仓储课程设计 鲍摩瓦尔夫选址
物流设施选址

多设施选址模型
集合覆盖模型
最大覆盖模型
P-中值模型
P-中值模型
贪婪取走算法
第一步
• 令当前选中设 施点数k=m, 即所有m个候 选位置都选中
第二步
• 将每个需求点 指派给k个设施 点中离其距离 最近的一个设 施点。
• 求出总运输费 用Z
第三步
• 若k=p,得到k 个设施点及各 需求点的指派 结果,停止
6 14 2 4 9 70
7 20 30 2 11 60
8 24 12 6 22 100
多设施选址模型
集合覆盖模型
最大覆盖模型
P-中值模型
例 3-6
第二步 ➢分别对取走候选点1,2,3,4进行分析 ,并计算各自的费用增量:
✓取走候选点3,结果(1,1,1,4,4,2,4,2), Z=3620,费用增量ΔZ=1140
8 24 12 6 22 100
多设施选址模型
6
第二步 ➢分别对取走候选点1,2,3,4进行分析 ,并计算各自的费用增量:
✓取走候选点4,结果(1,1,1,2,3,2,3,3), Z=3520,费用增量ΔZ=1040
1 2 100
1
400
4
4
5
7 120
1 4 12 20 6 100
2 2 10 25 10 50
3 3 4 16 14 120
i
4 6 5 9 2 80 5 18 12 7 3 200
6 14 2 4 9 70
7 20 30 2 11 60
8 24 12 6 22 100
多设施选址模型
集合覆盖模型
最大覆盖模型
P-中值模型
例 3-6
第一步
基于鲍摩_瓦尔夫模型的配送中心选址

基于鲍摩_瓦尔夫模型的配送中心选址
鲍摩_瓦尔夫模型是一种最小配送成本模型,用于确定终端顾客需求点和配送中心的
最佳位置,在传统市场分析中广泛应用。
该模型的基本假设是,顾客需求点的需求量恒定,且距离配送中心越远,配送成本越高。
选择配送中心的最佳位置可能涉及多个因素,例如人口密度、土地成本、运输成本等。
在执行模型分析之前,应先考虑与配送相关的各种因素,以确定权衡决策所需的权重。
首先,要确定可行的候选地点,并确定重点考虑的因素。
然后,收集这些因素的数据,并将其用于计算每个地点的相对宜居指数。
接着,可以利用鲍摩_瓦尔夫模型来计算每个候选地点的最小配送成本。
此时,需要
指定每个需求点的需求量,以及连接每个需求点和候选配送中心的距离。
一旦计算得出最
小配送成本,可以从中选择一个“最优”的配送中心位置。
有许多工具和技术可以帮助执行上述任务,例如GIS(地理信息系统),它可以绘制地图、计算距离和执行统计分析。
除此之外,采用交通状况分析工具可以考虑道路交通流量
和容量等因素,这些因素也可以影响最终的配送成本。
需要注意的是,在执行鲍摩_瓦尔夫模型时,仅考虑了成本因素,而没有考虑其他与
顾客相关的因素,例如品牌声誉和购买体验。
因此,在最终选址方案中,应该综合考虑珂
以平衡各类因素,以取得最优的运营效益。
基于鲍摩—瓦尔夫模型的配送中心选址研究

基于鲍摩—瓦尔夫模型的配送中心选址研究作者:张音来源:《中国市场》2015年第02期[摘要]本文在国内外相关文献的基础上,用鲍摩-瓦尔夫模型解决配送中心选址问题,并在文中运用了一个简单而具有代表性的案例分析,显示了鲍摩-瓦尔夫模型的优缺点。
[关键词]配送中心;选址;鲍摩-瓦尔夫模型[DOI]10-13939/j-cnki-zgsc-2015-02-0081 引言在《物流手册》中,对配送中心有专门的定义:配送中心是从供应者手中接收多种大量的货物,进行倒装、分类、保管、流通加工和情报处理等作业,然后按照众多需要者的订货要求备齐货物,以令人满意的服务水平进行配送的设施。
配送中心(Distribution Center,DC)是实现配送业务的现代化流通设施。
配送中的“货物配备”是配送中心主要的业务,是全部由它完成的;而送货既可以完全由它承担,也可以利用社会货运企业来完成。
配送中心在以下几个方面发挥较好的作用:减少交易次数和流通环节;产生规模效益;减少客户库存,提高库存保证程度;与多家厂商建立业务合作关系,能有效而迅速地反馈信息,控制商品质量。
配送中心是现代电子商务活动中开展配送活动的物质技术基础。
配送中心的功能主要有:采购功能、存储保管功能、配组功能、分拣功能、分装功能、集散功能、流通加工功能、送货功能、传递功能、衔接功能、服务功能等。
2 鲍摩-瓦尔夫模型简介2-1 鲍摩-瓦尔夫模型描述鲍摩-瓦尔夫模型又称为多节点单品种选址模型。
该模型是从一组候选地点选择若干个位置作为配送中心,使得从已知若干资源点,经过这几个设施网点,向若干个客户运送一种产品时,使得运费、保管费、建设费和发送费总的成本最小。
用鲍摩-瓦尔夫模型解决配送中心选址问题时,将问题简单化,是在考虑过其他因素的基础上使得成本最小化,从而体现模型的简便有效。
2-2 鲍摩-瓦尔夫模型所要解决的问题从n个候选的地点中选中若干个位置作为配送中心,使得从已知m个资源点(如工厂),经过这n个配送中心,向q个客户运送同一种产品时,总的物流布局成本(包括相应的配送中心变动成本)为最小,也可能存在从某资源点i直接将产品送往某个客户点k。
B1鲍摩——瓦尔夫模型选址方法

B1鲍摩——瓦尔夫模型选址方法瓦尔夫模型,又称鲍摩—瓦尔夫模型(The Baumo-Walpole Model),是一种用于选址决策的数学模型。
该模型适用于研究解决选址问题时的决策过程,并可作为指导决策者做出最佳选址决策的工具。
瓦尔夫模型的特点是综合考虑了各个因素对于选址决策的重要性,并进行了权衡。
瓦尔夫模型的基本原则是通过对选址因素进行评估,并为每个因素赋予适当的权重,然后将各因素的权重和评估值相乘,得到每个选址候选点的综合评分,最终选择评分最高的候选点作为最佳选址。
瓦尔夫模型的四个主要步骤如下:1.识别选址因素:选址因素是影响选址决策的各种因素,如用地成本、交通便利性、市场需求、竞争状况等。
在这一步骤中,需要对选址问题进行全面分析,确定所有与选址相关的因素。
3.赋予权重:为每个选址因素赋予适当的权重,以反映其在选址决策中的重要性。
权重的确定可以通过专家意见征询、决策者的权衡等方式进行。
一般来说,权重应尽可能客观地反映各因素的重要性。
4.综合评分:将每个选址因素的权重和评估值相乘,得到每个选址候选点的综合评分。
评分最高的候选点被选择为最佳选址。
在这一步骤中,可以使用数学模型或电子表格等工具进行计算。
瓦尔夫模型的优点是综合考虑了各种因素的重要性,并能够准确评估每个选址候选点的优劣。
然而,该模型也存在一些局限性,例如对于一些主观因素的评估可能存在误差,以及权重的确定可能会受到决策者主观意愿的影响。
总之,瓦尔夫模型是一种较为科学和系统的选址方法,可以为选址决策者提供决策支持。
但在实际应用中,需要根据具体情况对模型进行适当的改进和调整,以使其更符合实际情况。
仓储技术与管理课程设计仓储设施选址问题研究

山东交通学院仓储技术与管理课程设计说明书题目:仓储设施选址问题研究院(系)别交通与物流工程系专业物流工程班级学号姓名指导教师二○一二年三月课程设计任务书题目仓储设施选址问题研究系 (部) 交通与物流工程系专业物流工程班级学生姓名学号3 月 5 日至 3 月9 日共 1 周指导教师(签字)系主任(签字)2012年3 月2 日3 / 25摘要进入二十一世纪以来,随着世界市场由传统的相对稳定演变成动态多变,物流企业所面临的社会、经济、制造环境与客户需求都发生了明显的变化。
物流企业在既要满足顾客及时、准确的交货要求,又要保持相对较低的物流成本的情况下,纷纷对原有的流通渠道进行变革和创新。
同时仓储业作为现代物流系统中的三大支柱之一,面对需求方式出现了个性化、多样化的变化,生产方式也变为多品种、小批量的柔性生产方式的情况下,其功能也从重视保管效率逐渐变为重视流通功能的实现。
因此,在现代物流环境下,仓储设施规划、布局应的合理性和科学性变得越来越重要,合理的仓储设施选址不仅可以节约物流成本,还可以提高物流企业的服务效率,增强企业竞争力。
文章将对重心法、遗传算法、层次分析法三种选址方法的基本原理和优缺点进行简单地介绍,并使用层次分析法对华安仓储进行案例分析,借此了解熟悉仓储设施选址的过程和方法。
关键词:仓储设施,选址,层次分析法,物流I / 25目录1仓储设施选址 (1)1.1现代仓储业特点 (1)1.2仓储设施选址的影响因素 (2)1.3研究仓储设施选址的意义与必要性 (3)2仓储设施选址的方法介绍 (4)2.1重心法 (4)2.2遗传算法 (4)2.2.1遗传算法的基本原理 (4)2.2.2遗传算法的优缺点 (5)2.3层次分析法 (6)2.3.1层次分析法的基本原理 (6)2.3.2层次分析法的优缺点 (7)3案例分析 (9)3.1华安仓储简介 (9)3.2评选步骤 (9)设计体会及今后的改进意见 (15)参考文献 (16)i / 251仓储设施选址1.1现代仓储业特点在现代物流环境下仓储业有了很大的改观,主要表现在以下几个方面。
基于鲍莫尔—沃尔夫模型的农产品配送中心选址问题研究

【相关文献】
[1]杨波:《多品种随机数学模型的物流配送中心选址问题》,载于《中国管理科学》2003年第2期。
[2]周爱莲、李旭宏、毛海军:《一类企业物流中心动态选址模型研究》,载于《系统工程学报》2011年第3期。
[3]方磊、何建敏:《综合AHP和目标规划方法的应急系统选址规划模型》,载于《系统工程理论与实践》2003年第12期。
基于鲍莫尔—沃尔夫模型的农产品配送中心选址问题研究
李远远;刘礼帅
【期刊名称】《经济研究参考》
【年(卷),期】2015(000)029
【总页数】3页(P90-92)
【作 者】李远远;刘礼帅
【作者单位】广西社科规划办;桂林电子科技大学
【正文语种】中 文
合理选择配送中心可在满足相应节点需求量的同时有效降低物流成本。本文在分析影响农产品配送中心选址因素的前提下,利用鲍莫尔—沃尔夫选址模型进行选址,并通过实例验证该选址模型的实用性。
(一)自然环境。
农产品物流中心选址受自然环境约束大。一方面,农产品保质期短、易腐易损的特性决定了在选址时要考虑温度、湿度等有关自然条件;另一方面,农产品种类繁多,分布范围广,因此在存储过程中,必须采用先进的技术来保证农产品的鲜活度。
(二)市场特性。
一方面,农业作业对象固定,农产品产能受自然条件约束大;另一方面,大部分农产品是必需品,需求弹性小,因而其供、需弹性小,容易导致价格波动。因此农产品配送中心选址要与农产品的资源分布和农产品的需求分布相适应。
鲍摩-瓦尔夫(Baumol-Wolfe)模型
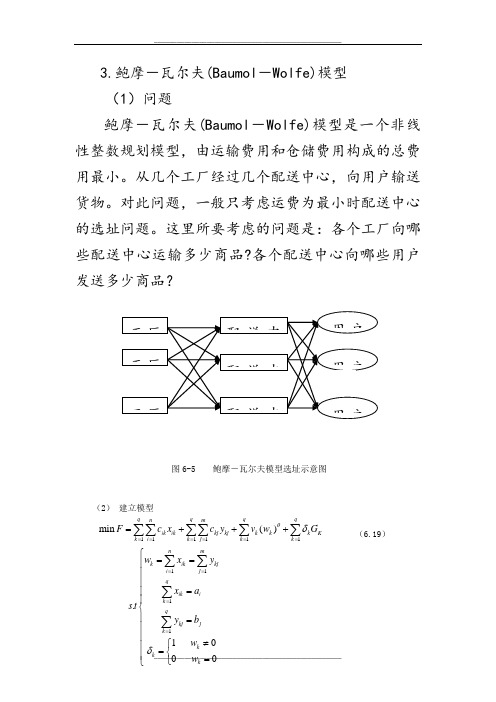
3.鲍摩-瓦尔夫(Baumol -Wolfe)模型(1)问题鲍摩-瓦尔夫(Baumol -Wolfe)模型是一个非线性整数规划模型,由运输费用和仓储费用构成的总费用最小。
从几个工厂经过几个配送中心,向用户输送货物。
对此问题,一般只考虑运费为最小时配送中心的选址问题。
这里所要考虑的问题是:各个工厂向哪些配送中心运输多少商品?各个配送中心向哪些用户发送多少商品?图6-5 鲍摩-瓦尔夫模型选址示意图(2) 建立模型(6.19)1111111111min ().10q q q q n m ik ik kj kj k k k K k i k j k k n m k ik kj i j q ik i k q kj j k k F c x c y v w G w x y x a s t y b w θδ===========+++⎧==⎪⎪⎪=⎪⎪⎨⎪=⎪⎪≠⎧⎪∑∑∑∑∑∑∑∑∑∑式中c ik —从工厂到配送中心,每单位运量的运输费:X ik —从工厂到配送中心运送的运量;c kj —通过配送中心向用户发送单位运量的运费;Y ki —从配送中心到用户运送的运量;W k —通过配送中心的运量;V k —配送中心的单位运量的可变费用;G k —配送中心的固定费用(与其规模无关的固定费用);θ—规模指数系数(0<θ<1);δk—为备选网点k 是否选中的决策变量(0--1 变量)。
总费用函数F(x)的第一项是工厂到节点的运输费用,第二项是节点到需求点的运输费用,第三项是配送中心的可变费用,第四项是配送中心的固定费用。
(3)模型的求解启发式算法是在可接受的费用内寻找最好的解的技术,但不一定能保证所得解的可行性和最优性。
鲍摩-瓦尔夫(Baumol -Wolfe)模型求解思想,通过求解边际成本,对规模仓储进行分段线性化。
边际成本表示网点在一定规模下的单位货物储存费用 ,即存储费用率,用边际成本成本代替可变费用率,从而把非线性函数转化为线性。
基于Baumol-Wolk法(保莫法)的物流网络节点选址策略研究.

基于Baumol-Wolk法(保莫法)的物流网络节点选址策略研究摘要本文介绍了物流网络节点以及物流网络节点选址的现状及其意义,介绍了多个仓库选址及保莫法的基本原理与优势,分析了保莫法在物流网络节点选择中的具体应用,本文认为合理选址不仅影响到物流中心本身的运营成本、运营绩效、竞争战略和未来的发展,而且还影响到上游的供应商、下游的分销商或零售商的物流成本以及物流战略和竞争战略,甚至影响到区域经济的发展。
文章结合实际详细的案例作出详细的说明。
关键词:物流节点,节点选址,保莫法及应用1.绪论1.1研究背景现代物流的快速发展促进了物流中心的建设。
随着我国经济的飞速发展,市场竞争已越来越激烈,在经济日益全球化的今天,物流作为企业的第三利润源泉,正受到广泛的重视,并面临着前所未有的发展机遇。
国家政策的出台推动了现代物流的发展进程。
商品物流配送自20世纪80年代中后期在我国流通领域出现以来,因其能够适应社会化大生产专业化分工与协作的要求,减少流通环节、节约流通费用、加快商流和物流速度、实现社会资源的优化配置等特点,受到了政府主管部门和流通企业的广泛重视。
国家已明确将发展商品物流配送作为深化流通领域营销方式改革、实现流通现代化的一项重要内容,并已列入国家流通产业发展政策。
因此,发展现代化物流是现代物流业的发展方向。
1.2物流网络节点物流网络节点是指物流网络中连接物流线路的结节之处。
广义的物流节点是指所有进行物资中转、集散和储运的节点,包括港口、空港、火车货运站、公路枢纽、大型公共仓库及现代物流(配送)中心、物流园区等。
狭义的物流节点仅指现代物流意义的物流(配送)中心、物流园区和配送网点。
所有的物流活动都是在线路和节点上进行的。
物流节点对优化整个物流网络起着重要作用,从发展来看,它不仅执行一般的物流职能,而且越来越多地执行指挥调度、信息等神经中枢的职能,是整个物流网络的灵魂所在,因而更加受到人们的重视。
所以,在有的场合也称之为物流据点,对于特别执行中枢功能的又称物流中枢或物流枢纽。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章背景1.1企业背景长沙鸿运商贸有限公司主要长期主营:生产明火、防风、直冲、台式、礼类等几千余种不同款式及打火机散件和打火机专用气体-丁烷气供应,打火机组装设备的专业厂家.主要型号有:721 透明机、309透明机、501、606、739 透明机725、105喷砂机208 、309包纸725五彩直打、投影机、闪灯机、绿双瓶、防风机、双色机、磨砂啄木鸟、斜打机王、皮纹机、熊猫大元、中元、实色双瓶机、黑三角、小六角、插花大圆、透明中圆、熊猫大圆等。
1.2公司发展的机遇和存在的问题鸿运公司在国内有两个生产基地,经统计和预测分析,其用户大致分布在8个区域,现为了提高物流效率而实行商流物流分离,需在全国建立配送中心,初步规划有5处配送中心候选地W1、W2、W3、W4、W5。
已知配送中心的单位可变费用Vhj依次分别为75、80、75、80、70元;各生产基地的生产能力和各区域用户的需求量、生产基地到配送中心和配送中心到用户的单位运费的具体数据见表1-1和表1-2。
(取θ=1/2,运费单位为元/t)。
表1-1 生产基地到配送中心的单位运费及工厂生产能力表1-2 配送中心到用户的单位运费及用户的需求量1.3 优化的必要性配送中心是从事货物配备(集货、加工、分货、拣选、配货)和组织对用户的送货,以提高水平实现销售和供应服务的现代流通设施。
配送中心是现代物流的重要组成部分,它的上游是制造商,下游是用户,在整个物流系统中起着承上启下的作用。
而配送中心位置的确定又是物流系统分析中的核心内容,配送中心合理的选址能够减少货物运输费用,大幅度地降低运营成本,从而获得最大的利润;同时,合理的配送中心能使物流系统有效运作,为企业提供优质服务,最终实现低成本,为企业增加更大的利润;配送中心位置的选择也将显著影响实际运营的效率与成本,以及日后仓储规模的扩充与发展。
第二章配送中心相关理论与分析2.1配送中心概述及其选址的原则2.1.1 配送中心概述根据物流手册的定义,配送中心是从供应者手中接受多种大量的货物,进行倒装、分类、保管、流通加工和情报处理等作业,然后按照众多需要者的订货要求备齐货物,以令人满意的服务水平进行配送的设施。
配送中心的功能主要有:采购功能、存储保管功能、配组功能、分拣功能、分装功能、流通加工功能、送货功能、物流信息汇总即传递功能、衔接功能、服务功能。
配送中心一般都具有这些功能,对其中某一功能的重视程度不同决定了该配送中心的性质。
配送中心的功能会影响它的选址、房室构造、规模和设施等。
功能概括如下(图2-1)图2-1 配送中心的功能2.1.2配送中心选址的原则配送中心选址过程应同时遵守适应性原则、协调性原则、经济性原则和战略性原则。
a)适应性原则。
配送中心的选址必须与国家以及省市的区域经济发展方针、政策向适应,与国家物流资源分布和需求分布相适应,与国民经济和社会发展相适应。
b)协调性原则。
配送中心的选址应将国家的物流网络作为一个大系统来考虑,是配送中心的设施设备在地域分布、物流作业生产力、技术水平等方面互相协调。
c)经济性原则。
配送中心的发展过程中,有关选址的费用,主要包括建设费用以及经营费用两个部分,配送中心的选址定在市区还是郊区,其未来物流辅助设施的建设规模以及建设费用、物流运输费用等是不同的,选址是应当以总的费用最低作为配送中心选址的经济性原则。
d)战略性原则。
配送中心的选址,应具有战略眼光。
一是要考虑全局,二是要考虑长远。
局部要服从全局,目前利益要服从长远利益,既要考虑目前的实际需要,又要考虑日后发展的可能2.2 配送中心选址的影响因素(一)货物分布和数量这是配送中心的对象,如货物来源和去向的分布情况,历史和现在以及将来的预测和发展趋势等。
配送中心应尽可能地与生产地和配送区域形成短距离优化。
货物数量是随配送规模的增长而不断增长的,货物增长率越高,越是要求配送中心选址更加合理,从而减少输送过程中不必要的浪费。
(二)运输条件物流配送中心的选址应该接近交通运输枢纽,使配送中心形成物流过程中的一个恰当的结点。
在有条件的情况下,配送中心应尽可能靠近铁路货运站、港口及公路。
(三)用地条件物流配送中心的占地问题在土地日益昂贵的今天显得越来越重要。
配送中心是利用现有土地还是重新征地,值得权衡,而且地价因素以及是否符合政府规划要求等等,在建设配送中心是都要进行综合考虑。
(四)商品流动企业生产的消费品随着人口的转移而变化,应该根据这种情况更好地为企业的配送系统定位。
同时,工业产品市场也会转移变化。
为了确定原材料和半成品等商品的流动变化情况,在进行物流配送中心的选址时,应考虑有关商品流动的具体情况。
(五)其他因素如劳动力、运输与服务的方便程度、投资额的限制等。
2.3配送中心选址方法及决策步骤2.3.1 配送中心选址方法(一)定性分析法。
定性分析法主要是根据选址影响因素和选址原则,依靠专家或管理人员丰富的经验、知识及其综合分析能力,确定配送中心的具体选址。
主要有专家打分法、德尔菲法。
定性方法的优点是注重历史经验,简单易行。
其缺点是容易犯经验主义和主观主义的错误,并且当可选地点较多时,不易做出理想的决策,导致决策的可靠性不高。
(二)定量分析法。
定量的方法主要包括重心法、鲍摩-沃尔夫法、运输规划法、Cluster法、CFLP法、混合0-1整数规划法、双层规划法、遗传算法等。
定量方法选址的优点是能求出比较准确可信的解。
其中,重心法是研究单个物流配送中心选址的常用方法,这种方法将物流系统中的需求点和资源点看成是分布在某一平面范围内的物流系统,各点的需求量和资源量分别看成是物体的重量,物体系统的重心作为物流网点的最佳设置点。
2.3.2 配送中心选址的决策步骤第三章 规划方案设计3.1 选址模型的建立鲍摩—瓦尔夫法(Baumol-Wolfe )是属于非线性规划,并且以逐次求解运输问题为思路的启发式解法。
它的目标函数是使从有限数量的工厂,经过有限数量的配送中心,向有限数量的用户运输货品所需要的成本最小,即:)()()()(,,i ii i ii ijk kj i ij ki ijk I r F I u X h c x f ∑∑∑+++=θ● ki c ——从工厂k 到配送中心i 每单位运量的运输费; ● ij h ——从配送中心i 向用户j 发送单位运量的运费: ● ijk X ——从工厂k 通过配送中心i 向用户j 运送的运量; ● i I ——通过配送中心i 的运量;● i u ——配送中心i 的单位运量的可变费用; ● i F ——配送中心i 的固定费用; 它主要适用于如图3-1所示的物流系统。
图3-1 物流企业配送网络图如上图所示,从k个工厂经过配送中心m个,向n个用户输送货物。
对此问题,一般只考虑运费最小时配送中心的选址问题。
这里需要考虑的问题是:各个工厂向哪些配送中心输送多少商品?各个配送中心向哪些用户发送多少商品?在什么情况下运输效果最好、总成本最小?从以下几个方面分析:1.基本思想:在保证货物运输高效、安全、顺畅的前提下,通过对模型求解找出是总费用最小的运输方案,来确定每个配送中心的取舍。
总费用=总运输费用+ 可变费用+固定费用。
2.基本假设:配送中心选址问题属于最小成本问题,建立数学模型的基本假设如下:(1)工厂到配送中心间的整车运输成本,及配送中心到用户的零担运输成本,都与运输量程线性关系。
(2)用户的位置及需求量为已知。
(3)配送中心的容量可满足需求点要求。
(4)配送中心的候选位置及其变动成本为已知。
在上述四项假设条件下,求解配送中心的个数、规模大小及位置,以使运输成本及可变费用之和最小。
3.2 选址模型的算法探讨整个求解过程的基本思路是:首先,列出从生产基地经过配送中心到用户的最小运费单价表,在此费用表的基础上按照“运输问题”求解配送中心j 运量(初次解)和总的运输费用;其次,根据上述所求的运量求变动费用,从而得到初次总的运费和变动费用;第三,对变动费用函数求微分使其边际费用最小,在此基础上集合生产企业到配送中心的运费表和配送中心到用户的费用表,再列出最小单位费用表,再据此求解运输问题,得到经过配送中心j 的运量(第二次解)。
如此反复直到第n 次的解接近或等于第(n-1)次的解,即得到了近似最优解或最优解。
根据所得最优解可以判断是否应该建设配送中心j 。
当然在实际运用中,还应结合固定费用进行综合分析比较,再作决策。
简言之,该模型的计算方法是首先给出费用的最初值,求初始解;然后进行迭代计算,使其逐步接近费用最小的运输规划。
3.2.1 算法的收敛性收敛性主要是从数学知识的角度来说的,一判断函数有无最优解(是否存在最大值或最小值)。
由数学知识可知,总费用函数)()()()(,,i ii i ii ijk kj i ij ki ijk I r F I u X h c x f ∑∑∑+++=θ可以看成是自变量ijk X 的一次函数,且费用函数的一阶倒数存在,∑+=kj i ij ki ijk h c X f ,,)()( 又一阶导数0)(,,>+∑kj i ij ki h c ,所以同样根据数学知识可知:次函数收敛,且一定存在最优值,即总费用最小。
3.3选址模型的求解(一)初始解要求最初的工厂到用户问(k ,j)的运费相对最小,也就是要求工厂到配送中心间的运费率c ki 和配送中心到用户间的发送费率h ij 之和为最小 ,即:)()(000min ij ki ij ki ikj h c h c c +=+=表3-1生产基地到用户的最小运费生产基地用户F 1W 1 W 1 W 1 W 5 W 3 W 3 W 2 W 2 1218 10 13 10 13 11 11W 5 W 5 W 5 W 5 W 3 W 4 W 4 W 4 注:阴影部分的字母为使用的配送中心;数字为最小费用用表上作业法(最小元素法)求解运输问题得初始解,表3-2-2中的数字为其通过的运量表 3-2需求量 101010155151015由表3-2可得出各配送中心的通过量(I 0):W 1为25t,、W 2为10t 、W 3为5t 、W 4为30t 、W 5为20t ,则运输费用为:Y 0=ijk kj i ij ki x h c ∑+,,)(=12×10+18×5+10×10+10×5+11×10+15×5+10×15+8×15+8×15=935(元)配送中心的可变费用为(θ=1/2):V 0=θ)(0i ii I u ∑=75×25+ 80×10+ 75×5+80×30+ 70×20=1547(元)所以总运费和可变费用为:C 0=Y 0+V 0=2482(元)(二) 求二次解在初始解的基础上结合由通过量计算各配送中心的可变费用即11)(--θθn ii I u ,使工厂到配送中心间的运费率ki c 和配送中心到用户间的发送费率ij h 和相应的可变费用之和最小。
