勾股定理竞赛试卷(含解答)讲解学习
勾股定理综合难题。竞赛
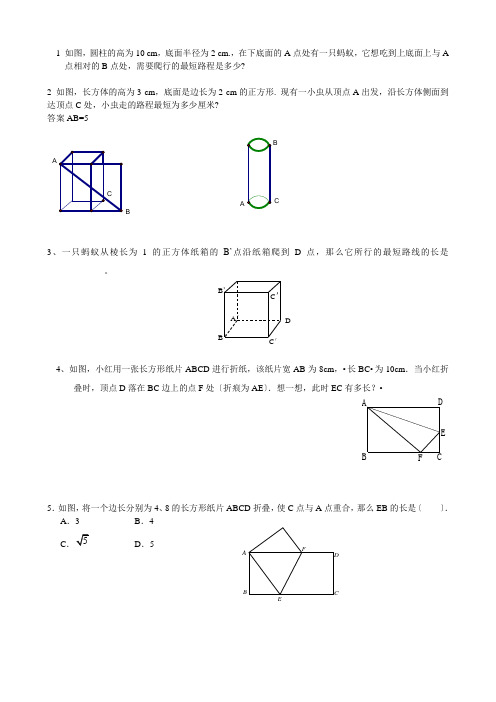
CBA D EF1 如图,圆柱的高为10 cm ,底面半径为2 cm.,在下底面的A 点处有一只蚂蚁,它想吃到上底面上与A点相对的B 点处,需要爬行的最短路程是多少?2 如图,长方体的高为3 cm ,底面是边长为2 cm 的正方形. 现有一小虫从顶点A 出发,沿长方体侧面到达顶点C 处,小虫走的路程最短为多少厘米? 答案AB=5AB3、一只蚂蚁从棱长为1的正方体纸箱的B’点沿纸箱爬到D 点,那么它所行的最短路线的长是_____________。
4、如图,小红用一张长方形纸片ABCD 进行折纸,该纸片宽AB 为8cm ,•长BC•为10cm .当小红折叠时,顶点D 落在BC 边上的点F 处〔折痕为AE 〕.想一想,此时EC 有多长?•5.如图,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与A 点重合,那么EB 的长是〔 〕. A .3 B .4 C D .5BCAFEDCBAB ’C ’B ′A ′C ′DC D 6.:如图,在△ABC 中,∠C=90°,∠B=30°,AB 的垂直平分线交BC 于D ,垂足为E ,BD=4cm .求AC 的长.7、如图,有一个直角三角形纸片,两直角边AC=6,BC=8,现将直角边AC 沿直线AD 折叠,使其落在斜边AB 上,且与AE 重合,那么CD 的长为8、如图,在矩形ABCD 中,,6=AB 将矩形ABCD 折叠,使点B 与点D 重合,C 落在C '处,假设21::=BE AE ,那么折痕EF 的长为 。
9、如图,:点E 是正方形ABCD 的BC 边上的点,现将△DCE 沿折痕DE 向上翻折,使DC 落在对角线DB 上,那么EB ∶CE =_________.10、如图,AD 是△ABC 的中线,∠ADC =45o ,把△ADC 沿AD 对折,点C 落在C´的位置,假设BC =2,那么BC´=_________.E题5图FBC ′ BA CD A C11.如图1,有一块直角三角形纸片,两直角边AC =6cm ,BC =8cm ,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,那么CD 等于〔 〕A.2cmB.3 cmC.4 cmD.5 cm12、有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗?13、如图,在△ABC 中,∠B=90,AB=BC=6,把△ABC 进行折叠,使点A 与点D 重合,BD:DC=1:2,折痕为EF ,点E 在AB 上,点F 在AC 上,求EC 的长。
2022年必考点解析沪科版八年级数学下册第18章 勾股定理综合测评试卷(含答案详解)

八年级数学下册第18章勾股定理综合测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、若等腰三角形两边长分别为6和8,则底边上的高等于()A.B C.D.102、如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要()A.8 cm B.10 cm C.12 cm D.15 cm3、以下列长度的三条线段为边,能组成直角三角形的是()A.4,5,6 B.8,15,17 C.2,3,4 D.1,34、如图,四棱柱的高为9米,底面是边长为6米的正方形,一只蚂蚁从如图的顶点A开始,爬向顶点B.那么它爬行的最短路程为()A.10米B.12米C.15米D.20米5、下列长度的三条线段能组成直角三角形的是()A.5,11,12 B.4,5,6 C.4,6,8 D.5,12,136、如图,在Rt△ABC中,∠CBA=60°,斜边AB=10,分别以△ABC的三边长为边在AB上方作正方形,S1,S2,S3,S4,S5分别表示对应阴影部分的面积,则S1+S2+S3+S4+S5=()A.50 B.C.100 D.7、下列条件中,能判断△ABC是直角三角形的是()A.a:b:c=3:4:4 B.a=1,b,cC.∠A:∠B:∠C=3:4:5 D.a2:b2:c2=3:4:58、以下列各组线段为边作三角形,不能..作出直角三角形的是()A .1,2B .6,8,10C .3,7,8D .0.3,0.4,0.59、如图,在等腰1Rt OAA 中,190OAA ∠=︒,1OA =,以OA 1为直角边作等腰12Rt OA A ,以OA 2为直角边作等腰23Rt OA A ,则2n OA 的长度为( )A .2nB .C .2nD .210、如图,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的点B '处,点A 的对应点为点A ',3B C '=,则AM 的长为( )A .1.8B .2C .2.3D 第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、已知:点A 的坐标为()3,4,点B 坐标为()1,1-,那么点A 和点B 两点间的距离是______.2、如图,点P 是∠AOB 的角平分线上一点,过点P 作PC ∥OA 交OB 于点C ,过点P 作PD ⊥OA 于点D ,若∠AOB =60°,OC =2,则PD =_____________.3、如图,在平面直角坐标系中,5AB AC ==,点B ,C 的坐标分别是()5,2,()5,8,则点A 的坐标是______.4、直角三角形中,根据勾股定理,已知两边可求第三边: Rt △ABC 中,∠C =90°,a ,b ,c 分别为内角A ,B ,C 的对边,(1)若已知边a ,b ,则c =_____(2)若已知边a ,c ,则b = _____(3)若已知边b ,c ,则a =_____.5、如图,已知Rt ABC 中,90ACB ∠=︒,4AC BC ==,动点M 满足1AM =,将线段CM 绕点C 顺时针旋转90︒得到线段CN ,连接AN ,则AN 的最小值为_________.三、解答题(5小题,每小题10分,共计50分)1、滑撑杆在悬窗中应用广泛.如图,某款滑撑杆由滑道OC ,撑杆AB 、BC 组成,滑道OC 固定在窗台上.悬窗关闭或打开过程中,撑杆AB 、BC 的长度始终保持不变.当悬窗关闭时,如图①,此时点A 与点O 重合,撑杆AB 、BC 恰与滑道OC 完全重合;当悬窗完全打开时,如图②,此时撑杆AB 与撑杆BC 恰成直角,即90B ∠=︒,测量得12cm OA =,撑杆15cm AB =,求滑道OC 的长度.2、如图,在△ABC 和△DEB 中,AC ∥BE ,∠C =90°,AB =DE ,点D 为BC 的中点,12AC BC =. (1)求证:△ABC ≌△DEB .(2)连结AE ,若BC =4,直接写出AE 的长.3、如图在55⨯的正方形网格中,每个小正方形的顶点称为格点.点A ,点B 都在格点上,按下列要求画图.(1)在图①中,AB 为一边画ABC ,使点C 在格点上,且ABC 是轴对称图形;(2)在图②中,AB 为一腰画等腰三角形,使点C 在格点上;(3)在图③中,AB 为底边画等腰三角形,使点C 在格点上.4、一个三角形三边长分别为a ,b ,c .(1)当a =3,b =4时,① c 的取值范围是________;② 若这个三角形是直角三角形,则c 的值是________;(2)当三边长满足3a b c b ++=时, ① 若两边长为3和4,则第三边的值是________;② 在作图区内,尺规作图,保留作图痕迹,不写作法:已知两边长为a ,c (a <c ),求作长度为b 的线段(标注出相关线段的长度).5、在平面直角坐标系xOy 中,对于点P 给出如下定义:点P 到图形1G 上各点的最短距离为1d ,点P 到图形2G 上各点的最短距离为2d ,若12d d =,就称点P 是图形1G 和图形2G 的一个“等距点”.已知点()6,0A ,()0,6B .(1)在点()6,0D -,()3,0E ,()0,3F 中,______是点A 和点O 的“等距点”;(2)在点()2,1G --,()2,2H ,()3,6I 中,______是线段OA 和OB 的“等距点”;(3)点(),0C m 为x 轴上一点,点P 既是点A 和点C 的“等距点”,又是线段OA 和OB 的“等距点”.①当8m =时,是否存在满足条件的点P ,如果存在请求出满足条件的点P 的坐标,如果不存在请说明理由;②若点P 在OAB 内,请直接写出满足条件的m 的取值范围.-参考答案-一、单选题1、C【分析】因为题目没有说明哪个边为腰哪个边为底,所以需要讨论,①当6为腰时,此时等腰三角形的边长为6、6、8;②当8为腰时,此时等腰三角形的边长为6、8、8;然后根据等腰三角形的高垂直平分底边可运用勾股定理的知识求出高.【详解】解:∵△ABC 是等腰三角形,AB =AC ,AD ⊥BC ,∴BD =CD ,边长为6和8的等腰三角形有6、6、8与6、8、8两种情况,①当三边是6、6、8时,底边上的高AD②当三边是6、8、8时,同理求出底边上的高AD故选C.【点睛】本题主要考查了勾股定理和等腰三角形的性质,解题的关键在于能够利用分类讨论的思想求解.2、B【分析】立体图形展开后,利用勾股定理求解.【详解】解:将长方体沿着AB边侧面展开,并连接'AB,如下图所示:由题意及图可知:'13138AB cm=,=+++=,''6AA cm两点之间,线段最短,故'AB的长即是细线最短的长度,''∆中,由勾股定理可知:'10Rt AABAB cm===,故所用细线最短需要10cm.故选:B .【点睛】本题主要是考查了勾股定理求最短路径、两点之间线段最短以及立体图形的侧面展开图,因此,正确得到立体图形的侧面展开图,熟练运用勾股定理求边长,是解决此类问题的关键.3、B【分析】根据勾股定理的逆定理:若三角形三边分别为a ,b ,c ,满足222+=a b c ,则该三角形是以c 为斜边的直角三角形,由此依次计算验证即可.【详解】解:A 、22245416+=≠,则长为4,5,6的线段不能组成直角三角形,不合题意;B 、22281528917+==,则长为8,15,17的线段能组成直角三角形,符合题意;C 、22223134+=≠,则长为2,3,4的线段不能组成直角三角形,不合题意;D 、222133+=≠,则长为13的线段不能组成直角三角形,不合题意;故选:B .【点睛】本题考查勾股定理的逆定理,掌握并熟练运用勾股定理的逆定理是解题关键.4、C【分析】将立体图形展开,有两种不同的展法,连接AB ,利用勾股定理求出AB 的长,找出最短的即可.【详解】解:如图,(1)AB(2)AB15,由于15则蚂蚁爬行的最短路程为15米.故选:C.【点睛】本题考查了平面展开--最短路径问题,要注意,展开时要根据实际情况将图形安不同形式展开,再计算.5、D【分析】先分别求出两小边的平方和和最长边的平方,再看看是否相等即可.【详解】解:A.∵52+112=25+121=146,122=144,∴52+112≠122,即三角形不是直角三角形,故本选项不符合题意;B.∵42+52=16+25=41,62=36,∴42+52≠62,即三角形不是直角三角形,故本选项不符合题意;C.∵42+62=16+36=52,82=64,∴42+62≠82,即三角形不是直角三角形,故本选项不符合题意;D.∵52+122=25+144=169,132=169,∴52+122=132,即三角形是直角三角形,故本选项符合题意;故选:D.【点睛】本题考查了勾股定理的逆定理,能熟记勾股定理的逆定理是解此题的关键,注意:如果一个三角形的两边a、b的平方和等于最长边c的平方,那么这个三角形是直角三角形.6、B【分析】根据题意过D作DN⊥BF于N,连接DI,进而结合全等三角形的判定与性质得出S1+S2+S3+S4+S5=Rt△ABC的面积×4进行分析计算即可.【详解】解:在Rt△ABC中,∠CBA=60°,斜边AB=10,∴BC=12AB=5,AC过D作DN⊥BF于N,连接DI,在△ACB和△BND中,90 ACB BNDCAB NBD AD BD ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩,∴△ACB≌△BND(AAS),同理,Rt△MND≌Rt△OCB,∴MD=OB,∠DMN=∠BOC,∴EM=DO,∴DN=BC=CI,∵DN ∥CI ,∴四边形DNCI 是平行四边形,∵∠NCI =90°,∴四边形DNCI 是矩形,∴∠DIC =90°,∴D 、I 、H 三点共线,∵∠F =∠DIO =90°,∠EMF =∠DMN =∠BOC =∠DOI ,∴△FME ≌△DOI (AAS ),∵图中S 2=S Rt△DOI ,S △BOC =S △MND ,∴S 2+S 4=S Rt△ABC .S 3=S △ABC ,在Rt△AGE 和Rt△ABC 中,AE AB AG AC =⎧⎨=⎩, ∴Rt△AGE ≌Rt△ACB (HL ),同理,Rt△DNB ≌Rt△BHD ,∴S 1+S 2+S 3+S 4+S 5=S 1+S 3+(S 2+S 4)+S 5=Rt△ABC 的面积+Rt△ABC 的面积+Rt△ABC 的面积+Rt△ABC 的面积=Rt△ABC 的面积×4=故选:B .【点睛】本题考查勾股定理的应用和全等三角形的判定,解题的关键是将勾股定理和正方形的面积公式进行灵活的结合和应用.7、B【分析】根据勾股定理的逆定理,以及三角形的内角等于180︒逐项判断即可.【详解】A ,设3a x =,4b x ,4=c x ,此时()()()222344x x x +≠,故ABC 不能构成直角三角形,故不符合题意;B ,2221+=,故ABC 能构成直角三角形,故符合题意C ,::3:4:5A B C ∠∠∠=且180A B C ∠+∠+∠=︒,设3A x ∠=,4B x ∠=,5C x ∠=,则有12180x =︒,所以15x =︒,则75C ∠=︒,故ABC 不能构成直角三角形,故不符合题意;D ,设23a x =,24b x =,25c x =,则345x x x +≠,即222a b c +≠,故ABC 不能构成直角三角形,故不符合题意;故选:B【点睛】本题考查了勾股定理的逆定理,和三角形的内角和等知识,能熟记勾股定理的逆定理内容和三角形内角和等于180︒是解题关键.8、C【分析】先求出两小边的平方和,再求出最大边的平方,看看是否相等即可.【详解】解:A 、∵2221+2=5=,∴以1,2B 、∵62+82=36+64=100=102,∴以6,8,10为边的三角形是直角三角形,故本选项不符合题意;C 、∵32+72=9+49=58≠82,∴以3,7,8为边的三角形不是直角三角形,故本选项符合题意;D 、∵0.32+0.42=0.09+0,16=0.25=0.52,∴以0.3,0.4,0.5为边的三角形是直角三角形,故本选项不符合题意;故选:C .【点评】本题考查了勾股定理的逆定理,能熟记勾股定理的逆定理的内容是解此题的关键,注意:勾股定理的逆定理是:如果一个三角形的两边a 、b 的平方和等于第三边c 的平方,那么这个三角形是直角三角形.9、C【分析】利用等腰直角三角形的性质以及勾股定理分别求出各边长,进而得出答案.【详解】解:∵△OAA 1为等腰直角三角形,OA =1,∴AA 1=OA=1,OA 11;∵△OA 1A 2为等腰直角三角形,∴A1A2=OA1OA2OA1=2=2;∵△OA2A3为等腰直角三角形,∴A2A3=OA2=2,OA323;∵△OA3A4为等腰直角三角形,∴A3A4=OA3,OA4OA3=4=4,∵△OA4A5为等腰直角三角形,∴A4A5=OA4=4,OA545.OA的长度为2n=2n,∴2n故选C.【点睛】本题考查了等腰直角三角形的性质以及勾股定理,熟练应用勾股定理得出是解题关键.10、B【分析】连接BM,MB′,由于CB′=3,则DB′=6,在Rt△ABM和Rt△MDB′中由勾股定理求得AM的值.【详解】解:连接BM,MB′,设AM=x,在Rt △ABM 中,AB 2+AM 2=BM 2,在Rt △MDB ′中,B ′M 2=MD 2+DB ′2,∵折叠,∴MB =MB ′,∴AB 2+AM 2= MD 2+DB ′2,即92+x 2=(9-x )2+(9-3)2,解得x =2,即AM =2,故选:B .【点睛】本题考查了翻折的性质,对应边相等,利用了勾股定理建立方程求解.二、填空题1、5【分析】根据两点间距离公式求解即可.【详解】∵点A 的坐标为()3,4,点B 坐标为(1,1)-,∴点A 和点B 5=.故答案为:5.【点睛】本题考查两点间距离,若11(,)A x y ,22(,)B x y ,则两点间的距离是AB =点间距离公式是解题的关键.2【分析】作PE OB ⊥,则PD PE =,由等腰三角形的性质可得,2OC PC ==,在Rt PCE △中,利用勾股定理即可求解.【详解】解:作PE OB ⊥,如下图:∵OP 平分AOB ∠,PE OB ⊥,PD OA ⊥,∴PD PE =,1302AOP BOP AOB ∠=∠=∠=︒,∵PC OA ∥,∴30DOP OPC POC ∠=∠=︒=∠,∴2OC PC ==,60PCE POC OPC ∠=∠+∠=︒,在Rt PCE △中,2PC =,60PCE ∠=︒,∴30CPE ∠=︒ ∴112CE CP ==,由勾股定理得,PE【点睛】此题考查了角平分线的性质,勾股定理,三角形外角的性质,等腰三角形的判定与性质以及含30直角三角形的性质等,解题的关键是灵活运用相关性质进行求解.3、()1,5A【分析】如图,过A 作AD BC ⊥于,D 证明BC x ⊥轴,则AD x ∥轴,826,BC 再利用等腰三角形的性质求解3,BD = 利用勾股定理求解4,AD = 从而可得答案.【详解】解:如图,过A 作AD BC ⊥于,D5,2,5,8,B CBC x ∴⊥轴,则AD x ∥轴,826,BC5,AB AC3,BD CD 224,ADAB BD541,325,A A D x y y1,5.A故答案为:()1,5A【点睛】本题考查的是等腰三角形的性质,坐标与图形,勾股定理的应用,掌握“坐标与线段长度的关系”是解本题的关键.4【分析】(1)(2)(3)根据勾股定理及题意可直接进行求解.【详解】解:(1)若已知边a ,b ,则根据勾股定理得c(2)若已知边a ,c ,则根据勾股定理得b =(3)若已知边b ,c ,则根据勾股定理得a【点睛】 本题主要考查勾股定理,熟练掌握勾股定理是解题的关键.5、1##【分析】证明△AMC ≌△BNC ,可得1BN AM ==,再根据三角形三边关系得出当点N 落在线段AB 上时,AN 最小,求出最小值即可.【详解】解:∵线段CM 绕点C 顺时针旋转90︒得到线段CN ,∴MC NC =,90MCN ∠=︒,∵90ACB ∠=︒,4AC BC ==,∴ACM BCN ∠=∠,AB =∴△AMC ≌△BNC ,∴1BN AM ==,∵1AN AB BN ≥-=∴AN 的最小值为1;故答案为:1.【点睛】本题考查了全等三角形的判定与性质,勾股定理,解题关键是证明三角形全等,得出1BN AM ==,根据三角形三边关系取得最小值.三、解答题1、滑道OC 的长度为51cm .【分析】设OC m =cm ,可得出(15)BC m =-cm ,(12)AC m =-cm ,在在Rt △ABC 中,根据勾股定理可得m 的值,由此可得结论.【详解】解:设OC m =cm ,则由图①可知(15)BC OC AB m =-=- cm ,由图②可知(12)AC OC OA m =-=-cm ,∵90B ∠=︒,∴在Rt△ABC 中,根据勾股定理可得,222AB BC AC +=,∴22215(15)(12)m m +-=-,解得51m =,∴滑道OC 的长度为51cm .【点睛】本题考查勾股定理的应用,能结合撑杆AB 、BC 的长度始终保持不变正确表示出BC 和AC 是解题关键.2、(1)见解析;(2)【分析】(1)根据平行可得∠DBE =90°,再由HL 定理证明直角三角形全等即可;(2)构造Rt AHE ,利用矩形性质和勾股定理即可求出AE 长.【详解】(1)∵AC ∥BE ,∴∠C +∠DBE =180°.∴∠DBE =180°-∠C =180°-90°=90°.∴△ABC 和△DEB 都是直角三角形.∵点D 为BC 的中点,12AC BC =,∴AC =DB . ∵AB =DE ,∴Rt △ABC ≌Rt △DEB (HL ).(2)AE =过程如下:连接AE 、过A 点作AH ⊥BE ,∵∠C =90°,∠DBE =90°.∴AC BH ∥,AH BC ∥,∴AH =BC =4, 122BH AC BC ===,∴2EH EB EH =-=,在Rt AHE 中,AE =【点睛】本题主要考查了直角三角形全等的判定和勾股定理解三角形,解题关键是构造直角三角形,利用用平行线间的距离处处相等得线段AH =BC ,从而利用勾股定理求AE .3、(1)见详解;(2)见详解;(3)见详解.【分析】(1)先根据以AB 为边△ABC 是轴对称图形,得出△ABC 为等腰三角形,AB 长为3,画以AB 为腰的等腰直角三角形即可;(2)先根据勾股定理求出AB 的长,利用平移画出点C 即可;(3)先求出以AB 为底等腰直角三角形腰长AC C 即可.【详解】解:(1)∵以AB 为边△ABC 是轴对称图形,∴△ABC 为等腰三角形,AB 长为3,画以AB为直角边,点B为直角顶点△ABC如图也可画以AB为直角边,点A为直角顶点△ABC如图;(2)根据勾股定理ABAB,以点A为顶角顶点根据勾股定理构建横1竖3,或横3竖1;点A向左1格再向下平移3格得C1,连结AC1,C1B,得等腰△ABC1,点A向右3格再向上平移1格得C2,连结AC2,BC2,得等腰△ABC2,点A向右3格再向下平移1格得C3,连结AC3,BC3,得等腰△ABC3,点B向右3格再向上平移1格得C4,连结AC4,BC4,得等腰△ABC4,点B向右3格再向下平移1格得C5,连结AC5,BC5,得等腰△ABC5,点B向右1格再向上平移3格得C6,连结AC6,BC6,得等腰△ABC6;(3)AB为底边画等腰三角形,等腰直角三角形腰长为m,根据勾股定理222AB AC BC=+,22+m m =,解得m =1竖2,或横2竖1得图形,点A 向右平移2格,再向下平移1格得点C 1,连结AC 1,BC 1,得等腰三角形ABC 1,点A 向左平移1格,再向下平移2格得点C 2,连结AC 2,BC 2,得等腰三角形ABC 2.【点睛】本题考查网格作图,图形平移性质,勾股定理应用,等腰直角三角形性质,轴对称性质,掌握网格作图,图形平移性质,勾股定理应用,等腰直角三角形性质,轴对称性质是解题关键.4、(1)①17c <<或5;(2)①2或72或5;②图见解析.【分析】(1)①根据三角形的三边关系定理即可得;②分斜边长为b 和斜边长为c 两种情况,分别利用勾股定理即可得;(2)①先根据已知等式得出2a c b +=,再分,a c 中有一个为3,4b =;,a c 中有一个为4,3b =;,a c 中有一个为3,另一个为4三种情况,分别代入2a c b +=求解即可得; ②先画出射线AM ,再在射线AM 上作线段AB a ,然后在射线BM 上作线段BC c =,最后作线段AC 的垂直平分线,交AC 于点D 即可得.【详解】解:(1)①由三角形的三边关系定理得:4334c -<<+,即17c <<,故答案为:17c <<;②当斜边长为b 时,c ===当斜边长为c 时,2222345c a b ,综上,c 5,或5;(2)①由3a b c b ++=得:2a c b +=, 因此,分以下三种情况:当,a c 中有一个为3,4b =时,不妨设3a =,则17c <<,将3,4a b ==代入2a c b +=得:324c +=⨯,解得5c =,符合题设,当,a c 中有一个为4,3b =时,不妨设4a =,则17c <<,将4,3a b ==代入2a c b +=得:423c +=⨯,解得2c =,符合题设,当,a c 中有一个为3,另一个为4时,不妨设3,4a c ==,则17b <<,将3,4a c ==代入2a c b +=得:342b +=,解得72b =,符合题设, 综上,第三边的值是2或72或5,故答案为:2或72或5; ②由3a b c b ++=得:2a c b +=, 如图,线段AD 即为所求.【点睛】本题考查了勾股定理、三角形的三边关系定理、作线段和线段垂直平分线(尺规作图)等知识点,较难的是题(2)①,正确分三种情况讨论是解题关键.5、(1)点E ;(2)点H ;(3)①存在,点P 的坐标为(7,7);②60m -<<【分析】(1)根据“等距点”的定义,即可求解;(2)根据“等距点”的定义,即可求解;(3)①根据点P 是线段OA 和OB 的“等距点”,可设点P (x ,x )且x >0,再由点P 是点A 和点C 的“等距点”,可得22AP CP = ,从而得到()()222286x x x x -+=-+ ,即可求解;②根据点P 是线段OA 和OB 的“等距点”, 点P 在∠AOB 的角平分线上,可设点P (a ,a )且a >0,根据OA =OB ,可得OP 平分线段AB ,再由点P 在OAB 内,可得0<<3a ,根据点P 是点A 和点C 的“等距点”,可得22AP CP = ,从而得到()()22226a m a a a -+=-+,整理得到()()()2666m a m m -=+-,即可求解. 【详解】解:(1)根据题意得:()6612AD =--= ,633AE =-= ,AF = , 6OD = ,3OE = ,3OF = , ∴AE OE = ,∴点()3,0E 是点A 和点O 的“等距点”;(2)根据题意得:线段OA 在x 轴上,线段OB 在y 轴上,∴点()2,1G --到线段OA 的距离为1,到线段OB 的距离为2,点()2,2H 到线段OA 的距离为2,到线段OB 的距离为2,点()3,6I 到线段OA 的距离为6,到线段OB 的距离为3,∴点()2,2H 到线段OA 的距离和到线段OB 的距离相等,∴点()2,2H 是线段OA 和OB 的“等距点”;(3)①存在,点P 的坐标为(7,7),理由如下:∵点P 是线段OA 和OB 的“等距点”,且线段OA 在x 轴上,线段OB 在y 轴上,∴可设点P (x ,x )且x >0,∵点P 是点A 和点C 的“等距点”,∴22AP CP = ,∵点C (8,0),()6,0A ,∴()()222286x x x x -+=-+ ,解得:7x = ,∴点P 的坐标为(7,7);②如图,∵点P 是线段OA 和OB 的“等距点”,且线段OA 在x 轴上,线段OB 在y 轴上,∴点P 在∠AOB 的角平分线上,可设点P (a ,a )且a >0,∵()6,0A ,()0,6B .∴OA =OB =6,∴OP 平分线段AB ,∵点P 在OAB 内,∴当点P 位于AB 上时, 此时点P 为AB 的中点,∴此时点P 的坐标为6060,22++⎛⎫ ⎪⎝⎭,即()3,3 , ∴0<<3a ,∵点P 是点A 和点C 的“等距点”,∴22AP CP = ,∵点(),0C m ,()6,0A ,∴()()22226a m a a a -+=-+, 整理得:()()()2666m a m m -=+- ,当6m = 时,点C (6,0),此时点C 、A 重合,则a =6(不合题意,舍去),当6m ≠时,62m a += , ∴6032m +<<,解得:60m -<< , 即若点P 在OAB 内,满足条件的m 的取值范围为60m -<<.【点睛】本题主要考查了平面直角坐标系内两点间的距离,点到坐标轴的距离,等腰三角形的性质,角平分线的判定等知识,理解新定义,利用数形结合思想解答是解题的关键.。
勾股定理测试题及答案

勾股定理测试题及答案一、选择题(每题2分,共10分)1. 直角三角形的两直角边长分别为3和4,斜边长为______。
A. 5B. 6C. 7D. 82. 如果一个三角形的三边长分别为3,4,5,那么这个三角形是______。
A. 直角三角形B. 钝角三角形C. 锐角三角形D. 不是三角形3. 一个三角形的两边长分别为5和12,斜边长为13,那么这个三角形是______。
A. 直角三角形B. 等边三角形C. 等腰三角形D. 其他三角形4. 直角三角形的斜边长为10,一条直角边长为6,另一条直角边长为______。
A. 4B. 6C. 8D. 105. 如果一个三角形的三边长满足勾股定理,那么这个三角形一定是______。
A. 直角三角形B. 等边三角形C. 等腰三角形D. 锐角三角形二、填空题(每题2分,共10分)6. 若直角三角形的两条直角边分别为a和b,斜边为c,则a² + b²= ______。
7. 已知直角三角形的一条直角边长为9,斜边长为10,另一条直角边长为 ______。
8. 如果一个三角形的三边长分别为6,8和10,那么这个三角形是______ 。
9. 直角三角形的两条直角边分别为3和4,那么斜边长为 ______ 。
10. 如果一个三角形的三边长分别为7,24和25,那么这个三角形是______ 。
三、解答题(每题5分,共10分)11. 已知直角三角形的两条直角边分别为5和12,求斜边的长度。
12. 一个三角形的三边长分别为7,24和25,判断这个三角形是否为直角三角形,并说明理由。
四、证明题(每题10分,共20分)13. 证明:如果一个三角形的三边长分别为a,b和c,且满足a² + b² = c²,那么这个三角形是直角三角形。
14. 证明:在一个直角三角形中,斜边是最长边。
答案:1. A2. A3. A4. C5. A6. c²7. 78. 直角三角形9. 510. 直角三角形11. 斜边长度为1312. 是直角三角形,因为7² + 24² = 25²13. 证明略14. 证明略。
数学数学勾股定理试题含答案

一、选择题1.如图:在△ABC 中,∠B=45°,D 是AB 边上一点,连接CD ,过A 作AF ⊥CD 交CD 于G ,交BC 于点F .已知AC=CD ,CG=3,DG=1,则下列结论正确的是( )①∠ACD=2∠FAB ②27ACD S ∆= ③272CF=- ④ AC=AF A .①②③ B .①②③④ C .②③④ D .①③④2.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由三角形较长直角边长为a ,较短直角边长为b ,若(a +b )2=21,大正方形的面积为13,则小正方形的面积为( )A .3B .4C .5D .63.如果正整数a 、b 、c 满足等式222+=a b c ,那么正整数a 、b 、c 叫做勾股数.某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x y +的值为( )A .47B .62C .79D .984.如图,正方形ABCD 的边长为2,其面积标记为S 1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S 2,…按照此规律继续下去,则S 2016的值为( )A.(22)2013B.(22)2014C.(12)2013D.(12)20145.如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,D为BC边上的一点,现将直角边AC沿直线AD折叠,使AC落在斜边AB上,且与AE重合,则CD的长为()A.2cm B.2.5cm C.3cm D.4cm6.下列各组线段能构成直角三角形的一组是()A.30,40,60B.7,12,13C.6,8,10D.3,4,67.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是()A.245B.5 C.6 D.88.已知三组数据:①2,3,4;②3,4,5;③1,2,5,分别以每组数据中的三个数为三角形的三边长,能构成直角三角形的是()A.②B.①②C.①③D.②③9.如图,点A和点B在数轴上对应的数分别是4和2,分别以点A和点B为圆心,线段AB的长度为半径画弧,在数轴的上方交于点C.再以原点O为圆心,OC为半径画弧,与数轴的正半轴交于点M,则点M对应的数为()A .3.5B .23C .13D .36210.已知三角形的两边分别为3、4,要使该三角形为直角三角形,则第三边的长为( )A .5B .7C .5或7D .3或4二、填空题11.如图,在平面直角坐标系中,等腰直角三角形OA 1A 2的直角边OA 1在y 轴的正半轴上,且OA 1=A 1A 2=1,以OA 2为直角边作第二个等腰直角三角形OA 2A 3,以OA 3为直角边作第三个等腰直角三角形OA 3A 4,…,依此规律,得到等腰直角三角形OA 2018A 2019,则点A 2019的坐标为________.12.如图,RT ABC ,90ACB ∠=︒,6AC =,8BC =,将边AC 沿CE 翻折,使点A 落在AB 上的点D 处;再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B '处,两条折痕与斜边AB 分别交于点E 、F ,则B FC '△的面积为______.13.如图,在四边形ABCD 中,22AD =,3CD =,45ABC ACB ADC ∠=∠=∠=︒,则BD 的长为__________.14.如图,在Rt ABC ∆中,90ABC ∠=,DE 垂直平分AC ,垂足为F ,//AD BC ,且3AB =,4BC =,则AD 的长为______.15.如图,长方形ABCD 中,∠A =∠ABC =∠BCD =∠D =90°,AB =CD =6,AD =BC =10,点E 为射线AD 上的一个动点,若△ABE 与△A ′BE 关于直线BE 对称,当△A ′BC 为直角三角形时,AE 的长为______.16.如图,长方体纸箱的长、宽、高分别为50cm 、30cm 、60cm ,一只蚂蚁从点A 处沿着纸箱的表面爬到点B 处.蚂蚁爬行的最短路程为_______cm.17.一块直角三角形绿地,两直角边长分别为3m ,4m ,现在要将绿地扩充成等腰三角形,且扩充时只能延长长为3m 的直角边,则扩充后等腰三角形绿地的面积为____m 2.18.已知a 、b 、c 是△ABC 三边的长,且满足关系式2222()0c a b a b --+-=,则△ABC 的形状为___________19.如图,在Rt ABC ∆中,90ACB ∠=,2AC BC ==,D 为BC 边上一动点,作如图所示的AED ∆使得AE AD =,且45EAD ∠=,连接EC ,则EC 的最小值为__________.20.如图的实线部分是由Rt ABC ∆经过两次折叠得到的.首先将Rt ABC ∆沿高CH 折叠,使点B 落在斜边上的点B '处,再沿CM 折叠,使点A 落在CB '的延长线上的点A '处.若图中90ACB ∠=︒,15cm BC =,20cm AC =,则MB '的长为______.三、解答题△中,∠ACB = ∠DCE=90°.21.如图,在两个等腰直角ABC和CDE(1)观察猜想:如图1,点E在BC上,线段AE与BD的数量关系是,位置关系是;△绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?(2)探究证明:把CDE说明理由;△绕点C在平面内自由旋转,若AC = BC=10,DE=12,当A、E、(3)拓展延伸:把CDED三点在直线上时,请直接写出 AD的长.22.如图1,在△ABC中,AB=AC,∠BAC=90°,D为AC边上一动点,且不与点A点C重合,连接BD并延长,在BD延长线上取一点E,使AE=AB,连接CE.(1)若∠AED=20°,则∠DEC=度;(2)若∠AED=a,试探索∠AED与∠AEC有怎样的数量关系?并证明你的猜想;(3)如图2,过点A作AF⊥BE于点F,AF的延长线与EC的延长线交于点H,求证:EH2+CH2=2AE2.23.如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm 的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).(1)若点P在AC上,且满足PA=PB时,求出此时t的值;(2)若点P恰好在∠BAC的角平分线上,求t的值;(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.24.如果一个三角形的两条边的和是第三边的两倍,则称这个三角形是“优三角形”,这两条边的比称为“优比”(若这两边不等,则优比为较大边与较小边的比),记为k . (1)命题:“等边三角形为优三角形,其优比为1”,是真命题还是假命题?(2)已知ABC 为优三角形,AB c =,AC b =,BC a =,①如图1,若90ACB ∠=︒,b a ≥,6b =,求a 的值.②如图2,若c b a ≥≥,求优比k 的取值范围.(3)已知ABC 是优三角形,且120ABC ∠=︒,4BC =,求ABC 的面积.25.(1)如图1,在Rt ABC ∆中,90ACB ∠=︒,60A ∠=︒,CD 平分ACB ∠. 求证:CA AD BC +=.小明为解决上面的问题作了如下思考:作ADC ∆关于直线CD 的对称图形A DC '∆,∵CD 平分ACB ∠,∴A '点落在CB 上,且CA CA '=,A D AD '=.因此,要证的问题转化为只要证出A D A B ''=即可. 请根据小明的思考,写出该问题完整的证明过程.(2)参照(1)中小明的思考方法,解答下列问题:如图3,在四边形ABCD 中,AC 平分BAD ∠,10BC CD ==,17AC =,9AD =,求AB 的长.26.如图,在△ABC 中,∠C =90°,把△ABC 沿直线DE 折叠,使△ADE 与△BDE 重合.(1)若∠A =35°,则∠CBD 的度数为________;(2)若AC =8,BC =6,求AD 的长;(3)当AB =m(m>0),△ABC 的面积为m +1时,求△BCD 的周长.(用含m 的代数式表示)27.已知ABC ∆中,90ACB ∠=︒,AC BC =,过顶点A 作射线AP .(1)当射线AP 在BAC ∠外部时,如图①,点D 在射线AP 上,连结CD 、BD ,已知21AD n =-,21AB n =+,2BD n =(1n >).①试证明ABD ∆是直角三角形;②求线段CD 的长.(用含n 的代数式表示)(2)当射线AP 在BAC ∠内部时,如图②,过点B 作BD AP ⊥于点D ,连结CD ,请写出线段AD 、BD 、CD 的数量关系,并说明理由.28.如图,己知Rt ABC ∆,90ACB ∠=︒,30BAC ∠=︒,斜边4AB =,ED 为AB 垂直平分线,且23DE =,连接DB ,DA .(1)直接写出BC =__________,AC =__________;(2)求证:ABD ∆是等边三角形;(3)如图,连接CD ,作BF CD ⊥,垂足为点F ,直接写出BF 的长;(4)P 是直线AC 上的一点,且13CP AC =,连接PE ,直接写出PE 的长. 29.如图1,在正方形ABCD 中,点E ,F 分别是AC ,BC 上的点,且满足DE ⊥EF ,垂足为点E ,连接DF .(1)求∠EDF= (填度数);(2)延长DE 交AB 于点G ,连接FG ,如图2,猜想AG ,GF ,FC 三者的数量关系,并给出证明;(3)①若AB=6,G 是AB 的中点,求△BFG 的面积;②设AG=a ,CF=b ,△BFG 的面积记为S ,试确定S 与a ,b 的关系,并说明理由.30.已知,矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .(1)如图1,连接AF 、CE .求证:四边形AFCE 为菱形.(2)如图1,求AF 的长.(3)如图2,动点P 、Q 分别从A 、C 两点同时出发,沿△AFB 和△CDE 各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,点P 的速度为每秒1cm ,设运动时间为t 秒.①问在运动的过程中,以A 、P 、C 、Q 四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t 和点Q 的速度;若不可能,请说明理由.②若点Q 的速度为每秒0.8cm ,当A 、P 、C 、Q 四点为顶点的四边形是平行四边形时,求t 的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】过点C 作CH AB ⊥于点H ,根据等腰三角形的性质得到1802ACD CDA ∠=︒-∠,根据AF CD ⊥得到90FAB CDA ∠=︒-∠,可以证得①是正确的,利用勾股定理求出AG 的长,算出三角形ACD 的面积证明②是正确的,再根据角度之间的关系证明AFC ACF ∠=∠,得到④是正确的,最后利用勾股定理求出CF 的长,得到③是正确的.【详解】解:如图,过点C 作CH AB ⊥于点H ,∵AC CD =,∴CAD CDA ∠=∠,1802ACD CDA ∠=︒-∠,∵AF CD ⊥,∴90AGD ∠=︒,∴90FAB CDA ∠=︒-∠,∴2ACD FAB ∠=∠,故①正确;∵3CG =,1DG =,∴314CD CG DG =+=+=,∴4AC CD ==,在Rt ACG 中,221697AG AC CG =--=, ∴1272ACD S AG CD =⋅= ∵90CHB ∠=︒,45B ∠=︒,∴45HCB ∠=︒,∵AC CD =,CH AD ⊥, ∴12ACH HCD ACD ∠=∠=∠, ∵45AFC B FAB FAB ∠=∠+∠=︒+∠,45ACF ACH HCB ACH ∠=∠+∠=∠+︒,12ACH ACD FAB ∠=∠=∠, ∴AFC ACF ∠=∠,∴4AC AF ==,故④正确; ∴47GF AF AG =-=-在Rt CGF 中,()2222347272CF CG GF =+=+-=,故③正确.故选:B .【点睛】本题考查几何的综合证明,解题的关键是掌握等腰三角形的性质和判定,勾股定理和三角形的外角和定理.2.C解析:C【分析】观察图形可知,小正方形的面积=大正方形的面积-4个直角三角形的面积,利用已知2()a b + =21,大正方形的面积为13,可以得以直角三角形的面积,进而求出答案。
难点详解沪科版八年级数学下册第18章 勾股定理专题测试试卷(含答案详解)

八年级数学下册第18章 勾股定理专题测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,在ABC 中,90ABC ∠=︒,BD AC ⊥,垂足为D .如果6AC =,3BC =,则BD 的长为( )A .2B .32C .D 2、下列长度的三条线段能组成直角三角形的是( )A .3,4,5B .2,3,5C .0.2, 0.3, 0.5D .13,14,153、下列四组数据中,不能..作为直角三角形的三边长的是( ) A .5,13,12 B .6,8,10 C .9,12,15 D .3,4,64、点P (-3,4)到坐标原点的距离是( )A .3B .4C .-4D .55、下列各组数中,不能作为直角三角形的三边的是( )A .3,4,5B .2,3C .8,15,17D .23,24,256、以下列各组线段为边作三角形,能构成直角三角形的是( )A .2,3,5B .6,8,9C .5,12,13D .6,12,137、下列条件:①222b c a =-;②C A B ∠=∠-∠;③111::::345a b c =;④::3:4:5A B C ∠∠∠=,能判定ABC 是直角三角形的有( )A .4个B .3个C .2个D .1个8、现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图(1)已知云梯最多只能伸长到15m ,消防车高3m .救人时云梯伸长至最长,在完成从12m 高处救人后,还要从15m 高处救人,这时消防车要从原处再向着火的楼房靠近的距离AC 为( )A .3米B .5米C .7米D .9米9、图中字母A 所代表的正方形的面积为( ).A .64B .8C .16D .610、已知一个直角三角形两直角边边长分别为6和8,则斜边边长为( )A .10B .C .15D .10或第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,在△DEF 中,∠D =90°,DG :GE =1:3,GE =GF ,Q 是EF 上一动点,过点Q 作QM ⊥DE 于M ,QN ⊥GF 于N ,EF =QM +QN 的长是___________.2、如今人们锻炼身体的意识日渐增强,但是发现少数人保护环境的意识仍显淡薄,应提醒注意.下图是房山某公园的一角,有人为了抄近道而避开路的拐角ABC ∠(90ABC ∠=︒),于是在草坪内走出了一条不该有的“捷径路AC ” .已知30AB =米,40BC =米,他们踩坏了______米的草坪,只为少走______米的路.3、如图,线段10AB =,45A B ∠=∠=︒,AC BD ==E 、F 为线段AB 上两点从下面4个条件中:①5CE DF ==;②AF BE =;③7CE DF ==;④CEB DEA ∠=∠,选择一个条件,使得ACE 和BDF 全等.则所有满足的条件是______(填序号)4、已知三角形的三边分别是6,8,10,则最长边上的高等于______.5、如图,在四边形ABCE 中,∠B =∠A ,∠E =90°,点D 在AB 上,AD ∶BD =5∶11,连接CD ,若点D 在CE 的垂直平分线上且满足∠A =2∠BDC ,CE =10,则线段AB 的长为______.三、解答题(5小题,每小题10分,共计50分)1、如图,△ABC 中,∠ABC =45°,F 是高AD 和高BE 的交点,AC BD =2.求线段DF 的长度.2、阅读下列一段文字,然后回答问题.已知在平面内两点()111,P x y 、()222,P x y ,其两点间的距离12PP =连线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为21x x -或21y y -.(1)已知A 、B 两点在平行于y 轴的直线上,点A 的纵坐标为4,点B 的纵坐标为1-,试求A 、B 两点之间的距离;(2)已知一个三角形各顶点坐标为(1,6)D 、(2,2)E -、(4,2)F ,你能判定此三角形的形状吗?说明理由.(3)在(2)的条件下,平面直角坐标系中,在x 轴上找一点P ,使PD PF +的长度最短,求出点P 的坐标以及PD PF +的最短长度.3、已知:△ABC 是等腰直角三角形,动点P 在斜边AB 所在的直线上,以PC 为直角边作等腰直角三角形PCQ ,其中∠PCQ =90°,探究并解决以下问题:(1)如图1,若点P 在线段AB 上,且AC =4,PA PB = ,PC = .②猜想:222,,PA PB PQ 三者之间的数量关系为 .(2)如图2,若点P 在线段AB 的延长线上,则在(1)中所猜想的结论仍然成立,请你利用图2给出证明过程.(3)若动点P 满足13PA PB =,请直接写出PC AC的值.(提示:请你利用备用图探究)4、若实数b 的立方根为2,且实数a ,b ,c 2(4)8b a c +-+=.(1)求23a b c -+的值;(2)若a ,b ,c 是△ABC 的三边,试判断三角形的形状.5、(问题背景)学校数学兴趣小组在专题学习中遇到一个几何问题:如图1,已知等边ABC ,D 是ABC 外一点,连接AD 、CD 、BD ,若30ADC ∠=︒,3AD =,5BD =,求CD 的长.该小组在研究如图2中OMN OPQ ≅中得到启示,于是作出如图3,从而获得了以下的解题思路,请你帮忙完善解题过程.解:如图3所示,以DC 为边作等边CDE △,连接AE .∵ABC ,DCE 是等边三角形,∴BC AC =,DC EC =,60BCA DCE ∠=∠=︒.∴BCA ACD ∠+∠= ACD +∠,∴BCD ACE ∠=∠,∴ ,∴5AE BD ==,∵30ADC ∠=︒,60CDE ∠=︒,∴90ADE ADC CDE ∠=∠+∠=︒.∵3AD =,∴CD DE == .(尝试应用)如图4,在ABC 中,45ABC ∠=︒,AB =4BC =,以AC 为直角边,A 为直角顶点作等腰直角ACD △,求BD 的长.(拓展创新)如图5,在ABC 中,4AB =,8AC =,以BC 为边向往外作等腰BCD △,BD CD =,120BDC ∠=︒,连接AD ,求AD 的最大值.-参考答案-一、单选题1、D【分析】先根据勾股定理求出AB ,再利用三角形面积求出BD 即可.【详解】解:∵90ABC ∠=︒,6AC =,3BC =,∴根据勾股定理AB ==,∵BD AC ⊥,∴S △ABC =1122AB BC AC BD ⋅=⋅,即113622BD ⨯=⨯⋅,解得:BD =故选择D .【点睛】 本题考查直角三角形的性质,勾股定理,三角形面积等积式,掌握直角三角形的性质,勾股定理,三角形面积等积式是解题关键.2、A【分析】只要验证两小边的平方和等于最长边的平方即可判断是直角三角形.【详解】解:A. 2223+4=5∴能组成直角三角形,故A 符合题意;B. 2222+35≠∴不能组成直角三角形,故B 不符合题意;C. 2220.2+0.30.5≠∴不能组成直角三角形,故C 不符合题意;D. 222111()+()()345≠∴不能组成直角三角形,故D 不符合题意, 故选:A .【点睛】本题考查勾股定理的逆定理,是重要考点,掌握相关知识是解题关键.3、D【分析】根据勾股定理的逆定理进行判断即可.【详解】解:A 、22251213+=,故A 不符合题意.B 、2226810+=,故B 不符合题意.C 、22291215+=,故C 不符合题意.D 、222346+≠,故D 符合题意.故选:D .【点睛】本题主要是考查了勾股定理的逆定理,熟练利用勾股定理来判定三角形是否为直角三角形,是解决本题的关键.4、D【分析】利用两点之间的距离公式即可得.【详解】解:点(3,4)P -到坐标原点(0,0)5,故选:D.【点睛】本题考查了两点之间的距离公式,熟练掌握两点之间的距离公式是解题关键.5、D【分析】由题意直接根据勾股定理的逆定理即如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形,如果没有这种关系,这个就不是直角三角形进行分析判断即可.【详解】解:A、32+42=52,符合勾股定理的逆定理,故选项错误;B、22223+=,符合勾股定理的逆定理,故选项错误;C、82+152=172,符合勾股定理的逆定理,故选项错误;D、∵(32)2+(42)2=81+256=337,(52)2=625,∴(32)2+(42)2≠(52)2,不符合勾股定理的逆定理即此时三角形不是直角三角形,故选项正确.故选:D.【点睛】本题考查勾股定理的逆定理,注意掌握在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.6、C【分析】根据两小边的平方和是否等于最长边的平方进行判断是否是直角三角形.【详解】A、选项:222+=≠,不能构成直角三角形,故本选项不符合题意;23135B、选项:222+=≠,不能构成直角三角形,故本选项不符合题意;681009C 、选项:22251216913+==,能构成直角三角形,故本选项符合题意;D 、选项:22261218013+=≠,不能构成直角三角形,故本选项不符合题意;故选:C【点睛】考查勾股定理的逆定理的应用,判断三角形是否为直角三角形只要验证两小边的平方和等于最长边的平方即可.7、C【分析】根据三角形的内角和定理以及勾股定理的逆定理即可得到结论.【详解】解:①222b c a =-即222+=a b c ,△ABC 是直角三角形,故①符合题意;②∵∠A +∠B +∠C =180°,∠C =∠A −∠B ,∴∠A +∠B +∠A −∠B =180°,即∠A =90°,∴△ABC 是直角三角形,故②符合题意; ③∵111::::345a b c =,设a =3k,b =4k ,c =5k , 则222543k k k ⎛⎫⎛⎫⎛⎫+≠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ∴△ABC 不是直角三角形,故③不合题意;④∵::3:4:5A B C ∠∠∠=,∴∠C =5345++×180°=75°,故不是直角三角形;故④不合题意. 综上,符合题意的有①②,共2个,【点睛】本题主要考查了直角三角形的判定方法.①如果三角形中有一个角是直角,那么这个三角形是直角三角形;②如果一个三角形的三边a ,b ,c 满足a 2+b 2=c 2,那么这个三角形是直角三角形.8、A【分析】根据题意结合图形可得:3OE =m ,1239OB =-=m ,15312OD =-=m ,15AB CD ==m ,在两个直角三角形ABO ∆和ΔΔΔΔ中,分别运用勾股定理求出AO ,CO ,即可得出移动的距离.【详解】解:如图所示:3OE =m ,1239OB =-=m ,15312OD =-=m ,15AB CD ==m ,在Rt ABO ∆中,12AO ==m ,在ΔΔΔΔΔΔ中,9CO m ,3AC AO CO =-=m ,故选:A .题目主要考查勾股定理的应用,理解题意,找出相应的线段运用勾股定理是解题关键.9、A【分析】根据勾股定理和正方形的性质即可得出结果.【详解】解:根据勾股定理以及正方形的面积公式知:以直角三角形的两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,所以A=289-225=64.故选:A.【点睛】本题考查了勾股定理,以及正方形的面积公式,勾股定理最大的贡献就是沟通“数”与“形”的关系,它的验证和利用都体现了数形结合的思想,即把图形的性质问题转化为数量关系的问题来解决.能否由实际的问题,联想到用勾股定理的知识来求解是本题的关键.10、A【分析】已知两直角边边长分别为6和8,利用勾股定理求斜边即可.【详解】解:∵一个直角三角形两直角边边长分别为6和8,斜边边长,∴斜边边长为10.故选A.【点睛】本题考查了利用勾股定理解直角三角形的能力,当已知条件中明确直角边或斜边,直接应用勾股定理,如果条件不明确时那条边是斜边,要注意讨论.二、填空题1、4【分析】连接QG 解直角三角形求出DF ,再证明QM QN DF +=,即可解决问题.【详解】解:连接QG .:1:3DG GE =,∴可以假设DG k =,3EG k =,GF EG =,90D ∠=︒,3FG k ∴=,DF , 4EF =222EF DE DF =+,2248168k k ∴=+,k ∴或,4DF ∴=,111222EFG S EG DF EG QM GF QN ∆=⋅⋅=⋅⋅+⋅⋅,4QM QN DF ∴+==, 故答案为:4.【点睛】本题考查解直角三角形,勾股定理,等腰三角形的性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.2、50 20【分析】根据勾股定理计算AC ,计算AB +BC -AC 的值即可.【详解】∵90ABC ∠=︒,30AB =,40BC =,∴AC (米),∴AB +BC -AC =30+40-50=20(米),故答案为:50,20.【点睛】本题考查了勾股定理,准确用定理计算是解题的关键.3、②③④【分析】条件①利用SSA 不能证明全等;条件②可以用SAS 证明两个三角形全等;条件③先证明Rt CME Rt DNF ≌,再利用AAS 即可证明ACE BDF ≌;条件④可利用AAS 证明两个三角形全等.【详解】解:①如图1,过C 作CM AB ⊥于M ,过D 作DN AB ⊥于N ,∵45A B ∠=∠=︒,∴ACM △和BDN 是等腰直角三角形,∵AC BD ==∴4CM DN ==,∵45<<∵5CE DF ==∴符合条件的E 和F 在线段AB 上各有两个点,如图1,ACE 不一定和BDF 全等,故①不符合题意;②如图2,∵AF BE =,∴AE BF =在ACE 和BDF 中,∵AC BD A B AE BF =⎧⎪∠=∠⎨⎪=⎩, ∴()ACE BDF SAS ≌,故②符合题意;③如图3,过C 作CM AB ⊥于M ,过D 作DN AB ⊥于N ,由①知CM DN =∵7CE DF ==,且7>,∴E 和F 在线段AB 上各存在一个点,在Rt CME 和Rt DNF △中,∵CM DN CB DF =⎧⎨=⎩, ∴()Rt CME Rt DNF HL ≌,∴CEM DFN ∠=∠,在ACE 和BDF 中,∵A B CEM DFN AC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()ACE BDF AAS ≌,故③符合题意;④如图4,∵CEB DFA ∠=∠,∴AEC BFD ∠=∠,在ACE 和BDF 中,∵A B AEC DFB AC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()ACE BDF AAS ≌,故④符合题意.故答案为:②③④.【点睛】本题主要考查了全等三角形的性质与判定,解题的关键在于能够熟练掌握全等三角形的性质与判定条件.4、245【分析】根据勾股定理的逆定理,得这个三角形是直角三角形;根据直角三角形的面积计算,即可得到答案.【详解】∵三角形的三边分别是6,8,10,又∵2226810+=∴这个三角形是直角三角形∵12⨯最长边上的高110682⨯=⨯⨯ ∴最长边上的高为:6824105⨯= 故答案为:245. 【点睛】本题考查了勾股定理逆定理的知识;解题的关键是熟练掌握勾股定理的逆定理,从而完成求解. 5、554【分析】根据题意过点D 作DG ⊥EC ,CF ⊥AB ,连接AC 、DE ,先证明△ADE ≅△BCD 和△GDC ≅△FDC ,进而设AD =BC =5x ,AE = BD =11x ,AF =y ,则BF =16x -y ,通过勾股定理建立方程求解即可.【详解】解:过点D 作DG ⊥EC ,CF ⊥AB ,连接AC 、DE ,∵点D 在CE 的垂直平分线上,DG ⊥EC ,∴DE =DC ,EDG CDG ∠=∠,∵∠AEC =90°,DG ⊥EC ,∠EAD =2∠BDC ,∴//AE DG ,2,EAD GDF BDC AED GDE ∠=∠=∠∠=∠,∴BDC CDG EDG AED ∠=∠=∠=∠,∵∠B=∠EAD,BDC AED∠=∠,DE=DC,∴△ADE≅△BCD,AE=BD,∵DG⊥EC,CF⊥AB,BDC CDG∠=∠,CD=CD,∴△GDC≅△FDC,又∵CE=10,CG=CE,∴CF=CG=5,∵AD∶BD=5∶11,设AD=BC=5x,AE= BD=11x,AF=y,则BF=16x-y,由勾股定理AC2=AE2+CE2=CF2+AF2得到121x2+100=25+y2①由勾股定理得BC2=CF2+BF2得到25x2=25+(16x-y)2②联立①②可解得54x=,∴5551144 BD=⨯=.故答案为:554.【点睛】本题考查全等三角形的判定与性质以及勾股定理的应用和垂直平分线性质,熟练掌握通过垂直平分线性质和角平分线性质构造全等三角形是解题的关键.三、解答题1、1【分析】由勾股定理可求CD=1,由“AAS”可证△BFD≌△ACD,可得CD=DF=1.【详解】解:∵AD 和BE 是△ABC 的高,∴∠ADB =∠ADC =∠BEC =90°.∴∠C +∠DAC =90°;∠C +∠DBF =90°.∴∠DAC =∠DBF .∵∠ABC =45°,∴∠DAB =45°.∴∠ABC =∠DAB .∴DA =DB .在△ADC 与△BDF 中,ADC BDF DA DBDAC DBF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADC ≌△BDF (ASA ).∴AC =BF在Rt △BDF 中,∠BDF =90°,∴BD 2+DF 2=BF 2.∵BD =2,BF∴DF =1【点睛】本题考查了全等三角形的判定和性质,勾股定理,等腰直角三角形的性质,掌握全等三角形的判定定理是本题的关键.2、(1)5;(2)能,理由见解析;(3)13,04⎛⎫ ⎪⎝⎭【分析】(1)根据文字提供的计算公式计算即可;(2)根据文字中提供的两点间的距离公式分别求出DE 、DF 、EF 的长度,再根据三边的长度即可作出判断;(3)画好图,作点F 关于x 轴的对称点G ,连接DG ,则DG 与x 轴的交点P 即为使PD +PF 最短,然后有待定系数法求出直线DG 的解析式即可求得点P 的坐标,由两点间距离也可求得最小值.【详解】(1)∵A 、B 两点在平行于y 轴的直线上∴AB =4(1)5--=即A 、B 两点间的距离为5(2)能判定△DEF 的形状由两点间距离公式得:5DE =,5DF =,4(2)6EF =--=∵DE =DF∴△DEF 是等腰三角形(3)如图,作点F 关于x 轴的对称点G ,连接DG ,则DG 与x 轴的交点P 即为使PD +PF 最小 由对称性知:点G 的坐标为(4,2)-,且PG =PF∴PD +PF =PD +PG ≥DG即PD +PF 的最小值为线段DG 的长设直线DG 的解析式为(0)y kx b k =+≠,把D 、G 的坐标分别代入得:642k b k b +=⎧⎨+=-⎩ 解得:83263k b ⎧=-⎪⎪⎨⎪=⎪⎩即直线DG 的解析式为82633y x =-+ 上式中令y =0,即826033x -+=,解得134x = 即点P 的坐标为13,04⎛⎫ ⎪⎝⎭ 由两点间距离得:DG=DG =所以PD +PF【点睛】本题是材料阅读题,考查了等腰三角形的判定,待定系数法求一次函数的解析式,两点间线段最短,关键是读懂文字中提供的两点间距离公式,把两条线段的和的最小值问题转化为两点间线段最短问题.3、(1)①AP 2+BP 2=PQ 2;(2)见解析;(3【分析】(1)①在等腰直角三角形ACB中,由勾股定理先求得AB的长,然后根据PA的长,可求得PB的长,再利用SAS证明△APC≌△BQC,得出BQ=AP CBQ=∠A=45°,那么△PBQ为直角三角形,依据勾股定理求出PQ=PC;②过点C作CD⊥AB,垂足为D,由△ACB为等腰直角三角形,可求得:CD=AD=DB,然后根据AP=DC-PD,PB=DC+PD,可证明AP2+BP2=2PC2,因为在Rt△PCQ中,PQ2=2CP2,所以可得出AP2+BP2=PQ2的结论;(2)过点C作CD⊥AB,垂足为D,则可证明AP2+BP2=2PC2,在Rt△PCQ中,PQ2=2CP2,可得出AP2+BP2=PQ2的结论;(3)根据点P所在的位置画出图形,然后依据题目中的比值关系求得PA、PD的长(用含有CD的式子表示),然后在Rt△ACD和Rt△PCD中由勾股定理求得AC和PC的长度即可.【详解】解:(1)如图①.连接BQ,①△ABC是等腰直角三角形,AC=4,∴AB∵PA∴PB==∵△ABC和△PCQ均为等腰直角三角形,∴AC=BC,∠ACP=∠BCQ,PC=CQ,∴△APC≌△BQC(SAS).∴BQ =AP CBQ =∠A =45°.∴△PBQ 为直角三角形.∴PQ =∵22220PC PQ ==,∴PC =故答案为:②如图①.过点C 作CD ⊥AB ,垂足为D .∵△ACB 为等腰直角三角形,CD ⊥AB ,∴CD =AD =DB .∵AP 2=(AD -PD )2=(DC -PD )2=DC 2-2DC •PD +PD 2,PB 2=(DB +PD )2=(DC +DP )2=CD 2+2DC •PD +PD 2,∴AP 2+BP 2=2CD 2+2PD 2,∵在Rt △PCD 中,由勾股定理可知:PC 2=DC 2+PD 2,∴AP 2+BP 2=2PC 2.∵△CPQ 为等腰直角三角形,∴2PC 2=PQ 2.∴AP 2+BP 2=PQ 2;故答案为:AP2+BP2=PQ2;(2)如图②:过点C作CD⊥AB,垂足为D.∵△ACB为等腰直角三角形,CD⊥AB,∴CD=AD=DB.∵AP2=(AD+PD)2=(DC+PD)2=CD2+2DC•PD+PD2,PB2=(DP-BD)2=(PD-DC)2=DC2-2DC•PD+PD2,∴AP2+BP2=2CD2+2PD2,∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,∴AP2+BP2=2PC2.∵△CPQ为等腰直角三角形,∴2PC2=PQ2.∴AP2+BP2=PQ2;(3)如图③:过点C作CD⊥AB,垂足为D.①点P位于点P1处时.∵111 3P APB=,∴P1A=14AB=12CD,11122PD AD CD==,在Rt△P1CD中,由勾股定理得:1PC==,在Rt△ACD中,由勾股定理得:AC=,∴1PCAC==②当点P位于点P2处时.∵2213P AP B=,∴P2A=12AB=CD,222P D P A AD CD=+=,在Rt△P2CD中,由勾股定理得:2P C,在Rt△ACD中,由勾股定理得:AC=,∴2P CAC=综合上述,PCAC【点睛】本题主要考查的是等腰直角三角形的性质和勾股定理的应用,以及全等三角形的判定和性质,正确作出辅助线,根据等腰直角三角形的性质得CD =AD =DB ,将PA 、PB 、PQ 、AC 、PC 用含DC 的式子表示出来是解题的关键.注意运用数形结合的思想和分类讨论的思想进行求解.4、(1)232a b c -+=-;(2)△ABC 是直角三角形.【分析】(1)先根据立方根的定义求出b 的值,然后根据非负数的性质求出a 、c 的值,最后代值计算即可;(2)根据(1)所求,利用勾股定理的逆定理求解即可.【详解】解:(1)∵实数b 的立方根是2,∴b =8,2(4)8b a c +-+=,28(4)8a c +-+=,2(4)0a c -+=,0≥,2(4)0a c -+≥,∴6040a a c -=⎧⎨-+=⎩, ∴a =6,c =10,∴232638102a b c -+=⨯-⨯+=-;(2)∵a 2+b 2=36+64=100,c 2=100,∴a 2+b 2=c 2.∴△ABC 是直角三角形.【点睛】本题主要考查了立方根,非负数的性质,代数式求值,勾股定理的逆定理,熟知相关知识是解题的关键.5、 [问题背景]DCE ∠;BCD ACE ≌;4;[尝试应用][拓展创新]【分析】[问题背景]根据等式的性质,三角形全等的判定与性质,勾股定理填空即可;[尝试应用]以AB 为直角边,A 为直角顶点作等腰Rt ABF ,连接,,AF BF CF ,进而证明BAD FAC △≌△,根据勾股定理求得FC ,即可求得BD 的长;[拓展创新] 以DA 为腰,作等腰DAG △,DA DG =,120ADG ∠=︒,过点D 作DH AG ⊥,同理证明ABD GCD ≌,进而根据含30度角的直角三角形的性质,勾股定理求得,DH AH ,根据三角形三边关系确定AD 最大值时,,,A C G 三点共线,进而即可求得AD 的最大值.【详解】[问题背景] 解:如图3所示,以DC 为边作等边CDE △,连接AE .∵ABC ,DCE 是等边三角形,∴BC AC =,DC EC =,60BCA DCE ∠=∠=︒.∴BCA ACD ∠+∠=DCE ∠ACD +∠,∴BCD ACE ∠=∠,∴BCD ACE ≌,∴5AE BD ==,∵30ADC ∠=︒,60CDE ∠=︒,∴90ADE ADC CDE ∠=∠+∠=︒.∵3AD =,∴CD DE ==4.[尝试应用] 解:如图4所示,以AB 为直角边,A 为直角顶点作等腰Rt ABF ,连接,,AF BF CF .∵DAC △,FAB 是等腰直角三角形, ∴AF AB =,AD AC =,90FAB DAC ∠=∠=︒. ∴BAF FAD CAD FAD ∠+∠=∠+∠, ∴FAC BAD ∠=∠,∴BAD FAC △≌△,∴AF AB ==2FB ∴==∵45ABC ∠=︒,45ABF ∠=︒, ∴90FBC ABF ABC ∠=∠+∠=︒. ∵4BC =,∴BD FC =[拓展创新]解:如图,以DA 为腰,作等腰DAG △,DA DG =,120ADG ∠=︒,过点D 作DH AG ⊥,90,30DHA HAD ∴∠=︒∠=︒,12AH HG AG == 12HD AD ∴=AH AD ∴==即AD == ∵DBC △,DAG △是等腰三角形,,DC DB DG DA ∴==∴GDA CDA CDB CDA ∠-∠=∠-∠GDC ADB ∴∠=∠∴ABD GCD ≌4CG AB ∴==AD =AG = 则当AG 取得最大值时,AD 取得最大12AG CG AC AB AC ≤+=+=当,,A C G 三点共线时,AD 取得最大值,如图,AD ∴AG == 【点睛】本题考查了等腰三角形的性质与判定,三角形全等的性质与判定,勾股定理,线段最值问题,从题干部分理解作等腰三角形辅助线是解题的关键.。
强化训练-北师大版八年级数学上册第一章勾股定理专项测评练习题(含答案详解)

北师大版八年级数学上册第一章勾股定理专项测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出()A.直角三角形的面积B.最大正方形的面积C.较小两个正方形重叠部分的面积D.最大正方形与直角三角形的面积和2、如图,△ABC中,90∠=,以其三边分别向外侧作正方形,然后将整个图形放置于如图所示ACB的长方形中,若要求图中两个阴影部分面积之和,则只需知道()A.以BC为边的正方形面积B.以AC为边的正方形面积C.以AB为边的正方形面积D.△ABC的面积3、在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是()A.如果∠A-∠B=∠C,那么△ABC是直角三角形B.如果a2=b2-c2,那么△ABC是直角三角形,且∠C=90°C.如果∠A︰∠B︰∠C=1︰3︰2,那么△ABC是直角三角形D.如果a2︰b2︰c2=9︰16︰25,那么△ABC是直角三角形4、下列各组数:①3、4、5 ②4、5、6 ③2.5、6、6.5 ④8、15、17,其中是勾股数的有( )A.4组B.3组C.2组D.1组5、有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了上图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是()A.1 B.2021 C.2020 D.20196、如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖A处的最短距离是()A B.10厘米C.D.8厘米7、如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的点中任取一点C,使△ABC为直角三角形的概率是()A.12B.25C.47D.378、一个直角三角形的两条直角边边长分别为6和8,则斜边上的高为()A.4.5 B.4.6 C.4.8 D.59、如图,长方形纸片ABCD中,AB=3cm,AD=9cm,将此长方形纸片折叠,使点D与点B重合,点C落在点H的位置,折痕为EF,则△ABE的面积为()A.6cm2B.8cm2C.10cm2D.12cm210、如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是()A.48 B.60C.76 D.80第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、《九章算术》中有“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:有一根竹子原来高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?如图,设折断处距离地面x尺,根据题意,可列方程为______.2、如图,一艘轮船位于灯塔P的南偏东60︒方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东45︒方向上的B处,此时B处与灯塔P的距离为___________海里(结果保留根号).3、如图,矩形ABCD中,AD=6,AB=8.点E为边DC上的一个动点,△AD'E与△ADE关于直线AE对称,当△CD'E为直角三角形时,DE的长为__.4、如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶点A在AC上滑动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,滑竿顶端A下滑________米.5、无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有__________cm.三、解答题(5小题,每小题10分,共计50分)1、如图,CE⊥AB于点E,BD⊥AC于点D,AB=AC.(1)求证:△ABD≌△ACE.(2)连接BC,若AD=6,CD=4,求△ABC的面积.2、如图,在△ABC和△DEB中,AC∥BE,∠C=90°,AB=DE,点D为BC的中点,12AC BC=.(1)求证:△ABC≌△DEB.(2)连结AE,若BC=4,直接写出AE的长.3、如图,在△ABC中,∠C=90°,M是BC的中点,MD⊥AB于D,求证:222AD AC BD=+.4、在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.5、做4个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,再做一个边长为c的正方形,把它们按如图的方式拼成正方形,请用这个图证明勾股定理.-参考答案-一、单选题1、C【解析】【分析】根据勾股定理得到c2=a2+b2,根据正方形的面积公式、长方形的面积公式计算即可.【详解】设直角三角形的斜边长为c,较长直角边为b,较短直角边为a,由勾股定理得,c 2=a 2+b 2,阴影部分的面积=c 2-b 2-a (c-b )=a 2-ac+ab=a (a+b-c ),较小两个正方形重叠部分的长=a-(c-b ),宽=a ,则较小两个正方形重叠部分底面积=a (a+b-c ),∴知道图中阴影部分的面积,则一定能求出较小两个正方形重叠部分的面积,故选C .【考点】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a ,b ,斜边长为c ,那么a 2+b 2=c 2.2、D【解析】【分析】如图所示,过点C 作CN ⊥AB 于N ,延长AB 、BA 分别交正方形两边于H 、E ,证明△ADE ≌△CAN 得到=ADE CAN S S △△,AE =CN 同理可证△BGH ≌△CBN ,得到=BGH CBN S S △△,BH =CN ,则==ADE BGH CAN CBN ABC S S S S S ++△△△△△,即可推出=5ABC S S △阴影由此即可得到答案.【详解】解:如图所示,过点C 作CN ⊥AB 于N ,延长AB 、BA 分别交正方形两边于H 、E ,∴∠CNA =∠DEA =∠DAC =90°,∴∠DAE +∠EDA =∠DAE +∠CAN =90°,∴∠ADE =∠CAN ,又∵AD =CA ,∴△ADE ≌△CAN (AAS ),∴=ADE CAN S S △△,AE =CN同理可证△BGH ≌△CBN ,∴=BGH CBN S S △△,BH =CN∴==ADE BGH CAN CBN ABC S S S S S ++△△△△△,∴=ABC S AB AE AB BH S ⋅+⋅+△阴影=2ABC AB CN S ⋅+△=5ABC S △,∴只需要知道△ABC 的面积的面积即可求出阴影部分的面积,故选D【考点】本题主要考查了全等三角形的性质与判定,解题的关键在于能够正确作出辅助线,构造全等三角形.3、B【解析】【分析】根据勾股定理的逆定理、三角形内角和定理、直角三角形定义即可.【详解】解:A 、∵∠A -∠B =∠C ,∴∠A=∠B+∠C,∵∠A+∠B+∠C=180°,∴∠A=90°,∴△ABC是直角三角形,此选项正确;B、如果a2=b2-c2,∴a2+c2=b2,∴△ABC是直角三角形且∠B=90°,此选项不正确;C、如果∠A:∠B:∠C=1:3:2,设∠A=x,则∠B=3x,∠C=2x,则x+3x+2x=180°,解得:x=30°,则3x=90°,∴△ABC是直角三角形,此选项正确;D、如果a2:b2:c2=9:16:25,则a2+b2=c2,∴△ABC是直角三角形,此选项正确;故选:B.【考点】本题考查了三角形内角和,勾股定理的逆定理,如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.4、C【解析】【详解】解:∵32+42=52,①符合勾股数的定义;∵42+52≠62,②不符合勾股数的定义;∵2.5和6.5不是正整数,③不符合勾股数的定义;∵82+152=172,④符合勾股数的定义,是勾股数的有:①④,共2组,故选:C.5、B【解析】【分析】根据勾股定理求出“生长”了1次后形成的图形中所有的正方形的面积和,结合图形总结规律,根据规律解答即可.【详解】解:由题意得,正方形A的面积为1,由勾股定理得,正方形B的面积+正方形C的面积=1,∴“生长”了1次后形成的图形中所有的正方形的面积和为2,同理可得,“生长”了2次后形成的图形中所有的正方形的面积和为3,∴“生长”了3次后形成的图形中所有的正方形的面积和为4,……∴“生长”了2020次后形成的图形中所有的正方形的面积和为2021,故选:B.【考点】本题考查了勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.6、B【解析】【分析】把圆柱沿着点A所在母线展开,把圆柱上最短距离转化为将军饮马河型最短问题求解即可.【详解】把圆柱沿着点A所在母线展开,如图所示,作点A的对称点B,连接PB,则PB为所求,根据题意,得PC=8,BC=6,根据勾股定理,得PB=10,故选B.【考点】本题考查了圆柱上的最短问题,利用圆柱展开,把问题转化为将军饮马河问题,灵活使用勾股定理是解题的关键.7、C【解析】【分析】找到可以组成直角三角形的点,根据概率公式解答即可.【详解】解:如图,1C,2C,C,4C均可与点A和B组成直角三角形.34P ,7故选:C.【考点】本题考查了概率公式,解题的关键是掌握如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)mn =.8、C【解析】【分析】根据勾股定理求出斜边的长,再根据面积法求出斜边的高.【详解】解:设斜边长为c,高为h.由勾股定理可得:c2=62+82,则 c=10 ,直角三角形面积S=12×6×8=12×c×h,可得h=4.8 ,故选:C.【考点】本题考查了勾股定理,利用勾股定理求直角三角形的边长和利用面积法求直角三角形的高是解决此类题的关键.9、A【解析】【分析】根据折叠的条件可得:BE DE=,在Rt BAE中,利用勾股定理就可以求解.【详解】将此长方形折叠,使点B与点D重合,9cmAD=,9BE AE ∴=-,根据勾股定理得:229(9)AE AE +=-,解得:4(cm)AE =.21436(cm )2ABES ∴=⨯⨯=. 故选:A .【考点】本题考查了利用勾股定理解直角三角形,掌握直角三角形两直角边的平方和等于斜边的平方是解题的关键.10、C【解析】【详解】解:∵∠AEB =90°,AE =6,BE =8,∴AB 10∴S 阴影部分=S 正方形ABCD -SRt △ABE =102-1682⨯⨯=100-24=76.故选:C.二、填空题1、2223(10)x x +=-【解析】【分析】根据勾股定理即可得出结论.【详解】解:设未折断的竹干长为x 尺,根据题意可列方程为:2223(10)x x +=-.故答案为:2223(10)x x +=-.【考点】本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.2、.【解析】【分析】先作PC ⊥AB 于点C ,然后利用勾股定理进行求解即可.【详解】解:如图,作PC ⊥AB 于点C ,在Rt △APC 中,AP =50海里,∠APC =90°-60°=30°,∴1252AC AP ==海里,PC =在Rt △PCB 中,PC=BPC =90°-45°=45°,∴PC =BC =∴PB ==故答案为:【考点】此题主要考查了勾股定理的应用-方向角问题,求三角形的边或高的问题一般可以转化为用勾股定理解决问题,解决的方法就是作高线.3、3或6【解析】【分析】分两种情况分别求解,(1)当∠CED′=90°时,如图(1),根据轴对称的性质得∠AED =∠AED′=45′,得DE =AD =6;(2)当∠ED′A =90°时,如图(2),根据轴对称的性质得∠AD′E =∠D ,AD′=AD ,DE =D′E ,得A 、D′、C 在同一直线上,根据勾股定理得AC =10,设DE =D′E =x ,则EC =CD −DE =8−x ,根据勾股定理得,D′E 2+D′C 2=EC 2,代入相关的值,计算即可.【详解】解:当∠CED′=90°时,如图(1),∵∠CED′=90°,×90°=45°,根据轴对称的性质得∠AED=∠AED′=12∵∠D=90°,∴△ADE是等腰直角三角形,∴DE=AD=6;(2)当∠ED′A=90°时,如图(2),根据轴对称的性质得∠AD′E=∠D=90°,AD′=AD,DE=D′E,△CD′E为直角三角形,即∠CD′E=90°,∴∠AD′E+∠CD′E=180°,∴A、D′、C在同一直线上,根据勾股定理得10AC=,∴CD′=10−6=4,设DE=D′E=x,则EC=CD−DE=8−x,在Rt△D′EC中,D′E2+D′C2=EC2,即x2+16=(8−x)2,解得x=3,即DE=3;综上所述:DE的长为3或6;故答案为:3或6.【考点】本题考查了矩形的性质、勾股定理、轴对称的性质,熟练掌握矩形的性质、勾股定理、轴对称的性质的综合应用,分情况讨论,作出图形是解题关键.4、0.5【解析】【详解】结合题意可知AB=DE=2.5米,BC=1.5米,BD=0.5米,∠C=90°,(米).∵BD=0.5米,∴CD=2米,(米),∴AE=AC-EC=0.5(米).故答案为0.5.点睛:本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.5、5【解析】【分析】根据题意直接利用勾股定理得出杯子内的筷子长度,进而得出答案.【详解】解:由题意可得:15,则木筷露在杯子外面的部分至少有:20−15=5(cm ).故答案为5.【考点】此题主要考查了勾股定理的应用,正确得出杯子内筷子的长是解决问题的关键.三、解答题1、 (1)见解析(2)40【解析】【分析】(1)根据题目所给条件证()ABD ACE AAS ≌即可;(2)由ABD ACE △≌△可得10AB AC AD CD ==+=,由勾股定理可求BD ,即可求解;(1)证明:∵,CE AB BD AC ⊥⊥,∴90ADB AEC ∠=∠=︒,∵,AB AC A A =∠=∠,∴()ABD ACE AAS ≌.(2)解:∵ABD ACE △≌△,∴10AB AC AD CD ==+=,在Rt ABD △中,8BD ,∴111084022ABC S AC BD =⋅=⨯⨯=△.【考点】本题主要考查三角形的全等证明、勾股定理,掌握三角形的全等证明及性质是解题的关键.2、(1)见解析;(2)【解析】【分析】(1)根据平行可得∠DBE =90°,再由HL 定理证明直角三角形全等即可;(2)构造Rt AHE ,利用矩形性质和勾股定理即可求出AE 长.【详解】(1)∵AC ∥BE ,∴∠C +∠DBE =180°.∴∠DBE =180°-∠C =180°-90°=90°.∴△ABC 和△DEB 都是直角三角形.∵点D 为BC 的中点,12AC BC =,∴AC =DB . ∵AB =DE ,∴Rt △ABC ≌Rt △DEB (HL ).(2)AE =过程如下:连接AE 、过A 点作AH ⊥BE ,∵∠C =90°,∠DBE =90°.∴AC BH ∥,AH BC ∥,∴AH =BC =4, 122BH AC BC ===,∴2EH EB EH =-=,在Rt AHE 中,AE =【考点】本题主要考查了直角三角形全等的判定和勾股定理解三角形,解题关键是构造直角三角形,利用用平行线间的距离处处相等得线段AH =BC ,从而利用勾股定理求AE .3、见解析【解析】【分析】连接AM得到三个直角三角形,运用勾股定理分别表示出AD²、AM²、BM²进行代换就可以最后得到所要证明的结果.【详解】证明:连接MA,∵MD⊥AB,∴AD2=AM2-MD2,BM2=BD2+MD2,∵∠C=90°,∴AM2=AC2+CM2∵M为BC中点,∴BM=MC.∴AD2=AC2+BD2【考点】本题考查了勾股定理,三次运用勾股定理进行代换计算即可求出结果,另外准确作出辅助线也是正确解出的重要因素.4、84.【解析】【详解】解:作AD⊥BC于D,如图所示:设BD = x ,则14CD x =-.在Rt △ABD 中,由勾股定理得:2222215AD AB BD x =-=-,在Rt △ACD 中,由勾股定理得:()222221314AD AC CD x =-=--,∴2215x -=()221314x --,解之得:9x =.∴12AD =. ∴1·2ABC S BC AD ∆= 11412842=⨯⨯=. 5、见详解.【解析】【分析】利用4个直角三角形全等,根据=4+AEH ABCD EFGH S S S ∆正方形正方形列式,整理即可.【详解】证明:如图,AE BF CG DH a ====,AH DG CF BE b ====,HE EF FG GH c ====,∵=4+AEH ABCD EFGH S S S ∆正方形正方形,即()22142a b ab c +=⋅⋅+ ∴22222a ab b ab c ++=+,∴222+=a b c .【考点】本题考查了勾股定理的验证,运用拼图的方式,即利用两种不同的方法计算同一个图形的面积来验证勾股定理是解决本题的关键.。
勾股定理测试题及答案

勾股定理测试题及答案1. 计算下列直角三角形的斜边长度:a. 直角边长度分别为 3cm 和 4cmb. 直角边长度分别为 5cm 和 12cmc. 斜边长度为 10cm,直角边长度分别为 6cm 和 xcm2. 判断以下三角形是否为直角三角形,并说明理由:a. 三边长度分别为 3cm, 4cm, 5cmb. 三边长度分别为 8cm, 15cm, 17cmc. 三边长度分别为 7cm, 24cm, 25cm3. 已知一个直角三角形的斜边长度为 13cm,一条直角边长度为 5cm,求另一条直角边的长度。
4. 一个直角三角形的斜边和一条直角边的长度之比为 5:2,如果斜边长度为 20cm,求另一条直角边的长度。
答案1.a. 根据勾股定理,斜边长度等于两直角边长度的平方和的平方根。
因此,√(3² + 4²) = √(9 + 16) = √25 = 5cm。
b. 同样地,斜边长度为√(5² + 12²) = √(25 + 144) =√169 = 13cm。
c. 设另一条直角边长度为 y,则√(x² + 6²) = 10,解得 x²= 100 - 36 = 64,所以 x = 8cm。
2.a. 3² + 4² = 9 + 16 = 25,等于 5²,所以这是一个直角三角形。
b. 8² + 15² = 64 + 225 = 289,等于 17²,所以这也是一个直角三角形。
c. 7² + 24² = 49 + 576 = 625,不等于 25²,所以这不是一个直角三角形。
3. 设另一条直角边长度为 y,则根据勾股定理,5² + y² = 13²,解得 y² = 169 - 25 = 144,所以 y = 12cm。
八年级数学下册勾股定理习题(附答案)(含答案)

C勾股定理评估试卷(1)一、选择题(每小题3分,共30分)1. 直角三角形一直角边长为12,另两条边长均为自然数,则其周长为( ). (A )30 (B )28 (C )56 (D )不能确定2. 直角三角形的斜边比一直角边长2 cm ,另一直角边长为6 cm ,则它的斜边长(A )4 cm(B )8 cm (C )10 cm(D )12 cm3. 已知一个Rt △的两边长分别为3和4,则第三边长的平方是( ) (A )25(B )14(C )7(D )7或254. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) (A )13 (B )8 (C )25 (D )645. 五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )715242520715202425157252024257202415(A)(B)(C)(D)6. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )(A ) 钝角三角形 (B ) 锐角三角形 (C ) 直角三角形 (D ) 等腰三角形. 7. 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( ) (A ) 25 (B ) 12.5 (C ) 9 (D ) 8.5 8. 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( ) (A ) 等边三角形 (B ) 钝角三角形 (C ) 直角三角形 (D ) 锐角三角形.9.△ABC 是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°,AC=30米,AB=50米,如果要在这块空地上种植草皮,按每平方米草皮a 元计算,那么共需要资金( ). (A )50a 元 (B )600a 元 (C )1200a 元 (D )1500a 元 10.如图,A B ⊥CD 于B ,△ABD 和△BCE 都是等腰直角三角形,如果CD=17,BE=5,那么AC 的长为( ).(A )12 (B )7 (C )5 (D )135米3米(第10题) (第11题) (第14题)二、填空题(每小题3分,24分)11. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.12. 在直角三角形ABC 中,斜边AB =2,则222AB AC BC ++=______. 13. 直角三角形的三边长为连续偶数,则其周长为 .14. 如图,在△ABC 中,∠C=90°,BC=3,AC=4.以斜边AB 为直径作半圆,则这个半圆的面积是____________.(第15题) (第16题) (第17题) 15. 如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞___________米. 16. 如图,△ABC 中,∠C =90°,AB 垂直平分线交BC 于D若BC =8,AD =5,则AC 等于______________. 17. 如图,四边形ABCD 是正方形,AE 垂直于BE ,且AE =3,BE =4,阴影部分的面积是______.18. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A ,B ,C ,D 的面积之和为___________cm 2.EABCDBDE ABCD第18题图7cm三、解答题(每小题8分,共40分)19. 11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题:“小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树跟有多远?20. 如图,已知一等腰三角形的周长是16,底边上的高是4.求这个三角形各边的长.21. 如图,A 、B 两个小集镇在河流CD 的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A 、B 两镇供水,铺设水管的费用为每千米3万,请你在河流CD 上选择水厂的位置M ,使铺设水管的费用最节省,并求出总费用是多少?22. 如图所示的一块地,∠ADC=90°,AD=12m ,CD=9m ,AB=39m ,BC=36m ,求这块地的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理竞赛试卷(含解答)八年级数学《勾股定理》竞赛试卷(时间:120分钟,总分:120分)一、选择题(每小题5分,共25分)1、△ABC 周长是24,M 是AB 的中点MC=MA=5,则△ABC 的面积是( )A .12;B .16;C .24;D .302、如图,在正方形ABCD 中,N 是CD 的中点,M 是AD 上异于D 的点,且∠NMB=∠MBC ,则AM :AB=( ) A .31; B .33; C .21; D .63第(1)题图 第(2)题图第(3)题图3、如图,已知O 是矩形ABCD 内一点,且OA=1,OB=3,OC=4,那么OD 的长为( ) A.2; B.22; C.23; D.34、如图,P 为正方形ABCD 内一点,PA=PB=10,并且P 点到CD 边的距离也等于10,那么,正方形ABCD 的面积是( )A .200;B .225;C .256;D .150+1025、如图,矩形ABCD 中,AB=20,BC=10,若在AB 、AC 上各取一点N 、M ,使得BM+MN 的值最小,这个最小值为( ) A .12; B .102; C .16; D .20二、填空题(每小题5分,共25分) 第(5)题图6、如图,△ABC 中,AB=AC=2,BC 边上有10个不同的点1021,,P P P ,记C P B P AP M i i i i ⋅+=2(i = 1,2,……,10),那么, 1021M M M +++ =_________。
(6)题图7、如图,设∠MPN=20°,A为OM 上一点,OA=43,D 为ON 上一点,OD=83,C 为AM 上任一点,B 是OD 上任意一点,那么折线ABCD的长最小为__________。
第(7)题图第(8)题图8、如图,四边形ABCD 是直角梯形,且AB=BC=2AB ,PA=1,PB=2,PC=3,那么梯形ABCD 的面积=__________。
9、若x + y = 12,那么9422+++y x 的最小值=___________。
10、已知一个直角三角形的边长都是整数,且周长的数值等于面积的数值,那么这个三角形的三边长分别为____________。
三、解答题(共70分)11、(本题10分)如图△ABC 三边长分别是BC=17,CA=18,AB=19,过△ABC 内的点P 向△ABC 三边分别作垂线PD ,PE ,PF ,且BD+CE+AF=27,求BD+BF 的长度。
12、(本题15分)如图,在△ABC 中,AB=2,AC=3, ∠A=∠BCD=45°,求BC 的长及△BDC 的面积。
13、(本题15分)设a,b,c,d 都是正数。
求证:ad d b a c b cd d c a 2222222222+++>+++++14、(本题15分)如图,四边形ABCD 中, ∠ABC=135°,∠BCD=120°,AB=6,BC=5-3,CD=6,求AD 。
15、(本题15分)如图,正方形ABCD 内一点E ,E 到A 、B 、C 三点的距离之和的最小值为62+,求此正方形的边长。
答案一、选择题 1.C 2.A 3.B 4.C 5.C 解答:1.∵MA=MB=MC=5, ∴∠ACB=90°知周长是24,则AC+BC=14,AC 2+BC 2=102,∴2AC ·BC=(AC+BC)2-(AC 2+BC 2) = 142-102=4×24 ∴2421=⋅=∆BC AC S ABC2.如图,延长MN 交BC 的延长线于T ,设MB 的中点为O ,连TO ,则△BAM ∽△TOB∴AM :MB=OB :BT∴MB 2=2AM ·BT (1)令DN=1,CT=MD=k ,则AM=2 – k 所以BM=222)2(4k AM AB -+=+BT= 2 + k 代入(1),得4 + (2 – k )2= 2 (2 – k ) (2 + k ) 所以 k = 34所以AM :AB=32:2 = 313.如图,过O 作EF ⊥AD 于E ,交BC 于F ;过O 作GH ⊥DC 于G ,交AB 于H设CF=x ,FB = y, AH = s, HB = x, 所以OG=x, DG = s所以OF 2=OB 2- BF 2=OC 2-CF 2 即42- x 2=32- y 2所以x 2- y 2= 16 – 9 =7 (1) 同理有OH 2=12- s 2= 32- t 2 所以t 2- s 2= 32- 12= 8 (2) 又因为OH 2+HB 2=OB 2 即y 2+ t 2= 9(1)-(2)得(x 2+s 2) – (y 2+ t 2) = – 122222 所以OD 2=x 2+ s 2= (y 2+ t 2) – 1 = 9 – 1 = 8 所以OD=224.如图,过P 作EF ⊥AB 于E ,交CD 于F ,则PF ⊥CD所以PF=PA=PB=10,E 为AB 中点 设PE = x ,则AB=AD=10 + x 所以AE=21AB=21(10 + x)在Rt △PAE 中,PA 2=PE 2+AE 2所以102= x 2+ [21(10 + x )]2 所以x = 6所以正方形ABCD 面积=AB 2=(10 + 6)2 = 256 5.如图,作B 关于AC 的对称点B ',连A B ',则N 点关于AC 的对称点N '在A B '上, 这时,B 到M 到N 的最小值等于B →M →N '的最小值,等于B 到A B '的距离BH ',连B 与A B '和DC 的交点P ,则ABP S ∆=21×20×10=100,由对称知识,∠PAC=∠BAC=∠PCA所以PA=PC , 令PA=x ,则PC=x ,PD=20 – x , 在Rt △ADP 中,PA 2=PD 2+AD 2所以 x 2 = (20 – x )2 + 102 所以 x = 12.5 因为ABP S ∆=21PA ·BH '所以BH '=165.1221002=⨯=∆PAS ABP二、填空题 1.40; 2.12; 3.223415+;4.13;5.6,8,10或5,12,13 解答:1.如图,作AD ⊥BC 于D ,在Rt △ABD 和Rt △AP i D 中,AB 2=AD 2+BD 2222D P AD AP i i +=所以22222)(D P AD BD AD AP AB i i +-+=-BP C P D P BD D P BD D P BD i i i i i ⋅=-+=-=))((22所以422==⋅=AB B P C P AP i i i 所以4=i M所以401021=+++M M M1.如图,作A 关于ON 的对称点A ',D 关于OM 的对称点D ',连结A 'B ,CD ',则A 'B=AB ,C 'D=CD ,从而AB+BC+CD=A 'B+BC+CD '≥A 'D '因为∠A 'ON=∠MON=∠MOD '=20°,所以∠A 'OD '=60°又因为OA '=OA=43,OD '=OD=83,所以OD '=2OA '即△OD 'A '为直角三角形,且∠OA 'D '=90° 所以A 'D '=12)34()38(222'2'=-=-OA OD所以,折线ABCD 的长的最小值是12 3.如图,作PM ⊥AB 于M ,PN ⊥BC 于N , 设AB = m, PM = x, PN = y ,则⎪⎩⎪⎨⎧=+-=-+=+)3(9)()2(1)()1(4222222y x m y m x y x 由(2)、(3)分别得,12222=+-+y my m x (3) 92222=+-+x mx m y (4)将(1)代入(4)得;2303222mm y my m +=⇒=+- 将(1)代入(5)得;2505222mm x mx m -=⇒=-- 把x,y 的表达式分别代入(1)得0171024=+-m m 因为m 2>0 所以m 2=5+22所以 AB=22521,225,225+=+=+=AD BC m 所以223415)(21+=⋅+=AB BC AD S ABCD4.如图,AB=12,AC=2,BD=3,且AB ⊥AC ,AB ⊥BD ,P 在AB 上且PA=x ,PB=y ,连PC ,PD ,在Rt △CAP 和Rt △DBP 中9,4222222+=+=+=+=y PB BD PD x PA AC PC如图,P 点在0P 位置时,PC+PD 的值最小,为线段CD 的长度,而 CD=1312)32(22=++13。
所以9422+++y x 的最小值为5.设三边长为a,b,c ,其中c 是斜边,则有⎪⎩⎪⎨⎧=++=+)3(2)1(222ab c b a c b a (2)代入(1)得222)2(b a ab b a --=+ 即0)844(4=+--b a ab ab 因为ab ≠0 所以ab – 4a – 4b + 8 = 0所以484-+=b a (a,b 为正整数)所以b – 4 = 1,2,4,8,所以b = 5,6,8,12;a = 12,8,6,5;c = 13,10,10,13,所以,三边长为6,8,10或5,12,13三、解答题1.如图,连结PA,PB ,PC ,设BD=x ,CE=y ,AF=z ,则DC=17-x ,EA=18 – y ,FB = 19 –z在Rt △PBD 和Rt △PFB 中,有2222)19(PF z PD x +-=+同理有:22222222)18()17(PE y PF z PD x PE y +-=++-=+将以上三式相加,得222222)19()18()17(z y x z y x -+-+-=++即17x + 18y + 19z = 487又因为x + y + z = 27,所以x = z – 1,所以BD + BF = x + (19 – z ) = z – 1 + 19 – z = 18 2.如图,作CE ⊥AB 于E , 则CE=AE=2622=AC 所以BE=AB-AE=2 -26426-= 又222BE CE BC +=所以BC=1662722-=-=+BE CE再过D 作DF ⊥BC ,交CB 延长线于F ,并设DF=CF=x ,则BF= x – BC = x + 1 -6 又Rt △DFB ∽Rt △CEB ,所以DF :BF=CE :BE ,即x :(x + 1 -6) = 264:26- 所以x = 2623+所以4692623)16(2121+=+⨯-⨯=⋅=∆DF BC S BCD 2.如图,构造一个边长为(a + b)、(c + d)的矩形ABCD ,在Rt △ABE 中,BE=22AB AE + 所以BE=cd d c a d c a 2)(22222+++=++在Rt △BCF 中,BF=ab d b a d b a CF BC 2)(2222222+++=++=+在R t △DEF 中,EF=2222c b DF DE +=+在△BEF 中,BE+EF>BF 即ab d b a c b cd d c a 2222222222+++>+++++3.如图,过A 作AE ∥BC 交CD 于E ,则∠1=45°,∠2=60°, 过B 作BF ⊥AE 于F ,作CG ⊥AE 于G ,则Rt △ABF 为等腰直角三角形,BCFG 为矩形,又因为AB=6,BC=5-3,所以BF=AF=22AB=3,所以CG=BF=3,所以CE=32CG=2,EG=31CG=1所以AE=AF+FG+GE=AF+BC+GE=6DE=CD-EC=6-2=4过D 作DM ⊥AE 延长线于M∠MED=180°-∠AED=180°-∠BCD=180°-120°=60°所以EM=21DE=2,DM=23DE=23在Rt △AMD 中,AD=192)32()26(2222=++=+DM AM5.如图,以A 为中心,将△ABE 旋转60°到△AMN ,连NB ,MB ,则AE+EB+EC=AN+MN+EC因为AE=AN ,∠NAE=60°所以AE=NE所以AE+EB+EC=MN+NE+EC当AE+EB+EC 取最小值时,折线MNEC 成为线段,且MC=62+,∠MBC=150°在Rt △PMC 中,设BC=x ,PM=x PB x 23,2= 所以222)23()2()62(x x x ++=+ 所以x = 2, BC=2。
