第四章 地下水向完整井的稳定运动
地下水动力学习题

地下水动力学习题————————————————————————————————作者: ————————————————————————————————日期:ﻩ常见思考题A.填空及判断题第一章 渗流理论基础§1.1 渗流的基本概念一、填空题:1. 地下水动力学是研究地下水在________、________、和____________、中运动规律的科学,通常把_________ __________称为多孔介质,而其中的岩石颗粒称为_____。
多孔介质的特点是________、______、_______________和_______。
2. 地下水在多孔介质中存在的主要形式有______、______、______和______,而地下水动力学主要研究______的运动规律。
3.在多孔介质中,不连通的或一端封闭的孔隙对地下水运动来说是________,但对贮 ①(编者认为应称为渗流速度,但考虑到习惯用语,故书中仍沿用渗透速度。
)水来说却是______。
4·假想水流的_______、_______、___________________ 以及 ___________、都与真实水流相同,假想水流充满________________。
5.地下水过水断面包括________和___________所占据的面积。
渗透速度是____上的平均速度,而实际速度是_______________的平均速度。
6.在渗流中,水头一般是指__________,不同数值的等水头面(线)永远_________。
7.在渗流场中,把大小等于__________,方向沿着_______的法线,并指向水头_____方向的矢量,称为水力坡度。
水力坡度在空间直角坐标系中的三个分量分别为__________、___________和_________。
8.渗流运动要素包括______、_______、______和_______等等。
水文地质-地下水的运动
第三节 地下水向井的稳定运动
四、裘布依公式的讨论
(2)抽水井流量与井径的关系
但实际情况远非如此,井径 对流量的影响比Dupuit公 式反映的关系要大得多。
第三节 地下水向井的稳定运动
四、裘布依公式的讨论
(3)水跃对裘布依公式计算结果的影响
在潜水的出口处一般都存 在渗出面。当潜水流入井 中时也存在渗出面,也称水 跃,即井壁水位hs高于井 中水位hw(图4一10),而潜 水井的Dupuit公式并没有 考虑渗出面的存在。
H Z p
图4-5 流网示意图
在渗流场中,把水头值相等的点连成线或面就构成了等水 头线或等水头面。
流网是由等水头线和流线所组成的正交网格。流网直观地 描述了渗流场(或流速场)的特征。它可以是正方形、长 方形或曲边方形。
第二节 地下水运动规律
水流类型
一维流任意点的水力坡度均相等(
图4-6a);
s1=1.00 m s2=1.75 m s3=2.50 m 求K?
Q1=4500 m3/d; Q2=7850 m3/d; Q3=11250 m3/d;
第三节 地下水向井的稳定运动
五、地下水流向非完整井和直线边界附近的完整井
1、承压水非完整井 当α=1时,A=0,就变成 完整井公式,当α很小, A值很大,则公式变为:
第三节 地下水向井的稳定运动
五、地下水流向非完整井和直线边界附近的完整井
2、潜水非完整井 潜水非完整井可以看做上段 是潜水完整井,下段是承压 水非完整井。这样可以近似 的看做总流量Q等于两段Q1 和Q2的和。
第三节 地下水向井的稳定运动
裘布衣假设:
天然水力坡度为0,井附近水力坡度<1/4; 含水层是均质各向同性的,含水层的底板
地下水动力学(第四章_地下水向完整井的非稳定运动-2-专)

s s t s 1 2 lg t t lg t lg t t lg t lg t lg t lg t t 2 * 2.3Q r Tt 2 4Tt * B e 2.3t t 4T 2s
r B B
2. 拐点法 (1)原理 r 2* Tt ① 拐点的斜率 * 2 s Q 1 4Tt B e 前面,水头下降速度中,给出 t 4T t 则 r Tt
s s lg t Q 1 e t lg t t 4T t
2. 水头下降速度 r 2* Tt * 2 s Q 1 4Tt B e t 4T t 前面推出无越流时的公式:
s Q 1 e t 4T t
r 2* 4Tt
相比,越流含水层水位下降速度比无越流含水层慢。 当t足够大时,
s Q t 4Tt
s 2.3Q e lg t 4T
r 2* Tt * 2 4Tt B
将此二式代入得: 得
s 2.3Q B e lg t p 4T
r
即拐点处的斜率为:
2.3Q ip e 4T
r B
② 拐点处降深
Q r 1 sp K 0 s max 4T B 2
r 0
lim r
s , t Q r 2T
下弱透水层:
2 s2 * s T2 2 2 2 z t s2 r,z, 0 0 s2 r, ,t 0 0 s2 r,m2,t s r,t
水文地质第四章1

3、当抽水井是建在无充分就地补给(无定 水头)广阔分布的含水层之中。若观测孔中 的s值在s-lgr曲线上能连成直线,则可根据 观测井的数据用裘布依型公式来计算含水层 的渗透系数
4、在取水量远小于补给量的地区,可以先 用上述方法求得含水层的渗透系数,然后 再用裘布依公式大致推测在不同取水量的 情况下境内及附近的地下水位降值
只有当雷诺数小于1~10时地下水运动才服 从达西公式。 大多情况下地下水的雷诺数一般不超过1; 例如,地下水以u=10m/d的流速在粒径为 20mm的卵石层中运动,卵石间的孔隙直径 为3mm(0.003m),当地下水温为15℃时, 运动粘滞系数γ=0.1m2/d,则雷诺数为?
(二)非线性渗透定律
当地下水在岩石的大孔隙,大裂隙,大溶洞中及取 水构筑物附近流动时,Re>10,紊流。 紊流运动的规律称为谢才公式(哲才公式)
D、地下水径流从水位高处向低处流动
达西定律要满足条件为( ) A、地下水流的雷诺数Re<1~10 B、地下水流的雷诺数1~10<Re<20~60 C、地下水流的雷诺数Re>20~60 D、地下水流的雷诺数可以为任何值
一潜水含水层均质,各向同性,渗透系数 为15m/d,其中某过水断面A的面积为 100m2,水位为38m,距离A断面100米的 断面B的水位为36m,则断面A的日过流量 是( )m3
裘布依公式推导的假设条件
1、水力坡度:天然水力坡度等于零,抽水时为了 用流线倾角的正切代替正弦,则井附近的水力坡 度不大于1/4。 2、含水层是均质各向同性的,含水层的底板是隔 水的。 3、边界条件:抽水时影响半径的范围内无入渗, 无蒸发,每个过水断面上流量不变;在影响半径 范围以外的地方流量为零;在影响半径的圆周上 为定水头边界。 4、抽水井内及附近都是二维流(即抽水井内不同 深度处的水头降低是相同的。
《地下水动力学》课程总结

求水文地质参数
K、T、μ、μ*、B…
计算运动要素
Q、q、H、s、t….
模型识别
判断水文地质条件 如边界性质
1、介质(为描述介质特性提出的一些概念)
连续介质模型-典型单元体 渗透性:
渗透系数(K)、等效渗透系数 均质、非均质 各向同性、各向异性
2、渗流场
渗流特征 运动要素:实际流速、渗透流速、质点流速、单个孔隙
5、水文地质参数及获取方法
渗透系数K 入渗强度W 导水系数T=KM 弹性释水系数μ* 给水度μ 阻越流系数B 压力传导系数a =T/ μ*
配线法 直线图解法 水位恢复资料法
1、达西定律
dH Q = -KA
ds
dH v = -K
ds
适用条件:1<Re<10的层流
2、 Dupuit假定,Dupuit微分方程
Kz
∂ ∂z
s(r, H 0 ,t )
=
-μ
∂ ∂t
s(r, H 0 ,t )
方程解析解
s(r, z, t) Q
4 T
1
0
4
yJ 0
(
y
2
)[ 0
(
y)
n ( y)]dy
n 1
• 纽曼解的特点
5、地下水向不完整井的运动
• 不完整井流特点(三点)
• 地下水向不完整井的稳定运动
井底进水的承压水不完整井(空间汇点法)
井壁进水的承压水不完整井(空间汇线法)
∫ Q
s = 4πK(z2 - z1)
[z2
1
+
z1 (z - η)2 +r 2
1
]dη
(z + η)2 +r 2
地下水向完整井的稳定流动
地下水动力学
第三章 地下水向完整井的稳定运动
在三种常见水文地质条件下,推广应用Dupuit公式 (1)巨厚含水层中的潜水井
当井中降深H0-hw<<H0时,H0+hw≈2H0
地下水动力学
第三章 地下水向完整井的稳定运动
设距潜水井r1,和r2处的降深分别为s1和s2:
修正降深 公式同承压水
地下水动力学
地下水动力学
第三章 地下水向完整井的稳定运动
§3一3 非线性流情况下的地下水向完整井的稳定运动
在少数情况下,地下水不服从Darcy定律,其流动 是非线性的
一、承压水井 当地下水运动服从Chezy公式时
分离变量,在井壁和任意r断面之间积分,得:
地下水动力学
第三章 地下水向完整井的稳定运动
当地下水运动服从式J=av+bv2时,有:
因此,井管外面的水头高于井管内部的水头。
地下水动力学
第三章 地下水向完整井的稳定运动
过滤器周围填砾的井(gravel-packed well) 井周围的降深比未填砾时要小。 此时,井损仍然存在,如井径 仍用过滤器直径会造成较大的 计算误差。因此,引进了有效 井半径的概念。有效井半径是 由井轴到井管外壁某一点的水 平距离。在该点,按稳定流计 算的理论降深正好等于过滤器 外壁的实际降深。
地下水动力学
第三章 地下水向完整井的稳定运动
§3一2 地下水向承压水井和潜水井的稳定流动
一、承压水井的Dupuit公式 可以把在无限含水层中的抽水情况设想为一半径为R的 圆形岛状含水层的情况。岛边界上的水头H0保持不变。 水流有如下特征: ①水流为水平径向流,即流线为指向井轴的径向直线, 等水头面为以井为共轴的圆柱面,并和过水断面一致; ②通过各过水断面的流量处处相等,并等于井的流量。
地下水动力学(周志芳,王锦国编著)PPT模板

0 3 3.1.3非线性流情况下的地下水向完 整井的稳定运动
0 4 3.1.4越流含水层中地下水向承压水 井的稳定流动
0 5 3.1.5地下水向干扰井群的稳定运动
0 6 3.1.6井损与有效井径及其确定方法
第三章井附近 的地下水运动
3.2地下水向完整井的非稳定运 动
3.2.2有越流 补给的完整 井流
3.2.1承压含 水层中的完 整井流
3.2.3潜水完 整井流的 Boulton模型
第三章井附近 的地下水运动
3.3地下水向边界附近完整井的运 动
3.3.1镜像法原 理及直线边界
附近的井流
01
3 . 3 . 3 条 形 03 含水层中的
井流
02 3 . 3 . 2 扇 形 含水层中的 井流
第三章井附近的地下水运动
第一章地下水 运动基础
第一章地下水运动基础
1.1地下水运动的基本 概念
1.3流体运动的描述方 法
1.5地下水运动的控制 方程
1.2渗流基本定律
1.4流网
1.6地下水运动的数学 模型及其求解方法
第一章地下水运动基础
1.1地下水运动的基本概念
A
1.1.1多孔 介质中的
地下水
B
1.1.2地下 水和多孔 介质的性
第三章井附近 的地下水运动
第三章井附近的地 下水运动
3.1地下水向完整井的稳定运动 3.2地下水向完整井的非稳定运动 3.3地下水向边界附近完整井的运动 3.4地下水向不完整井的运动
第三章井附近 的地下水运动
3.1地下水向完整井的稳定运 动
0 1 3.1.1概述 0 2 3.1.2地下水向承压水井和潜水井的
2.1河渠间地下水的稳定运 动
3地下水向完整井的稳定运动
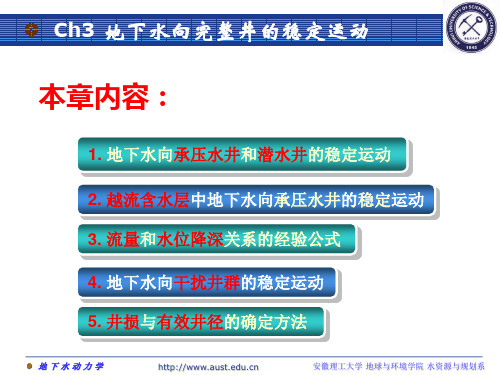
Q r2 H 2 H1 s1 s2 ln 2KM r1
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch3 地下水向完整井的稳定运动
6、承压水头分布方程(降落曲线方程):
Q R ln 联立求解方程: H 0 hw 2KM rw
安徽理工大学 地球与环境学院 水资源与规划系
Ch3 地下水向完整井的稳定运动
三、Dupuit公式的推广
1、巨厚含水层中的潜水井
H 0 hw
2 2
Q R ln K rw
Q R H 0 hw ln K ( H 0 hw ) rw
当井中降深H0-hw<<H0时,H0=hw,H0+hw=2H0,于是得近似式:
安徽理工大学 地球与环境学院 水资源与规划系
Ch3 地下水向完整井的稳定运动
3、潜水井Dupuit公式的推导过程
d dh2 r 0 dr dr h rR H 0 h r r hw
w
① 积分:
dh r C1 dr
2
② 通过任一断面的流量相等,并等于 抽水井的流量Q,由Darcy定律:
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch3 地下水向完整井的稳定运动
4、有一个观测孔时:
距抽水井中心r处有一个观测孔,水位为H,在rw和r两断面间积分得:
Q r H hw sw s ln 2KM rw
5、有两个观测孔时(承压水井的Thiem公式):
有两个观测孔距抽水井中心的距离分别为r1和r2,水位分别为H1和H2, 在r1和r2两断面间积分得:
Q 1 dr 2KM r H0 R1 Q hw dH 2KM rw r dr Q R H 0 hw ln 2KM rw sw Q R ln 2KM rw
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 地下水向完整井的稳定运动
一、名词解释
1. 潜水完整井:贯穿整个潜水层,在全部潜水层上都安装过滤器,并能全面进水的水井。
2. 承压不完整井:不完全贯穿,没有完全揭露承压含水层,只有井底和部分含水层能进水的水井。
3. 降深:从井中抽水,井周围附近含水层的水流入井中,井中和井附近的水位将降低,水位降低值称为水位降深,简称降深。
4. 井损:井管外面的水通过过滤器的孔眼进入井内造成的水头损失和井管内部水向上运动至水泵吸水口的途中造成的水头损失,两者统称为井损。
5. 有效井半径:有限井半径是从井轴到井管外壁某一点的水平距离。
在该点上,按稳定流理论计算的降深等于过滤器外壁的实际降深。
7. 叠加原理:如H1,H2,……,Hn 是关于水头H 的线性偏微分方程的特解,C1,C2,……,Cn 为任意常数,则这些特解的线性组合:∑==n
i i i H C H 1,也是该
非齐次方程的解。
8. 干扰井:各井之间的距离小于影响半径时,彼此的降深和流量会发生干扰,这样的井称为干扰井。
二、填空题
1. 根据揭露含水层的厚度和进水条件,抽水井可分为完整井和非完整井两类。
2. 承压水井和潜水井是根据水井所揭露的含水层类型来划分的。
3. 从井中抽水时,水位降深在井中心处最大,而在降落漏斗的边缘处最小。
4. 对于潜水稳定井流,抽出的水量主要等于降落漏斗的体积乘以给水度;而对于承压水井,抽出的水量则等于降落漏斗的体积乘以弹性贮水系数。
5. 对潜水井来说,测压管进水口处的水头不等于测压管所在地的潜水位。
6. 填砾的承压完整抽水井,其井管外面的测压水头要高于井管里面的测压水头。
7. 地下水向承压水井稳定运动的特点是:流线为指向井轴的径向直线;等水头面为以井为共轴的圆柱面;各断面流量相等。
8. 由于裘布依公式没有考虑渗出面的存在,所以,仅当r>H 0时,用裘布依公式计算的浸润曲线才是准确的。
9. 在承压含水层中进行稳定流抽水时,通过距井轴不同距离的过水断面上流量处处相等,且都等于井的流量 。
12. 常见的Q ~Sw 曲线类型有直线型、抛物线型 、幂函数曲线数型和对数曲线型四种。
14. 在均质各向同性含水层中,如果抽水前地下水面水平,抽水后形成对称 的降落漏斗;如果地下水面有一定的坡度, 抽水后则形成不对称 的降落漏斗。
15. 在承压水井中抽水,当Q 较小时,井损可以忽略不计;而当大流量抽水 时,井损在总降深中占有很大的比例。
三、判断题
1. 在安装过滤器的承压含水层中抽水时,井壁内外水位不同的主要原因是由于存在井损的缘故。
(√)
2. 抽水井附近渗透性的增大会导致井中及其附近的水位降深也随之增大。
(×)
3. 无论是潜水井还是承压水井都可以产生水跃。
(×)
4. 在无补给的无限含水层中抽水时,水位永远达不到稳定。
(√)
5. 潜水井的流量和水位降深之间是二次抛物线关系。
这说明,流量随降深的增大而增大,但流量增加的幅度愈来愈小。
(√)
6. 按裘布依公式计算出来的浸润曲线,在抽水井附近往往高于实际的浸润曲线。
(×)
7. 由于渗出面的存在,裘布依公式中的抽水井水位Hw 应该用井壁外水位Hs 来代替。
(×)
8. 对越流含水层中的稳定井流来说,抽水量完全来自井附近的越流补给量。
(√)
9. 可以利用降深很小时的抽水试验资料所建立的Q-Sw 关系式来预测大降深时的流量。
(×)
10. 井损随水井抽水量的增大而增大。
(√)
四、计算题
1. 某承压含水层中有一口直径为0.20 m 的抽水井,在距抽水井527 m 远处设有一个观测孔。
含水层厚5
2.20 m ,渗透系数为11.12 m/d 。
试求井内水位降深为
6.61 m ,观测孔水位降深为0.78 m 时的抽水井流量。
1、解:
()()d /15.24811
.0527ln 78.061.620.5212.112ln 2ln 23m r r s s KM Q r r KM Q s s w w w w =-⨯⨯⨯⨯=-=⇒=-πππ
2. 在厚度为27.50 m 的承压含水层中有一口抽水井和两个观测孔。
已知渗透系数为34 m/d ,抽水时,距抽水井50 m 处观测孔的水位降深为0.30 m 、110 m 处观测孔的水位降深为0.16 m 。
试求抽水井的流量。
2、解:
()()d m r r s s KM Q r r KM Q s s /14.104350
110ln 16.030.050.27342ln 2ln 2312211221=-⨯⨯⨯⨯=-=⇒=-πππ
3. 某潜水含水层中的抽水井,直径为200 mm ,影响半径为100 m ,含水层厚度为20 m ,当抽水量为273 m 3/d 时,稳定水位降深为2 m 。
试求当水位降深为5 m 时,未来直径为400 mm 的生产井的涌水量。
3、解:(1)计算含水层的渗透系数
()()d m r R s s H Q K w w /90.71
.0100ln 22202273ln 2w 0=⨯⨯-⨯=-=ππ (2)计算涌水量
()()d m r R
K s s H Q w w /73.6982.0100ln 90.755202ln 23w 0=⨯⨯⨯-⨯=-=π
π
4. 设承压含水层厚13.50 m ,初始水位为20 m ,有一口半径为0.06 m 的抽水井分布在含水层中。
当以1080 m 3/d 流量抽水时,抽水井的稳定水位为17.35 m ,影响半径为175 m 。
试求含水层的渗透系数。
4、解:
()()d m r R h H M Q K r R KM Q s h H w w w w w /33.3806.0175ln 35.172050.1321080ln 2ln 200=-⨯⨯⨯=-=⇒=
=-πππ。
