固体物理第三章2
固体物理-第三章 金属自由电子论讲解

3.1.量子自由电子理论
I2=(1/2!)-(E-EF)2(-f/E) dE 不难算出, I0=1(d-函数积分), I1=0 (根据d-函数的性质) 为了计算I2, 而令h=(E-EF)/kBT,于是, I2=[(kBT)2/2]-{h2/[(eh+1)(e-h+1)] }dh=(pkBT)2/6
波长),可见k为电子的波矢, 是3 维空间矢量. r:电 子的位置矢量。
由波函数的归一化性质:vy*(r) y(r)d(r)=1, v:金属体积, 假设为立方体,边长为L,把3.1.1.3式 代入归一化式子, 得: A=L-3/2=V-1/2, 所以
y(r)= V-1/2eik•r 3.1.1.4, 此即自由电子的本征态。 由周期性边界条件, y(x,y,z)= y(x+L,y,z) = y(x,y+L,z) = y(x,y,z+L)
一状态的电子具有确定的动量ħk和能量ħ2k2/(2m),因而 具有确定的速度,v=ħk/m,故一个k全面反映了自由电子 的一个状态,简称态。
2. k-空间
以kx, ky , kz 为坐标轴建立的 波矢空间叫k-空间。电子的 本征态可以用该空间的一点
来代表。点的坐标由3.1.1.5 式确定。
3.1.量子自由电子理论
T>0K的费米能EF 把3.1.2.2和3.1.3.1代入3.1.3.2, 分步积分, 得:
N= (-2C/3) 0 E3/2(f/E) dE 3.1.3.3 令G(E)= 2C E3/2/3, 3.1.3.3.式化简为 N= 0G(E) (-f/E) dE 3.1.3.4 (-f/E)函数具有类似d函数的特性,仅仅在EF附近kBT范 围内才有显著的值,且为E-EF偶函数. 由于(-f/E)函数 具有这些性质,把G(E)在EF附近展开为泰勒级数, 且积分 下限写成 -,不会影响积分值. 3.1.3.4化为:
《固体物理·黄昆》第三章

氢键结合的情况可写成通式:
X-H…Y。 式中 X 、 Y 代表 F 、 O 、 N 等电负 性大而原子半径较小的非金属原 子, X 和 Y 可以是两种相同的元 素,也可以是两种不同的元素。 d F l H F H F
归纳起来,氢键形成的条件是:
A)有与电负性大(X)的原子相结合的氢原子;
B) 有一个电负性也很大,含有孤对电子并带有部分负 电荷的原子(Y); C)X与Y的原子半径都要较小。
氯化钠型 —— NaCl、KCl、AgBr、PbS、MgO (配位数6) 氯化铯型 —— CsCl、 TlBr、 TlI(配位数8)
离子结合成分较大的半导体材料ZnS等(配位数4)
2. 离子晶体结合的性质
1) 系统内能的计算 晶体内能 : 1)所有离子库仑相互作用能(吸引作用)
2) 和重叠排斥能之和(排斥作用)
具体晶体的内聚能(晶格能)参见周期表,有一定的规律性: 惰性气体晶体<碱金属<过渡族金属(共价晶体)
两粒子间的相互作用 相互作用能.
f(r) 和u(r)分别表示相互 作用力和相互作用势 则:
u (r ) f (r ) r
U 排斥 r
f (r )
B rn
u (r )
pij A12= j'
12
12.13188
pij A6= j'
6
14.45392
物理意义:
晶体总的势能:
—— 非极性分子晶体的晶格常数、结合能和体变模量 晶格常数
平衡状态体变模量
晶体的结合能
分子晶体: 常温下是气态的物质如:Cl2,SO2,HCl, H2, O2, He, Ne, Ar, Xe等在低温下依靠范德瓦耳斯力结合成的晶体.
(完整版)固体物理胡安第三章课后答案

3.1 在单原子组成的一维点阵中,若假设每个原子所受的作用力左右不同,其力常数如图所示相间变化,且21。
试证明在这样的系统中,格波仍存在着声频支和光频支,其格波频率为21221221212)2(sin 411M)(qa 证明:第2n 个原子所受的力121122221212121222)()()(n nn n nn nnuu u u u u u F 第2n+1个原子所受的力nn n n nn nnu u u u u u u F 22121122112221222112)()()(这两个原子的运动方程:212222112121122112222()()n n n n nn n nmu u u u mu u u u &&&&方程的解qan t inqan t in Beu Aeu 2)12(122)2(2代入到运动方程,可以得到BA e eBmAB eeAmqaiqa iq a i q a i )()(21222122122212经整理,有)()(22122212221221B mA eeB eeAmqa iqa iqa iq ai 若A ,B 有非零解,系数行列式满足22212122221212,,aai q i q a a i q i q me eee m根据上式,有21221221212)2(sin 411M)(qa 3.3(a) 设单原子链长度L=Na波矢取值2qhNa每个波矢的宽度2qNa,状态密度2Na dq 间隔内的状态数2Nadq ,对应±q ,ω取相同值因此22Na dqdq一维单原子链色散关系,4sin 2aqm 令4,sin2aq m两边微分得到cos22aaq ddq将220cos12aq 代入到0cos22aaq ddq22222,2a dq ddq da频率分布函数2222122122Na NaN dadq3.4三维晶格振动的态密度为3(2)V 根据态密度定义3()(2)|()|qV dS q r =对2qAq两边微分得到2d q Aqdq在球面上2qd Aq dq,半径01qA代入到态密度函数得到21/23323/2144,2422qV qV AV AAAq最小截止频率m001/223/234mmV dd NA可得2/32min 06N AV所以1/2min 023/2,4VA在0min或时,是不存在频率ω的分布的,也就不会有频率分布的密度。
固体物理第三章1-2

小振动,U(r)与U(a) 差别不大,在平衡位置泰勒级数展开:
3 1 d 2U 1 d U dU 2 3 U ( r ) U a r a 2 r a 3 r a ...... 2 dr a 6 dr a dr a
A 2 1 2 2 Mm 2 1 2 O 2 Mm
1 2 16 Mm qa 2 2 1 2 ( M m ) ( M m ) sin 2 ( ) 2 1 2 1 2 16 Mm qa 2 2 1 2 ( M m ) ( M m ) sin 2 ( ) 2 1 2
与单原子一维晶格类似:上述方程具有下述格波形式解
2n i q a t 2
u2 n Ae
Ae
i ( qnat )
u2 n1 B' e
2n i q( )a qbt 2
Be
i ( qnat )
U2n / u2n+1表示同一原胞中两种不等价原子的位移
相互作用力:
r = un+1 + a -un
2 1 d 3U dU d U 2 r a r a ...... f ( r ) 2 3 2 dr a dr a dr a
= 0
(d2U/dr2)a =
玻恩—卡门边界条件下平衡位置运动方程组的通解:
un Ae
i ( qnat )
A为振幅,是圆频率,qna是第n个 原子在t=0时刻的振动相位
《固体物理基础》晶格振动与晶体的热学性质

一、三维简单格子
二、三维复式格子
三、第一布里渊区
四、周期性边界条件
◇一个原胞内有P
个不同原子,则
有3P个不同的振
动模式,其中3支 声学波。
◇具有N个原胞的 晶体中共有3PN个
振动模式,其中
3N个声学波, 3N(P-1)个光学波。
四、周期性边界条件 总结
§ 3.4 声子
声子:晶格振动中格波的能量量子
二、一维单原子链的振动
格波
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
周期性边界条件
玻恩—卡曼边界条件
二、一维单原子链的振动
周期性边界条件
即q有N个独立的取值—晶格中的原胞数第一布
◇非弹性X射线散射、非弹性中子散射、可见光 的非弹性散射。
§ 3.4 声子
§ 3.4 声子
90K下钠晶体沿三个方向的色散关系
§ 3.5 晶格热容
一、晶格振动的平均能量
热力学中,固体定容热容:
根据经典理论,每一个自由度的平均能量是kBT, kBT/2为平均动能,kBT/2为平均势能,若固体有
N个原子,总平均能量: 取N=1摩尔原子数,摩尔热容是:
二、一维单原子链的振动
一维单原子链的振动
二、一维单原子链的振动
简谐近似下的运动方程
二、一维单Hale Waihona Puke 子链的振动简谐近似下的运动方程
在简谐近似下,原子的相互作用像一个弹 簧振子。一维原子链是一个耦合谐振子,各原 子的振动相互关联传播,形成格波。
固体物理 第三章_ 晶体中的缺陷

4
由以上讨论可知: 刃位错: 外加切应力的方向、原子的滑移方向和位错 线的运动方向是相互平行的。 螺位错: 外加切应力的方向与原子的滑移方向平行, 原子的滑移方向与螺位错的运动方向垂直。 在左右两部分受到向上和向下的切应力的作 用时,位错线向前移动,直到位错线移动到 尽头表面,这时左右两部分整个相对滑移b 的距离,晶体产生形变。
固体物理第三章
1. 热缺陷:由热起伏的原因所产生的空位和填隙原 子,又叫热缺陷,它们的产生与温度直接有关
(a) 肖脱基缺陷
(b)弗伦克耳缺陷
(c) 间隙原子
固体物理第三章
( a )肖特基缺陷 (vacancy) :原子脱离正常格点 移动到晶体表面的正常位置,在原子格点位置 留下空位,称为肖特基缺陷。 (b)弗伦克尔缺陷(Frenkel defect),原子脱离格 点后,形成一个间隙原子和一个空位。称为弗 伦克尔缺陷。 (c)间隙原子(interstitial):如果一个原子从正常 表面位置挤进完整晶格中的间隙位置则称为间 隙原子,由于原子已经排列在各个格点上,为 了容纳间隙原子,其周围的原子必定受到相当 大的挤压。
固体物理第三章 固体物理第三章
产生位错的外力: 机械应力:挤压、拉伸、切割、研磨 热应力:温度梯度、热胀冷缩 晶格失配: 晶体内部已经存在位错,只用较小的外力就 可推动这些位错移动,原来的位错成为了位错 源,位错源引起位错的增殖,有位错源的晶体 屈服强度降低。 晶体的屈服强度强烈地依赖于温度的变化。 T升高,原子热运动加剧,晶体的屈服强度下 降,容易产生范性形变。
固体物理第三章
在实际晶体中,由于存在某种缺陷,所以晶 面的滑移过程,可能是晶面的一部分原子 先发生滑移,然后推动同晶面的另一部分 原子滑移。按照这样的循序渐移,最后使 上方的晶面相对于下方的晶面有了滑移。 1934 年, Taylor( 泰勒 ), orowan( 奥罗万 ) 和 Polanyi( 波拉尼)彼此独立提出滑移是借助 于位错在晶体中运动实现的,成功解释了 理论切应力比实验值低得多的矛盾。
固体物理 第三章 晶格振动
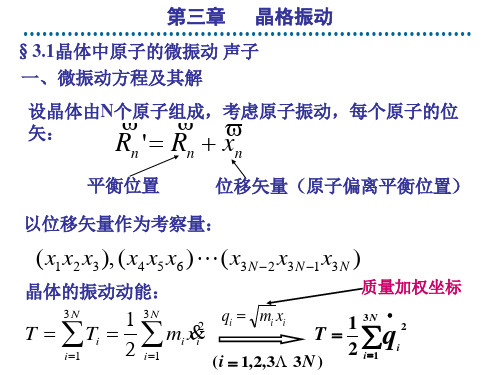
1 2 T = ∑q 2 i =1 i
3N •
3.1晶体中原子的微振动 3.1晶体中原子的微振动 声子 晶体振动势能U (qi ) 按 qi 的幂将势能在平衡位置附近展开为泰勒级数 ∂U 1 ∂ 2U U = U0 + ∑ ( ) 0 qi + ∑ ( ) 0 qi q j + 高阶项 ∂q i 2 ij ∂qi ∂q j i 其中 U 0 = 0 平衡位置处的势能为零势能点
xn = x N + n
又 : xn = Ae
i ( kna − ωt )
又 − π < k ≤ π s = − N + 1,− N + 2⋯⋯ N 共有N个取值 : a a 2 2 2
=1 e ⇒ 2π ⋅ s, = N+ 2π ,− π + 2 2π ,..., π 有N种均匀分布的分立取值 种均匀分布的分立取值 a L a L a 2π L 间隔∆k = ,密度 ,第一布里渊区倒格点数N。 L 2π
, ( l =1, 2, ⋯ 3N )
Ql = Ql0 sin(ωl t + α 1 )
1 ε l = (Q l + ωl2Ql2 ) 2
• 2
能量量子化
1 εl = (nl + )hυl 2
3.2 一维布拉菲格子的晶格振动 一、简谐近似
du 1 d 2u u( x) ≈ u( x0 ) + ∆x + (∆x)2 2 dx r0 2 dx x
3.1晶体中原子的微振动 声子 3.1晶体中原子的微振动 晶格振动模式
质量加权坐标下: 质量加权坐标下:
•• 3N
↔
独立的谐振子
↔
声子
固体物理课后习题解答(黄昆版)第三章

固体物理课后习题解答(黄昆版)第三章黄昆固体物理习题解答第三章晶格振动与晶体的热学性质3.1 已知⼀维单原⼦链,其中第j个格波,在第个格点引起的位移为,µ= anj j sin(ωj_j+ σj) ,σj为任意个相位因⼦,并已知在较⾼温度下每个格波的平均能量为,具体计算每个原⼦的平⽅平均位移。
解:任意⼀个原⼦的位移是所有格波引起的位移的叠加,即µn= ∑ µnj=∑ a j sin(ωj t naq j+σj)j j(1)µ2 n =∑µjnj∑µj*nj=µj2nj+ µ µnj*nj′j j′由于µ µnj?nj数⽬⾮常⼤的数量级,⽽且取正或取负⼏率相等,因此上式得第2 项与第⼀项µ相⽐是⼀⼩量,可以忽略不计。
所以2= ∑ µ 2njn j由于µnj是时间的周期性函数,其长时间平均等于⼀个周期内的时间平均值为µ 2 = 1 T∫0 2 ω+σ 1 2 j aj sin( t naqjj j)dt a=j(2)T0 2已知较⾼温度下的每个格波的能量为KT,µnj的动能时间平均值为1 L T ?1 ?dµ 2 ?ρw a2 T 1= ∫∫dx0?ρnj?= j j∫0 2 ω+ σ= ρ 2 2 T??dt L a sin( t naq)dt w Lanj T0 0 0 ? 2 ?dt??2T0 j j j j 4 j j其中L 是原⼦链的长度,ρ使质量密度,T0为周期。
1221所以Tnj= ρ w La j j=KT(3)4 2µKT因此将此式代⼊(2)式有nj2 = ρωL 2 jµ所以每个原⼦的平均位移为2== ∑ µ 2= ∑KT= KT∑1n njρωL2ρLω2j j j j j3.2 讨论N 个原胞的⼀维双原⼦链(相邻原⼦间距为a),其2N 格波解,当M=m 时与⼀维单原⼦链的结果⼀⼀对应.解答(初稿)作者季正华- 1 -黄昆固体物理习题解答解:如上图所⽰,质量为M 的原⼦位于2n-1,2n+1,2n+3 ……质量为m 的原⼦位于2n,2n+2,2n+4 ……⽜顿运动⽅程:..mµ2n= ?βµ(22n?µ2n+1 ?µ2n?1)..Mµ2n+1 = ?βµ(22n+1 ?µ2n+2 ?µ2n)体系为N 个原胞,则有2N 个独⽴的⽅程i na q⽅程解的形式:iµ2n=Ae[ωt?(2 ) ] µ2n+1=Be[ω?(2n+1)aq]na qµ=将µ2n=Ae[ωt?(2 ) ]2n+1 Be i[ωt?(2n+1) aq]代回到运动⽅程得到若A、B 有⾮零的解,系数⾏列式满⾜:两种不同的格波的⾊散关系:——第⼀布⾥渊区解答(初稿)作者季正华- 2 -第⼀布⾥渊区允许 q 的数⽬黄昆固体物理习题解答对应⼀个 q 有两⽀格波:⼀⽀声学波和⼀⽀光学波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
U U U0 i 1 ui
3N
2 1 3N U ui 2 u u i , j 1 i j 0
ui u j , 0
因在平衡位置势能取极小值,所以上式右端第二项为零,若取U0为能 量零点,并略去二次以上的高次项,得到
上一节关于晶格的运动方程之所以能够化成线性齐次方程组,是
简谐近似的结果,即忽略原子相互作用的非线性项得到的。
处理小振动问题的理论方法和主要结果--做为晶格振动这部分
内容的理论基础。
在第二章已经讨论过,当原子处于平衡位置时,原子间的相互
作用势能
1 A B ' U0 m n 2 i j r r ij ij
用独立简谐振子来表述。
下面根据分析力学原理,引入简正坐标,直接过渡到量子理论, 并引入声子概念--晶格振动中的简谐振子的能量量子。
数学处理:通过引入简正坐标,将晶格振动总能量(哈密顿量)= 动能 +
势能(化成)= 独立简谐振子能量之和
一、简谐近似和简正坐标
从经典力学的观点,晶格振动是一个典型的小振动问题,凡是力 学体系自平衡位置发生微小偏移时,该力学体系的运动都是小振动。
(9)
代表q空间均匀分布的点子。 若 K 是倒格矢,则 q q' q K h h
u
l p
不变。
因此q的取值可限制在第一布里渊区之内。
h3 h1 h2 q b1 b2 b3 (10) N1 N2 N3
波矢q的点阵具有周期性,均匀分布。 其中
b1 b2 b3 是波矢q的基矢,最小重复单元的体积为 , , N1 N 2 N3
对于有N个原胞的三维晶体,每个原胞有n个原子,每个原子有3个
自由度,所以晶体的总自由度数也是3nN。 概括起来,得到以下结论: • 波矢q增加一个倒格矢,原子的位移保持不变。--第一布里渊区。
• 晶格振动的波矢数目Nq等于晶体的原胞数N;
• 格波振动模式数目Nω等于晶体中所有原子的自由度数之和3nN 。
倒空间原 胞体积
b1 b2 b3 ( 2 ) 3 ( 2 ) 3 N1 N 2 N 3 N N V
原胞体积
一个重复单元对应一个波矢点,单位波矢空间内的波矢数目,
即波矢密度为
波矢密度: q
1
(2 ) 3 V N N h , 另由边界条件: 2 2
l X p Rl rp
l X p Rl rp
rp :原胞内第p个原子的位置矢量。
l 该原子相对于平衡点的位移为 u p 它沿坐标轴的分量为 u l p
x, y, z; Rl l1a1 l2a2 l3a3
(3)
Ap 有非零解的条件是系数行列式等于零,可解出3n个实根。
由此可得到3n个色散关系
j j (q), j 1,2,3n
每个色散关系代表一支格波,共有3n支格波。
格波的色散关系中,有3支当 q 0, 0,
ω- Ai v- Ai (q) q (i 1,2,3)
即
e
iq N i ai
1(8)
也就是说
h1 q N1a1 2 h1 , x1 N1 h2 q N 2a2 2 h2 , x2 N2 h3 q N 3 a3 2 h3 , x3 N3
应用到关系
(9)
ai bj 2 ij
b1 / 2 , b2 / 2 , b3 / 2 ,
b1 / 2 b1
b2 / 2 b3
b2 / 2 b2
Vq b1 b2 b3
* • •
此即倒空间原胞体积 可见第一布里渊区的体积(q的取值范围)即为倒空间原胞体积
V N N q q Vq N 3 3 (2 ) (2 )
1 3 N 2U U 2 i , j 1 ui u j
ui u j 0
上式即为简谐近似下,势能的表示式,包含了位移交叉项。
处理小振动问题一般都取简谐近似。 对于一个具体的物理问题是否可以采用简谐近似,要看在简谐 近似条件下得到的理论结果是否与实验相一致。 在有些物理问题中就需要考虑高阶项的作用,称为非谐作用。
简正坐标与原子的位移坐标之间的正交变换关系:
m i ui a ij Q j
j 1
3N
在简正坐标中,势能和动能化成:
1 3N 2 2 U i Qi , 2 i 1
1 3N 2 T Qi 2 i 1
1 3N 2 2 U i Qi , 2 i 1
1 3N 2 T Qi 2 i 1
l l1 u u p
l l1 u u p
l l1 u u p
l2 p
l2 p
l2 p
l3 l1 N1 l2 u p
l3 l1 u
l3 l1 u
l l u u 1 p l l u u 1 p
l l u u 1 p
l2 p l2 p
l2 p
l3 l1 N1 l2 u p l3 l1 u
l3 l1 u
§3.3 简正振动
声子
理论考虑:前面根据牛顿定理用直接解运动方程的方法,求解一维 链的振动模,得出如下结论: 晶体中原子的集体振动-----格波,可展开成简谐平面波的线性 迭加。 当振动微弱时(即相当于简谐近似情况),每个格波就是一个简 谐波,格波之间的相互作用可忽略,形成独立格波模式。 在玻恩-卡门周期性边界条件下,得到分立的独立格波模式,可
l3 l2 N 2 l3 (5) p l2 l3 N 3 p
或写成
u Rl N 1 a 1 u Rl u Rl N 2 a 2 u Rl (6) u Rl N 3 a 3 u Rl
N1 N h1 1 2 2 N N 2 h2 2 2 2 N N 3 h3 3 2 2
q hi bi (i 1,2,3) Ni
V (2 ) 3
1, 2, 3
则q在三个基矢方向上 的长度为:
b1 b q 1 2 2 b b 2 q 2 2 2 b b 3 q 3 2 2
是原子(l,p)与原 子(l’,p’)之间的准 弹性力系数
l , l ' 1, 2 N ;
p, p' 1, 2n; x, y, z
上式是3nN个相耦合的运动方程组。
把一维晶格动力学方程的试解加以推广,设三维晶格行波试解为:
l i Rl rp q t u A e p p i q Rl t Ap e (2)
q x1b1 x2b2 x3b3 (4)
Hale Waihona Puke h1 , h2 , h3 为整数。代回(4)式:
q x1b1 x2b2 x3b3 (4)
q h h1 h b1 2 b2 3 b3 (10) N1 N2 N3
h1 N1 h x2 2 N2 h3 x3 N3 x1
N个原子体系的势能函数为:
3N 1 2 N个原子体系的动能函数为:T m u i i 2 i 1
为了消去势能中的交叉项,使问题简化,引入简正坐标:
Q1,Q2 , , Q3 N
ui ui (Q Q3 N ) 1 , Q2 ,......, i 1 ,2,........, 3N
e
如果q改变一个倒格子矢量 K h b h b h b m 1 1 2 2 3 3 由于 R K 2 h l h l h l l h 1 1 2 2 3 3 不影响位相因子,因而对格波的描述没有任何区别。将波矢q的
取值限制在一个倒格原胞范围内—简约布里渊区。
对每一个波矢q,有3n个 j (q) 与之对应,每一组 , q 表示 晶格的一种振动模式,由此可知三维晶体中振动模式数目为3nN个。
每个原胞中,n个不同原子平衡位置的相对坐标为: r 1, r 2 , r n
第p个原子在 方向的运动方程为:
' ' l l, l l l uα u β (1) α m pu φαβ p p p, p' p' ' ' l pβ
3 (2) *
即:第一布里渊区里共有 N N1 N 2 N 3 个q值。
从三维晶格行波试解:
l i q Rl t u A e ( 2) p p
可以看出,q的作用只在于确定不同原胞之间振动位相的联系, 具体表现在位相因子:
i q Rl
取最小值。 相互作用势能是原子偏离平衡位置位移的函数。N个原子的位移
矢量共有3N个分量,写成
ui ( i 1, 2, 3 N )
原子相互作用势能是这些位移分量的函数,即
U U ( u1 , u2 , , u3 N )
将
U U ( u1 , u2 , , u3 N )
在平衡位置展开成泰勒级数
振动系统的拉格朗日函数为:
1 3N 2 1 3N 2 2 L T U Qi i Qi 2 i 1 2 i 1
Ap A p e
iq r p
na
振幅Apα与指标l 无关,因为它对于一个确定的q,任意元胞中第p 个原子在α方向上的运动有相同的振幅。
