电工电子技术基础第2章
电工电子技术基础第二章直流电路分析 ppt课件
结点数 N=4 支路数 B=6
（取其中三个方程）
PPT课件
6
b
列电压方程
I2
abda :
I1
I6
E4 I6R6 I4 R4 I1R1
a I3 I4
R6
c
I5 bcdb :
0 I2R2 I5R5 I6R6
+E3
d R3
adca : I4R4 I5R5 E3 E4 I3R3
对每个结点有
I 0
3. 列写B-（N-1)个KVL电压
方程 对每个回路有
E U
4. 解联立方程组
PPT课件
5
I1 a
b I2
I6
R6
I3 I4
d
+E3
R3
列电流方程
结点a： I3 I4 I1
c 结点b： I1 I6 I2
I5
结点c： I2 I5 I3
结点d： I4 I6 I5
基本思路
对于包含B条支路N个节点的电路，若假 设任一节点作为参考节点，则其余N－1个节点 对于参考节点的电压称为节点电压。节点电压 是一组独立完备的电压变量。以节点电压作为 未知变量并按一定规则列写电路方程的方法称 为节点电压法。一旦解得各节点电压，根据 KVL可解出电路中所有的支路电压，再由电路 各元件的VCR关系可进一步求得各支路电流。
3、会用叠加定理、戴维宁定理求解复杂电路中的电压、电流、功率等。
PPT课件
1
对于简单电路，通过串、并联关系即可 求解。如：
R
R
R
+ E 2R 2R 2R 2R
-
PPT课件
+
电工电子技术-第2章 正弦交流电路
•
I m = 14.1∠36.9°A
其有效值相量为：I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的，所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值，幅角对应正弦量的初相。
i u u、i 即时对应！ R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相！
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
（2）电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子，一个复数乘以j相当于在复
平面上逆时针旋转90°；除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的，电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中，一定要根据复数所在象
限正确写出幅角的值。如：
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3
电工电子技术第2章
第2章 正弦交流电路
在交流电路中，因各电流和电压多 +j A 为同一频率的正弦量，故可用有向线段 b r 来表示正弦量的最大值(有效值) Im 、 ψ Um(I、U)和初相ψ ，称为正弦量的相量。 O a +1 在正弦量的大写字母上打“•”表示，如 图2-5 有向线段的表示正弦量 幅值电流、电压相量用 I m、 m表示，有 U • U 效值电流、电压相量用 I 、 表示。将电 U • 路中各电压、电流的相量画在同一坐标 φ I ψ 中，这样的图形称为相量图。 ψ 同频率的u和i可用图2-6相量图表示。 图2-6 u和i的相量图 即 超前 Iφ°，I或 U滞后φ°。 U
第2章 正弦交流电路
2.1
正弦交流电的基本概念
正弦交流电压和电流的大小和方向都按正弦规律 作周期性变化，波形如图2-1a。
u U m s in ( t u ) i I m s in ( t i )
(2-1)
为便于分析，在电路中电压参考方向用“+”、“–” 标出，电流参考方向用实线箭头表示；电压、电流实 际方向用虚线箭头表示如图2-1b、c所示
第2章 正弦交流电路
u Im O φ Ψu Ψi i Um
u
i
t
T
图2-2 u和i相位不等的正弦量波形图
当φ=0º 时，称u、I同相；当φ=180º 时，称u比i反相； 当φ=±90º 时，称u与i正交 。 u i u i
u i
ui
u
i
t
u
i
O a) 同相
t O
b) 反相
O c)正交
t
图2-3 正弦量的同相、反相和正交
第2章 正弦交流电路
电工与电子技术第2章
+
−
i
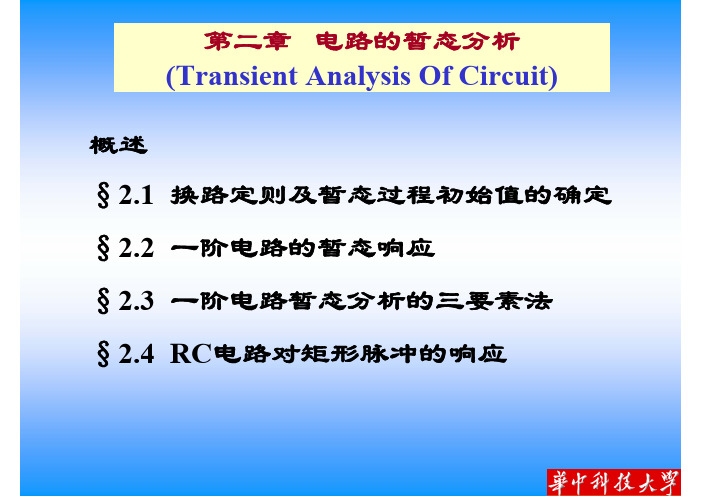
t→∞结束暂态,进入新稳态
uR C
uC 变量值需标明时刻：
uC(0-)、uC(0+)、uC(∞)、uC (t)
例2:求uC(0+)、 iC(0+),设S动作前电路稳定
R2 4 = 12 × = 8V uC (0-) = U S 2+4 R1 + R 2
根据换路定则：uc ( 0 ) = uc ( 0 ) = 8 V
S V R uR
US = 0.5A i L( 0 + ) = i L( 0 − ) = R
uR ( 0 + ) = iL ( 0 + ) × R = 0.5 × 20 = 10V
u(0+ ) = − iL (0+ ) × R0 = 0.5 × 10 × 103 = −5000V
uL (0 + ) = u( 0 + ) − uR (0 + ) = −5000 − 10 = −5010V
RC电路的暂态响应
uC = U 0 e
−t / τ
τ=RC 越大, 暂态过程越长 一阶RC零输入电路的 暂态响应曲线 为RC放电过程
(t ≥ 0) (t＞0) (t＞0)
i C
U0
uR = −Βιβλιοθήκη 0e−t / τU 0 −t / τ i=− e R
t=0
R uR
0 i U0 uC − R − U 0
+
−
t=0-
换 路
t=0+
t
换路前后虽电路不同,但换路后 瞬间uC和iL保持不变。
0 暂态过程
换路定则只对uC和iL,其他电量都会发生突变
电工电子技术第二章
L
di dt
代入上式得
L diL dt
RiL
US
(2-16)
式（2-16）为一阶线性常系数非齐次微分方程，解此方程可得
iL (t)
US R
(1
t
e
)
iL ()(1
t
e
)（
t 0）
（2-17）
其中 L 是电路的时间常数
R
电阻上的电压
Rt
uR (t) RiL US (1 e L ) （ t 0 ）
已在稳t=定0时，将则开L相关当闭于合短，路iL (0，) 此 iL时(0电) 感IS中的电流，为此iL时(0，) 电IS感元。
件储有能量。它将通R过 放电，从而产生电压和电流，如图
2-7（b）所示。
可见，电感电流和电感电压都是从初始值开始。随时间按同
一
上一页 下一页 返回
2.2 一阶电路的零输入响应
一阶电路中仅有一个储能元件（电感或电容），如果在换路 瞬间储能元件原来就有能量储存，那么即使电路中并无外施 电源存在，换路后电路中仍有电压、电流。这是因为储能元 件所储存的能量要通过电路中的电阻以热能的形式放出。
2.2.1RC电路的零输入响应
电路如图2-3所示，开关S在位置1时，电容C已被电源充电到 U0，若在时把开关从位置1打到位置2，则电容C与电阻R相联 接，独立电源US 不再作用于电路，此时根据换路定律，有， 电容C将通过电阻R放电，电路中的响应完全由电容电压的初
2.1换路定律及电路初始条件的确定
前面各章所研究的电路，无论是直流电路，还是周期性交流电 路，所有的激励和响应，在一定的时间内都是恒定不变或按周 期规律变动的，这种工作状态称为稳定状态，简称稳态。然而， 实际电路经常可能发生开关的通断、元件参数的变化、连接方 式的改变等情况，这些情况统称为换路。电路发生换路时，通 常要引起电路稳定状态的改变，电路要从一个稳态进入另一个 稳态。 由于换路引起的稳定状态的改变，必然伴随着能量的改变。在 含有电容、电感储能元件的电路中，这些元件上能量的积累和 释放需要一定的时间。如果储能的变化是即时完成的，这就意 味着功率为无限大，这在实际上是不可能的。也就是说，储能 不可能跃变，需要有一个过渡过程。这就是所谓的动态过程。 实际电路中的过渡过程往往是短暂的，故又称为暂态过程，简 称暂态。
《电子电工技术》课件——第二章 单相交流电路
例2：已知相量，求瞬时值。
已知两个频率都为 1000 Hz 的正弦电流其相量形
式为： I1 100 60 A I2 10 e j30 A
求： i1、i2
解：
2
f
2 1000 6280
rad s
i1 100 2 sin(6280t 60 ) A
i2 10 2 sin(6280t 30 ) A
u i
90
U
IL
t
I I
C. 有效值 U IL
定义： X L L
则： U I X L
U IL
感抗（Ω） XL
感抗（XL =ωL ）是频率的函数， 表示电感电路中电压、 电流有效值之间的关系，且只对正弦波有效。
ω
d. 相量关系
U
则：U I L e j90 I ( jX )
L
设： I I0
设： U1 a1 jb1 U 2 a2 jb2
则：
U U1 U2 (a1 a2 ) j(b1 b2 ) Ue j
2. 乘法运算
： 设
U1 U1e j1 U 2 U 2e j2
则： 3. 除法运算
U U1 U 2 U1 U 2 e j(12 )
则：
U1 U 2
U1 U2
U e j
U
指数式 极坐标形式
三、正弦量的相量运算
1、相量图运算
例：同频率正弦波相加 -- 平行四边形法则
u1 2U1 sin t 1
u2 2U2 sin t 2
U 2
U
同频率正弦波的 相量画在一起， 构成相量图。
2
1 U1
U U1 U 2
相量的复数运算
1. 加 、减运算
《电工与电子技术》第2章试题库
昆明冶金高等专科学校西校区《电工与电子技术》第二章正弦交流电路试题一、填空题1、一个工频正弦电压的最大值为20伏，t = 0时，其瞬时值为10伏，该正弦电压的瞬时值表达式u = 。
2、在纯电感正弦交流电路中，电压有效值不变，增加电源频率时，电路中电流将。
3、在R、L、C串联正弦交流电路中，当X L X C时，电路呈感性；当X L X C时，电路呈容性；当X L X C时；电路发生谐振。
4、正弦交流电的三要素为、和。
5、提高功率因数的意义在于既了电源设备的利用率，同时又了线路的功率及电压损耗。
6、一个电感线圈接在Ｕ＝120Ｖ的直流电源上，电流为20A，若接在Ｕ＝220Ｖ的工频交流电源上，则电流为28.2A，线圈的电阻Ｒ＝_ __欧，感抗XＬ＝______欧。
7、RLC串联电路的端电压=10√2sin(2500t+10o)V，当C=8F时电路消耗的功率最大Pmax=100W，则L=mH，Q=Var。
8、已知某电炉接在220V的正弦交流电源上，取用功率500W，电炉的电阻R=，4小时消耗的电能W=。
9、纯电阻电路的功率因数为，纯电容电路的功率因数为。
10、串联谐振时，电路的阻抗，电流，电感上的电压电容上的电压。
二、选择题（将正确答案的序号填人括号中）1、交流电的周期越长，说明交流电变化得（ ）。
a 、越快；b 、越慢 。
2、电路中某元件两端的电压u = 2202sin314t 伏，通过的电流i= 10cos314t 安，则该元件是（ ）。
a 、电阻；b 、电感；c 、电容 。
3、一度电可供“220V40W ”的灯泡正常发光的时间是（ ）。
a 、20小时；b 、45小时；c 、25小时。
4、已知两正弦量 i 1 =10sin(314t+900)安,i 2=10sin(628t+300)安，则（ ）。
a 、i 1超前i 2 600；b 、i 1滞后i 2 600；c 、不能判断相位差 。
5、在正弦电压不变的情况下，给电阻、电感串联电路再并联电容后，（ ）。
电工电子技术基础习题答案解析
第1章电路的基本知识1.1电路的概念 (1) 略(2) 电路通常由电源、负载和中间环节(导线和开关)等部分组成。
A •电源的作用：将其他形式的能转换成电能。
B •负载的作用：将电能转换成其他形式的能。
C •中间环节的作用：传递、分配和控制电能。
1.2电路中的主要物理量 (1) 零、负电位、正电位 (2) 3、1.5、3、1.5、0、3 (3) -7,-5 1.3电阻 (1) 3: 4 (2)查表1.3，知锰铜合金的电阻率 J =4.4 10亠」m1.4欧姆定律 (1)电动势、内压降(2)当R= R 时，电路处于开路状态，其特点是电路中电流为零，电源端电压等于电 源电动势；当R=0时，电路处于短路状态，其特点是短路电流极大，电源端电压等于。
由于I =0.22A=220mA . 50mA ，故此人有生命危险。
1.5电功与电功率P 40(2)略(3) W 二Ult =220 0.2 7200 = 316800J思考与练习一、 判断题1" 2. X 3. V 4. X 5. V 6. X 7. X 8. V 9. X 二、 选择题1. C2. C3. B4. B5. B6. B7. C8. B根据t ，得1RS 3 0.21 10 P 4.4如0二=1.43 m(3)U 220R "1000= 0.22 A(1)t=W 二空£=25h三、填空题1 •正、相反；2•参考点；3•负极、正极； 4 •高、低、低、高； 5•材料、长度、横截面积、 R - ； 6• 1800、土 5%; 7. 220S四、计算题1 • U ab =V a -V b =10 - 5 = 5VU bc *b-V c =5-(-5) =10 V U ac 二V a-V c =10 -(-5) =15V U ca - —U ac - - 15VR = U420门I0.2 220100 10(2)U =IR =2 100=200V(3) U r =lr =2 10 =20V 4.( 1)P =UI = 220 4 =880W(2)W 二 Pt =880 1800 =1584000J2 2(3) Q =l Rt =4 0.5 1800 =14400J(4) E =W -Q =1584000 -14400 =1569600 J第2章直流电路的分析与计算2.1电阻的连接(1) I mb =0.5AR 1 4U 2 = IR 2 =0.5 20 =10V U U U 2 =210 =12VR 2故 P 2』P 二10 28 =14WR 2 202. I24 120= 0.2A 3・(1)(2)由于P P 2 R 1 U 2 R 2 R 1WORD 格式整理10(3) (a ) R ab(b) R ab(R R)RR 」R 3(R R) R (c) R ab=R=1门R (2 R)RR（汀）R32 —Q 52.2基尔霍夫定律 (1) 5、3、6、3 (2) 假设I 2、I 3的方向和回路绕行方向如图 I 1 R 1 1 3R 3 = E 1 12 R 2 T 3 R 3 = E2 0.008 I 2 =丨3 0.008 50 8OI3 =3 I 丨2艮 +8013 =12解得 =0.0245 A=24.5mA =0.0325 A=32.5mA R 2 = 384门2.3电压源与电流源的等效变换 （1） I s =—、不变、并、E — I s r 、不变、r （2） （ a ）把两个电压源等效变换为电流源，如图- ----1Q0Q200 n 10¥ a -O rn,evO匸(a)2.2（ a ）所示。
电工电子技术基础知识
u3 Um sin(t 240 ) Um sin(t 120 )
Um
u1
u2
u3
0
–Um
2
t
也可用相量表示：
U1 U U 2 U U 3 U
0o 120o 120o
•
U3 120°
120°
•
U2
•
U1 120°
三相电压相量图
对称正弦量特点为： U1 U 2 U 2 0
频率相同、幅值相等、相 位互差120°的三相电压称为
平，则输出F 为低电平；只
R
有输入A、B 全为高电平时，
A
输出F 才为高电平。可见输
F 入与输出呈现与逻辑关系： B
与逻辑关系表达式
F = AB
与逻辑关系逻辑符号：
A
&
F
B
2、 二极管或门
与逻辑关系真值表：
AB F
00 0 01 0 10 0 11 1
A
只要输入A、B中一个为高
B
F 电平，则输出F 为高电平；
1、 常量之间的关系（常量：0和1）
加： 0+0=0 乘：0 ·0=0 非：0 1
0+1=1 1+1=1
0 ·1=0 1 ·1=1
1 0
2、变量和常量的关系（变量：A、B、C…）
加：A+0=A 乘: A ·0=0
A+1=1
A ·1=A
A+A=A
A ·A=A
3、与普通代数相似的定理
非：A A 0
1 电流
一、电流定义
带电粒子或电荷在电场力作用下的定向运动
形成电流。单位时间内流过导体截面的电荷量定义为
《电工与电子技术基础》第2章正弦交流电路习题解答
67
（1）i= u Z
（2）I= U R + XC
（3）
I
=
R
U − jωC
（4）I= U Z
（7） I = − j U ωC
（5）U=UR+UC
（8）
I
=
j
U ωC
（6）U =UR + UC
解：在
R、C
串联电路中，总阻抗 Z
=
R
−
j
X
C
=
R
−
j
1 ωc
而 Z=
R2
+
X
2 C
I = U Z
L = XL =
8
= 25.5 (mH)
2πf 2 × 3.14 × 50
2.10 题 2.10 图中，U1=40V，U2=30V，i=10sin314t A，则 U 为多少？写出其瞬时值表 达式。
解：由电路图可知，电压 u1 与电流 i 同方向，而电压 u2 超前电流 i90º，所以
U=
U12
+
U
2.2 两个频率相同的正弦交流电流，它们的有效值是 I1=8A，I2=6A，求在下面各种情况 下，合成电流的有效值。
（1）i1 与 i2 同相。 （2）i1 与 i2 反相。 （3）i1 超前 i2 90º角度。 （4）i1 滞后 i2 60º角度。
解：（1） I = I1 + I2 = 8 + 6 = 14 （A）
− j4 2 − j2
=
2+
2j
+
− j4(2 + j2) (2 − j2)(2 + j2)
=3+
j (Ω)
电工学(下册)电子技术基础-第2章-习题解答
习 题 22.1 电路如图2.1所示，1k ΩR =，测得D 5V U =，试问二极管VD 是否良好（设外电路无虚焊）？解：内部PN 结或电极已开路，D 已损坏。
2.2 电路如图2.2所示，二极管导通电压D(on)U 约为0.7V ，试分别估算开关断开和闭合时输出电压o U 的数值。
图2.1 习题2.1电路图 图2.2 习题2.2电路图解： S 断开：断开VD ，D 5V U =。
所以VD 导通，o 50.7 4.3V U =-=S 闭合：断开VD ，)V (1125D-=⨯+-=RR RU ，所以VD 截止，o 6V U = 2.3 分析判断图2.3所示各电路中二极管是导通还是截止，并计算电压ab U ，设图中的二极管都是理想的。
图2.3 习题2.3电路图解：（a ）断开VD ，U D =5+5=10V>0，VD 导通 ，ab 5V U =-；（b）断开VD，D2151V23U=-⨯=-+，VD截止ab252V23U=⨯=+；（c）断开VD1 VD2，D1D212V,5127VU U==-+=，所以VD1优先导通，U D2= −5V，VD2截止，U ab=0V；(d) ）断开VD1 VD2，D1D212V,12517VU U==+=所以 VD2优先导通，D15VU=- VD1截止，ab5VU=-2.4 一个无标记的二极管，分别用a和b表示其两只引脚，利用模拟万用表测量其电阻。
当红表笔接a，黑表笔接b时，测得电阻值为500。
当红表笔接b，黑表笔接a时，测得电阻值为100k。
问哪一端是二极管阳极?解：b端是阳极2.5 二极管电路如图 2.4(a)所示，设输入电压i()u t波形如图 2.4(b)所示，在05mst<<的时间间隔内，试绘出输出电压o()u t的波形，设二极管是理想的。
图2.4 习题2.5电路图解：i()2tu t=，断开VD，D6iu u=-，当Du>时，VD导通，即3st>，60.2630.20.2iouu t-=⨯+=++当Du<时，VD截止，即3st<，6Vou=()ou tt/ms2.6 在图2.5所示的电路中，设二极管为理想的，已知i30sin(V)u tω=，试分别画出输出电压ou的波形，并标出幅值。
《电工电子技术基础》第2章 电路的基本分析方法
第2章 电路的基本分析方法 ——电源等效变换
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——电源等效变换
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——电源等效变换
如图2.2.11所示，计算电路中流过2 Ω电阻的电流I。
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——叠加定理
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——叠加定理
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——叠加定理
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法——戴维宁定理
2.5 戴维宁定理
复杂电路中有时只需要计算其中某一条支路的响应，此时可 以将这条支路划出，而把其余部分看作一个有源二端网络。 有源二端网络 具有两个出线端的内含独立电源的电路 无源二端网络 不含独立电源的二端网络
回路，网孔的数目就等于总的独立回路数。
I1
I3
I2 I II
III
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——支路电流法
4.选取独立结点电流方程和独立回路电压方程组成联列方程组。
I1
I3
I1+I2 － I3=0 R1I1 － R2I2=US1 － US2
I2 I II
R2I2+R3I3=US2
III
5.方程总数等于支路总数，也就是所要求的变量数，方程组
有唯一的解。解方程组，可得到各支路电流I1、I2和I3。
I1
US1(R2 R3 ) R1R2 R2 R3
US2 R3 R3R1
电工电子技术基础与应用第2章 电路的分析方法
72
I=
A = 4A
6 + 12
2.2 支路电流法
1．支路电流法 支路电流法就是以支路电流为变量，根据
基尔霍夫电流定律和基尔霍夫电压定律， 列出节点电流方程和回路电压方程，求解 支路电流的方法。支路电流法是分析电路 最基本的方法之一。 2．支路电流法的解题步骤
2．支路电流法的解题步骤
o
IS
I
31.2 电压源与电流源的等效变换
1．等效变换方法 因为对外接负载来说这两个电源提供的电
压和电流完全相同，所以
因此，一个恒压源US与内阻R0串联的电路 可以等效为一个恒流源IS与内阻RS并联的电
路。如图所示。
I
+
RS
+
U
R
U_S
_
IS
R'S
I +
U
R
_
在电压源和电流源等效过程中，两种电路模 型的极性必须一致，即电流源流出电流的一 端与电压源正极性端对应。
=
6.5V
4、使用叠加定理时的注意事项：
1)只能用来计算线性电路的电流和电压， 对非线性电路，叠加定理不适用。
2)叠加时要注意电流和电压的参考方向， 求其代数和。
3)不能用叠加定理直接计算功率。因为
功率 P I 2 R (I 2 I 2 )R I 2 R I 2 R
理想电流源所在 处开路。
有源二端网络变换为电压源模型后，一个复杂的 电路就变为一个简单的电路，就可以直接用全电 路的欧姆定律，来求取该电路的电流和端电压。
2）当电流源单独作用时，电压源不作用，在该电 压源处用短路代替。
+ US _
电工电子技术及应用第2章
弦量；只有同频率的正弦量其相量才能相互运算，
才能画在同一个复平面上。
画在同一个复平面上表示相量的图称为相量图。
相量与正弦量的关系
U U
对应关系
Umsin( t )
不相等！！
例2-9
已知正弦电压、电流为 u 220 2 sin(t π )V，
i
+ +
R
i
us
u
π
2π
o
t
T
a)
b)
图2-1
Байду номын сангаас 一、正弦量的三要素
1.振幅值（最大值） 正弦量在任一时刻的值称为瞬 时值，用小写字母表示， 如
u
i、 u
, 分别表示电流及
u1 u2
电压的瞬时值。正弦量瞬时值
中的最大值称为振幅值也叫最 大值或峰值，用大写字母加下
o
Um2
Um1
t
图2-2
标m表示，如Im、Um , 分别表
6.55 j2.45 6.99 159.5
A B 685 11 130 0.52 j5.98 (7.07 j8.43)
7.59 j14.41 16.2962.2
例2-8
已知复数 A 4 j3 B 3 j4 ，求AB和A/B。
起点不同，正弦量的初相不同，因此初相与计时
起点的选择有关。我们规定初相|ψ |不超过π 弧 度，即-π ≤ψ ≤π 。图2-3所示是不同初相时的 几种正弦电流的波形图。
在选定参考方向下，已知正弦量的解析 式为 i 10sin( 314t 240 )A 。试求正弦量的 振幅、频率、周期、角频率和初相。
电工电子技术及应用第二章单相正弦交流电路习题
《学习指导与练习》上的题(P21)二、单项选择题1.两个正弦交流电流的解析式是i 1=2202sin(10πt+3π)A ，i 2=311sin(10πt －3π)A 。
在这两个式子中两个交流电流相同的量是（ ）。
【C 】A. 最大值和初相位B. 有效值和初相位C. 最大值、有效值和周期D. 最大值、有效值、周期和初相位2.对照明用交流电u=380sin(100πt －2π)V 的说法正确的是（ ）。
【A 】A. 1S 内交流电压有100次达到最大值B. 交流电的有效值为220VC. 初相位为π/2D. 1S 内交流电压有50次过零3.当两个同频率正弦量的初相位相等时，下列表述正确的是（ ）。
【D 】 A. 两个正弦量的最大值和有效值相等 B. 两个正弦量的计时起点一定相同C. 判断两个正弦量是否同时到达最大值和零值，还须由计时起点确定D. 两个正弦量同时到达最大值和零值4.在正弦量的有效值相量表示法中，下列说法正确的是（ ）。
【B 】 A. 相量的长度等于正弦量的最大值 B. 相量的长度等于正弦量的有效值 C. 相量与横轴的夹角等于正弦量的相位 D. 相量与横轴的夹角等于正弦量的初相位5.已知某交流电流，t=0时的瞬时值i 0=10A ，初相位ψ0=30°，则这个正弦交流电的有效值为（ ）。
【C 】 A. 20AB. 202AC. 14.14D. 10A6.电容器上标有“30μF ，600V ”的字样，600V 的电压是指（ ）。
【A 】 A. 额定电压B. 最小电压C. 正常工作时必须加的电压D. 交流电压有效值7.电感量一定的线圈，如果产生的自感电动势大，则反映该线圈中通过的电流（ ）。
【D 】 A. 数值大B. 变化量大C. 时间快D. 变化率大11.线圈电感的单位是（ ）。
【A 】A.亨【利】B. 法【拉】C. 高【斯】D. 韦【伯】12.一个空心线圈，当通过它的电流为8A 时，电感为36mH ；若通过它的电流为4A 时，则（ ）。
【精品】J__《电工电子技术基础》电子教案_电工电子技术课件_第2章 正弦交流电路
电感元件上电压、电流的有效值关系为：
U=LI=2πf LI=IXL
其中：
XL=2πf L=ωL称为电感元件的电抗，简称感抗。 感抗反映了电感元件对正弦交流电流的阻碍作用；
感抗的单位与电阻相同，也是欧姆【Ω】。
感抗与哪些 因素有关？
XL与频率成正比；与电感量L成正比
直流下频率f =0，所以XL=0。L 相当于短路。
平均功率用大写 ！
例
“220V、100W”和“220V、40W”灯泡的电阻？ U2 2202 解： R100 484 P 100 U2 2202 R40 1210 P 40 显然，在相同电压下，负载的电阻与功率成反比。
第3页
2.3.2 电感元件
1. 电感元件上的电压、电流关系
耐压为220V的电容 器，能否用在180V 的正弦交流电源上 ？
U=180V，则Um≈255V
255V>220V 不能用在180V正弦电源上！
u
何谓反相？ 同相？相位 正交？超前 ？滞后？
u1
u2
u3
u4
ωt
u1与u2反相； u1与u4同相；u3与u4正交； u3超前u490°；u3滞后u290°。
第3页
p<0
2. 平均功率（有功功率）P
P=0，电感元件不耗能。 3. 无功功率Q
U Q ULI I X L XL
2
2
Q反映了电感元件与电源之间能量交换的规模。
问题与讨论 1. 电源电压不变，当电路的频率变化时， 通过电感元件的电流发生变化吗？
f 变化时XL随之变化，导致电流i 变化。
则 p ic u I Cm cost U m sint
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第2章 正弦交流电路
2.2 正弦量的表示法
2.2.2 正弦交流电的相量表示法
一个正弦电压u=Umsin（ωt+φ）V的有效值相量表达式可写成
•
U U
有一正弦电流 i=14.14sin（ωt+60º）A，写出它的相量表达式。
解： Im=14.14A I= 0.707Im=0.707×14.14 A =10A φ=60º
2
在电工学中常把振幅值、角频率和初相称为正弦交流电的三要素。
第2章 正弦交流电路
2.1 交流电
2.1.2 表征正弦交流电的物理量
相位差是指两个同频率正弦量的初相之差。 若u1=Um1sin（ωt+φ1）V，u2=Um2sin（ωt+φ2）V则两者的相位差为：
φ12=φ1－φ2
当φ12＞0时，u1超前于u2； 当φ12＜0时，u1滞后于u2。
同时存在
当φ12=0时，称u1与u2同相； 当φ12=π/2时，称u1与u2正交； 当φ12=π时，称u1与u2反相。
第2章 正弦交流电路
2.1 交流电
2.1.2 表征正弦交流电的物理量
有效值是指在相同的时间内让一直流电流和一交流电流通过相同的 电阻，当两者产生的热量相等时，就用直流电流的大小作为交流电流的
相量图 ：
•
• UR I
u i
+1
第2章 正弦交流电路
2.3 电阻性交流电路
2.3.2 电阻元件上的功率
瞬时功率指的是电阻元件在某一瞬间的
功率，用p表示，单位为瓦特，写作W。
i
p=uRi ＞0
u
R uR
说明电阻总是在消耗功率。
电阻性交流电路
平均功率简称为功率，指的是电阻在一个 周期内消耗功率的平均值，又叫有功功率。用 P表示，单位为瓦特，写作W。
一个正弦电压u=Umsin（ωt+φu）V可以表示为下图 ：
•
Um
u
+1
第2章 正弦交流电路
2.2 正弦量的表示法
2.2.2 正弦交流电的相量表示法
复数的表示方法
+j
b
r
θ O
A=a+jb
a
+1
代数表示形式： A=a+jb
极坐标形式 ： A=r∠θ
r a2 b2
arctan b
a a=rcosθ b=rsinθ
u Um
0
T
2
T 3T 2
2T
t
正弦电压（电流）完成一个循环所用的时间称为一个周期，用T 表示，单位是秒（s）。1s内完成的循环次数称为频率，用 f 表示，单 位是赫兹（Hz）。可知 f=1/T 。
第2章 正弦交流电路
2.1 交流电
2.1.2 表征正弦交流电的物理量
解析式 u=Umsin（ωt+φ）中的ω称为角频率，表示单位时间内正 弦量变化的电角度，它的单位是弧度/秒（rad/s）。周期、频率、角频
u u(t1)
O t1
t
第2章 正弦交流电路
2.1 交流电
2.1.2 表征正弦交流电的物理量
正弦量瞬时值中最大的值叫做振幅值，电压的振幅值用Um表示。 从最大值到最小值称为峰-峰值，电压的峰-峰值用Up-p表示。
u
u
Um
Um
Up-p
O
t
O
t
-Um
第2章 正弦交流电路2.1 交流电21.2 表征正弦交流电的物理量
•
I I 1060oA
第2章 正弦交流电路
2.3 电阻性交流电路
2.3.1 电阻元件上电压与电流的关系
已知 i=ImsinωtA 流过电阻R，
i
则 uR=Ri=RImsinωt=URmsinωtV 可得
振幅值关系式： URm=RIm
u
R uR
有效值关系式： UR=RI
相量关系式：U•
R
•
I
R
电阻性交流电路
第2章 正弦交流电路
本章要点 了解正弦交流电的基本概念及相关物理量。 学会正弦量的各种表示法及各种方法之间的转换。 掌握电阻性电路中电压、电流间的相量关系及功率计算。 掌握电感性电路中电压、电流间的相量关系及功率计算。 掌握电容性电路中电压、电流间的相量关系及功率计算。 掌握RLC串联电路电压、电流间的相量关系及功率计算。
率都是表示正弦量变化快慢的物理量，三者之间存在如下关系：
ω=2π/T=2πf
u
角频率不同的两个正弦量
u1
u2
O
t
第2章 正弦交流电路
2.1 交流电
2.1.2 表征正弦交流电的物理量
解析式 u=Umsin（ωt+φ）中的（ωt+φ）称为相位，φ称为初相。
u
初相不同的两个正弦量
Um
u1
2
O
2
u2
3 2 ωt
u1=10sin314tV u(V)
10
u2=15sin（314t+π/3）V
u(V) 15
O
2
3 2 ωt
2
O
3
2 3
5 2 ωt
3
第2章 正弦交流电路
2.2 正弦量的表示法
2.2.2 正弦交流电的相量表示法
正弦交流电还可以用具有大小和方向的旋转矢量来表示，即：用矢 量的长度表示正弦交流电的有效值（或最大值）；用矢量与横轴的夹角 表示正弦交流电的初相角，这就是正弦量的相量表示法。
uL
L
di dt
L为电感元件的自感系数，单位为亨[利]（H），还有毫亨（mH）
和微亨（μH），三者存在如下关系:
1H=103mH
1 mH =103μH
第2章 正弦交流电路
2.4 电感性交流电路
2.4.1 电感元件上电压与电流的关系
已知电流i=ImsinωtA流过电感L，产生电压uL
i
uL
L
di dt
第2章 正弦交流电路
2.1 交流电
2.1.1 正弦交流电的基本概念
u
O
t1
t2
t
大小和方向按照正弦规律变化的电压称作正弦交流电压。正弦交 流电压通常表示为解析式
u=Umsin（ωt+φ）
第2章 正弦交流电路
2.1 交流电
2.1.2 表征正弦交流电的物理量
在某一时刻电压、电流的大小称为瞬时值，用u（t）、i（t）表示。
有效值。用 I 表示。
I
Im 2
0.707Im
同理
U
Um 2
0.707Um
平均值是对正弦量在半个周期求其平均值，用Iav或Uav表示。
Iav=0.637Im Uav=0.637Um
第2章 正弦交流电路
2.2 正弦量的表示法
2.2.1 正弦交流电的波形图
通过画出正弦电压所对应的正弦曲线可以直观地看出电压的变化过 程，正弦量的这种表示方法称为波形图法。
P=URI=UR2/R=I2R
第2章 正弦交流电路
2.4 电感性交流电路
2.4.1 电感元件上电压与电流的关系
电感元件又叫电感线圈，是一种用导线绕制而成的元器件，通 常简称为电感。
当给一个电感通以变化的电流时，在电感的两端会产生感应电
压，称为自感电压，这种现象称为自感现象。自感电压用uL表示，
通常写作：