线性系统大作业题目一
线性系统设计大作业

第一章 背景1.1自相关函数自相关函数是信号在时域中特性的平均度量,它用来描述信号在一个时刻的取值与另一时刻取值的依赖关系,对于离散信号r 长度为N ,记为{r(k),k=0,1,2,…,N-1}。
该信号的自相关函数为101R()[()()]N i r i i N ττ-==+∑()()r i r i N ττ+=+-伪随机信号在每个采样点k 信号值为-a 或a ,其自相关函数为自相关函数就是信号x(t)和它的时移信号()x t τ+乘积的平均值,它是时移变量τ的函数。
自相关函数具有如下主要性质:(1)自相关函数为偶函数,xy R ()τ=xy R ()τ-,其图形对称于纵轴。
因此,不论时移方向是导前还是滞后(τ为正或负),函数值不变。
(2)当τ=0时,自相关函数具有最大值,且等于信号的均方值,即(3)周期信号的自相关函数仍为同频率的周期信号。
自相关函数的典型应用包括:检测淹没在随机噪声中的周期信号。
由于周期信号的自相关函数仍是周期性的,而随机噪声信号随着延迟增加,它的自相关函数将减到零。
因此在一定延迟时间后,被干扰信号的自相关函数中就只保留了周期信号的信息,而排除了随机信号的干扰。
1.2互相关函数互相关函数,表示的是两个时间序列之间和同一个时间序列在任意两个不同时刻的取值之间的相关程度,即互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1,t2的取值之间的相关程度。
随机信号x(t)和y(t)的互相关函数xy R ()τ定义为xy R ()[()()]n m x n m y n +∞=-∞=-∑系统脉冲响应的测定。
在随机激励试验中,假如以随机白噪声作为试验信号输入被测系统,则输入信号与输出信号的互相关函数R() 就是被测系统的脉冲xy响应。
这种测量方法的优点可以在系统正常工作过程中测量。
测量时,其他信号都与试验信号无关,因而对互相关函数没有影响,不影响脉冲响应的测量。
第二章 基于Hankel 阵的实现2.1 Markov 系数概述对于严格真有理分式111111...()...n n nnn n nb s b s b G s s a s a s a ----+++=+++ 用多项式除法按指数级数展开12()(0)+(1)(2)...g s h h s h s --=++∵传递函数是严格真有理分式 ∴(0)=0hG(s)按Markov 矩阵展开成1(1)(1)1G(s)=C[SI-A]()()i i i i i B CA s G s h i s ∞--+=∞-+==⇒=∑∑我们把{(1),(2),(3)...}h h h 称为Markov 系数。
线性系统作业1
线性系统作业
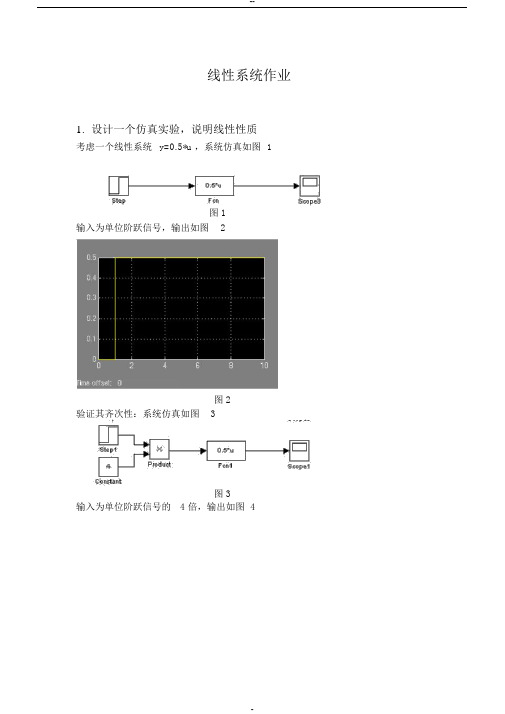
1.设计一个仿真实验,说明线性性质
考虑一个线性系统y=0.5*u ,系统仿真如图1
图 1
输入为单位阶跃信号,输出如图2
图 2
验证其齐次性:系统仿真如图3
图 3
输入为单位阶跃信号的 4 倍,输出如图 4
图 4
验证其叠加性,系统仿真如图 5
图 5
输入为两个单位输入信号,输出如图 6
图 6
从图 4、图 6 中我们可以看出线性系统的齐次性和叠加性
2. 构造两个零状态等价系统,其稳定性不同,用仿真说明,在
初始条件相同时,系统输出可能不同。
m
m 先构造两个零状态等价系统,可知道其 D= B C A B ( ⋯) D , CA
m=0,1,2,
0, 1 1 1, 3
1
取 A 1 , B ,C 0,1 , D 0 则得 A 1, , B , C 0,1 , D 1, 0 2 0
0,1
x 1
0,1 x
系统 1 为 x
1u , y
1,0
1,3
x 1
0,1 x
系统 2 为 x
2u , y
1,0
用 MATLAB 仿真系统如图 7
图 7
当输入为正弦信号,两个系统的初始状态均为0 时,输入如图 8
图 8
1 时,输入如图 9当输入为正弦信号,两个系统的初始状态均为
图9
从图 8、图 9 上可以看出在初始条件相同时的两个零状态等价系统,初始状态为0 时系统输出几乎相同,初始状态为 1 时系统输出不同。
线性系统理论大作业

目录题目一 (2)(一)状态反馈加积分器校正的输出反馈系统设计 (2)(1)建立被控对象的状态空间模型,并判断系统性质 (2)(2)状态反馈增益矩阵和积分增益常数的设计 (4)(3)全维观测器设计 (6)(4)如何在闭环调速系统中增加限流环节 (8)(二)二次型最优全状态反馈控制和按负载扰动前馈补偿的复合控制系统设计 (8)(1)线性二次型最优全状态反馈设计 (8)(2)降维观测器设计 (13)题目二 (15)(1)判断系统是否存在最优控制律 (15)(2)非零给定点的最优控制设计和仿真分析 (16)(3)权矩阵的各权值对动态性能影响分析 (17)题目一(一)状态反馈加积分器校正的输出反馈系统设计 (1)建立被控对象的状态空间模型,并判断系统性质1)画出与题目对应的模拟结构图,如图1所示:图1原始系统结构图取状态变量为1x =n ,2x =d I ,3x =d u ,控制输入u=c u1222212333375375111T Le la la la s s s C x x T GD GD C x x x x RT T RT K xx u T T ⎧=-⎪⎪⎪=--+⎨⎪⎪=-+⎪⎩将已知参数代人并设输出y=n=1x ,得被控对象的状态空间表达式为L x Ax Bu ET y Cx=++=其中,237500039.768011=-3.696-17.85727.05600-588.235100T ela lala s C GD C A RT T RT T ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦,000=023529.41s s B K T ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦,2375-30.4880=000GD E ⎡⎤-⎢⎥⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,[]100C = 2)检查被控系统的结构性质判断系统能控性、能观性、稳定性 程序如下:A=[0 39.768 0;-3.696 -17.857 27.056;0 0 -588.235]; B=[0;0;23529.41];C=[1 0 0]; Qc=ctrb(A,B); Qo=obsv(A,C); L=length(A); if rank(Qc)==Ldisp('系统是状态完全能控'); elsedisp('系统是状态不完全能控'); endif rank(Qo)==Ldisp('系统是状态完全能观'); elsedisp('系统是状态不完全能观'); enddisp(eig(A))%利用A 的特征值判断系统稳定性 运行结果:系统是状态完全能控 系统是状态完全能观 1.0e+02 *-0.0893 + 0.0820i -0.0893 - 0.0820i -5.8823 + 0.0000i由于矩阵A 全部特征值均具有负实部,因此系统渐近稳定。
华电线性系统理论大作业

而前文已经得出导轨的动能 Tw ,因此两式相加得系统的动能 T 为:
2 2 2 2 1 x T Tb Tw m x x2 a Ib I w a 2 R
是导轨相对于水平线的倾斜角。
图 1.球杆系统简图
2.2 拉格朗日法建模
为了对球杆系统进行研究, 我们先对其进行建模, 一般来说, 这种球杆系统, 运用拉格朗日方程建立其数学模型比较方便,拉格朗日方程如下:
d T T V R U t dt q q ' q ' q
v v' w r
其中 v ' 是小球相对于导轨的线速度,其数值等于 x ,负号是指方向与规定 的正方向相反, 指的是导轨的角速度,即 a ,r 是小球的质心在坐标系中的位 置向量,计算式如下:
R x 0 x x a v 0 0 R xa a 0 0 0
其中 T 为系统的动能,包括小球的转动的动能,导轨转动的动能等,V 为系 统的势能, 包括重力势能弹性势能等等, 能量耗散函数为 R ,q
q1 , q2 ....qk
T
1
为广义坐标向量,其中 k 代表系统的自由度,即完全描述系统运动特性需要的坐 标数目,关于自由度在下文会具体分析, u 为作用于系统的外力。 以下为各个变量所表示的物理意义,M:导轨的质量,g:重力加速度 r:小 球的半径 I b :球的惯性力矩, I w :杆的惯性力矩,x:球的相对横坐标,y:球 的相对纵坐标, :小球相对于导轨的转角,a:导轨与水平线的夹角,球杆系 统受力分析如下:
线性系统作业

P130T10系统的状态方程为X(t )AX(t )Bu(t )=+其中, ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=10,0010B A 试将它离散化,并求出当输入和初始条件分别为⎥⎦⎤⎢⎣⎡==01)0(),(1)(x t t u 时方程在采样时刻的近似解了。
解 取采样周期T=0.05秒,编写和执行以下的m-文件:>> A=[0 1;0 0];>> B=[0;1];>> [G ,H]=c2d(A,B,0.05)得到G =1.0000 0.05000 1.0000H =0.00130.0500因此,所求的离散化状态空间模型是)(0500.00013.00000.100500.00000.1)1(t u k x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+用以下Matlab 程序求离散后状态方程的解,>> syms s t x0 x tao phi phi0;>> G=[1.0000 0.0500;0 1.0000];I=[1 0;0 1];H=[0.0013 0.0500];>> syms s t x0 x tao phi phi0;>> G=[1.0000 0.0500;0 1.0000];I=[1 0;0 1];H=[0.0013;0.0500];>> E=s*I-G;C=det(E);D=collect(inv(E));>> phi0=ilaplace(D);x0=[1;0];x1=phi0*x0;>> phi=subs(phi0,'t',(t-tao));>> F=phi*H*1;x2=int(F,tao,0,t);>> x=collect(x1+x2)得到x =2497/2500*exp(t)+3/2500+1/400*t*exp(t)-1/20+1/20*exp(t)这表示⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-++=t t t e te e t x 20120140012500325002497)( P274T16设有n 阶系统()(1)110()n n n x a x a xa x u t --++++= 其中u(t)是控制函数,试写出使泛函()102t m t J x c u d t⎡⎤=-+⎣⎦⎰ 取极小值的欧拉方程。
线性系统理论试题

x&1 x&2
=
−7
0
x&3 0
0 −5 0
0 x1 0
0
x2
+
4
−1 x3 7
0
0 5
u1 u2
解:由于对角规范型中 B 包含元素全为零的行,故系统不完全能控。
3.(约当规范形判据的应用)判断下面系统的能控性和能观性
1 1 0 0 0 1
x&
=
0 0
1 0
0 1
u = e(t),输出变量 y = uc。
解:
e
=
uc
+
R
⋅C
duc dt
, x& = − 1 x + 1 u RC RC
, y=x
2.(由输入输出描述建立状态空间描述)系统的传递函数如下,求系统的状态空 间描述
G(s)
=
s3
s2 + s + 5 + 6 s2 + 12 s
+
4
0 解:可控标准形, x& = 0
s −1 0 1 det(sI − A) = 0 s −1 0 = (s −1)2 (s − 2) = 0
0 0 s−2
则系统特征值为 λ1 = 1( λ1 的代数重数 σ1 = 2 ), λ2 = 2 ( λ2 的代数重数 σ 2 = 1 )。 (2)有重特征值,判断是否可以化为对角规范形
对于 2 重特征值 λ1 = 1,它所对应的特征矩阵
1 0
υ11
= 1,υ22
= 1 ,得到
2
个属于二重特征值 λ1
= 1的特征向量υ1
=
0
清华线性系统控制理论作业一参考解答

2.(根据框图写出状态空间描述) 图2.2中描述了列车悬浮系统的工作原理,其中,1、2、3、 4为电磁装置,车辆通过电磁力的作用,悬浮于轨道上。磁悬浮控制系统的目的是通过调整 电磁作用力的输入,保证列车在运行过程中的平稳。这里我们考虑车辆运行过程中产在x和y 轴两个方向的位移,给出其线形化系统框图如图2.1所示
描述,其中g 是重力加速度常数,如图3所示,h 是自行车质心距地面高度,w 是两个轮子 与地面接触点的距离, b 是自行车质心投影与后轮和地面接触点的距离。 试给出该线性系统 的一个状态空间描述。
图3 参考文献: [3.1] Bicycles, motorcycles, and models-single-track vechicle modeling and control, IEEE Control Systems Magazine, October, 2006. 参考解答:
作业一
1.(线性化)已知倒立摆系统满足如下非线性状态方程
1 (t ) x2 (t ) x 2 (t ) ( g / l ) sin x1 (t ) u (t ) x
通过线性化给出系统在平衡解 [ x1 (), x2 ()] [0,0] , u () 0 的邻域内的线性模型。 参考解答:
图 2.2
参考解答:
注意状态变量的维数. 3. (从传递函数得到状态方程描述)图3中给出了解释自行车姿态动态平衡的原理图示。在 前进速度保持为定常v 的假设下,车把转角 对车身姿态角 的作用在平衡点( =0, =0)附近范围内可用微分方程
g v2 bv h hw wh
图2.1 这里A11=[100 0;0 200] B21=[10 -3;-5 16] C22=[1 1;1 -1]。 这里输入向量u是控制的作用力, 也就是车辆的加速度量, 输出向量y是车辆在两个轴方向的 位移量,通过间隙传感器测量。试列写出系统的状态空间模型。 参考文献: [2.1] H2 and H∞ control for MagLev vehicles,IEEE Control System Magazine, 1998 [2.2] Experimental comparison of linear and nonlinear controllers for a magnetic suspension, Proceedings of the 2000 IEEE International Conference on Control Applications,2000 [2.3] 广义线性磁悬浮对象的H∞控制问题,西安交通大学学报,Feb,2000
第一篇线性系统理论习题答案

9-7 设有三维状态方程
⎡0 ⎤ ⎢1 ⎥ ⎢ ⎥ ⎢ ⎣1 ⎥ ⎦
1 s + s +1 s 2 s + s +1
2
0
⎤ 0 ⎥ ⎥ ⎡0 ⎤ s 2 + 2 s 1⎥ = 3 0 ⎥ ⎢ ⎢ s −1 ⎥ ⎥ 1 ⎥ ⎢ ⎣1⎥ ⎦ s − 1⎥ ⎦
⎡ R M ⎤ ⎡ R −1 ∵⎢ ⎥×⎢ ⎣0 T ⎦ ⎣ 0
− R −1 MT −1 ⎤ ⎡ R −1 ⎥=⎢ T− ⎦ ⎣ 0
⎡R M ⎤ ∴⎢ ⎥ ⎣0 T ⎦
9-10 解
−1
⎡ R −1 =⎢ ⎣ 0
− R −1 MT −1 ⎤ ⎥ T −1 ⎦
−1
对可控标准形 A 和 b ,计算 ( sI − A) b
+
v2
& 2 = x1 + y = x1 − C 2 x
写成矩阵形式为
1 1 x2 + U R2 R2
图 9-1 RLC 网络
⎡ R1 − & x ⎡ 1 ⎤ ⎢ L1 ⎢x ⎥=⎢ ⎣ &2 ⎦ ⎢ 0 ⎢ ⎣
⎤ ⎡ 1 ⎤ 0 ⎥ x ⎡ ⎤ ⎢ L ⎥ ⎥ ⎢ 1 ⎥ + ⎢ 1 ⎥U − 1 ⎥ ⎣ x2 ⎦ ⎢ − 1 ⎥ ⎢ R2 C 2 ⎥ ⎦ ⎣ R2 C 2 ⎥ ⎦
x1 , x 2 有下列关系存在 x1 = x1 + x 2 x 2 = − x1 − 2 x 2
试求系统在 x 坐标中的状态方程。 解 ①
&1 = x & = x2 x &2 = & & = −2 x1 − 3 x 2 + u x x
