2.1群的线性表示.ppt
《近世代数》PPT课件

a b a b ,(m m )o a b d a b(m m )o
10.01.2021
编辑ppt
18
2.2 多项式剩余类环和域
1.域上多项式的定义
– 多项式与码字的关系:桥梁;
• 多项式的系数表示
;
• x的幂次表示
;
– 域上的多项式
• 针对系数定义;
• 例如二进制系数多项式,称为二元域GF(2)上的 多项式。
编辑ppt
28
(1) 常数总是多项式的因子。
(2) 一个多项式 f(x) 是否为既约多项式 与所定义的域有关。
(3) 一个多项式既约的充要条件:多项 式Pl(x) 不能分解成两个次数低于Pl(x) 的多项式的乘积。
(4) 完全分解:n次多项式最多能分解成 n个一次多项式的乘积,被称为完全分 解。
(5) 一次多项式一定是既约的。
(3)加法和乘法之间满足如下分配率 (distributive) :
a(bc) abac
(bc)a baca
则称F是一个域。
10.01.2021
编辑ppt
6
(1)域的阶(针对群中元素的个数),记 为q。
(2)有限域或伽逻华(Galois)域,表示为:
GF(q)。
–域将
10.01.2021
和
编辑ppt
联系在一起?
7
例2-3
– F1:有理数全体、实数全体对加法和乘法都 分别构成域,分别称为有理数域和实数域。
– F2:0、1两个元素模2加构成域;由于该域 中只有两个元素,记为GF(2)。
10.01.2021
编辑ppt
8
• 定理:
– 设p为质数,则整数全体关于p模的剩余类: 0,1,2,…,p-1,在模p的运算下(p模相 加和相乘),构成p阶有限域GF(p)。
数学高等代数第五版

目 录
• 引言 • 线性方程组与矩阵 • 向量空间与线性变换 • 多项式与行列式 • 线性方程组的解法 • 线性变换的矩阵表示 • 二次型与矩阵的相似对角化 • 总结与展望
01 引言
课程简介
高等代数是数学的一个重要分支,主 要研究线性代数、多项式、群、环和 域等抽象代数结构及其性质和关系。
常用的解法包括高斯消元法、LU 分解法、迭代法等,可以根据具 体情况选择合适的解法。
线性方程组在各个领域都有广泛 的应用,如物理、工程、经济等。
矩阵的基本概念
矩阵的定义
矩阵是一个由数字组成的矩形阵列,行和列都有 一定的数量。
矩阵的元素
矩阵中的每个元素都有其行标和列标,表示其在 矩阵中的位置。
矩阵的维度
相似变换
如果存在一个可逆矩阵P,使得$P^{-1}AP=B$,并且B的特征值和特征 向量与A相同,则称A经过相似变换得到B。
矩阵的特征多项式与特征值
特征多项式
对于一个给定的矩阵A,存在一个多项式$f(lambda)$,使得 $f(lambda)=0$是A的特征方程,这个多项式称为矩阵A的特征多项式。
高等代数作为大学数学专业的一门必 修课程,对于培养学生的逻辑思维、 抽象思维和数学素养具有重要意义。
学习高等代数的重要性
培养数学思维
高等代数作为数学专业的基础课程,通过学习代数结构和性质,可以培养学生的数学思维和逻辑推理 能力。
应用领域广泛
高等代数在科学、工程、经济、金融等领域有广泛应用,如线性方程组求解、矩阵计算、数据降维、 机器学习等领域都需要用到高等代数的知识。
深化数学理解
学习高等代数有助于学生深化对中学阶段数学知识的理解,如代数方程、平面几何、解析几何等,能 够更好地理解和应用这些知识。
群论 群的线性表示 基础

1 0 0 0 1 e1 , e2 , en 0 0 0 1
线性变换:
矢量:
x1 x2 x x n
封闭性 分配律
●
a(XY)=(aX)Y=X(aY) 数与矢量可对易
这样的线性空间V称为线性代数或代数。 (可)结合代数:满足 (XY)Z=X(YZ) 的代数
2) 群代数:
● (线性)代数是在线性空间上定义矢量乘法, 现 在群空间上定义矢量乘法 ● 规则 数与数: 普通数的乘法
群元素与群元素: 群元素的乘积规则 即
PG
给出了D(S)与S间一一对应关系
按惯例算符乘积定义为两个算符的相继作用 矩阵之间按照矩阵乘积规则相乘, 则 算符乘积和矩阵乘积仍按照上式一一对应 这种算符与其矩阵形式一一对应或多一对应关系在乘积中保 持不变的性质,在群论中会经常遇到,只给出这一次证明 证明:算符与其矩阵形式一一对应关系对它们乘积保持不变
2) 由乘法表写出群的正则表示 方法:♣ 群元素S的正则表示中,矩阵形式由 乘法表中S所在行的乘积元素决定
♣ 表示矩阵中第R列不为零的矩阵元素所在行 就是乘法表S行中R列的乘积元素标记的行
S R
E C4 C42 C43 mx my σu σv
按列写
σv
σv my σu mx C43 C4 C42 E
RG SG
矢量
矢量分量
基
自然基:以群元素作为基
3. 群代数
1) 线性代数: 若在线性空间引入矢量乘法, 则要求线性空间关于乘法是封闭的,且满足分配律,即 若V是数域K上的线性空间,在V中可以定义乘法
对 X,Y,Z∈V, a∈K 满足
分子的对称和群
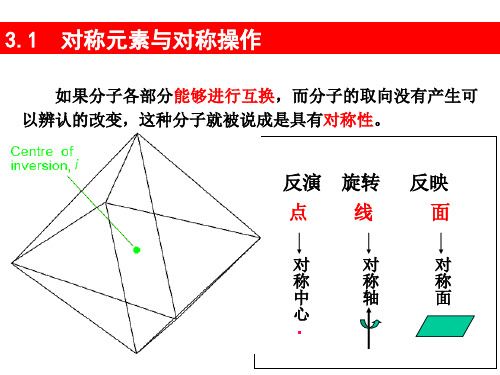
(正四面体构型的分子)
对称元素:3个C2,4个C3,3个S4 , 6个d
ˆ ,4C ˆ ,4C ˆ 2 ,3S ˆ1 ,3S ˆ 3 ,6 ˆ ,3C ˆd Td E 2 3 3 4 4
C3 C2 (S4)
24阶群
Cபைடு நூலகம்4
P4
d
CH4、P4、GeH4、SO42-、ClO4-、CrO4-、MnO4-
Cn
C2
阶数:2n
C2 C2
C2
D2
[Co(dien)2]3+
C2
D3
[Co(en)3]3+
2) Dnh群 对称元素: E,Cn,nC2,h, (nv, Sn) 阶数:4n
C2H4, N2O4 D2h
C6H6 D6h
重叠式C2H6
D3h
Cl Cl Re Re Cl Cl
Cl
Cl Cl Cl
Cl Cl Re Re Cl Cl
Cl
Cl Cl Cl
找出对称元素
PCl5
Mn(CO)5I
§3.2 点对称操作群(点群)
3.2.1 群的定义、群阶
3.2.2 主要点群
3.2.3 分子点群的确定
3.2.1 群的定义、群阶
我们称元素的某个集合形成一个群,群有着严格 的定义:“封闭性、结合律成立、存在恒等元素、存 在逆元素”。群中元素的个数,称作群阶。
C 6 H6
PtCl42
-
CO2
N2F2
SiF4
BF3
对称中心的性质
• 通过中心连续进行两次反演,分子中所有 原子均回到起始位置,得到起始构型的恒 等构型,其效应等于不动,即i2=E。由此 推得,i2n=i2=E; i2n+1=i, n为整数.
第二章_群表示理论

第二章 群表示理论基础§2.1 群表示【定义2.1】 (线性空间)数域K (实数域R 或复数域C )上的线性空间V 是一个向量集合,}{x V=;该集合定义了加法和数乘两种二元运算,且集合V 在加法运算下构成交换群,满足:,唯一逆元)()(唯一单位元,有o x x x x o x x o o x z y x z y x x y y x V z y x=+-=-+=+=+++=+++=+∈∀,)()(,, 数乘运算KV →V 满足:x x x b x a x b a ya x a y x a xb a x ab K b a=+=++=+=∈∀1)()()()(,,【定义2.2】 (线性无关和维数)线性空间V 中,任意n 个向量n x x x,,,21,其线性组合02211=+++n n x a x a x a当且仅当021====n a a a 时成立,则称此n 个向量线性无关,否则它们线性相关。
线性空间中线性无关向量的最大个数m ,称为空间V 的维数,记为dim V = m 。
【定义2.3】 (基矢)设V 是n 维线性空间,则V 中任意一组n 个线性无关的向量,称为空间V 的基矢,记为),,,(21n e e e 。
空间中任意矢量均可表示为n 个基矢的线性组合,∑=n ii i e x x。
矩阵形式:n i i i e e e e e e 0000121+++++=+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0100][,0100),,(21i n i e e e e e⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛==∑=n n n i ni i x x x x x x x e e e e x x 2121211][,),,,(【定义2.4】 (线性变换)线性变换A 是将V 映入V 的线性映射,满足:)()()(,)(,:,,,y A x aA y x a A V x A V V A K a V y x+=+∈→∈∈∀线性变换的矩阵形式:采用列矢量记法⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛====⎪⎪⎪⎪⎭⎫⎝⎛=='====∑∑∑∑∑∑∑∑n n n nn n n n i j ij j i iiij jj jj j nj j j n ii ij j j jjj j j j y y e e e x x A A A A e e e x a e e a x e x A x A a a a e e e e a e e A e y y e x x y x A 12111111212121),,,(),,,())()(),,,()(,,)(故有矩阵形式:⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=n n nn n n y y x x A A A A y x A 111111],[]][[ 若0]det[≠A ,则称线性变换A 非奇异,A 有逆变换A -1,[A -1]=[A ]-1。
群论课件ppt

元素数量是有限的集合。
03
02
置换
将一个有限集合的元素重新排列。
乘法
置换之间的运算。
04
循环群
01
02
03
循环群
由一个元素生成的群,即 置换群中所有元素都是该 元素的循环。
循环
将一个元素替换为另一个 元素,其它元素保持不变 。
元素生成
由一个元素开始,通过重 复应用某种变换得到的所 有元素。
群论课件
目录
• 群论基础 • 置换群 • 群论的应用 • 群表示论 • 群论中的问题与挑战 • 群论与其他数学领域的联系
01
CATALOGUE
群论基础
群的定义
群是由一个集合和定义在这个集合上 的一个二元运算所组成的一个代数结 构。这个二元运算被称为群中的“乘 法”。
群中的元素可以是有理数、整数、矩 阵、变换等,具体取决于实际应用和 研究领域。
群论与几何学的联系
对称性
群论在几何学中广泛应用于描述对称性。例 如,晶体学中的晶格结构可以用群论来描述 其对称性。此外,在几何图形中,我们也可 以用群论来描述图形的对称变换。
几何形状的分类
通过群论的方法,我们可以对几何形状进行 分类。例如,根据其对称性,我们可以将几 何形状分为不同的类型。这种分类方法有助 于我们更好地理解和研究几何形状的性质和
群表示是群论中一个重要的概念,它有助于将群的结构和性质转化为线性 代数的语言,从而更好地理解和研究群。
特征标与维数
01
特征标是群表示的一个重要概念 ,它描述了群在某个向量空间上 的作用方式。
02
特征标是一个函数,将群中的每 元素映射到复数域上,它反映
了群元素的性质和作用方式。
群论(1)第二章

cos µ ¡ sin µ 0 D(R) = @ sin µ cos µ 0 A 0 0 1
0
1
可以验证,D(R)构成平面转 动群的真实表示。(练习)
例2:
系统哈密顿量H,本征值E的能级m重简并
Hù = Eù; ¹ = 1; 2; ¢ ¢ ¢ ; m
G = fRi g
系统的对称变换构成群
,有
m X j=1
Ãj [D(R)D(S)]jk
(1)G与D(G)建立了对应关系 (2)对应关系的性质由变换 群的性质与基矢量的选取决 定
RS -> D(R)D(S)=D(RS) D(G)构成群G在线性空间V上 的表示,V也称为D(G)的表 示空间
例1:平面转动群的二维表示
平面转动R,逆时针转theta角
8 <1 DP R(S) = : 0 if P = T = SR if P 6= SR
这样的矩阵构成群,与G同构,构成群G的g维表示,称 为正则表示,表示空间为群空间。
正则表示的特征标
对角元
DRR (S) =
8 <1 : 0
if R = SR if R 6= SR
if S = E if S 6= E
D1也是可约表示 根本原因 V3 (x; y; z) = V2 (x; y) © V1 (z)
逆向思维
有群G不变的两个线性空间w(n维)和w’(m维),则有两 表示空间上的群表示C(G)和B(G) 将两线性空间直和,得到更高维(n+m)的线性空间
群G即有n+m维的可约表示
该表示的表示空间为V=w+w’
X X=
群论第三章A

0 1 0 3 0 − 1 , D′( F ) = 2 2 1 3 0 − 2 2
定义: 定义:群 G{E , A, B, ⋯} 表示 D(G ){D(E ), D( A), D(B ), ⋯} 则
trD (E ) = ∑ D (E )ii ≡ χ (E )
也是它们的表示,但无意义 即:
D( E ) = D( A) = D( B ) = ⋯ = (1)
称为恒等表示
3.1.2 等价表示和特征标
定理:若 D(G ){D(E ), D( A), D(B ), ⋯} 为群 G{E , A, B,⋯} G的表示。 证:∵ D(A)D(B) = D(AB)
−1 −1 −1 −1 ∴ (xD( A)x )(xD(B )x ) = xD( A)D(B )x = xD( AB )x
γ
PRϕα (r ) = ∑ ϕ β (r )D( R ) βα
β
则:PS PRϕα ( r ) = PS ∑ ϕ β ( r )D( R) βα = ∑ [PSϕ β ( r )]D ( R ) βα
β β
= ∑ ∑ ϕγ (r )D ( S )γβ D ( R) βα = ∑ ϕγ ( r ) ∑ D ( S )γβ D ( R ) βα β γ γ β = ∑ ϕγ (r )[D( S ) D ( R )]γα
且PR ↔ R; PS ↔ S ; PR PS = PRS ↔ RS ;⋯
∴{R}和{PR}有相同的表示,同构。
ϕ ′′(r ) = Ps PRϕ (r ) ϕ ′′(r ) = ϕ (r )
r ′′ = SRr r = ( SR) −1 r ′′
ϕ ′′(r ′′) = ϕ (( SR) −1 r ′′) ϕ ′′(r ) = ϕ (( SR) −1 r ) = PSRϕ (r ) ∴ Ps PRϕ (r ) = PSRϕ (r )
