巧借轴对称求最短距离
七年级数学 轴对称之—最短距离

轴对称之——最短距离类型一、两点之间线段最短例1:已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P 是对角线BD上一点,则PM+PN的最小值= .例2:如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是.例3、如图,在Rt△ABC中∠ACB=90°,AC=BC=8,CD=2,点P是AB上的一的动点,求:PC+PD的最小值。
例4、如图,在矩形ABCD中,AB=2,AD=4,E为CD边的中点,P为BC边上的任一点,那么,AP+EP的最小值为。
例5、如图,已知⊙O的直径MN=1,点A在圆上,且∠AMN的度数为30°,点B是弧AN的中点,点P在直径MN上运动,求BP+AP的最小值.例6、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底5cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿5cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为?例7:如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC 沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是.例8:如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是().例9:如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一个动点,则PA+PC的最小值为().A. B. C. D.2例10(一定两动)如图∠AOB=45°,角内有一点P,PO=10,在两角边上有两点Q、R(均不同于点O),则△PQR的周长最小值是当△PQR周长最小时,∠QPR的度数=例11(两定两动)如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.类型二、垂线段最短例12、如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值为。
用轴对称求最短距离

用轴对称求最短距离在研究几条线段长之和(差)的最小或最大值时,常常需要把这些线段集中到一起,然后将其与某条长度固定的线段进行比较。
把其中的部分特殊点进行恰当的轴对称变换,是实现这一目标的有效手段。
现举例说明,供同学们参考。
一、为了在已知直线上寻找与同侧两点距离之和最小的点,可通过轴对称变换,把同侧两点转化为异侧两点,再利用“三角形任意两边之和大于第三边”来确定例1. 如图1,牧童在A处放牧,其家在B处,A、B到河岸l的距离分别为AC、BD,,且A处到河岸CD中点的距离为500m。
(1)如牧童从A处将马牵到河边饮水后再回家,试问:在何处饮水,所走路程最短?(2)最短的路程是多少?解析:这个问题可简述为“已知直线CD和直线CD同侧的两点A,B,在直线CD 上求一点M,使最小。
”(1)如图2,先作点A关于直线CD的对称点,再连接交CD于点M,则点M为所求的点。
证明如下:在CD上任取一点,连接、、、AM。
点A、关于直线CD对称,点M、在CD上,。
最小。
(2)由(1)知,,。
故M为CD中点,且最短路程为。
二、在涉及折线段长的最值问题的,一般是通过多次轴对称变换,利用两点之间线段最短求最值。
例2. 如图3,牧童家在A处。
现在牧童要先带马到河边(图中用直线a表示)饮水,再到草地(图中用直线b表示)吃草,然后回家。
问:牧童让马在何处饮水、吃草,所走的总路程最短?解析:设点B、点C分别是马饮水、吃草处,本题即是要求线段长之和AB+BC+CA 的最小值。
我们通常需要把它和固定线段相比较。
可通过轴对称变换,把这些线段放在同一直线上,利用两点之间线段最短来解决。
如图4所示,分别作点A关于直线a的对称点A”,点A关于直线b的对称点A””。
连接A”A””。
A”A””交直线a于点B,交直线b于点C,则AB+BC+CA=A”B+BC+CA””=A”A””。
而对其他地点B”、C”,也都可以同样转化为A”B”+B”C”+C”A””,即为A”、A””两点间的折线段的长。
利用轴对称求两点一线型最短距离

利用轴对称求“两点一线”型最短距离几何模型:模型:“两点一线”模型条件:如图,A、B是直线l同旁的两个定点.+的值最小.问题:在直线l上确定一点P,使PA PB方法:作点A关于直线l的对称点A',连结A B'交l于点P,+=的值最小.则PA PB A B'模型应用:一. 两点一线间的对称二.三角形中的对称1.如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边上的中点,E是AB边上的一动点,则EC+ED的最小值是__2.如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是.三.四边形中的对称1.如图,正方形ABCD的边长为8, M在DC上,且DM=2,N是AC上的动点,则DN+MN的最小值为多少?2.如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连结BD,由正方形对称性可知,B与D关于直线AC对称.连结ED交AC于P,则+的最小值是___________;PB PE△是等边三角形,点E在正方形3.如图所示,正方形ABCD的面积为12,ABE+的和最小,则这个最小值为()ABCD内,在对角线AC上有一点P,使PD PEA.B.C.3 D四.圆中的对称1.如图,已知点A 是⊙O 上的一个六等分点,点B 是弧AN 的中点,点P 是半径ON 上的动点,若⊙O 的半径长为1,求AP+BP 的最小值。
2.如图,O ⊙的半径为2,点A B C 、、在O ⊙上,OA OB ⊥,60AOC ∠=°,P 是OB 上一动点,求PA PC +的最小值;五.立体图形中的对称如图是一个没有上盖的圆柱形食品盒,一只蚂蚁在盒外表面的A 处,它想吃到盒内表面对侧中点B 处的食物,已知盒高h =10cm ,底面圆的周长为32cm ,A 距离下底面3cm .请你帮小蚂蚁算一算,为了吃到食物,它爬行的最短路程为 cm .课堂练习: 1.如图,在菱形ABCD 中,对角线AC=6,BD=8,点E 、F 分别是边AB 、BC 的中点,点P 在AC 上运动,在运动过程中,存在PE+PF 的最小值,则这个最小值是 .2.如图,在梯形ABCD 中,AB ∥CD ,∠BAD=90°,AB=6,对角线AC 平分∠BAD ,点E 在AB 上,且AE=2 (AE <AD ),点P 是AC 上的动点,则PE+PB 的最小值是 .3.如图,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点,5.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为.6.如图,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为 cm.7.在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,则线段AT长度的最大值与最小值之和为(计算结果不取近似值).8.如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N 分别是边AB、BC的中点,则PM+PN的最小值是.9.如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若PM+PB 的最小值是3,则AB长为.解答题:1.如图,45AOB∠=°,P是AOB∠内一点,10PO=,Q R、分别是OA OB、上的动点,求PQR△周长的最小值.2.一次函数y kx b=+的图象与x、y轴分别交于点A(2,0),B(0,4).(1)求该函数的解析式;(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点坐标.ABPRQ图3中考题综合演练:1.(1)观察发现:如(a)图,若点A,B在直线l同侧,在直线l上找一点P,使AP+BP 的值最小.做法如下:作点B关于直线l的对称点B',连接AB',与直线l的交点就是所求的点P.再如(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.做法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为.(2)实践运用:如(c)图,已知⊙O的直径CD为4,∠AOD的度数为60°,点B是AD^的中点,在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.(3)拓展延伸:如(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留作图痕迹,不必写出作法.2.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.⑴求证:△AMB≌△ENB;⑵①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;3 时,求正方形的边长.⑶当AM+BM+CM的最小值为1。
中考专题复习:利用轴对称解决最短距离问题

主备人单位日期2019.5 课型复习课课题专题复习:最短距离学习目标1.能够通过观察找出最短距离问题的基本模型。
2.能够运用基本方法找出最短距离。
3.能够利用勾股定理、相似、三角函数等相关知识解决计算问题。
教学过程一、问题引入:1、如下图,在直线异侧各有点A、B,在直线上找一点p,使PA+PB最小。
2、如下图,在直线同侧各有点A、B,在直线上找一点p,使PA+PB最小。
二、1.在几何背景中的应用例1、如图正方形ABCD的边长为4,P为对角线上任意一点。
若E为边BC 的中点,求PE+PB的最小值______变式:如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为.师生笔记例2.(东营中考)在⊙O中,AB是⊙O的直径,且AB=8cm, M是AB上一动点,,CM+DM的最小值是__________.例3.如图,菱形ABCD中,∠BAD=60°,AB=4,点M是AB中点,P是对角线AC上的一个动点,则PM+PB的最小值是_______2.在函数背景中的应用例4、如图,已知二次函数y=ax2-4x+c 的图象与坐标轴交于点A(-1,0)和点B(0,-5).(1)求该二次函数的解析式;(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.求出△ABP周长的最小值,求出点P的坐标.变式、如图,抛物线y=ax2+bx+c 经过点A(1,0)、B(4,0)、C (0,3 ).(1)求抛物线的解析式;(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由。
课堂小结:1、知识点:2、基本数学模型:。
利用轴对称求最短距离精修订

分析:由题意知:首先找点D或者点E关于AC所在直线的对称点。由正方形的轴对称性不难发现:点B即是点D关于直线AC的对称点,则连接BE与线段AC的交点即为P点。那么PD+PE的最小值实际上就是线段BE的长度,BE=2。
(2)、以正方形为媒介的最短距离问题:
如下图,正方形ABCD边长为2,△ABE为等边三角形,且点E在正方形ABCD内部,在对角线AC上找一点P,使PD+PE最小,则这个最小值为多少?
(3)、以圆为媒介的最短距离问题:
如下图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,
∠AOB=60°,P是OB上一动点,求PA+PC的最小值
(4)、以二次函数为媒介的最短距离:
如下图,抛物线y=x^2+2x-3与x轴交与A、B两点,与y轴交与点C,对称轴上存在一点P,使△PBC周长最小,求P点坐标。
三、巩固加深:
(5)、以三角形为媒介的最短距离问题:
如下图,在锐角△ABC 中,AB=4,∠BAC=45°,∠BAC的角平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少
分析:由AD是∠BAC的角平分线得,点N关于直线AD对称的点N′一定在线段AC上,则直线AD是线段NN′的垂直平分线,则MN=MN′,则求BM+MN的最小值就是求BM+MN′的最小值。易知点B、M、N′三点共线时BM+MN′最小,根据“点到直线上点的距离中垂线段最短”得:过点B作AC的垂线,垂足为N′′,则BN′′的长度就是BM+MN′的最小值,也就是BM+MN的最小值。由△ABN′′为等腰直角三角形,AB=4立得。
利用图形的对称性(轴对称)求最短路径问题
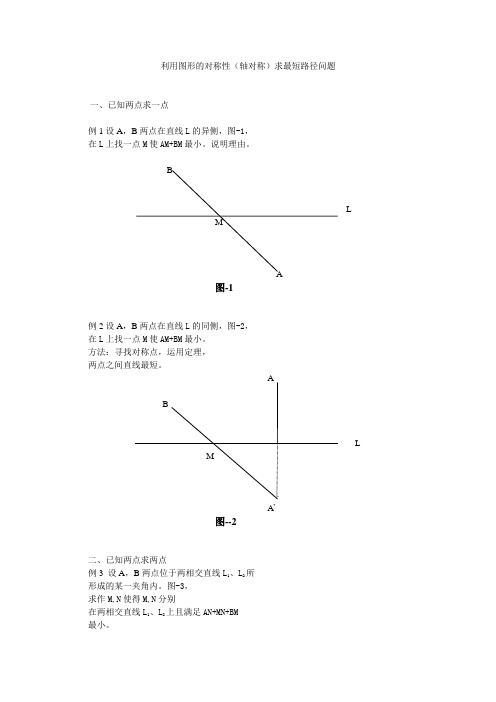
利用图形的对称性(轴对称)求最短路径问题一、已知两点求一点例1设A,B两点在直线L的异侧,图-1,在L上找一点M使AM+BM最小。
说明理由。
BLMA图-1例2设A,B两点在直线L的同侧,图-2,在L上找一点M使AM+BM最小。
方法:寻找对称点,运用定理,两点之间直线最短。
ABLMA’图--2二、已知两点求两点例3 设A,B两点位于两相交直线L1、L2所形成的某一夹角内。
图-3,求作M,N使得M,N分别在两相交直线L1、L2上且满足AN+MN+BM最小。
L1B’. AM . BL2NA’图--3例4 设P,Q两点位于锐角 ABC的BC边上,有两动点M,N分别位于另外两边上,图-4,求作M,N使四边形PQNM的周长最短。
P’ BM PQCA N图--4Q’三、已知一点求两点例5 点P位于三角形的某一边上,动点M,N分别位于另外两边上。
图-5,试作M,N使得❒PMN周长最短。
P’ BPMA N CP’’图—5例6 点P位于两相交直线L1,L2所形成的夹角内,动点M,N分别位于两直线上。
图-6,试作M,N使得❒PMN周长最短。
L2PML1N图-6我们将这些情况放在直角坐标系下考虑。
第一种情况:设A,B两点都在第一象限,直线L与X轴重合,M点在X轴上,且使AM+BM最小。
求(1)M点的坐标。
(2)AM+BM的长度。
第二种情况设A,B两点,B点在第Ⅰ象限,M,N分别在Y轴,X轴上,A点分别在第Ⅰ象限,第Ⅱ象限,第Ⅲ象限,第Ⅳ象限时,试求(1)M,N的坐标,使得AM+MN+BN最小,并求出最小值。
(2)两动点M,N到达何处时,四边形AMNB周长最短。
Y训练题1.已知,AB是圆O的直径,P、Q是圆O上的两点,且直线PQ//AB,M是直径AB是上动点,试问:∆PQM周长最短时,M点处于何处?并证明。
A B【思路】由于三角形∆PQM的一边PQ是定长,因此要使它的周长最短就是要求动点M到点P、Q的距离之和最短。
利用图形的对称性,作Q关于直线AB的对称点Q’,连接PQ’,它与AB相交于M即为所求。
利用轴对称求最短距离

利用轴对称求最短距离轴对称知识在近来的中考题中,经常出现,笔者浏览最近几年各地的中考试题,发现各地中考试题除考察轴对称图形的基本知识和性质,还考察了利用轴对称知识解决最短距离问题,这类问题在各地中考试题中,屡见不鲜,如何利用轴对称的性质解决最短距离问题呢?根据本人多年从事初三数学教学工作的一些体会。
概括一些一些常见的题型。
一、基础知识如图直线l 同侧有两点A 、B ,在直线l 上找点P ,使得PA+PB 最短,并简要说明理由。
解:作点关于直线l 的对称点A ′,连A ′B 交直线l 于点P,则点P 即为所求,此时PA+PB=PA ′+PB= A ′B 。
A 1二、典型例题:A 组(1)以菱形为载体的最短距离问题:如图所示,菱形ABCD 中, ∠ BAD=60°,AB=4,M 是AB 的中点,P 是对角线AC 上的一个动点,则PM+PB 的最小值是_________。
解:∵菱形ABCD 是以AC 为对称轴的轴对称图形。
∴点B 关于直线AC 的对称点为点D,ABLP连接DM 交AC 于点P,则PM+PB 的最小值即为线段DM,此时DM=32 ∴PM+PM 的最小值为32.(2)以矩形为载体求最短距离问题在矩形ABCD 中,AB=2,AD=4,E 为为边CD 中点。
P 为边BC 上的任一点,求PA+EP 的最小值。
解:作点A 关于BC 的对称点A ′,连A ′E 交BC 于点P,则点P 为所求,此时PA+PE 的最小值即为A ′E,过点E ,作EF ⊥AB , A ′E=2243 =5 ∴PA+PE 的最小值为5。
MA A 1ED如图所示,正方形ABCD 的边长为2,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上找一点P,使PD+PE 最小,则这个最小值为_________.解:∵正方形ABCD 是以AC 为对称轴的轴对称图形。
∴点B 关于点D 关于AC 对称 ∵BE 即为PD+PE 的最小值 ∴PD+PE 的最小值为2(4) 以圆形为载体的最短距离问题:如图,⊙O 的半径为2,点A 、B 、C 在⊙O 上,OA ⊥OB, ∠ABC=60°,P 是OB 上一动点,求PA+PC 的最小值。
(完整版)利用轴对称求最短距离

利用轴对称求最短距离一、问题引入:1、如下图,在直线异侧各有点A、B,在直线上找一点p,使PA+PB最小。
分析:根据“两点之间线段最短”,可知:连接AB,与直线的交点即为P点.此基本类型为:一线(直线)两定点(点A、B)。
分析:作点A关于直线的对称点A′,连接AA′,则直线就是线段AA′的垂直平分线,根据“垂直2、如下图,在直线同侧各有点A、B,在直线上找一点p,使平分线上一点到线段两PA+PB最小。
端点的距离相等”可得,直线上任一点到点A的距离都等于到点A′的距离。
事实上,这个问题就可以转化成:在直线异侧各有点A′、B,在直线上找一点p,使PA′+PB最小。
即:一线两定点的问题。
由(1)得,连接BA′,与直线的交点即为点P。
分析:由题意知:首先找二、典型例题:点B或者点M关于AC所(1)、以菱形为媒介的最短距离问题:在直线的对称点。
由菱形如下图,菱形ABCD中,∠BAD=60°,AB=4,点M是AB中点,的轴对称性不难发现:点P是对角线AC上的一个动点,则PM+PB的最小值是多少?D即是点B关于直线AC的对称点,则连接DM与线段AC的交点即为P点。
那么PM+PB的最小值实际上就是线段DM的长度分析:由题意知:首先找(2)、以正方形为媒介的最短距离问题:点D或者点E关于AC所如下图,正方形ABCD边长为2,△ABE为等边三角形,且点E在直线的对称点。
由正方在正方形ABCD内部,在对角线AC上找一点P,使PD+PE最小,形的轴对称性不难发现:则这个最小值为多少?点B即是点D关于直线AC的对称点,则连接BE与线段AC的交点即为P点。
那么PD+PE的最小值实际上就是线段BE的长度,BE=2。
分析:由题意知:首先找(3)、以圆为媒介的最短距离问题:点A或者点C关于OB所如下图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,在直线的对称点。
由圆的∠AOB=60°,P是OB上一动点,求PA+PC的最小值轴对称性不难发现:延长AO交圆于点A′,则点A′即是点A关于直线OB的对称点,则连接CA′与线段OB的交点即为P点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图5 l 图1 巧借轴对称求最短距离
大家知道“两点之间线段最短”,是解决最短距离问题的依据,在实际问题中,我们常碰到求不在一条直线上的两条或三条线段和的最小值问题,要解决这类问题,可借助轴对称的性质,将不在同一直线上的线段和转化为两点之间的距离问题.
例1如图1,公路l 两旁有两工厂A 、B ,现要在公路上建一仓库.
⑴若要使仓库到A 、B 两工厂的距离相等,仓库应建在何处?
⑵若要使仓库到A 、B 两工厂的距离之和最短,仓库应建在何处?
分析:⑴线段的垂直平分线的性质“线段垂直平分线上的点到这条线段两端点的距离相等”可知仓库应建在AB 的垂直平分线上,又因为仓库在公路上,所以AB 的垂直平分线与公路l 的交点即为仓库应建的地点. ⑵ 如果A 、B 两点在直线l 的两侧,那么连接AB 与l 的交点即为所求,由于现在A 、B 两点在l 的同侧,因此可考虑作A (或B )点关于l 的对称点C ,由轴对称的性质可知,直线l 上任意一点到A 、C 的距离相等,这样就把直线l 上一点到点A 的距离转化为到点C 的距离,因此连接CB 与l 的交点即为所求.
解:⑴如图2,作AB 的垂直平分线交l 于点P ,点P 就是所要求作的仓库的位置.
⑵如图3,作点A 关于l 的对称点C ,连接AC 交l 于点D ,点D 就是所要求作的仓库的位置.
例2如图4,已知牧马营地在点M 处,每天牧马人要赶着马群到河边饮水.
⑴求到河边饮水的最短路线.
⑵如果饮完水后,需再到草地吃草,然后回到营地,试设计出最短的牧马路线图.
分析:这是一道实际问题,从中抽象出数学问题是解题的首要a 的最短距离. ⑵可抽象得到
这样的数学模型:直线a 、b 间有一点M ,试分别在a 、b . 要求.
解:⑴如图5,过点M 作MA ⊥a 于A ,MA 即为最短路线.
⑵如图6,分别作点M 关于a 、b 的对称点A 、B ,连接AB 分别交a 、b 于点C 、D ,则最短的牧马路线为:M →C →D →M.
图4 l 图2 l
点评:⑴利用垂线段最短获解. ⑵中点A、M关于直线a对称,则可得到CA=CM,同理DM=DB,所以MC+CD +DB=AC+CD+DB,这实际上将ΔMCD的周长,即三条不在同一直线上的线段和转化成了两点之间的距离问题,由于“两点之间,线段最短”,因此连接AB与直线a、b的交点即为所求的两点.。
