电子教案-自动控制原理及其应用(第4版_黄坚)课件-4.4
自动控制原理电子教案
自动控制原理电子教案第一章：绪论1.1 自动控制的概念解释自动控制的定义强调自动控制在现代工业和日常生活中的重要性1.2 自动控制系统的分类介绍开环控制系统和闭环控制系统解释数字控制系统和模拟控制系统的区别1.3 自动控制系统的性能指标介绍稳定性、线性、收敛性和鲁棒性等性能指标解释这些指标对系统性能的影响第二章：反馈控制系统2.1 反馈控制系统的组成介绍控制器、执行器和传感器的功能和作用2.2 反馈控制系统的类型解释正反馈和负反馈的区别和应用场景2.3 控制器的设计方法介绍PID控制器和模糊控制器的原理和方法第三章：线性系统的状态空间分析3.1 状态空间表示法介绍状态空间的概念和数学表示方法3.2 状态方程和输出方程推导状态方程和输出方程的求解方法3.3 线性系统的可控性和可观测性解释可控性和可观测性的概念和判断方法第四章：非线性控制系统分析4.1 非线性系统的分类介绍线性与非线性的区别和常见的非线性特性4.2 非线性方程的求解方法解释求解非线性方程的数值方法和解析方法4.3 非线性控制系统的稳定性分析介绍李雅普诺夫理论和Lyapunov 函数的应用第五章：现代控制理论5.1 现代控制理论的概念解释现代控制理论的背景和发展5.2 鲁棒控制理论介绍鲁棒控制的概念和设计方法5.3 自适应控制理论解释自适应控制的概念和应用场景第六章：控制系统的设计方法6.1 系统设计的基本原则介绍控制系统设计中的稳定性、准确性和快速性原则6.2 控制器设计方法详细讲解PID控制器、模糊控制器、自适应控制器的设计步骤和注意事项6.3 系统仿真与实验介绍使用MATLAB等工具进行控制系统仿真的方法强调实验在控制系统教学和工程应用中的重要性第七章：线性调节器的设计7.1 调节器的作用与分类解释调节器的作用以及比例、积分、微分调节器的特点7.2 调节器的设计方法介绍Ziegler-Nichols方法等经典调节器设计方法7.3 调节器的参数整定讲解如何通过观察系统响应来整定调节器参数第八章：系统辩识8.1 系统辩识的基本概念解释系统辩识的目的和方法8.2 输入输出数据采集介绍如何采集系统的输入输出数据8.3 系统模型的建立与参数估计讲解如何根据采集到的数据建立数学模型并进行参数估计第九章：数字控制系统9.1 数字控制系统的组成介绍数字控制系统的硬件和软件组成部分9.2 数字控制算法详细讲解离散PID控制、模糊控制等数字控制算法9.3 数字控制器的实现介绍如何实现数字控制器，包括硬件实现和软件实现第十章：自动控制系统的应用10.1 工业自动化讲解自动控制系统在工业生产中的应用案例10.2 家居自动化介绍自动控制系统在智能家居中的应用案例10.3 汽车自动化探讨自动控制系统在现代汽车工业中的应用案例重点和难点解析重点环节：1. 自动控制的概念和分类2. 反馈控制系统的组成和类型3. 状态空间分析方法4. 非线性控制系统分析5. 现代控制理论6. 控制系统的设计方法和步骤7. 调节器的设计和参数整定8. 系统辩识的方法和模型建立9. 数字控制系统的组成和算法实现10. 自动控制系统的应用案例难点解析：1. 自动控制的概念和分类：理解自动控制的基本原理和不同类型控制系统的特点。
自动控制原理及应用课件
控制算法设计
采用位置闭环控制算法，根据位置误 差调节执行机构的输出，实现位置的 精确控制。
抗干扰措施
设计滤波器、隔离电路等抗干扰措施， 提高系统对外部干扰的抵抗能力。
07
现代控制理论在自动控制中应用
状态空间法描述动态系统
01
状态变量的定义与 性质
状态变量是描述系统动态行为的 最小变量集，具有可观测性和可 控制性。
极限环与振荡
研究相平面上可能出现的极限环及其性质， 分析系统的振荡行为。
描述函数法分析非线性系统
描述函数的性质
研究描述函数的幅值、相位等特性，分析非 线性系统的频率响应。
描述函数的概念
用一次谐波分量近似表示非线性环节的输入 输出关系。
描述函数法的应用
利用描述函数法分析非线性系统的稳定性、 自振频率等动态特性。
利用数学表达式描述系统的输入-输出关系，便 于理论分析和计算。
表格描述法
通过列出系统在不同输入下的输出值，形成输入输出对应表，方便查阅和对比。
相平面法分析非线性系统
相平面的概念
在相平面上绘制系统状态变量的轨迹，反映 系统的动态行为。
平衡点与稳定性
通过分析相平面上的平衡点及其性质，判断 系统的稳定性。
03
Z变换在离散系统分 析和设计中的应用
利用Z变换可以分析离散系统的稳定 性、因果性和频率响应等特性，进而 进行系统设计和优化。同时，Z变换 也可以用于数字滤波器的设计和分析 等应用领域。ຫໍສະໝຸດ 05非线性系统分析
非线性特性描述方法
图形描述法
通过绘制系统的输入-输出特性曲线，直观展示 非线性特性。
解析描述法
02
状态空间方程的建 立
自动控制原理电子教案
一、教案基本信息自动控制原理电子教案课时安排：45分钟教学目标：1. 理解自动控制的基本概念和原理。
2. 掌握自动控制系统的分类和特点。
3. 了解常用自动控制器的原理和应用。
教学方法：1. 讲授：讲解自动控制的基本概念、原理和特点。
2. 互动：提问和回答，让学生积极参与课堂讨论。
3. 案例分析：分析实际应用中的自动控制系统，加深学生对知识的理解。
教学工具：1. 投影仪：用于展示PPT和视频资料。
2. 计算机：用于播放教学视频和演示软件。
二、教学内容和步骤1. 自动控制的基本概念（5分钟）讲解自动控制系统的定义、作用和基本组成。
通过举例说明自动控制系统在实际中的应用，如温度控制、速度控制等。
2. 自动控制系统的分类和特点（10分钟）讲解自动控制系统的分类，包括线性系统和非线性系统、连续系统和离散系统、开环系统和闭环系统等。
介绍各种系统的特点和应用场景。
3. 常用自动控制器原理和应用（15分钟）介绍常用的自动控制器，如PID控制器、模糊控制器、神经网络控制器等。
讲解其原理和结构，并通过实际案例分析其应用。
4. 课堂互动（5分钟）提问和回答环节，让学生积极参与课堂讨论，巩固所学知识。
可以设置一些选择题或简答题，检查学生对自动控制原理的理解。
三、教学评价1. 课堂表现：观察学生在课堂上的参与程度、提问和回答问题的积极性等。
2. 作业完成情况：检查学生作业的完成质量，包括答案的正确性、解题思路的清晰性等。
3. 课程测试：在课程结束后进行一次测试，检验学生对自动控制原理的掌握程度。
四、教学资源1.PPT：制作精美的PPT，用于展示教学内容和实例。
2. 视频资料：收集相关自动控制原理的教学视频，用于辅助讲解和演示。
3. 案例分析：挑选一些实际应用中的自动控制系统案例，用于分析和学习。
五、教学拓展1. 开展课后讨论：鼓励学生在课后组成学习小组，针对课堂所学内容进行讨论和交流。
2. 参观实验室：组织学生参观自动控制实验室，实地了解自动控制系统的原理和应用。
《自动控制原理》电子教案
5
《自动控制原理》电子教案
《自动控制原理》课程实验教学大纲
一、实验教学目标与基本要求
《自动控制原理》课程实验通过上机使用 ＭＡＴＬＡＢ 软件，使学生初步掌握 ＭＡＴＬＡＢ 软件在控制理论中的 基本应用，学会利用 ＭＡＴＬＡＢ 软件分析控制系统，从而加深对自动控制系统的认识，帮助理解经典自动控 制的相关理论和分析方法。通过本课程上机实验，要求学生对 ＭＡＴＬＡＢ 软件有一个基本的了解，掌握 ＭＡＴＬＡＢ 软件中基本数组和矩阵的表示方法，掌握 ＭＡＴＬＡＢ 软件的基本绘图功能，学会 ＭＡＴＬＡＢ 软件中自动控制理论 常用函数的使用，学会在 ＭＡＴＬＡＢ 软件工作窗口进行交互式仿真和使用 Ｍ＿Ｆｉｌｅ 格式的基本编程方法，初步
制系统的性能。了解开环零、极点对系统性能的影响。
5．熟悉频率分析法分析控制系统性能的方法 熟悉典型环节频率特性的求取以及频率特性曲线，掌握系统开环对数频率特性曲线、极坐标曲线绘制 的基本方法。了解根据开环对数频率特性曲线分析闭环系统性能的方法。熟悉用奈奎斯特稳定判据判断系
1
《自动控制原理》电子教案
４．频率法反馈校正的基本原理和方法（选讲）
（七）非线性控制系统 了解非线性系统与线性系统的区别，了解非线性特性和非线性系统的主要特征，学会非线性系统的描 述函数分析方法，了解非线性系统的相平面分析法（选讲）。
3
《自动控制原理》电子教案
１． 非线性系统的基本概念
２． 典型非线性特性、非线性系统的主要特征
三、实验方法、特点与基本要求
本课程实验采用计算机 ＭＡＴＬＡＢ 软件仿真方法，其特点是利用 ＭＡＴＬＡＢ 软件丰富的功能函数、灵活的编 程和调试手段以及强大的人机交互和图形输出功能，可以实现对控制系统直观和方便的分析和设计。
《自动控制原理》电子教案
自动控制原理电子教案第 1 次课授课时间2学时授课题目（章、节）第一章绪论（1-3节）主要内容1．自动控制在各领域的应用2．自动控制的作用3．自动控制定义：自动控制就是在没有人直接参与的情况下，利用控制器使被控对象（或过程）的某些物理量自动地按预先给定的规律去运行。
4．自动控制系统的基本职能元件及基本框图等5．开环控制与闭环控制目的与要求了解自动控制系统的基本职能元件、基本术语及方框图掌握自动控制定义掌握开环、闭环控制的定义、基本框图重点与难点重点：自动控制的定义、开环控制与闭环控制的定义及框图教学手段授课、例题讲解思考题或作业题1-2１．１ 引言 无论是人们的日常生活、工业生产，还是空间探索、导弹制导等尖端科技领域中，自动控制技术无所不在、无所不能。
自动控制理论和技术已经渗透到社会、经济和科学研究的各个方面。
自动控制技术是建立在控制论基础上的，而控制论研究的是控制的一般性理论，它不具体面对某一类控制系统的，因此它是一门以理论为主的课程。
自动控制理论是一门理论性和工程性的综合科学。
１．控制理论的基础观念 控制理论是建立在有可能发展一种方法来研究各式各样系统中控制过程这一基础上的理论（也即，它是研究系统共性的控制过程的理论，可以把实际对象的物理涵义抽象出来，因此，它一定是以数学工具作为主要研究手段的）。
２．控制理论的研究对象 控制论的研究是面向系统的。
广义地讲：控制论是研究信息的产生、转换、传递、控制和预报的科学； 狭义地讲：根据期望的输出来改变控制输入，使系统的输出能达到某中预期的效果。
３．控制论与数学及自动化技术的关系 控制论是应用数学的一个分支，它的某些理论的研究还要借助于抽象数学。
而控制论的研究成果若要应用于实际工程中，就必须在理论概念与用来解决这些实际问题的实用方法之间架起一座桥梁。
１．２ 自动控制和自动控制系统 １．２．１自动控制问题的提出 人们存在着一种普遍的要求或希望，即要求某些物理量维持在某种特定的（如恒定不变或按某种规律变化或跟踪某个变化的量等等）标准上。
电子教案-自动控制原理及其应用(第4版_黄坚)课件-2.1
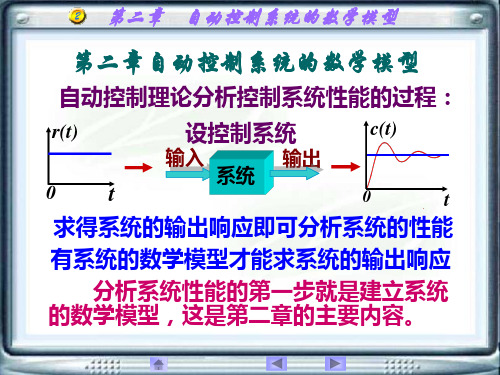
r(t)
c(t)
分析系统性能的第二步就是解微分方 程，工程中常采用拉氏变换法求解。
返回
系统组成：
(1) 中确间定变输量入关和系输式出: 输F入K量(t)=k输y(出t) 量
(2) 初F始B(微t)=分f 方dyd(程tt) 组
根据a=牛Fd=2d顿ymt(2t第a) 二定律
F(t)–FB(t)–FK(t)=ma
弹簧系数k
F(t)
弹簧
质量
m
y(t) 阻尼器
阻尼系数f
(3)消除中间变量
m
d2y(t) dt2
+
f
dy(t) dt
+ky(t)=F(t)
第一节 控制系统的微分方程
3．他激直流电动机
系统组成：
电他根定转根枢机T励 设Tue激据电 T子子据ee定b+d-=-电mu磁=直=T机输R磁CL基d=u义iCTRLd时aam电f3流械入Le-时尔Ga3G:n7T=ii间d7d压D5N电S运DTf+T间霍5C=2afL常2转飞i输反动=动mRf=常夫3CGa磁C矩轮7数0Ra电RLdmn出d机D方数定5力导eiCataa系惯d势2电构磁程e线线d+律d数量系ndted路成场式2b有t数n2T载 的 转等m+T流 作矩效3aG7导 用，d图d5Di2udtCn22线 力使=d:R+m-+uu3C在 产转aTdf7G5m.磁 生子Dd电Cdddn2tmnt场了转RL源电+i+.nadand受电动d机nTn=t=e到磁。反CuT负CudLe电de载eTb势f
第二章的主要内容有：
第二章 自动控制系统的数学模型
第一节 控制系统的微分方程
一、建立微分方程的一般步骤
电子教案-自动控制原理及其应用(第4版_黄坚)课件-4.3
ω=∞ ω=0
-1
0
Re
0
Re
修正
π
2
修正
-π
ω=0+
相角变化量为p180o ，系统是稳定的。
相角变化量为p180o ，系统是稳定的。
第三节 用频率特性法分析系统稳定性
(c) ω=0+
Im
υ=3
-1 ω=∞ ω=0
0
Re
修正
-3π2
(d) ω=0+
π 2
Im
υ=1 p=1
ω=∞
ω=0
-1 0 Re
修正方法： 在ω=0+开始， 逆时针方向补画一
个半径无穷大、相角为υ900 的大圆弧。 即ω=0→0+ 曲线
第三节 用频率特性法分析系统稳定性
例 υ为积分环节的个数， p为不稳定极点
的个数，试判断闭环系统的稳定性。
解：
系统的奈氏曲线如图
(a)
Im υ=1
(b)
Im υ=2
ω=∞ ω=0
ω=0+ -1
一、开环频率特性和闭环特征式的关系
R系(S)统-的结G=(构Ks)j∏f=C图n∏i1((=Tsn1()Tjsi+s+1G设1)()s开)==K环NjM∏p=n1i∏1传(1=(sn(1s(-ss)递p)-js)函i)H数(s)：=
M2(s) N2(s)
FF((ss))的的H零极(s)点点 系系G统统(s)开闭H(环环s)=特特NM征征(s(方方s))=程程MN式式11((s的的s))NM根根22((ss))
从下往上的负穿越次数为N-。
起始或终止于负实轴上为1/2 奈氏稳定判据可表述为：N=N N
次穿p越。 =2
电子教案-自动控制原理及其应用(第4版_黄坚)课件-6.6
Kp=lzi→m1G(z)
则有
e*(∞)=
1 1+Kp
第六节 离散控制系统的稳态误差分析
二、单位斜坡输入时系统的 稳态误差
e*(定几∞)义种=((K12(l设K系v3i下情))z=m→)v系=统zl况面v(1vi→zvzlm==统-i→的讨按=1m101T121)的静系论T1(1z输态(。统-+Kze1eG-1入*速e)v*开1(=(*(∞)(∞(z为度z(环∞zl))Kz)-i→=m=-1)·K误r脉1=1(Π∞)irmz)=0ΠjTKn1Π2T-1差=1iR冲m(-=Π11n1jvz(1=z((-()z-2z1系z传z2(z---z)1ip=Πjz)=-数=n)递ipj1)K)T1((j：)zzTr函z=l--Πi→izp1m=m常=数1)(j1)2z∞(数-z分z1-i1)成)=G0(z)
K)
z→1
则有
e*(∞)=
1 Kv
第六节 离散控制系统的稳态误差分析
三、单位加速度输入时系统的 稳态误差
KKaa((==31(2))KTe)1T定K1*a2vv(2=aez∞vl==义=izl*→=mi→T)20(1m=11∞T系121((l2)zzzi统=→Kz=lm1--i→11lma1iz的(TR))m11→z22(2(-(z(静1z1lzzK-z→i)-)K1Πm-jr=21态=1n1)Π(ri1m2=)()(ΠTziG2m11zΠz=jn加(-=-12--(zK(1111(pz1z-(zz+(速)r-zz)j-)zΠ)21i2-ziGm1)=+ΠGpji)n度1)=(31-(j12z()z=)z-误)ez)0-*=ip·)(T差0∞j)22e)z系(*=(z(=ze∞-数+1常*K)(1)1=返∞3：a数)∞)回=∞
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四节 用频率特性法分析系统性能
4．二阶系统开环频率特性与动态性能的关系
开环传递函数：
G(s)=
ωn2 s(s+2ζωn
)
G(ωj
)=
ωj
ωn2 (ωj +2ζωn
)
Aω(
)=ω
ω
ωn2 2+(2ζωn
)2
φ ω( )=-90o- tg-12ζωωn
L(ω ) dB
20
-20dB/dec
ωc
0
2ζωn
+20 0
-40dB/dec
ωc
ω
闭-函4环0数d传B为可/递d：近eφc似的(s认直)=为线1+ω整sω。2sc22c个2 =曲s2ω+线ωc2 是-c220 一处稳条于定斜临状率界态为
中频段斜率为-40dB/dec ，所占频率区
间不能过宽，否则系统平稳性难以满足要求。
通常，取中频段斜率为-20dB/dec 。
40
40
σ%
30
20
20
0
10
0 0.2 0.4 0.6 0.8 1.0ζ
第四节 用频率特性法分析系统性能
(2)ωc 、γ与ts 之间的关系
根据：
得
ts=ζω3n ωc=ωn 4ζ 4+1 -2ζ 2
tsω·c= 3
4ζ 4+1 -2ζ 4ζ
2ζ 4+1 -2ζ
2
得 ts·ωc=tgγ6
σ%= e-ζπ 1-ζ 2100%
ωc=ωn 4ζ 4+1 -2ζ 2
σ%
140
80
ζ与γ、=1σ8%0o+之φ间(ω的c )
120 100
70 60
=180关o-9系0o曲-tg线-12ζωωc n
=γtg越-1大2ζω反ω，cn之σ=亦%tg-然1越4ζ。小4+2ζ；1 -2ζ 2
80
50
60
闭环传递函数为： ωc
0 -20
ωc
ω
-φ20(dsB)可=/1d近+ecωs似的sc 认直=ω为1线c s1整。+1个曲线t是s≈3一T条=ω斜3c 率为
第四节 用频率特性法分析系统性能
(2) 中频段的斜率与动态性能的关系
设系统如图:
L(ω ) dB
开环传递 函数：
G(s)≈
K s2
=ωs2c2
第四节 用频率特性法分析系统性能
3 ．高频段
一般 L(ω )=20lg|G(jω )|<<0
即
|G(ωj )|<<1
φ|
(ωj
)|=
|G(ωj )| |1+G(ωj )|
≈ |G(ωj )|
高频段反映了系统对高频干扰信号的
抑制能力。高频段的分贝值越低，系统的
抗干扰能力越强。高频段对应系统的小时
间常数，对系统动态性能影响不大。
M0
(1) 零频幅值Mo
0.707M(0)
(((432ω幅)M程))M=带频谐谐o度0=o谐的=宽最1振振闭上幅M时振闭频大频峰环反频(，峰ω环率值率值峰映值)输值=幅ω与ωM值了M降出反br值Mr零系出(到与0映γ频)=统现0输了.幅7的时MM入0系值M7m快的o相M统(之0速频ω0等的时b比性率)，相=的。。。0ω没对.频r7在0有稳率ω7一bM误定。定0差性的。ω
可求=得(1- ωωn22M)1+γ=j2Mζ mω=ωn =2ζM1(1ω-2)ζe2jα(ω)
第四节 用频率特性法分析系统性能
由上述分析可见：
对于二阶系统，当0 ≤ζ ≤ 0.707时，幅 频特性的谐振峰值Mr与系统的阻尼比ζ有 着对应关系，因而Mr反映了系统的平稳 性；再由ts=3 /ζωn推知，ωr 越大，则ts越 小，所以ωr反映了系统的快速性。
第四节 用频率特性法分析系统性能
一 、开环频率特性与闭环系统性能的关系
常将开环频率特性分成低、中、高三 个频段。
L(ω ) dB
低频段 中频段
高频段
-40dB/dec
0
ω1
ωc ω2
-20dB/dec
ω
-40dB/dec
三个频段分别与系统性能有对应关系， 下面具体讨论。
第四节 用频率特性法分析系统性能
-180
第四节 用频率特性法分析系统性能
二、闭环频率特性与时域指标的关系
根据开环频率特性来分析系统的性能 是控制系统分析和设计的一种主要方法， 它的特点是简便实用。但在工程实际中， 有时也需了解闭环频率特性的基本概念和 二阶系统中闭环频域指标与时域指标的关 系。
第四节 用频率特性法分析系统性能
1. 闭环频率特性及频域指标
第四节 用频率特性法分析系统性能
设 M0=1
根据
M(ω)=0.707M0=0.707 可求得
ωb=ωn (1-2ζ2)+ 2-4ζ2+4ζ4
ζ一定的情况下,ωb越大，则ωn越大， ts越小。ωb表征了控制系统的响应速度。
1．低频段
低频段由积分环节和比例环节构成：
G(s)=
K sυ
G(jω)= (ωj Kυ)
可对知数：幅频特性为：
L(ω曲)线=2位0l置gA越(ω高) ，
L(ω ) dB
K值越大=2；0lg低ωKυ频段斜
υ=0 υ=1
率越负=，20积lg分K-环v20节lgω 数 性越能根 图多越据所。好分示系。析的统可结稳得果态如：
第四节 用频率特性法分析系统性能
2．二阶系统闭环频域指标与时域指标的关系
M(ω)二= 阶(系1Φ-统ω(ωsn)的22=1)标C+R2(准(sζs))式ω=ωns2+2αζ(ωωωnn)2s=+tgω-1n2
2ζω/ωn 1-ω2/ωn
闭ω环γ=Φ频ω令(n率jω特)=1性-2(jdζω2Md)2(ω+ω2)ζωω0=nn≤02(ζj≤ω0)得.7+0ω7n2
20
γσ=%=1=891=0t08soo0=+e-oω7-ζ-π2φ9c.0t63(ωg1γo8-ζ-co2t)=1=g013-107s(%0.6.=525×o7%6.3)
0 -20
0
-90
-
L(ω
φ (ω
20 θc(s)
s(0.5s+1)
) dB
-20dB/dec
ωc
2
)
γ
ω
-40dB/dec
ω
ζ=γ/100=0.176
ω
-20
-40dB/dec
φ (ω )
0
ω
-90
γ
-180
平稳性: σ% γ
快速性: ts ωc
第四节 用频率特性法分析系统性能
(1) 相位裕量γ和超调量σ% 之间的关系
Aω( )=ωcωc2ω+(n22ζωn )2=1 得 ωc4+4ζ ω2 n2ωc2-ωn4=0
0<ζ< 0.707近似为
γ (ωc)=100ζ
0
-20υ ν
K
υ=2 K
Kω
第四节 用频率特性法分析系统性能
2. 中频段
反穿映越了穿频系越率统频ω动率c 反态ωc映响附了应近系的的统平区响稳段应性为的和中快快频速速段性性。。。它
(1) 穿越频率ωc与动态性能的关系
设系统如图:
开环传递 函数：
G(s)≈
Ks =ωsc
L(ω ) dB
+20
-20dB/dec
调节时间 ts 与ωc以及γ有关。γ不 变时，穿越频率ωc 越大，调节时间越 短。
第四节 用频率特性法分析系统性能
例 分析随动系统的性能，求出系统的频
域指标ωc、γ和时域指标σ%、 ts。
随动系统结构如图 θr(s)
可解ω得：n：= 04ζ.2G5ω40+(ωsc12)≈c=-12ζs(02ω.=25c60s=.+561.3)
闭环传递函数为
Φ(s)=
G(s) 1+G(s)
闭环频率特性：
Φ(jω)=
G(jω) 1+G(jω)
=M(ω)ejαω
已知G(jω)曲线上的一点，便可求得
Φ(jω)曲线上的一点，用这种方法逐点绘
制出闭频率特性曲线。
第四节 用频率特性法分析系统性能
闭环幅频特性曲线
系统的闭环频率
M(ω)
指标主要有：
Mm