尺规作图专题复习(八上)
初二上册数学尺规作图练习题

初二上册数学尺规作图练习题尺规作图是数学中的一项重要技能,本文将为你提供一些初二上册数学尺规作图练习题,帮助你巩固这一技巧。
1. 作一个正三角形ABC,已知边长为5cm。
首先,使用尺子在纸上画一条直线段,作为边AB的长度,标记为点A和点B。
接下来,以点A为圆心,以边长为半径,使用圆规画一个圆弧,交直线段AB于点C。
连接点B和C,得到正三角形ABC。
2. 作一个等边五边形ABCDE,已知边长为6cm。
先绘制一个正三角形ABC,其中AB的长度为6cm,并连接点C和点A。
接着,以点C为圆心,以边长为半径,使用圆规画一个圆弧,交直线段AC于点D。
再以点D为圆心,以边长为半径,使用圆规画一个圆弧,交直线段AD于点E。
连接点E与点B,得到等边五边形ABCDE。
3. 作一个平行四边形ABCD,已知边长AB为7cm,AD为5cm,且AD平行于BC。
首先,使用尺子在纸上作一条长度为7cm的直线段,标记为点A 和点B。
接下来,以点A为起点,使用圆规在直线上切取长度为5cm 的线段,标记为点D。
连接点B和点D,得到平行四边形ABCD。
通过以上练习题,我们可以巩固尺规作图的技巧。
在进行尺规作图时,需要注意以下几点:
- 确定给定的边长或者角度,合理利用这些已知信息;
- 使用尺规和圆规进行绘图时,要保持工具的垂直和水平;
- 使用直尺时,要注意尺子的一端与绘图纸对齐,以确保准确度。
希望通过这些练习题,你能更好地掌握初二上册数学尺规作图的方法和技巧。
请继续进行更多的练习,熟能生巧!。
(完整版)八上数学尺规作图归纳总结

八上数学教师辅导讲义学员编号:年级:新初二课时数:学员姓名:辅导科目:数学学科教师:赵老师课题尺规作图授课日期及时段教学目的教学内容一、知识梳理(一)尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
(二)五种基本作图:1、作一条线段等于已知线段;已知:如图,线段a .求作:线段AB,使AB = a . 訂〈己知)作法:A 1H p①作射线AP;:作线段等干记知线段)②在射线AP上截取AB=a .则线段AB就是所求作的图形。
2、作一个角等于已知角;3、作已知线段的垂直平分线;已知:如图,线段MN.求作:点O,使MO=NQ即0是MN的中点)作法:完美WORD 格式.整理①分别以M N为圆心,大于1/2MN的相同线段为半径画弧,两弧相交于P, Q;②连接PQ交MN于O.则点O就是所求作的MN的中点。
(试问:PQ与MN有何关系?)4、作已知角的角平分线;已知:如图,/ AOB求作:射线OP,使/ AOP=Z BOP (即卩OP平分/ AOB 。
作法:①以O为圆心,任意长度为半径画弧,分别交OA OB于M N;②分别以M N为圆心,大于1/2MN的相同线段为半径画弧,两弧交/ AOB内于P;③作射线OP则射线OP就是/ AOB的角平分线。
5、过一点作已知直线的垂线;①以已知点为圆心,以任意长为半径作弧,交直线于②分别以A、B为圆心,以大于1/2AB长为半径分别作弧,两弧分别交于点M点N;③连接MN则直线MN为所求作的直线。
6、过直线外一点作直线的平行线(三)尺规作图拓展(1)已知三边作三角形。
已知:如图,线段a, b, c.求作:△ ABC 使AB = c , AC = b , BC = a.作法:(作线段的中点)(作角平分线)B两点;--------------------- b(巳知)(已知三边作三凭形)作线段AB = c ;以A 为圆心b 为半径作弧,以 B 为圆心 为半径作弧与前弧相交于 C ;连接AC, BG则厶ABC 就是所求作的三角形。
人教版八年级上册数学期末复习6专题六 作图专题

则H即为工厂位置.
四、网格作图
13.如图,在平面直角坐标系中,△ABC的顶点A(0,1), B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1; (2)将△A1B1C1沿x轴方向向左平移3个单位长度后得到
△A2B2C2,写出顶点 A2,B2,C2的坐标.
解:如图,作出AB和BC的中垂线,相交于点P, 则点P是所求的到三村距离相等的点
11.如图,在△ABC中,AB=AC,∠BAC=120°. (1)用尺规作出AB的垂直平分线交AB于点E,交BC于点F. (2)若BF=3,求CF的长度.
解:(1)如图所示:
(2)连接AF.
∵AB=AC,∠BAC=120°
∴∠B=∠C=
1 2
(180°-120°)=30°
又由(1)知BF=AF
∴∠FAB=∠B=30°
∴∠FAC=120°-30°=90°
∴CF=2AF=2BF=2×3=6
12. 如图,已知甲村和乙村靠近公路a,b,为了发展经济, 甲、乙两村准备合建一个工厂,经协商,工厂必须满足 以下要求:
(1)到两村的距离相等; (2)到两条公路的距离相等.你能帮忙确定工厂的位置吗?
解:如图
15.如图,在平面直角坐标系中,△ABC的三个顶点分别为 A(2,3),B(3,1),C(-2,-2).
(1)请在图中作出△ABC关于y轴的轴对称图形△A′B′C′(A,B,C 的对称点分别是A′,B′,C′),并直接写出A′,B′,C′的坐标.
(2)求△A′B′C′的面积.
解:(1)如图所示,点A′(-2,3), B′(-3,1),C′(2,-2);
解:设a、b相交于点O.甲村为点E,乙村为点D.
第05讲 尺规作图(1个知识点+7大题型+18道强化训练)(教师版) 24-25学年八年级数学上册
第05讲 尺规作图(1个知识点+7大题型+18道强化训练)课程标准学习目标①掌握尺规作图的方法;②学会用尺规作图画角、画边;①掌握尺规作图的方法;②学会用尺规作图画角、画边;知识点01:尺规作图尺规作图:在几何作图中,我们把用没有刻度的直尺和圆规作图,简称尺规作图。
1.基本作图 作等量线段、作等量角、作线段的和差倍、作角的和差倍、2.作线段的中垂线、作角的平分线、中垂线角平分线在一起作、3.作三角形 知三边、知两边夹角、知两角夹边、知一边及该边上的高作法:有规定名称时需格外注意字母的标注注意务必考虑三角形的各要素(类比于三角形全等的判定条件)。
【即学即练1】1.(23-24七年级下·四川成都·期末)如图,已知AOB Ð,以点O 为圆心,任意长度为半径画弧,分别交OA 、OB 于点E 、F ,再以点E 为圆心,EF 的长为半径画弧,交前弧于点D ,画射线OD .若27AOB Ð=°,则AOD Ð的度数为( )A .27°B .54°C .63°D .36°【答案】A 【分析】本题考查了全等三角形的判定与性质,基本作图知识,解题的关键是熟练掌握基本知识.根据作图过程可得OD OE OF ==,EF DE =,利用SSS 证明ODE OFE ≌V V ,即可得出结果.【详解】解∶由作图过程可得OD OE OF ==,EF DE =,∴()SSS ODE OFE ≌V V ,∴27EOD EOF Ð=Ð=°,故选∶A .【即学即练2】2.(24-25七年级上·山东·随堂练习)如图,点C 在AOB Ð的边OB 上,用尺规作出了NCE AOD Ð=Ð,作图痕迹中,弧FG 是( )A .以点C 为圆心,OD 为半径的弧B .以点C 为圆心,DM 为半径的弧C .以点E 为圆心,OD 为半径的弧D .以点E 为圆心,DM 为半径的弧【答案】D 【分析】本题主要考查尺规作角等于已知角,掌握其作法是解题的关键,弧FG 是以点E 为圆心,以DM 为半径作的弧,运用作一个角等于已知角可得答案.【详解】解:根据作一个角等于已知角可得弧FG 是以点E 为圆心,DM 为半径的弧.故选:D .【即学即练3】3.(23-24七年级下·全国·假期作业)下列作图属于尺规作图的是( )A .用量角器画出AOB Ð的平分线OCB .已知a Ð,作AOB Ð,使2AOB a Ð=Ð.C .用刻度尺画线段3cmAB =D .用三角板过点P 作AB 的垂线【答案】B【分析】本题考查了尺规作图的定义,掌握尺规作图的定义是解题的关键.根据尺规作图的定义,逐项分析即可,尺规作图是指仅用没有刻度的直尺和圆规作图【详解】解:A .用量角器画出AOB Ð的平分线OC 借助了量角器,不符合题意B.借助直尺和圆规作AOB Ð,使2AOB a Ð=Ð,符合题意;C.画线段3cm AB =,借助了带刻度的直尺或三角板,不符合题意;D .用三角尺过点P 作AB 的垂线,借助了三角尺的直角,不符合题意;故选:B .【即学即练4】4.(23-24七年级下·辽宁锦州·期末)如图,已知ABC V ,按如下步骤作图:①分别以点A 和B 为圆心,以大于12AB 的长为半径作弧,两弧相交于点E 和F ;②作直线EF ,分别交AB BC ,于点M ,N ;③连接AN ,若2,AM ACN =V 的周长为12,则ABC V 的周长为( )A .16B .15C .14D .13【答案】A 【分析】本题考查了基本作图—垂直平分线作图,垂直平分线的性质,解题的关键是熟练掌握垂直平分线的性质;根据作图可知MN 为AB 的垂直平分线,进而可得224AB AM BM AN BN ====,,即可求解【详解】解:根据作图可知:MN 为AB 的垂直平分线,224AB AM BM AN BN\====,12ACN C AN CN AC =++=V Q 12BN CN AC \++=41216ABC C AB BN CN AC V \=+++=+=故选:A题型01 尺规作一个角等于已知角1.(23-24八年级上·山东菏泽·期中)尺规作图:已知线段a 和a Ð.作一个ABC V ,使AB a =,AC 2a =,BAC a Ð=Ð.(要求:不写作法,保留作图痕迹)【答案】图见解析【分析】本题考查基本尺规作图,根据尺规作一个角等于已知角和尺规作线段的步骤画图即可.【详解】解:如图,ABC V 即为所求作:2.(23-24八年级上·陕西延安·期中)在ABC V 中,点D 是AB 上一点,请用尺规作图法,在BC 边上找一点E ,使得∥D E A C .(保留作图痕迹,不写作法)【答案】见解析【分析】题考查基本尺规作图—作一个角等于已知角,平行线的判定,解题的关键是作CAD BDE Ð=Ð,由同位角相等两直线平行即可得到DE AC P .【详解】如图,点E 即为所作.3.(21-22八年级上·陕西铜川·期末)如图,点B 是射线AC 上一点,请用尺规作图法,求出线段BE ,使得BE AD ∥.(不写作法,保留作图痕迹)【答案】见解析【分析】以点A 为圆心,任意长为半径作弧,交AD 、AC 于F 、G ,以点B 为圆心,AF 为半径作弧,交AC于点H ,以点H 为圆心,FG 为半径作弧,交前弧于点P ,连接BP ,如图1,延长BP 到点E ,可得DAB EBC Ð=Ð,则BE AD ∥;如图2,反向延长BP 到点E ,可得DAB ABE Ð=Ð,则BE AD ∥.【详解】解:如图1,线段BE 为所作.如图2,线段BE 为所作.【点睛】此题考查了尺规作图,作角等于已知角,平行线的判定定理,同位角相等两直线平行,内错角相等两直线平行,熟记平行线的判定定理是解题的关键.4.(22-23七年级下·陕西汉中·期中)如图,已知AOB Ð,利用尺规作NMC Ð,使2NMC AOB Ð=Ð.(保留作图痕迹,不写作法)【答案】见解析【分析】根据尺规作图,即倍角作图,即可作图.【详解】解:如图,NMC Ð即为所作,【点睛】本题考查了尺规作图知识,解题关键是理解2NMC AOB Ð=Ð.5.(22-23七年级下·广东佛山·阶段练习)如图,已知锐角a Ð和平角AOB Ð,在AOB Ð内部求作AOC Ð,使AOC Ð与a Ð互补.(不要求尺规作图)【答案】见解析【分析】以O 为顶点,OB 为一边,作BOC a Ð=,即可得出AOC Ð.【详解】解:如图所示,AOC Ð即为所求..【点睛】本题主要考查作一个角等于已知角及互为补角的两个角的性质,熟练掌握作一个角等于已知角是解题关键.题型02 尺规作角的和、差6.(21-22七年级下·甘肃白银·期中)作图题.已知,,a b ÐÐ,且a Ð大于Ðb ,求作AOB a b Ð=Ð-Ð(不写作法,保留作图痕迹,不在原图上作图)【答案】图见解析【分析】本题考查尺规作图—作一个角等于已知两角的差,根据尺规作角的方法,进行作图即可.【详解】解:如图,AOB Ð即为所求.7.(23-24七年级下·山东青岛·单元测试)已知:AOB Ð,求作:COD Ð,使2COD AOB Ð=Ð.【答案】见解析【分析】此题主要考查了作一个角等于已知角的基本作图, 关键是熟练掌握基本作图的方法.先利用尺规作一个等于已知角的方法作出MOC AOB Ð=Ð,然后作出MOD AOB Ð=Ð即可.【详解】如图所示,COD Ð即为所求.8.(23-24七年级上·江苏南京·期末)如图为一副三角尺,其中60,45a b °°Ð=Ð=,作120,15ABC DEF °°Ð=Ð=.(要求:尺规作图,保留作图痕迹,不写作法)【答案】图见解析【分析】本题考查尺规作角,根据尺规作角的方法,作图即可.掌握尺规作角的方法,是解题的关键.【详解】解:如图,,ABC DEF ÐÐ即为所求;9.(23-24七年级上·江苏南京·阶段练习)如图,已知a b ÐÐ、,利用直尺和圆规画AOB Ð,使AOB Ð的大小为a b Ð+Ð.(不写作法,保留作图痕迹.)【答案】见解析【分析】本题主要考查了尺规作图——作一个角等于已知角.先作AOC a Ð=Ð,再作BOC b Ð=Ð,即可求解.【详解】解:如图,AOB Ð即为所求.10.(23-24七年级上·江苏南京·阶段练习)如图,已知ABC V 的三边长分别为a b c B C Ða Ðb ==,,,,,利用直尺和圆规完成下列作图(不写作法,保留作图痕迹).(1)作线段EF a c =-;(2)作POQ a b Ð=+.【答案】(1)见详解(2)见详解【分析】本题考查了作一个与已知角相等的角以及线段:(1)先画出一条射线,以端点O 为圆心,分别以AB BC ,为半径画弧,与射线的交点分别为E 点和F 点,即可作答.(2)先画出一条射线,以端点O 为圆心,取MC 的长度为半径,画弧,交点为M ¢,再以点M ¢为圆心,MN 的长度为半径,画弧,交点为N ¢,此时N OM b ¢¢Ð=;以端点O 为圆心,取BP ¢¢的长度为半径,画弧,交点为P ¢,再以点P ¢为圆心,Q P ¢¢¢¢的长度为半径,画弧,交点为Q ¢,此时P OQ a ¢¢Ð=;故POQ a bÐ=+【详解】(1)解:如图:(2)解:如图所示:题型03 过直线外一点作这条直线的平行11.(23-24七年级下·福建福州·期末)如图,已知MON Ð,A 、B 分别是射线OM ON ,上的点.(1)尺规作图;在MON Ð的内部确定一点C ,使得BC OA ∥且BC OA =(保留作图痕迹,不写作法);(2)在(1)中,连接OC ,仅用无刻度直尺在线段OC 上确定一点D ,使得OD CD =,并证明.【答案】(1)见解析(2)见解析【分析】本题考查了全等三角形的判定及性质、尺规作图;熟练掌握尺规作图的作法及全等三角形的判定及性质是解题的关键.(1)根据尺规作图作角及线段的作法即可求解;(2)利用AAS 证得AOD BCD V V ≌,进而可求证结论;【详解】(1)解:如图所示,线段BC即为所求.(2)证明:连接AB ,与AC 交点即为D 点,∵BC OA ∥,∴AOD BCD Ð=Ð,又ADO BDC Ð=Ð,由(1)得BC OA =,∴在AOD △与BCD △中,AOD BCD ADO BDC BC OA Ð=ÐìïÐ=Ðíï=î,∴()AAS AOD BCD V V ≌,∴OD CD =.12.(23-24七年级下·辽宁辽阳·期中)已知:如图,在ABC V 中,D 为AB 的中点,E 是BC 上一点,DEB ACB Ð=Ð.(1)过点D 作DF BC ∥交AC 于点F (尺规作图,不写作法,保留作图痕迹);(2)求证:AF DE =.【答案】(1)见解析(2)见解析【分析】本题主要考查了平行线的尺规作图,平行线的性质与判定,全等三角形的性质与判定:(1)根据平行线的尺规作图方法作图即可;(2)先证明AC DE ∥,得到A BDE Ð=Ð,再由平行线的性质得到ADF B Ð=Ð,由线段中点的定义得到AD DB =,则可证明()ASA ADF DBE V V ≌,即可证明AF DE =.【详解】(1)解:如图所示,即为所求;(2)证明:∵DEB ACB Ð=Ð,∴AC DE ∥,∴A BDE Ð=Ð,∵DF BC ∥,∴ADF B Ð=Ð,∵点D 为AB 的中点,∴AD DB =,∴()ASA ADF DBE V V ≌,∴AF DE =.13.(23-24七年级下·辽宁丹东·期中)如图,已知Rt ABC △,90B Ð=°用尺规过点A 作直线MN ,使得MN BC ∥.(保留作图痕迹,不写作法)【答案】见解析【分析】本题主要考查了平行线的尺规作图,根据平行线的尺规作图方法作图即可.【详解】解:如图所示,直线MN即为所求.14.(2024·陕西西安·模拟预测)如图,在四边形ABCD中,点P为边AD上一点,请用尺规作图法,在边BC 上求作一点Q,使得P、Q到AB的距离相等.【答案】见解析∥交BC于Q,则点Q即为所【分析】本题主要考查了平行线的性质和平行线的尺规作图,过点P作PQ AB求.∥交BC于Q,则点Q即为所求.【详解】解:如图所示,过点P作PQ AB由平行线间间距相等可得P、Q到AB的距离相等.15.(23-24七年级下·福建宁德·期中)如图,已知三角形ABC,点E是AB上一点.(1)尺规作图:在BC 上找到一点F ,使得BFE C Ð=Ð;(不写作法,保留作图痕迹)(2)在(1)的条件下,连接CE ,若110EFC Ð=°,且CE 平分ACB Ð,求FEC Ð的度数.(2)解:∵EF BC ∥,∴FEC ACE ACF =∠∠,∠∵CE 平分ACB Ð,∴1352ACE ACF ==∠∠题型04 尺规作图——作三角形16.(23-24七年级下·辽宁本溪·期末)尺规作图:如图,线段BC 和一副三角尺,其中60,45a b °°Ð=Ð=.求作:以线段BC 为一条边作ABC V ,使得60,75ABC BAC ÐÐ=°=°.(要求:保留作图痕迹,不写作法)【答案】见解析【分析】本题考查尺规作三角形,根据尺规作角的方法作出60ABC Ð=°,45ACB Ð=°即可.掌握尺规作角的方法,是解题的关键.【详解】因为6075ABC BAC Ð=°Ð=°,所以45ACB Ð=°如图所示,ABC V 即为所求.17.(24-25八年级上·全国·假期作业)已知:如图,线段a 、b 、c .求作:ABC V ,使得BC a =,AC b =,AB c =.(保留作图痕迹,不写作法)【答案】见解析【分析】本题考查了作图-作三角形,首先画AB c =,再以B 为圆心,a 为半径画弧,以A 为圆心,b 为半径画弧,两弧交于一点C ,连接BC ,AC ,即可得到ABC V .【详解】解:如图所示,ABC V 就是所求的三角形.18.(23-24七年级下·河北保定·阶段练习)如图,已知Ðb 和线段a ,求作ABC V ,使得A b Ð=Ð,2B b Ð=Ð,边AB a =.(用圆规、直尺作图,不写作法,但要保留作图痕迹)【答案】见解析【分析】本题考查作图-复杂作图,解题的关键是熟练掌握五种基本作图,属于中考常考题型.作射线AM ,在射线AN 上截取AB a =,在AB 的上方分别作EAB b Ð=,2FBA b Ð=,AE 交BF 于点C ,ABC V 即为所求.【详解】解:如图,ABC V 即为所求.19.(23-24七年级下·辽宁沈阳·期中)尺规作图:(不写作法,保留作图痕迹)已知:已知线段a ,b 和aÐ求作:ABC V 使BC a =,AC b =,BAC aÐ=Ð【答案】见解析【分析】本题考查作三角形,解题的关键是熟练掌握五种基本作图.作MAN a Ð=,在射线AN 上截取线段AC ,使得AC b =,以B 为圆心,a 为半径作弧,交AM 于点B ,B ¢,连接BC ,B C ¢,ABC V 或AB C ¢V 即为所求.【详解】解:如图,ABC V 或AB C ¢V 即为所求.20.(23-24九年级下·湖南长沙·期中)人教版初中数学教科书八年级上册第37—38页告诉我们作一个三角形与已知三角形全等的方法:已知:ABC V .求作:A B C ¢¢¢V ,使得A B C ABC ¢¢¢V V ≌.作法:如图.(1)画DA E A ¢Ð=Ð;(2)在射线A D ¢上截取A B AB ¢¢=,在射线A E ¢上截取A C AC ¢=;(3)连接线段B C ¢¢,则A B C ¢¢¢V 即为所求作的三角形.请你根据以上材料完成下列问题:(1)完成下面证明过程(将正确答案填在相应的空上):证明:由作图可知,在A B C ¢¢¢V 和ABC V 中,()()A B AB DA E A C ì=ïÐ=¢¢¢¢=¢Ðíïî∴A B C ¢¢¢≌______.△(2)这种作一个三角形与已知三角形全等的方法的依据是______(填序号)①AAS ②ASA ③SAS ④SSS【答案】(1)A ;AC ;ABCV (2)③【分析】本题考查了作图-复杂作图,全等三角形的判定等知识:(1)根据作图信息,利用“SAS ”证明三角形全等即可;(2)利用(1)中证明可得结论.【详解】(1)解:由作图可知,在A B C ¢¢¢V 和ABC V 中,A B AB DA E A A C AC =ìïÐ=Т¢¢¢¢íï=î,∴()SAS A B C ABC ¢¢¢V V ≌,故答案为:A ;AC ;ABCV (2)解:这种作一个三角形与已知三角形全等的方法的依据是SAS ,故答案为:③.题型05 结合尺规作图的全等问题21.(22-23七年级下·辽宁沈阳·期末)如图,在所给正方形网格图中完成下列各题:(1)画出所有与格点ABC V (顶点均在格点上)全等的格点三角形,使它与ABC V 有且只有一条公共边,你画出了______ 个符合要求的格点三角形,分别记作______ ;(2)在DE 上画出点P ,使得PAC △的周长最小;(3)若网格上的最小正方形的边长为1,直接写出ABC V 的面积为______ .(3)ABC V 的面积133132=´-´´故答案为:72.22.(20-21七年级下·广东佛山·期中)作一个角等于已知角的方法:已知:AOBÐ求作:A O B ¢¢¢Ð,使A O B AOB ¢¢¢Ð=Ð,作法:(1)如图,以点O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C 、D ;(2)画一条射线O A ¢¢,以点O ¢为圆心,OC 长为半径画弧,交O A ¢¢于点C ¢;(3)以点C ¢为圆心,CD 长为半径画弧,与第2步中所画的弧相交于点D ¢;(4)过点D ¢画射线O B ¢¢,则A O B AOB ¢¢¢Ð=Ð.请你根据提供的材料完成下列问题.(1)请你证明A O B AOB ¢¢¢Ð=Ð.(2)这种作一个角等于已知角的方法的依据是________________________.【答案】(1)见解析(2)SSS【分析】(1)由作图过程得到相应条件,再根据SSS 证明即可;(2)根据作图过程可得这种作一个角等于已知角的方法的依据是SSS .【详解】(1)解:证明:在C O D ¢¢¢△和COD △中,O C OC O D OD C D CD=ìï=íï=¢¢¢¢¢î¢,\(SSS)C O D COD ¢¢¢△≌△,A OB AOB ¢¢¢\Ð=Ð.(2)这种作一个角等于已知角的方法的依据是SSS .故答案为:SSS【点睛】本题考查了作图-应用与设计作图,全等三角形的判定,解决本题的关键是掌握作一个角等于已知角的方法.23.(22-23八年级上·吉林长春·期末)图①、图②均为44´的正方形网格,每个小正方形的顶点称为格点,边长均为1.在图①、图②中按下列要求各画一个三角形.要求:(1)三角形的三个顶点都在格点上.(2)与ABC V 全等,且位置不同.【答案】(1)见解析(2)见解析【分析】(1)利用全等三角形的判定方法,画出图形即可;(2)利用全等三角形的判定方法,画出图形即可.【详解】(1)如图,ECB V 即为所求(2)如图,DEF V 即为所求【点睛】本题考查作图,全等三角形的判定的知识,解题的关键是理解题意,灵活运用所学知识解决问题.24.(22-23八年级上·江苏连云港·期中)如图,在58´的正方形网格中,每个小正方形的边长均为1,ABC V 的三个顶点都在小正方形的顶点上.(1)在图1中画ABD △(点D 在小正方形的顶点上),使得ABD △与ABC V 全等,且点D 在直线AB 的下方(点D 与点C 不重合);(2)在图2中画ABE V (点E 在小正方形的顶点上),使得ABE V 与ABC V 全等,且AC BE P ;【答案】(1)见解析(2)见解析【分析】(1)根据轴对称图形的性质找出点C 的对应点D ,连接AD ,BD 即可;(2)根据中心对称图形的性质找出点C 的对应点E ,连接AE ,BE 即可.【详解】(1)解:利用轴对称图形的性质找出点C 的对应点D ,连接AD ,BD ,则ABD △即为所求作的三角形,如图所示:(2)解:利用中心对称图形的性质找出点C 的对应点E ,连接AE ,BE ,则ABE V 即为所求作的三角形,如图所示:【点睛】本题主要考查了网格作图,解决问题的关键是熟练掌握运用轴对称性质中心对称性质确定对应点,解题的关键是确定点D 和点E 的位置.25.(22-23八年级上·湖北荆门·期中)如图,ABC V 的顶点A 、B 、C 都在小正方形的顶点上,试在方格纸上按下列要求画格点三角形(三角形的顶点在格点上),只需画出一个即可:V全等的三角形,且有条公共边:(1)在图(1)中画出与ABCV全等的三角形,且有一个公共顶点:(2)在图(2)中画出与ABCV全等的三角形,且有一个公共角.(3)在图(3)中画出与ABC【答案】(1)见解析(2)见解析(3)见解析【分析】(1)可根据全等三角形判定中的边边边(SSS)为依据作图;(2 )(3)可根据全等三角形的判定中的边角边(SAS)为依据作图.V即为所求(答案不唯一),【详解】(1)解:如图1,AB C¢;(2)解:如图2,BEF△即为所求,;(3)解:如图3,CDE V 即为所求,.【点睛】本题考查的是作图-复杂作图,熟知全等三角形的作法是解答此题的关键.题型06 作角平分线26.(23-24七年级下·陕西榆林·期末)如图,在ABC V 中,请用尺规作图法作出BAC Ð的平分线.(保留作图痕迹,不写作法)【答案】见解析【分析】本题主要考查了尺规作一个角的平分线,根据尺规作一个角的平分线的方法,进行作图即可.【详解】解:AD 即为所求作的BAC Ð的平分线.27.(23-24六年级下·上海宝山·期末)如图,已知点A 、O 、B 在一条直线上,2AOC COD Ð=Ð.(1)利用直尺和圆规作BOD Ð的平分线OE ;(2)如果77COE Ð=o ,求COD Ð的大小.(2)解:∵2AOC COD Ð=Ð,∴设COD x Ð=,则2AOC x Ð=,∴180180BOD AOC COD Ð=°-Ð-Ð=∵射线OE 是BOD Ð的平分线,D 到点B 和点C 的距离相等,且到边AC ,BC 的距离也相等.【答案】见解析【分析】本题考查了尺规作图,线段垂直平分线的性质,角平分线的性质,熟练掌握以上知识点是解题的关键.根据线段垂直平分线的作法作出BC 的垂直平分线,再根据角平分线的作法作ACB Ð的角平分线,两线的交点即为所求.【详解】作线段BC 的垂直平分线MN ,作CT 平分ACB Ð,MN 交CT 于点D ,如图所示,D 点即为所求,29.(2024·陕西西安·一模)已知ABC V ,请在AB 边上确定一点P ,使得点P 到AC BC 、的距离相等.(尺规作图,不写做法,保留作图痕迹)【答案】见解析【分析】题目主要考查角平分线的作法及性质,根据题意点P 到AC BC 、的距离相等得出作角平分线,然后作图即可,熟练掌握作图方法是解题关键.【详解】解:如图所示:点P 即为所求.30.(23-24八年级下·江西吉安·期末)如图,在ABC V 中,902ACB BC AC Ð=°=,,将ABC V 向右平移一定距离后,得到DEF V ,且E 为BC 的中点,请你用无刻度的直尺按下列要求作图.(1)在图1中,作出ACB Ð的平分线CP ;(2)在图2中,作一个以C 为顶点的直角(已知直角除外)【答案】(1)见解析(2)见解析【分析】本题考查了尺规作图——作角平分线及作垂线,(1)尺规作出ACB Ð的平分线CP 即可;(2)尺规过点C 作BC 垂线即可;【详解】(1)解:ACB Ð的平分线CP 即为所求;(2)BCH Ð即为所求作直角.题型07 作垂线31.(23-24七年级下·山东枣庄·期末)如图,在ABC V 中,10cm AB =,6cm AC =.(1)利用尺规作BC 边的垂直平分线,交AB 于点D ,交BC 于点E ;(保留作图痕迹,不写作法)(2)在(1)的条件下,连接CD ,求ACD V 的周长.【答案】(1)见解析(2)16cm【分析】本题主要考查了尺规作图,线段垂直平分线的性质:(1)根据作已知线段的垂直平分线的作法画出图形,即可;(2)根据线段垂直平分线的性质可得CD BD =,从而得到ACD V 的周长为:AC AD CD AC AD BD AC AB ++=++=+,即可求解.【详解】(1)解:如图所示,直线DE 即为所求;(2)解:因为DE 是BC 的垂直平分线.所以CD BD =.所以ACD V 的周长为:AC AD CD AC AD BD AC AB ++=++=+,因为10cm AB =,6cm AC =.所以ACD V 的周长为:()61016cm AC AB +=+=.32.(24-25八年级上·全国·假期作业)如图,已知点A 、点B 以及直线l .(1)用尺规作图的方法在直线l 上求作一点P ,使PA PB =.(保留作图痕迹,不要求写出作法);(2)在(1)中所作的图中,若AM PN =,BN PM =,求证:MAP NPB Ð=Ð.【答案】(1)见解析(2)见解析【分析】(1)利用线段垂直平分线的尺规作图法,作出AB 的垂直平分线得出即可;(2)利用全等三角形的判定方法以及利用其性质得出即可.此题主要考查了基本作图以及全等三角形的判定与性质,熟练应用线段垂直平分线的性质是解题关键.【详解】(1)解:如图所示:(2)解:在V AMP 和BNP △中Q AM PN PM BN AP BP =ìï=íï=î,(SSS)AMP PNB \V V ≌MAP NPB \Ð=Ð.33.(23-24七年级下·陕西榆林·期末)如图,在Rt ABC △中,请用尺规作图法作AB 边上的高CD 交AB 于点D .(不写作法,保留作图痕迹)【答案】见解析【分析】本题考查作垂线,过点C 作CD AB ^于点D ,则CD 为所求.【详解】解:如图,线段CD 为所求.34.(23-24七年级下·北京怀柔·期末)如图,点O 在直线l 外,点A 在直线l 上,连接OA .选择适当的工具作图.(1)在直线l 上作点B ,使得OB l ^于点B ;(2)连接OB ;(3)在直线l 上取一点C (不与A ,B 重合),连接OC ;(4)在OA ,OB ,OC 中,线段 最短,依据是 .【答案】(1)见解析(2)见解析(3)见解析(4)OB ;垂线段最短【分析】本题考查作图-基本作图,垂线段最短等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.(1)作OB ^直线l 即可;(2)连接OB 即可;(3)在直线l 上取一点C (不与A ,B 重合),连接OC 即可;(4)根据垂线段最短即可.【详解】(1)解:如图,点B 即为所求;(2)解:如图,连接OB 即可;(3)解:如图,点C 即为所求;(4)解:根据垂线段最短可知,线段OB 最短,故答案为:OB ,垂线段最短.35.(23-24七年级下·辽宁沈阳·阶段练习)如图,ABC V 中,AB AC =.(1)尺规作图(保留作图痕迹,不写作法):①作A Ð的角平分线,交BC 于点H ;②作AB 边的垂直平分线,垂足为点D ,交AH 于点O ;(2)连接BO ,OC ,求证:OA OC =.【答案】(1)见解析(2)见解析【分析】本题考查了尺规作图,全等三角形的判定和性质,线段垂直平分线的性质.(1)利用尺规作图作出角平分线,线段垂直平分线即可;(2)证明()SAS BAO CAO V V ≌,得到OB OC =,再根据线段垂直平分线的性质得到OB OA =,即可证明OA OC =.【详解】(1)解:所作图形如图所示:;(2)证明:由作图知BAH CAH Ð=Ð,又AB AC =,AO AO =,∴()SAS BAO CAO V V ≌,∴OB OC =,∵OD 是AB 边的垂直平分线,∴OB OA =,∴OA OC =.A 夯实基础1.(2024·河北·中考真题)观察图中尺规作图的痕迹,可得线段BD 一定是ABC V 的( )A.角平分线B.高线C.中位线D.中线【答案】B^,从而可得答案.【分析】本题考查的是三角形的高的定义,作线段的垂线,根据作图痕迹可得BD AC^,【详解】解:由作图可得:BD ACV的高线;∴线段BD一定是ABC故选B2.(23-24七年级下·广东佛山·期末)如图,作一个角等于已知角(尺规作图)的正确顺序是()A.①⑤②④③B.①②④⑤③C.①④③⑤②D.②①③④⑤【答案】A【分析】此题主要考查了基本作图,熟练掌握尺规作一个角等于已知角的作法是解题的关键.【详解】解:根据用尺规作一个角等于已知角的作图步骤可知正确的是:①⑤②④③.故选:A.3.(22-23八年级上·湖北武汉·期中)已知村政府现要在如图所示区域内,修建到AB,CD,EF三条公路距离相等的加油站P,则加油站的选址共有种选择.【答案】4【分析】本题考查了角平分线的性质的灵活应用,注意:三角形的外角平分线的交点不要漏掉,思考问题要全面.加V的内角角平分线的交点处或外角的角平分线的交点油站到三条公路的距离相等,那么加油站应该建在ABC处,故满足要求的加油站位置共有4个,作出其中一个即可.【详解】解:满足要求的加油站位置共有4个,如图所示,点1P 即为所求.(答案不唯一,画出2P ,3P ,4P 也可以)故答案为:4.4.(23-24八年级上·江苏常州·阶段练习)如图,已知AOB Ð,以点O 为圆心,任意长度为半径画弧①,分别交OA ,OB 于点E ,F ,再以点E 为圆心,EF 的长为半径画弧,交弧①于点D ,画射线OD .若26AOB Ð=°,则AOD Ð的度数为 .【答案】26°/26度【分析】本题考查了全等三角形的判定与性质,基本作图知识,解题的关键是熟练掌握基本知识.根据作图过程可得OD OE OF ==,EF DE =,利用SSS 证明ODE OFE △≌△,即可得出结果.【详解】解:根据作图过程可知:OD OE OF ==,EF DE =,∴()SSS ODE OFE V V ≌,∴26AOD AOB Ð=Ð=°.故答案为:26°.5.(23-24七年级下·陕西榆林·期末)如图,已知四边形ABCD ,利用尺规作图法作ABC Ð的平分线交CD 于点E .(不写作法,保留作图痕迹)【答案】见解析【分析】本题考查尺规作图-作角的平分线,熟悉作图步骤是解答的关键.根据作角平分线的方法步骤作图即可.【详解】解:如图,射线BE 即为所求作:6.(23-24八年级下·甘肃兰州·期中)如图,作出ABC V 的BC 边上的高.(用尺规完成作图,只保留作图痕迹,不要求写出作法)【答案】作图见详解【分析】本题考查了作图−基本作图:熟练掌握5种基本作图是解决问题的关键.利用基本作图,过A 点作BC 的垂线即可.【详解】解:如图,线段AD 即为所求,B 能力提升1.(23-24七年级下·辽宁锦州·期末)如图,已知ABC V ,按如下步骤作图:①分别以点A 和B 为圆心,以大于12AB 的长为半径作弧,两弧相交于点E 和F ;②作直线EF ,分别交AB BC ,于点M ,N ;③连接AN ,若2,AM ACN =V 的周长为12,则ABC V 的周长为( )A .16B .15C .14D .13【答案】A 【分析】本题考查了基本作图—垂直平分线作图,垂直平分线的性质,解题的关键是熟练掌握垂直平分线的性质;根据作图可知MN 为AB 的垂直平分线,进而可得224AB AM BM AN BN ====,,即可求解【详解】解:根据作图可知:MN 为AB 的垂直平分线,224AB AM BM AN BN\====,12ACN C AN CN AC =++=V Q 12BN CN AC \++=41216ABC C AB BN CN AC V \=+++=+=故选:A2.(2024·湖北黄石·三模)如图所示,在ABC V 中,90C Ð=°,以顶点A 为圆心,取适当长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以点M ,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线AP 交边BC 于点D ,若3CD =,则点D 到AB 的距离是( )A .1B .2C .3D .4【答案】C 【分析】本题考查了作图-基本作图:角平分线的作法;由作法得AP 是BAC Ð的角平分线,,然后根据角平分线的性质求解.【详解】解:由题可知,AP 是BAC Ð的角平分线,\点P 到AB 和AC 的距离相等,90C Ð=°Q ,3CD =,DC AC \^,\点D 到AC 的距离为CD 的长,即点D 到AC 的距离为3,∴点D 到AB 的距离为3.。
八上数学:尺规作图专练

6. 已知∠AOB=60°,以 O 为圆心,以任意长为半径作弧,交 OA,OB 于点 M,
N,分别以点 M,N 为圆心,以大于 1 MN 的长度为半径作弧,两弧在 2
∠AOB 内交于点 P,以 OP 为边作∠POC=15°,则∠BOC 的度数为( )
A.15°
B.45°
C.15°或 30°
D.15°或 45°
6
7. 如图,已知锐角∠AOB. ︵
(1)在射线 OA 上取一点 C,以点 O 为圆心,OC 长为半径作 PQ ,交射线 OB 于点 D,连接 CD;
︵ (2)分别以点 C,D 为圆心,CD 长为半径作弧,交PQ于点 M,N; (3)连接 OM,MN. 根据以上作图过程及所作图形,给出下列结论:
①∠COM=∠COD; ②若 OM=MN,则∠AOB=20°; ③MN∥CD; ④MN=3CD. 其中正确的结论是__________.(填序号)
9. 在数学课上,老师提出如下问题: 尺规作图:作一条线段的垂直平分线. 已知:线段 AB.
小芸的作法如下: 如图,
(1)分别以点 A 和点 B 为圆心,大于 1 AB 的长为半径作弧,两弧相交于 C, 2
D 两点; (2)作直线 CD. 老师说,小芸的作法正确. 请回答,小芸的作图依据是____________________________.
2
8. 已知:∠AOB. 求作:∠AOB 的平分线. 作法:①以点 O 为圆心,适当长为半径作弧,分别交 OA,OB 于点 M,N; ②分别以点 M,N 为圆心,大于 1 MN 的长为半径作弧,两弧在∠AOB 内部 2 交于点 C; ③作射线 OC.射线 OC 即为所求. 上述作图用到了全等三角形的判定方法,这个方法是__________.
八上第二章尺规作图专题训练(有答案)
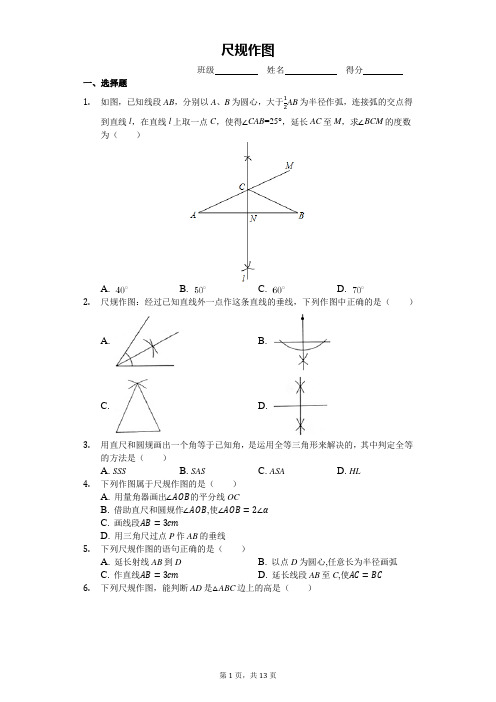
尺规作图班级姓名得分一、选择题1.如图,已知线段AB,分别以A、B为圆心,大于1AB为半径作弧,连接弧的交点得2到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为()A. B. C. D.2.尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是()A. B.C. D.3.用直尺和圆规画出一个角等于已知角,是运用全等三角形来解决的,其中判定全等的方法是()A. SSSB. SASC. ASAD. HL4.下列作图属于尺规作图的是()A. 用量角器画出∠AOB的平分线OCB. 借助直尺和圆规作∠AOB,使∠AOB=2∠αC. 画线段AB=3cmD. 用三角尺过点P作AB的垂线5.下列尺规作图的语句正确的是()A. 延长射线AB到DB. 以点D为圆心,任意长为半径画弧C. 作直线AB=3cmD. 延长线段AB至C,使AC=BC6.下列尺规作图,能判断AD是△ABC边上的高是()A. B.C. D.7.已知:直线AB和AB外一点C.作法:(1)任意取一点K,使K和C在AB的两旁.(2)以C为圆心,CK长为半径作弧,交AB于点D和E.DE的长为半径作弧,(3)分别以D和E为圆心,大于12两弧交于点F.(4)作直线CF,直线CF就是所求的垂线.这个作图是()A. 平分已知角B. 作一个角等于已知角C. 过直线上一点作此直线的垂线D. 过直线外一点作此直线的垂线二、填空题8.如图,在△ABC中,用直尺和圆规作AB、AC的垂直平分线,分别交AB、AC于点D、E,连接DE.若BC=10cm,则DE=______cm.9.如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,BC)为半径作弧,两弧相交于点D,连接以相同长(大于12AD,BD,CD.若∠MBD=40°,则∠NCD的度数为______.10.小为同学和小辰同学研究一个数学问题:尺规作图:作三角形的高线.已知:△ABC.尺规作图:作BC边上的高AD.他们的作法如下:BE长为半径画弧,两弧交于点F.①分别以B,E为圆心,大于12②连接AF,与BC交于点D,则线段AD即为所求.③以A为圈心,AB为半径画弧,与BC交于点E.老师说:“你们的作法思路正确,但作图顺序不对.”请回答:其中顺序正确的作图步骤是(填写序号)______.判断线段AD为BC边上的高的作图依据是______.11.如图,以点O为圆心,任意长为半径画弧,与射线OP交于点A,再以点A为圆心,OA长为半径画弧,两弧交于点B,画射线OB,则∠AOB=_________°.12.如图,在△ABC中,∠C=90°,分别以点A,B为圆心,大于1AB长为半径作弧,两2弧分别交于M,N两点,过M,N两点的直线交BC于点D,若AC=2,∠B=15°,则BD的长______.13.如图,用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取______,再分别过点M,N作OA、OB的垂线,交点为P,画射线OP,可利用______(填写判定方法)证明△POM≌△PON,然后根据______得∠POM=∠PON,则OP平分∠AOB.14.如图,画线段PQ的垂直平分线.PQ长为半径画弧,两弧分解:(1)分别以点_________和点_________为圆心,大于12别交于点________和点________;(2)过点________和点________作直线,则直线________就是线段PQ的垂直平分线.15.如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:①以点A为圆心,小于AC的长为半径.画弧,分别交AB、AC于点E、F;EF的长为半径画弧,两②分别以点E、F为圆心,大于12弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为______.三、解答题16.如图,在△ABC中,∠A>∠B.(1)作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);(2)在(1)的条件下,连接AE,若∠B=50°,求∠AEC的度数.17.如图,已知∠AOB及点C、D,求作一点P,使PC=PD,并且使点P到OA、OB的距离相等.(尺规作图)18.如图,已知△ABC,∠BAC=90°,(1)尺规作图:作∠ABC的平分线交AC于D点(保留作图痕迹,不写作法)(2)若∠C=30°,求证:DC=DB.19.如图,已知在△ABC中,BC=4,AC=8.(1)作边AB的垂直平分线MN,交AC于点D,连接BD(用尺规作图,保留作图痕迹,不要求写作法);(2)在(1)的条件下,求△BCD的周长.20.如图,在△ABC中,AB=AC,∠BAC=120°.(1)尺规作图:作线段AB的垂直平分线DE,交BC于点D,交AB于点E(保留作图痕迹,不写作法);DC.(2)求证:BD=1221.如图,已知△ABC.(1)请用尺规作图作出AC的垂直平分线,垂足为点D,交AB于点E(保留作图痕迹,不要求写作法);(2)连接CE,如果△ABC的周长为27,DC的长为5,求△BCE的周长.答案和解析1.【答案】B【解析】解:∵由作法可知直线l是线段AB的垂直平分线,∴AC=BC,∴∠CAB=∠CBA=25°,∴∠BCM=∠CAB+∠CBA=25°+25°=50°.故选:B.根据作法可知直线l是线段AB的垂直平分线,故可得出AC=BC,再由三角形外角的性质即可得出结论.本题考查的是作图-基本作图,熟知线段垂直平分线的作法是解答此题的关键.2.【答案】B【解析】已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.作法:(1)任意取一点K,使K和C在AB的两旁.(2)以C为圆心,CK的长为半径作弧,交AB于点D和E.DE的长为半径作弧,两(3)分别以D和E为圆心,大于12弧交于点F,(4)作直线CF.直线CF就是所求的垂线.故选:B.根据过直线外一点向直线作垂线即可.此题主要考查了过一点作直线的垂线,熟练掌握基本作图方法是解决问题的关键.3.【答案】A【解析】解:用直尺和圆规画出一个角等于已知角,是运用了SSS定理来判定全等的,故选:A.根据作一个角等于已知角的做法可得答案.此题主要考查了全等三角形的判定,以及作一个角等于已知角的做法,关键是熟练掌握作一个角等于已知角的做法.4.【答案】B【解析】解:根据尺规作图的定义可知:助直尺和圆规作∠AOB,使∠AOB=2∠α属于尺规作图,故选:B.根据尺规作图的定义即可判定.本题考查尺规作图的定义,解题的关键是理解尺规作图的定义,属于中考基础题.5.【答案】B【解析】解:A.根据射线AB是从A向B无限延伸,故延长射线AB到D是错误的;B.根据圆心和半径长即可确定弧线的形状,故以点D为圆心,任意长为半径画弧是正确的;C.根据直线的长度无法测量,故作直线AB=3cm是错误的;D.延长线段AB至C,则AC>BC,故使AC=BC是错误的;故选:B.根据线段、射线以及直线的概念,利用尺规作图的方法进行判断即可得出正确的结论.本题主要考查了尺规作图的定义的运用,解题时注意:尺规作图是指用没有刻度的直尺和圆规作图,只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.6.【答案】B【解析】解:过点A作BC的垂线,垂足为D,故选:B.过点A作BC的垂线,垂足为D,则AD即为所求.本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图7.【答案】D【解析】解:利用作法得CF⊥AB,所以这个作图为过直线外一点作此直线的垂线.故选:D.利用基本作图(过一点作直线的垂线)进行判断.本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.8.【答案】5【解析】【分析】此题主要考查了基本作图以及线段垂直平分线的性质,三角形的中位线的性质,正确得出DE是△ABC的中位线是解题关键.直接利用线段垂直平分线的性质得出DE是△ABC的中位线,进而得出答案.【解答】解:∵用直尺和圆规作AB、AC的垂直平分线,∴D为AB的中点,E为AC的中点,∴DE是△ABC的中位线,∴DE=1BC=5cm.2故答案为5.9.【答案】40°【解析】解:∵AB=AC,DB=DC,∴∠ABC=∠ACB,∠DBC=∠DCB,∴∠ABD=∠ACD,∴∠MBD=∠NCD=40°,故答案为:40°根据等腰三角形的性质得到∠ABC=∠ACB,∠DBC=∠DCB,则∠ABD=∠ACD,然后根据邻补角得出∠MBD=∠NCD.本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).10.【答案】③①②到线段两点的距离相等的点在线段的垂直平分线上【解析】解:作法如下:先以A为圈心,AB为半径画弧,与BC交于点E,再分别以B,BE长为半径画弧,两弧交于点F,然后连接AF,与BC交于点D,因E为圆心,大于12为根据到线段两点的距离相等的点在线段的垂直平分线上,所以线段AD⊥BC,即AD 为高.故答案为③①②;到线段两点的距离相等的点在线段的垂直平分线上.利用基本作图(作已知线段的垂直平分线)可得到正确的作图步骤,然后根据线段垂直平分线的性质定理的逆定理可判断AD⊥BC.本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).11.【答案】60【解析】【分析】本题考查了尺规作图和等边三角的判断,解题的关键是能根据尺规作图得到相等的线段.由尺规作图可知AO=BO=AB,由此可得△AOB是等边三角形,得出∠AOB的度数.【解答】解:由作图可得:AO=BO=AB,∴△AOB是等边三角形,∴∠AOB=60°.故答案为60.12.【答案】4【解析】解:连接AD,如图,由作法得MN垂直平分AB,则DA=DB,∴∠B=∠BAD=15°,∴∠ADC=∠B+∠BAD=30°,在Rt△ADC中,AD=2AC=4,∴BD=DA=4.故答案为4.连接AD,如图,由作法得MN垂直平分AB,则DA=DB,根据等腰三角形性质和三角形外角性质得到∠ADC=30°,所以AD=2AC=4,从而得到BD的长.本题考查了作图-基本作图:熟练掌握5种基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了线段垂直平分线的性质.13.【答案】OM=ON;HL;全等三角形的对应角相等【解析】解:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA、OB的垂线,交点为P,画射线OP,可利用HL(填写判定方法)证明△POM≌△PON,然后根据全等三角形的对应角相等得∠POM=∠PON,则OP平分∠AOB.故答案为:OM=ON,HL,全等三角形的对应角相等.根据作图的作法得到OM=ON,根据全等三角形的判定定理得到HL,根据全等三角形的性质得到结论.本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了全等三角形的判定方法.14.【答案】(1)P;Q;M;N;(2)M;N;MN.【解析】【分析】本题主要考查线段的垂直平分线的画法,需熟练掌握作图语言才能解决问题.通过观察可发现是作线段PQ的垂直平分线.【解答】解:通过观察可发现是作线段PQ的垂直平分线,根据线段的垂直平分线的画法,PQ的长为半径作弧,两弧分别交于点M和点所以分别以点P和点Q为圆心,以大于12N,再过点M和点N作直线,则直线MN就是线段PQ的垂直平分线.故答案为(1)P;Q;M;N;(2)M;N;MN.15.【答案】65°【解析】解:解法一:连接EF.∵点E、F是以点A为圆心,小于AC的长为半径画弧,分别与AB、AC的交点,∴AF=AE;∴△AEF是等腰三角形;EF的长为半径画弧,两弧相交于点G;又∵分别以点E、F为圆心,大于12∴AG是线段EF的垂直平分线,∴AG平分∠CAB,∵∠ABC=40°∴∠CAB=50°,∴∠CAD=25°;在△ADC中,∠C=90°,∠CAD=25°,∴∠ADC=65°(直角三角形中的两个锐角互余);解法二:根据已知条件中的作图步骤知,AG是∠CAB的平分线,∵∠CAB=50°,∴∠CAD=25°;在△ADC中,∠C=90°,∠CAD=25°,∴∠ADC=65°(直角三角形中的两个锐角互余);故答案是:65°.根据已知条件中的作图步骤知,AG是∠CAB的平分线,根据角平分线的性质解答即可.本题综合考查了作图--复杂作图,直角三角形的性质.根据作图过程推知AG是∠CAB 平分线是解答此题的关键.16.【答案】解:(1)如图所示;(2)∵DE是AB的垂直平分线,∴AE=BE,∴∠EAB=∠B=50°,∴∠AEC=∠EAB+∠B=100°.【解析】(1)根据题意作出图形即可;(2)由于DE是AB的垂直平分线,得到AE=BE,根据等腰三角形的性质得到∠EAB=∠B=50°,由三角形的外角的性质即可得到结论.本题考查了作图-基本作图,线段垂直平分线的性质,三角形的外角的性质,等腰三角形的性质,熟练掌握线段垂直平分线的性质是解题的关键.17.【答案】解:(1)以O为圆心,以任意长为半径画弧,交OA、OB于M、N两点,MN长为半径画弧,两弧交于K点,(2)再以M、N为圆心,大于12(3)作射线OK,(4)分别以C、D为圆心画弧,两弧分别交于H、T两点,连接HT,(5)CD的垂直平分线与∠AOB的角平分线交点即为P点【解析】本题考查了尺规作图的一般作法.解答本题的关键在于知道怎么作出线段CD的垂直平分线及∠AOB的角平分线,通过两条直线的交点即为我们所要求的P点.18.【答案】(1)解:射线BD即为所求;(2)∵∠A=90°,∠C=30°,∴∠ABC=90°-30°=60°,∵BD平分∠ABC,∠ABC=30°,∴∠CBD=12∴∠C=∠CBD=30°,∴DC=DB.【解析】(1)根据角平分线的作法求出角平分线BD;(2)想办法证明∠C=∠CBD即可;本题考查作图-基本作图,等腰三角形的判断等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.19.【答案】解:(1)(2):∵MN 是AB 的垂直平分线.∴AD =BD∴△BCD 的周长=BD +CD +BC=AD +CD +BC=AC +BC =8+4=12【解析】此题主要考查了基本作图,关键是掌握线段垂直平分线的作法和性质.垂直平分线上任意一点,到线段两端点的距离相等.(1)根据线段垂直平分线的作法作图即可;(2)根据线段垂直平分线的性质可得“DB =DC ,进而得到AD +DC =AD +BD =5cm ,然后可得周长.20.【答案】(1)解:如图,DE 为所作;(2)证明:连接AD ,如图,∵AB =AC ,∴∠B =∠C =12(180°-∠BAC )=12(180°-120°)=30°, ∵DE 垂直平分AB ,∴DA =DB ,∴∠DAB =∠B =30°,∴∠CAD =120°-30°=90°,在Rt △ADC 中,AD =12CD ,∴BD =12CD .【解析】(1)利用基本作图(作已知线段的垂直平分线)作出DE 垂直平分AB ; (2)连接AD ,如图,先利用等腰三角形的性质和三角形内角和计算出∠B =∠C =30°,再根据线段垂直平分线的性质得DA =DB ,则∠DAB =∠B =30°,接着计算出∠CAD =90°,利用含30度的直角三角形三边的关系得到AD =12CD ,从而得到结论.∴BD =12CD .本题考查了作图-基本作图:熟练掌握5种基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).21.【答案】解:(1)如图,DE为所作;(2)∵DE垂直平分AC,∴EA=EC,AD=CD=5,∴AC=10,∵△ABC的周长=AB+BC+AC=27,∴AB+BC=27-10=17,∴△AEC的周长=BE+EC+BC=BE+AE+BC=AB+BC=17.【解析】(1)利用基本作图作DE垂直平分AC;(2)根据线段垂直平分线的性质得到EA=EC,AD=CD=5,则利用△ABC的周长得到AB+BC=17,然后根据等线段代换可求出△AEC的周长.本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).。
尺规作图专题
探索10:如图,在一组平行线 1、 2两侧各有两点 、 ,在 1、 2间找一条线段MN,使 ⊥ 1并且使得AM+MN+NB之和最短.
2【解析】
(1)问题描述
已知:直线MN外一点P
求作:直线a,使得点P在直线a上,且垂直于直线MN
(2)作法提要
(3)基本原理
5.尺规作图5-------过直线外一点做已知直线的平行线(选学)
(1)问题描述
已知:直线MN外一点P
求作:直线a,使得点P在直线a上,且平行于直线MN
(2)作法提要
(3)基本原理
专题2————与三角形有关的“心”
(1)原理分析
(2)应用举例
如图,三条公路两两相交,交点分别为A,B,C.现计划修建一个油库,要求到三条公路的居理想等,请你说出可以选择的地址
2到点的距离相等
(1)原理分析
(2)应用举例
如图,在公路l的同旁有两座城市A,B,为了方便市民就医治疗,政府决定在公路边建一所医院,这所医院应该建在什么位置,能使这两座城市到这个医院的距离相等?作图说明。
八年级上册尺规作图专题
专题1————尺规作图
1.尺规作图1------做线段等于已知线段
(1)问题描述
已知:线段AB
求作:线段CD,CD=AB
(2)作法提要
(3)基本原理
2.尺规作图2------做三角形与已知三角形全等
(1)问题描述
已知:三角形ABC
求作:三角形DEF,使得ABC DEF
(3)作法提要
使 的周长最小.
【解析】
探索7:如图,点 在锐角 的内部,在 边上求作一点 ,在 边上求作一点 ,
使 最小.
【解析】
八年级上尺规作图常见题
学习资料八年级上尺规作图常见类型题在几何里,把限定用直尺和圆规来画图,称为尺规作图.最基本,最常用的尺规作图,通常称基本作图. 其中,直尺是没有刻度的;一些复杂的尺规作图都是由基本作图组成的.以前学过的”作一条线段等于已知线段”,就是一种基本作图. 下面再介绍几种基本作图:1、作一条线段等于已知线段(七年级下);2、作一个角等于已知角;(第36页)3、平分已知角;(第48页)4、过一点作已知直线的垂线;(第62页例1)5、作已知线段的垂直平分线;(第63页例2) 第一类:用尺规作图作一个角等于已知角。
已知:∠AOB 。
求作:∠A ′O ′B ′=∠AOB 。
(只保留作图痕迹,写出结论,不写作图过程)第二类:用尺规作图作一个角等于已知角;例1:已知:∠AOB 。
角平分线的性质: 求作:∠AOB 的角平分线。
练习: 1、(书本49页思考)如图,要在S 区建一个集贸市场, 使它到两条路的距离相等,并且交叉点200m,这个集贸 市场应建在何处?(比例尺为1:10 000)2、如图,在直线MN 上求作一点P ,使点P 到∠AOB 两边的距离相等3、(书本55页第6题拓展)如图,三条笔直的公路将地面分成7块区域, 是否存在到这三条公路距离相等的点,请用尺规作图做出这些点。
并证明 这些点到这三条公路距离相等。
A OB A O B S学习资料第三类:用尺规作图过一点做已知直线的垂线。
(一)过直线上一点做这条直线的垂线; (二)过直线外一点做这条直线的垂线。
已知:点C 是直线AB 上的一点; 已知:点C 是直线AB 外的一点; 求作:AB 的垂线,使它经过点C. 求作:AB 的垂线,使它经过点C.四、用尺规作图作已知线段的垂直平分线垂直平分线的性质: 例2、已知线段AB ;求作:线段AB 的垂直平分线。
练习: 1、(书本66页第10题)如图,路边有A 、B 两个小区, 要在公路m 上修建一个公交车站,请问公交车站建在哪 能使车站到两小区的距离相等?2、(书本66页第13题拓展)如图,在△ABC 中,确定一点使它到三个顶点的距离相等,并给于证明。
初中数学人教版八年级上册第11章专题突破:尺规作图讲义
初中数学人教版八年级上册实用资料尺规作图(讲义)➢课前预习1.尺规作图是指用没有刻度的直尺和圆规作图,其中“尺”指没有刻度的直尺,作用是作线;“规”指_________,作用是_______和_______.2.读一读,背一背常见的几何语言,并在旁边画一画:①连接AB;②延长线段AB到点C,使BC=AB;③延长线段AB交线段CD的延长线于点E;④过点A作AB∥CD;⑤过点A作AB⊥CD于点E.➢知识点睛1.基本作图:①作一条线段等于已知线段;②作一个角等于已知角;③作已知角的角平分线.书写作法时注意:________________,________________.2.应用作图:①______________________,设计作图方案;②调用__________________完成图形.➢精讲精练1.作一条线段等于已知线段.已知:如图,线段a.求作:线段AB,使AB=a.作法:(1)作射线AP;(2)以_________为圆心,_______为半径作弧,交射线AP于点B.___________即为所求.),作一条线段,使它等于2a-b.2.已知线段a,b(a bab3.作一个角等于已知角.已知:如图,∠ABC.求作:∠DEF,使∠DEF=∠ABC.A作法:(1)作射线EF ;(2)以________为圆心,_______为半径作弧,交BA于点M ,交BC 于点N ;(3)以____为圆心,____为半径作弧,交EF 于点P ; (4)____________,__________作弧,交前弧于点D ; (5)作射线ED . ∠DEF ______________.证明:如图,连接________,________.在___________和___________中,______________________________________________________⎧⎪⎨⎪⎩(已作)(已作)(已作) ∴____________________( ) ∴____________________4. 作一个已知角的倍角.5. 过直线外一点作已知直线的平行线.已知:如图,A 是直线MN 外一点. 求作:直线AB ,使AB ∥MN .NMA6.已知两边及夹角作三角形.已知:如图,线段m,n,∠α.求作:△ABC,使∠A=∠α,AB=m,AC=n.αn m7.作已知角的角平分线.已知:如图,∠AOB.求作:射线OP,使∠AOP=∠BOP(即OP平分∠AOB).AOB作法:(1)________________,__________________作弧,交OA于点M,交OB于点N;(2)分别以______,______为圆心,______________为半径作弧,两弧在________________交于点P;(3)_________________________.______________________________.8.作已知角的四等分线.已知:如图,∠AOB.求作:射线OP,OQ,OM,使∠AOP=∠POQ=∠QOM=∠MOB(即OP,OQ,OM四等分∠AOB).AOB9.为打造“宜居城市”,某市拟在新竣工的扇形广场的内部修建一个音乐喷泉,要求音乐喷泉M在广场的两个入口P,Q的连线上(P,Q的位置如图所示),且到广场两边AB,AC的距离相等.请在题目给的原图上利用尺规作图作出音乐喷泉M的位置(不写作法,保留作图痕迹).10.请画出草图,解决下列问题:(1)在△ABC中,点D是AC边的中点,连接BD,若AB=5,BC=3,则△ABD和△BCD的周长的差是____________.(2)在△ABC中,BD平分∠ABC交AC于点D,过D作DE∥BC交AB 于点E,则∠AED和∠EDB的数量关系是________________________.(3)已知:在△ABC中,BO平分∠ABC,CO平分∠ACB,BO与CO交于点O,过点O作DE∥BC交AB于D,交AC于E,则DE_____BD+CE(选填“>”、“<”或“=”).(4)已知:在△ABC中,CE平分∠ACB交AB于E,过点E作ED∥AC 交BC于D,过D作DF∥CE交AB于F,则∠EDF和∠BDF的数量关系是_____________________.(5)已知:在△ABC中,∠A=80°,AB=AC,BD平分 ABC交AC于点D,CE ⊥BD交BD延长线于点E,则∠ECD=_______.(6)若等腰三角形一腰的垂直平分线与另一腰所在的直线夹角为40°,则此等腰三角形的顶角为______________.【参考答案】➢课前预习1.圆规、度量、截取2.略➢知识点睛1.点线取名称,作弧说心径2.①画出草图②基本作图➢精讲精练1.点A a长线段AB图略2. 略3. 作法:(1)作射线EF ;(2)以 点B 为圆心,任意长为半径作弧,交BA 于点M ,交BC 于点N ;(3)以点E 为圆心,BM 长为半径作弧,交EF 于点P ; (4)以点P 为圆心,MN 长为半径作弧,交前弧于点D ; (5)作射线ED . DEF ∠即为所求. 证明:连接MN ,DP . 在BMN △和EDP △中BM EDBN EP MN DP =⎧⎪=⎨⎪=⎩(已作)(已作)(已作) SSS BMN EDP DEF ABC ≅∠=∠∴△△()∴ 4. 略 5. 略 6. 略7. (1)以点O 为圆心 任意长为半径(2)点M点N大于12MN 长AOB ∠内部(3)作射线OP 射线OP 即为所求 8. 略 9. 略 10. (1)2 (2)2AED EDB ∠=∠ (3)=(4)EDF BDF ∠=∠ (5)15°(6)50°或130°。
八年级上册尺规作图知识点
八年级上册尺规作图知识点尺规作图是中学数学最基础的一部分之一,也是非常重要的一部分。
在八年级上册,学生们将进行深入的尺规作图学习。
本文将介绍八年级上册尺规作图知识点。
第一部分:基础知识在学习尺规作图之前,需要了解一些基础知识。
首先是尺规作图的基本规则和对象。
尺规作图只能使用尺子和圆规,只能作直线和圆。
直线是通过尺子进行作图的,而圆是通过圆规进行作图的。
因此,尺规作图的基本规则是使用尺子和圆规,只能作直线和圆。
其次是尺规作图的基础术语。
直线和圆都有一些基础的术语。
直线上的点称为点,在直线上画出的小段称为线段,在直线上的两个点之间画出的直线称为线段。
圆的中心为圆心,圆的周围称为圆周,圆周上的点称为点。
第二部分:尺规作图的主要步骤尺规作图的主要步骤如下:1.画出给定的直线和圆。
2.通过尺规,从给定的直线或圆的一个点开始作出需要的线段或圆。
3.通过圆规,从圆心或圆周上的点开始作出需要的圆。
4.用尺规或圆规测量所画出的线段或圆的大小。
第三部分:尺规作图的基本构造在学习尺规作图时,需要了解一些基本的构造。
以下是一些基本的尺规构造:1. 画直线段:这是尺规作图中最基础的构造之一。
利用尺子可以快速精准地画出直线段。
2. 画平行线:利用尺子可以相对较容易地画出平行线。
3. 画垂直线:画出两条互相垂直的线通常被称为画出垂直线。
4. 作圆:圆可以通过圆规方便地作出。
圆的大小只需要通过圆规测量就可以得知。
5. 作垂线:利用圆规可以方便地作出垂线。
第四部分:尺规作图的高级构造在掌握了基础构造之后,学习尺规作图的高级构造就变得相对容易。
以下是一些高级构造:1.倍增线段:掌握倍增线段的构造可以快速且准确地将线段长度增大或减小。
2.三分线段:三分线段是尺规作图中另一个重要的概念。
掌握三分线段的构造可以将任意线段三等分。
3.求平均数:通过尺规作图可以快速求出一组数的平均数。
总结:尺规作图是中学数学的基础之一。
在八年级上册,学生将学习到更深入的尺规作图知识,如基础构造和高级构造。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 1
尺规作图专题复习
一、关于尺规作图
用 和 准确地按要求作出图形。
不利用...直尺的刻度,三角板现有的角度,及量角器。
二、几种基本作图
1、画一条线段等于已知线段
如图1,MN 为已知线段,用直尺和圆规准确地画一条线段AC 与MN 相等。
步骤:
1、画 AB ,
2、然后用 量出线段 的长,再在 AB 上截取AC =MN , 那么,线段AC 就是所要画的线段. 2、画一个角等于已知角
如图2所示,∠AOB 为已知角,试按下列步骤用圆规和直尺准确地画∠A ′O ′B ′等于∠AOB .
步骤:
1、 画射线O ′A ′.
2、 以点O 为圆心,以适当长为半径画弧,交OA 于C ,交OB 于D .
3、 以点O ′为圆心,以OC 长为半径画弧,交O ′A ′于C ′.
4、 以点C ′为圆心,以CD 长为半径画弧,交前一条弧于D ′.
5、 经过点D ′画射线O ′B ′.∠A ′O ′B ′就是所要画的角. 3、画已知线段的垂直平分线
定义: 于一条线段并且 这条线段的直线,叫做线段的垂直平分线(或叫中垂线。
) 如图所示,已知线段AB ,画出它的垂直平分线. 步骤:
1、 以点A 为圆心,以大于AB 一半的长为半径画弧;
2、 以点B 为圆心,以同样的长为半径画弧,
3、 两弧的交点分别记为C 、D ,连结CD ,则CD 是线段AB 的垂直平分线.
4、画角平分线
利用直尺和圆规把一个角二等分. 已知:如图3,∠AOB 求作:射线OC ,使∠AOC =∠BOC 步骤:
1、OA 和OB 上,分别截取OD 、OE ,使OD =OE
2、分别以D 、E 为圆心,大于 的长为半径作弧,在∠AOB 内,两弧交于点C
3、作射线OC ,OC 就是所求的射线。
5、作已知直线垂线
(1)过直线上一点作一条直线与已知直线垂直 如图,点A 在1l 上,过点A 作直线2l ,使得1l ⊥2l 作法:
1、以点A 为圆心,以为适当长为半径画弧交1l 于B 、C
2、分别以点B 、C 为圆心,以大于2
1
BC 为半径,在1l 一侧作弧,交点为D 3、连接AD
那么,AD 就是所求的直线直线2l
(2)过直线上一点作一条直线与已知直线垂直
1、以点A 为圆心,以大于点A 到1l 的距离的长度为半径画弧交1l 于B 、C
o B A
图2A
l 1
A
l 1
o B A
图2
2、分别以点B 、C 为圆心,以大于
2
1
BC 为半径,在另一侧作弧,交点为D 3、连接AD 那么,AD 就是所求的直线直线2l
练习一
1、如图,画一个等腰△ABC ,使得底边BC=a ,它的高AD=h
2、如图,已知∠AOB 及M 、N 两点,求作:点P ,使点P 到∠AOB 的两边距离相等,且到M 、N 的两点也距离相等。
3
己知一个三角形三条边分别为a ,b ,c 求作这个三角形。
4、己知三角形的两条边及其夹角,求作三角形
已知一个三角形的两条边分别为a ,b ,这两条边夹角为∠a ,求作这个三角形
5、已知三角形的两角及其夹边,求作三角形
巳知一个三角形的两角分别为∠a ∠β夹边为a 求作这个三角形。
6、己知三角形的两角及其中一角的对边,求作三角形
O
已知三角形的两角分别为∠a ∠β,∠a 的对边为∠a,求作这个三角形
5.己知一直角边和斜边求作三角形
己知一个直角三角形的一条直角边为a ,斜边长为b ,求作这个三角形。
6、如图,做出△BCD 关于直线l 的对称图形。
7、如图所示,如果将军从马棚M 出发,先赶到河OA 上的某一位置P ,再马上赶到河OB 上的某一位置Q ,然后立即返
回校场N .请为将军重新设计一条路线(即选择点P 和Q),使得总路程MP +PQ +QN 最短.
8、如图,已知直线A B 和A B 外一点P ,作一条经过点P 的直线C D ,使C D ∥A B .
l
B C
D
9、如图,已知△ABC,求作AC边上的高。
A
B C
10、已知:如图,甲、乙、丙三人做接力游戏,开始时甲站在∠AOB内的P点,乙站在OA上的定点Q,丙站在OB 上且可以移动.游戏规则:甲将接力棒转给乙,乙将接力棒转给丙,最后丙跑至终点P处.若甲、乙、丙三人速度相同,试用尺规作图找出丙必须站在OB上的何处,使得他们完成接力所用的时间最短?(不写作法,保留作图痕迹)。
