第七章 单 元 选 择_ 非线性分析
合集下载
自动控制原理第七章非线性控制系统的分析
X X
这里，M=3，h=1
负倒描述函数为
N 1 X
X
12 1 1 2
X
X 1
X 1, N 1 X , N 1
必有极值
d N 1X 令
0 dX
得 X 2
N 1 2
2
0.523
12
1
1 2
2
6
X： 1 2
-N-1(X)： 0.523
2.自振的稳定性分析
在A点，振幅XA，频率A。
扰动：
X : A点 C点 C点被G(j)轨迹包围，不稳定，
振幅 ，工作点由C点向B点运动；
A点一个不稳 定的极限环。
X : A点 D点 D点不被G(j)轨迹包围，稳定，
振幅 ，工作点由D点左移。
在B点，振幅XB，频率B 。 扰动：
X : B点 E点 E点不被G(j) 轨迹包围，稳定，
振幅 ，工作点由E点到B点；
X : B点 F点 F点被G(j)轨迹包围，不稳定，
振幅 ，工作点由F回到B点。
B点呈现稳定的自激振荡:振幅XB ,频率B。
3.闭环系统稳定性判别步骤
1）绘制非线性部分的负倒描述函数曲线和线 性部分的频率特性曲线。
2）若G(j)曲线不包围“-N-1(X)”曲线，则系统稳定。 若G(j)曲线包围“-N-1(X) ”曲线，系统不稳定。 若G(j)曲线与“-N-1(X)”曲线相交，系统出现自振。
3）若G(j )曲线与“-N-1(X)”曲线有交点，做以 下性能分析：
（1）不稳定的极限环
（2）稳定的极限环 计算自振频率和幅值。
例1：非线性系统如图所示,其中非线性特性为 具有死区的继电器,分析系统的稳定性。
0e
这里，M=3，h=1
负倒描述函数为
N 1 X
X
12 1 1 2
X
X 1
X 1, N 1 X , N 1
必有极值
d N 1X 令
0 dX
得 X 2
N 1 2
2
0.523
12
1
1 2
2
6
X： 1 2
-N-1(X)： 0.523
2.自振的稳定性分析
在A点，振幅XA，频率A。
扰动：
X : A点 C点 C点被G(j)轨迹包围，不稳定，
振幅 ，工作点由C点向B点运动；
A点一个不稳 定的极限环。
X : A点 D点 D点不被G(j)轨迹包围，稳定，
振幅 ，工作点由D点左移。
在B点，振幅XB，频率B 。 扰动：
X : B点 E点 E点不被G(j) 轨迹包围，稳定，
振幅 ，工作点由E点到B点；
X : B点 F点 F点被G(j)轨迹包围，不稳定，
振幅 ，工作点由F回到B点。
B点呈现稳定的自激振荡:振幅XB ,频率B。
3.闭环系统稳定性判别步骤
1）绘制非线性部分的负倒描述函数曲线和线 性部分的频率特性曲线。
2）若G(j)曲线不包围“-N-1(X)”曲线，则系统稳定。 若G(j)曲线包围“-N-1(X) ”曲线，系统不稳定。 若G(j)曲线与“-N-1(X)”曲线相交，系统出现自振。
3）若G(j )曲线与“-N-1(X)”曲线有交点，做以 下性能分析：
（1）不稳定的极限环
（2）稳定的极限环 计算自振频率和幅值。
例1：非线性系统如图所示,其中非线性特性为 具有死区的继电器,分析系统的稳定性。
0e
非线性系统分析方法
解：1. 死去继电特性的描述函数
4M N(X)
1 ( )2
X
X
2. 绘制描述函数的负倒数特性
1
X
N(X ) 4M 1 ( )2
X
3. 绘制线性部分的极坐标图
4. 判断稳定性，分析两曲线相交点的性质
1 N(X)
X
-1.56 300 400 B -1 -0.5
X 130 A 140
120 G(j)
趋于奇点 远离奇点 包围奇点
例：二阶线性定常系统
••
•
x 2n x n2 x 0
试分析其奇点运动性质。
dx/dt x
稳定节点
••
•
x 2n x n2 x 0
dx/dt x
1
稳定节点
相轨迹趋于原点，该奇点称为 稳定节点
••
•
x 2n xn2 x 0
dx/dt x
1
不稳定节点
相轨迹远离原点，该奇点为 不稳定节点
者是自持振荡的
自持振荡点 a 振荡幅值=Xa
振荡频率=a
Im Re
X a
0
1 G(j) N ( X )
例：已知死区继电非线性系统如图
R(s)
+M
460
C(s)
+-
- -M
( j)(0.01 j 1)(0.005 j 1)
继电参数： M 1.7 死区参数：Δ 0.7 应用描述函数法作系统分析。
•
x
-1 -5/4
-3/2
-5/3
=
-2
-3/7
-3
-5 - x
3
1 1/3
0 -3/4 -1/2 -1/3
非线性系统的分析 (3)
第七章 非线性系统的分析
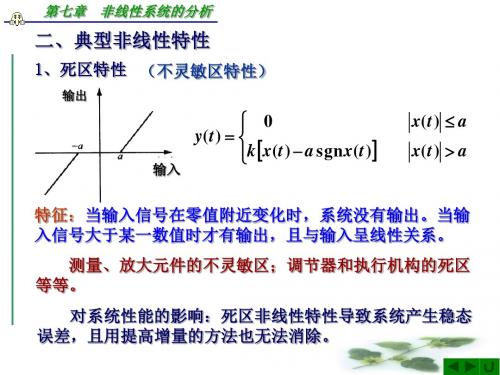
2、饱和特性
输出
k x( t ) y( t ) ka sgn x( t )
输入
x( t ) a x( t ) a
特征：当输入信号超出其线性范 围后，输出信号不再随输入信号 变化而保持恒定。
放大器的饱和输出特性、磁饱和、元件的行程限制、 功率限制等等。 饱和特性对系统性能的影响： 使系统在大信号作用下开环增益下降，因而降低了 稳态精度。
继电器特性对系统性能的影响
带死区的继电特性，将会增加系统的定位误差，对 其他动态性能的影响，类似于死区、饱和非线性特 性的综合效果
第七章 非线性系统的分析
三、非线性系统的特点
１、系统的稳定性
非线性系统的稳定性不仅与系统的结构参数有关， 而且与初始状态有关。 ２、系统的自持振荡 非线性系统即使无外界作用，也可能会发生某一 固定振幅和频率的振荡，称为自持振荡。
第七章 非线性系统的分析
7-2 相平面分析法
相平面法是Poincare在1885年首先提出来 的，它是一种求解一、二阶微分方程的图解法。 这种方法的实质是将系统的运动过程形象 地转化为相平面上一个点的移动，通过研究这 个点移动的轨迹，就能获得系统运动规律的全 部信息。 由于它能比较直观、准确、全面地表征系 统的运动状态，因而获得广泛应用。
第七章 非线性系统的分析
用x1、x2描述 二阶系统常微分方程方程的解，也就是 用质点的状态来表示该质点的运动。在物理学中，状态又称 为相。
把由x1—x2所组成的平面坐标系称为相平面，系统的一 个状态则对应于相平面上的一个点。
当t变化时，系统状态在相平面上移动的轨迹称为相轨 迹。
而与不同初始状态对应的一簇相轨迹所组成的图叫做 相平面图。 利用相平面图分析系统性能的方法称为相平面法。
第7章非线性系统分析
描述函数的定义是：输入为正弦函数时，输 出的基波分量与输入正弦量的复数比。
其数学表达式为
N
X
R
X
Y1
sin(t X sint
1)
Y1 X
1
A12 B12 arctan A1
A1
1
2
y(t) costdt
0
X
B1
1
B1
2
y(t ) sin tdt
0
7.3 非线性特性的描述函数法
（2）举例说明描述函数
(1) 降低了定位精度，增大了系统的静差。 (2) 使系统动态响应的振荡加剧，稳定性变坏。
7.2 非线性环节及其对系统结构的影响
4.摩擦特性
Mf
M1 •
M2
•
M f 摩擦力矩
转速
M1 静摩擦力矩
M 2 动摩擦力矩
7.2 非线性环节及其对系统结构的影响
摩擦特性的影响
(1)对随动系统而言，摩擦会增加静差，降低精 度。
7.2 非线性环节及其对系统结构的影响
2.饱和特性
x1 a ，等效增益 为常值，即线性段 斜率；
而 x1 a ，输出饱
和，等效增益随输 入信号的加大逐渐 减小。
7.2 非线性环节及其对系统结构的影响
饱和特性的影响
(1) 饱和特性使系统开环增益下降， 对动态响应的 平稳性有利。
(2) 如果饱和点过低，则在提高系统平稳性的同时， 将使系统的快速性和稳态跟踪精度有所下降。
7.3 非线性特性的描述函数法
KX sint
y(t) Ka
0 t 1 1 t / 2
∵ y(t) 单值奇对称， A0 0 A1 0
B1
4
非线性分析简介
非线性分析简介非线性分析是数学中一个重要的分支，研究的对象是非线性系统。
在实际生活和科学研究中，许多系统都是非线性的，因此非线性分析具有广泛的应用价值。
本文将简要介绍非线性分析的基本概念、方法和应用。
一、非线性系统的特点在介绍非线性分析之前，首先需要了解非线性系统的特点。
与线性系统相比，非线性系统具有以下几个显著的特点：1. 非线性系统的响应与输入之间不满足叠加原理，即系统的输出不是输入的简单线性组合。
2. 非线性系统的行为复杂多样，可能出现周期性运动、混沌现象等。
3. 非线性系统的稳定性分析更加困难，存在更多的稳定性条件和现象。
二、非线性分析的基本概念1. 非线性方程：非线性系统的数学模型通常由非线性方程描述，如非线性微分方程、非线性差分方程等。
2. 非线性动力学：研究非线性系统随时间演化的规律，包括稳定性、周期性、混沌等性质。
3. 非线性控制：设计能够有效控制非线性系统的控制器，使系统达到期望的状态或性能。
三、非线性分析的方法1. 线性化方法：将非线性系统在某一工作点附近进行泰勒展开，得到近似的线性系统，然后应用线性系统的方法进行分析。
2. 相图分析：通过构建相空间中的相图，观察系统在相空间中的轨迹和稳定性，揭示系统的动力学行为。
3. 数值模拟：利用计算机进行数值模拟，求解非线性系统的数值解，研究系统的演化过程和特性。
4. 非线性优化：通过优化方法寻找非线性系统的最优控制策略或参数配置，使系统达到最佳性能。
四、非线性分析的应用1. 混沌理论：非线性分析在混沌理论中有重要应用，揭示了一些看似混乱的系统背后的规律和特性。
2. 生物系统：生物系统中存在许多非线性现象，如神经元网络、生物钟等，非线性分析有助于理解和模拟这些系统。
3. 控制工程：许多实际控制系统是非线性的，非线性分析为设计高效的控制器提供了理论支持和方法指导。
4. 物理学：非线性分析在物理学中有广泛应用，如流体力学、光学等领域，帮助揭示复杂系统的行为规律。
7第七章__非线性系统的分析
３、频率响应畸变
非线性系统在输入为正弦函数时，输出为包含一定数 量的高次谐波的非正弦周期函数。
第七章 非线性系统的分析
线性系统分析可用叠加原理，在典型输入信号下系 统分析的结果也适用于其它情况。
非线性系统不能应用叠加原理，没有一种通用的方 法来处理各种非线性问题。 对非线性系统分析研究的重点是： （1）系统是否稳定； （2）有无自持振荡； （3）若存在自持振荡，确定自持振荡的频率和振幅； （4）研究消除或减弱自持振荡的方法。
第七章 非线性系统的分析
6、
,
1
2
为一正一负两实根
jω
x
×
×
λ1
0
λ2
x
系统的自由运动是发散运动，原点处的奇点称为鞍点。 以上6种奇点，类似的奇点在非线性系统中也常见到。
第七章 非线性系统的分析
二阶系统的相轨迹总结：
极点分布 奇点
中心点
相迹图
极点分布 奇点
鞍 点
相迹图
稳定的 焦点
不稳定 的焦点
第七章 非线性系统的分析
借助Matlab等软件工具可以方便地绘制非线性系统的相平面 图。 例1：有死区继电器非线性的系统框图如下
r 常数
＋
e
1 -1 1 -1
y
1 S ( S 1)
C
阻尼自然振荡角频率 n 1rad / s ，阻尼比 前面对奇点的分类，可知为稳定焦点。
1 系统线性部分的传递函数 G ( S ) ，该二阶系统的无 S ( S 1)
第七章 非线性系统的分析
4、 (-1 0)
jω
× 0 ×
x
x
系统的自由运动是发散振荡。相轨迹是以原点出发的螺旋线， 原点处的奇点称为不稳定焦点。
非线性控制系统分析(《自动控制原理》课件)
出发的相轨迹曲线互不相交. 如果在相平面上某些点的
d x/ dx 0/ 0, 即曲线在这一点上的斜率不定, 可有无穷多
条相轨迹通过这一点, 称这一点为系统的平衡点, 或叫奇
点.
在相平面的上方(如下图) ,
由于
x
0所以
x总是朝大的
x
A(x0 ,
x0 )
方向变化, 故相轨迹上的点总是按图 中箭头所指从左向右移动. 在相平面
u0
0
u(t) u(t) G(s) c(t)
u0
上图中, 大方框表示一具有理想继电特性的非线性环节, G(s) 表示非线性系统中线性部分的传递函数.
非线性的特性是各种各样的, 教材图及 表给出了一些工程上常见的典型非线性特性.
7-2非线性控制系统的特征
非线性控制系统有如下两个基本特征: (1)非线性控制系统的基本数学模型是非线性微分方程 (2)非线性控制系统的性能不仅与系统本身的结构和参
0
x
的下方,
由于
x
0
所以
x
总是朝小的
方向变化, 故相轨迹上的点总是按图中箭
箭头所指从右向左移动. 在 x 轴上, 由于
x 0, 即 x不变化, 达到最大值或最小值, 故相轨迹曲线
与 x 轴的交点处的切线总垂直于x 轴.
2. 相轨迹作图法
先以线性系统为例, 说明相轨迹曲线的画法.
(1)解析法
数有关, 还与系统的初始状态及输入信号的形式和大小 有关.
由于非线性控制系统的基本数学模型是非线性微分 方程, 而从数学上讲, 非线性微分方程没有一个统一的 解法, 再由于第二个特征, 对非线性控制系统也没有一 个统一的分析和设计的方法, 只能具体问题具体对待.
第七章 非线性系统的分析
自激振荡或自振荡,如图所示。 自振荡是人们特别感兴趣的一个 问题,对它的研究有很大的实际意义。
Nanjing University of Technology
四、非线性系统的正弦输入响应 正弦信号作用下，线性系统的输出是与输入信 号同频率的正弦信号。 而非线性系统在正弦信号作用下的响应则很复 杂，一般不是正弦信号，但仍是周期信号；有 时输出信号频率为输入频率的倍频、分频等现 象。 非线性系统响应还有其他与线性系统不同的现 象,无法用线性系统的理论来解释。在一些情况 下,引入某些非线性环节,使系统获得比线性系 统更为优异的性能。实际上大多数智能控制都 属于非线性控制范畴。
Nanjing University of Technology
图7-6-3非线性控制系统的稳定性分析
二、自振荡分析
Nanjing University of Technology
• 若复平面中-1／N (X)曲线与G (j)曲线有交点,则该交 点对应着可能的等幅振荡,问题是这个等幅振荡能否稳 定地存在？也就是说,如果系统受到某个扰动使振荡的 振幅发生变化,系统是否具有恢复到扰动前的等幅振荡 状态的能力？如果系统具备这种能力,则该等幅振荡能 够稳定地存在,并能被观察到,称这个稳定的等幅振荡为 自持振荡。反之,振荡不能稳定地存在,必然转移到其它 运动状态(收敛到零或发散)。 • 以图7-6-3(c) 为例进行分析。图中-1／N (X)曲线与G (j)曲线有两个交点a和b, 对应于不同的振荡频率和振 幅。对a点,振幅及频率为Xa及 (j),若由于扰动使振 荡的振幅略有增大,这时工作点将沿-1／N (X)曲线由a 点移动到c点。由于c点不被G (j)所包围,故系统进入稳 定区,周期振荡的振幅要衰减,并逐步恢复到Xa,即自动返 回原状态；若由于扰动使振荡的振幅略有减小,这时工 作点将沿-1／N (X)曲线由a 点转移到d点，由
Nanjing University of Technology
四、非线性系统的正弦输入响应 正弦信号作用下，线性系统的输出是与输入信 号同频率的正弦信号。 而非线性系统在正弦信号作用下的响应则很复 杂，一般不是正弦信号，但仍是周期信号；有 时输出信号频率为输入频率的倍频、分频等现 象。 非线性系统响应还有其他与线性系统不同的现 象,无法用线性系统的理论来解释。在一些情况 下,引入某些非线性环节,使系统获得比线性系 统更为优异的性能。实际上大多数智能控制都 属于非线性控制范畴。
Nanjing University of Technology
图7-6-3非线性控制系统的稳定性分析
二、自振荡分析
Nanjing University of Technology
• 若复平面中-1／N (X)曲线与G (j)曲线有交点,则该交 点对应着可能的等幅振荡,问题是这个等幅振荡能否稳 定地存在？也就是说,如果系统受到某个扰动使振荡的 振幅发生变化,系统是否具有恢复到扰动前的等幅振荡 状态的能力？如果系统具备这种能力,则该等幅振荡能 够稳定地存在,并能被观察到,称这个稳定的等幅振荡为 自持振荡。反之,振荡不能稳定地存在,必然转移到其它 运动状态(收敛到零或发散)。 • 以图7-6-3(c) 为例进行分析。图中-1／N (X)曲线与G (j)曲线有两个交点a和b, 对应于不同的振荡频率和振 幅。对a点,振幅及频率为Xa及 (j),若由于扰动使振 荡的振幅略有增大,这时工作点将沿-1／N (X)曲线由a 点移动到c点。由于c点不被G (j)所包围,故系统进入稳 定区,周期振荡的振幅要衰减,并逐步恢复到Xa,即自动返 回原状态；若由于扰动使振荡的振幅略有减小,这时工 作点将沿-1／N (X)曲线由a 点转移到d点，由
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M
M
x
M
M
微体积纯弯曲变形中，平直断面 保持平直，上下两边变成圆弧， xy = 0。
完全积分低阶单元变形中，上下两边 保持直线，不再保持直角， xy不等 于0。
October 18, 2000
单元选取 – 5.7版本
7-5
剪切锁定实例
PL 3EI tip 1.0 2 3EI kGAL
7-10
非协调模式
低阶完全积分单元的形函数可被表示常曲率状态的模式所增强，这些 增加的模式作为内在的自由度，因其导致网格的缝隙和重叠而被称为 非协调模式。
F 2F
F 2F F 非协调模式
F 2F
F 2F F
F
F
无非协调模式
单元选取 – 5.7版本
7-11
October 18, 2000
非协调模式
3
P
当长宽比增加时，在弯曲时完全积 分低阶单元将发生锁定。
如 Plane82 的二阶单元不会发生 剪切锁定问题 (二次形函数允许边 部弯曲)。
Number of Normalized Deflection of a Cantilever Beam Elements tip deflection (Plane42) (depth/length = 1/100) Depth Length Exclude Extra shapes 0.02 0.02 0.02 0.07
7-15
单元选取 – 5.7版本
一致缩减积分
• 一致缩减积分 (URI) 采用比精确数值积分所需阶数低的低阶积 分规则进行积分。这将导致单元变形更加容易，有助于消除剪 切锁定和体积锁定。
• URI不需要附加的自由度。 文件减小，单元计算所需CPU时间缩 短 (尤其对于材料非线性)。 然而URI会引起应变能为零的变形 模式，这被称为零能量或沙漏模式。
October 18, 2000
单元选取 – 5.7版本
7-23
推荐使用的实体单元
线性分析 • 对于线性分析采用有非协调模式的一阶单元 (非退化形状的 Plane42, Solid45)，二阶单元适用于高应力梯度和应力集中区 域中。
• 采用 Solid92 进行高性能求解。
• 具有缩减积分的Solid95 单元适用于要求泊松比接近0.5 的大部 分问题。
Plane182 3.75 4.4531 4.5825 5.0399 5.0602 5.0623
Plane42 w/ extra shape 3.7745 4.4837 4.6143 5.0763 5.0968 5.0989
Plane42 w/o extra shape 3.7236 4.4037 4.5227 4.1971 1.7 0.2441
October 18, 2000
单元选取 – 5.7版本
7-24
推荐使用的实体单元(续)
几乎不可压缩材料 (塑性) • 可忽略弯曲的体结构变形采用 Plane182, Solid185 选择缩减积 分 (B-Bar)。 • 对于小应变应用采用非协调模式单元 Plane42, Solid45。 • 对于大应变应用采用具有URI(特别对于大模型)的Plane182 和 Solid185 或具有URI的 Solid95 。也可以采用 Visco106, Visco107 和 Visco108 单元(甚至对于与速率无关的塑性)。
低阶单元 & URI
• URI 导致沙漏模式， 如不加以检查，沙漏模式可引起网格的 不可控变形。为控制沙漏模式 ANSYS 使用一个小的沙漏刚度 来控制变形的零能量模式。
• 当使用URI和低阶单元时应避免点载荷和点约束，为得到精确 的应力预测还需要细化网格。
• 尽管沙漏行为使验证问题解时增加了需检查的项目，但这些单 元在非线性分析中是非常高效的。
任何情况下都应监察“ 虚假能量”， 最好使“ 虚假能量” 与总能量的比值(AENE/SENE)小于 5%。
October 18, 2000
单元选取 – 5.7版本
7-20
二次单元 & URI
• 采用一致缩减积分的二次单元没有低阶单元的沙漏困难。
• Plane82 采用 2 x 2 高斯积分规则，只有一个零能量模式，并 且只要模型中有不止一个单元，零能量模式就不会传播。
October 18, 2000
单元选取 – 5.7版本
7-16
沙漏模式
• 沙漏模式是由于变形而引起零应变能的变 形模式。
• 如右图所示两例，在只有一个积分点的低 阶单元中，此单个积分点未获得任何单元 应变能。这可导致出现不切实际的行为。
October 18, 2000
单元选取 – 5.7版本
7-17
第 七 章
单 元 选 择
－非线性分析
单元算法
• 传统位移协调方法 Solid45 KEYOPT(1)=1 由于剪切锁定而很少使用 • 非协调模式 (额外形函数) Solid45 缺省选项，弯曲变形 • 选择缩减积分 (B-Bar) 几乎不可压缩材料，体积变形
• 一致缩减积分 (URI) 几乎不可压缩材料，弯曲变形
• 体积锁定可出现于不同的应力状态中，包括平面应变、轴对称和 3-D 应力。对于平面应力不会发生体积锁定。
October 18, 2000
单元选取 – 5.7版本
7-8
体积锁定实例
厚壁轴对称圆筒的径向位移
Poisson's ratio 0 0.25 0.3 0.49 0.499 0.4999
October 18, 2000
Analytical 3.75 4.4531 4.5825 5.0399 5.0602 5.0623
Plane42 w/ extra shape 3.7745 4.4837 4.6143 5.0763 5.0968 5.0989
单元选取 – 5.7版本
Plane42 w/o extra shape 3.7236 4.4037 4.5227 4.1971 1.7 0.2441
*** 警告 *** 区域2的网格包含 PLANE42 三角形，这些三角形单元在弯曲中过于刚硬， 如有可能采用二次(6或 8 节点)单元。
October 18, 2000
单元选取 – 5.7版本
7-12
非协调模式
非协调模式以附加公式为代价增 加精度：
悬臂梁的挠曲 (厚度/长度 = 1/100)
Number of Elements Depth Length Normalized tip deflection (Plane42) Include Extra shapes 0.9972 0.9973 0.9974 0.9993 Exclude Extra shapes 0.02 0.02 0.02 0.07
7-6
网格细分一般无助于剪切锁定!
1 4 10 10
October 18, 2000
10 10 10 20
单元选取 – 5.7版本
体积锁定
• 当材料特性是几乎不可压缩的并使用完全积分单元时发生体积锁 定 (泊松比约为 0.5)， 不可压缩性能存在于超弹性材料或塑性流 动中。 在单元中出现伪压应力，从而使单元对于不会引起任何体 积变化的变形“ 过于刚硬”。
• 注意：由于剪切锁定和体积锁定，此公式的低阶单元极少使用。
October 18, 2000
单元选取 – 5.7版本
7-4
剪切锁定
在弯曲问题中，完全积分低阶单元呈现“ 过分刚硬”。在弯曲中这种 公式包括实际上并不存在的剪切应变，称为寄生剪切。 (从纯弯曲中 的梁理论可知剪切应变 xy = 0)
y
October 18, 2000
单元选取 – 5.7版本
7-14
B-Bar 实例
厚壁轴对称圆筒的径向位移
Poisson's ratio 0 0.25 0.3 0.49 0.499 0.4999
October 18, 2000
Analytical 3.75 4.4531 4.5825 5.0399 5.0602 5.0623
URI 67 808 82
October 18, 7-22
U-P 混合公式
• U-P 混合公式除位移外还把静水压力作为一个单独的自由度， 且位移和压力自由度分别使用单独的插值函数。
• U-P 混合公式非常适合于不可压缩材料模型，如橡胶和橡胶类 材料。
• 采用此种公式的 ANSYS 单元包括超弹性单元 Hyper56、 Hyper58、 Hyper74 和 Hyper158; 以及粘塑性实体单元 Visco106、 Visco107和 Visco108。
7-9
体积锁定
• 体积锁定可通过压应力“ 棋盘状”模式 (相邻单元间变化显著) 检 测出。 在超弹性模型中可用单元等值线绘图(PLESOL)绘制静水压 力(HPRES)等值线来验证此行为。
• 如怀疑存在体积锁定，可试细分高静水压力区域的网格或改变单 元类型。
October 18, 2000
单元选取 – 5.7版本
• 任何情况下都应该监控由沙漏模式产生的“ 虚假能量”，可 以用单元表格项 AENE 来存储“ 虚假能量”。
October 18, 2000
单元选取 – 5.7版本
7-19
沙漏控制
如果模型中发生沙漏模式，推荐采取的步骤按优先顺序排列如 下所示： • • • • 去掉点载荷和点约束 细化网格 采用其它可选单元类型 增大沙漏刚度缩放因子
• 选择缩减积分 (B-Bar)在几乎不可压缩材料中用单元平均体积 应变代替积分点应变从而消除体积锁定。 B-Bar 把 B 矩阵分 成两部分，即体积应变 (主应变) 和偏差应变。
• B-Bar 的优势在于其不增加求解中的自由度数。 • 推荐将 B-Bar 公式用于体积变形塑性应用中，因对于B-Bar仍 存在剪切锁定问题 (弯曲) 。