《自动控制原理》第3章 系统时间响应的性能指标
合集下载
自动控制原理(3-1)

动态性能指标定义1
hh((tt))
AA
超超调调量量σσ%% ==
AA BB
110000%%
峰峰值值时时间间ttpp BB
上上 升升 时时间间ttrr
调调节节时时间间ttss
tt
动态性能指标定义2 h(t)
调节时间 ts
上升时间tr
t
动态性能指标定义3
h(t)
A
σ%=
A B
100%
B tr tp
一阶系统对典型输入的输出响应
输入信号
输出响应
1(t) 1-e-t/T t≥0
δ(t)
1 et T t 0
T
t
t-T(1-e-t/T) t≥0
1 t2
1 t 2 Tt T 2 (1 et T ) t 0
2
2
由表可见,单位脉冲 响应与单位阶跃响应 的一阶导数、单位斜 坡响应的二阶导数、 单位加速度响应的三 阶导数相等。
自动控制原理
朱亚萍 zhuyp@ 杭州电子科技大学自动化学院
第三章 线性系统的时域分析法
3.1 系统时间响应的性能指标 3.2 一阶系统的暂态响应 3.3 二阶系统的暂态响应 3.4 高阶系统的暂态响应 3.5 线性系统的稳定性分析 3.6 控制系统的稳态误差 3.7 利用MATLAB对控制系统进行时域分析
超调量σ%:指响应的最大偏离量h(tp)与终值 h(∞)的差与终值h(∞)比的百分数,即
% h(tp ) h() 100%
h()
在实际应用中,常用的动态性能指标多为上升 时间tr、调整时间ts和超调量σ%。 用上升时间tr或峰值时间tp评价系统的响应速度; 用超调量σ%评价系统的阻尼程度;
自动控制原理第三章

σ % = 0没有超调,非周期响应,
惯性环节亦称非周期环节。
t s = 3 T ( ± 5 % 误差带 t s = 4 T ( ± 2 % 误差带 T 越小, )
C(t)
1 1/T斜率 0.632
h (t ) = 1 − e − t /T
)
0
系统的快速性越好。
T
t
1.
一阶系统的结构图如图所示,若kt=0.1,试求系统的调节时间ts,如果要求 ts= 0.1秒。试求反馈系数应取多大?
§3-1 控制系统的时域指标
h(t)
σ
1.0
误 差 带 5%或 2%
td 0.5
h(∞)
0
tr tp ts
控制系统的时域性能指标,是根据系统在单位阶跃函数作用下的时间 响应——单位阶跃响应确定的,通常以y(t)表示。
1、超调量σ% 、超调量 响应曲线超出稳态值的最大偏差与稳态值之比。 y (t ) − y (∞) 即 超调量表示系统响应过冲的 σ% = × 100% y (∞ ) 程度 。 2、上升时间tr 响应曲线从零首次上升到稳态值h(∞)所需的时间,称为 上升时间。对于响应曲线无振荡的系统,tr是响应曲线从 tr 稳态值的10%上升到90 %所需的时间。 延迟时间td:响应曲线第一次到达终值一半所需的时间。 3、峰值时间tp
§3-2 一阶系统的阶跃响应
一、一阶系统的数学模型
dy (t ) + y (t ) = x(t ),T为时间常数。 dt 1 k 1 = , k = 为开环增益 开环传递函数:G0 ( s) = T Ts s G0 ( s) Y ( s) 1 闭环传递函数:G(s) = = = X ( s) 1 + G0 ( s) Ts + 1 微分方程为:T
《自动控制原理》第三章自动控制系统的时域分析和性能指标

i1 n
]
epjt
j
(spj)
j1
j1
limc(t) 0的充要条件是 p j具有负实部
t
二.劳斯(Routh)稳定判据
闭环特征方程
a nsn a n 1 sn 1 a 1 s a 0 0
必要条件
ai0. ai0
劳斯表
sn s n1 s n2
| | |
a a n
n2
a a n 1
n3
b1 b2
或:系统的全部闭环极点都在复数平面的虚轴上左半部。
m
设闭环的传递函数:
(s)
c(s) R(s)
k (s zi )
i 1 n
(s p j )
P j 称为闭环特征方程的根或极点 j1
n
(s pj ) 0 称为闭环特征方程
j1
若R(s)=1,则C(s)= s m
k (szi)
n
c(t)L1[c(s)]L1[
t 3、峰值时间 p
误差带
4 、最大超调量
%
C C ( )
% max
100 %
C ( )
ts
5 、调节时间
ts
(
0 . 05
0
.
02
)
6、振荡次N数
e e 7、稳态误差 ss
1C()(对单位阶跃) 输入
ss
第三节 一阶系统的动态性能指标
一.一阶系统的瞬态响应
R(s) -
K0 T 0S 1
s5 | 1 3 2
s4 | 1 3 2
s3 | 4 6
s2
|
3 2
2
s1
|
2 3
s0 | 2
自动控制原理(胡寿松版)课件第三章讲解

1. 0<ζ<1 欠阻尼
第三节 二阶系统的时域分析
第三节 二阶系统的时域分析
二阶系统的传递函数 开环传递函数:
2 n G( s) = s( s 2n )
闭环传递函数:
C ( s) = 2 2 R(s) s 2n s n
2 n
第三节 二阶系统的时域分析 二阶系统的特征方程为
s 2n s = 0
2 2 n
第二节 一阶系统的时域分析
性能指标
1. 平稳性:
非周期、无振荡, =0 2. 快速性ts:
t = 3T时,c(t ) = 0.95 [对应5%误差带 ] t = 4T时,c(t ) = 0.98 [对应2%误差带 ]
3.准确性 ess:
ess = 1 - c() = 0
第二节 一阶系统的时域分析
当控制系统的数学模型为一阶微分 方程时,称其为一阶系统.
一阶系统的动态结构图 闭环传递函数为 C(s) = 1 Ф(s)= R(s) Ts+1 时间常数
R(s)
-
E(s)
1 TS
C(s)
第二节 一阶系统的时域分析
二、一阶系统时域响应及性能分析 1.单位阶跃响应
单位阶跃响应曲线 一阶系统没 : 系统在单位阶跃信号作 单位阶跃响应 c(t) 有超调,系统的 用下的输出响应 . 1 动态性能指标为 0.98 1 0.95 R(s)= s 一阶系统单位阶跃响应: 0.86 调节时间: 0.632 1 1 1 1 1 • ts = C(s)= 3T Ф (± 5%) (s) · s =Ts+1 s = s - s+ 1 T 0 T 4T 2T 3T t ( ± 2%) ts拉氏反变换: = 4T c(t)=1-e-t/T
自动控制原理课件之第三章 (一) 时域性能指标,时域分析 (1)
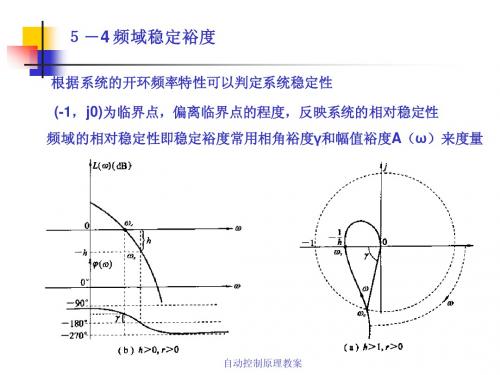
5-4 频域稳定裕度
根据系统的开环频率特性可以判定系统稳定性 (-1,j0)为临界点,偏离临界点的程度,反映系统的相对稳定性 频域的相对稳定性即稳定裕度常用相角裕度γ和幅值裕度A(ω)来度量
自动控制原理教案
相角裕度γ和幅值裕度A(ω)定义
相角裕度γ 设ωc为系统的截止频率
A ( c ) G ( j c ) H ( c ) 1
1 G ( j x ) H ( x )
对数坐标下 h 20 lg G ( j x ) H ( x )
幅值裕度h的含义是,对于闭环稳定系统,如果系统开环幅频特性再增大h倍, 则系统将处于临界稳定状态
自动控制原理教案
例5—12
已知单位反馈系统
G (s) K ( s 1)
3
设k分别为4和10时,试确定系统的稳定裕度。 解 系统开环频率特性
180 G ( j c ) H ( c )
相角裕度γ的含义是,对于闭环稳定系统,如果系统开环相频特性再 滞后γ度,则系统将处于临界稳定状态。 幅值裕度 设ωx为系统的穿越频率 定义幅值裕度为
h
( x ) G ( j x ) H ( x ) ( 2 k 1)
上例中减小开环增益可以增大系统的相角裕度,
但会增大系统的稳态误差,一般要求相角裕度达到 45º ~70º ,为满足这一要求在截止频率附近的斜率大 于-40dB/dec,且有一定的宽度. 若兼顾系统的稳态误差和过度过程的要求,有 必要应用校正方法
自动控制原理教案
自动控制原理教案
例5—13 典型二阶系统相角裕度γ
典型二阶系统如图所示,试确定系统的相角裕度γ。 解 典型二阶系统的开环频率特性为
G ( j )
根据系统的开环频率特性可以判定系统稳定性 (-1,j0)为临界点,偏离临界点的程度,反映系统的相对稳定性 频域的相对稳定性即稳定裕度常用相角裕度γ和幅值裕度A(ω)来度量
自动控制原理教案
相角裕度γ和幅值裕度A(ω)定义
相角裕度γ 设ωc为系统的截止频率
A ( c ) G ( j c ) H ( c ) 1
1 G ( j x ) H ( x )
对数坐标下 h 20 lg G ( j x ) H ( x )
幅值裕度h的含义是,对于闭环稳定系统,如果系统开环幅频特性再增大h倍, 则系统将处于临界稳定状态
自动控制原理教案
例5—12
已知单位反馈系统
G (s) K ( s 1)
3
设k分别为4和10时,试确定系统的稳定裕度。 解 系统开环频率特性
180 G ( j c ) H ( c )
相角裕度γ的含义是,对于闭环稳定系统,如果系统开环相频特性再 滞后γ度,则系统将处于临界稳定状态。 幅值裕度 设ωx为系统的穿越频率 定义幅值裕度为
h
( x ) G ( j x ) H ( x ) ( 2 k 1)
上例中减小开环增益可以增大系统的相角裕度,
但会增大系统的稳态误差,一般要求相角裕度达到 45º ~70º ,为满足这一要求在截止频率附近的斜率大 于-40dB/dec,且有一定的宽度. 若兼顾系统的稳态误差和过度过程的要求,有 必要应用校正方法
自动控制原理教案
自动控制原理教案
例5—13 典型二阶系统相角裕度γ
典型二阶系统如图所示,试确定系统的相角裕度γ。 解 典型二阶系统的开环频率特性为
G ( j )
(自动控制原理)3一阶系统的时间响应及动态性能

一阶系统具有简单的结构和易于控制的特点,常见于温度和速度控制等应用场景。了解一阶系统的时间响应和 动态性能对于设计和优化控制系统至关重要。
(自动控制原理)3一阶系 统的时间响应及动态性能
本节介绍一阶系统的定义、特点以及时间响应,探讨影响动态性能的因素和 常见应用场景,并讨论比例控制、积分控制和比例积分控制方法。
一阶系统的定义和特点
定义
一阶系统是指具有一个能量存储元件和一个能 量传递元件的线性系பைடு நூலகம்。
特点
一阶系统具有简单的结构、易于分析和控制、 但响应速度较慢。
一阶系统的时间响应
1
零状态响应
当输入信号改变时,系统从初始状态开始的响应。
2
零输入响应
当输入信号为零时,系统由初始状态跟踪到平衡状态的响应。
3
控制一阶系统的方法
比例控制、积分控制和比例积分控制。
一阶系统的动态性能指标
1 响应速度
衡量系统从初始状态到达稳定状态所需的时间。
2 超调量
描述系统响应超过稳态值的程度。
3 阻尼比
描述系统振荡响应的衰减程度。
影响一阶系统动态性能的因素
1 系统增益
增加系统增益可以加快响应速度,但可能导致超调量增加。
2 时延效应
时延会影响系统的稳定性和响应速度。
常见应用场景
温度控制
一阶系统常用于室内温度控制,如空调、恒温器等。
速度控制
一阶系统可用于调节电机速度,如风扇、电动车等。
结论
(自动控制原理)3一阶系 统的时间响应及动态性能
本节介绍一阶系统的定义、特点以及时间响应,探讨影响动态性能的因素和 常见应用场景,并讨论比例控制、积分控制和比例积分控制方法。
一阶系统的定义和特点
定义
一阶系统是指具有一个能量存储元件和一个能 量传递元件的线性系பைடு நூலகம்。
特点
一阶系统具有简单的结构、易于分析和控制、 但响应速度较慢。
一阶系统的时间响应
1
零状态响应
当输入信号改变时,系统从初始状态开始的响应。
2
零输入响应
当输入信号为零时,系统由初始状态跟踪到平衡状态的响应。
3
控制一阶系统的方法
比例控制、积分控制和比例积分控制。
一阶系统的动态性能指标
1 响应速度
衡量系统从初始状态到达稳定状态所需的时间。
2 超调量
描述系统响应超过稳态值的程度。
3 阻尼比
描述系统振荡响应的衰减程度。
影响一阶系统动态性能的因素
1 系统增益
增加系统增益可以加快响应速度,但可能导致超调量增加。
2 时延效应
时延会影响系统的稳定性和响应速度。
常见应用场景
温度控制
一阶系统常用于室内温度控制,如空调、恒温器等。
速度控制
一阶系统可用于调节电机速度,如风扇、电动车等。
结论
第三章 自动控制系统的时域分析(1)《自动控制原理与系统》

第二节 一阶系统的动态响应
凡是以一阶微分方程作为运动方程的控制系统,成为一阶系统
一、一阶系统的数学模型
一阶系统的时域微分方程为
T dc (t ) c(t ) r (t ) dt
式中c(t)和r(t)分别为系统的输出、输入量;T为时间 常数,具有时间“秒”的量纲,此外时间常数T也是表征系 统惯性的一个主要参数,所以一阶系统也称为惯性环节 在初始条件为零时两边取拉氏变换,可得其闭环传递函数为
)] T
这里,输入信号t是输出量的期望值。上式还表明,一阶系统在 跟踪单位斜波输入信号时,输出量与输入量存在跟踪误差,其 稳态误差值与系统的“T”的值相等。一阶系统在跟踪斜波输入 信号,所带来的原理上的位置误差,只能通过减小时间常数T来 降低,而不能最终消除它
第三章 自动控制系统的时域分析
4.单位冲激响应 单位脉冲函数是单位阶跃函数的一阶 导数。因此其单位脉冲响应是单位阶 跃响应的一阶导数
r(t)=A sinωt
周期性输入信号
第三章 自动控制系统的时域分析
二、动态过程与稳态过程
在典型输入信号作用下,任何一个控制系统的时间响应都是由 动态过程和稳态过程组成 1.动态过程
又称为过渡过程或暂态过程,是指系统从初始状态到接近最终 状态的响应过程。 2.稳态过程
稳态过程是指时间t趋于无穷时的系统输出状态。
第三章 自动控制系统的时域分析
第三节 二阶系统的动态响应
凡是由二阶微分方程描述的系统,称为二阶系统。在控制工程 中的许多系统都是二阶系统,如电学系统、力学系统等。即使 是高阶系统,在简化系统分析的情况下有许多也可以近似成二 阶系统。因此,二阶系统的性能分析在自动控制系统分析中有 非常重要的地位。
一、二阶系统的数学模型
[精品]自动控制原理课件之第三章(一)时域性能指标,时域分析
![[精品]自动控制原理课件之第三章(一)时域性能指标,时域分析](https://img.taocdn.com/s3/m/34f843ec5022aaea998f0f7d.png)
90 arctg
2 n
根据定义
1 c 4 2 2 ( 4 1 2 ) n
相角裕度γ
180 G ( jc )
180 90 arctg
4
c 2 n arctg 2 n c
2 1 2
arctg[2 ( 4 1 2 ) ]
故 20lg ( j) 3(dB)
b
系统带宽频率与带宽
一阶和二阶系统,带宽和系统参数具有解析关系。
自动控制原理教案
一阶系统的带宽: 一阶系统: 因为
1 (s) Ts 1
, 按带宽定义1 1 Fra bibliotekT 2b2
( j 0) 1
20lg ( jb ) 20lg
( ) 180 ( )
其中γ(ω)表示相角相对于-180º的相移。 开环频率特性可以表示为
G( j ) A( )e j[180 ( )] A( )[ cos ( ) j sin ( )]
自动控制原理教案
系统闭环和开环频域指标的关系 闭环幅频特性
自动控制原理教案
系统闭环和开环频域指标的关系 1.系统开环指标截止频率ωc与闭环指标带宽频率ωb有着密切的关系。
ωc 大的系统 ωb大
2. 闭环振荡性能指标谐振峰值Mr和开环指标相角裕度γ都能
表征系统的稳定程度. 证明 设系统开环相频特性可以表示为
1 1 M r M (r ) sin (r ) sin
解 因为该系统为I型系统,单位速度输入下的稳态误差为 查表
1 K 9 K
60
0.62 % e
/ 1 2
7.5%
K 2 1 n , 2n n 2 K 11.6 T T 3.5 ts 0.506
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
延迟时间
00..11 h()
0 tr tp ts
允许误差
0.02或 0.05
t
h(t)
Mp超 调 量
1 h() 00.9.9 h()
td
0.05.5 h()
00..11 h() 0
tr tp
上升时间 ts
Ch2 控制系统的数学模型
允许误差 0.02或 0.05
t
h(t)
Mp超 调 量
1 h() 00.9.9 h()
❑数学模型
Ch3 线性系统的时域分析法
r(t)
1
c(t )
Ts + 1
C(s) = 1 R(s) Ts + 1
极点 s=-1/T
二、单位阶跃响应
Ch3 线性系统的时域分析法
1. 输入 r(t)=1(t)
C(s)=G(s)R(s) = 1 1 Ts +1 s
=1− T s Ts +1
h(t ) = L−1[C ( s)]
% = h(tp ) − h() 100%
h()
Ch3 线性系统的时域分析法
(1)tr、tp评价系统的响应速度; (2) ts同时反映响应速度和阻尼程度。 (3)σ%评价系统的阻尼程度。
2、稳态性能
Ch3 线性系统的时域分析法
稳态误差---描述系统稳态性能的一种 性能指标。
是系统控制精度或抗扰能力的一种度量。
Ch3 线性系统的时域分析法
4.加速度函数
f (t ) = 1 t 2 , 2
L 1 t 2 2
=
1 s3
t 0
考察系统对于输入加速度信号的运动规律或 对加速度信号的跟踪能力。
5.正弦函数
f (t) = Asint
L(Asint) =
A s2 +2
Ch3 线性系统的时域分析法
考察系统对于输入周期变化信号的跟踪 能力。
Ch3 线性系统的时域分析法
当典型输入信号为单位脉冲信号 时,可以通过系统的输出相应曲 线得到系统的闭环传递函数。
四、单位斜坡响应
Ch3 线性系统的时域分析法
二、动态过程与稳态过程
动态过程: 过渡过程/瞬态过程。 指系统在典型输入信号作用下,系统输
出量从初始状态到最终状态的响应过程。
稳态过程: 指系统在典型输入信号作用下,当t→∞
时,系统输出量的表现形式。 稳态响应。表征系统输出量最终复现输入
量的程度,提供有关稳态误差的信息。
Ch3 线性系统的时域分析法
三、动态性能与稳态性能
Ch3 线性系统的时域分析法
当动态过程收敛时,研究系统的动态性 能才有意义
1、动态性能
假定系统在单位阶跃输入信号作用前处 于静止状态,而输出量及其各阶导数均等于 零。
h(t)
Mp超 调 量
1 h() 00.9.9 h()
td
0.05.5 h()
−t
= 1−e T
t0
−t
h(t) = 1− e T t 0
Ch3 线性系Biblioteka 的时域分析法时间t 0 T
2T 3T 4T … ∞
h(t) 0 0.632 0.865 0.95 0.982 … 1
−t
h(t) = 1− e T t 0
Ch3 线性系统的时域分析法
dh(t) 1 =
dt t=0 T
Mp超 调 量
1 h() 00.9.9 h()
td
0.05.5 h()
00..11 h()
0 tr tp ts
% = h(tp ) − h() 100%
允 许 误h(差)
0.02或 0.05
t
Ch3 线性系统的时域分析法
td 响应曲线第一次到达稳态值一半所需的时间。 tr 响应从稳态值10%-90%所用时间。 tp 响应超过稳态值到第一个峰值所用时间。 ts 响应到达并保持在稳态值5%内所用时间。 σ% 最大偏离量与稳态值的差比上稳态值。
C(s) = K R(s) Ts +1
确定增益K,时间常数T?
三、单位脉冲响应
Ch3 线性系统的时域分析法
r(t)=δ(t)
C(s)=G(s)R(s) = 1 Ts +1
k(t ) = L−1[C ( s)]
=
1
−t
eT
T
t0
k(t) =
1
−t
eT
T
t0
Ch3 线性系统的时域分析法
曲线特点:
1当t=0时,最大值1/T 2当t→∞,幅值衰减到0 3一阶系统对于脉冲扰动 信号,具有自动调节能 力。
R(s)
G(s)
C(s)
为了评价线性系统时间响应的性能指标,需要 研究控制系统在典型输入信号作用下的时间响 应过程。
一、典型输入信号
Ch3 线性系统的时域分析法
1 单位阶跃函数
f(t)
0 0
0
t
e−stdt = 1
s
考察系统对输入恒 值信号的保持能力。
工作状态突然改变, 突然受到恒定输入 作用。
L1(t) = 1
s
Ch3 线性系统的时域分析法
2.(单位)脉冲函数δ(t)
L( (t)) = 1
冲击输入量。
0
考察系统在脉冲扰
动后的复位运动或
系统的调节能力。
3 单位斜坡函数
0
Ch3 线性系统的时域分析法
f (t) = t , t 0
L(t ) =
1 s2
输入随时间渐变
考察系统对输入等速 t 度信号的跟踪能力。
td
0.05.5 h()
00..11 h() 0
tr tp
峰值时间 ts
Ch2 控制系统的数学模型
允许误差 0.02或 0.05
t
h(t)
Mp超 调 量
1 h() 00.9.9 h()
td
0.05.5 h()
00..11 h()
0 tr tp ts
允许误差 0.02或 0.05
t 调节时间
h(t)
Ch3 线性系统的时域分析法
第三章 线性系统的时域分析法
Ch3 线性系统的时域分析法
本章内容
❖ 系统时间响应的性能指标 ❖ 一阶系统的时域分析 ❖ 二阶系统的时域分析 ❖ 高阶系统的时域分析 ❖ 线性系统的稳定性分析 ❖ 线性系统的稳态误差计算
Ch3 线性系统的时域分析法
3.1 系统时间响应的性能指标
当t→∞时,系统的输出量不等于输入 量(或输入量的函数),则系统存在稳态误
差。 误差:e(t)=r(t)-c(t) 稳态误差:ess=e(∞)
Ch3 线性系统的时域分析法
3.2 一阶系统的时域分析
一、一阶系统的数学模型
❑ 一阶系统: ❑ 由一阶微分方程描述的控制系统
T dc(t) + c(t) = r(t) dt
dh(t) =0
dt t=
Ch3 线性系统的时域分析法
一阶系统单位阶跃响应曲线特点
1)一阶惯性环节的阶跃响应无振荡, 能趋于稳态值。
2)T=0+时刻,系统运动的变化率最大。 3)t=3T或 4T时,输出基本达到稳态值。 4)稳态特性:
系统阶跃响应的稳态误差为零。
思考: 如何用实验法确定一阶系统参数?
