两次串联超前校正
自动控制原理超前网络及其串联校正
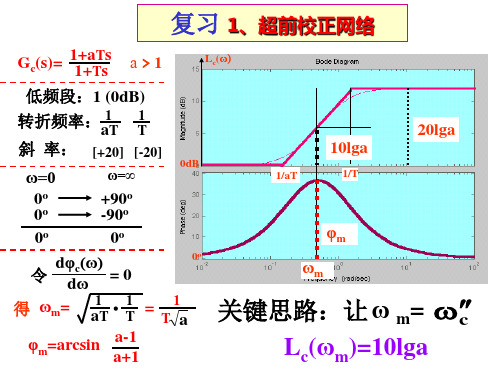
Gc(s)=
1+bTS 1+TS
b<1
低频段: 1 (0dB)
转折频率:
1 T
1 bT
斜 率: [-20]1 [+20]
T
ω=0 ω=∞
0o
+90o
0o
-90o
0o
0o
1
bTω=10 b1T时
1 bT
c(ω) ≈ -5o~ -9o
Lc(ω)= 20lgb
4、串联滞后 校正 步骤:
确定开环增益K
根据稳态误差的要求
2)反馈信号是从系统前向通道的某一元件的输出端引出的, 这 就是说, 信号是从功率电平较高的点传向电平较低的点。 因而通常不必采用附加的放大器。因此, 它所需的元件数往 往比串联校正少, 所用的校正装置也比较简单。
3)反馈校正在系统内部形成了一个局部闭合回路, 作用在这个回 路上的各种扰动, 受到局部负反馈的影响, 往往被削弱。
适当选择反馈校正装置的形式和参数,可使已校正系统性能满足 给定性能指标的要求。
2、复合校正
1) 概念
也就是说, 系统对扰动的敏感度低, 这样可减轻测量元件负担, 提高测量的准确性, 对于控制系统的性能也是有利的。
基本原理:用反馈校正装置包围待校正系统中对动态性能改善
有重大防碍作用的某些环节,形成一个局部反馈回路;在局部反馈 回路的幅值远大于1的条件下,局部反馈回路的特性主要取决于反 馈校正装置,与被包围的部分无关。
根据响应速度要求选择系统的截止频率 ,c 及响应衰减因
子 1 a,确定方法:
20
lg
a
L(
'' c
)
20
lg
'' c
串联超前校正和滞后校正的不同之处

串联超前校正和滞后校正的不同之处在控制系统中,超前校正和滞后校正是两种常见的校正方法。
它们都是为了提高系统的稳定性和性能而采取的措施。
然而,它们的实现方式和效果却有很大的不同。
本文将从理论和实践两个方面,分别探讨串联超前校正和滞后校正的不同之处。
一、理论分析1. 超前校正超前校正是指在控制系统中,通过提前控制信号的相位,使得系统的相位裕度增加,从而提高系统的稳定性和响应速度。
具体来说,超前校正是通过在控制信号中加入一个比例项和一个积分项,来提高系统的相位裕度。
这样,系统就能更快地响应外部干扰和变化,从而提高系统的性能。
2. 滞后校正滞后校正是指在控制系统中,通过延迟控制信号的相位,使得系统的相位裕度减小,从而提高系统的稳定性和抗干扰能力。
具体来说,滞后校正是通过在控制信号中加入一个比例项和一个微分项,来减小系统的相位裕度。
这样,系统就能更好地抵抗外部干扰和变化,从而提高系统的性能。
二、实践应用1. 超前校正超前校正在实践中的应用非常广泛。
例如,在电力系统中,超前校正可以用来提高电力系统的稳定性和响应速度。
在机械控制系统中,超前校正可以用来提高机械系统的精度和响应速度。
在化工生产中,超前校正可以用来提高化工生产的稳定性和生产效率。
2. 滞后校正滞后校正在实践中的应用也非常广泛。
例如,在飞行控制系统中,滞后校正可以用来提高飞行器的稳定性和抗干扰能力。
在汽车控制系统中,滞后校正可以用来提高汽车的稳定性和安全性。
在医疗设备中,滞后校正可以用来提高医疗设备的精度和稳定性。
总之,串联超前校正和滞后校正是两种常见的校正方法,它们都是为了提高系统的稳定性和性能而采取的措施。
然而,它们的实现方式和效果却有很大的不同。
在实践中,我们需要根据具体的应用场景和需求,选择合适的校正方法,以达到最佳的控制效果。
实验四:连续系统串联超前校正

实验目的
1. 加深理解串联校正装置对系统动态性 能的校正作用。 2. 对给定系统进行串联校正设计,并通 过模拟实验检验设计的正确性。
实验内容
串联超前校正
系统模拟电路图(含结构图)如下,图中开关S断开对应未校正 情况, 接通对应超前校正:
实验步骤
1.连接被测量典型环节的模拟电路。电路的输入U1接A/D、 D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入。检 查无误后接通电源。
2.开关S放在断开位置。 3.选中 [实验课题→ 连续系统串联校正→超前校正] 菜单项,鼠 标单击将弹出参数设置窗口。系统加入阶跃信号。参数设置完成 后鼠标单击确认测量系统阶跃响应,并记录最大超调量Mp和调节 时间ts。
4.开关S接通,重复步骤3,将两次所测的波形进行比较。 并将测量结 果记入下表中:
超前校正系统 指标
阶跃响应曲线
Mp tp(秒) ts(秒)
校正前
校正后
实验报告
1.计算串联校正装置的传递函数 Gc(s)和校正 网络参数。
2.画出校正后系统的对数坐标图,并求出校 正后系统的ωc及γ 。
3.比较校正前后系统的阶跃响应曲线及性能 指标,说明校正装置的作用。
付出总有回报
祝愿大家不断ቤተ መጻሕፍቲ ባይዱ步!
自控课程设计实验报告串联超前校正滞后装置

课题:串联超前校正滞后装置专业:电气工程及其自动化班级:组长:组员:指导教师:设计日期:成绩:超前校正课程设计报告一、设计目的(1)把握操纵系统设计与校正的步骤和方式。
(2)把握对操纵系统相角裕度、稳态误差、剪切频率、相角穿越频率和增益裕度的求取方式。
(3)把握利用Matlab 对操纵系统分析的技术。
熟悉MATLAB 这一解决具体工程问题的标准软件,能熟练地应用MATLAB 软件解决操纵理论中的复杂和工程实际问题,并给以后的模糊操纵理论、最优操纵理论和多变量操纵理论等奠定基础。
(4)提高操纵系统设计和分析能力。
二、设计要求与内容已知单位负反馈系统的开环传递函数0()(1)(0.251)K G S S S S =++,试用频率法设计串联校正装置,要求校正后系统的静态速度误差系数1v K 5s -≥,系统的相角裕度045γ≥,校正后的剪切频率2C rad s ω≥已知参数和设计要求:1.前期基础知识,要紧包括MATLAB 系统要素,MATLAB 语言的变量与语句,MATLAB 的矩阵和矩阵元素,数值输入与输出格式,MATLAB 系统工作空间信息,和MATLAB 的在线帮忙功能等。
2.操纵系统模型,要紧包括模型成立、模型变换、模型简化,Laplace 变换等等。
3.操纵系统的时域分析,要紧包括系统的各类响应、性能指标的获取、零极点对系统性能的阻碍、高阶系统的近似研究,操纵系统的稳固性分析,操纵系统的稳态误差的求取。
4.操纵系统的根轨迹分析,要紧包括多回路系统的根轨迹、零度根轨迹、纯迟延系统根轨迹和操纵系统的根轨迹分析。
5.操纵系统的频域分析,要紧包括系统Bode图、Nyquist图、稳固性判据和系统的频域响应。
6.操纵系统的校正,要紧包括根轨迹法超前校正、频域法超前校正、频域法滞后校正和校正前后的性能分析。
三、实现进程1、系统概述所谓校正,确实是在系统中加入一些其参数能够依照需要而改变的机构或装置,使系统整个特性发生转变,从而知足给定的各项性能指标。
串联超前校正

串联超前校正简单的超前网络若在系统的前向通路上(一般是串联于两级放大器之间),就构成了串联超前校正。
给系统串入串联超前校正,减少对数幅频特性在幅值穿越频率上的负斜率,可以有效地改善原系统的平稳性和稳定性,并可以提高系统的频带宽度,对快速性也将产生有利的影响,但是超前校正很难使原系统的低频段特性得到改善。
如果采取进一步开环增益的办法,使低频段上移,则系统的平稳性有所下移;幅频段过分上移,还会大大削弱系统干扰能力。
故超前校正对提高系统稳态精度的作用是很小的。
利用Bode 图设计超前校正网络超前校正的基本原理是利用超前网络的相位特性去增大系统的相位裕度,以改善系统的瞬态响应,具体设计步骤如下。
(1)求出满足稳态指标的开环放大系数K 值。
(2)根据求得的K 值,画出未校正系统的Bode 图,并计算出其幅值穿越频率c ω、相位裕度γ、幅度裕度g K 。
(3)确定需要对系统增加的相位超前m ϕ,m ϕ可表示为m ϕ=∆--γγ'式中,'γ 和γ 分别表示期望的相位裕度和未校正系统(原系统)的相位裕度,∆为增加超前网络后使幅值穿越频率向右方移动所带来的原系统相位的滞后量,一般该滞后量为 5~12。
(4)确定α值。
(5)确定校正后系统的幅值穿越频率'c ω。
为了最大限度利用超前网络的相位超前量。
'c ω应与m ω相重合,即 'c ω 应选在未校正系统的αωlg 10)(-=L 处。
(6)确定校正装置的传递函数。
令)/(1'αωωT c m ==,从而求出超前校正为了的两个转折频率 ⎩⎨⎧==T T αωω1112由此得出校正装置具有的传递函数为111121)(++=++=Ts Ts s sG s αωω(7)验证校正后系统的相位裕度γ。
MATLAB ProgramK0=1000;n1=1;d1=([1 0],[1 2]); sope= tf(K0*n1,d1);[mag,phase,w] =bode(sope);gama=45;[mu,pu]=bode(sope,w); gam=gama*pi/180;alfa=(1-sin(gam))/(1+sin(gam));adb=20*log10(mu);am=10*log10(alfa); ca=adb+am;wc=spline(adb,w,am); T=1/(wc*sqrt(alfa));alfat=alfa*T;Gc=tf([T 1],[alfat 1])MATLAB ProgramK0=1000;n1=1;d1=conv([1 0],[1 2]); S1=tf(K0*n1,d1);N2=[0.04916 1];d2=[0.008434 1]; S2=tf(n2,d2);sope=s1*s2;[mag,phase,w]=bode(sope);Margin(mag,phase,w);。
两次串联超前校正

课程设计任务书2012 —2013学年第1学期电子与信息工程系电气工程及其自动化专业 10-1班级课程设计名称:自动控制原理课程设计设计题目:串联超前校正装置的设计完成期限:自 2012年12—月日至2012年12月14日共1周设计依据、要求及主要内容:设单位反馈系统的开环传递函数为:G(s):s(s+1)(0.6s + 1)(0.001s + 1) 要求校正后系统的幅值裕度大于10dB,相角裕度 _40,试设计串联超前校正装置。
基本要求:1、对原系统进行分析,绘制原系统的单位阶跃响应曲线,2、绘制原系统的Bode图,确定原系统的幅值裕度和相角裕度。
3、绘制原系统的Nyquist曲线。
4、绘制原系统的根轨迹。
5、设计校正装置,绘制校正装置的 Bode图。
&绘制校正后系统的Bode图、确定校正后系统的幅值裕度和相角裕度。
7、绘制校正后系统的单位阶跃响应曲线。
8、绘制校正后系统的Nyquist曲线。
9、绘制校正后系统的根轨迹。
指导教师(签字): ____________________________教研室主任(签字):________________________ 批准日期:2012年12月8日目录一、绪论 (3)二、原系统分析 (5)2.1原系统的单位阶跃响应曲线 (5)2.2原系统的Bode图 (5)2.3原系统的Nyquist 曲线 (6)2.4原系统的根轨迹 (6)三、校正装置设计 (7)3.1校正装置参数的确定 (7)3.2校正装置的Bode图 (7)四、校正后系统的分析 (7)4.1 校正后系统的Bode图 (8)4.2二次校正系统分析 (8)五、二次校正后系统的分析 (8)5.1二次校正后系统的Bode图 (9)5.2校正后系统的单位阶跃响应曲线 (9)5.3校正后系统的Nyquist 曲线 (9)5.4校正后系统的根轨迹 (10)六、总结 (10)七、附图 (11)七、参考文献 (16)、绪论完成一个控制系统的设计任务,往往需要经过理论和实践的反复比较才可以 得到比较合理的结构形式和满意的性能,在用分析法进行串联校正时,校正环节的结构通常采用超前校正、滞后校正、滞后超前校正这三种类型,也就是工程上 常用的PID 调节器。
串联超前校正

串联超前校正
连锁校正,又称前兆校正或预见性校正,是一种利用模型的预测能力,检测并校正潜在的故障,以改善系统安全和可靠性的方法。
指的是根据集成到系统的模型,以及基于时间的监测,识别和修复潜在的故障和风险。
这些模型可以追踪和分析数据,帮助用户明确可能出现故障的部件和时间,使其能够有效预防和配置预案,
实现以预防为主的预见性维护。
实施连锁校正的过程常常包括三个步骤:监测,诊断和修复。
在监测阶段,系统通过检测易受攻击和失效的部件来收集参数、信号、统计等数据;然后,在诊断阶段,系统利用这些数据,基于模型和标准,通过运行环境和抽样等方式,辨认并分析出可能出现的缺陷;最后,在修复阶段,系统根据缺陷的严重性,制定并应用相应的维护方案,以保持系统的正常运行。
传统的故障检测和预防技术偏重于主动修复,即当出现故障时,系统会自动重启以修复故障。
而连锁校正则以预见为主,采用必要的现行管理和体制,将隐藏的故障原因提前发现,并制定合理的控制方案,来有效的减少故障的发生概率。
这种预防性的主动定期维护,可以很好的有效利用资源,有效减少无用功,加强系统安全性和可靠性,从而使组织节省维护成本,提高维修效率。
6.5 串联滞后-超前校正

γ = 180° 90° tan 1 ω c tan 1 0.125ω c = 16.6°
原系统不稳定,不能满足性能指标要求.
3在未校正系统对数幅频特性上,选择斜率从-20dB/dec 在未校正系统对数幅频特性上,选择斜率从变为-40dB/dec的转折频率作为校正网络超前部分的转折 变为-40dB/dec的转折频率作为校正网络超前部分的转折 频率:ω =1. 频率:ωb=1.
ωa
′ tan 1 0.11ω c′ = 50°
6校验已校正系统的各项性能指标. 静态速度误差系数 Kv=20(1/s) 相角裕度 γ ′′ = 180° + tan 1 2.33 × 2.2 90° tan 1 0.125 × 2.2
tan 1 21.2 × 2.2 tan 1 0.11× 2.2 = 51.21°
20 20 = = 9 .1 α = ′ ω c′ 2 .2
此时,滞后此时,滞后-超前校正网络的传递函数可写为 s (1 + )(1 + s ) ωa Gc ( s ) = 9.1s (1 + )(1 + 0.11s )
ωa
5根据相角裕度要求,估算校正网络滞后部分的转折频率ωa. 根据相角裕度要求,估算校正网络滞后部分的转折频率ω 校正后系统的开环传递函数 20(1 + Gc ( s )G0 ( s ) = s (1 + 0.125s )(1 + s ) )(1 + 0.11s )
例 6-5 设某单位反馈系统,其开环传递函数 K G0 ( s ) = s ( s + 1)(0.125s + 1) 要求K =20(1/s),相位裕度γ=50°,调节时间t 不超过4s,试 要求Kv=20(1/s),相位裕度γ=50°,调节时间ts不超过4s,试 设计串联滞后设计串联滞后-超前校正装置,使系统满足性能指标要求. 解:1确定开环增益K 解:1确定开环增益K=Kv=20 2作未校正系统对数幅频特性渐近曲线,如图6-22所 作未校正系统对数幅频特性渐近曲线,如图6 22所 示.由图得未校正系统截止频率ω =4.47rad/s,相位 示.由图得未校正系统截止频率ωc=4.47rad/s,相位 裕度γ 16.6° 裕度γ=-16.6°. 20 20 lg =0 ωc=4.47rad/s ωc ωc
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计任务书2012 —2013 学年第 1 学期电子与信息工程 系 电气工程及其自动化 专业 10-1 班级 课程设计名称: 自动控制原理课程设计设计题目: 串联超前校正装置的设计完成期限:自 2012 年12 月 10 日至 2012 年 12 月 14 日共 1 周 设计依据、要求及主要内容: 设单位反馈系统的开环传递函数为:)1001.0)(16.0)(1(5)(+++=s s s s s G 要求校正后系统的幅值裕度大于10dB ,相角裕度 40≥γ,试设计串联超前校正装置。
基本要求:1、对原系统进行分析,绘制原系统的单位阶跃响应曲线,2、绘制原系统的Bode 图,确定原系统的幅值裕度和相角裕度。
3、绘制原系统的Nyquist 曲线。
4、绘制原系统的根轨迹。
5、设计校正装置,绘制校正装置的Bode 图。
6、绘制校正后系统的Bode 图、确定校正后系统的幅值裕度和相角裕度。
7、绘制校正后系统的单位阶跃响应曲线。
8、绘制校正后系统的Nyquist 曲线。
9、绘制校正后系统的根轨迹。
指导教师(签字):教研室主任(签字):批准日期:2012年12月8日目录一、绪论 (3)二、原系统分析 (5)2.1 原系统的单位阶跃响应曲线 (5)2.2 原系统的Bode图 (5)2.3 原系统的Nyquist曲线 (6)2.4 原系统的根轨迹 (6)三、校正装置设计 (7)3.1 校正装置参数的确定 (7)3.2 校正装置的Bode图 (7)四、校正后系统的分析 (7)4.1 校正后系统的Bode图 (8)4.2 二次校正系统分析 (8)五、二次校正后系统的分析 (8)5.1二次校正后系统的Bode图 (9)5.2校正后系统的单位阶跃响应曲线 (9)5.3 校正后系统的Nyquist曲线 (9)5.4 校正后系统的根轨迹 (10)六、总结 (10)七、附图 (11)七、参考文献 (16)一、绪论完成一个控制系统的设计任务,往往需要经过理论和实践的反复比较才可以得到比较合理的结构形式和满意的性能,在用分析法进行串联校正时,校正环节的结构通常采用超前校正、滞后校正、滞后超前校正这三种类型,也就是工程上常用的PID 调节器。
本次课设采用的超前超前校正的基本原理是利用超前相角补偿系统的滞后相角,改善系统的动态性能,如增加相角裕度,提高系统稳定性能等,而由于计算机技术的发展,matlab 在控制器设计,仿真和分析方面得到广泛应用。
本次课设采用用Matlab 软件对系统进行了计算机仿真,分析未校正系统的动态性能和超前校正后系统是否满足相应动态性能要求。
超前校正就是在前向通道中串联传递函数为:()()()111G c ++⋅==Ts aTs a s R s C s 其中:C R R R R T 2121+= 1221>+=R R R a 通常 a 为分度系数,T 叫时间常数,由式(2-1)可知,采用无源超前网络进行串联校正 时,整个系统的开环增益要下降 a 倍,因此需要提高放大器增益交易补偿. 如果对无源超前网络传递函数的衰减由放大器增 益所补偿,则()11++=Ts aTs s aG c 上式称为超前校正装置的传递函数。
无源超前校正网络的对数频率特性如图1。
图1无源超前校正网络的对数频率特性显然,超前校正对频率在1/aT 和1/T 之间的输入信号有微分作用,在该频率范围内,输出信号相角比输入信号相角超前,超前网络的名称由此而得。
因此超前校正的基本原理就是利用超前相角补偿系统的滞后相角,改善系统的动态性能,如增加相位裕度,提高系统的稳定性等。
下面先求取超前校正的最大超前相角m ϕ及取得最大超前相角的频率mω,则像频特性: ()ωϕc =arctanaT ω-arctanT ω()()()221T 1d ωωωϕωT T a aT d c +-+= 当(),0=ωϕωd d e 则有:T a m 1=ω 从而有:aa T a T T a aT 1arctan arctan 1arctan 1arctan m -=-=ϕ =11arcsin 21arctan 111arctan +-=-=+-a a a a aa a a 既当T a m 1=ω时,超前相角最大为11arcsin m +-=a a ϕ,可以看出m ϕ只与a 有关这一点对于超前校正是相当重要的超前校正RC 网络图如图2。
图2超前校正RC 网络图二、原系统分析 设单位反馈系统的开环传递函数为:)1001.0)(16.0)(1(5)(+++=s s s s s G 要求校正后系统的幅值裕度大于10dB ,相角裕度 40≥γ,试设计串联超前校正装置。
2.1 原系统的单位阶跃响应曲线用MATLAB 求出对原系统进行分析,绘制原系统的单位阶跃响应曲线如图1所示num=[5];den=[0.0006 0.6016 1.601 1 0];sys=tf(num,den);sys1=feedback(sys,1);t=0:0.1:45;step(sys1,t)hold ongridhold off2.2 原系统的Bode 图应用MATLAB 绘制出开环系统Bode 图如图2所示由Bode 图可知,幅值裕度dB h 48.5-=,相角裕度 2.16-=γ。
num=[5];den=[0.0006 0.6016 1.601 1 0];sys=tf(num,den);margin(sys)hold ongridhold off2.3 原系统的Nyquist 曲线原系统的Nyquist 曲线如图3所示num=[5];den=[0.0006 0.6016 1.601 1 0];sys=tf(num,den);nyquist(sys)hold onplot([-1],[0],'o')gtext('-1')hold off2.4 原系统的根轨迹原系统的根轨迹如图4所示num=[5];den=[0.0006 0.6016 1.601 1 0];sys=tf(num,den);rlocus(sys)hold onplot([0],[0])gtext('0')plot([-2],[0])gtext('-2')plot([-5],[0])gtext('-5')hold off三、校正装置设计3.1 校正装置参数的确定校正前截止频率s rad w c /73.1=,相角裕度γo o 402.16<-=,可知相角裕度不满足要求,由此考虑加入串联超前校正系统。
为了满足校正后的系统的相角裕度︒≥40γ的条件,故需要加入 m θ='γ-[γ-(︒︒12~5)]=︒40-[︒-2.16-(︒︒12~5)], 然后再根据2.6211sinarg =+-=a a m θ求出7.15=a 。
跟据系统对相角裕度的要求,确定校正后系统的截止频率'c ω,由式10lg )(lg 20'c W A +α=0,由此可求得02.3c ='ω计算校正装置的时间常数T 。
由于a T W W m c 1'==,由此可以解出T=0.084.则校正装置的传递函数为()1084.013188.1s G c ++=s s 3.2 校正装置的Bode 图如图5num=[1.3188 1];den=[0.084 1];sys=tf(num,den);bode(sys)grid四、校正后系统的分析 校正后的传递函数为:)1084.0)(1001.0)(16.0)(1()13188.1(5)(+++++=s s s s s s s G4.1 校正后系统的Bode 图如图6num=[5];den=[0.0006 0.6016 1.601 1 0];sys1=tf(num,den);num1=[1.3188 1];den1=[0.084 1];sys2=tf(num1,den1);sys3=sys1*sys2;margin(sys3)Grid4.2 二次校正系统分析如图6所示相角裕度o r 407.18<=,可知相角裕度不满足要求,由此考虑在次加入串联超前校正系统进行二次校正。
故需要加入m θ='γ-[γ-(︒︒12~5)]=o 50-[︒7.18-(︒︒12~5)], 然后再根据4.4311sin arg =+-=a a m θ求出365.5=a 。
跟据系统对相角裕度的要求,确定校正后系统的截止频率"c ω,由式10lg )''(lg 20c W A +α=0,由此可求得7.4''c =ω计算校正装置的时间常数T 。
由于aT W W m c 1''==,由此可以解出T=0.092. 则二次校正装置的传递函数为()1092.0149.0s "G c ++=s s 五、二次校正后系统的分析校正后的传递函数为:)1092.0)(1084.0)(1001.0)(16.0)(1()149.0)(13188.1(5)(+++++++=s s s s s s s s G5.1二次校正后系统的Bode 图 num=[5];den=[0.0006 0.6016 1.601 1 0]; sys1=tf(num,den);num1=[1.3188 1];den1=[0.084 1];sys2=tf(num1,den1);num2=[0.49 1];den2=[0.092 1];sys3=tf(num2,den2);sys4=sys1*sys2*sys3;margin(sys4)Grid如图7所示,由图可知h=12.1dB, 8.43=γ满足系统要求5.2校正后系统的单位阶跃响应曲线 如图8num=[5];den=[0.0006 0.6016 1.601 1 0]; sys1=tf(num,den);num1=[1.3188 1];den1=[0.084 1];sys2=tf(num1,den1);num2=[0.49 1];den2=[0.092 1];sys3=tf(num2,den2);sys4=sys1*sys2*sys3;sys5=feedback(sys4 ,1);t=0:0.1:6;step(sys5,t)5.3 校正后系统的Nyquist 曲线 如图9num=[5];den=[0.0006 0.6016 1.601 1 0]; sys1=tf(num,den);num1=[1.3188 1];den1=[0.084 1];sys2=tf(num1,den1);num2=[0.49 1];den2=[0.092 1];sys3=tf(num2,den2);sys4=sys1*sys2*sys3; nyquist(sys4)hold onplot([-1],[0],'o')gtext('-1')hold off5.4 校正后系统的根轨迹如图10num=[5];den=[0.0006 0.6016 1.601 1 0]; sys1=tf(num,den);num1=[1.3188 1];den1=[0.084 1];sys2=tf(num1,den1);num2=[0.49 1];den2=[0.092 1];sys3=tf(num2,den2);sys4=sys1*sys2*sys3;rlocus(sys4)六、总结七、附图(1)校正前单位阶跃响应图1图2 (3)校正前系统的Nyquist曲线图3图4 (5)校正装置的Bode图。
