圆锥摆、漏斗摆
圆锥摆的原理

圆锥摆的原理圆锥摆是一种有趣且神秘的物理现象,它涉及到多个物理学原理的综合作用。
下面我将详细介绍圆锥摆的原理。
圆锥摆是由一个线绳或细杆连接球状物体悬挂在顶端,线绳的另一端连接到一个固定点。
当球状物体被推离平衡位置后,它将在水平面内飞快旋转,并维持着一条固定的轨道。
圆锥摆的运动原理可以通过以下几个步骤来理解:第一步是球体离心力的作用。
当球体被推离平衡位置后,线绳产生张力,并将球体拉向固定点。
由于球体在线绳上受到的拉力不是竖直的,它分解成两个分力:一个竖直向下的重力分力,与一个水平向心的张力分力。
这个向心力被称为离心力,它的大小与球体离开平衡位置的距离成正比。
第二步是离心力与球体的质量产生的加速度之间的关系。
根据牛顿第二定律,物体受到的合力等于质量与加速度的乘积。
在圆锥摆中,离心力是球体受到的唯一水平合力,因此可以用离心力除以球体质量来计算加速度。
第三步是加速度与速度之间的关系。
根据牛顿第二定律,加速度等于速度的导数。
在圆锥摆中,球体在水平面内沿着一条曲线运动,因此需要使用速度的矢量表示。
这时,加速度被定义为速度的变化率,或者说,速度的瞬时变化量。
在圆锥摆中,加速度的大小等于球体在轨道上的速度大小除以转向半径。
第四步是速度与位置之间的关系。
速度是位置的导数。
如果球体在垂直于轨道平面的方向上运动,那么球体在该方向上的速度和加速度将为零。
因此,球体的运动轨迹将位于轨道平面内。
通过上述分析,我们可以得出圆锥摆的运动原理总结如下:1. 球体离心力的作用使得球体朝着固定点移动。
2. 离心力与球体质量产生的加速度成正比。
3. 加速度与速度之间存在导数关系。
4. 球体在轨道平面上运动,因为在垂直于轨道平面的方向上速度和加速度为零。
总之,圆锥摆的运动原理涉及到离心力、加速度、速度和位置之间的多个物理学原理的综合作用。
这种物理现象不仅可以帮助我们更好地理解自然界中的运动规律,还有助于培养我们对科学的好奇心和研究精神。
圆锥摆知识点总结

圆锥摆知识点总结1. 圆锥摆的结构和原理圆锥摆主要由一个圆锥形的摆体和一根摆线组成。
摆线上缠绕着一根细线,细线的一端固定在摆体上,另一端系着小球。
当小球被拉向摆体时,细线会绕着摆体旋转,产生圆锥形的摆动运动。
圆锥摆的运动原理主要依赖于惯性和引力。
当摆线被拉向摆体时,球的惯性会使它向外运动,而摆线的张力会使其朝摆心方向旋转。
这种旋转运动会使球回到静止状态,形成周期性的摆动。
2. 圆锥摆的运动规律圆锥摆的摆动运动具有几个基本的规律。
首先是周期性,也就是摆体在一个周期内完成上下摆动的时间。
其次是振幅,即摆体摆动的角度大小。
此外,还有摆体摆动时的角速度和角加速度等运动参数。
圆锥摆的运动规律可以用物理学的公式来描述。
例如,摆体的周期T可以用摆长L和重力加速度g表示:T=2π√(L/g)。
振幅的大小则取决于摆体的初速度和初位移。
3. 圆锥摆的应用圆锥摆作为一种科学玩具,常常被用来演示物理学原理。
它能够直观地展示力学和动力学的基本原理,如万有引力、周期振动和谐波运动等。
通过观察圆锥摆的摆动过程,可以更清晰地理解这些物理现象。
在科学研究中,圆锥摆也被用来研究摆动运动的特性和规律。
通过对摆体的振动频率、振幅和周期的测量,可以得到一些有用的物理参数,如物体的惯性、摆长和所受的力等。
这些数据对于研究其他力学或者动力学问题有一定的参考价值。
此外,圆锥摆还可以被用来制作科学装置和教学实验。
它的摆动运动非常稳定,可以用来研究和展示许多物理现象。
因此,圆锥摆在物理实验室和教学课堂中有着广泛的应用。
4. 圆锥摆的改进和发展近年来,随着科学技术的进步,圆锥摆也得到了一些改进和发展。
一些科研机构和高校利用先进的材料和工艺制作了更为精密的圆锥摆,提高了其测量精度和稳定性。
另外,一些科研团队还在研究如何利用圆锥摆来进行科学研究。
他们试图通过对摆动运动的微小变化进行观测和测量,来探索一些新的物理现象或者发展新的测量仪器。
这些工作有助于提高圆锥摆的科研价值和应用前景。
08 生活 漏斗圆锥摆1
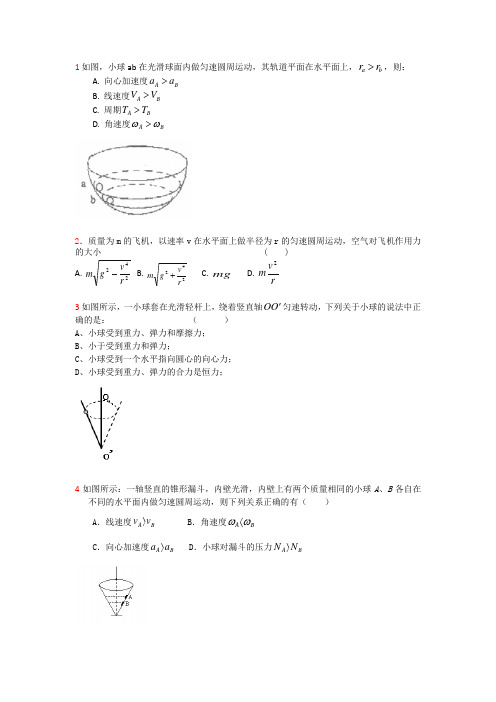
1如图,小球ab 在光滑球面内做匀速圆周运动,其轨道平面在水平面上,b a r r >,则:A. 向心加速度B A a a >B. 线速度B A V V >C. 周期B A T T >D. 角速度B A ωω>2.质量为m 的飞机,以速率v 在水平面上做半径为r 的匀速圆周运动,空气对飞机作用力的大小 ( )A .242r v g m - B .242rv g m + C .mg D .r v m 23如图所示,一小球套在光滑轻杆上,绕着竖直轴O O '匀速转动,下列关于小球的说法中正确的是: ( ) A 、小球受到重力、弹力和摩擦力; B 、小于受到重力和弹力;C 、小球受到一个水平指向圆心的向心力;D 、小球受到重力、弹力的合力是恒力;4如图所示:一轴竖直的锥形漏斗,内壁光滑,内壁上有两个质量相同的小球A 、B 各自在不同的水平面内做匀速圆周运动,则下列关系正确的有( )A .线速度B A v v 〉 B .角速度B A ωω〈C .向心加速度B A a a 〉D .小球对漏斗的压力B A N N 〉5在光滑的圆锥漏斗的内壁,有两个质量相等的小球A、B,它们分别紧贴漏斗,在不同水平面上做匀速圆周运动,如图所示,则下列说法正确的是()A.小球A的速率大于小球B的速率B.小球A的速率小于小球B的速率C.小球A对漏斗壁的压力大于小球B对漏斗壁的压力D.小球A的转动周期小于小球B 的转动周期6如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在图中所示位置的水平面内作匀速率圆周运动,则以下判断正确的是A.球A的线速度大于球B的线速度B.球A的向心加速度小于球B的向心加速度C.球A对筒壁的压力等于球B对筒壁的压力D.球A的运动周期大于球B的运动周期AB7.有一种杂技表演叫“飞车走壁”。
由杂技演员驾驶摩托车沿圆台形表演台的侧壁,做匀速圆周运动。
圆锥摆模型

专题:圆锥摆模型(水平面内的圆周运动)教学目标物理观念:通过圆锥摆模型的分析,会在具体问题中分析向心力的来源,会寻找圆心,计算半径,列出方程求解物理量。
科学思维:运用函数思想构建所求物理量的函数关系,并利用函数关系处理物理问题。
科学探究:通过圆锥摆模型的分析,体会物理模型的重要性,并能将相关模型等效成圆锥摆模型。
科学态度与责任:通过圆锥摆模型的分析,培养学生将物理知识应用于生活的意识。
教学重难点:重点:通过圆锥摆模型的分析,会在具体问题中分析向心力的来源,会寻找圆心,计算半径,列出方程求解物理量。
难点:1.运用函数思想构建所求物理量的函数关系,并利用函数关系处理物理问题。
2.通过圆锥摆模型的分析,体会物理模型的重要性,并能将相关模型等效成圆锥摆。
模型。
教学过程:复习导入:向心力的表达式。
新课教学一.圆锥摆模型的受力特点受两个力,且两个力的合力沿水平方向,物体在水平面内做匀速圆周运动。
二.圆锥摆的相关规律1.摆球的加速度2.摆球的线速度3.摆球的周期和角速度4.摆线得拉力5.两种圆锥摆分析对甲:由a =g tan θ知A 、B 的向心加速度大小相等。
由a =ω2r 知ωA <ωB ,由a =v 2r 知v A >v B 对乙:由T =2πhg 知摆高h 相同,则ωA =ωB ,由v =ωr 知v A >v B ,由a =ω2r知a A >a B 。
三.案例分析例1、如图所示,两根长度相同的细线分别系有两个完全相同的小球,细线的上端都系于O 点.设法让两个小球均在各自的水平面上做匀速圆周运动.已知L 1跟竖直方向的夹角为60°,L 2跟竖直方向的夹角为30°,下列说法正确的是( )A .细线L 1和细线L 2所受的拉力大小之比为1:√3B .小球m 1和m 2的角速度大小之比为1:1C .小球m 1和m 2的向心力大小之比为3:1D .小球m 1和m 2的线速度大小之比为3√3:1练习1、A 、B 两质量相同的质点用轻质细线悬挂在同一点O ,在同一水平面上做匀速圆周运动,如图所示,则( ) A .A 的加速度一定比B 的加速度小 B .A 的线速度一定比B 的线速度小 C .A 的角速度一定等于B 的角速度D .A 所受细线的拉力一定等于B 所受的细线的拉力例2:如图所示,用一根质量不计、不可伸长的细绳,一端系一可视为质点的小球,另一端固定在O 点。
圆锥摆问题

解:设转盘转动的角速度为ω时,钢绳与竖直方 向的夹角为θ
座椅到中性轴的距离为:R=r+Lsinθ
对座椅分析有:F向=mgtanθ=mRω2 联力两式,解得:
g tan r L sin
θ
F向
mg
tan
1、向心加速度的计算:
an
Fn m
g
tan
θ角一定,故an恒定。
2、周期T、角速度ω、线速度v的计算(设匀速圆周运
动的平面离漏斗尖端距离为h)
由:
Fn
mg
tan
m( 2 )2 h tan
T
m 2h tan
mv 2
h tan
得: T 2 tan h
g g l cos h
式中h=lcosθ为摆球的轨道平面到悬点的距离, 即圆锥摆的高度。由这些公式可知,高度相同 的圆锥摆的T、f和ω相等,与m、l和θ无关。
5、漏斗摆:物体在光滑的漏斗形容器内 壁的某水平面上做匀速圆周运动。漏斗摆
的力学特点:物体只受两个力,竖直向下
的重力,垂直于漏斗壁的弹力,两个力的 合力水平指向转轴,其向心力表达式为:
F向
ma向
mg
tan
m
l
v2
sin
m2l sin
m
2
T
2
l
sin
m2f
2l sin
向心加速度可表示为:
a向
F向 m
g tan
v2
l sin
2l sin
2
T
2
使物体圆锥摆的方法

使物体圆锥摆的方法
将物体转化为圆锥摆的方法有几种,下面介绍其中两种常见的方法:
1.线绳摆法:这是一种基本的圆锥摆方法。
需要准备一个重
物(例如小珠子或小铅块)和一根线或绳子。
首先,将线或绳子系在重物上,确保重物悬挂在空中。
然后,通过旋转着线或绳子,使重物绕着你所期望的圆锥轨迹运动。
你可以调整线的长度和旋转速度来改变圆锥的大小和形状。
2.旋转台面法:这种方法需要一个平滑的旋转台面或转盘。
将物体放置在旋转台面的边缘上,并以较高的旋转速度将台面转动起来。
当台面旋转时,物体将被离心力推向台面的边缘。
通过调整旋转台面的速度和物体离中心的距离,可以产生不同大小和形状的圆锥运动。
请注意,进行圆锥摆实验时需要确保安全,特别是当使用高速旋转台面时。
遵循相关的安全规定,确保周围环境安全,并小心操作以避免任何伤害。
另外,还有其他方法可以实现圆锥摆,例如使用电动机、弧度坐标系和角动量守恒等方法实现。
这些方法可能需要更多的设备和技术支持。
圆锥摆总结
圆锥摆总结引言圆锥摆是一种具有特殊运动形式的物体,它可以通过自身的旋转而实现平衡。
本文将介绍圆锥摆的基本原理、应用领域以及未来发展方向。
1. 圆锥摆的基本原理圆锥摆的运动原理可以总结为以下几点:•重力和离心力的平衡:圆锥摆的运动是通过重力和离心力之间的平衡实现的。
当圆锥摆旋转时,重力会使得摆的质心向下,而离心力会使得摆的质心向外。
•建立稳定的摆动轨道:为了建立稳定的摆动轨道,摆的底部需要具有一定的倾斜角度,并且摆动的半径需要逐渐减小。
这样可以使得重力和离心力恰好相等,从而实现平衡。
2. 圆锥摆的应用领域圆锥摆在科学研究和工程领域有着广泛的应用。
以下是一些常见的应用领域:2.1 天文学圆锥摆可以模拟行星和卫星的轨道运动。
科学家可以通过观察圆锥摆的运动来研究行星和卫星的运动规律,从而帮助解开宇宙的奥秘。
2.2 工程学圆锥摆可以用于建筑物的结构分析和抗震设计。
通过模拟地震时建筑物的摆动情况,科学家可以评估建筑物的抗震性能,并优化设计方案。
2.3 教育圆锥摆也常用于物理实验教学。
通过操纵圆锥摆的各种参数,学生可以直观地观察到重力和离心力的作用,从而更好地理解物理原理。
3. 圆锥摆的未来发展方向圆锥摆作为一种有趣而又实用的物体,未来还有很大的发展潜力。
以下是一些可能的发展方向:3.1 精确控制技术未来可以开发出更加精确的控制技术,使得圆锥摆的运动更加稳定和可控。
这将有助于提高圆锥摆的应用范围,并扩大其在科学研究和工程领域的应用。
3.2 多维度摆动目前的圆锥摆主要是在一个平面上进行摆动,未来可以进一步发展多维度摆动的圆锥摆。
这将带来更加丰富的运动形式,并开辟新的实验和研究领域。
3.3 生物医学应用圆锥摆的平衡运动可以模拟人体的动态平衡。
未来可以将圆锥摆应用于康复医学领域,帮助恢复平衡功能的患者进行康复训练。
结论圆锥摆作为一种具有特殊运动形式的物体,具有广泛的应用领域和未来发展的潜力。
我们可以通过深入研究圆锥摆的原理,加强控制技术的发展,进一步推动圆锥摆在科学研究、工程应用和教育领域的发展。
《6.4 “圆锥摆”专题》教案
●圆锥摆:天花板上有一个悬点,下方通过一根细绳悬挂着小球,小球旋转形成圆平面,
与两边的悬绳(母线)组合,就构成了数学中“圆锥”的形状。
学美术的同学可能会遇到石膏模型,有时候上边是不是还插一个圆柱?高度相同的圆锥摆,角速度相同;线速度与旋转半径成正比。
与“同轴转动模型”类似。
●漏斗摆:由对称性,圆锥摆尖尖朝上,就像金字塔;漏斗摆尖尖朝下,与长颈漏斗、分
液漏斗有点像?漏斗摆是如何运转的呢?用一根刚性的绳连接小球,抓住绳子的下端旋转,小球在上方的平面内做匀速圆周运动就形成了漏斗摆。
●应用:圆锥摆与漏斗摆受力的本质相同。
主要应用于:“超级飞椅”、“花样滑冰”、“火
车转弯”、“飞车走壁”等模型。
圆锥摆变形记之“双线圆锥摆”
圆锥摆变形记之 双线圆锥摆高安强(临沂华盛教育集团ꎬ山东临沂276017)摘㊀要:圆锥摆是圆周运动的重要物理模型ꎬ根据双线圆锥摆的绕线方式分成四类ꎬ并对每一类进行方法提升和总结.关键词:双线圆锥摆ꎻ向心力ꎻ临界角速度中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)22-0127-03收稿日期:2023-05-05作者简介:高安强(1977.9-)ꎬ男ꎬ本科ꎬ中学一级教师ꎬ从事高中物理教学研究.㊀㊀圆锥摆[1]是高中的圆周运动的重要物理模型ꎬ圆锥摆的变形较多ꎬ例如光滑漏斗内壁圆锥摆㊁粗糙漏斗内壁圆锥摆㊁粗糙漏斗外壁圆锥摆㊁光滑漏斗外壁挂绳圆锥摆㊁双线圆锥摆等等.很多初学者在学习圆锥摆时ꎬ因为圆锥摆及其变形内容繁多ꎬ理不清头绪而至烦恼不已ꎬ为了解决初学者的这些困扰ꎬ下面就对圆锥摆的变形之一 双线圆锥摆进行讨论和总结.1双线在两边如图1ꎬ两绳在水平方向的分力之差充当向心力ꎻ竖直方向的分力与重力的合力等于零.图1㊀双线在两边例题1㊀如图1所示ꎬ在固定的竖直杆上固定水平杆ꎬ二杆垂直ꎬ把两根轻绳初端系在水平杆的O㊁A两点ꎬ两绳的末端都系在同一个小球上ꎬ小球的质量为mꎬ并且OA=OB=AB=lꎬ现让竖直杆匀速转动ꎬ三角形OAB始终在竖直平面内ꎬg为重力加速度ꎬ不计空气阻力ꎬ则下列说法正确的是(㊀㊀).A.当杆转动角速度增加时ꎬOB绳上的拉力变大和AB绳上拉力减小B.两绳都拉直的角速度的范围为0ɤωɤ2glC.两绳都拉直的角速度的范围为0ɤωɤ3glD.若转动的角速度ω2=2glꎬOB绳上的拉力大小为FOB=2mg解析㊀A:对小球受力分析ꎬ则水平方向:FOBcos60ʎ-FABcos60ʎ=mlcos60ʎω2①竖直方向:FOBsin60ʎ+FABsin60ʎ=mg②721由①②两式解得FAB=3mg3-12mlω2FOB=3mg3+12mlω2当杆转动角速度ω增加时ꎬOB绳上的拉力变大和AB绳上拉力减小ꎬ故选项A正确ꎻBC:根据圆锥摆的受力特点ꎬmgtan30ʎ=mlsin30ʎω2得ω=glcos30ʎ=233时ꎬAB绳子只是拉紧ꎬ拉力刚好等于零故两绳都拉直的角速度的范围为0ɤωɤ233ꎬBC错ꎻD:若转动的角速度ω2=2glꎬAB绳子的弹力33mg+mgꎬ选项D错.答案:A2一线的拉力或一线拉力竖直方向的分力等于摆球的重力㊀㊀(1)如图2(a)所示ꎬ在角速度变化的过程中ꎬ因为绳a上的拉力大小不变ꎬ大小等于mgꎻ绳b上的拉力充当向心力.(2)如图2(b)所示ꎬ绳上的拉力大小不变ꎬ竖直方向的分力等于重力ꎻ水平分力和筒壁的支持力的合力充当向心力ꎻ当然筒壁的支持力可能等于零.图2㊀竖直方向拉力或拉力的分力与重力平衡例题2㊀如图3所示ꎬ竖直圆桶的内壁光滑ꎬ绕中心轴做匀速圆周运动ꎬ轻绳的另一端系于圆桶上表面圆心ꎬ另一端系有一个质量为m的物体ꎬ且物块贴着圆桶内表面随圆桶一起转动ꎬ轻绳与竖直方向的夹角等于60ʎꎬ轻绳的长度等于2mꎬ物块的质量等于1kgꎬ则(㊀㊀).A.小物块圆周运动的向心力等于绳子水平方向的分力B.当ω=10rad/s时ꎬ桶对物块的弹力等于为零C.当ω=20rad/s时ꎬ绳子的拉力等于20ND.当ω=20rad/s时ꎬ筒壁的弹力等于390N图3㊀例2题图解析㊀A:小物块圆周运动的向心力等于绳子沿着水平方向的分力和筒壁的弹力之和ꎬ故A错ꎻB:根据圆锥摆的受力特点mgtanθ=mlsinθω2得ꎬω=glcosθꎬ当角速度ω=glcosθ=102ˑ12=10rad/s时ꎬ筒壁的弹力等于零ꎬB正确ꎻC:当角速度ωȡ10rad/s时ꎬ绳子上的拉力不变ꎬ根据Fcos60ʎ=mgꎬ解得F=2mgꎬ故C正确ꎻD:向心力的大小等于Fsinθ+FN=mlsinθω2ꎬ代入数据解得FN=3903Nꎬ故D错误.答案:BC3双线在一边双线圆锥摆如图4(a)㊁图4(b)㊁图4(c)所示ꎬ三种情况下的临界状态都可以利用离心趋势找出来.(1)当转轴不转动时ꎬ图4(a)㊁图4(b)㊁821图4(c)ꎬ三种情况下的小球都会紧靠在转轴上ꎬ此时AC绳拉紧而BC绳松弛.小球不离开转轴.图4㊀双线在一边当0ɤωɤgL1cosα时ꎬ图4(a)㊁图4(b)㊁图4(c)中的小球开始离开转轴ꎬ且只有AC绳拉紧ꎬ而BC绳松弛.(2)在图4(a)㊁图4(c)中ꎬ当ω>gL1cosα时ꎬ两绳都张紧.(3)在图4(b)中ꎬ当gL1cosα<ω<gL2cosβ时ꎬAC㊁BC两绳都张紧ꎻ当ω>gL2cosβ时ꎬAC绳松弛ꎬBC绳张紧ꎻ例题3㊀如图5(a)所示ꎬ竖直细杆下端固定在位于地面上的水平转盘上ꎬ一质量为m的1kg小球接上长度均为L=2m不可伸长的两相同的轻质细线a㊁bꎬa细线的另一端结在竖直细杆顶点Aꎬ细线b的另一端结在杆的中点BꎬAB长度为l=L.当杆随水平转盘绕竖直中心轴匀速转动时ꎬ将带动小球在水平面内做匀速圆周运动ꎬ如图5(b).不计空气阻力ꎬ重力加速度为g.则(㊀㊀).图5㊀例3题目A.杆转动的角速度时ω=2g3rad/sꎬb绳上的拉力等于零B.当细线b刚好拉直时ꎬ杆转动的角速度ω=2gC.当ω=2g时ꎬa绳上的拉力等于(2033+10)ND.当ω=2g时ꎬb绳上的拉力等于(4033-20)N解析㊀AB:根据圆锥摆的受力特点mgtan60ʎ=mLsin60ʎω2ꎬ当细线b刚好拉直时ꎬω=gLcos60ʎ=2gL=gꎬ故选项B错误ꎻ因为ω=2g3rad/s<gꎬ故b绳还没有被拉直ꎬ故b绳上的拉力等于零ꎬA选项正确.CD:对摆球受力分析如图5(c)所示ꎬ列方程Facos30ʎ+Fbcos30ʎ=mLsin60ʎω2①Fasin30ʎ=Fbsin30ʎ+mg②解得两绳上的拉力等于Fa=30NFb=10N故CD错.答案:A解答双线圆锥摆的关键还是对摆球受力分析清楚ꎬ建立坐标系ꎬ在建立坐标系时ꎬ要注意两轴的方向ꎬ一定要有一个轴指向圆心ꎬ这样求出这个轴上的合外力即为向心力ꎬ另一个轴上合外力等于零.另外需要明确两个绳子出现和消失拉力的临界点.参考文献:[1]张颖ꎬ梁旭.普通高中教科书 物理必修:第二册[M].北京:人民教育出版社ꎬ2019:32.[责任编辑:李㊀璟]921。
《5.6 圆锥摆问题》PPT
2
2
l m2n l
2
4、周期、频率和角速度的计算 根据向心加速度公式,有: 2 a向 g tan(静力学) l sin (动力学)
g g l cos h l cos h T 2 2 g g
θ
h
l
1 f 2
g 1 l cos 2
g h
v gh
可见,h增大,线速度增大,角速度减小,周期增大。
应用
飞走壁
漏斗摆
1、向心加速度的计算: θ角一定,故an恒定。
Fn g an m tan
2、周期T、角速度ω、线速度v的计算(设匀速圆周运 动的平面离漏斗尖端距离为h) 2 m g 2 m v 2 2 由: F m ( ) h tan m h tan n tan T h tan h g 得: T 2 tan 2 g h tan
圆锥摆问题
圆锥摆受力分析
竖直方向:F cosθ=mg
F
O
l
θ
水平方向: F合=Fsinθ F合=mω2l sinθ
θ
m
F合
O'
ω
mg
特点: 1、圆锥摆模型的受力
只受两个力:竖直向下的重力和沿摆线方向的拉 力,二力的合力就是摆球做圆周运动的向心力,如图。 2、向心力和向心加速度的计算 设摆球的质量为m,摆长为L,与竖直方向的夹角为θ, 摆球的线速度、角速度、周期和频率依次为v、ω、T、 和f,如图,r=l*sinθ 向心力可表示为: 2 2
二、漏斗摆(倒圆锥摆): 物体在光滑的漏斗形容器内壁的某水平面 上做匀速圆周运动。漏斗摆的力学特点: 物体只受两个力,竖直向下的重力,垂直 于漏斗壁的弹力,两个力的合力水平指向 转轴,其向心力表达式为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对向心加速度的进一步理解
1. 如何理解向心加速度的含义:
速度矢量的方向应当用它与空间某一确定方向(如坐标轴)之间的夹角来描述.做匀速圆周运动的物体其速度方向(圆周的切线方向)时刻在变化,在时间内速度方向变化的角度等于半径在相同时间内转过的角度,如做匀速圆周运动的物体在一个周期内半径转过弧度,速度方向变化的角度也是弧度.因此,确切描述速度方向变化快慢的,应该是角速度,
即.
上式表示了单位时间内速度方向变化的角度,即速度方向变化的快慢.角速度相等,速度方向变化的快慢相同.
由向心加速度公式可知,向心加速度的大小除与角速度有关外,还与半径或线速度的大小有关,从看,向心加速度等于线速度与角速度的乘积.
例如:在绕固定轴转动的圆盘上,半径不同的、、三点,它们有相同的角速度,但线速度不同,,,,如图所示.因此它们的速度方向变化快慢是相同的,但向心加速度的大小却不相等,.
又如:A、B两个物体分别沿半径为和做圆周运动,,它们的角速度不同,设,因此它们的线速度的关系为,显然,这两个物体有相同的向心加速度,即.但速度方向变化的快慢却不同.
综上所述:向心加速度是由于速度方向变化而引起的速度矢量的变化率.速度方向变化是向心加速度存在的前提条件,但向心加速度的大小并不简单地表示速度方向变化的快慢,确切地说:当半径一定时,向心加速度的大小反映了速度方向变化的快慢,当线速度一定时,向心加速度的大小正比于速度方向变化的快慢.
2.向心加速度的分析计算公式:
①已知v、r,则;
②已知ω、r,则;
③已知T、r,则;
④已知ω、v,则.
3.向心加速度的公式也适用于非匀速圆周运动.
向心加速度不一定是物体做圆周运动的实际加速度。
对于匀速圆周运动,其所受的合外力就是向心力,只产生向心加速度,因而匀速圆周运动的向心加速度是其实际加速度。
对于非匀速圆周运动,例如竖直平面内的圆周运动,如图所示,小球的合力不指向圆心,因而其实际加速度也不指向圆心,此时的向心加速度只是它的一个分加速度。
此时,向心加速度仍满足:.
4.与r的关系图象,如图所示.
由图象可以看出:与r成正比还是反比,要看恒定还是恒定,即:当一定时,与r成反比;当一定时,与r成正比.
圆锥摆:
(1)理想圆锥摆模型的力学特点.
①圆锥摆模型的结构特点--一根质量和伸长可以不计的线,系一个可以视为质点的摆球,在水平面内做匀速圆周运动,且在摆线沿顶点位置不变的圆锥面上运动。
②圆锥摆模型的受力特点--只受两个力:竖直向下的重力(mg)和沿摆线方向的拉力(F),二
力的合力就是摆球做圆周运动的向心力(),如图所示。
(2)向心力和向心加速度的计算.
设摆球的质量为m,摆长为l,与竖直方向的夹角为θ,摆球的线速度、角速度、周期和频率依次为v、ω、T和f.
如上图所示,根据不同的条件,向心力可以表示为:
.
向心加速度可表示为:
.
(3)摆线拉力的计算.
计算摆线的拉力,有两种基本思路:
①当θ角已知时,.
②当θ角未知时,
(4)周期T、频率f和角速度ω的计算.
根据向心加速度公式,有,,
.
式中为摆球的轨道平面到悬点的距离,即圆锥摆的高度。
由这些公式可知,高度相同的圆锥摆,即等高圆锥摆的T、f和ω相等,与m、l和θ无关,如图所示。
漏斗摆
漏斗摆就是物体在光滑的漏斗形容器内壁的某水平面上做匀速圆周运动。
漏斗摆式匀速圆周运动的基本模型之一。
(1)漏斗摆的力学特点:物体只受两个力,竖直向下的重力mg,垂直于漏斗壁的弹力
,两个力的合力水平指向转轴,其向心力。
如图所示。
(2)向心加速度的计算.
,θ角一定,故恒定。
(3)周期T、角速度ω、线速度v的计算.
(设匀速圆周运动的平面离漏斗尖端距离为h)
由,得,
由,得,
由,得.
可见,h增大,线速度增大,角速度减小,周期增大。
