20082009学年度第二学期期末试卷
2008-2009第二学期概率统计期末试题

2008-2009 学年 第二学期期末A一、单项选择题(每小题3分,满分18分)1、设随机变量),0(~2i i N X σ,2,1=i,则下列说法中正确的是( )。
(A )12(,)X X 必服从二维正态分布; (B )12()0E X X =; (C )2(A )(C )1)≥。
3当c 4(A) 4σ; (B) 42σ; (C) 46σ; (D) 43σ 。
5、设B A ,为任意两事件,则下列关系成立的有( )(A) A B B A =-+)( ;(B) ()A B B A B +-=- ;(C) A B B A =+-)( ;(D) ()A B B AB -+=.6、从9~0这十个数码中任意取出4个排成一串数码,则数码恰成四位偶数的概率为: (A )4190 ;(B )12;(C )4090;(D )3290 。
二、填空题(每小题3分,满分18分)1、设有n 个球,每个球都能以同样的概率N1落到N 个格子)(n N ≥的每一个格子中, 则恰有n 个格子中各有一个球的概率为 。
2、一盒子内装有5个红球,15个白球,从中不放回取10次,每次取一个球,则第5次取到的是红球的概率为 。
3、袋中装有编号8~1的八个球,从中任取3个,则最小号码为偶数的概率为 。
4、对目标进行射击,直到击中目标为止, 若每次击中目标的概率为)10(<<p p ,记5、Y f6、设1nii X =,2=S 三、,以X(1)五、, 求()Y X E +及()XY E 。
六、(满分12分)设总体),(~21σμN X ,),(~22σμN Y ,且X 与Y 相互独立;n X X X ,,,21⋅⋅⋅;12,,,m Y Y Y ⋅⋅⋅别是来自X 和Y 的样本,令11n i i X X n ==∑,11m i i Y Y m ==∑ ,22111()1n i i S X X n ==--∑, 试求:(1)X 服从的分布,Y 服从的分布; (2X Y 服从的分布;(3)统计量T =服从的的分布。
2008—2009学年下期期末测试

2008—2009学年下期期末测试八年级 数学 参考答案一、1.A ; 2.D ; 3.B ; 4.A ; 5.D ; 6.C ;二、7.x ﹥3; 8. (2)(2)x x -+; 9. ≠45-; 10. 1B ∠=∠或2C ∠=∠或AE AD AC AB =; 11. 2; 12. x <-1; 13. 105; 14. 4; 15. 154. 三、解答题16.解:解不等式①,得1x -≥.………2分 解不等式②,得3x <.………4分 不等式①、②的解集在数轴上表示如下:∴原不等式组的解集为13x -<≤.………6分17.解:4)221(22--÷-+p p p p )1()2)(2(222--+⨯-+-=p p p p p p 12-+=p p . …………4分 (其中通分1分,除法变乘法1分,分子分母分解因式1分,化简1分)在-3 < p < 3中的整数p 是-2,-1,0,1,2, ……………………………………5分根据题意,这里p 仅能取-1,此时原式 = 21-.…………………………………6分 18.解:设摩托车的速度是x 千米/时;则汽车速度是1.5x 千米/时.根据题意得:…………1分,60155.13030=-x x …………3分 解这个方程得:x =40. …………5分 经检验x =40是原方程的解.当x =40时;1.5x =60. …………7分答:摩托车的速度是40千米/时;则汽车速度是60千米/时.…………8分19.证明:∵∠1=∠2+∠B ,∴∠2=∠1-∠B =60°-40°=20°. ………2分又∵∠G =40°,∴∠2=∠G . ………3分∵EG ∥AD ,∴∠2=∠BAD ,∠G =∠CAD . ………5分∴∠BAD =∠CAD .∴AD 平分∠BAC . ………8分20.(1)a=8,b =12,c =0.3. (每对一个给1分)…………………………3分(2)略 (画对一个直方图给1分)……………………………………5分(3)算出样本中噪声声级小于75dB 的测量点的频率是0.3 .………………7分0.3×300=90.∴在这一时刻噪声声级小于75dB 的测量点约有90个.……………………8分21.(1)2,326,a b b a -=⎧⎨-=⎩12,10.a b =⎧∴⎨=⎩………………2分 (2)设购买污水处理设备A 型设备x 台,B 型设备(10)x -台,则:1210(10)105,x x +-≤ ………………3分2.5.x ∴≤ ……………………4分 x 取非负整数,012.x ∴=,, ……………………5分 ∴有三种购买方案:①A 型设备0台,B 型设备10台;②A 型设备1台,B 型设备9台;③A 型设备2台,B 型设备8台. …………………6分(3)由题意:240200(10)2040,x x +-≥ ……………………7分1x ∴≥.又 2.5,x ≤x ∴为1,2. ……………………………8分当1x =时,购买资金为:121109102⨯+⨯=(万元);当2x =时,购买资金为:122108104⨯+⨯=(万元).∴为了节约资金,应选购A 型设备1台,B 型设备9台.………………9分22.(1)△PF A 与△ABE 相似.…………………1分理由如下:由正方形ABCD 知AD BC ∥, PAF AEB ∴∠=∠.又90PFA ABE ∠=∠=,PFA ABE ∴△∽△. …………………3分(2)解:若EFP ABE △∽△,则PEF EAB ∠=∠,∴必有PE AB ∥. ∴四边形ABEP 为矩形.∴P A =EB =4,即x =4. ………………6分若PFE ABE △∽△,则PEF AEB ∠=∠. 而PAF AEB ∠=∠,PEF PAF ∴∠=∠,PE PA ∴=. PF AE ⊥,∴点F 为AE 的中点, ∵5480482222==+=+=BE AB AE , ∴5221==AE EF . …………8分 由PE EF AE EB =,即45254=PE 得PE =10,即x =10, …………9分 ∴满足条件的x 的值为4或10. ……………10分。
2008—2009学年下期期末测试

2008—2009学年下期期末测试高中二年级 数学(文科) 参考答案一. 选择题ACADC ABDAB DB 二. 填空题(13)60 (14)1825 (15)1240(16) 10 三.解答题(17)解: (Ⅰ)记事件A 为“甲投篮一次且投中”,事件B 为“乙投篮一次且投中”,则事件A ,B 相互独立且()0.8,()0.5.p A p B == ………1分所以()1()0.2,()1()0.5.p A p A p B p B =-==-=………3分故甲、乙各投蓝一次,均没有投中的概率()()()0.20.50.1.p A B p A p B ⋅=⋅=⨯=………5分 (Ⅱ)记事件C 为“甲投篮两次且投中两次”,事件D 为“乙投篮两次且只投中一次”,则事件C ,D 相互独立且()0.80.80.64,()0.50.50.50.50.5.p C p D =⨯==⨯+⨯= ………8分故甲、乙各投蓝两次,其中甲投中两次,乙只投中一次的概率为:()()()0.640.50.32.p C D p C p D ⋅=⋅=⨯= ………10分(18)解: (Ⅰ)由题意4412=-n n C C .…………2分解得118n =-或.…………4分 由n ∈+N 得n =11. …………6分(Ⅱ)由二项式定理得,展开式的通项33311(11)42211111r r rrr r T C xxC x---+=⋅⋅=⋅. …………8分令33110r -=得3=r . …………10分所以展开式中的常数项为展开式的第4项1654=T . ……12分(19)解:(Ⅰ)设CB 1与C 1B 的交点为E ,连结DE . ………2分 ∵D 是AB 的中点,E 是BC 1的中点.∴DE //AC 1. ………4分 ∵DE ⊂平面CDB 1,AC 1⊄平面CDB 1.∴AC 1//平面CDB 1. ………6分 (Ⅱ)∵DE //AC 1,∴∠CED 为AC 1与B 1C 所成的角. ………8分在△CED 中,ED 112AC ==15151,,2222CD AB CE CB ==== ………10分8cos5522252544CED+∴∠==⋅-∴异面直线AC1与B1C所成角的余弦值为5……………………12分(20)解:(Ⅰ)由题知,符合题意的检测方法即前四次中恰有一次检测到正品,第五次检测到最后一件次品.……………2分下面分两步进行:第一步:先确定一件正品的排法有1164C C种方法;第二步:再确定四件次品的排法有44A种方法;……………4分由分步计数原理得,所有不同检测方法的方法数为114644576C C A⋅=种. ……………6分(Ⅱ)由题知,将全部次品检测出的情况有两类:第一类:前五次恰检测出三件次品,第六次检测出第四件次品, 这样的检测的方法有224654C A A⋅种;…8分第二类:前六次检测出全部的正品,则剩余的四件必为次品,这样的检测方法总数共有66A种.…………10分由分类计数原理得,所有不同检测方法数为224654C A A⋅+66A=7920. …………12分(21)解:(Ⅰ)作ADEM⊥于M,∵ABCDPA平面⊥,∴ABCDEM平面⊥.作,于NACMN⊥ACNENE⊥,则连结.∴ENM∠为二面角的平面角.…………4分∵aAMaPAEM323131===,,∴aaAMMN33233260sin=⋅=︒⋅=,∴33tan==∠MNEMENM,∴︒=∠30ENM,∴二面角DACE--的大小为︒30.………8分(Ⅱ)BF∥平面AEC.…………9分PE Q FQ BF BQ AC BD O OE =取中点,连结、、,设,连,则OE ∥BQ ,QF ∥CE ,∴ 平面BQF ∥平面ACE ,…………11分 ∴ BF ∥平面ACE .…………12分(22)解:令,,k k k A B C 分别表示甲、乙、丙在第k 局中获胜.(Ⅰ)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满3局比赛还未停止的概率为 12312333111()().224P AC B P B C A +=+= …………6分 (Ⅱ)比赛停止时已打的局数不超过4局,即比赛停止时已打局数分别为2、3、4,其对应的概率分别为123P P P 、、,…………7分依题意有:且1121222111()();222P P A A P B B =+=+= 212312333111()();224P P AC C P B C C =+=+= 31234123444111()().228P P AC B B P B C A A =+=+=…………10分 所以事件A 发生的概率()p A =1117.2488++= …………12分。
南海区2008-2009学年度第二学期期末考试八年级数学试卷

初二数学下学期第20周晚测试卷班别: 姓名: 学号: 成绩:一.选择题(每小题4分,共32分)1.已知y x >,那么下列不等式一定成立的是( )A 、66-<-y xB 、y x 33<C 、y x 22-<-D 、1212+->+-y x2.如图1,是小孔成像原理的示意图,根据图1所标注的尺寸,这支蜡烛在暗盒中所成的像CD 的长是( )A 、cm 61B 、cm 31C 、cm 21 D 、cm 1 3.如图2能说明21∠>∠的是( )4.为了了解三水区老年人的健康状况,在以下的抽样调查中,你认为样本选择较合适的是( )A 、在西南公园晨练的100位老人;B 、到三水人民医院随机抽查的100位老人;C 、100位女性老人;D 、到区户籍管理处从各乡村任意抽取的100位老人。
5.如图3,是四个视力表中不同的“E ”,它们距同一测试点O 的距离各不相同,则在O 点测得视力相同的“E ”是()A 、①和②B 、①和③C 、②和③D 、①,②和④6.如图4、5,在边长为a 的正方形中挖掉一个边长为b 的小正方形(b a >)。
把余下的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )A 、))((22b a b a b a -+=-B 、2222)(b ab a b a +-=-C 、2222)(b ab a b a ++=+D 、)(2b a a ab a +=+7.如图6,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h 为( )A 、158B 、1C 、34D 、58 8.设n 为整数,则25)12(2-+n 一定能被( )整除A 、6B 、5C 、8D 、12二、填空题(每小题5分,共20分)9.已知4,6==+xy y x ,则y x xy 22+的值为 .10.跳远训练时,甲、乙两同学在相同条件下各跳10次,统计得,他们的平均成绩都是5.68,甲的方差为0.3, 乙的方差为0.4,那么成绩较为稳定的是 .(填“甲”或“乙”)11.因式分解:22121196x y -= .12.已知点C 是线段AB 的黄金分割点,AC >BC ,以AC 为边的正方形的面积为1S ,以BC,AB 为边的矩形的面积为2S ,则1S 与2S 的大小关系为 .三、解答题:(16~20题每小题6分,21~23题每小题8分,24题10分,25题11分,共75分)13. 解下列方程:11322x x x-+=--14.一群女生住若干间宿舍,若每间住4人,则19人无房住;若每间住6人,则有一间宿舍住不满.你知道有多少间宿舍,多少名女生吗?15. 如图,。
20082009学年第二学期下学期期末考试试题

商丘市2008-2009学年度第二学期期末考试试题高一生物注意事项:1.本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,第I卷1至4页,第II卷5至8页,共100分;考试时间为90分钟。
2.请把密封线内的项目和座号写在指定位置,把准考证号、第I卷答案用2B铅笔填涂在答题卡上;第II卷答案直接答于第II卷相应位置。
3.交卷时,只交答题卡和第II卷。
第I卷(选择题,共50分)一、选择题(本大题共25小题,每小题2分,共50分。
在每个题目列出的四个选项中,只有一个选项是最符合题目要求的。
)1.在证明DNA是遗传物质的实验中,赫尔希和蔡斯分别用32P和35S标记噬菌体的DNA和蛋白质,在下图中标记元素所在部位依次是A.①、④B.②、④ C.①、⑤ D.③、⑤2.构成烟草花叶病毒、噬菌体和烟草体内遗传物质的碱基种类依次是A.8、4、2 B.8、4、4 C.4、4、5 D.4、4、43.下列各组中不属于相对性状的是A.水稻早熟和晚熟B.豌豆的紫花和红花C.小麦的抗病和易感病D.绵羊的长毛和细毛4.假设某大肠杆菌含14N的DNA相对分子质量为a;而含15N的DNA分子,其相对分子质量为b。
现将含15N的DNA大肠杆菌再培养在14N的培养基中,子二代DNA的相对分子质量平均为A.(a+b)/2B.(3a+b)/4C.(2a+3b)/2D.(a+3b)/45.某双链DNA分子中,已知其中一条链中碱基数目比例关系为(A+T)/(G+C)=0.4,则另一条链中(A+T)/(G+C)为A. 1.25B. 0.4C. 0.6D. 无法确定6.一对表现正常的夫妇,生了一个孩子既是红绿色盲又是XYY的两病兼发的患者,从根本上说,前一病因与父母中的哪一方有关?后一病因形成发生在什么时期A.与父亲有关、减数第一次分裂B.与母亲有关、减数第一次分裂C.与母亲有关、减数第二次分裂D.与父母亲都有关、受精作用7.遗传信息和遗传密码子分别位于A.DNA和信使RNA上B.DNA和转运RNA上C.信使RNA和转运RNA上D.染色体和基因上8.一条染色体可能含有一条双链DNA分子,那么一条染色单体含有A.一条双链DNA分子B.一条单链DNA分子C.二条双链DNA分子D.二条单链DNA分子9.某成年男子是一种隐性致病基因的携带者,他下列那种细胞可能不含致病基因A.大脑中某些神经元B.精原细胞C.所有体细胞D. 某些精细胞10.将单个的脱氧核苷酸连接成DNA分子的主要的酶A.DNA连接酶 B.限制性核酸内切酶 C.DNA解旋酶 D.DNA聚合酶11.玉米籽粒黄果皮对白果皮为显性,让白果皮作母本,纯合的黄果皮作父本杂交,F2代植株所结的籽粒A.全为白果皮B.全为黄果皮C.黄果皮与白果皮为1︰1D.黄果皮与白果皮为3︰112.在人类中,多指是由显性基因控制的。
2008~2009学年度第二学期南昌市期末终结性
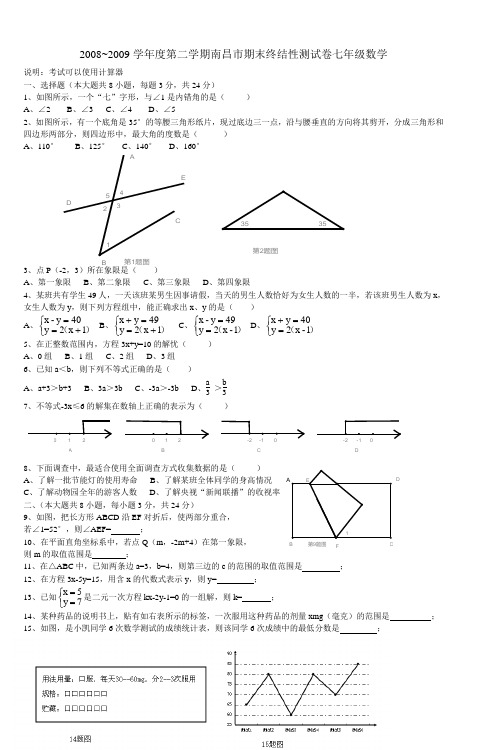
第2题图第1题图BA B C D第9题图F DCB 2008~2009学年度第二学期南昌市期末终结性测试卷七年级数学说明:考试可以使用计算器一、选择题(本大题共8小题,每题3分,共24分)1、如图所示,一个“七”字形,与∠1是内错角的是( ) A 、∠2 B 、∠3 C 、∠4 D 、∠52、如图所示,有一个底角是35°的等腰三角形纸片,现过底边三一点,沿与腰垂直的方向将其剪开,分成三角形和四边形两部分,则四边形中,最大角的度数是( ) A 、110° B 、125° C 、140° D 、160°3、点P (-2,3)所在象限是( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限4、某班共有学生49人,一天该班某男生因事请假,当天的男生人数恰好为女生人数的一半,若该班男生人数为x ,女生人数为y ,则下列方程组中,能正确求出x 、y 的是( ) A 、⎩⎨⎧+==)(1x 2y 40y -x B 、⎩⎨⎧+==+)(1x 2y 49y x C 、⎩⎨⎧==)(1-x 2y 49y -x D 、⎩⎨⎧==+)(1-x 2y 40y x 5、在正整数范围内,方程3x+y=10的解忧( )A 、0组B 、1组C 、2组D 、3组6、已知a <b ,则下列不等式正确的是( )A 、a+3>b+3B 、3a >3bC 、-3a >-3bD 、a 3 >b37、不等式-3x ≤6的解集在数轴上正确的表示为( )8、下面调查中,最适合使用全面调查方式收集数据的是( )A 、了解一批节能灯的使用寿命B 、了解某班全体同学的身高情况C 、了解动物园全年的游客人数D 、了解央视“新闻联播”的收视率 二、(本大题共8小题,每小题3分,共24分)9、如图,把长方形ABCD 沿EF 对折后,使两部分重合, 若∠1=52°,则∠AEF= ; 10、在平面直角坐标系中,若点Q (m ,-2m+4)在第一象限, 则m 的取值范围是 ;11、在△ABC 中,已知两条边a=3,b=4,则第三边的c 的范围的取值范围是 ; 12、在方程3x-5y=15,用含x 的代数式表示y ,则y= ; 13、已知⎩⎨⎧==7y 5x 是二元一次方程kx-2y-1=0的一组解,则k= ;14、某种药品的说明书上,贴有如右表所示的标签,一次服用这种药品的剂量xmg (毫克)的范围是 ; 15、如图,是小凯同学6次数学测试的成绩统计表,则该同学6次成绩中的最低分数是 ;16、本学期实验中学组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下:若用同一小班的计划人数与报名人数的比值来衡量进入该班的难易程度,学生中对于进入各活动小班的难易有以下预测:○1篮球和航模都能进;○2舞蹈比写作容易;○3写作比奥数容易;○4舞蹈比奥数容易,则预测正确的有(填序号即可)三、解下列方程组、不等式(组)(本大题共4小题,每小题6分,共24分)17、⎩⎨⎧=+=+4yx26y3x418、⎪⎩⎪⎨⎧=+=+4yx23yx221-x5)(19、2x-13-5x+12≤120、⎩⎨⎧≤≥5x2-363-x9四、应用题(本大题共2小题,每小题8分,共16分)今有甲、乙两个旅行团,已知甲团人数不小于50人,乙团人数不超过100人,若分别购票,两团共计应付门票费1950元,若合在一起作为一个团体购票,总计应付门票费1545元(1)请你判断乙团的人数是否也不少于50人?(2)求甲、乙两旅行团各有多少人?(3)甲旅行团单独购票,有无更省钱的方案?说明理由?22、“你记得父母的生日吗?”这是某中学在七年级学生中开展主题为“感恩“教育时设置的一个问题,有以下四个选项:A、父母生日都记得;B、只记得母亲的生日;C、只记得父亲的生日;D、父母生日都不记得。
2008-2009学年第二学期期末初二数学试卷张春凤

A BCDE2008-2009学年第二学期期末初二数学试卷(薄弱校)玉渊潭中学 出卷人: 张春凤 王慧 满分120分 2009年5月一、选择题(下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在相应的表格内,每小题4分,共32分)x 的取值范围是( ) A. x >1 B. x ≥1 C. x <1 D. x ≤1 2.把方程x(x+2)=5(x-2)化成一般式,则a 、b 、c 的值分别是( ) A .1,-3,10 B. 1,7,-10 C. 1,-5,12 D.1,3,23.实验表明,人体内某种细胞的形状可近似地看作球,它的直径约为0.00000156m ,将0.00000156用科学记数法表示是( )A .50.15610-⨯ B .50.15610⨯ C .61.5610-⨯ D .61.5610⨯ 4.若点(1,2y -)、),1(2y 、),3(3y 都在反比例函数xy 2-=的图象上,则321,,y y y 的大小关系是( )A.231y y y <<B.312y y y <<C.321y y y <<D.132y y y << 5.平行四边形ABCD 中,∠C=108°,BE 平分∠ABC ,则∠ABE 等于( ). A. 18° B. 36° C. 72° D. 108°6.一个三角形的三边的长分别是3,4,5,则这个三角形最长边上的高是( ) A. 4 B. 52 C. 125 D. 103GF EDCBAE FD CBA 7.若m 人需a 天完成某项工程,则这样的人(m+n)个完成这项工程需要的天数是( )A. a+mB.ma m n + C.a m n + D. m nam+ 8.将七个边长都为1cm 的正方形如图3所示摆放,点A 1、A 2、A 3、A 4、A 5、A 6、A 7分别是这七个正方形的中心,则这七个正方形重叠形成的重叠部分的面积是( )A .241cmB .2741cm ⎪⎭⎫⎝⎛C .247cm D .223cm 二、填空题(共4道小题,每小题4分 ,共16分) 9.方程224x x =的根为 . 10.如果03)2(2=-++y x ,那么=x y .11.如图,梯形ABCD 中,AD ∥BC ,AC 、BD 是对角线,E 、F 分别是BD 、AC 的中点,且EF=3.若上底AD 的长是4,则下底BC 的长是 .11题 12题12.如图,正方形ABCD 的边长为2,E 是AB 边上一点,四边形 EFGB 也是正方形,则△AFC 的面积是 .三、解答题(共13道题,共72分) 13.(本小题满分5分)计算: 12)31()3(1310+--+--π14.(本小题满分5分)计算:2118)12)(12()12(2+--++-15.(本小题满分5分)计算:b a ba a +--12216.(本小题满分5分)解方程:32121---=-xx x17.(本小题满分5分)已知 x-4y=0,求)2(44222y x y xy x yx -⋅+-+的值18.(本小题满分5分)已知:如图,E 、F 是□ABCD 的对角线AC 上的两个点,且AE=CF.求证:四边形DEBF 是平行四边形.19.(本小题满分5分)已知:平面直角坐标系xoy 中,反比例函数x k y =的图象与xy 5=的图象关于x 轴对称,又与直线y=ax+4交于点A(m, 5). 求:(1) A 点的坐标;(2)确定a 的值.20.(本小题满分5分)已知:如图,矩形ABCD 中AB=3,BC=5,折叠矩形的一边BC ,使点B 落在AD 边的F 处,求:折痕EC 的长.AE BCDFFC DB EA21.(本小题满分5分)印度数学家什迦罗(1141年-1225年)曾提出过“荷花问题”:平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?请用学过的数学知识回答这个问题。
昆山市2008~2009学年第二学期期末考试试卷 初二数学

初二数学(考试时间:120分钟,满分100分)一、选择题(每小题3分,共24分)1.银原子的直径为0.0003微米,用科学记数法可表示为A.3×104微米B.3×10-4微米C.3×10-3微米D.0.3×103微米2.若分式132xx+-的值为零,则x等于A.0 B.1 C.23D.-13.若x=2xx-的值为A.0 B C.D.4.△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是A.1:6 B.1:5 C.1:4 D.1:25.一台机床在十天内每天生产的产品中,每天出现的次品个数依次为(单位:个)0,2,0,2,3,3,2,3,1,2那么,这十天中次品个数的A.平均数为1.8 B.众数为3 C.中位数1.5 D.方差为2 6.在□ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CB F∽△CDE,则BF的长为A.5 B.1.8C.6.4 D.8.27.去年5月23日8时40分,哈尔滨铁路局一列满载2400吨“爱心”大米的专列向四川灾区进发,途中除3次更换车头等原因必须停车外,一路快速行驶,经过80小时到达成都.描述上述过程的大致图象是(t 为时间,v 为速度)8.在直角坐标系中,已知点A(-2,0),B(0,4),C(0,3),过点C 作直线交x 轴于点D ,使得以C 、O 、D 为顶点的三角形与△AOB 相似,这样的直线最多可作 A .1条 B .2条 C .3条 D .4条 二、填空题(每小题2分,共20分)9.函数y =x 的取值范围_____________.10.命题“两全等三角形的面积相等”的逆命题是___________________. 11.若五个数1,5,3,2,x 的平均为3,则这组数据的方差为__________. 12.若点P(-2m+1,3)在第二象限,则m 的取值范围_____________. 13.若反比例函数y=(k -1)x k2-5的图象经过二、四象限,则k=___________.14.已知:157x y y -=,则xy=___________. 15.如图是小孔成像原理的示意图,根据图中标注的尺寸, 如果物体AB 的高度为36 cm ,那么它在暗盒中所成 的像CD 的高度应为_________cm .16.如图E 是平行四边形ABCD 的边AD 上的点,AE=12ED .BE 交AC 于F ,则AF FC=___________. 17.已知数据2、4、6、7、a 的中位数为4,极差为6.则a=_________. 18.如图,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点, 且CF=14CD ,下列结论:①∠BA E=30°②△AB E ∽△AEF ③A E ⊥EF ④△AD F ∽ECF其中正确结论为__________________.(只需填写序号)三、解答题(本大题共10题,满分56分,解答应写出必要的解答过程、推理步骤或文字说明)19.(本题共2小题,每小题3分,共6分)(1)()1120092-⎛⎫-+ ⎪⎝⎭(2)化简:()22212x x x x x x x +--÷++-20.(本题4分)先化简,再求值:21111x x x x ⎛⎫⎛⎫-÷+ ⎪ ⎪+-⎝⎭⎝⎭,其中x =.21.(本题4分)如图,AB=AD,AC=AE,∠1=∠2求证:BC=DE22.(本题5分)如图,在△ABC中,∠BAC=2∠C.(1)在图中作出△ABC的内角平分钱AD.(要求:尺规作图,保留作图痕迹,不写证明)(2)在已作出的图形中,写出一对相似三角形,并说明理由.23.(本题5分)在平面直角坐标系中,有A(0,1),B(-1,0),C(1,0)三点.(1)若点D与A,B,C三点构成平行四边形,请写出所有符合条件的点D的坐标;(2)选择(1)中符合条件的一点D,求直线BD的解析式.24.(本题6分)某同学进行社会调查,随机抽查了某个地区的20个家庭的年收入情况,并绘制了统计图.请你根据统计图给出的信息回答:(1)填写完成下表:(2)这20个家庭年平均收入为多少万元?(3)样本中的中位数是多少万元?众数是多少万元?25.(本题6分)为预防“甲型H1N1流感”,某校对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:(1)求药物燃烧时y与x的函数关系式;(2)求药物燃烧后y与x的函数关系式;(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?26.(本题6 分)□ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=12 CD.(1)求证:△AB F∽△CEB;(2)若△DEF的面积为2,求□ABCD的面积.27.(本题6分)如图,在矩形ABCD中,点E在BC上,EF⊥DE交AB于点F,连结AE,DF.(1)若EF=ED(如图①),求证:△AB E∽△FED;(2)若点E在BC上运动(如图②,点E不与点B,C重合),试问△AB E∽△FED是否仍然成立?若不成立,请举出反例;若成立,请说明理由.28.(本题8分)如图,菱形ABCD的边长为12厘米,∠A=60°,P从点A出发沿线路AB —BD作匀速运动,点Q从点D同时出发沿线路DC—CB—BA作匀速运动.(1)求BD的长;(2)已知质点P,Q运动的速度分别为4厘米/秒、5厘米/秒,经过6秒后,P,Q分别到达M,N两点,若按角的大小进行分类,请你确定△AMN是哪一类三角形,并说明理由;(3)设题(2)中的质点P,Q分别从M,N同时沿原路返回,质点P的速度不变,质点Q的速度改变为a厘米/秒,经过1.5秒后,P,Q分别到达E,F两点,若△BEF 与题(2)中的△AMN相似,试求a的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008---2009学年度第二学期期末试卷
北师大版教材二年级数学
一、你的口算进步了吗?(4分)
790-500= 28÷4= 73+50= 5900-2000=
51÷7= 71-26=1600-700= 6×7=
二、填空。
(16分其中3小题3分,其余每空1分)
1、在()÷6=4……(),第二个括号最多只能填()
2、两千零八十写作:()
3、按照从小到大排列下面各数:3050、5030、5003、350、3500、53
()<()<()<()<()<()
4、选择合适的单位填空(km、m 、dm、cm、mm)
数学书厚约5()二年级的小红高128()
深圳到广州大约120() 1分硬币大约有1()厚。
5、用0、1、2、3四个数组成的最大四位数是(),最小的四位数是()。
6、在计算35-35÷7 时要先算()法,再算()法。
7、长方形有四个()角。
三、判断题(5分)
()1、在有余数的除法里余数一定要比除数小。
()2、锐角比直角大。
()3、五位数都比四位数大。
()4、当你看《中国地图》时,你的左边就是地图的西方。
()5、一个角有一个顶点,两条边。
四、计算。
(30分)
1、脱式计算下面的题。
(9分)
88-(23+46)63-56÷7 9×8+68
= = =
= = =
2、竖式计算下面的题,带*的验算。
(21分)
* 457+326= * 4100-648=
验算验算
62÷8= 36÷4= 261+425= 210+356+902= 896-253+74= 五、你会迷失方向吗?(12分)
1、从邮局出发向____方走____站到少年宫,再向____方走___站到了育才路,
再向___方走____站到电影院,再向____方走____站到居民区。
2、小华坐了4站在医院下车,她可能在哪上的车?
3、医院在育才路的__ __方;幸福路在少年宫的__ __方。
六、我会动手做:(10分)
1、在右面的方格里涂色,要求在不同
位置涂一个三角形、一个平行四边形。
2、把序号填在相应的方框内。
①②③④⑤⑥
直角锐角钝角
七、根据统计图回答下面问题。
(6分)
下面是同学们参加兴趣小组的统计图:
趣味数学
美术小组
科技小组
足球小组
人数
0 1 2 3 4 5 6 7 8 9 10 11 12
(1)一共调查了______名同学。
(2)参加______小组的人数最多,______小组的人数最少,差____人。
(3)参加______小组的是______小组人数的2倍。
八、小调查:(5分)
星期一二三四五六日营业额/
168 226 174 295 414 492 477 元
这周星期_______收入最高,星期_______收入最低。
星期三和星期四共收入多少元?
=(元)
(12分)
买一副羽毛球拍和5个羽毛球共需多少钱?
买一个足球和一副羽毛球拍,妈妈付200元,应找回去多少钱?
30元钱可以买几个羽毛球,还剩多少元?。
