解直角三角形复习湘教版
最新湘教版九年级数学下册 第18讲 解直角三角形
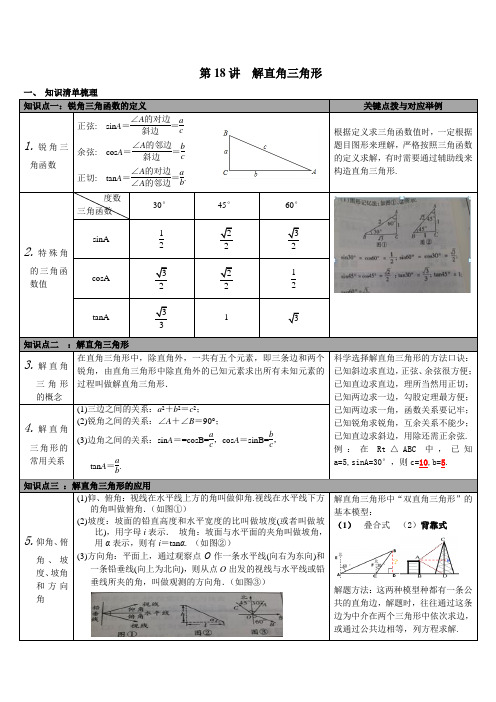
解直角三角形中“双直角三角形”的基本模型:
(1)叠合式(2)背靠式
解题方法:这两种模型种都有一条公共的直角边,解题时,往往通过这条边为中介在两个三角形中依次求边,或通过公共边相等,列方程求解.Βιβλιοθήκη 三角函数30°45°
60°
sinA
cosA
tanA
1
知识点二:解直角三角形
3.解直角三角形的概念
在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形.
科学选择解直角三角形的方法口诀:
已知斜边求直边,正弦、余弦很方便;
已知直边求直边,理所当然用正切;
(3)边角之间的关系:sinA==cosB= ,cosA=sinB= ,
tanA= .
知识点三:解直角三角形的应用
5.仰角、俯角、坡度、坡角和方向角
(1)仰、俯角:视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角.(如图①)
(2)坡度:坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比),用字母i表示.坡角:坡面与水平面的夹角叫做坡角,用α表示,则有i=tanα.(如图②)
第18讲解直角三角形
一、知识清单梳理
知识点一:锐角三角函数的定义
关键点拨与对应举例
1.锐角三角函数
正弦:sinA= =
余弦:cosA= =
正切:tanA= = .
根据定义求三角函数值时,一定根据题目图形来理解,严格按照三角函数的定义求解,有时需要通过辅助线来构造直角三角形.
专题1-9 《直角三角形》全章复习与巩固(知识讲解)-八年级数学下册(湘教版)

1.9 《直角三角形》全章复习与巩固(知识讲解)【复习目标】1.了解直角三角形的概念,理解直角三角形的性质和判定;2.能用直角三角形的性质和判定解决简单问题;3.会运用直角三角形的知识解决有关问题.【知识梳理】要点一、直角三角形定义1.直角三角形定义:有一个角是直角的三角形叫做直角三角形.要点二、直角三角形性质(1)直角三角形中两锐角互余.(2)直角三角形中,30°锐角所对的直角边等于斜边的一半.(3)在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.(4)勾股定理:直角三角形中,两条直角边的平方和等于斜边的平方.(5)勾股定理逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.(6)直角三角形中,斜边上的中线等于斜边的一半.要点三、直角三角形的判定(1)有两内角互余的三角形是直角三角形.(2)一条边上的中线等于该边的一半,则这条边所对的角是直角,这个三角形是直角三角形.(3)如果三角形两边的平方和等于第三边的平方,则这个三角形是直角三角形,第三边为斜边.要点四、判定直角三角形全等的一般方法由三角形全等的条件可知,对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形就全等了.这里用到的是“AAS”,“ASA”或“SAS”判定定理. 要点五、判定直角三角形全等的特殊方法——斜边,直角边定理在两个直角三角形中,有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).这个判定方法是直角三角形所独有的,一般三角形不具备.【典型例题】类型一、直角三角形的性质1.已知:如图,在△ABC中,AB=AC=2a,∠ABC=∠ACB=15°,CD是腰AB上的高.求CD的长.【答案】CD=a【思路点拨】根据三角形的外角的性质得∠DAC=30°,再根据含30°角的直角三角形的性质可得DC=a.解:∵∠ABC=∠ACB=15°∴∠DAC=30°∵CD是腰AB上的高AB=AC=2a∴AC=2CD∴CD=a【点拨】此题主要考查含30°的直角三角形的性质,解题的关键是利用等腰三角形得出含30°角的直角三角形.2 已知,在,ABC中,,ACB,90°,CD,AB垂足为D,BC,6,AC,8,求AB与CD 的长.【答案】AB=10∠CD=4.8.解∠在△ABC中∠∠ACB=90°∠CD⊥AB垂足为D∠BC=6∠AC=8∠由勾股定理得∠AB=∵S△ABC=12AB•CD=12AC•BC∠∴CD=AC BCAB⋅=8610⨯=4.8∠【点拨】在直角三角形ABC中∠利用勾股定理求出AB的长∠再利用等面积法求出CD的长即可.3.已知:如图,在△ABC中,∠A=30°,∠ACB=90°,M、D分别为AB、MB的中点. 求证:CD⊥AB.【思路点拨】由∠ACB=90°,M为AB的中点.根据直角三角形斜边上的中线等于斜边的一半得到CM12=AB=BM,再根据在直角三角形中,30°所对的边等于斜边的一半得到CB12=AB=BM,则CM=CB,而D为MB的中点,根据等腰三角形的性质即可得到结论.解∵∠ACB=90°,M为AB中点,∴CM12=AB=BM.∵∠ACB=90°,∠A=30°,∴CB12=AB=BM,∴CM=CB.∵D为MB的中点,∴CD⊥BM,即CD⊥AB.【点拨】本题考查了含30°的直角三角形的性质:30°所对的边等于斜边的一半;也考查了直角三角形斜边上的中线等于斜边的一半以及等腰三角形的性质.类型二、直角三角形全等的判定——“HL”4、已知:如图,AB⊥BD,CD⊥BD,AD=BC.求证:(1)AB=CD:(2)AD∥BC.【思路点拨】先由“HL”证Rt△ABD≌Rt△CDB,再由内错角相等证两直线平行.证明:(1)∵AB⊥BD,CD⊥BD,∴∠ABD =∠CDB =90°在Rt △ABD 和Rt △CDB 中,∴Rt △ABD ≌Rt △CDB (HL )∴AB =CD (全等三角形对应边相等)(2)由∠ADB =∠CBD∴AD ∥BC .【总结升华】证明两个直角三角形全等,首先考虑用斜边、直角边定理,再考虑用一般三角形全等的证明方法.举一反三:【变式】已知:如图,AE ⊥AB ,BC ⊥AB ,AE =AB ,ED =AC .求证:ED ⊥AC .证明:∵AE ⊥AB ,BC ⊥AB ,∴∠DAE =∠CBA =90°在Rt △DAE 与Rt △CBA 中,∴Rt △DAE ≌Rt △CBA (HL )∴∠E =∠CAB∵∠CAB +∠EAF =90°,∴∠E +∠EAF =90°,即∠AFE =90°即ED ⊥AC .5、 判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:AD BC BD DB ⎧⎨=⎩=ED AC AE AB ⎧⎨⎩==,(1)一个锐角和这个角的对边对应相等;( )(2)一个锐角和斜边对应相等; ( )(3)两直角边对应相等; ( )(4)一条直角边和斜边对应相等. ( )【答案】(1)全等,“AAS ”;(2)全等,“AAS ”;(3)全等,“SAS ”;(4)全等,“HL ”.【解析】理解题意,画出图形,根据全等三角形的判定来判断.【总结升华】直角三角形全等可用的判定方法有5种:SAS 、ASA 、AAS 、SSS 、HL. 举一反三:【变式】下列说法正确的有( )(1)一个锐角及斜边对应相等的两个直角三角形全等;(2)一个锐角及一条直角边对应相等的两个直角三角形全等;(3)两个锐角对应等的两个直角三角形全等;(4)有两条边相等的两个直角三角形全等;(5)有斜边和一条直角边对应相等的两个直角三角形全等.A.2个B.3个C.4个D.5个 【答案】C .解:(1)一个锐角及斜边对应相等的两个直角三角形全等,根据AAS 可判定两个直角三角形全等;(2)一个锐角及一条直角边对应相等的两个直角三角形全等,根据AAS 或ASA 可判定两个直角三角形全等;(3)两个锐角对应等的两个直角三角形全等,缺少“边”这个条件,故不可判定两个直角三角形全等;(4)有两条边相等的两个直角三角形全等,根据SAS 或HL 可判定两个直角三角形全等;(5)有斜边和一条直角边对应相等的两个直角三角形全等,根据HL 可判定两个直角三角形全等.所以说法正确的有4个.故选C .6、 如图,AB ⊥AC 于A ,BD ⊥CD 于D ,若AC=DB ,则下列结论中不正确的是( ) A .∠A=∠D B .∠ABC=∠DCBC .OB=OD D .OA=OD O BC DA【思路点拨】根据已知及全等三角形的判定方法进行分析,从而得到答案.做题时要结合已知条件与全等的判定方法逐一验证.【答案与解析】解:∵AB⊥AC于A,BD⊥CD于D∴∠A=∠D=90°(A正确)又∵AC=DB,BC=BC∴△ABC≌△DCB(HL)∴∠ABC=∠DCB(B正确)∴AB=CD又∵∠AOB=∠C∴△AOB≌△DOC(AAS)∴OA=OD(D正确)C中OD、OB不是对应边,不相等.故选C.【总结升华】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.类型三、直角三角形的折叠问题7.将一张矩形纸片如图所示折叠,使顶点落在点.已知,,则折痕的长为( )A. B. C. D.【思路点拨】直角三角形是常见的几何图形,在习题中比较多的利用数形结合解决相应的问题.常用的是两锐角互余,三边满足勾股定理和直角三角形中,30°角所对的边等于斜边的一半.【答案】C.【解析】由折叠可知,∠CED=∠C′ED =30°,因为在矩形ABCD中,∠C等于90°,CD=AB=2,所以在Rt△DCE中,DE=2CD=4.故选C.【总结升华】折叠题型一定要注意对应的边相等,对应的角相等.【变式】如图,一张直角三角形纸片,两直角边AC=4cm,BC=8cm,将△ABC折叠,点B与点A重合,折痕为DE,则DE的长为( ).A. B. C. D.5【答案】B.解析:由折叠可知,AD=BD,DE⊥AB,∴BE=AB设BD为x,则CD=8-x∵∠C=90°,AC=4,BC=8,∴AC2+BC2=AB2∴AB2=42+82=80,∴AB=,∴BE=在Rt△ACD中,AC2+CD2=AD2 ,∴42+(8-x)2=x2,解得x=5在Rt△BDE中,BE2+DE2=BD2,即()2+DE2=52,∴DE=,故选B.类型四、直角三角形的性质和判定综合运用8.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一直重型运输卡车P沿道路ON方向行驶的速度为18千米/时.(1)求对学校A的噪声影响最大时卡车P与学校A的距离;(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.。
湘教版八年级下册数学第一章直角三角形复习课件

正弦、余弦函数值在0到1之间,正切函数 值可正可负,且随着角度的增大而增大或减 小。
特殊角度下三角函数值记忆方法
30°、45°、60°等特殊角度的三 角函数值可通过几何图形或三角
函数表进行记忆。
利用三角函数之间的互相关系, 如tanA=sinA/cosA,可以通过 已知函数值推导出其他函数值。
制作三角函数卡片或表格,方便 随时查阅和记忆。
分类
按边长可分为普通直角三角形和 等腰直角三角形,其中等腰直角 三角形两腰相等。
直角三角形边与角关系
边长关系
对于直角三角形,满足勾股定理,即两直角边的平方和等于 斜边的平方。
角度关系
直角三角形两锐角互余,且满足三角函数的定义和性质。
勾股定理及其应用
勾股定理
在直角三角形中,两直角边的平方和 等于斜边的平方。
05 复习策略与备考建议
重点知识点回顾与总结
直角三角形的定义和性质
01
直角三角形是一个角为90度的三角形,它具有一些特殊的性质
和定理,如勾股定理等。
直角三角形的边角关系
02
在直角三角形中,角度和边长之间有一定的关系,如正弦、余
弦、正切等三角函数。
直角三角形的判定方法
03
通过给定的条件,如角度、边长等,可以判定一个三角形是否
湘教版八年级下册数学第一章直角 三角形复习课件
目 录
• 直角三角形基本概念与性质 • 直角三角形中的函数关系 • 解直角三角形方法技巧总结 • 直角三角形在几何证明题中应用 • 复习策略与备考建议
01 直角三角形基本概念与性 质
直角三角形定义及分类
定义
有一个角为90度的三角形称为直 角三角形。
构造直角三角形
八年级数学下第一单元直角三角形小结与复习湘教版全面版ppt课件

A E
C
B
D
9、 如图,AC=AD,∠C,∠D是直角,将上述条件标 注在图中,你能说明BC与BD相等吗?
C
解:在Rt△ACB和Rt△ADB中,则
A D
AB=AB,
B
AC=AD.
∴ Rt△ACB≌Rt△ADB (HL). ∴BC=BD
(全等三角形对应边相等).
10、已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE 交点F,CF=BF,求证:点F在∠A的平分线上.
二、直角三角形全等的判定: 斜边直角边定理:斜边和一条直角边对应相等的
两个直角三角形全等(可以简写成“斜边、直角边” 或“HL”).
三、角平分线的性质: 性质定理:角的平分线上的点到角的两边的距离
相等。 逆定理:角的内部到角的两边距离相等的点在角
的平分线上。
随堂练习
1.如图,AB ⊥DB,CD ⊥DB,下列说法错误的是( C )
知识梳理
一、直角三角形的性质和判定:
性质定理: 直角三角形的两个锐角互余。 直角三角形斜边上的中线等于斜边的一半。 直角三角形两直角边a,b的平方和,等于斜边c的
平方.
a2 + b2 =c2
判定定理: 有两个角互余的三角形是直角三角形。 如果三角形的三条边长,a,b,c满足关系:
a2 + b2 =c2 ,那么这个三角形是直角三角形。
光不会因你而停留,你却会随着光阴而老去。
有些事情注定会发生,有的结局早已就预见,那么就改变你可以改变的,适应你必须去适应的。面对幸与不幸,换一个角度,改变一种思维,也许心空就不再布满阴霾,头上就 是一片蔚蓝的天。一生能有多少属于我们的时光,很多事情,很多人已经渐渐模糊。而能随着岁月积淀下来,在心中无法忘却的,一定是触动心灵,甚至是刻骨铭心的,无论是 伤痛是欢愉。人生无论是得意还是失意,都不要错过了清早的晨曦,正午的骄阳,夕阳的绚烂,暮色中的朦胧。经历过很多世态炎凉之后,你终于能懂得:谁会在乎你?你又何 必要别人去在乎?生于斯世,赤条条的来,也将身无长物的离开,你在世上得到的,失去的,最终都会化作尘埃。原本就不曾带来什么,所以也谈不到失去什么,因此,对自己 经历的幸与不幸都应怀有一颗平常心有一颗平常心,面对人生小小的不如意或是飞来横祸就能坦然接受,知道人有旦夕祸福,这和命运没什么关系;有一颗平常心,面对台下的 鲜花掌声和头上的光环,身上的浮名都能清醒看待。花不常开,人不常在。再热闹华美的舞台也有谢幕的时候;再奢华的宴席,悠扬的乐曲,总有曲终人散的时刻。春去秋来, 我们无法让季节停留;同样如同季节一样无法挽留的还有我们匆匆的人生。谁会在乎你?生养我们的父母。纵使我们有千般不是,纵使我们变成了穷光蛋,唯有父母会依然在乎! 为你愁,为你笑,为你牵挂,为你满足。这风云变幻的世界,除了父母,不敢在断言还会有谁会永远的在乎你!看惯太多海誓山盟的感情最后星流云散;看过太多翻云覆雨的友 情灰飞烟灭。你春风得意时前呼后拥的都来锦上添花;你落寞孤寂时,曾见几人焦急赶来为你雪中送炭。其实,谁会在乎你?除了父母,只有你自己。父母待你再好,总要有离 开的时日;再恩爱夫妻,有时也会劳燕分飞,孩子之于你,就如同你和父母;管鲍贫交,俞伯牙和钟子期,这样的肝胆相照,从古至今有几人?不是把世界想的太悲观,世事白 云苍狗,要在纷纷扰扰的生活中,懂得爱惜自己。不羡慕如昙花一现的的流星,虽然灿烂,却是惊鸿一瞥;宁愿做一颗小小的暗淡的星子,即使不能同日月争辉,也有自己无可 取代的位置其实,也不该让每个人都来在乎自己,每个人的人生都是单行道,世上绝没有两片完全相同的树叶。大家生活得都不容易,都有自己方向。相识就是缘分吧,在一起 的时候,要多想着能为身边的人做点什么,而不是想着去得到和索取。与人为善,以直报怨,我们就会内心多一份宁静,生活多一份和谐没有谁会在乎你的时候,要学会每时每 刻的在乎自己。在不知不觉间,已经走到了人生的分水岭,回望过去生活的点滴,路也茫茫,心也茫茫。少不更事的年龄,做出了一件件现在想来啼笑皆非的事情:斜阳芳草里, 故作深沉地独对晚风夕照;风萧萧兮,渴望成为一代侠客;一遍遍地唱着罗大佑的《童年》,期待着做那个高年级的师兄;一天天地幻想,生活能轰轰烈烈。没有刀光剑影,没 有死去活来,青春就在浑浑噩噩、懵懵懂懂中悄然滑过。等到发觉逝去的美好,年华的可贵,已经被无可奈何地推到了滚滚红尘。从此,青春就一去不回头。没有了幻想和冲动, 日子就像白开水一样平淡,寂寞地走过一天天,一年年。涉世之初,还有几分棱角,有几许豪情。在碰了壁,折了腰之后,终于明白,生活不是童话,世上本没有白雪公主和青 蛙王子,原本是一张白纸似的人生,开始被染上了光怪陆离的色彩。你情愿也罢,被情愿也罢,生存,就要适应身不由己,言不由衷的生活。人到中年,突然明白了许多:人生 路漫漫,那是说给还不知道什么叫人生的人说的,人生其实很短暂,百年一瞬间;世事难预料,是至理名言,这一辈子,你遇见了谁,擦肩而过了谁,谁会是你真心的良朋益友,
湘教版八年级数学下册第1章 直角三角形 复习2

章末复习【知识与技能】1.系统了解本章的知识体系及知识内容.2.在熟练掌握直角三角形相关概念的基础上,进一步熟悉掌握直角三角形性质与判定的应用.3.在掌握角平分线性质及其逆定理的基础上将知识融汇贯通,进行一些提高训练.4.培养对知识综合掌握、综合运用的能力.【过程与方法】复习梳理本章的主要知识点,及应注意的问题.通过典型例题讲解和对应练习,使学生对本章知识达标.【情感态度】主动参与、积极探索、合作交流,发挥学习中主人翁意识,感受成功的乐趣,激发学生的学习兴趣,培养学生的动手操作能力和解决问题的能力.【教学重点】勾股定理及其逆定理,直角三角形的性质和判定,角平分线性质与判定在解决实际问题中的作用.【教学难点】综合运用直角三角形相关知识解决问题.一、知识框图,整体把握【教学说明】引导学生回顾本章知识点,展示结构框图,让学生对本章所学知识有个系统地把握.教学时,可以边回顾边建立结构图,逐步加深印象.二、释疑解惑,加深理解1.“斜边、直角边定理”是判定两个直角三角形全等所独有的,在运用该判定定理时,要注意全等的前提条件是两个直角三角形.2.本章的互逆定理:直角三角形的性质和判定定理,勾股定理及其逆定理,角平分线的性质定理及其逆定理等,注意它们之间的区别与联系.3.数形结合的思想:勾股定理体现了由形到数,而勾股定理的逆定理体现了由数到形.三、典例精析,复习新知例1 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,图中与∠A 互余的角有()A.0个B.1个C.2个D.3个【分析】由“直角三角形的两锐角互余”,可找出与∠A互余的角.∵∠ACB=90°,CD是AB边上的高,∴∠A+∠B=90°,∠A+∠ACD=90°,∴与∠A互余的角2个,故选C.例2 如图,一棵树在一次强台风中,从离地面5m处折断,倒下的部分与地面成30°角,如图所示,这棵树在折断前的高度是()A.10mB.15mC.5mD.20m.【分析】根据题意可以得直角三角形中,较短的直角边是5,再根据30°所对的直角边是斜边的一半,得斜边是10,从而求出大树的高度为10+5=15(m).故选B.例3 如图,已知△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为_______.【分析】∵AB=5cm,BC=12cm,AC=13cm,由勾股定理的逆定理得,△ABC是直角三角形,∵BD是AC边上的中线,∴BD=12AC=6.5cm.例4 一架长5米的梯子AB,斜立在一竖直的墙上,这时梯子底端距墙底3米.如果梯子的顶端沿墙下滑1米,梯子的底端在水平方向沿一条直线也将滑动1米吗?用所学知识,论证你的结论.【分析】由勾股定理求得AC=4(米),由题意得CD=AC-AD=4-1=3(米),再由勾股定理可求得CE的长,进而求出BE的长.解:是,理由如下:在Rt△ACB中,BC=3,AB=5,AC2+BC2=AB2,∴AC=4,DC=4-1=3,在Rt△DCE中,DC=3,DE=5,CE2+DC2=DE2,∴CE=4,∴BE=CE-CB=1,即梯子底端也滑动了1米.【教学说明】典型例题的分析解答,对学生解题有着非常重要的指导作用,教师在讲评的过程中,让学生明确本章的重点有哪些,难点在哪里,需要注意哪些,容易忽略什么,逐步加深印象,达到全面掌握.四、复习训练,巩固提高1.如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,若CD=2,那么BD等于()A.6B.4C.3D.22.如图,由四个全等的直角三角形拼成“赵爽弦图”。
八年级数学下册 第1章 直角三角形小结与复习(复习题1)课件(新版)湘教版

∴xy 1.
这个直角三角形的面积S 1 xy 1 . 22
10.如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线且
交BC于点D,DE⊥AB,垂足为点E,若AB=12 cm,求△DEB的周长.
解:AD是∠BAC的平分线,DE⊥AB于E, DC⊥AC于C, ∴DE=CD. 易证AE=AC=BC. ∴BD+DE+EB=BD+CD+EB=BC+EB
解: ∵D为AB的中点, AB=8, ∴AD=BD=4, 又在Rt△ABC中, ∠A=30°, ∴DE=2.
3.用计算器求图中的x (结果精确到0.1 m).
x 2.5 2 4.2 2 6.25 17.64 4.9 m
x 1.392-0.912 1.9321-0.8281 1.1 m
复习课件
八年级数学下册 第1章 直角三角形小结与复习(复习题1)课件(新版)湘教版
①
小结与复习
小结复习
1.直角三角形的两个锐角有什么关系? 2.直角三角形斜边上的中线与斜边有什么关系? 3.请用自己的语言叙述勾股定理及其逆定理. 4.判断两个直角三角形全等的方法有哪些? 5.角平分线有哪些性质?
4.判断由a,b, c组成的三角形是不是直角三角形.
(1)a=15,b=8,c=17;
(2)
a=
1 2
,b=1,c=
3 4
;
(3)a=1.5,b=2,c=2.5.
解:( 1) 15282= 172,
∴ 由 a,b,c组 成 的 三 角 形 是 直 角 三 角 形 . (2)122432≠12,
∴由a,b,c组成的三角形不是直角三角形.
=AE+EB=AB=12 cm. ∴△DEB的周长为12 cm.
湘教版(2012)初中数学九年级上册 4.4 直角三角形复习课 教案 .doc
例题2:如图△ADC与△ABD为直角三角形,E 为AD的中点。
BE和CE相等吗?请说明理由。
变式1:如图,AB⊥BD于B ,E为AD的中点,BE=CE, AC与CD垂直吗?请说明理由。
变式2:如图,已知△ABG中,AB⊥BD于B,AC⊥CD于C ,E为AD的中点,点F是BC的中点, 那么EF垂直BC吗?请说明理由。
计算:如上图,已知△ABG中,AB⊥BD于B,AC⊥CD于C ,E为AD的中点,点F是BC的中点, BC=6,EF=4,求线段AD的长度。
师生合作完成、体现教师引导、学生主体,充分让学生参与展示、小组合作等。
设计变式题让学生积极思考,对于类型习题进行演练,培养学生的直观想象及推理能力。
通过逻辑推理、数据分析,培养学生的运算能力,解题能力。
四、巩固提高1、下列三数不能作为一个直角三角形三边长的
是()
A 5、12、13
B 1、3、2
C 1、1、2
D 3、4、5
2、Rt△ABC中,两条边的长分别为6cm和8cm,
则第三边的长为
3、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB
于D,AB=4, BC=2,求线段CD的长度.
学生自主
完成
教师指导知识的综合
运用
此题一题多
解,培养学
生思维,激
E
B
A D
C
E
B
A D
C
G
F。
解直角三角形 第4课时 复习 课件(湘教版九年级全)
2、坡面与水平面的夹角叫做坡角。 设坡角为 ,坡度为i,则 i=tan =h:l 3、坡度越大,则坡角越大,坡面 就越陡.
例. 如图,拦水坝的横断面为梯形ABCD(图中i=1:3是指坡面的铅直 度DE与水平宽度CE的比),BC=30m,AF=6m,求:
(1)坡角a和β; (2)斜坡AB和坝顶宽AD的长(精确到0.1m) 解:(1)在Rt△AFB中,∠AFB=90° i=1:1.5 AF tan i 11.5 : 0.667 α BF B A D i=1:3 E β C
2 1.414, 3 1.732
tan 30 x 3 1 10 x 3 3
x x 10
x 5 3 5 15.1
15.1+1.44 16.5
化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用 相关知识,例如,当我们要测量如图所示大坝的高度h时,只要测出仰 角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所 示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a 和山坡长度l
l
α
l
h
α
h
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲” 的,怎样解决这样的问题呢?
我们设法“化曲为直,以直代曲”. 我们可以把山坡“化 整为零”地划分为一些小段,图表示其中一部分小段,划分小 段时,注意使每一小段上的山坡近似是“直”的,可以量出这 段坡长l1,测出相应的仰角a1,这样就可以算出这段山坡的高度 h1=l1sina1. l α h
解直角三角形的应用
坡度与坡角
在进行观察或测量时, 从下向上看,视线与水平线的夹角叫做仰角; 从上往下看,视线与水平线的夹角叫做俯角. 视线 铅 垂 仰角 线 水平线 俯角
湘教版九年级数学 4.3 解直角三角形(学习、上课课件)
感悟新知
知2-练
例2 [母题 教材 P123 练习 T2 ]根据下面的条件,解直角
三角形:在Rt△ABC中,∠C=90°,a=2 3 ,b=2.
解题秘方:紧扣“直角三角形的边角关系”选择 适合的关系式求解.
感悟新知
解:在Rt△ABC 中,∠C=90°, a=2 3,b=2,∴ c= a2+b2= 12+4=4. ∵ tan A=ab=223=3 ,∴∠A=60°, ∴∠B=90°-∠A=90°-60°=30°
知2-练
感悟新知
2-1.根据下面的条件解直角三角形:在 Rt △ ABC 中,知2-练 ∠ C=90 ° , a=20,c=20 2 . 解:在 Rt△ ABC 中,∠C=90°, ∵a=20,c=20 2, ∴b= c2-a2= 800-400=20. ∵sinA=ac=20202= 22, ∴∠A=45°,∴∠B=90°-∠A=90°-45°=45°.
知2-练
∴
AD=
1 2
AC=1,∴
CD=
AC 2 - AD 2=
22 - 12=
3.
在 Rt △ ADB 中, ∠ B = 45° , AD = 1,
∴ BD = AD = 1,∴ BC = BD+CD = 1+ 3 . 答案:C
感悟新知
知2-练
4-1. [ 期中·济南槐荫区 ] 如图, △ ABC 是边长 为 6 的等
第四章 锐角三角函数
4.3 解直角三角形
学习目标
1 课时讲解 解直角三角形的定义
直角三角形中的边角关系
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
感悟新知
知识点 1 解直角三角形的定义
初三数学解直角三角形及其应用知识精讲 湘教版
初三数学4.3 解直角三角形及其应用知识精讲湘教版【本讲教育信息】一. 教学内容:§4.3 解直角三角形及其应用【教学目标】知识与技能:1. 掌握利用直角三角形的边角关系,求解直角三角形。
2. 会利用解直角三角形解决实际问题。
过程与方法:经历利用解直角三角形解决实际问题的过程,体验用所学的知识解决实际问题。
情感、态度与价值观:进一步积累数学活动的经验,并在学习活动中学会与人合作交流。
二. 重点、难点:1. 教学重点:(1)掌握直角三角形中的边角关系。
(2)灵活地运用三角函数关系式解直角三角形。
(3)理解坡角、坡度、仰角、俯角、方位角等意义,能根据实际问题构建直角三角形的数学模型。
2. 教学难点:运用解直角三角形的方法解决实际问题,关键是能将实际问题转化为数学问题——解直角三角形。
三. 主要内容:(一)解直角三角形1. 定义:在直角三角形中,由除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。
+=a b c()三边之间的关系:(勾股定理)1222()两锐角之间的关系:∠∠290A B o+=(3)边角之间的关系:sin AA ac ==∠的对边斜边cosAA bc ==∠的邻边斜边tan AAAab ==∠的对边∠的邻边3. 解直角三角形的四种基本类型:已知直角三角形的两个基本元素(至少有一个是边),利用以上关系就可以求出其余的未知元素,其中恰当地选用边角关系是关键。
应注意以下原则:(1)有“斜”选“弦”,无“斜”选“切”。
(2)尽量使未知元素在分子的位置上,以便利用乘法运算求未知元素。
(3)尽量使用原始数据:以减少误差的积累,也可避免由于中间数据有错而产生新的误差。
4. 几个常用概念:(1)仰角:在测量时,从下向上看,视线与水平线的夹角叫仰角。
(2)俯角:在测量时,从上向下看,视线与水平线的夹角叫俯角。
坡面的铅直高度(h )和水平长度(l )的比,叫做坡面的坡度。
记作,,通常写成的形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题赏析
例6
如图,海岛A四周20海里周围内为暗礁区,一艘货轮由 东向西航行,在B处见岛A在北偏西60˚方向,航行24海 里到C处,见岛A在北偏西30˚方向,货轮继续向西航行, 有无触礁的危险?
解
过点A作AD⊥BC于D,设AD=x
∵ ∠NBA= 60˚, ∠N1BA= 30˚, ∴ ∠ABC=30˚, ∠ACD= 60˚,
M 解(2):设点E、F是以A为圆心,150km 为半径的圆与BM的交点,由题意得: ∴CE =√ 2 – AC2 = 90 AE ∴EF = 2CE = 2 x 90 = 180 180÷12 = 15小时
A
F
C E
∴A城受到沙尘暴影响的时间为
240 30°
B
答:A城将受到这次沙尘暴影响, 影响的时间为15小时。
当堂训练二
1,在Rt△ABC中,如果各边都扩大2倍,则锐角A的正 弦值和余弦值( A ) A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。 2,在△ABC中,若 sinA= √2 , tanB=√3,则∠C= 75° 2 tan B = √3 3, 在Rt△ABC中, ∠C=90°, AC= √3, AB=2,则 2 3 4,如果α和β都是锐角,且sinα=cosβ,则α与β的关系 是( B ) A,相等 B,互余 C,互补 D,不确定。 5,已知在Rt△ABC中, ∠C=90°,sinA= 1 ,则 cosB=( A ) 2 √3 1 √2 A, B, 2 C, 2 D, √3 2
2
A,9 B,10 C,11 D
A 6
2 1
2
当堂训练一
A,10 Л B,25 Л C,12.5 Л D,100 Л
R P
5,如图,图中直角三角形的两条直角边的长分别是6和8, 则图中半圆R的面积是( C )
Q
6, 池塘里一枝荷花高出水面20厘米,一阵劲风吹来,荷 花从根部向一边倾斜,顶端与水面平齐,如图,已知荷 花被风吹动的水平距离是60厘米,求池塘中水的深度。 (80厘米)
a
解直角三角形的依据
1、三边之间的关系 a2+b2=c2(勾股定理);
锐角之间的关系
∠ A+ ∠ B= 90º
B
边角之间的关系(锐角三角函数) sinA= a tgA= b a
c
cosA= b c b ctgA= a
A
c
a
b
C
2、 在△ABC中, S△ABC = 1 absinα 2
概念反馈
在解直角三角形及应用时经常接触到的一些概念
B
A
D
C
当堂训练二
3,由于过度采伐森林和破坏植被,我国部分地区频频 遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A 城的正南方向240km的B处,以每小时12km的速度向北 偏东30°方向移动,距沙尘暴中心150km的范围为受影响 区域。 (1)A城是否受到这次沙尘暴的影响,为什么? (2)若A城受这次沙尘暴的影响,那么遭受影响的时 M 间有多长? 解(1):过A作AC⊥BM,垂足为C, 在Rt△ABC中, ∠B = 30°, x 240 = 120 ∵AC = 120 < 150 ∴A城受到沙尘暴影响 ∴AC=
即 BD² +BC² DC² = ,所以△BCD是直角三角形 1 × 3×4+1 ×5×12=36 所以S四边形ABCD= 2 2
当堂训练一
1,以下列数据为三角形的边长,则不能构成直角三角形 的一组是( D ) A,3,4,5, B,5,12,13, C,6 ,8 ,10 D,7,8,9 2,如果直角三角形的两条边长为3厘米、4厘米,则其 12厘米或(7+√7)厘米 周长是---------------------------------------------。 3,如果直角三角形的两条直角边之和为7,斜边长为5, 6 则三角形的面积是-------------。 4,如图,有一张藏宝图,根据图中的数据,起点A与 B1 宝藏B的直线距离是( B ) 4
学习小结
一,知识小结:
本节课主要复习勾股定理、锐角三角函数、 勾股定理在解题中的应用,三角函数在解三角形 中的应用。
二,方法归纳;
在涉及四边形问题时,经常把四边形进行适 当分割,划分为三角形和特殊四边形,再借助特 殊四边形的特征和直角三角形知识解决问题。
巩固练习一
1,如图,在△ABC中, ∠C=90°,点D在BC上, A 3 BD=4,AD=BC, cos∠ADC= 5 求:(1)DC的长;(2)sinB的值
例题赏析
例5
如图,在△ ABC中,AD是BC边上的高, A
若tanB=cos∠DAC,
B (1)AC与BD相等吗?说明理由; D 12 (2)若sinC= ,BC=12,求AD的长。 13 解 (2) 在Rt △ACD中,因为sinC= 12 13 设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k, 2 所以BC=18k=12,故k= 3 2 所以AD=12× =8 3 C
巩固练习一
1,课本第119页复习题第1、2、3题。
2,如图,房屋的人字架为等腰三角形,中拄BC= 4√3 米,
∠A=30度,求跨度AD的长。
B
A D
3
C
例题赏析
2 (1)计算: sin60°· cot30°+cos ²45°= 例3 60° (2)如果tanA· cot60°=1,A=_________。 (3)已知cosα<0.5,那么锐角α的取值范围是( A )
1 2 A C
240 30 °
B
AB =
1 2
当堂训练二
3,由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘 暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向 240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙 尘暴中心150km的范围为受影响区域。 (1)A城是否受到这次沙尘暴的影响,为什么? (2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?
解直角三角形
(复习课)
学习目标
1,明确本章的知识结构。 2,回顾勾股定理的证明(拼图方法),进一步理解勾 股定理。 3,进一步理解三角函数的意义,熟悉特殊角的三角函 数值。
4,进一步掌握直角三角形的解法。
5,学会运用勾股定理和三角函数解决实际问题。
知识网络
互余 两个锐角_______ 斜边的一半 斜边上的中线等于_________
当堂训练二
6、植树节,某班同学决定去坡度为1︰2的山坡上 种树,要求株距(相邻两树间的水平距离)是6m, 3√5 斜坡上相邻两树间的坡面距离为 m.
A
i=1︰2
C B
7、如图为了测量小河的宽度,在河 的岸边选择B、C两点,在对岸选择 一个目标点A,测得∠BAC=75°, ∠ACB=45°;BC=48m, 求河宽 72-24√3 米
在Rt△ABE中,AE 2=AB2-BE2 AE=√252-72= 24 在Rt△CDE中,DE 2=CD2-CE2 DE=√ 252 –202=15
所以BD=DE–BE=15–7=8 Nhomakorabea米)答:梯子的底部滑开8米
E
B
D
例题赏析
例2 解
如图,AB=3,BC=12,CD=13,AD=4,∠BAD=90 ° 求四边形ABCD的面积。 B A 连结BD, 在Rt△ABD中, BD=√3² =5 +4² 又 BD² +BC² +12² =5² =169, D DC² =169, =13² C
A
30˚
N1
N
60˚
C B
在Rt△ADC中, CD=AD•ctg∠ACD= x•ctg60˚, D
在Rt△ADB中, BD=AD•ctg30˚= x•ctg30˚, ∴ x•ctg30˚- x•ctg60˚=24∴ x=
答:货轮无触礁危险。
∵ BD-CD=BC,BC=24
24 √ =12 3 > 20 ctg30˚- ctg60˚
直角三角形 30°角所对的直角边等于 斜边的一半 _____________ 解直角三角形
a² =c² +b² 勾股定理________________
锐角三角函数 边角关系________________
勾股定理拼图
b c b a a
a c c b a b
b
c
c
a
b
a
a² =c² +b²
c
c b
(1)仰角和俯角
(2)坡度 i= h
铅 直 线 仰角
视线
l
水平线
俯角
北
tgα= i (α为坡角)
视线
h α
A
(3)方向角
西
30° 东
l
B
O 45° 南
例题赏析
例1 一架25米长的梯子斜靠在墙上,梯子的底部离
墙脚7米,如果梯子的顶部滑下4米,梯子的底 部滑开多远? A 解 如图,根据题意知 AB=25,BE=7,AC=4 C
A, 60°<α<90° C,30°< α <90°
1 (4)如果√cosA – —
B, 0°< α <60° D, 0°< α <30°
2
+ | √3 tanB –3|=0 ) B,锐角三角形 D,等边三角形。
²
那么△ABC是( D A,直角三角形 C,钝角三角形
例题赏析
如图学校里有一块三角形形状的花圃ABC,现测得 例4 ∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块 C 花圃的面积? 解 过点C作CD⊥AB于D 在Rt△ADC中, ∠A=30°, AC=40, A B D ∴CD=20, AD=AC•cos30° √ =20 3 √ 在Rt△CDB中, CD=20 , CB=25, ∴DB= CB2 – CD2 = 15
