Petri网知识点
Petri网预备知识
Petri⽹预备知识死锁产⽣原因（1）互斥：同时争夺唯⼀资源（2）占⽤且等待（3）⽆抢占（4）循环等待死锁产⽣的原因及四个必要条件产⽣死锁的原因主要是：（1）因为系统资源不⾜。
（2）进程运⾏推进的顺序不合适。
（3）资源分配不当等。
如果系统资源充⾜，进程的资源请求都能够得到满⾜，死锁出现的可能性就很低，否则就会因争夺有限的资源⽽陷⼊死锁。
其次，进程运⾏推进顺序与速度不同，也可能产⽣死锁。
产⽣死锁的四个必要条件：（1）互斥条件：⼀个资源每次只能被⼀个进程使⽤。
这个资源只能是空闲待⽤或者分配给确定的任务，不可被两个或两个以上任务同时使⽤。
（2）请求与保持条件：⼀个进程因请求资源⽽阻塞时，对已获得的资源保持不放，更导致其他进程想获得资源⽽得不到资源，更导致进程瘫痪。
（3）不剥夺条件:进程已获得的资源，在末使⽤完之前，不能强⾏剥夺。
只有当正在使⽤这个资源的任务进程结束后，此资源才能被释放，被其他任务占⽤。
（4）循环等待条件:若⼲进程之间形成⼀种头尾相接的循环等待资源关系。
这四个条件是死锁的必要条件，只要系统发⽣死锁，这些条件必然成⽴，⽽只要上述条件之⼀不满⾜，就不会发⽣死锁。
死锁的解除与预防：理解了死锁的原因，尤其是产⽣死锁的四个必要条件，就可以最⼤可能地避免、预防和解除死锁。
所以，在系统设计、进程调度等⽅⾯注意如何不让这四个必要条件成⽴，如何确定资源的合理分配算法，避免进程永久占据系统资源。
此外，也要防⽌进程在处于等待状态的情况下占⽤资源。
因此，对资源的分配要给予合理的规划。
因此，前三个条件通常是满⾜的，⽽第四个条件可因资源的请求、分配和释放等因素，随时间⽽变化。
只要发⽣死锁，这四个条件必然都满⾜。
反之，只要有⼀个条件不满⾜，系统就不会发⽣死锁。
因此想要控制系统死锁的发⽣，必须破坏第四个条件即循环等待条件。
Petri⽹建模优势对系统中的并发、资源共享、冲突、相互抑制以及⾮确定性等有简单表⽰；（1）可以使⽤⾃顶向下和⾃底向上的设计⽅法，使系统具有不同的抽象层次；（2）从Petri ⽹模型可以直接⽣成控制代码；（3）良好定义的语义能够为系统的确认提供定性和定量的分析；（4）图形界⾯可给出系统的直观视图；（5） Petri ⽹可⽤于系统设计的各个阶段，从系统建模、分析、仿真、确认、性能评价到调度、控制和监控的整个过程。
petri网入门
petri网入门最近需要学习一个大系统，其中涉及到了petri网的知识，发现这东西非常好用，在这分享给大家吧！了解一些，总会用得上的:)文章引自：学习空间===========================Petri网是对离散并行系统的数学表示。
Petri网是1960年代由C.A.佩特里发明的，适合于描述异步的、并发的计算机系统模型。
Petri网既有严格的数学表述方式，也有直观的图形表达方式。
由于Petri网能表达并发的事件，被认为是自动化理论的一种。
研究领域趋向认为Petri网是所有流程定义语言之母。
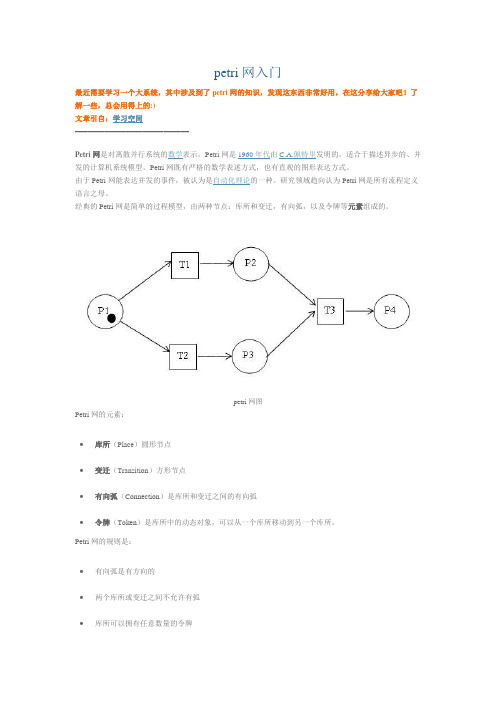
经典的Petri网是简单的过程模型，由两种节点：库所和变迁，有向弧，以及令牌等元素组成的。
petri网图Petri网的元素：•库所（Place）圆形节点•变迁（Transition）方形节点•有向弧（Connection）是库所和变迁之间的有向弧•令牌（Token）是库所中的动态对象，可以从一个库所移动到另一个库所。
Petri网的规则是：•有向弧是有方向的•两个库所或变迁之间不允许有弧•库所可以拥有任意数量的令牌行为如果一个变迁的每个输入库所（input place）都拥有令牌，该变迁即为被允许(enable)。
一个变迁被允许时，变迁将发生(fire)，输入库所(input place)的令牌被消耗，同时为输出库所(output place)产生令牌。
注意：•变迁的发生是原子的；•有两个变迁都被允许的可能，但是一次只能发生一个变迁；•如果出现一个变迁，其输入库所的个数与输出库所的个数不相等，令牌的个数将发生变化；•Petri网络是静态的；•Petri网的状态由令牌在库所的分布决定。
两个变迁争夺一个令牌的情形被称之为冲突多个弧连接两个节点的情况。
在输入库所和变迁之间的弧的个数决定了该变迁变为被允许需要的令牌的个数。
弧的个数决定了消耗/产生的令牌的个数。
第七章Petri网基础
18
§7.2.1 共享资源模型6
p active1
p active 2
t request 1
prequesting 1
trequest2 pidle
p requesting 2
t start 1
pacces sin g 1
t start 2
pacces sin g 2 pbusy
事件之间的同步距离(synchronic distance)
公平性(fairness)
4
§7.1 Petri 网发展概述5
Petri网模型的主要分析方法依赖于： 可达树(reachability tree) 关联矩阵和状态方程(incidence matrix and state equation) 不变量(invariants) 分析化简规则 Petri网的的纵向扩展： 条件/事件(C/E)网
PetriNets-owner@daimi.au.dk]] PetriNets-request@daimi.au.dk]]
[[World Wide Web URL:
http://www.daimi.au.dk/PetriNets/pnl/]]
[[Read before posting:http://www.daimi.au.dk/PetriNets/pnl/faq.html]]
9
§7.2 Petri网模型简介1
直观理解什么是Petri网，它们如何应用。 一个PN的结构元素包括： 位置(place)：描述可能的系统局部状态(条件或状 况)，例如，队列、缓冲、资源等。 变迁(transition)：描述修改系统状态的事件、动 作，例如，信息处理、发送、资源的存取等。 弧(arc)：使用两种方法规定局部状态和事件之间 的关系：引述事件能够发生的局部条件状态；由 事件所引发的局部状态的转换。
Petri网详细介绍与学习
模型改进
针对传统Petri网的不足，研究者们不断尝试对其进行改 进和优化，以提高其适用性和性能。例如，通过引入新 的元素或规则，改进Petri网的表达能力；优化Petri网的 推理算法，提高其推理速度等。
有界性、安全性与死锁
01
03
有界性
Petri网中的每个库所至多 包含有限个标记，且每个 变迁最多可以消耗和产生 有限个标记。
安全性
Petri网中不存在死锁状态 ，即对于任意一个状态， 总存在一个后继状态。
死锁
当Petri网中存在一个状态 ，从该状态无法通过任何 变迁到达其他状态时，称 该状态为死锁状态。
Petri网与其他建模方法的融合
融合方法
为了更好地描述和分析复杂系统，研究者们尝试将 Petri网与其他建模方法进行融合。例如，将Petri网与 流程图、状态图等图形化建模方法相结合，可以更直 观地描述系统的结构和行为。
融合优势
通过融合不同的建模方法，可以取长补短，提高对复 杂系统的描述和分析能力。同时，这种融合也有助于 推动不同领域之间的交叉和融合，促进多学科研究的 开展。
实例分析学习
案例分析
分析不同类型Petri网的特点和适用场景，如同步Petri 网、时间Petri网和有色Petri网等。
通过学习经典的Petri网实例，深入理解Petri网的实际 应用和建模技巧。
对比不同Petri网实例的建模效果，提高对Petri网的实 际操作能力和应用水平。
实践应用学习
Petri网模型专业知识课件
t1 t2
t3
t1 ， t2 ， t3同步能够发生变迁
同步(Synchronization)
p1
t1
t1旳激发当且仅当p1中有令牌
Petri网常见构造
合并(Merging)
t1
t2Байду номын сангаас
t3
p1
t1 ， t2 ， t3变迁后同步到达p1
紊乱(Confusion)
t1
t2
t3
制造系统库所分类
A库所—表达操作旳库所， A库所中一种 令牌表达操作正在执行 B库所—表达资源类库所，且资源数目固 定不变，如机床、机器人、传送系统等 C库所—表达资源类库所，且资源数目可 变，如托盘、夹具、零件等
在用Petri网对制造系统进行分析时， C库所 尤其主要，需要拟定此类资源数目（初始令牌 数）才不致使系统发生死锁或富裕。
Petri网图形表达
库所（place）用
表达
变迁（transition）用
表达
·
令牌（token）用 · 表达
流关系（F）用 表达
Petri网示例
Petri网
输入输出矩阵
Petri网特点
以图形方式描述系统，使复杂系统形象 化，有利于了解 能够分层建立Petri网，便于描述分布式 递阶系统 具有一套严密旳数学解析理论，能够分 析制造系统多种运营特征 不但能够描述制造系统静态特征，还能 够描述动态特征
状态元素：资源按其在系统中旳作用分类，每 一类存储一处，则该处抽象为一种相应旳状态 元素，称为S元素(state element)，资源旳状态 由相应元素旳状态表达 库所：状态元素又称库所（place），库所不但 表达一种场合而且表达在该厂所存储了一定旳 资源
第二章Petri网的基本概念及性质
Step3： If tT:M[t> Then
把M的标注改为“端点”，返回Step1
Step4： For 每个满足M[t> 的tT Do
4.1：
计算M[t>M’中的M’；
4.2： 4.3：
If 从M0 到M的有向路上存在M’’使M’’<M’ Then 找出使M’’(pj)< M’(pj)的分量j，把M’的第j个分量改为；
定义3.1. 设PN=(P,T;F, M0)为一个有界Petri网。PN的可达标识图定义为一个三元组 RG(PN)=(R(M0),E, L)，其中 E={(Mi,Mj)| Mi, Mj R(M0),tk T: Mi [ tk> Mj } L:E→T，L(Mi,Mj)= tk 当且仅当Mi [ tk> Mj 称R(M0)为顶点集，E为弧（边）集， 若L(Mi,Mj) = tk，则称tk为弧(Mi,Mj)的旁标。
p4
t2
t4
(0,1, ,0) 新
t1
t4
(1,0, ,0) 新旧 (0,0, ,1) 新
t3 (1,0, ,0) 旧新
可达标识图与可覆盖性树
定理3.1. PN是有界Petri网当且仅当 （按算法3.1构造的）CT(PN)中，每个 结点的标识向量都不含有分量。
对有界Petri网PN，按照算法3.1构造 出来的树结构称为PN的可达性树 （reachability tree），记为 RT(PN)。
t1
t3
M0 : (0,1,0)
p1
p2
p3
பைடு நூலகம்t1 t2
t3
t4
t2
t4
M1 : (1,0,0)
M2: (0,0,1)
第四部分Petri网的结构性质-121218-Basic
五、死锁与陷阱
定义4.14. 设N=(P,T;F)为一个网， P1 P。 •P1 P1• ，则称P1为网N 的一个死锁（Siphon） ；如果P1• •P1，则称P1为N的一个陷阱。
第四章 Petri网的结构性质
提纲
网的结构性质只由网的结构（基网）确定，而与网的初 始标识无关。
一、结构有界性和守恒性
二、可重复性和协调性 三、不变量 四、可重复向量 五、死锁与陷阱
一、结构有界性和守恒性
定义4.1. 设N=(P,T;F)为一个网。如果对N赋予任 意初始标识M0。网系统(N, M0)都是有界的，则称
定义4.8. 设N=(P,T;F)为一个网，|P|=m，|T|=n，A为N的关联矩阵。如果Y1 （ X1）是 网N的一个S-不变量（T-不变量），而且任意满足Y< Y1（X< X1）的m（n）维非负整 数向量Y（X）都不是网N的S-不变量（T-不变量），那么称Y1 （ X1）为网N的一个极 小S-不变量（极小T-不变量）。
三、不变量
定义4.9.设V1,V2,…,Vk和V都是非平凡的非负整数n维向量。如果存在 一组非负整数c1,c2,…,ck，使得 V= c1V1+c2V2+…+ckVk 则称向量V可以被V1,V2,…,Vk非负整系数线性表出，或称V是 V1,V2,…,Vk的非负整系数线性组合。 定理4.6. 一个网N的任意一个S-不变量（T-不变量）都是网N的极小 S-不变量（极小T-不变量）的非负整系数线性组合。
四、可重复向量
第四章Petri网结构性质
三、不变量
定义4.9.设V1,V2,…,Vk和V都是非平凡的非负整数n维向量。如果存在 一组非负整数c1,c2,…,ck，使得 V= c1V1+c2V2+…+ckVk 则称向量V可以被V1,V2,…,Vk非负整系数线性表出，或称V是 V1,V2,…,Vk的非负整系数线性组合。
定理4.6. 一个网N的任意一个S-不变量（T-不变量）都是网N的极小 S-不变量（极小T-不变量）的非负整系数线性组合。
第四章 Petri网的结构性质
提纲
网的结构性质只由网的结构（基网）确定，而与网的初 始标识无关。
一、结构有界性和守恒性 二、可重复性和协调性 三、不变量 四、可重复向量 五、死锁与陷阱
一、结构有界性和守恒性
定义4.1. 设N=(P,T;F)为一个网。如果对N赋予任 意初始标识M0。网系统(N, M0)都是有界的，则称 N为结构有界网。
M1 p 0
pP2
则对MR(M1)，都有
M p 0
pP2
五、死锁与陷阱
定理4.11. 设N=(P,T;F)为一个网，A为N的关联矩阵。 如果P1 ={pi1, pi2 ,…, pik} 为网的一个死锁（陷阱）的充分必
要条件是：A关于P1 列的列生成子阵中，每个非全零行至少包含一个“-1”（或“1”）元素。 M. D. Jeng and M. Y. Peng, “Generating minimal siphons and traps for Petri nets,” in IEEE International
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.一个经典的Petri网由四元组（库所，变迁，输入函数，输出函数）组成。
2.如果一个变迁的每个输入库所（input place）都拥有托肯，该变迁即为被允许(enable)。
一个变迁被允许时，变迁将发生(fire)，输入库所(input place)的托肯被消耗，同时为输出库所(output place)产生托肯。
3.高级模型：
为了解决经典Petri网中的问题，研究出了高级Petri网，在以下方面进行了扩展：o 令牌着色
一个令牌通常代表具有各种属性的对象，因此令牌拥有值（颜色）代表由令牌建模的对象的具体特征，如一个令牌代表一个工人（张三，28岁，经验3级）。
o 时间
为了进行分析，我们需要建模期间，延迟等，因此每一个令牌拥有一个时间戳，变迁决定生产出的令牌的延迟。
（这类Petri网模型规定每个变迁都具有有限的引发时延，其触发规则被修改为:每一个触发变迁都有一个时延过程;一个变迁一旦使能必须立即触发。
）
o 层次化
构造一个复杂性与数据流图相当的Petri网的机制。
子网是由库所，变迁和子网构成的网络。
o 时序
增加时序逻辑的定义，更好的描述行为过程
4.两个库所或变迁之间不允许有弧
5.有两个变迁都被允许的可能，但是一次只能发生一个变迁
6.Petri网络是静态的
7.Petri网的状态由托肯在库所的分布决定
8.两个变迁争夺一个托肯的情形被称之为冲突
9.多个弧连接两个节点的情况。
在输入库所和变迁之间的弧的个数决定了该变迁变为被允许需要的令牌的个数。
弧的个数决定了消耗/产生的令牌的个数
10.petri网基本概念：Petri网是一种用有向图及称为初始标识的初始状态表示的特殊的系统模型其中有向图由库所变迁以及从库所到变迁或者从变迁到库所的有向弧组成，称为Petri网结结构。
标识是一个m维数组(m为库所个数)，它的一元素对应一库所，取值为非负整数。
标识代表系统的状态。
11.不同类型的资源相应地，变迁的发生就可能不只是简单地复制和传递令牌，而是要对从输入库所取来的令牌经过加工，变成新颜色的令牌后再传递给输出库所这就是有色Petri网的两个特别之处:令牌是有颜色的，变迁的发生可以改变令牌的颜色。
12.
13.Petri网的归纳分析技术
归纳分析技术是针对Petri网的状态复杂性而提出的。
一般来说，一个规模不大的系统，可能会出现状态组合爆炸的危险，从而给分析带来困难，对此人们提出化简和分解的思想。
化简是将一个较复杂的Petri网简化成一个比较简单Petri网而又要保留一些性质不变的同态变换过程，这个过程减少了可达状态空间，通过对简单网的分析，能为理解原网性质提供充分的信息。
分解的思想即是分而治之，是将一个复杂的网系统分解成若干较为简单的网系统，分解过程也要保持一些性质不变。
这样，通过分析简单的子网系统便可以了解复杂的网系统。
14.Petri 网的扩展形式：
Petri 网在实际应用中有时会受到一些局限，人们在基本Petri 网的基础上，引入各种因素，得到各种Petri 网的扩展形式，主要有:抑制弧Petri 网模型，高级Petri 网，时间/时延Petri 网，随机Petri 网等等，下面将具有代表性的Petri 网模型介绍如下：
① 高级Petri 网模型：Petri 网面临的另一个问题是，为了某一个特别的操作建立模型从而必须建立复杂的编码。
一些学者认为，如果以某种方式来区别托肯，可使复杂编码容易实现。
目前的着色网(Colored Petri Net)和谓词变迁网(Predicate Transition Petri Net)就是这种思想的具体体现。
② 抑制弧Petri 网模型：首先对Petri 网模型的重要扩充就是附加一些新型的弧线。
早期模型的触发规则是当有一个以上的托肯驻留在每一个输入库所时，相应的变迁就可以触发，从而改变模型的状态。
抑制弧的定义则相反，当输入库所无托肯时变迁可以触发。
抑制弧的引入使Petri 网具备了零检验能力。
③ 时间/时延Petri 网：随着系统逻辑层分析的进一步深入，必须进行物理层的处理，时间是系统物理层上的一个重要参数。
建立含时间因素的系统分析模型对于实际系统来说是非常必要的。
在过去十年中，出现了两类含时间因素的基本Petri 网模型。
15.不带初始状态的Petri 网记为N = (P, T, F, W), 带有初始状态M0的Petri 网则记为(N, M0).
16.流关系F={(1t ,1p ),(2t ,2p )}
17.K, W, M 依次是N 上的容量函数，权函数和标识函数
18.)()(S T T S F ⨯⨯ ........“⨯为笛卡尔积”
笛卡尔积：笛卡尔乘积是指在数学中，两个集合X 和Y 的笛卡尓积（Cartesian product ），又称直积，表示为X × Y ，第一个对象是X 的成员而第二个对象是Y 的所有可能有序对的其中一个成员。
假设集合A={a, b}，集合B={0, 1, 2}，则两个集合的笛卡尔积为{(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}。
19.定义：称变迁t 是使能的，当且仅当变迁t 的所有输入库所都至少有1个令牌。
称变迁t 是激活的，当且仅当变迁t 是使能的且其护卫函数值为真。
20.考虑后备保护的故障模拟Petri网模型
利用主保护清除故障的过程是很简单的，但是，实际上保护装置(包括断路器和继电器)总会因为这样或者那样的原因拒动，而最终由后备保护来切除故障，现在来讨论这种情况下Petri网的构成。
根据保护动作原理，当系统中某一元件发生故障时，主保护和后备保护均检测到故障参数，由于主保护是瞬时动作，而后备保护需要一个延时才可能动作。
当主保护拒动时，经延时后故障参数仍然存在，则后备保护动作切除故障。
21.一个转移可点火，首先该转移必须允许点火，即转移使能。
一个转移使能的前提条件是该转移的每一个输入库所中被标记的托肯数至少等于该所到该转移的有向弧数。
也就是说一个转移的所有输入库所中至少包括一个托肯(假设每条有向弧的权均为1)。