精典平面几何题汇总适合初二
中考数学平面几何经典题
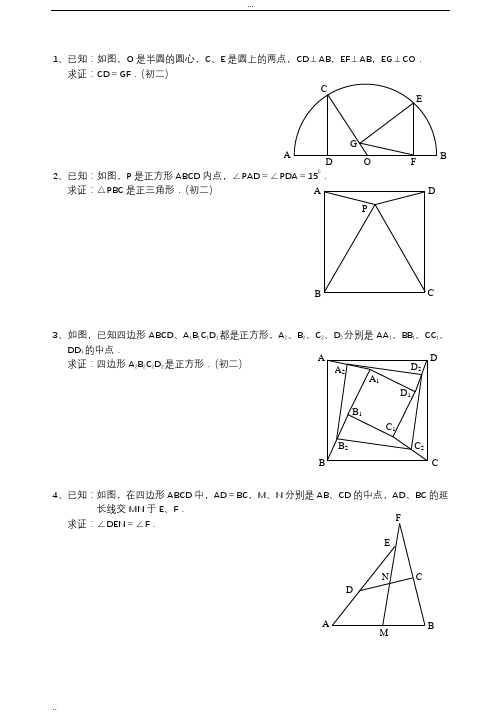
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABCP 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)D1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 200,求∠BED 的度数.1.如下图做GH ⊥AB,连接EO 。
(完整版)八年级数学几何经典题【含答案】
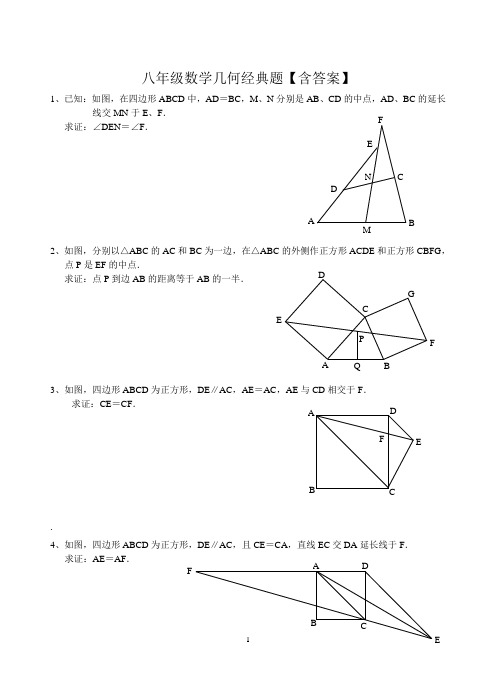
F八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF ..4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .B5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA,九年级数学【答案】1.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
八上平面几何难题集锦

八年级平面几何难题集锦1.如图,已知等边△ABC ,P 在AC 延长线上一点,以PA 为边作等边△APE,EC 延长线交BP 于M ,连接AM,求证:(1)BP=CE ; (2)试证明:EM-PM=AM.2.点C 为线段AB 上一点,△ACM, △CBN 都是等边三角形,线段AN,MC 交于点E ,BM,CN 交于点F 。
求证:(1)AN=MB.(2)将△ACM 绕点C 按逆时针方向旋转一定角度,如图②所示,其他条件不变,(1)中的结论是否依然成立? (3)AN 与BM 相交所夹锐角是否发生变化。
3.已知,如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AN AM =;(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立.BE A B AB 图①E 图②4.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作正三角形ABC 和正三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下五个结论:① AD=BE ; ② PQ ∥AE ; ③ AP=BQ ;④ DE=DP ; ⑤ ∠AOB=60° ⑥CP=CQ ⑦△CPQ 为等边三角形.⑧共有2对全等三角形 ⑨CO 平分∠AOP ⑩CO 平分∠BCD 恒成立的结论有______________(把你认为正确的序号都填上).5.已知:如图,ABC △是等边三角形,过AB 边上的点D 作DG BC ∥,交AC 于点G ,在GD 的延长线上取点E ,使DE DB =,连接AE CD ,.(1)求证:AGE DAC △≌△;(2)过点E 作EF DC ∥,交BC 于点F ,请你连接AF ,并判断AEF △是怎样的三角形,试证明你的结论.6.如图,以ABC △的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ,连结EG ,试判断ABC △与AEG △面积之间的关系,并说明理由.7.在ABC △中,2120A B B C A B C ==∠=,°,将ABC △绕点B 顺时针旋转角α(0<°α90)<°得A BC A B 111△,交AC 于点E ,11AC 分别交AC BC 、于D F 、两点.如图1,观察并猜想,在旋转过程中,线段1EA 与FC 有怎样的数量关系?并证明你的结论;ADBECF 1A1CADBECF 1A1CFABC E DO P QCGAE DB F8.如图所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .9.如图1,四边形ABCD 是正方形,M 是AB 延长线上一点。
八年级数学几何经典题【含答案】

八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.F 求证:∠DEN=∠F.ENCDABM2、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.D求证:点P到边AB的距离等于AB的一半.GCEPFAQB3、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.DAFEBC.4、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.ADFBC1E5、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.DA求证:PA=PF.FBPCE6、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.ADFPBEC 7如图,△ABC中,∠C为直角,∠A=30°,分别以AB、AC为边在△ABC的外侧作正△ABE与正△ACD,DE与AB交于F。
求证:EF=FD。
8如图,正方形ABCD中,E、F分别为AB、BC的中点,EC和DF相交于G,连接AG,求证:AG=AD。
9、已知在三角形ABC中,AD是BC边上的中线,E是AD上的一点,且BE=AC,延长BE交AC与F,求证AF=EF2,3九年级数学【答案】∠QMN=∠QNM,从而得出∠DEN=∠F。
1.AC并取其中点QQN和QM,所以可得∠QMF=∠F,∠QNM=∠DEN和EG+FH2E,C由△EGA≌△AIC,可得EG=AI,由△BFH≌△CBI,可得FH=BI。
4从而可得PQ=AI+BI 2=AB 2,从而得证3△A从而可得B ,G ,D 在一条直线上,可得△AGB ≌△CGB 。
推出AE=AG=AC=GC ,可得△AGC 为等边三角形。
0,既得∠EAC=300,从而可得∠AEC=750。
精典平面几何题汇总(适合初二)(完整资料).doc

【最新整理,下载后即可编辑】一、 等腰直角三角形题一∠ACB=90°,AC=BC,ED ⊥DF,D 为AB 中点 ①②12S △ABC =S △EDF +S △EFC ③S △EDF = 12S △ABC +S △EFC ①另知:DE ⊥AC, DF ⊥BC②E 、F 分别在AC 、BCA CB E AC BE F F②E、F分别在AC、BC题二已知∠BAC=90°,CD平分∠ACB,AC=AB,CD⊥AE,求证:CD=2(OA+OD)ABCACFDEO已知∠BAC=90°, AC=AB,D 为AB 中点, CD ⊥AE,求证:∠BDE=∠CDA换说法:求证A 到DE 的距离等于OA题四:已知∠BAC=90°, AC=AB,D 为AC 中点, CF ∥AB,求证:CF=ADA B CAD E O F已知∠ACB=90°, AC=BC,DA 平分∠BAC ,H 为AB 中点, BE ⊥AD,求证:CF=EC 。
判断:①AF=BE ,②AF=2BD ,③AF 垂直平分BE ,④AC+CF=AB ,⑤S △ACG = S △AHG ⑥AG=BD垂直角平分线题六:已知AB=AE ,BC=CA ,BC ⊥CA ,AD 平分∠BAC ,H 为AB 的中点。
求证:①△AFC ≌△BCE ②2DE=AF ,③判断△BDG 的形状并证明垂直角平分线A C E DB H G F D B H G F题七:已知∠B=45°,∠C=30°,DE⊥CA,AE=AF,GE=DF,求证:①△ADG为等腰直角三角形,②GC=2BD,③∠BAD=15°题八:已知正方形ABCD,DE=AD,DF=BD,求证:①BF平分∠DBC,②FH=2DG,③CD=CG,④S△CDG =SDHGE⑤G为FH中点ACEAB D CGEFABDEFC题九:已知∠A=90°,AB=AC ,EF ⊥AC ,D 为BC 的中点。
初中平面几何经典训练习题及答案
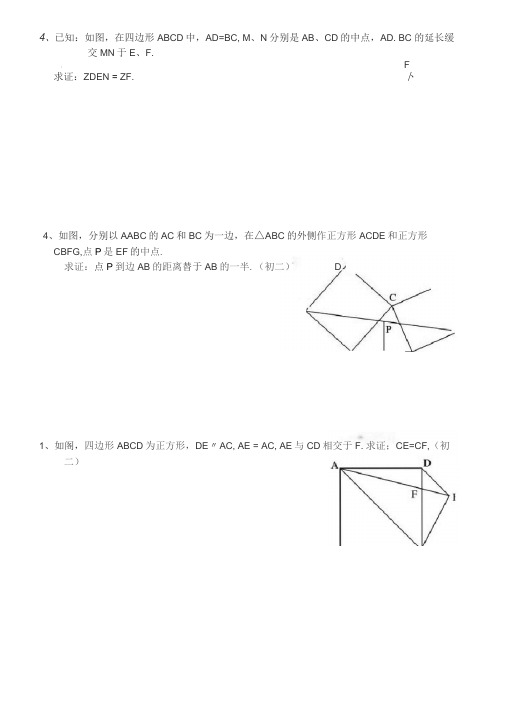
4、已知:如图,在四边形ABCD中,AD=BC, M、N分别是AB、CD的中点,AD. BC 的延长缓交MN于E、F.「 F求证:ZDEN = ZF. 卜4、如图,分别以AABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离替于AB的一半.(初二) D1、如阁,四边形ABCD为正方形,DE〃AC, AE = AC, AE与CD相交于F. 求证;CE=CF,(初二)lx已知:△回€?是正三角形,P是三角形内一点J"=3, PB=4, 求二NAPB的度数,(初二)2、设P是平行四辿形ABCD内部的一点,J1ZPBA=ZPDA.求证二/PAB=/PCB,(初二)4,平行四边形ABCD中,设E, F分别是BC, AB上的一点,AE与CF相交于Z且AE=CF.求证;ZDPA=ZI>PC.(初二)3、P为正方形AECD内的一点,并且PA=a, PB=2a, PC=3a,求正方形的边长.4.如图,ZXARC 中,NABC = NACE =耻()口、E 分别是AR, AC上的点,ZDCA=30° ZEBA = 2()^ 求/BED 的度数.A4.如下图连接AC I并取其中点Q,连接QM和QM,所以可得NQMF=/BZQNM-Z DEN fDZ QMN= ZQNM,从而得出/DEN=NR,4.过EC F点分别作AB所在直线的离EG, CL FL可得P Q=£C+F L J2由△EGA^AAIC 可得EG=AL 由&BFH空ZiCBI,可得FH=BL从而可得PQ=—=”,从而得帆1 .顺时针旋转AADE,到AAEG,连接CG由于N AEG 二N ADE=90C)+45 Z135"从而可得& G, D在一条直线上,可得A AGE丝△CGB, 推Hl AE M AGAC H GC,可得△AGC为箸边三角形』Z AGB=3O C\ 既得/EAC=30",从而可得/A EC=75r)2.连接BB作CH_LDE,可得四边形CGDH是正方形. 由AC=CE=2GC=2CH,可得/CEH=3d1 所以/CAE= Z CEA=乙AED=15(,,从而可知道NF=15,从而得出AE=AF=3.作FGJLCD, FE±BE,可以得出GFEC为正方形。
初二平面几何考试题及答案

初二平面几何考试题及答案一、选择题(每题2分,共20分)1. 下列哪个图形是轴对称图形?A. 正方形B. 圆C. 长方形D. 等边三角形答案:B2. 一个圆的半径为5cm,那么它的周长是多少?A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案:C3. 一个三角形的内角和是多少度?A. 90°B. 180°C. 360°D. 540°答案:B4. 一个平行四边形的对角线互相平分,那么这个平行四边形是:A. 矩形B. 菱形C. 梯形D. 不规则四边形答案:A5. 如果一个角是直角的补角,那么这个角的度数是多少?A. 45°B. 90°C. 135°D. 180°答案:A6. 一个正六边形的内角是多少度?A. 60°B. 90°C. 120°D. 180°答案:C7. 一个圆的面积公式是:A. πr²B. πdC. π(r+d)²D. πr²/48. 一个三角形的外角等于与它相邻的内角的:A. 补角B. 余角C. 相等D. 两倍答案:A9. 一个矩形的对角线相等,那么这个矩形是:A. 正方形B. 长方形C. 梯形D. 不规则四边形答案:A10. 一个圆的内接四边形的对角线互相垂直,那么这个四边形是:A. 矩形B. 菱形C. 梯形D. 平行四边形答案:B二、填空题(每题2分,共20分)11. 一个直角三角形的两条直角边分别为3cm和4cm,那么它的斜边长是________cm。
答案:512. 一个正五边形的每个内角是________度。
答案:10813. 如果一个三角形的三边长分别为a, b, c,且满足a² + b² = c²,那么这个三角形是________三角形。
答案:直角14. 一个圆的半径增加1cm,那么它的面积增加了________πcm²。
初二平面几何基础练习题

初二平面几何基础练习题1. 问题描述:在平面上给定一个等边三角形ABC,边长为10cm。
求三角形ABC的高和面积。
解答:设三角形ABC的高为h,由于ABC是等边三角形,所以三角形ABC也是等腰三角形。
连接AB的中点M与C,可得到三角形AMC。
由于AM与CM分别垂直于BC和AB,所以AM和CM就是三角形ABC的高。
根据勾股定理,三角形AMC的斜边AC等于三角形ABC的边长,即AC = 10cm。
由于三角形AMC是直角三角形,所以AM和CM相等,记为AM = CM = h。
根据勾股定理,有AC² = AM² + CM²,即10² = h²+ h² = 2h²。
解方程2h² = 100,可以得到h = √50 ≈ 7.07 cm。
三角形ABC的面积S可以通过底乘高的公式计算,即S = 0.5 × 10× h = 0.5 × 10 × 7.07 ≈ 35.35 cm²。
所以,三角形ABC的高为7.07 cm,面积为35.35 cm²。
2. 问题描述:在平面上给定一个矩形ABCD,已知AB = 12cm,BC = 8cm。
求矩形ABCD的对角线长度和周长。
解答:设矩形ABCD的对角线长度为d。
根据勾股定理,可以得到d² = AB² + BC² = 12² + 8² = 144 + 64 = 208。
解方程d² = 208,可以得到d = √208 ≈ 14.42 cm。
矩形ABCD的周长可以通过将四条边的长度相加得到,即周长 =AB + BC + CD + DA = 12 + 8 + 12 + 8 = 40 cm。
所以,矩形ABCD的对角线长度约为14.42 cm,周长为40 cm。
3. 问题描述:在平面上给定一个圆O,半径为6cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、等腰直角三角形题一∠ACB=90°,AC=BC,ED ⊥DF,D 为AB 中点 ①②12 S △ABC =S △EDF +S △EFC ③S △EDF = 12S △ABC +S△EFC①另知:DE ⊥AC, DF ⊥BC②E 、F 分别在AC 、BC②E 、F 分别在AC 、BCADCDF题二已知∠BAC=90°,CD 平分∠ACB ,AC=AB,CD ⊥AE,求证:CD=2(OA+OD ) 题三:已知∠BAC=90°, AC=AB,D 为AB 中点, CD ⊥AE,求证:∠BDE=∠CDA 换说法:求证A 到DE 的距离等于OA 题四:已知∠BAC=90°, AC=AB,D 为AC 中点, CF ∥AB,求证:CF=ADAABADODE D题五:已知∠ACB=90°, AC=BC,DA 平分∠BAC ,H 为AB 中点, BE ⊥AD,求证:CF=EC 。
判断:①AF=BE ,②AF=2BD ,③AF 垂直平分BE ,④AC+CF=AB ,⑤S △ACG = S △AHG ⑥AG=BD垂直角平分线 题六:已知AB=AE ,BC=CA ,BC ⊥CA ,AD 平分∠BAC ,H 为AB 的中点。
求证:①△AFC ≌△BCE ②2DE=AF ,③判断△BDG 的形状并证明垂直角平分线 题七:已知∠B=45°,∠C=30°,DE ⊥CA ,AE=AF ,GE=DF ,求证:①△ADG 为等腰直角三角形,②GC=2BD ,③∠BAD=15°FAC EDBHGFAC EDBHGF题八:已知正方形ABCD ,DE=AD ,DF=BD ,求证:①BF 平分∠DBC ,②FH=2DG ,③CD=CG , ④S △CDG =S DHGE ⑤G 为FH 中点 题九:已知∠A=90°,AB=AC ,EF ⊥AC ,D 为BC 的中点。
求证:① CF=AG ,②△DGF 为等腰直角三角形 题十:已知∠ACB=90°,AC=BC ,PA ⊥AB ,E 为AC 的中点,∠ACF=∠CBE ,CG 平分∠ACB 。
AABDCGEFAB DEFGH CGF求证:①AP=CG ,②CF=2PE ,③CD ⊥PB题十一:已知∠BAC=90°,AB=AC ,BE 平分∠ABC , D 为BC 的中点,M 为EF 中点。
求证:①DF=DN ,②AE=CN ,③△DMN 为等腰三角形,④∠BMD 为45°题十二:已知∠BAC=90°, AC=AB, ∠ABP=ACP , AQ ∥PC,求证:①AP 平分∠BAC ,②若BQ=PB+PA ,M 在BC 上,△BMP 为等腰三角形,求∠BMP 的度数CABAPFGDE ABDNF M EC二、等边三角形题一:已知△ABC 和△BDE 为等边三角形。
①图E 在AB 上,求证:∠AMC 为60°,②图E 在△ABC 内,试说明AM ,BM ,CM 之间的关系。
③图E 在△ABC 外,直接写出AM ,BM ,CM 之间的关系②图 ③图 题二:B已知△ABC 为等边三角形,BE=AF ,EG ⊥BF ,求证:①∠BCE=∠ABF ,②PE=2PG 题三:已知△ABC 和△BDEAMC题四:已知△ABC 为等边三角形,DE ⊥AB ,∠APE=60°,求证:BD=2CD以上为题库 题五:已知如图,△ABC 3,PB =4,PC =5.?求:∠APB 的度数.AM C旋转60度等边三角形CEF 与菱形ABCD 边长相等.??????????求证:(1)∠AEF=∠AFE????(2)角B 的度数三、30题一:已知∠A=90°, ∠ABC=60°, DB ⊥BC , ED ⊥EB, HD ⊥AB,BE 平分∠ABC ,F 为CD中点,求证:HF=EF ①30度直角三角形 题二:已知∠A=90°, ∠ABC=60°, DB ⊥BC , ED ⊥EB, HD ⊥AB,BE 平分∠ABC ,F 为CDB PD中点,判断AEF 形状,并说明理由。
②30度直角三角形 中线及中位线三、题一:∠O=ɑ, OA 1=OB 1, A 2B 1=B 1B 2,A 3B 2=B 2B 3,。
,∠A 2B 1B 2=b 1, ∠A 3B 2B 3=b 2, ∠A n+1B n B n+1=b n ,求b 1和b n 题二:BE 平分∠ABC ,AB=BE ,BD=BC ,EF ⊥AB ,求证:①△ABD ≌△EBC ,②BA+BC=2BF 题三:S △ABC =12,AB=AC ,BC=3,D 为BC 中点,EF 垂直平分AC ,P 为EF 上动点。
△PCD 周长最小值AOA 1 A 2B 1A 3B 2A 4B 3ɑAF EBC DCED题四:AE=AC ,∠1=∠2=∠3,求证:△BAC ≌△DAE 题五:将A 1沿DE 对折,∠1+∠2=100°,求∠A 1度数 题六:长方形ABCD ,AE=AM ,AF=AD ,则EF 与DM 有何关系?注意垂直题七:D 为BC 的中点,BG ∥AC ,DE ⊥GF ,求证:①BG=GF ,②BE+CF >EF 题八ABPFBA EDC F 1 23 1 A 1 E BCA2D DCF∠BAE=∠BCE=∠ACD=90,BC=CE ,求证:△ABC ≌△DEC 题九:∠BAC=90°,BE 平分∠ABC ,AG 平分∠DAC ,AD ⊥BC 。
结论:①∠BAD=∠C ,②AE=AF ,③∠EBC=∠C ,④EF=FG 。
其中正确的有 ③④在∠C=30°时成立,请证明 题十:∠A=105°,MN 垂直平分AE ,AB=CE ,求∠B 度数 题十一: P 为∠AOB 是定点,当△PMN 周长最小时,∠MPO=50°,求∠AOB 度数 题十二:BC=AC ,DB=DE, ∠BDE+∠ACB=180°,F 为AE 的中点。
求证:①CF ⊥DF ②∠ACB=90°,其他不变,证:CF ⊥DF 且CF=DF ,③∠ACB=60°其他不变,证:CF ⊥DF 且CD=2DF ① ②AB D G CEN F ABF CE MNOMPABNAB DEFCBAC FD③ 题十二:四边形ABCD ,∠EAF 的度数题十三:E 为ACD 到AC 距离六、与坐标相关的几何题 题一:A (2,0),B (0,-10),C 为x 轴正半轴上,OC=5OA ,求:①S △ABC ,②延长BA ,使PA=AB ,作PM ⊥OC 于M ,求P 坐标,③D 为第三象限内,BE ⊥CD 于E ,OF ⊥OD 交BE 延长线于F ①②题EEB C CB D EA③题二:K(2,2),l1⊥l2,①若AC=BD,证△AKC≌△DKB,②求OB+OC的值及S△ACK-S△OCD,③J为AK上的动点,不与A、K重合,作AE⊥DJ,求∠DEK度数l题三:B (0,8),A (-8,0),C (2,0)①AH ⊥BC ,求证:△AOP ≌△BOC ,且P 坐标;②在①条件下,连接OH ,证:∠AHO=∠CHO,③D 为AB 的中点,M 为y 负半轴上运动,DN ⊥MD 于D ,S △BDM -S △AND 是否变化,不变求值,变则变化范围。
①② ③题一:AC于点F.? 题二:B'CB=30度,求AE .OC ADxJEBCD题三:在等腰直角三角形ABC且PB=PD ,DE 垂直AC ,垂足为E 。
?AC=3a ,AP=x ,四边形PBDE 的面积为y ,求y 与x 之间的函数关系式。
题四:已知△ABC ,AD 是BC 边上的中线,分别以AB 边、AC 边为直角边向形外作等腰直角三角形。
求证:EF=2AD 题五:如图,等边三角形ABC 的边长为2,点P 和点Q 分别是从A 和C 两点同时出发,做匀速运动,且他们的速度相同,点P 沿射线AB 运动,Q 点沿点C 在BC 延长线上运动。
设PQ 与直线AC 相交于点D ,作PE ⊥AC 于点E ,当P 和Q 运动时,线段DE 的长度是否改变?证明你的结论。
B C ABOPDECEBAFCDEPDQ。
