达西渗透实验指导书
实验

• 1、实验目的 • 通过达西稳定流的渗流实验,加深对 达西定律的理解。
• 2、实验原理:
• 达西定律:
H1 H 2 Q KA KAJ L
QL K A( H1 H 2 )
式中:Q为渗透流量;A为渗流断面面积;H1,H2为1和 2断面上的测压水头值;L为1和2两断面间的距离;J为水 力坡度,圆筒中渗流属于均匀介质一维流动,渗流段内 各点的水力坡度均相等;K为比例系数,称为砂土的渗透 系数(也称水力传导系数)。
• 根据达西定律
式中:H(t)是随时间变化的水头差;l为砂柱的长度;A为砂柱的横断 面积;Q(t)是随时间变化的流量。 在dt时段内,通过砂柱断面的体积为:
根据水均衡原理,通过砂柱断面的水体积为 式中负号表示随着通过砂柱断面水体积(V)的增加,水头(H)值 在减小。由以上两个式子得到
水头H与时间呈半对数关系
• 3、实验装置
QL K A( H1 H 2 )
• 4、实验步骤:
QL K A( H1 H 2 )
ቤተ መጻሕፍቲ ባይዱ
• ①熟悉实验仪器,做好实验分工。插上电源,打开开关。 注意:刚开始将开关不要开到最大,防止水柱内水溢出。 • ②待水柱中液面稳定后,记录各个水柱中液面刻度H1,H2,H3。 • ③将烧杯放在左侧排水管处,接一定体积V的水,同时记录接水 时间t。 流量Q=V/t • ④用直尺量出过水断面直径a,计算出过水断面的面积A=π(a/2)2 。 • ⑤根据达西定律计算出渗透系数K值。
注:根据另外两组合中水柱中的测压水头值计算出另一个渗透系数K, 以此来验证前一组实验的准确性。
二、不稳定流渗流实验
• 1、实验目的 • 通过不稳定流条件下的渗流实验,加深对 达西定律的理解,从而认识到达西定律既 适用于稳定流条件也适用于不稳定流条件。 稳定流条件也适用于不稳定流条件。
实验二 达西实验

实验二 达西实验[实验目的]通过实验达到认识达西公式中的各项因素的关系。
[实验方法]利用渗透仪测量渗透系数K 。
[实验器材]渗透仪,秒表,量筒,钢尺,台秤,河砂等。
[实验步骤]实验步骤分两部分进行。
第一部分:装填试样,做测前准备。
1. 称取砂样4kg 。
2. 用钢直尺测量渗透仪的内径计算截面积(即过水断面积)W ,筒口至筒底的高度h 1。
3. 将上水管5与渗水口1连接,使水从筒的底部进入筒内,直到水面上升至底部的隔板。
4. 将砂子从筒的上部填入,每次填入200g 左右。
同时将上水管的流量调小,避免水流过大将砂子冲起。
应该使水从砂子的下面慢慢浸润上来,排除砂子中的气体。
直到砂样的顶部距溢流口1cm 高度即可停止填砂,用工具修平砂面。
将剩余的砂子称重算出加入试样的重量。
5. 将管5与管1断开,把渗水管1提高至筒口上方,并用滴定管架固定住。
6. 将管5引至筒口上面,使水直接注入渗透仪内的砂面上,并调整水量,保持液面至溢流口一平,直到测压管3、4的水头慢慢升起与筒内液面一平。
如果测压管的水头不能与筒内的水面一平,说明测压管内可能不通畅,需要排除故障,直至达到要求。
第二部分:测量渗水量1. 将管1的出水口移至渗透仪的32高度。
使水渗出,同时调整管5流量,保持筒内液面稳定在溢流口水平高度,避免由于渗水增大入水减少,使得筒内的水头不稳定,影响实验结果的正确。
2. 观察一段时间,直到测压管的水头稳定为止。
测量筒口至砂面的高度h 2,记录下测压管水头H 1、H 2。
3. 用量筒从管1口处测量渗水量Q ,同时用秒表计时间T 。
重复三次。
4. 将管1口移至渗透仪的31高度处,重复1~3步骤。
将实验的数据记录于下表。
5. 将管1口移至高于渗透仪的上口位置。
用木锤轻敲渗透仪的筒壁,使渗透仪内的砂面下沉1cm 左右。
重复实验步骤1~4。
6. 再一次用木锤敲击筒壁,使试样进一步下沉,重复实验步骤1~4。
每次敲击使得试样体积发生改变,随之空隙度发生变化,得出至少三组关于空隙度和渗透系数的数据。
不同填料的渗透系数测定实验——达西定律
不同填料的渗透系数测定实验——达西定律一、实验意义通过描绘流速与水头差的函数关系图,来确定渗透流量与水头损失的关系,从而来验证达西定律。
以及通过平行实验和对比实验,对数据进行比较处理,从而可知那些数据受到粒径的影响。
二、实验目的1.了解达西实验装置,通过稳定流条件下的渗流实验,测定不同粒径填料的渗透系数k 值。
2.加深理解渗流速度、水力梯度、渗透系数之间的关系,并验证达西定律。
二、实验仪器1.达西实验装置(自行设计),分别装有不同粒径的均质试样:①砂体(粒径<0.5mm ,0.7~1mm );②煤块(粒径5~10mm );③砖块(粒径5~10mm )。
2.秒表、量筒、直尺、温度计、电子称等。
三、实验原理室内渗透系数测定是根据达西关于多孔介质中地下水的线性渗透定律而设计的。
由达西定律,在常水头条件下,水流在单位时间内透过岩石空隙的流量(Q )与岩石的断面面积(ω)、水力坡度(I )成正比:测定不同试样的渗透系数。
H Q K K I Lωω∆==式中:Q ——渗透流量(cm 3); ω——过水断面面积(cm 2);∆H ——上下游过水断面的水头差(cm );L ——渗透途径(cm );I ——水力梯度。
由上式可推知,QV KIIω==,亦即,渗透系数在数值上等于水力坡度为1时,透过某单位过水断面的渗流量(亦即渗流速度)。
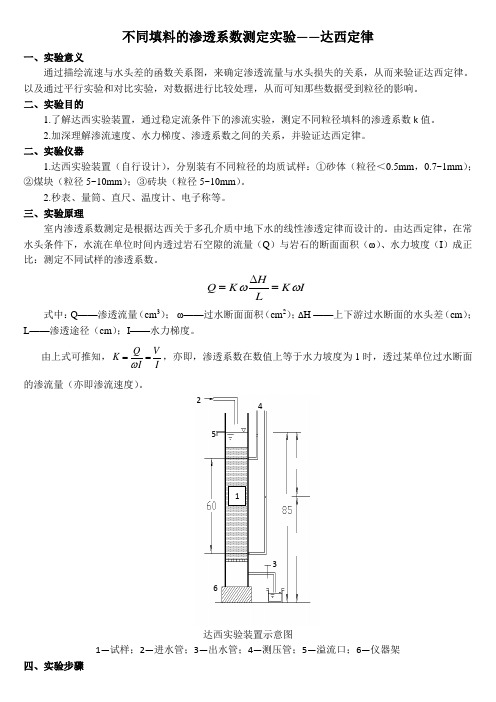
达西实验装置示意图1—试样;2—进水管;3—出水管;4—测压管;5—溢流口;6—仪器架四、实验步骤1234651.测量仪器的几何参数。
分别测量过水断面面积( ω )、测压管a 、b 的间距或渗透途径(L );记入(表1)。
2.调试仪器。
打开进水管,将水引入实验筒内,底部控制阀T 打开,此时要保持溢水管有少量水溢出,这时可以进行第一次实验。
3.测定水头待a 、b 两个测压管的水位稳定后,读出各测压管的水头值,记入(表1)中。
4.测定流量在进行步骤3的同时,利用秒表和量筒测量t 时间内水管流出的水体积,及时计算流量Q 。
达西渗流实验

达西渗流实验设计人:汪卓红程新颖班级:土木结构0101指导老师:毛根海教授日期:2003年12月6日浙江大学建筑工程学院水利实验室达西渗流实验一实验目的1 测定均质砂的渗透系数;2 测定渗过砂体的渗流量与水头损失的关系,验证达西定律;3 通过常水头线性渗流实验,进一步了解和掌握达西定律。
二实验装置1---水泵及供水箱 2---常水头供水箱 3---可水平移动的标尺4---测压管 5---塑料平板 6---橡皮管7---装砂圆筒 8---滤网 9---水桶10---进水阀门 11---出水阀门 12---溢流管嘴本实验装置是采用半自动循环系统供水,设计简洁,但非常实用,实验结果可靠。
三实验原理液体在孔隙介质中流动时,由于粘滞性作用将产生能量损失。
达西(Henri Darcy)在1852——1855年间通过实验,总结出渗流能量损失与渗流速度成一次方的线性规律,后人称为达西定律。
由于渗流流速很小,故流速水头可以忽略不计。
因此总水头H可用测管水头h来表示,水头损失hw可用测管水头差来表示,即H=h=z+p/γ, hw=h1-h2=Δh则水力坡度J可用测管水头坡度来表示:J=hw/L=(h1-h2)/L=Δh/L式中:L为两个测量管孔之间距离;h1与h2为两个侧压孔的测管水头。
达西通过大量实验,得到圆筒断面积A和水力坡度J成正比,并和土壤的透水性能有关,所建立基本关系式如下:Q=KAJv=Q/A=kJ式中v为渗流简化模型的断面平均流速;系数K为反映孔隙介质透水性能的综合系数,称为渗透系数。
实验中的渗流区为一圆柱形的均质砂体,属于均匀渗流,(本装置宜适用于中粗砂,细砂不是非常适合,因为常水头渗透实验本来就宜适用于粗土粒渗透系数的测定)可以认为各点的流动状态是相同的,任一点的渗流流速u等于断面平均渗流流速,因此达西定律也可以表示为:u=KJ上式表明,渗流的水力坡度,即单位距离上的水头损失与渗流流速的一次方成正比,因此称为渗流线性定律。
达西渗流实验报告

达西渗流实验报告引言达西渗流实验是一种通过测量孔隙介质中流体流动的实验,以研究孔隙介质的渗透性、渗透率等物理特性的方法。
本实验通过使用达西渗流仪对不同孔隙介质进行实验,研究不同孔隙率、不同渗透率条件下渗流的规律,为孔隙介质的研究提供一定的参考。
实验原理达西渗流实验是利用达西渗流仪对孔隙介质中流体流动进行测量的实验方法。
达西渗流仪包括一个圆筒形容器和一个注射器,通过注射器向圆筒形容器内注入一定压力的流体,使流体在孔隙介质中流动。
通过对流体流动的速度、压力等参数进行测量,可以得到孔隙介质的渗透性、渗透率等物理特性。
实验步骤1.准备工作(1)清洗达西渗流仪,将其内部和外部彻底清洗干净,以避免实验误差。
(2)准备不同孔隙率、不同渗透率的样品,将样品分别放入达西渗流仪容器中。
2.实验操作(1)将注射器插入达西渗流仪顶部,注入一定压力的流体,使其流经孔隙介质。
(2)测量流体流动的速度、压力等参数,记录实验数据。
3.实验结果分析(1)根据测量数据,计算孔隙介质的渗透性、渗透率等参数。
(2)分析不同孔隙率、不同渗透率条件下的流体流动规律和物理特性。
实验结果通过实验测量,我们得到了不同孔隙率、不同渗透率条件下的流体流动速度、压力等参数,计算出了孔隙介质的渗透性、渗透率等物理参数。
我们发现,不同孔隙率、不同渗透率条件下流体流动规律具有一定的差异,渗透率越大,流体流动速度越快,渗透性也越好。
此外,我们还发现,渗透率和孔隙率之间存在一定的关系,随着孔隙率的增加,渗透率也会增加。
结论通过达西渗流实验,我们得出了不同孔隙率、不同渗透率条件下的渗透性、渗透率等物理参数,研究了孔隙介质的渗透性、渗透率等物理特性。
本实验结果表明,渗透率和孔隙率之间存在一定的关系,随着孔隙率的增加,渗透率也会增加,同时渗透率越大,流体流动速度越快,渗透性也越好。
本实验结果对于孔隙介质的研究和应用具有一定的参考价值。
饱和渗透仪使用说明书汇总

饱和渗透实验指导书一、Darcy 定律水流状态可分为层流和紊流两种。
渗流在孔隙中的流线不产生旋涡,相互之间保持平行状态的水流称为层流(图1a ),低流速的地下水流表现为层流。
地下水的紊流状态只出现在高流速的场合,流线之间相互掺混(图1b )。
地下水流是层流还是紊流主要取决于流Lh称为水力坡降,常用 表示,则 Lh h L h i 21-==故 i ∞υ 于是,达西得到以下的实验式Ki =υ (厘米/秒或米/日) (1) 式中 K ——土的渗透系数(厘米/秒、米/日),即单位水力坡降时的υ。
通过截面积为A 的土体的渗流量Q 为度。
二、系数的范围及影响因素从式(2)可知,渗透系数表示水力坡降为1时的渗透速度,故具有速度单位,例如(厘米/秒)。
渗透系数与土的种类和性质等有关,它是土的渗透性指标。
表1列出几种土的渗透性系数的范围,可供参考。
影响渗透系数的因素很多,而且对于不同种类的土,影响的因素和程度又各不相同。
对于砾石土或砂土来说,颗粒级配对渗透系数影响最大,因为颗粒级配在很大程度上决定着土中的孔隙尺寸、形状及孔隙比等特征。
颗粒愈粗、愈均匀、愈浑圆时,土的渗透系数就愈大。
粘性土的渗透系数在很大程度上决定于矿物质成分及粘粒的含量。
粘土矿物中,以蒙脱土的亲水性最高,膨胀性最大,故含蒙脱土较多的土,其渗透系数较小。
颗粒越细,含粘粒越多的土,结合水的含水量也越高,其渗透性也越小。
渗透系数还与水温有关,因为水与土的渗透速度与水的动力粘滞系数成反比,渗透系数也就与动力粘滞系数成反比,而动力粘滞系数又决定于水温,所以,同一种土在不同温度下,将有不同的渗透系数值。
一般的,考虑到地下渗流的水温为10℃左右,故采用水温10℃时的渗透系数作为标准值,以便对取得的试验资料进行比较。
计算时必须把在某一温度T ℃时测定的渗透系数T K 换算为10℃时的渗透系数10K ,即1010μμTTK K = (3) 或近似地写成: TK K T03.074.010+=(4)式中T μ,10μ分别为T ℃和10℃时水的动力粘滞系数,标准温度各国均不一致,有10℃ ,15℃ ,20℃几种。
达西渗透实验指导书

达西渗透实验1实验目的(1) 测定均质沙的渗透系数k 值;(2) 测定通过沙体的渗透流量与水头损失的关系,验证达西定律。
(3) 通过试验,确定水流通过沙体的雷诺数,判别达西定律的适用范围。
2.实验设备与仪器实验设备由活动盛水容器、溢流板、进水管、滤板、盛沙桶、溢流管和测压管组成。
测量仪器为量筒、秒表、温度计。
3.实验原理液体在空隙介质中流动时,由于液体具有粘性,在液体流动中会引起水头损失1856年法国工程师H.Darcg 在装满沙的圆筒中进行实验。
因为渗流流速极为微小,所以流速水头可以忽略不计。
因此总水头H 可以用测压管水头h 来表示。
水头损失h w 可以用测压管水头差来表示,即γ/p Z h H +== (1) 21-h h h w = (2) 水力坡度可用测压管水头坡度来表示,即 Lh h L h J w 21-==达西分析了大量的实验资料表明,渗流量Q 与圆筒断面面积A 及水头损失h w 成正比,与断面间距L 成反比,并和土壤的透水性有关,达西得到了如下基本关系式L h h kAkAJ Q 21-== (3) Lh h k kJ A Qv 21-=== (4))/(AJ Q k = (5) 式中,v 为渗流的断面平均流速;γ/111p Z h +=,γ/222p Z h +=, k 为反映孔隙介质透水性能的一个综合系数,即渗透系数。
式(3)~(5)所表示的关系称为达西定律,它是渗流的基本定律。
由式(4)可以看出,渗透速度V 与水力坡度J 成线性关系,所以达西定律又称为线性渗流定律。
渗透系数k 是反映土壤透水性的一个综合指标,其大小主要取决于土壤颗粒的形状、大小、均匀程度以及地质构造等孔隙介质的特性,同时也和流体的物性如粘滞性和重度等有关。
因此k 值将随孔隙介质的不同而不同;对于同一介质,也因流体的不同而有差别;即使同一流体,当温度变化时重度和粘滞系数也有所变化,因而k 值也有所变化。
4渗流流态的判别地下水的运动也存在层流和紊流两种流态。
渗透探伤实验指导书及实验报告

渗透探伤实验指导书及实验报告一、实验目的:学会利用渗透探伤实验检测焊接等工件的表面或近表面的裂纹、气孔等缺陷。
更重要的是要同学们熟练的掌握并学会运用无损检测技术。
二、实验内容:利用带有荧光染料(荧光法)或红色染料(着色法)渗透剂的渗透作用,显现缺陷痕迹的无损检验法。
三、实验原理:在被检测工件表面涂覆某些渗透力较强的渗透液,在毛细作用下渗透液被渗入到工件表面开口的缺陷中,然后去除工件表面上多余的渗透液(保留渗透到表面缺陷中的渗透液),再在工件表面上涂上一层显象剂,缺陷中的渗透液在毛细作用下重新被吸到工件的表面,从而形成缺陷的痕迹。
根据在黑光(荧光渗透液)或白光(着色渗透液)下观察到的缺陷显示痕迹,作出缺陷的评定。
四、实验方法:渗透探伤的步骤:预处理(干燥,去除铁锈、氧化皮、油渍、污渍等)、渗透、中间清洗、干燥、显象、观察、质量评定。
五、实验步骤:1、预处理在渗透探伤前,应对受检表面及附近30㎜范围内进行清理,不得有污垢、锈蚀、焊渣、氧化皮等。
当受检表面妨碍显示时,应打磨或抛光处理。
在喷、涂渗透剂之前,需清洗受检表面,如用丙酮干擦,再用清洗剂将受检表面洗净,然后烘干或晾干。
2、渗透用浸浴、刷涂或喷涂等方法将渗透剂施加于受检表面。
采用喷涂法时,喷嘴距受检表面宜为20~30㎜,渗透剂必须湿润全部受检表面,并保证足够的渗透时间(一般为15~30min)。
若对细小的缺陷进行探测,可将工件预热到40~50℃然后进行渗透。
3、乳化当使用后乳化型渗透剂时,应在渗透后清洗前用浸浴、刷涂或喷涂方法将乳化剂施加于受检表面。
乳化剂的停留时间可根据受检表面的粗糙度及缺陷程度确定,一般为1~5min,然后用清水洗净。
4、清洗施加的渗透剂达到规定的渗透时间后,可用布将表面多余的渗透剂除去,然后用清洗剂清洗,但需注意不要把缺陷里面的渗透剂洗掉。
若采用水清洗渗透剂时,可用水喷法。
水喷法的水管压力为0.2Mpa,水温不超过43℃,当采用荧光渗透剂时,对不宜在设备中洗涤的大型零件,可用带软管的管子喷洗,且应由上往下进行,以避免留下一层难以去除的荧光薄膜。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
达西渗透实验
1实验目的
(1) 测定均质沙的渗透系数k 值;
(2) 测定通过沙体的渗透流量与水头损失的关系,验证达西定律。
(3) 通过试验,确定水流通过沙体的雷诺数,判别达西定律的适用范围。
2.实验设备与仪器
实验设备由活动盛水容器、溢流板、进水管、滤板、盛沙桶、溢流管和测压管组成。
测量仪器为量筒、秒表、温度计。
3.实验原理
液体在空隙介质中流动时,由于液体具有粘性,在液体流动中会引起水头损失
1856年法国工程师H.Darcg 在装满沙的圆筒中进行实验。
因为渗流流速极为微小,所以流速水头可以忽略不计。
因此总水头H 可以用测压管水头h 来表示。
水头损失h w 可以用测压管水头差来表示,即
γ/p Z h H +== (1) 21-h h h w = (2) 水力坡度可用测压管水头坡度来表示,即 L
h h L h J w 2
1-==
达西分析了大量的实验资料表明,渗流量Q 与圆筒断面面积A 及水头损失h w 成正
比,与断面间距L 成反比,并和土壤的透水性有关,达西得到了如下基本关系式
L h h kA
kAJ Q 2
1-== (3) L
h h k kJ A Q
v 21-=== (4)
)/(AJ Q k = (5) 式中,v 为渗流的断面平均流速;γ/111p Z h +=,γ/222p Z h +=, k 为反映孔隙介质透水性能的一个综合系数,即渗透系数。
式(3)~(5)所表示的关系称为达西定律,它是渗流的基本定律。
由式(4)可以看出,渗透速度V 与水力坡度J 成线性关系,所以达西定律又称为线性渗流定律。
渗透系数k 是反映土壤透水性的一个综合指标,其大小主要取决于土壤颗粒的形状、大小、均匀程度以及地质构造等孔隙介质的特性,同时也和流体的物性如粘滞性和重度等有关。
因此k 值将随孔隙介质的不同而不同;对于同一介质,也因流体的不同而有差别;即使同一流体,当温度变化时重度和粘滞系数也有所变化,因而k 值也有所变
化。
4渗流流态的判别
地下水的运动也存在层流和紊流两种流态。
判别渗流流态的方法很多,但常用的还是用雷诺数(Reynolds )来判别,最常用的公式为
γ
d
R e μ=
(6) ν=n μ (7)
式中,d 为代表颗粒的“有效”直径,有的取含水层颗粒的平均粒径,有的取d 10,d 10为直径比它小的颗粒占全部土重的10%时的土壤粒径;γ为水的运动粘滞系数。
n 为孔隙率。
如果求得的雷诺数小于临界雷诺数,则渗流运动处于层流状态;若大于临界雷诺数则为紊流状态。
对于渗流,用实验方法求临界雷诺数比较困难,不同作者的结果也不尽相同,有的作者求得临界雷诺数为150~300,有的求得该值为60~150,有的认为雷诺数的上限值是100,但巴甫洛夫求得的临界雷诺数为7~9。
为安全起见,一般可按R e =1.0作为渗流线性定律适用范围的上限值。
5.实验方法和步骤
(1)记录已知数据,如盛沙圆筒的直径D 、测压孔间距L 、沙样的粒径d 或d 10、土壤孔隙率n 等。
(2)将盛水盒放在适当位置,打开水泵,使盛水盒盛满水,并保持溢流状态。
(3)打开通往盛沙圆桶的阀门,使水流通过盛沙桶,并保持盛沙桶上部的溢水管有少量水溢出,待水流稳定后用测压管测量两测压管的压差,用量杯测量溢水管的流量。
用温度计测量水温。
(4)调节通往盛沙圆桶的阀门,改变流量,重复以上实验步骤N 次。
6.实验中注意的事项
(1)当渗流量为零时,两测压管水面应保持水平,如不水平,可能是测压管中有空气或测压管漏水,应排除空气或排除漏水后再实验。
(2)实验时流量不能过大,流量过大可能会使沙土浮动,也可能使雷诺数较大而超出达西实验的范围。
(3)实验时要始终保持盛水容器中的溢流板上有水流溢出,以保证水头为恒定流。
7.数据处理和结果分析
实验设备名称 仪器编号 同组学生姓名 已知数据: 盛沙圆通直径D = cm ;面积A = cm 2 ; 测压管距离L = cm
水温 T = ° 粘滞系数ν= cm 2/s ; 孔隙率n= 。
1.实验数据及计算成果
2.成果分析
(1)γ/111p Z h +=,γ/222p Z h +=,21-Δh h h =,=Q 体积/时间,A Q v /=,
L h h J /)-(21=,e R 用式(5)或式(6)计算。
注意计量单位。
(2)渗透系数k 用式(5)计算。
(3)点绘J v ~的关系曲线,其斜率即为渗透系数k 。
(4)求雷诺数,判断渗流是否符合达西渗透定律。
思考题
1.如何通过实验判别达西定律的适用范围。
2.达西定律适用的雷诺数范围是多少。
3.为什么说达西定律为线性定律。
