科学计数法 (1)
科学计数法(1)
〔难点突破〕
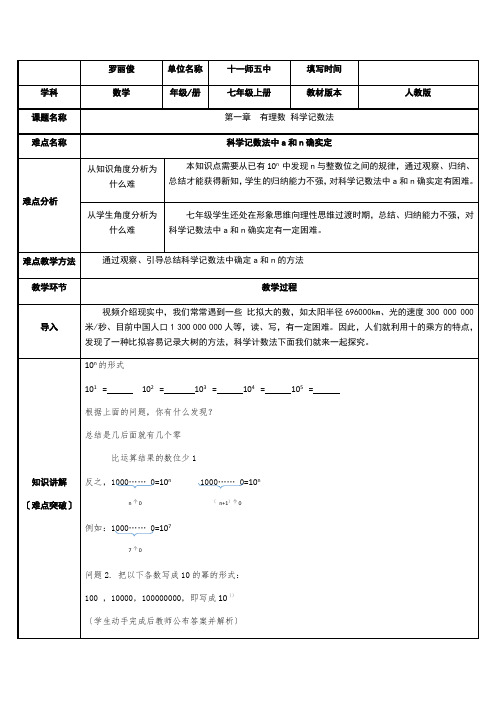
10n的形式
101=102=103=104=105=
根据上面的问题,你有什么发现?
总结是几后面就有几个零
比运算结果的数位少1
反之,1000……0=10n1000……0=10n
n个0〔n+1〕个0
例如:1000……0=107
7个0
问题2.把以下各数写成10的幂的形式:
100,10000,100000000,即写成10〔〕
又为了能够准确、快速确定n的值,引导学生发现n与小数点移动的位数有关,即n=整数位-1
××108
像这样,把一个大于10的数表示成a×10n的形式,〔1≤a<10,即n为正整数〕,这样的记数方法叫做科学记数法。
强调:1. a×10n中1≤a<10.
1.n =原数整数数位-1
对于小于-10的数也可以用科学记数法表示.
罗丽俊
单位名称
十一师五中
填写时间
学科
数学
年级/册
七年级上册
教材版本
人教版
课题名称
第一章 有理数 科学记数法
难点名称
科学记数法中a和n确实定
难点分析
从知识角度分析为什么难
本知识点需要从已有10n中发现n与整数位之间的规律,通过观察、归纳、总结才能获得新知,学生的归纳能力不强,对科学记数法中a和n确实定有困难。
小结
本节课我们把不易读、写的大数用科学记数法这一简洁的方法来表示,到达了化繁为简的目的,我们一起来回忆本节课所学内容:
科学记数法的定义:
科学记数法的形式:
科学记数法的要求:
通过本节课,让我们懂得一件复杂的事情,想要方便、快捷地表示出来,就需要我们认真地观察事物的特点,找出一定的规律,到达化繁为简的目的.
2017届中考数学冲刺复习第1章有理数06科学计数法、近似数

科学计数法 近似数一、 概念1、科学计数法把一个绝对值大于10的数记成10(110,)⨯≤<∈n a a n Z 的 形式,这种记数法叫做科学记数法.2、近似数与有效数字a 、只要采用和精确值近似的数来代替精确值去计算,就能使问题 令人满意地解决,这个和精确值近似的数值就叫这个精确值的近 似数。
b 、一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位. 例如、如果结果只取整数,那么按四舍五入的法则应为2,就叫 做精确到个位;如果结果取2位小数,则应为1.67,就叫做精确 到百分位(或叫精确到0.01)。
c 、从左边第一个不是0的数字起,到末位数字止,所有的数字都 叫做这个数的有效数字。
对于一个数取近似数,有效数字越多,精确度越高。
3、用科学计算器进行有理数的运算(1)计算器的简单介绍现在普通的计算器一般分为两类:⎧⎪⎧⎨⎨⎪⎩⎩简单计算器单行不按书写顺序输入科学计算器双行按书写顺序输入,可翻阅、修改二、典型例题例1:用四舍五入法,按括号中的要求把下列各数取近似数.(1)0.0198 (精确到0.001);(2)0.34082(精确到千分位);(3 )64.49 (精确到个位);(4)1.804 (保留2个有效数字);(5)1.804 (保留3个有效数字);(6)876000 (保留1个有效数字);(7)876000 (保留4个有效数字) .例2:选择(1)“全民行动,共同节约”,我国13亿人口如果都响应国家号 召每人每年节约1度电,一年可节约电1300000000度,这个数用科学记数法表示,正确的是( ).(A)1.30×109(B)1.3×109 (C)0.13×1010 (D)1.3×1010(2)已知:a =1.1×105,b =1.2×103,c =5.6×104,d =5.61×102,将a ,b ,c ,d 按从小到大顺序排列正确的是( ).(A)a <b <c <d(B)d <b <c <a (C)d <c <b <a (D)a <c <b <d(3)下列说法正确的有( ).①近似数1.60和近似数1.6的有效数字一样②近似数1.60和近似数1.6的精确度一样③近似数6百和600精确度是相同的④2.46万精确到万位,有三个有效数字⑤317500精确到千位可以表示为31.8万,也可表示为3.18×105 ⑥0.0502共有5个有效数字,它精确到万分位⑦近似数8.4和0.8的精确度一样(A) 1个 (B) 2个 (C) 3个 (D)4个例3.我们经常会看到“光年”和“纳米”这两个名称,你知道它们的 含义吗?(1)光年(1ight year)是天文学中使用的距离单位,符号是L. y .,主要用 于度量天体间的距离.1光年是光在真空中一年所走的距离:真空中光速 为299792.458千米/秒,1年≈60×60×24×365.25秒,故 1光年≈299792.458×60×60×24×365.25≈9.46×1210 (千米),即约等于 9.46万亿千米。
人教版七年级数学导学案科学计数法 (1)教案含同步练习课后作业

课题:科学记数法 【教】7017学习目标:1.了解科学记数法的意义;2.会用科学记数法表示大于10的数,能将用科学记数法表示的数还原成原数;3.能比较用科学记数法表示的两个数的大小.重点、难点:会用科学记数法表示大于10的数,能将用科学记数法表示的数还原成原数.【预习案】 1.现实中,我们会遇到一些较大的数.如,太阳半径约696000千米,光速约300000000米/秒,目前世界人口约6100000000人等.读、写这样大的数有一定的困难.2.观察10的乘方有如下的特点:102= ,103= ,104= ,….一般地,10的n 次幂等于 (在1的后面有n 个0)所以可以利用10的乘方表示一 些大数,例如567000000= = .读作“ ”. 这样不仅可以使书写简短,同时还便于读数.【探究案】探究一:科学记数法的意义及用科学记数法表示大于10的数.1.把一个大于10的数表示成na 10⨯的形式(其中a 是整数数位只有一位的数,n 是正整数),这种简便记数的方法称为科学记数法.2.注意①在n a 10⨯中,a 应满足1≤a <10,n 是正整数;②负数也可以用科学记数法表示,在n a 10⨯前面添上一个“-”即可.例1 用科学记数法表示下列各数:1000000, 57000000, -123000000000.思考:上面的式子中,等号左边整数的位数与右边10的指数有什么关系?用科学记数法表示一个n 位整数,其中10的指数是 .练习:1.下列各数是科学记数法的是( )A .0.582×104B .10.26×108C . 3.4×83D .2.05×1052.用科学记数法表示下列各数:10000,800000,56000000,-7400000.例2 用科学记数法表示下列各数:16万,1500亿,396×1015.练习:用科学记数法表示下列各数:5.26亿,17万亿,0.049×107.探究二:由用科学记数法表示的数转化为一般形式的数n例3 下列用科学记数法表示的数,原来各是什么数?(1)1×105 ; (2)5.18×103 ; (3)-7.24×106.练习:下列用科学记数法表示的数,原来各是什么数? (1)4×107 ; (2)7.04×105 ; (3)-3.96×106 .探究三:比较用科学记数法表示的两个数的大小例4比较大小(填“>”、“=”、“<”)(1)3.872×103 3.872×104 ; (2)4.8×1015 3.82×1015;(3)2.46×109 8.7×108 ; (4)-4.03×103 -3.8×104.归纳:设两个数为11011n a M ⨯=,21022n a M ⨯=(21,n n 为正整数a 1、a 2是正数) ⑴当21n n =,21a a >时,21M M >; ⑵当21n n >时,21M M >.小结:1.在n a 10⨯中,a 应满足1≤a <10,n 是正整数.2.用科学记数法表示一个n 位整数,其中10的指数是1-n .3.用科学记数法可以表示负数,在n a 10⨯前面添上一个“一”即可.【训练案】1.下列各数是科学记数法的是 ( )A .320×109B .4.7126×910C . -1.0009×101D .0.05×105 2.若71800000=7.18×10n ,则n 等于 ( )A . 6B . 7C . 8D . 93.用科学记数法表示下列各数:(1)1382000000= ; (2)-100000= ;(3)13亿= ; (4)345×106= ;4.写出以下用科学记数法表示的原数:(1)3.726×106= (2)-3.058×107=5.比较大小(填“>”、“=”、“<”)(1)3.14×107 3.14×108 (2)8.999×1012 7.201×1013(3)5.266×108 4.01×108 (4)-2.25×106 -8.25×1056.以下用科学记数法所表示的数:3.13×107 2.5×108 1.32×107 4.9×108其中最大的数是 ;最小的数是 .课题:科学记数法班级小组姓名得分1.用科学记数法表示:-3870000=.2.用科学记数法表示为-3.141×105的原数是.3.设n是一个正整数,则10n是 ( ) A.10个n相乘所得的积;B.是一个n位的整数;C.10后面有n个零的数;D.是一个(n+1)位的整数.4.用科学记数法表示1080000为 ( ) A.108×104B.10.8×105C.1.08×86D.0.108×1075.数3.76×10100的位数是 ( ) A.98B.99C.100 D.1016.用科学记数法表示下列各数:(1)1396290=;(2)-1741=;(3)-30003=;(4)+5001.03=.7.把下列用科学记数法表示的数写成原来的数:(1)-1.3×104=;(2)2.073×106=;(3)-2.71×104=;(4)1.001×102=;8.光速每纱约30万千米,用科学记数法表示是米/秒.9.下列数用科学记数法表示,正确的是()A.102000=10.2×104B.3100=3.1×103C.2020000=2.02×107D.423000=0.423×10410.已知m=25000用科学记数法表示为2.5×104,那么m2用科学记数法表示为()A.62.5×108B.6.25×109C.6.25×108D.6.25×10711.已知长方形的长为7×105mm,宽为5×104mm,求长方形的面积.12.把199 000 000用科学记数法写成1.99×10n-3的形式,求n的值13.用科学记数法表示下列各数:(1)太阳的半径约是696000千米;(2)据统计,全球每分钟约有85000吨污水排入江河湖海.14.一天有8.64×104秒,一年按365天计算,用科学记数法表示一年有多少秒?15.地球的质量为6×1013亿吨,太阳的质量是地球的质量的3.3×105倍,则太阳的质量为多少亿吨?16.比较大小(1)10.9×109与1.1×1010;(2)-5.64×109与-1.02×1010.。
科学计数法格式

科学计数法格式
科学计数法(Scientific Notation)是表示大数字的一种常用数学表示法。
它具有以下形式:
m×10^n
其中,m是数字的有效数字,n是乘方的指数。
一位有效数字的数字一般可以用科学计数法来表示,如4.8,一般可以用4.8×10^1来表示;而两位有效数字的数字,一般可以用9.72×10^1表示,向前移动一位,使得第一位为1,然后用指数n来补足原来的小数位数,这就是科学计数法。
以科学计数法表示一个数时,可以对两部分分别考虑,即数字和乘方;首先是数字,并非所有数字都可以用科学计数法表示,一般只有由1位或多位数字组成的有效数字可以用科学计数法表示,如果是由1位数字组成的,则记为m,如果是由多位数字组成的,则要求只有第一位是非零数字,其它位数可以是任意数字,这样的数可以将前导的部分看作一个整体,并将其记为m,如9.72以及1.173。
其次,科学计数法中也包含乘方,乘方为一个整数,可以正可以负;乘方的正负号可以从原数字看出来,也就是有效数字的位移,如果数字的小数点向前位移,则乘方就是正数,如9.72,位移一位变为乘方为1,如果坐标向后位移,则乘方为负数,如原数字为2.1732,向后位移三位变为乘方为-3,这就是科学计数法的基本原理。
综上所述,科学计数法是一种用于表示大数字的数学表示法,它是按照数字有效位数和乘方来表示的,将数字和乘方分别作为两部分考虑,有效数字采取1位或多位组成,乘方可以正可以负,它十分方便地将大数字简化成了几位简单的数字。
科学计数法1

1.5.2 科学记数法教材来源:初中七年级《数学(上册)》教科书/人民教育出版社2012版内容来源:初中七年级《数学(上册)》第一章第五节主题:科学记数法课时:1课时授课对象:七年级学生设计者:杨莹目标确定的依据1.课程标准相关要求了解科学记数法,在解决实际问题中,并会按问题的要求用科学记数法来表示数。
2.教材分析科学记数法是义务教育课程标准实验教科(人教版),七年级上册第一章第五节的内容。
之前,学生学习了有理数的加、减、乘、除、乘方等内容,本节课进一步学习大数的表示——科学记数法。
同时为学习物理、化学等知识的有力工具,并在实际生活中有着广泛的应用。
3.学情分析我班学生中农村学生占到90%以上,由于家长素质不高,对学生的行为规范养成非常不利,学习习惯差,小学基础薄弱,再加上七年级学生受年龄限制,认知能力有限,因此在教学中不宜过深。
学习目标1、熟记科学记数法的概念和符号表示,知道a和n的取值范围。
2、会用科学记数法表示绝对值大于10的数,并能把用科学记数法表示的数还原。
3、会解决与科学记数法有关的实际问题。
评价任务1、通过探讨感知科学记数法的生成,熟记科学记数法的概念,达成目标一。
2、通过教师引导和课堂练习会用科学记数法表示绝对值大于10的数,并会还原,达成目标二。
3、通过练习会实际应用科学记数法,达成目标三。
学习过程一、自主学习达成目标一1、阅读下列资料,感知大数:据有关资料统计:神十飞船在太空中大约飞行 10 080 000千米第六次人口普查时,中国人口约为1339724852人太阳的半径约为696 000 000米光的速度约为300 000 000米/秒像这样较大的数据,书写和阅读都有一定困难,那么有没有这样一种表示方法,使得这些大数易写,易读,易于计算呢?2、102=______ 103= ______ 104=________那么100 000=_________________ 10 000 000=__________1后面有11个0呢?同学们发现了什么?300 000又该如何表示呢?2600000呢?57600000呢?观察下面等式右边表示大数的式子,它们的形式都有什么特点?像这样,把一个数表示成a×10n的形式(其中1≤a<10,n是整数),既简单明了,又便于阅读和进行计算,这种记数法,习惯上叫科学记数法 (scientific notation) 。
人教版-数学-七年级上册-《科学计数法》知识点解读

《科学计数法》知识点解读学习目标:1.能了解科学记数法的意义.2.能掌握用科学记数法表示比较大的数.重点、难点:用科学记数法表示数.知识要点梳理:科学记数法:一般地,一个数可以表示成a×10n的形式,其中1≤a<10,n是整数,这种记数方法叫做科学记数法.注意:1.对于数目很大的数用科学记数法的形式表示起来又科学、又简单。
2.科学记数法的形式是由两个数的乘积组成的。
其中一个因数为a(1≤a<10),另一个因数为10n(n是比A的整数部分少1的正整数)。
3.用科学记数法表示数时,不改变数的符号,只是改变数的书写形式而已。
当有了负整数指数幂的时候,小于1的正数也可以用科学记数法表示。
例如:0.00001=10的负5次方,即小于1的正数也可以用科学记数法表示为a乘10 的负n次方的形式,其中a是正整数数位只有一位的正数,n是正整数。
4.在a×10n中,a的范围是1≤a<10,即可以取1但不能取10.而且在此范围外的数不能作为a.如:1300不能写作0.13×104.例1填空:(1)地球上的海洋面积为36100000千米2,用科学记数法表示为__________.(2)光速约3×108米/秒,用科学记数法表示的数的原数是__________.点拨:(1)用科学记数法写成a×10n,注意a的范围,原数共有8位,所以n =7.原数有单位,写成科学记数法也要带单位.(2)由a×10n还原,n=8,所以原数有9位.注意写单位.解:(1)3.61×107千米2.(2)300000000米/秒.注意:1.科学记数法形式与原数互化时,注意a的范围,n的取值.2.转化前带单位的,转化后也要有单位,一定不能漏.例2分别用科学记数法表示下列各数.(1)100万;(2)10000;(3)44;(4)0.000128-.点拨:(1)1万=10000,可先把100万写成数字再写成科学记数法的形式.(2)(3)(4)直接写成科学记数法形式即可.解:(1)100万=1000000=1×106=106.(2)10000=104.(3)44=4.4×10.(4)4-=-⨯0.000128 1.2810-说明:Ⅰ.在a×10n中,当a=1时,可省略,如:1×105=105.Ⅱ.对于44和4.4×101虽说数值相同,但写成4.4×10并非简化.所以科学记数法并非在所有数中都能起到简化作用,对于数位较少的数,用原数较方便.记住:Ⅲ.对于10n,n为几,则10n的原数就有几个零.例3设n为正整数,则10n是()A.10个n相乘B.10后面有n个零C.a=0D.是一个(n+1)位整数点拨:A错,应是10n表示n个10相乘;B错,10n共有n个零,10中已有一个零,故10后面有(n-1)个零;C当a=1时,a×10n=1×10n=10n,可有1.若a=0,a×10n=0;D在10n中,n是用原数的整数位数减1得来的,故原数有(n +1)位整数.解答:D.。
生活中的数据

生活中的数据知识要点:一、科学计数法:1.一般地,一个大于10的数可以表示成a×10n的形式,其中a是只有一位整数数位的数,n是正整数,这种记数方法叫做科学记数法。
(10的n次幂,在1后面就有n个0)。
2.科学记数法的表示分为两部分,如1.3×109,“×”前面一般为小数,“×”后为10的方幂,注意“×”前的小数应保持它的整数数位只有一位。
3.用科学记数法表示一个数时,10的指数比原数的整数位数少1。
二、扇形统计图:1.扇形统计图定义:利用圆和扇形来表示总体和部分的关系,即用圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分占总体的百分比的大小。
这样的统计图叫做扇形统计图(sector statistical chart)。
2.扇形统计图表明的是部分在总体中所占的百分比,等于该部分所对应的扇形圆心角的度数与360°的比,一般不能直接从图中得到具体数量,用圆代表的是总体1,圆大小与具体数量大小没有关系。
3.圆心角概念:顶点在圆心的角叫做圆心角。
4.会计算圆心角大小,扇形圆心角=该部分在总体中所占的百分比×360°。
5.画扇形统计图的步骤:先计算百分比,圆心角,画出扇形,标出百分比。
三、统计图的选择:三种统计图的各自特点:(1)条形统计图能清楚地表示出每个项目的具体数目;(2)折线统计图能清楚地反映事物的变化情况;(3)扇形统计图能清楚地表示出各部分在选择中所占的百分比。
例题解析:例题1、有一打字员每分钟可打150个字,要打100万字估计需要多少小时?(精确到1小时)。
思路点拨:以150个字为单位量,先算出打100万个字需要多少分钟,再折算成小时数。
解:由题意,得1000000÷(150×60)≈111(h)故打100万字需要约111h。
例题2、某养鱼户搞池塘养鱼已三年,头一年放养鲢鱼苗20000尾,其成活率为70%,在秋季捕捞时,随意捞出10尾鱼,称得每尾鱼的重量如下(单位:千克)0.80.9 1.2 1.30.80.9 1.1 1.0 1.20.8根据这10尾鱼的平均重量来估计这塘鱼的总产量多少千克?思路点拨:先计算出每条鱼的重量,然后乘以成活的条数,即为这塘鱼的总产量。
1.5科学计数法(1)

2008年北京奥 2008年北京奥 运会体育场— 运会体育场 —“鸟巢”能容 鸟巢” 鸟巢 91000位观众 位观众。 纳91000位观众。
2008年 2008年5月12日, 12日 在我国四川省汶川县 发生里氏8.0 8.0级强烈 发生里氏8.0级强烈 地震,面对地震灾难, 地震,面对地震灾难, 各级政府共投入抗震 救灾资金 22600000000元人 22600000000元人 民币。 民币。
1000= 103 = 106 1000 000= = 1000 000 000= 109 = 1000 000 000 000= 1012 = 100 …… 00 = 10n n个0 个 如果一个1后边有 后边有n个 ,这样的数可以简记作____ 如果一个 后边有 个0,这样的数可以简记作 10n
把一个数用科学记数法表示时, 把一个数用科学记数法表示时, 一般分两步进行: 一般分两步进行: (1)确定 a,1≤a<10,它是原数的小数 确定 < , 点向左移动后的结果 后的结果; 点向左移动后的结果; (2)确定 n,n 是比原数的整数位少 1 确定 , 的正整数. 的正整数.
本节学了哪些知识? 本节学了哪些知识? 科学记数法的一般形式是什么? 科学记数法的一般形式是什么? 把一个大于10的数表示成 把一个大于 的数表示成aX10n的形 式(其中a是整数数位只有一位的数,n 是整数数位只有一位的数, 是正整数),使用的是科学记数法。 ),使用的是科学记数法 是正整数),使用的是科学记数法。 (1≤a<10) 如何用科学记数法表示大数? 如何用科学记数法表示大数? 位整数, 用科学记数法表示一个n位整数,其 中10的指数是 n-1 的指数是
1、巩固练习: 、巩固练习: (1)、用科学记数法 、 写出下列各数: 写出下列各数: 104 10 000 = 800 000= 8X105 (2)、下列用科学记 、 数法写出的数, 数法写出的数,原 来分别是什么数? 来分别是什么数? 1X107= 10 000 000
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小数点原本的位置
400 000
小数点最后的位置
小数点向左移了5次
400 000 = 4 × 105
(b)
25 000 = 2.5 × 10 000 = 2.5 × 104
小数点原本的位置
25 000
小数点最后的位置
小数点向左移了4次
25 000 = 2.5 × 104
(c)
5 034 = 5.034 × 1 000 = 5.034 × 103
小数点原本的位置
5 034
小数点最后的位置
小数点向左移了3次
5 034 = 5.034 × 103
用科学记数法表示下列各数:
1 000 000,57 000 000,123 000 000 000 解:1 000 000=106 57 000 000=5.7X107 123 000 000 000=1.23X1011 观察:等号左边的位数与右边10的指数有什么关系? 右边10的指数等于左边整数位数减1
这节课你学到些什么?
1.遇到较大的数时可用科学记数法来表示? 一般形式: a×10n( 1≤a<10,n为正整数) 2.用科学记数法表示大数有什么好处? 用科学记数法,书写简短,同时还便于读数。
3.用科学记数法a×10n表示大数关键要注意两点: (1)1≤a<10. (2) n为原数整数位数减去1.
观察图片 世界人口6 100 000 000
把这个大数 简单记下来
6 100 000 000= 61X100 000 000= 6.1X1 000 000 000= 6.1X109 你能把567 000 000表示出来吗? 567X1 000 000 =5.67X100 000 000
=5.67X108
6
太阳的半径约为 696 000 000米
=6.96×108米
光的速度约为300 000 000米/秒
=3×108米/秒
下列用科学记数法写出的数,原来分别是什么数? 1X107= 10 000 000 4X103= 4 000
8.5X106= 8 500 000 7.04X105= 704 000 3.96X104= 39 600 1.96X104= 19 600
一个正常人的平均心跳速率是每分70次,一年 大约跳多少次?用科学记数法表示这个结果.
解: 70×60×24 ×365
= 36792000 =3.6792×107
答:一年大约跳3.6792×107 次。
生活中的大数
第五次人口普查时,中国人口约为1300 000 000人。
观察图片 世界人口6 100 000 000
北京故宫的占地面积约为721000m2
2008年北京 奥运会体育场 ——“鸟巢” 能容纳91000 位观众。
2008年5月12日 ,在我国四川省汶 川县发生里氏8.0 级强烈地震,面对 地震灾难,各级政 府共投入抗震救灾 资金 22600000000元 人民币。
9
2.76×10 (5) 27 600 000=_______________;
7
练习、下面信息中的数已经用科学记数法表 示了,你知道原数是多少吗? 8 (1)一口痰大约含有细菌1.3×10 个; 130 000 000 ___________________个 (2)温岭市去年总共缺水6.2×10 吨; 6 200 000 ____________________吨 (3)据中国电监会统计,我国今年预计将缺电 10 6×10 千瓦时; 60 000 000 000 ___________________千瓦时 4 24000 (4) 2.4×10 =________________.
把一个大于10的数表示成aX10n的形式(其中1≤a<10,
n是正整数),这种记数方法叫做科学记数法。
用科学记数法,书写简短,同时还便于读数。
第五次人口普查时,中国人口约为1300000000人。
用科学记数法表示
1 300 000 000人
怎样确定10 后面多少个零? 的指数呢?
1000000000 人 =1.3 ×109人 =1.3× 1
太阳半径约696 000千 米
月球的质量约为734万万亿吨
请 写 出 这 个 数 据
7,340,000,000,000,000,000吨
青藏铁路建设用于环保的投资大约11亿元。
这个数据是多少?
11,000,000,000元
721 000米2 1 300 000 000人 91 000个 22 600 000 000元 696 000 000米 300 000 000米 7 340 000 000 000 000 000吨 1 100 000 000 000元
1 a 10
n 是正整数
将下列数值写成科学记数法 a × 10n 。
(a) 400 000 = 4 × 100 000 = 4 × 105
(b)
400 000 = 40 × 10 000 = 40 × 104
此答案有 何问题?
此数不可大于 或等于10!
此数亦不 可小于1!
(a) 400 000 = 4 × 100 000 = 4 × 105
(1)如果一个数是6位整数,用科学记数 法表示它时,10的指数是___; 5 如果一个数有9位整数,那10的指数 8 是_______. (2) 用科学记数法表示一个n位整数,那 10的指数应是_________. n-1
a×10
n
中10的指数总比整数的位数少1
练习、用科学记数法表示下列数字. 1.3×10 (1)我国人口已达(1 300 000 000)_______; (2)我国去年发电总量约(2 000 000 000 000) 12 _____________ 千瓦时; 2×10 (3)三峡水电站的四台机组年内预计可发电 9 5.5×10 (5 500 000 000)度; ________9 460 000 000 000)千米; __________ 9.46×10
有简单的表示方法吗?
2.10 科学记数法
1000= 103 1000 000= 106
1000 000 000=109
1000 000 000 000= 1012
……
100 …… n个0 00 =10n
一般地,10的n次幂等于10…0(在1的后面有n个0), 所以就可以用10的乘方表示一些大数。
