数学中的切比雪夫逼近与最小二乘
数值分析之最小二乘法与最佳一致逼近

这里 ( x) 0是 [a, b]上的权函数,它表示不同点 ( xi , f ( xi ))
处的数据比重不同.
5
S ( x) a00 ( x) a11 ( x) ann ( x) (n m) 用最小二乘法求拟合曲线的问题,就是在
S ( x )中求一函数 y S * ( x), 使误差取得最小.
23
结果如下:
24
2
用正交多项式做最小二乘拟合
用最小二乘法得到的法方程组,其系数矩阵
n . G是病态的
(
(k 0,1,, n). (5.6) j 0 如果 0 ( x), 1 ( x), , n ( x) 是关于点集
k
, j )a j d k
{xi } (i 0,1,, m) 带权 ( xi ) (i 0,1,, m)
4 2.00 8.46 2.135
21
( 0 , y ) yi 9.404,
i 0 4
4
(1 , y ) xi yi 14.422.
i 0
故有法方程
5 A 7.50b 9.404, 7.50 A 11.875b 14.422.
解得
A 1.122, b 0.505, a e A 3.071.
使误差平方和
* 2 [ S ( x ) y ] i i i 0 2 i i 0 m m m
min
S ( x )
2 [ S ( x ) y ] , i i i 0
这里
S ( x) a00 ( x) a11 ( x) ann ( x)
(n m).
y S * ( x) 与所给数据{( xi , yi ), i 0,1,, m} 拟合.
最小二乘,切比雪夫,拉格朗日,牛顿,样条差值及仿真之令狐文艳创作

令狐文艳第一题:曲线拟合最小二乘法和切比雪夫的相同和不同,以及适用的场合令狐文艳背景及意义:在很多日常生活以及科研活动中,我们需要对一些离散的点集进行拟合,使得拟合的曲线尽量多的穿过所给出的离散点,并且误差小。
从而通过拟合的函数,找出离散点的规律,以此进行进一步的研究。
下面,就最小二乘法和切比雪夫两种拟合方法进行研究和分析。
1、最小二乘法它的标准是,所求得的拟合函数*()y S x =与给出的实际离散点{(,),0,1,,}i i x y i m =之间的误差平方和最小。
公式为:其中ϕ是规定区间上的线性无关函数族,01{,,,}m span ϕϕϕϕ=。
为了使问题提法更具一般性,在各自的离散点的区间中添加权函数()0x ω≥以表示各个离散点数据的比重不同。
要想求出函数*()S x ,就要求出其各阶系数,转而变成求多元函数极小点***01,,,n a a a其中:()j x ϕ取21,,,,n x x x的问题。
为了求取极值,其必要条件为 简化上式可得到矩阵形式其中01(,,,)T n a a a a =,01(,,,)T n d d d d =,要想使所求极值有唯一解,就要求G 非奇异。
又因()j x ϕ的组所组成向量为非奇异,则G 为非奇异,故而存在唯一的解*,0,1,.k k a a k n ==使得*()S x 为所求最优解。
例题:在相同离散点下用最小二乘法完成曲线拟合程序及结果如下clear all; clc; x0=1:10;y0=[1.1 3.5 9.7 2.6 9.4 6.5 5.6 2.1 6.5 5.9];plot(x0,y0,'o');hold on;x=1:0.1:10;hold on;q=polyfit(x0,y0,3);for i=1:length(x);y1(i)=q(4)+q(3)*x(i)+q(2)*x(i)*x(i)+q(1)*x(i)*x(i)*x(i) plot(x(i),y1(i),'*');hold on;end阶次为一的时候拟合曲线阶次为二的时候拟合曲线阶次为三时拟合曲线分析:最小二乘法的拟合需要提前确定离散点分布情况的阶次,即使是相同的离散点所拟合的多项式阶次不同所得曲线会有很大差异,并且当离散点的规律超过三次多项式的时候所拟合曲线的误差就会很大并出现病态问题。
叙述切比雪夫不等式

叙述切比雪夫不等式
【最新版】
目录
1.切比雪夫不等式的定义和背景
2.切比雪夫不等式的基本形式
3.切比雪夫不等式的应用举例
4.切比雪夫不等式的推广和发展
正文
1.切比雪夫不等式的定义和背景
切比雪夫不等式(Chebyshev"s inequality)是一种概率论中的基本不等式,由俄国数学家切比雪夫(Chebyshev)在 19 世纪末提出。
切比雪夫不等式用于估计一个随机变量偏离其数学期望的概率,为研究随机变量的分布和性质提供了一种有效的方法。
2.切比雪夫不等式的基本形式
切比雪夫不等式的基本形式如下:
对于任意实数 k > 0,随机变量 X 的数学期望为μ,方差为σ^2,则有
P(|X - μ| ≥ kσ) ≤ 1 / k^2
其中,P(A) 表示事件 A 发生的概率。
3.切比雪夫不等式的应用举例
假设我们要估计一个袋子里面装有 n 个红球和 k 个蓝球,从中随机抽取一个球,抽到红球的概率。
我们可以用切比雪夫不等式来估计这个概率。
设红球的概率为 p,蓝球的概率为 1-p,根据切比雪夫不等式,我们
可以得到:
P(抽到红球) ≥ 1 - 1/n^2
这意味着,当我们从袋子中抽取的次数越多,我们估计抽到红球的概率会越来越接近真实的概率。
4.切比雪夫不等式的推广和发展
切比雪夫不等式在概率论和统计学中有着广泛的应用。
随着研究领域的不断拓展,切比雪夫不等式也得到了不断的推广和发展。
例如,在多元随机变量的情况下,切比雪夫不等式可以推广到切比雪夫 - 马尔可夫不等式(Chebyshev-Markov inequality)等。
函数绝对值的最大值最小值问题切比雪夫逼近下的图像法
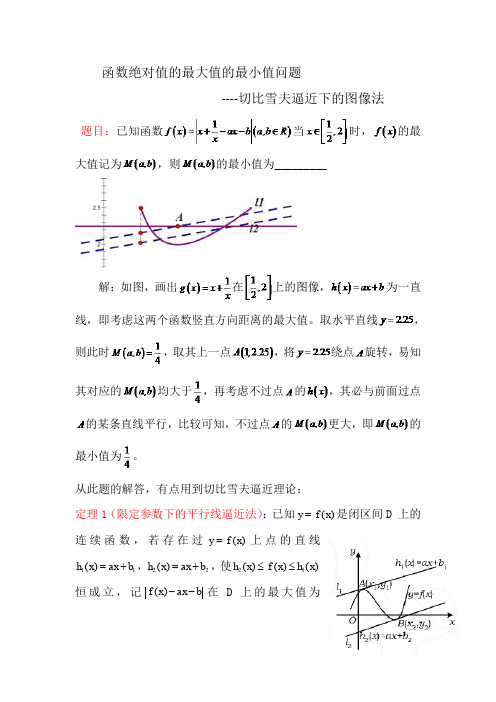
函数绝对值的最大值的最小值问题----切比雪夫逼近下的图像法 题目:已知函数当时,的最大值记为,则的最小值为_________解:如图,画出在上的图像,为一直线,即考虑这两个函数竖直方向距离的最大值。
取水平直线,则此时,取其上一点,将绕点旋转,易知其对应的均大于,再考虑不过点的,其必与前面过点的某条直线平行,比较可知,不过点的更大,即的最小值为。
从此题的解答,有点用到切比雪夫逼近理论:定理1(限定参数下的平行线逼近法):已知()y f x =是闭区间D 上的连续函数,若存在过()y f x =上点的直线11()h x ax b =+,22()h x ax b =+,使21()()()h x f x h x ≤≤恒成立,记()f x ax b --在D 上的最大值为(,)M a b ,则12(,)2b b M a b -≥ 推论1:已知()y f x =是闭区间D 上的连续函数,则()f x b -在D 上最大值为()M b ,则m a x mi n ()()(,)2fx fx Ma b -≥当且仅当max min()()2f x f x b +=时取等号。
接下来我们来尝试定理1及推论1的应用例1:(2016年4月浙江学考第18题)设函数2()f x ax b x=--,若对于任意正实数a 和实数b ,总存在0[1,2]x ∈,使得0()f x m ≥成立,则实数m 的取值范围是 。
解法1:(利用定理1) 记2ax b x--在[1,2]上的(,)M a b 最大值为 可知2()g x x=图像夹在两直线1()2h x ax a =-+,2()21(0)h x ax a a =-+>之间,由定理1得,(2)(12)1(,)22a a a M a b ---+≥=, 110,(,)22a a +>∈+∞,所以12m ≤ 解法2:由0a >,所以2()g x ax x =-在[1,2]单调递减,max min ()2,()12g x a g x a =-=-,(2)(12)1(,)22a a a M ab ---+≥=, 所以12a m +≤对0a >恒成立,11(,)22a +∈+∞,可得12m ≤ 上面我们用定理1及推论1很好的解决了例1,若题目条件中0a >变为任意实数a ,由于此时2()g x ax x =-的最值不容易求,所以我们需要更加一般的方法来解决。
指数函数与对数函数的函数逼近与最小二乘法

指数函数与对数函数的函数逼近与最小二乘法在数学中,指数函数和对数函数是非常常见且重要的函数。
它们在许多领域中扮演着重要的角色,例如物理学、经济学和统计学等。
本文将讨论指数函数和对数函数的函数逼近问题,并介绍最小二乘法在函数逼近中的应用。
一、指数函数的函数逼近指数函数可以表示为y = a^x的形式,其中a为底数,x为指数。
指数函数具有与底数a有关的特定增长率。
当底数a>1时,函数呈现增长趋势;当0<a<1时,函数呈现下降趋势。
在实际问题中,我们经常需要通过已知的数据去逼近一个未知的指数函数。
最常用的方法是使用最小二乘法进行函数逼近。
最小二乘法通过优化参数估计,来找到最能拟合给定数据的指数函数。
最小二乘法的基本原理是使得观测值与预测值之间的误差平方和最小化。
对于指数函数逼近,我们可以使用以下步骤:1. 收集指数函数的已知数据,包括自变量x和对应的函数值y。
2. 取对数转化:计算ln(y),将指数函数转化为对数函数。
3. 建立线性方程:将对数函数转化为线性方程,形式为ln(y) =ln(a)·x + ln(b)。
4. 进行最小二乘拟合:对转化后的线性方程应用最小二乘法,计算出拟合的参数估计值ln(a)和ln(b)。
5. 反转转化:根据拟合得到的ln(a)和ln(b),反转转化为a和b,得到拟合的指数函数。
通过这样的方法,我们可以使用最小二乘法逼近给定的指数函数,并找到最能拟合已知数据的指数函数。
二、对数函数的函数逼近对数函数可以表示为y = log_a(x)的形式,其中a为底数,x为对数的真数。
对数函数具有与底数a有关的特定增长率。
当底数a>1时,函数呈现增长趋势;当0<a<1时,函数呈现下降趋势。
对于对数函数的函数逼近,我们同样可以使用最小二乘法进行拟合。
以下是逼近对数函数的步骤:1. 收集对数函数的已知数据,包括自变量x和对应的函数值y。
2. 建立线性方程:将对数函数转化为线性方程,形式为y = a·ln(x)+ b。
两个随机变量切比雪夫不等式

两个随机变量切比雪夫不等式(实用版)目录1.切比雪夫不等式的定义和背景2.切比雪夫不等式的应用3.切比雪夫不等式的举例说明正文【1.切比雪夫不等式的定义和背景】切比雪夫不等式(Chebyshev"s inequality)是一种概率论中的基本不等式,用于估计一个随机变量的偏差。
切比雪夫不等式可以告诉我们,在给定的概率分布下,某个随机变量的取值偏离其数学期望的程度。
这个不等式的名字来源于 19 世纪俄国数学家切比雪夫(Pafnuty Chebyshev)。
设随机变量 X 的概率密度函数为 f(x),数学期望为μ,方差为σ,则切比雪夫不等式可以表示为:P(|X - μ| ≥ kσ) ≤ 1/k其中,k 为常数,称为切比雪夫常数。
【2.切比雪夫不等式的应用】切比雪夫不等式在概率论和统计学中有广泛应用,例如:- 估计随机变量的偏差:切比雪夫不等式可以用来估计一个随机变量的取值偏离其数学期望的程度。
- 风险管理:在金融领域,切比雪夫不等式可以用来估计投资组合的风险,帮助投资者制定合理的风险管理策略。
- 统计推断:在统计学中,切比雪夫不等式可以用来估计样本均值的置信区间,从而对总体均值进行估计。
【3.切比雪夫不等式的举例说明】假设有一个随机变量 X,其概率密度函数为 f(x),数学期望为μ,方差为σ。
现在我们想要知道,在给定的置信水平下,X 的取值偏离μ的程度。
根据切比雪夫不等式,我们可以计算出切比雪夫常数 k,然后得到 X 的取值偏离μ的置信区间。
例如,若置信水平为 95%,则 k=1.96(查表可得)。
假设我们要估计 X 的取值偏离μ的程度,可以计算:P(|X - μ| ≥ 1.96σ) ≤ 1/(1.96) = 0.05这意味着,在 95% 的置信水平下,X 的取值偏离μ的程度不会超过1.96σ。
概率论第四章-切比雪夫不等式

设随机变量X 设随机变量X 有数学期望 E = µ, 方 D =σ2 X 差 X 对任意 ε > 0, 不等式
P{| X −µ |≥ε}≤σ2 / ε2
或 成立, P{| X −µ |<ε}≥1−σ / ε 成立,
1
2
|x−µ |
2
ε
2
f (x)dx ≤ ∫
2
|x−µ |2
≤
ε
∫(x−µ)
f (x)dx
σ = 2 ε
ε
2
f (x)dx
2
是 于 P{| X −µ |<ε}≥1−σ / ε
2
2
P{| X −µ |≥ε}≤σ2 / ε2
P{| X −µ |<ε}≥1−σ / ε
2
2
切比雪夫不等式 证明切贝谢夫大数定律; 说明 (1)证明切贝谢夫大数定律; (2)表明D(X)描述了X偏离E(X)的离散程度; 表明D 描述了X偏离E 的离散程度; (3)给出X的分布未知时,事件 给出X的分布未知时, 概率的一个大致估计。 概率的一个大致估计。 大致估计 |X|X-E(X)|<ε的
不等式的其它形式
例1 估计 解
的概率
例2一电网有1万盏路灯, 晚上每盏灯开的概率为0.7. 一电网有1万盏路灯, 晚上每盏灯开的概率为0.7. 求同时开的灯数在6800至7200之间的概率。 求同时开的灯数在6800至7200之间的概率。 6800 之间的概率 解 为同时开的灯数。 设X 为同时开的灯数。 用二项分布
2 2
称此式为切比晓夫不等式. 称此式为切比晓夫不等式.
P{| X −µ |≥ε}≤σ2 / ε2
切比雪夫不等式xi

切比雪夫不等式xi切比雪夫不等式xi是19月科学家乔治切比雪夫发现的一个重要的数学定理,也被称为“切比雪夫不等式”。
它与其他不等式有着根本的不同,它只能定义有限多个未知数,而不是无限多个未知数。
它是数学家和科学家们许多工作和研究中不可或缺的重要理论。
历史上,切比雪夫不等式是由俄罗斯数学家切比雪夫发现的。
切比雪夫发现这个不等式有助于描述多变量函数的最大值和最小值。
它被用来给出多变量的解析解,从而为多变量函数的计算打开了大门。
此外,它还被用来推导数学空间的完备性定理,证明某些数学定理的正确性。
切比雪夫不等式的原理非常简单:如果两个变量(a和b)满足不等式xi,则它们之间的差值不能超过常数xi,即:|a - b|此外,它还表明如果N个变量满足不等式xi,则它们之间差值的大小不能超过N-1倍的常数xi:|a1 - a2||a2 - a3||an-1 - an|这是切比雪夫不等式xi的核心原理,它表明不等式xi对多变量函数的行为具有极大的约束力。
迄今为止,切比雪夫不等式一直是数学界的一个重要问题,因为它的许多应用可以帮助解决难题。
例如,它可以用来优化多变量函数,求解最佳参数,以及构建函数图像。
此外,它还可以引入数值近似解,有效解决多变量函数的极值点查找问题。
可以看出,切比雪夫不等式xi是一个伟大的数学定理,它的发现为数学研究提供了极大的帮助。
它的基本原理既简单又有效,因此一直被许多学者所重视。
它的强大优势可以帮助研究人员解决复杂的数学问题,从而为科学的发展做出重大贡献。
总之,切比雪夫不等式是一个著名的数学定理,由于它极大地促进了数学研究的发展,因此得到了众多学者的赞誉和推崇。
它将为科学界做出更多贡献,持续推动数学研究的发展,并且将来还会帮助解决更多科学难题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学中的切比雪夫逼近与最小二乘数学中的切比雪夫逼近与最小二乘是两种常见的函数逼近方法。
它
们在实际问题中的应用广泛,并且在数学领域有着重要的理论基础。
本文将分别介绍切比雪夫逼近和最小二乘的基本原理和应用,并且对
二者进行比较分析。
一、切比雪夫逼近
切比雪夫逼近是一种基于切比雪夫多项式的函数逼近方法。
切比雪
夫多项式是指满足以下条件的多项式:
$$T_n(x) = \cos(n\arccos(x))$$
其中,$n$ 是多项式的阶数,$-1\leq x \leq 1$。
根据切比雪夫逼近定理,对于任意给定的函数 $f(x)$,在闭区间 $[-1,1]$ 上存在一个切比雪夫多项式 $P_n(x)$,使得在该区间上的切比雪
夫范数最小:
$$\|f(x)-P_n(x)\|_{\infty} = \min_{T_n(x)} \|f(x)-T_n(x)\|_{\infty}$$
其中,$\| \cdot \|_{\infty}$ 表示切比雪夫范数,即函数的最大差值。
切比雪夫逼近方法的优点是可以在给定的误差限下找到最优逼近多
项式,并且能够保证逼近误差在整个区间上得到均匀分布。
但是该方
法在实际计算中由于多项式的高阶会导致计算量较大,同时由于切比
雪夫多项式在区间端点处存在震荡现象,因此需要额外加工边界条件。
二、最小二乘法
最小二乘法是一种通过最小化残差平方和来求取逼近函数的方法。
给定一组数据点 $(x_i, y_i)$,其中 $x_i$ 是自变量,$y_i$ 是因变量,我们希望找到一个函数 $f(x)$,使得在这些数据点上的误差最小。
最小二乘法的目标是使得残差平方和最小:
$$\min \sum_{i=1}^{m} (y_i - f(x_i))^2$$
最小二乘法的解可以通过求解线性方程组来得到。
具体地,假设函数 $f(x)$ 可以表示为一个多项式形式:
$$f(x) = \sum_{j=0}^{n} a_j x^j$$
其中,$n$ 是多项式的阶数,$a_j$ 是待求系数。
带入数据点 $(x_i, y_i)$,可以得到一个线性方程组:
$$\begin{pmatrix} 1 & x_1 & x_1^2 & \cdots & x_1^n \\ 1 & x_2 &
x_2^2 & \cdots & x_2^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_m & x_m^2 & \cdots & x_m^n \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_n \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{pmatrix}$$
通过求解上述线性方程组,可以得到多项式的系数,并且满足最小二乘法的要求。
最小二乘法适用于各种类型的函数逼近问题,并且具有良好的数值稳定性。
三、切比雪夫逼近与最小二乘法的比较
切比雪夫逼近和最小二乘法都是常见的函数逼近方法,但在具体应用中存在一些差异。
首先,在计算复杂度方面,切比雪夫逼近需要求解切比雪夫多项式的系数,而最小二乘法需要求解线性方程组。
一般情况下,最小二乘法的计算复杂度较低,特别是当多项式的阶数较高时。
其次,在逼近效果方面,切比雪夫逼近能够在给定的误差限下找到最优逼近多项式,并且逼近误差在整个区间上均匀分布。
最小二乘法则是通过最小化残差平方和来确定逼近函数,在数据点附近的逼近效果较好。
最后,在数值稳定性方面,最小二乘法更加稳定,对于数据中的噪声和异常值相对较为鲁棒。
而切比雪夫逼近对于数据的分布情况较为敏感,需要注意选择合适的切比雪夫多项式阶数和区间。
综上所述,切比雪夫逼近与最小二乘法都是重要的函数逼近方法,在数学中有着广泛的应用。
选择合适的方法需要根据具体的应用场景和要求进行综合考虑。
无论选择哪种方法,在实际问题中都需要注意数值计算的稳定性和逼近效果的准确性。
