安徽大学离散数学(上)试卷及参考答案

合集下载

《离散数学》(上)试卷(A卷)及参考答案

安徽大学20 09 — 20 10 学年第 1 学期《离散数学》考试试卷（A 卷）（时间120分钟）院/系专业姓名学号一、单项选择题（每小题2分，共20分）1. 设:P 天没下雪，:Q 我去镇上，则命题“天正在下雪，我没去镇上”可符号化为（ D ）A.Q P ⌝→⌝；B. P Q ⌝→⌝；C.Q P ⌝∧；D. Q P ⌝∧⌝。

2.下列命题是重言式的是（ C ）A.)()(P Q Q P →∧→；B. )()(Q P P Q P ↔↔↔∧；C. )(Q P Q P →→∧；D. Q P R Q P ∧⌝∧⌝∨→))((。

3. 设解释R 如下：论域D 为实数集，a=0, f(x,y)=x-y, A(x,y):x<y.下列公式在R 下为真的是( )A.(∀x)(∀y)(∀z)(A(x,y)→A(f(x,z),f(y,z)))B.(∀x)A(f(a,x),a)C.(∀x)(∀y)（A(f(x,y),x))D.(∀x)(∀y)(A(x,y)→A(f(x,a),a))4. 对任意集合,,A B C ，下列结论正确的是（ B ）A. C A C B B A ∉⇒∉∧∉][；B. C A C B B A ∈⇒⊆∧∈][；C. C A C B B A ∉⇒∉∧∈][；D. C A C B B A ∈⇒∈∧⊆][。

5. 9．关于{,,}X a b c =到{1,2,3}Y =的函数{,1,,1,,3}f a b c =<><><>，下列结论不正确的是（）A 、1({3}){}f c -=； B 、1(3)f c -=； C 、({}){3}f c =； D 、()3f c =。

6. 设I 为整数集合，则I 上的二元关系}4|||,{=-><=y x y x R 具有（ B ）A.自反性和对称性；B.反自反性和对称性；C.反自反性和传递性；D.反对称性和传递性。

2006-2007(1A)离散数学期末试卷答案

安徽大学2006-2007学年第1学期《离散数学》期末考试试卷答案（A 卷）（时间120分钟）一、选择题（每小题2分，共20分）1．C;2.D;3.C;4.B;5.A;6.C;7.B;8.D;9.C;10.A二、填空题（每空2分，共32分）1．}5{；}}5{,{φ；}4,3,1{2．4，1，2，53．{<1,2>,<2,4>,<3,3>,<1,1>,<2,2>,<4,4>}；{<1,2>,<2,4>,<3,3>,<2,1>,<4,2>}；{<1,2>,<2,4>,<3,3>,<1,4>}4．252,525．⊆，满射，⊇，单射三、综合题（第2小题16分，其它各小题8分，共48分）1．P R Q P A →⌝∨∧⇔))((P R Q P ∨⌝∨∧⌝⇔))((P R Q P ∨∧⌝∨⌝⇔))((P R Q R P ∨∧⌝∨∧⌝⇔)()( 2分))()(()()(())()((R R Q Q P P P R Q Q Q R P ⌝∨∧⌝∨∧∨⌝∨∧∧⌝∨∨⌝∧∧⌝⇔ 4分∨∧⌝∧⌝∨∧⌝∧∨∧⌝∧⌝∨∧∧⌝⇔)()()()(R Q P R Q P R Q P R Q P)()()()(R Q P R Q P R Q P R Q P ⌝∧⌝∧∨∧⌝∧∨⌝∧∧∨∧∧∨∧∧∨∧⌝∧∨∧⌝∧⌝∨∧∧⌝⇔)()()()(R Q P R Q P R Q P R Q P)()(R Q P R Q P ⌝∧⌝∧∨⌝∧∧（主析取范式） 6分)()(R Q P R Q P A ⌝∧∧⌝∨⌝∧⌝∧⌝⇔⌝∴ ))()(()(R Q P R Q P A A ⌝∧∧⌝∨⌝∧⌝∧⌝⌝⇔⌝⌝⇔)()(R Q P R Q P ∨⌝∨∧∨∨⇔（主合取范式） 8分2．①证明：(1) P S ∨⌝ P 1分(2) S P （附加前提） 2分(3) P T (1),(2) I 3分(4) )(R Q P →→ P 4分(5) R Q → T (3),(4) I 5分(6) Q P 6分(7) R T (5),(6) I 7分(8) R S → CP (2),(7) 8分②证明：(1) )(x xF ∃ P 1分(2) )(c F ES (1) 2分(3) )))()(()((x R y Q x F x ∧→∀ P 3分(4) ))()(()(c R y Q c F ∧→ US (3) 4分(5) )()(c R y Q ∧ T (2),(4) I 5分(6) )(c R T (5) I 6分(7) )()(c R c F ∧ T (2),(6) I 7分(8) ))()((x R x F x ∧∃ EG (7) 8分3．解：⊆><),(A ρ的哈斯图如下图所示。

离散数学试题与答案试卷一

权数1，4，9，16，25，36，49，64，81，100构造一棵最优二叉树。（7分）
试卷二答案：
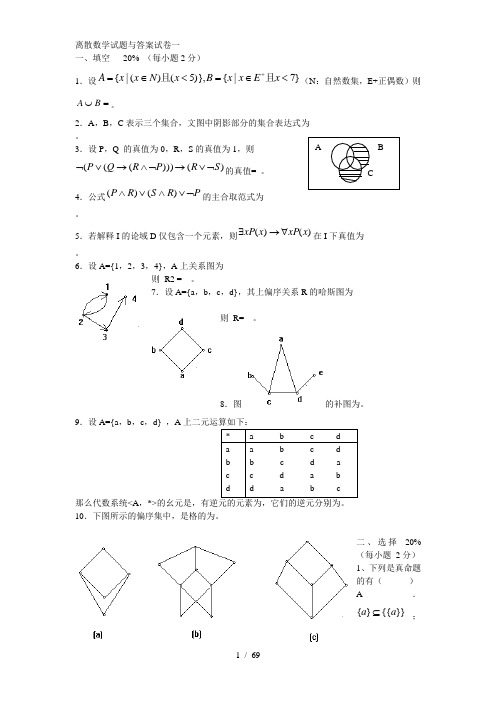
填空20%（每小题2分）
1、； 2、T 3、 4、R={<2,2>,<2,3>,<2,4>,<2,5>,<2,6>,<3,2>,<3,3>,<3,4>,<3,5>,<3,6>,<4,5>,<4,6>,<5,2>,<5,3>,<5,4>,<5,5>,<5,6>}； 5、R={<1,2>,<1,3>,<2,1>}；R={<1,1>,<2,2>,<3,3>} 6、a；否；有7、Klein四元群；循环群8、B 9、；图中无奇度结点且连通10、渗釤呛俨匀谔鱉调硯錦鋇絨钞。
前提：、结论： ……3分
① P
② P
③ US②
④ T①I
⑤ T③④I
⑥ T①I
⑦ T⑤⑥I
⑧ EG⑦……11分
３、１0分
证明：
。
4、8分
证明：设G中两奇数度结点分别为u和v，若u，v不连通，则G至少有两个连通分支G1、G2，使得u和v分别属于G1和G2，于是G1和G2中各含有1个奇数度结点，这与图论基本定理矛盾，因而u，v一定连通。铙誅卧泻噦圣骋贶頂廡缝勵罴。
选择20%（每小题2分）
题目
1
2
3
4
5
6
7
8
9
10Biblioteka 答案B、DD；DD
B
D
A

安徽大学期末试卷离散数学期末试卷及答案.doc

一．判断题（共10小题，每题1分，共10分）在各题末尾的括号内画表示正确，画表示错误：1．设p、q为任意命题公式，则(p∧q)∨p ⇔ p ( )2．∀x(F(y)→G(x)) ⇔ F(y)→∃xG(x)。

( )3．初级回路一定是简单回路。

( )4．自然映射是双射。

( )5．对于给定的集合及其上的二元运算，可逆元素的逆元是唯一的。

( )6．群的运算是可交换的。

( )7．自然数集关于数的加法和乘法<N，+， >构成环。

( )8．若无向连通图G中有桥，则G的点连通度和边连通度皆为1。

( )9．设A={a,b,c},则A上的关系R={<a,b>,<a,c>}是传递的。

( )10．设A、B、C为任意集合，则A⨯(B⨯C)=(A⨯B)⨯C。

( )二、填空题（共10题，每题3分，共30分）11．设p：天气热。

q：他去游泳。

则命题“只有天气热，他才去游泳”可符号化为。

12．设M(x)：x是人。

S(x)：x到过月球。

则命题“有人到过月球”可符号化为。

13．p↔q的主合取范式是。

14．完全二部图K r,s（r < s）的边连通度等于。

15．设A={a,b}，,则A上共有个不同的偏序关系。

16．模6加群<Z6，⊕>中，4是阶元。

17．设A={1,2,3,4,5}上的关系R={<1,3>,<1,5>,<2,5>,<3,3>,<4,5>}，则R的传递闭包t(R) = 。

.18．已知有向图D的度数列为(2,3,2,3)，出度列为(1,2,1,1)，则有向图D的入度列为。

19．n阶无向简单连通图G的生成树有条边。

20．7阶圈的点色数是。

三、运算题（共5小题，每小题8分，共40分）21．求∃xF(x)→∃yG(x,y)的前束范式。

22．已知无向图G有11条边，2度和3度顶点各两个，其余为4度顶点，求G 的顶点数。

离散数学考试题及详细参考答案

离散数学考试题(后附详细答案)一、命题符号化（共6小题，每小题3分，共计18分）1.用命题逻辑把下列命题符号化a)假如上午不下雨，我去看电影，否则就在家里读书或看报。

b)我今天进城，除非下雨。

c)仅当你走，我将留下。

2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x，总存在y使得xy=1。

c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B，使得f(a)=b.二、简答题（共6道题，共32分）1.求命题公式(P→(Q→R)) (R→(Q→P))的主析取范式、主合取范式，并写出所有成真赋值。

（5分）2.设个体域为{1,2,3}，求下列命题的真值（4分）a)x y(x+y=4)b)y x (x+y=4)3.求x(F(x)→G(x))→(xF(x)→xG(x))的前束范式。

（4分）4.判断下面命题的真假，并说明原因。

（每小题2分，共4分）a)（A B）－C=(A-B) (A-C)b)若f是从集合A到集合B的入射函数，则|A|≤|B|5.设A是有穷集，|A|=5，问（每小题2分，共4分）a)A上有多少种不同的等价关系？b)从A到A的不同双射函数有多少个？6.设有偏序集<A,≤>，其哈斯图如图1，求子集B={b,d,e}的最小元，最大元、极大元、极小元、上界集合、下界集合、上确界、下确界，(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合，R为实数集合，求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N（写出即可）(6分)三、证明题（共3小题，共计40分）1.使用构造性证明，证明下面推理的有效性。

（每小题5分，共10分）a)A→(B∧C),(E→ F)→ C, B→(A∧ S) B→Eb)x(P(x)→ Q(x)), x(Q(x)∨R(x))，x R(x) x P(x)2.设R1是A上的等价关系，R2是B上的等价关系，A≠ 且B≠ ，关系R满足：<<x1,y1>,<x2,y2>>∈R，当且仅当< x1, x2>∈R1且<y1,y2>∈R2。

2005-2006(1A)离散数学期末试卷

《离散数学》试卷共3页第1页安徽大学2005-2006学年第一学期《离散数学》期末考试试卷（A 卷）（时间120分钟）年级院系专业姓名学号座位号一、选择题（每小题2分，共20分）1．下列语句中哪个是真命题？（）A ．我正在说谎。

B ．严禁吸烟。

C ．如果521=+，那么雪是黑的。

D ．如果321=+，那么雪是黑的。

2．命题公式R Q P ∧→的对偶式为：（） A ．)(R Q P ∨→ B ．)(R Q P ∨∧⌝ C ．)(R Q P ∧∨⌝ D ．)(R Q P ∨∧3．命题公式R Q P →∧⌝)(的主析取范式中含极小项的个数为：（） A ．0 B ．3 C ．5 D ．8 4．谓词公式(,)x yP x y ∀∃的否定式是：（） A ．(,)x y P x y ∀∀⌝ B ．(,)x y P x y ∃∀⌝C ．(,)x y P x y ∀∃⌝D ．(,)x y P x y ∃∃⌝ 5．下列命题中，假命题的是：（）A ．}}{{}{x x x ∈B ．}}{{}{}{x x x -⊆C ．若x x A }{=，则A x ∈且A x ⊆D ．φ=-B A ⇔B A = 6．设集合A 上有n 个元素，则A 上的既对称又反对称的二元关系共有（） A ．0个 B ．2n 个 C ．2n 个 D ．2n个7．下列},,{c b a X =上的关系式中，不具有传递性质的是：（） A ．},{1><=b a R B ．},,,{2><><=c a b a R C ．},,,{3><><=a a b a R D ．},,,{4><><=c b b a R8．设}2,1,0{=A ，},{b a B =，则从A 到B 的全函数有多少个？（） A ．32+个 B ．32个 C ．32⨯个 D ．23个9．I 是整数集合，函数f 定义为：I I →，x x x f 2)(-=，则f 是：（） A ．单射 B ．满射 C ．双射 D ．非单射也非满射 10．下列无限集合中，哪个集合的基数不等于c 。

《离散数学》考试试卷(试卷库14卷)及答案

第 1 页/共 4 页《离散数学》考试试卷（试卷库14卷）试题总分： 100 分考试时限：120 分钟一、选择题（每题2分，共20分）1. 下述命题公式中，是重言式的为( )（A ）)()(q p q p ∨→∧ （B ）q p ∨))()((p q q p →∨→⇔（C ）q q p ∧→⌝)(（D ）q q p →⌝∧)(2. 对任意集合A,B,C,下列结论正确的是（）（A ）若A ⊆B,B ∈C,则A ⊆C ；（B ）若A ∈B,B⊆C,则A ⊆C ；（C ）若A ⊆B,B ∈C,则A ∈C ；（D ）若A ∈B,B ⊆C,则A ∈C ； 3. 设} 3 ,2 ,1 {=S ，定义S S ⨯上的等价关系,,则由R 产生的S S ⨯上一个划分共有( )个分块。

（A ）4（B ）5（C ）6（D ）94. 下列偏序集( )能构成格5. 连通图G 是一棵树当且仅当G 中( )（A ）有些边是割边（B ）每条边都是割边（C ）所有边都不是割边（D ）图中存在一条欧拉路径6. 有n 个结点)3(≥n ，m 条边的连通简单图是平面图的必要条件( )（A ） 63-≤n m（B ）63-≤m n （C ）63-≥n m （D ） 63-≥m n7. 设P,Q 的真值为0,R,S 的真值为1,则下面命题公式中真值为1的是（）（A ）R →P （B ）Q ∧S （C ）P S （D ）Q ∨R 8. 在图G=<V,E>中,结点总度数与边数的关系是（）（A ）deg()2||i v E =（B ）deg()||i v E =（C ）deg()2||iv Vv E ∈=∑（D ）deg()||iv Vv E ∈=∑9. 设有33盏灯,拟公用一个电源,则至少需有五插头的接线板数（）（A ）７（B ）８（C ）９（D ）１４ 10. 设集合A 上有四个元素,则A 上的不同的等价关系的个数为（）（A ）11 （B ）14 （C ）17（D ）15二、填空题（每题2分，共20分）1. 设A={a ，b ，c ，d}，其上偏序关系R 的哈斯图为则R= 。

安徽大学离散数学期末考试试卷 (5)

安徽大学20 11 —20 12 学年第 1 学期《离散数学（上）》考试试卷（B 卷）（闭卷时间120分钟）考场登记表序号一、单项选择题（每小题2分，共20分）1. 在下述公式中是重言式为（） A ．()()P Q P Q ∧→∨； B ．()(()())P Q P Q Q P ↔↔→∧→； C ．()P Q Q ⌝→∧；D ．()P P Q ↔∨。

2. 设{,{1},{1,2}}S =∅，则2S有（）个元素。

A ．3；B ．6；C ．7；D ．8 。

3.下列各项中，右侧结论不能从其左侧前提有效推出的是（） A. )()()),()((x xG x xM x G x M x ∃⇒∃→∀； B. )()()),()((x xF x B x x B x F x ∃⇒⌝∀→⌝∀；C. )()())()((x xQ x xP x Q x P x ∀→∀⇒→∀；D. )()())()((x xQ x xP x Q x P x ∀∨∀⇒∨∀。

4.对任意集合D C B A ,,,，下列结论不正确的是（）A.)()()(C B C A C B A ---=--；B.)()()(C A B A C B A ⋂⋃-=--； C.)()()()(D B C A D C B A ⋃-⋂=-⋂-； D.)()()()(D B C A D C B A -⋃-=⋃-⋃。

5. 量词的约束范围称为量词的（）A. 定义域；B. 个体域；C. 辖域；D. 值域。

6. 设个体域为{,}A a b = ,公式()()xP x xS x ∀∧∃在A 上消去量词后应为（） A.()()P x S x ∧； B.()()()()()P a P b S a S b ∧∧∨； C.()()P a P b ∧； D.()()()()P a P b S a S b ∧∧∨。

7.设},,{c b a X =，X I 是X 上恒等关系，要使R c a a c c b b a I X ⋃><><><><⋃},,,,,,,{为X 上的等价关系，R 应取（）A. },,,{><><c b a b ；B. },,,{><><a c a b ；C. },,,{><><b c a b ；D. },,,{><><a b c a 。

离散考试试题及答案

离散考试试题及答案一、选择题（每题5分，共20分）1. 在离散数学中，下列哪个概念不是布尔代数的基本运算？A. 与B. 或C. 非D. 模答案：D2. 集合论中，下列哪个符号表示“属于”关系？A. ∈B. ∉C. ⊆D. ⊂答案：A3. 命题逻辑中，下列哪个符号表示“蕴含”关系？A. ∧B. ∨C. →D. ↔答案：C4. 关系R在集合A上是自反的，意味着什么？A. 对于所有a∈A，(a, a)∈RB. 对于所有a∈A，(a, a)∉RC. 对于所有a∈A，(a, b)∈RD. 对于所有a∈A，(a, b)∉R答案：A二、填空题（每题5分，共20分）1. 一个集合的基数是集合中元素的________。

答案：数量2. 在有向图中，如果存在一条从顶点u到顶点v的路径，则称顶点v 是顶点u的________。

答案：可达的3. 一个图是连通的，当且仅当图中任意两个顶点都是________。

答案：连通的4. 在命题逻辑中，一个命题的否定是________。

答案：它的对立命题三、简答题（每题10分，共30分）1. 请解释什么是图的哈密顿回路。

答案：哈密顿回路是一个图中的闭合回路，它恰好访问图中的每个顶点一次。

2. 描述一下什么是二元关系，并给出一个例子。

答案：二元关系是定义在两个集合上的一个关系，它关联了第一个集合中的元素和第二个集合中的元素。

例如，小于关系是数字集合上的一个二元关系。

3. 什么是图的生成树？答案：图的生成树是图的一个子图，它包含图中的所有顶点，并且是一棵树，即它是连通的且没有环。

四、计算题（每题15分，共30分）1. 给定一个集合A={1,2,3,4,5}，计算它的幂集。

答案：幂集P(A)={∅, {1}, {2}, {3}, {4}, {5}, {1,2}, {1,3}, {1,4}, {1,5}, {2,3}, {2,4}, {2,5}, {3,4}, {3,5}, {4,5},{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}, {1,2,3,4}, {1,2,3,5}, {1,2,4,5}, {1,3,4,5}, {2,3,4,5}, {1,2,3,4,5}, A}。

离散数学考试题及答案

离散数学考试题及答案一、选择题（每题5分，共20分）1. 下列哪个选项不是离散数学的研究对象？A. 图论B. 组合数学C. 微积分D. 逻辑学答案：C2. 在逻辑学中，下列哪个命题是真命题？A. 如果今天是周一，那么明天是周二。

B. 如果今天是周一，那么明天是周三。

C. 如果今天是周一，那么明天是周四。

D. 如果今天是周一，那么明天是周五。

答案：A3. 在集合论中，下列哪个符号表示集合的并集？A. ∩B. ∪C. ⊆D. ⊂答案：B4. 在图论中，下列哪个术语描述的是图中的顶点集合？A. 边B. 路径C. 子图D. 顶点答案：D二、填空题（每题5分，共20分）1. 如果一个集合A包含5个元素，那么它的子集个数是______。

答案：322. 在逻辑学中，如果命题P和命题Q都是真命题，那么复合命题“P且Q”的真值是______。

答案：真3. 在图论中，如果一个图的顶点数为n，那么它的最大边数是______。

答案：n(n-1)/24. 如果一个二叉树的深度为3，那么它最多包含______个节点。

答案：7三、简答题（每题10分，共30分）1. 请简述什么是图的连通性，并给出一个例子。

答案：图的连通性是指在图中任意两个顶点之间都存在一条路径。

例如，在一个完全图K3中，任意两个顶点之间都可以通过一条边直接连接，因此它是连通的。

2. 解释什么是逻辑蕴含，并给出一个例子。

答案：逻辑蕴含是指如果一个命题P为真，则另一个命题Q也必须为真。

例如，命题P：“如果今天是周一”，命题Q：“明天是周二”。

如果今天是周一，那么根据逻辑蕴含，明天必须是周二。

3. 请描述什么是二叉搜索树，并给出它的一个性质。

答案：二叉搜索树是一种特殊的二叉树，其中每个节点的左子树只包含小于当前节点的数，右子树只包含大于当前节点的数。

它的一个性质是中序遍历可以得到一个有序序列。

四、计算题（每题15分，共30分）1. 给定一个集合A={1, 2, 3, 4, 5}，请计算它的幂集，并列出所有元素。

离散数学试题及答案

离散数学试题及答案一、选择题（每题2分，共20分）1. 在集合论中，下列哪个选项不是集合的运算？A. 并集B. 交集C. 差集D. 乘法2. 命题逻辑中，下列哪个命题是真命题？A. (P ∧ ¬P) → QB. (P ∨ Q) ∧ ¬(P ∧ Q)C. P → (Q → P)D. (P → Q) ∧ (Q → R) → (P → R)3. 函数f: A → B，如果f是单射，那么下列哪个选项是正确的？A. A中不同的元素在B中可能有相同的像B. B中每个元素都有原像C. A中不同的元素在B中有不同的像D. B中不同的元素在A中有不同的原像4. 在图论中，下列哪个选项不是图的基本术语？A. 顶点B. 边C. 邻接D. 矩阵5. 组合数学中，从n个不同元素中取出k个元素的组合数记作C(n, k)，下列哪个选项是错误的？A. C(n, k) = C(n, n-k)B. C(n, 0) = 1C. C(n, 1) = nD. C(n, k) = C(k, n)6. 关系R是A×B上的二元关系，下列哪个选项不是关系R的性质？A. 自反性B. 对称性C. 传递性D. 可数性7. 在命题逻辑中，下列哪个命题等价于P ∨ (Q ∧ R)？A. (P ∨ Q) ∧ (P ∨ R)B. (P ∧ Q) ∨ (P ∧ R)C. (P ∨ Q) ∨ RD. (P ∨ Q) ∧ R8. 集合{1, 2, 3}的幂集含有多少个元素？A. 3B. 6C. 8D. 99. 在图论中，下列哪个选项不是树的性质？A. 无环B. 至少有两个顶点C. 任意两个顶点都由唯一路径连接D. 至少有一个环10. 在集合论中，下列哪个选项是正确的？A. 空集是任何集合的子集B. 任何集合都是其自身的超集C. 空集是任何非空集合的真子集D. 空集是其自身的并集二、简答题（每题10分，共30分）11. 简述命题逻辑中的德摩根定律，并给出一个例子。

2006-2007(1A)离散数学期末试卷及答案2006-2007(1A)离散数学期末试卷及答案

安徽大学2006-2007学年第1学期《离散数学》期末考试试卷（A 卷）（时间120分钟）开课院（系、部）姓名学号 .1A C 2A 3I.A 4A C 5A 6R I.III. R R ⋅不是传递的A 、仅I ；B 、仅II ；C 、I 和II ；D 、全真。

7．R 是二元关系且4R R =，则一定是传递的是（）A 、4R ；B 、3R ；C 、2R ； D 、R 。

8．设1R 和2R 是非空集合A 上的等价关系，确定下列各式，哪些是A 上的等价关系（）A 、1R A A -⨯； B 、21R R -； C 、21R R ； D 、21R R 。

9．函数:f X Y →可逆的充要条件是：（）A 、AB =； B 、||||A B =；C 、f 为双射；D 、f 为满射。

10．下列集合中，哪个集合的基数与其他集合的基数不同（）A 、n N （N 为自然数集，N n ∈）； B 、NN （N 为自然数集）； C 、R R ⨯（R 为实数集）； D 、x 坐标轴上所有闭区间集合；二、填空题（每小题2分，共32分）1．全集}5,4,3,2,1{=U ，}5,1{=A ，}4,3,2,1{=B ，}5,2{=C ，则可求出：=B A _________________________________；=)()(C A ρρ ___________________________；=C _____________________________________。

2．设=A B B A B A -B A ⊕3．设{=A )(R r )(R s )(R t4．设5．设函数f (1f f -(1f f-当f 为当f 为三、综合题（第2小题16分，其它各小题8分，共48分）1．求命题公式P R Q P →⌝∨∧))((的主析取范式与主合取范式（要求用等值演算的方法求解）。

（8分）2①(P →②前提：3．设集合}}{},b a 的分）4．设RR 是5．已知f :①f ②f ③计算})0({1-f 。

离散数学考试题目及答案

离散数学考试题目及答案1. 试述命题逻辑中的等价关系和蕴含关系。

答案：命题逻辑中的等价关系是指两个命题在所有可能的真值赋值下都具有相同的真值。

若命题P和Q等价，则记作P⇔Q。

蕴含关系是指如果命题P为真，则命题Q也为真，但Q为真时P不一定为真。

若命题P蕴含Q，则记作P→Q。

2. 证明：若集合A和B的交集非空，则它们的并集包含A和B。

答案：设x属于A∩B，即x同时属于A和B。

根据并集的定义，若元素属于A或B，则它属于A∪B。

因此，x属于A∪B。

由于x是任意属于A∩B的元素，所以A∩B≠∅意味着A∪B至少包含A∩B中的所有元素，即A∪B包含A和B。

3. 给定一个有向图G，如何判断G中是否存在环？答案：判断有向图G中是否存在环，可以采用深度优先搜索（DFS）算法。

在DFS过程中，记录每个顶点的访问状态，如果遇到一个已访问过的顶点，且该顶点不是当前路径的直接前驱，则表示存在环。

4. 描述有限自动机的组成部分及其功能。

答案：有限自动机由以下几部分组成：输入字母表、状态集合、转移函数、初始状态和接受状态集合。

输入字母表定义了自动机可以接收的符号集合；状态集合包含了自动机所有可能的状态；转移函数定义了在给定输入符号和当前状态的情况下，自动机如何转移到下一个状态；初始状态是自动机开始工作时的状态；接受状态集合包含了所有使自动机接受输入字符串的状态。

5. 什么是图的连通分量？如何确定一个无向图的连通分量？答案：图的连通分量是指图中最大的连通子图。

在一个无向图中，如果两个顶点之间存在路径，则称这两个顶点是连通的。

确定无向图的连通分量可以通过深度优先搜索（DFS）或广度优先搜索（BFS）算法。

从任一顶点开始搜索，搜索过程中访问的所有顶点构成一个连通分量。

重复此过程，直到所有顶点都被访问过，即可确定图中所有连通分量。

《离散数学》试题及标准答案解析

《离散数学》试题及标准答案解析⼀、填空题1设集合A,B，其中A＝{1,2,3}, B= {1,2}, 则A - B＝____________________; ρ(A) - ρ(B)＝ __________________________ .2. 设有限集合A, |A| = n, 则 |ρ(A×A)| = __________________________.3.设集合A = {a, b}, B = {1, 2}, 则从A到B的所有映射是__________________________ _____________, 其中双射的是__________________________.4. 已知命题公式G＝?(P→Q)∧R，则G的主析取范式是_________________________________________________________________________________________.6设A、B为两个集合, A= {1,2,4}, B = {3,4}, 则从A?B＝_________________________; A?B＝_________________________;A－B＝ _____________________ .7. 设R是集合A上的等价关系，则R所具有的关系的三个特性是______________________, ________________________, _______________________________.8. 设命题公式G＝?(P→(Q∧R))，则使公式G为真的解释有__________________________，_____________________________, __________________________.9. 设集合A＝{1,2,3,4}, A上的关系R1= {(1,4),(2,3),(3,2)}, R2= {(2,1),(3,2),(4,3)}, 则R1?R2 = ________________________,R2? R1 =____________________________, R12 =________________________.10. 设有限集A, B，|A| = m, |B| = n, 则| |ρ(A?B)| = _____________________________. 11设A,B,R是三个集合，其中R是实数集，A = {x | -1≤x≤1, x∈R}, B = {x | 0≤x < 2, x∈R},则A-B = __________________________ , B-A =__________________________ , A∩B = __________________________ , .13.设集合A＝{2, 3, 4, 5, 6}，R是A上的整除，则R以集合形式(列举法)记为__________________________________________________________________.14. 设⼀阶逻辑公式G = ?xP(x)→?xQ(x)，则G的前束范式是__________________________ _____.16. 设谓词的定义域为{a, b},将表达式?xR(x)→?xS(x)中量词消除，写成与之对应的命题公式是__________________________________________________________________________.17. 设集合A＝{1, 2, 3, 4}，A上的⼆元关系R＝{(1,1),(1,2),(2,3)}, S＝{(1,3),(2,3),(3,2)}。

2005-2006(1A)离散数学期末试卷答案

安徽大学2005-2006学年第一学期《离散数学》期末考试试卷（A 卷答案）一、选择题（2⨯10=20分）C,B,C,B,D,D,D,B,A,A二、填空题（每空2分，总2⨯15=30分）1．Q P →，Q P ⌝∧，Q P ↔2．))()((x Q x R x →⌝∀，))()()((x Z x R x Q x ⌝∧∧∃3．}}{}},{{}},{,{,{φφφφφ4．}1{和}2{，}2,1{，φ，无5．92，56．}3,4,4,3,4,4,3,3,1,2,2,1,2,2,1,1{><><><><><><><><7．B B f f ⊆-))((1，))((1B f f B -⊆三、计算题（每小题8分，总2⨯8=16分）1. 用等值演算法求命题公式(())()P Q R P Q ⌝∧∨→⌝→的主析取范式和主合取范式。

解：(())()(())()(())()()()(())()()P Q R P Q P Q R P Q P Q R P Q P Q P Q RP Q Q RP R P Q R P Q R ⌝∧∨→⌝→⇔∧∨∨⌝⌝∨⇔∧∨∨∧⌝⇔∧∨∧⌝∨⇔∧∨⌝∨⇔∨⇔∨∨∧∨⌝∨（主合取范式）4分(02)(1,3,4,5,6,7)()()()()()()P Q R P Q R P Q R P Q R P Q R P Q R ⇔⇔⇔⌝∧⌝∧∨⌝∧∧∨∧⌝∧⌝∨∧⌝∧∨∧∧⌝∨∧∧∏∑（主析取范式），8分 2．设3=A ，16)(=B ρ，64)(=B A ρ，试求B ，B A ，B A -和B A ⊕。

解：因为16)(=B ρ，所以4=B ；因为64)(=B A ρ，所以6=B A （2分）。

于是集合B A ,的文氏图如下：所以，1=B A （4分），2=-B A （6分），5=⊕B A （8分）。

四、证明题（1、2小题每小题9分，3、4小题每小题8分，总分34）1．用CP 规则证明)(R Q P ∨⌝∨⌝，)(S R Q →→，P ⇒S Q →。

大学《离散数学》期末考试试卷及答案 (6)

《离散数学》试卷共3页第1页安徽大学2005-2006学年第一学期《离散数学》期末考试试卷（A 卷）（时间120分钟）年级院系专业姓名学号座位号一、选择题（每小题2分，共20分）1．下列语句中哪个是真命题？（ C ）A ．我正在说谎。

B ．严禁吸烟。

C ．如果521=+，那么雪是黑的。

D ．如果321=+，那么雪是黑的。

2．命题公式R Q P ∧→的对偶式为：（ A ） A ．)(R Q P ∨→ B ．)(R Q P ∨∧⌝ C ．)(R Q P ∧∨⌝ D ．)(R Q P ∨∧3．命题公式R Q P →∧⌝)(的主析取范式中含极小项的个数为：（ C ） A ．0 B ．3 C ．5 D ．8 4．谓词公式(,)x yP x y ∀∃的否定式是：（ B ） A ．(,)x y P x y ∀∀⌝ B ．(,)x y P x y ∃∀⌝C ．(,)x y P x y ∀∃⌝D ．(,)x y P x y ∃∃⌝ 5．下列命题中，假命题的是：（ D ）A ．}}{{}{x x x ∈B ．}}{{}{}{x x x -⊆C ．若x x A }{=，则A x ∈且A x ⊆D ．φ=-B A ⇔B A = 6．设集合A 上有n 个元素，则A 上的既对称又反对称的二元关系共有（ D ） A ．0个 B ．2n 个 C ．2n 个 D ．2n个7．下列},,{c b a X =上的关系式中，不具有传递性质的是：（ B ） A ．},{1><=b a R B ．},,,{2><><=c a b a R C ．},,,{3><><=a a b a R D ．},,,{4><><=c b b a R8．设}2,1,0{=A ，},{b a B =，则从A 到B 的全函数有多少个？（ A ） A ．32+个 B ．32个 C ．32⨯个 D ．23个9．I 是整数集合，函数f 定义为：I I →，x x x f 2)(-=，则f 是：（） A ．单射 B ．满射 C ．双射 D ．非单射也非满射 10．下列无限集合中，哪个集合的基数不等于c 。

离散数学考试试题及答案

离散数学考试试题及答案一、选择题（每题2分，共20分）1. 在集合论中，以下哪个选项表示“属于”关系？A. ⊆B. ⊂C. ∈D. ⊇答案：C2. 以下哪个命题是真命题？A. p ∧ ¬pB. p ∨ ¬pC. p → ¬pD. ¬(p → q) → p答案：B3. 以下哪个选项是命题逻辑中的德摩根定律？A. ¬(p ∨ q) = ¬p ∧ ¬qB. ¬(p ∧ q) = ¬p ∨ ¬qC. ¬(p → q) = p ∧ ¬qD. ¬(p ∨ q) = ¬p ∨ ¬q答案：A4. 以下哪个选项是命题逻辑中的蕴含等价？A. p → q ≡ ¬p ∨ qB. p → q ≡ ¬q → ¬pC. p → q ≡ p ∨ ¬qD. p → q ≡ ¬p ∧ q答案：A5. 以下哪个选项是关系的性质？A. 反身性B. 对称性C. 传递性D. 所有选项都是答案：D6. 以下哪个选项是图论中的有向图？A. 无向图中的边没有方向B. 有向图中的边有方向C. 混合图中的边既有方向也有无方向D. 所有选项都是答案：B7. 在图论中，以下哪个选项是树的性质？A. 树是无环的B. 树是连通的C. 树是无向图D. 所有选项都是答案：D8. 以下哪个选项是布尔代数的基本运算？A. 与（AND）B. 或（OR）C. 非（NOT）D. 所有选项都是答案：D9. 以下哪个选项是组合数学中的排列？A. 从n个不同元素中取出m个元素的组合B. 从n个不同元素中取出m个元素的排列C. 从n个相同元素中取出m个元素的组合D. 从n个相同元素中取出m个元素的排列答案：B10. 以下哪个选项是集合论中的幂集？A. 一个集合的所有子集的集合B. 一个集合的所有真子集的集合C. 一个集合的所有超集的集合D. 一个集合的所有子集的个数答案：A二、简答题（每题10分，共30分）1. 简述命题逻辑中的等价命题是什么？答案：等价命题是指两个命题在所有可能的真值赋值下都具有相同真值的命题。

离散数学试题与参考答案

《离散数学》试题及答案一、选择题：本题共5小题，每小题3分，共15分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 命题公式Q Q P →∨)(为 ( )(A) 矛盾式 (B) 可满足式 (C) 重言式 (D) 合取范式2．设P 表示“天下大雨”， Q 表示“他在室内运动”，则命题“除非天下大雨，否则他不在室内运动”符号化为（）。

(A)． P Q →； (B)．P Q ∧； (C)．P Q ⌝→⌝； (D)．P Q ⌝∨．3.设集合A ={{1,2,3}, {4,5}, {6,7,8}}，则下式为真的是( )(A) 1∈A (B) {1,2, 3}⊆A(C) {{4,5}}⊂A (D) ∅∈A4. 设A ＝{1,2},B ={a ,b ,c },C ={c ,d }, 则A ×(B ⋂C )= ( )(A) {<1,c >,<2,c >} (B) {<c ,1>,<2,c >} (C) {<c ,1><c ,2>,} (D) {<1,c >,<c ,2>}5. 设G 如右图：那么G 不是( ). (A)哈密顿图； (B)完全图；(C)欧拉图； (D) 平面图.二、填空题：本大题共5小题，每小题4分，共206. 设集合A ={∅,{a }}，则A 的幂集P (A )=7. 设集合A ={1,2,3,4 }, B ={6,8,12}, A 到B 的关系R ＝},,2,{B y A x x y y x ∈∈=><,那么R －1＝8. 在“同学，老乡，亲戚，朋友”四个关系中_______是等价关系.9. 写出一个不含“→”的逻辑联结词的完备集 .10.设X ＝{a ,b ,c }，R 是X 上的二元关系，其关系矩阵为 M R ＝⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001001101，那么R 的关系图为三、证明题（共30分）11. （10分）已知A 、B 、C 是三个集合，证明A ∩(B ∪C)=(A ∩B)∪(A ∩C)12. （10分）构造证明：(P →(Q →S))∧(⌝R ∨P)∧Q ⇒R →S13.（10分）证明（0,1）与[0,1)，[0,1)与[0,1]等势。