第9章 弯曲变形

第9章教学方案——弯曲变形
第9章 弯曲变形
9.1 弯曲变形概述
9.1.1弯曲变形问题的工程实例
弯曲变形:当杆件受弯时,杆件的轴线由直线变成曲线,称为弯曲变形。
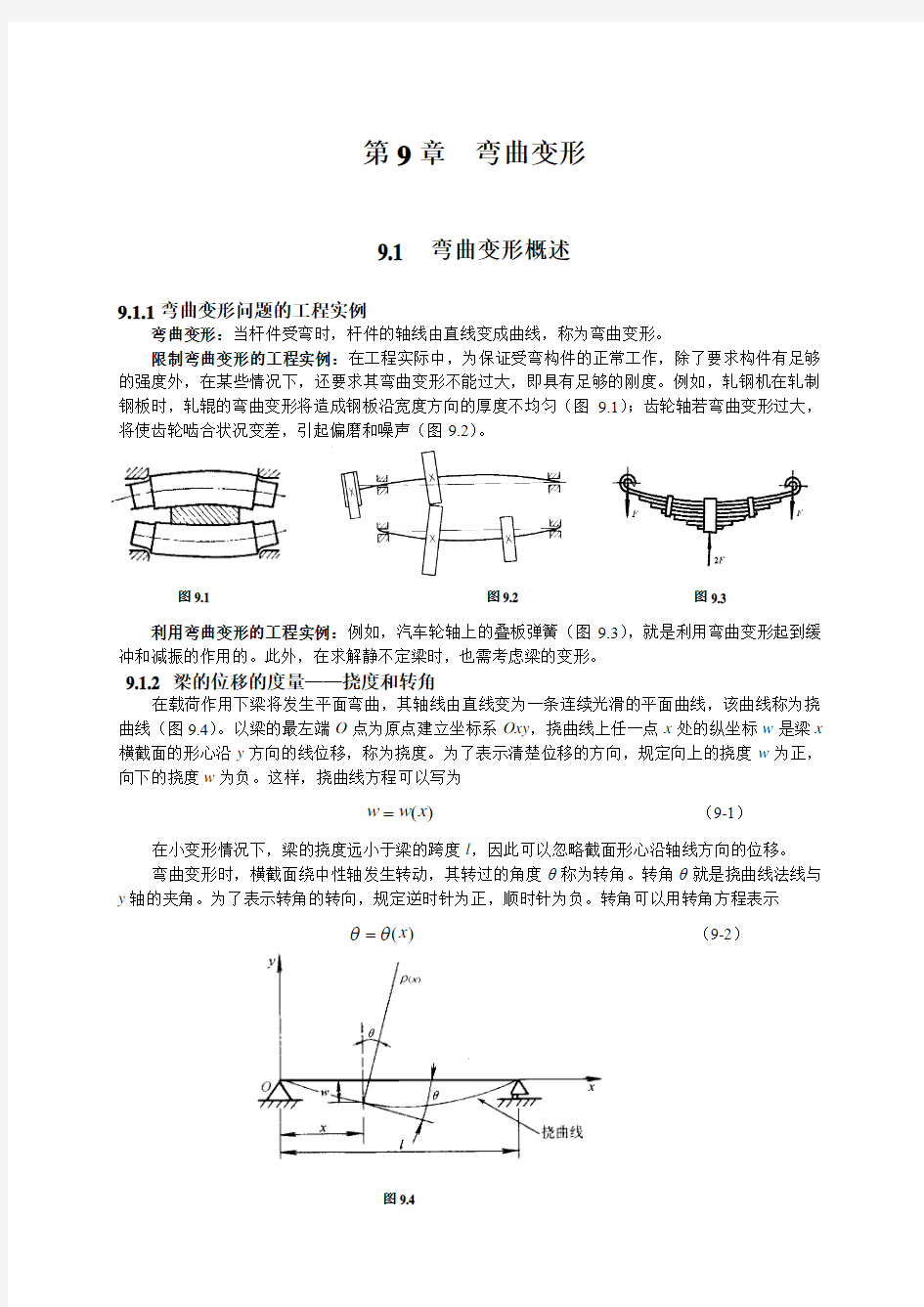
限制弯曲变形的工程实例:在工程实际中,为保证受弯构件的正常工作,除了要求构件有足够的强度外,在某些情况下,还要求其弯曲变形不能过大,即具有足够的刚度。例如,轧钢机在轧制钢板时,轧辊的弯曲变形将造成钢板沿宽度方向的厚度不均匀(图9.1);齿轮轴若弯曲变形过大,将使齿轮啮合状况变差,引起偏磨和噪声(图9.2)。
利用弯曲变形的工程实例:例如,汽车轮轴上的叠板弹簧(图9.3),就是利用弯曲变形起到缓冲和减振的作用的。此外,在求解静不定梁时,也需考虑梁的变形。
9.1.2 梁的位移的度量——挠度和转角
在载荷作用下梁将发生平面弯曲,其轴线由直线变为一条连续光滑的平面曲线,该曲线称为挠曲线(图9.4)。以梁的最左端O 点为原点建立坐标系Oxy ,挠曲线上任一点x 处的纵坐标w 是梁x 横截面的形心沿y 方向的线位移,称为挠度。为了表示清楚位移的方向,规定向上的挠度w 为正,向下的挠度w 为负。这样,挠曲线方程可以写为
)(x w w = (9-1)
在小变形情况下,梁的挠度远小于梁的跨度l ,因此可以忽略截面形心沿轴线方向的位移。 弯曲变形时,横截面绕中性轴发生转动,其转过的角度θ称为转角。转角θ就是挠曲线法线与y 轴的夹角。为了表示转角的转向,规定逆时针为正,顺时针为负。转角可以用转角方程表示
)(x θθ=
(9-2)
9.1.3 挠度和转角的关系
弯曲变形用挠度w 和转角θ这两个位移量来度量。由图9.4可以看出,转角θ与挠曲线在该点的切线倾角相等。在小变形情况下
x
w
d d tan =
≈θθ (9-3) 即横截面的转角可以用该点处挠曲线切线的斜率表示。只要知道挠曲线方程,就能确定梁上任一横截面的挠度和转角。
9.1.4 梁的刚度条件
在工程实际中,为了保证弯曲杆件的正常工作,有时会限定梁的最大挠度和最大转角,得到刚度条件
[][]??
?
??≤≤θθmax max f w (9-4)
式中,[f ]和[θ]分别为许用挠度和许用转角。
9.2 挠曲线微分方程及其积分
9.2.1 挠曲线微分方程
在纯弯曲时,挠曲线曲率1/ρ与弯矩M 的关系为式(8-1),即
EI
M
=
ρ
1
在横力弯曲时,如果是细长梁,剪力对变形的影响可以忽略,上式仍然成立,但曲率和弯矩都是x 的函数,即
()()EI
x M x =ρ1 (a ) )(x w w =上任一点的曲率为
()2
3
22
2d d 1d d 1
???
???????? ??+±=x w x w x ρ (b )
()EI x M x w =
±2
2d d (c )根据弯矩的符号规定和挠曲线二阶导数与曲率中心方位的关系,在所取坐标系下弯矩M 的正负号始终与2
2d d x
w
的正负号一致
()EI x M x w =
2
2d d (9-5) 式(9-5)即为梁的挠曲线微分方程。
9.2.2 挠曲线微分方程的积分
对式(9-5)积分一次,得转角方程
C x EI
M x w +==
?d d d θ (9-6a ) 再积分—次.可得挠曲线方程
D Cx x x EI M w ++??
?
??=??d d (9-6b )
式中C 、D 为积分常数。当梁为等截面梁时,EI 为常数,可以提到积分符号外面。如果梁的弯矩方程是分段函数,则上面的积分式也应分段积分。
9.2.3 积分常数的确定
积分常数C 和D 可以通过梁上某些位置的已知挠度和转角或应满足的变形关系来确定。
支承条件:支座处的挠度或转角是已知的。例如铰支座处的挠度为零,则在图9.6(a )中,在x =0和x =l 处,w A =w B =0;又如固定端约束处的挠度和转角均为零,则在图9.6(b )中,在x =0处,w A =0、θA =0。只要将这些数据代入式(9-6)中就可确定C 和D 。
连续光滑条件:因为挠曲线是一条连续光滑的曲线,所以在梁的积分分段点处,通过左右两段弯矩方程积分算出的挠度和转角是相等的。例如图9.7所示梁在集中力F 作用点A 处,有连续光滑条件为w A 左=w A 右和θA 左=θA 右。
9.2.4 用积分法求梁的位移
对(9-5)式进行积分,并根据约束条件和连续光滑条件确定积分常数,再将已确定的积分常数代回积分式,即可得到梁的挠曲线方程和转角方程,从而可确定任一截面的挠度及转角。这种求梁的位移的方法称为积分法。
在工程计算中,习惯用f 表示梁特定截面处的挠度。
【例9-1】简支梁AB 受均布载荷q 作用,如图9.8所示。建立梁的挠曲线方程和转角方程,并计算最大挠度和最大转角。 解:(1)计算支反力,列弯矩方程和挠曲线微分方程
通过平衡方程可得
2
ql F F By Ay =
= 弯矩方程为
故挠曲线微分方程为
)(2d d 22
2x lx EI q
x
w -= (2)对挠曲线微分方程积分
将上式积分两次,得
C x lx EI q x w +???
?
??-==322d d 32θ 和 D Cx x lx EI q w ++???
? ??-=126243 (3)确定积分常数
将约束条件x =0处w =0和x =l 处w =0代入上式中,可得
D =0,和EI
ql C 243
-=
(4)建立挠曲线方程和转角方程
将C 、D 值代入积分式,分别得到挠曲线方程和转角方程
()
()
3
323434624224l x lx EI q x l x lx EI
q
w --=--=
θ
(5)计算最大挠度和最大转角
全梁上的弯矩都为正,所以梁的挠曲线是一条上凹的曲线,又根据结构和载荷的对称性,可画
2
22)(2
qx x ql x qx x F x M Ay -
=-=
出挠曲线的大致形状如图9.8中所示。在梁中点处有最大挠度,在梁的支座A 、B 处有最大转角。将相应的x 坐标代入挠曲线方程和转角方程中,得
EI
ql EI
ql w f x l
x 2438453
max 4
2
max -
==-
====θ
θ和 负号表示其变形方向与规定的正向相反。
【例9-2】图9.9所示简支梁在C 点作用一集中力F ,梁的抗弯刚度为EI ,求梁的挠曲线方程和转角方程。 解:(1)计算支反力,列弯矩方程
通过平衡方程可得
l
Fa F l
Fb F By Ay =
=
, 分段列弯矩方程 AC 段 )0()(111a x x l
Fb x M ≤≤=
CB 段
)()()(2222l x a a x F x l
Fb
x M ≤≤--=
(2)分段列挠曲线微分方程并积分
分别列AC 和CD 段的挠曲线微分方程,并两次积分,结果见下表。
(3)确定积分常数
积分出现4个常数,需4个条件来确定。因为挠曲线是连续光滑的曲线,在两段交界面C 处,由(a 1)式确定的转角和由(a 2)式确定的转角相等;由(b 1)式确定的挠度和由(b 2)确定的挠度相等。即
2
23
31132
2
2126
)
(662
)(22D a C a a F a l Fb D a C a l Fb C a a F a l Fb C a l Fb ++--=+++--=+ 由此可得: C 1=C 2, D 1=D 2
在梁的A 、B 两端有铰支座,根据约束条件有 当x 1=0时, EIw =D 1=0
当x 2=l 时, 06
)(6223
3=++--=
D l C a l F l l Fb EIw
可得
)(6,022
2121b l l
Fb C C D D --
==== (4)建立挠曲线方程和转角方程
如果要求梁上的最大挠度和最大转角,可以首先根据挠曲线的大致形状判断最大值出现的截面
位置。最大转角出现在两端截面上,在(c 1)式和(c 2)式中分别代入x 1=0和x 2=l ,得
EIl
a l Fa
b EIl b l Fab B A 6)
(,6)(+=+-
=θθ
若a >b ,可以断定θB 为最大转角。
最大挠度可以用求极值的方法计算。可以证明,梁的最大挠度所在位置非常接近于梁的中点,因此常用简支梁中点的挠度来代替梁的最大挠度。则有
)43(48222
max b l EI
Fb
w f l x --
=≈= 积分法是求梁的变形的基本方法,它可以直接运用积分求得梁的挠曲线方程和转角方程,进而求出特定截面的挠度或转角。
9.3 用叠加法求梁的位移
在实际工程中,粱上可能同时作用几种载荷,此时若用积分法计算其位移,则计算过程比较烦琐,计算工作量大。由于研究的是小变形,材料处于线弹性阶段,因此所计算的梁的位移与梁上的载荷成线性关系。所以,当梁上同时作用几种载荷时,可先分别求出每一载荷单独作用时所引起的位移,然后计算这些位移的代数和,即为各载荷同时作用时所引起的位移。这种计算弯曲变形的方法称为叠加法。
为了使用方便,将各种常见载荷作用下的简单梁的转角和挠度计算公式及挠曲线方程列于表9-1中。利用表格,按叠加法计算梁在多个载荷共同作用下所引起的位移是很方便的。
9.3.1 多个载荷作用时求梁的位移的叠加法
根据叠加法,几个载荷共同作用下梁任意横截面上的位移,等于每个荷载单独作用时该截面位移的代数和。
【例9-3】求图9.10(a )所示梁C 截面的挠度和B 截面的转角。设EI 为常数。
解:(1)梁的位移的分解
梁上有集度为q 的均布载荷和集中力F 作用,其C 截面的挠度和B 截面的转角为两个载荷单独作用下位移的代数和。即
F
B q B B F
C q C C f f f )()()()(θθθ+=+=
(2)在均布力作用下
B 截面转角查表9-1中第7栏可得
EI
ql q B 24)(3
=
θ C 截面的挠度可以通过查表9-1中第7栏的挠曲线方程,代入坐标值l x 3
2
=
计算。即 EI ql l l l l EI l q f q C 972113232224)32
()(4323-
=???
???????? ??+??? ??--= (3)在集中力F 作用下
B 截面转角查表9-1中第6栏可得
EI
ql EI Fl EIl l l l l F F B 8158156323132)(3
2==?
?? ??+???=θ
C 截面的挠度可以通过查表9-1中第6栏的两段中的任一段挠曲线方程,代入坐标值l x 3
2
=计算。即
EI ql EI Fl l l l EIl l l F f F C 24352435332632
3)(43222-=-
=???
???????? ??-??? ??-??-= (4)叠加
EI
ql
EI ql EI ql EI
ql EI ql EI ql f f f F B q B B F C q C C 6486781524)()(97231243597211)()(3
334
44=
+=+=-
=--=+=θθθ
【例9-4】 如图9.11(a )所示悬臂梁,其抗弯刚度EI 为常数,求B 点转角和挠度。 解:(1)在F 单独作用下: 查表9-1中第2
(2)在q单独作用下:
查表9-1中第3栏可得
由于CB段没有弯矩作用,挠曲线保持直线状态,而两段挠曲线在C点应相切,所以B点的转角和挠度为
(3)在F和q共同作用下:
9.3.2 逐段刚化法
在有些情况下,梁上某截面的位移是由几段梁的弯曲变形共同引起的。在计算其位移时,可以分别计算各段梁单独变形引起的该截面的位移,然后代数求和,这种分析方法称为逐段刚化法。对于表9-1中没有列出的外伸梁情况以及变截面梁情况,常用逐段刚化法分析。在梁上作用多个载荷情况下,可以先分解成单个载荷作用情形,然后分别用逐段刚化法分析,再进行位移叠加。下面通过举例说明其分析方法和特点。
【例9-5】图9.12(a )所示外伸梁,在C 处作用集中力F ,梁的EI 、l 、a 已知。求C 截面的挠度和转角。
解:该梁由AB 、BC 两段组成,梁在C 截面的挠度和转角等于两段梁分别变形时在该截面引起的挠度和转角的代数和。
(1)刚化AB 段,只考虑BC 段的变形 如图9.12(b )所示,AB 不变形,保持原来的直线形态;BC 发生弯曲,在B 点与AB 连续光滑连接,所以B 点没有转角位移,因此可以将B 截面处视为固定端,将BC 段看成悬臂梁。
查表9-1第2栏可得
(2)刚化BC 段,只考虑AB 段的变形
如图9.12(c )所示,AB 发生弯曲;CB 不变形,保持原来的直线形态,在B 点与AB 保持连续光滑连接。F 力对AB 段的作用可以用将F 力等效简化到B 点得到的一个力F 和一个力偶Fa 代替。因为力在BC 段的等效不改变对AB 的作用效果,即没有改变AB 段的弯矩,所以这种简化是可行的。简化到B 点的F 力作用在支座上,不会使AB 梁变形;力偶Fa 的作用可以查表9-1中第4栏,得到
EI
Fal
EI ml B 33-==
θ 则由AB 段变形引起的C 点的转角和挠度为
EI
l
Fa a w EI Fal C C B C 3,32222
-=?=-==θθθ
(3)叠加
梁C 截面的总挠度和总转角为
)
23(632)
(3332
212
2321l a EI
Fa
EI Fal EI Fa l a EI
Fa EI l Fa EI Fa w w w C C C C C C +-=--=+=+-=--=+=θθθ 【例9-6】求图9.13(a )所示悬臂梁端截面A 的挠度。
解:(1)刚化BC 段,只考虑AB 段的变形
如图9.13(b )所示,B 点可以看成固定端,查表9-1中第3栏得
EI
ql w A 841
= ( ) 在查表时可以发现,表中固定端位置与题中情况正好相反,这样在使用表格数据时有时会出现符号相反的情况,如本图中A 截面的转角方向为逆时针,应取正号。为了不出现错误,通常将变形后的挠曲线大致形状画出,根据变形方向确定符号,也可用箭头标明位移方向。
(2)刚化AB 段,只考虑BC 段的变形
将载荷等效简化到B 点,得到一个力ql 和一个力偶2
2
1ql ,分别计算力偶和力作用下在B 点产生的挠度和转角。查表9-1中第1、2栏可得
EI
ql EI l ql EI l
ql w EI
ql EI l ql EI l
ql B B 12732212214322322=
?+?==
?+?=θ
则A 点的挠度
EI
ql l EI ql EI ql l w w B B A 12191274
342
=?+=+=θ
(3)叠加
EI
ql EI ql EI ql w w w A A A 2441121984442
1=+=+=
9.4 简单静不定梁
9.4.1 静不定梁的概念
前面分析过的梁,如简支梁和悬臂梁等,其支座反力和内力仅用静力平衡条件就可全部确定,
这种梁称为静定梁。在工程实际中,为了提高梁的强度和刚度,往往在静定梁上增加一个或几个约束,此时梁的支座反力和内力用静力平衡条件不能全部确定,这种梁称为静不定梁或超静定梁。例如在图9.14(a )所示悬臂梁的自由端B 加一支座,未知约束反力增加一个,该梁由静定梁变为了静不定梁,如图9.14(b )。
9.4.2 变形比较法求解简单静不定梁
在静不定梁中,那些超过维持梁平衡所必需的约束称为多余约束,对应的支座反力称为多余约束反力。由于多余约束的存在,使得未知力的数目多于能够建立的独立平衡方程的数目,两者之差称为静不定次数。为确定静不定梁的全部约束反力,必须根据梁的变形情况建立补充方程式。解除静不定梁上的多余约束,变为一个静定梁。这个静定梁为原静不定梁的基本静定梁,两个梁应具有相同的受力和变形。
为了使基本静定梁的受力和变形与原静不定梁完全相同,作用在基本静定梁上的外力除了原来的载荷外,还应加上多余约束反力;同时还要求基本静定梁在多余约束处的挠度或转角满足该约束的限制条件。例如,在图9.14(b )中,若将B 端的可动铰支座作为多余约束,则可得到图9.14(c )所示的基本静定梁;且该梁应满足
w B =0 或 w B =(w B )q +(w B )FRB =0
这就是梁应满足的变形协调条件。
根据变形条件和力与变形间的物理关系可以建立补充方程。由此可以求出多余约束反力,进而
图
9.15
图9.16
求解梁的内力、应力和变形。这种通过比较多余约束处的变形,建立变形协调关系,求解静不定梁的方法称为变形比较法。
变形比较法解静不定梁步骤:第一,去掉多余约束,使静不定梁变成基本静定梁,并施加与多余约束对应的约束反力;第二,比较多余约束处的变形情况,建立变形协调关系;第三,将力与变形之间的物理关系代入变形条件,得到补充方程,求出多余约束反力。
解静不定梁时,选择哪个约束为多余约束并不是固定的,可以根据方便求解的原则确定。选取的多余约束不同,得到的基本静定梁的形式和变形条件也不同。例如图9.14(b )所示静不定梁也可选阻止A 端转动的约束为多余约束,相应的多余约束反力为力偶矩M A 。解除这一多余约束后,固定端将变为固定铰支座;相应的基本静定梁为简支梁,如图9.15所示。该梁应满足的变形关系为A 端的转角为零,即
0=+=A
AM Aq A θθθ
最后利用物理关系得到补充方程,求解可以得到与前面相同的结果。
【例9-7】房屋建筑中某一等截面梁简化为均布载荷作用下的双跨梁,如图9.16(a )所示。试求梁的全部约束反力。 解:(1)确定基本静定梁
解除C 点的约束,加上相应的约束反力F RC ,得到基本静定梁如图9.16(b )所示。
(2)变形协调条件
C 点由于支座的约束,梁的挠度为零,即
0=+=R C CF Cq C w w w
(3)建立补充方程
查表9-1中第5、7栏可得
EI l F EI l F w RC RC CF R C
648)2(33==, EI
ql EI l q w Cq 245384)2(544-=-=
代入变形关系可得补充方程为
062453
4=+-EI
l F EI ql RC 解得
ql F RC 4
5=
(4)列平衡方程,求解其他约束反力
0220=?-?-?=∑l F l F l ql M
RB RC A
020
=-++=∑ql F F F Y RC RB RA
解得
ql F F RB RA 8
3=
= 在求出梁上作用的全部外力后,就可以进一步分析梁的内力、应力、强度和变形了。
第12章 薄板的小挠度弯曲问题
第十二章薄板的小挠度弯曲问题知识点 薄板的基本概念 薄板的位移与应变分量 薄板广义力 薄板小挠度弯曲问题基本方程薄板自由边界条件的简化 薄板的莱维解 矩形简支薄板的挠度基尔霍夫假设 薄板应力 广义位移与薄板的平衡 薄板的典型边界条件 薄板自由边界角点边界条件挠度函数的分解 一、内容介绍 薄板是工程结构中的一种常用构件,它是由两个平行面和垂直于它们的柱面所围成的物体,几何特征是其高度远小于底面尺寸,简称板。薄板的弯曲变形属于弹性力学空间问题,由于数学求解的复杂性,因此,需要首先建立应力和变形分布的基本假设。 根据薄板的外载荷和几何特征,外力为横向载荷,厚度远小于薄板的平面宽度,可以忽略一些次要因素,引入一些基本变形假设,抽象建立薄板弯曲的力学模型。薄板的小挠度弯曲理论是由基尔霍夫基本假设作为基础的。 根据基尔霍夫假设,采用位移解法,就是以挠度函数作为基本未知量求解。因此,首先将薄板的应力、应变和内力用挠度函数表达。然后根据薄板单元体的平衡,建立挠度函数表达到平衡方程。 对于薄板问题,边界条件的处理与弹性力学平面等问题有所不同,典型形式有几何边界、混合边界和面力边界条件。 二、重点 1、基尔霍夫假设; 2、薄板的应力、广义力和广义位移; 3、薄板小 挠度弯曲问题的基本方程;4、薄板的典型边界条件及其简化。 §12.1 薄板的基本概念和基本假设
学习要点: 本节讨论薄板的基本概念和基本假设。 薄板主要几何特征是板的中面和厚度。首先,根据几何尺寸,定义薄板为0.5≤δ/b≥1/80,并且挠度小于厚度的五分之一,属于小挠度问题。对于小挠度薄板,在横向载荷作用下,将主要产生弯曲变形。 根据薄板的外载荷和几何特征,外力为横向载荷,厚度远小于薄板的平面宽度,可以忽略一些次要因素,引入一些基本变形假设,抽象建立薄板弯曲的力学模型。 薄板的小挠度弯曲理论是由三个基本假设作为基础的,因为这些基本假设是由基尔霍夫首先提出的,因此又称为基尔霍夫假设。 根据上述假设建立的薄板小挠度弯曲理论是弹性力学的经典理论,长期应用于工程问题的分析。实践证明是完全正确的。 学习思路: 1、薄板基本概念; 2、基尔霍夫假设 1、薄板基本概念 薄板是工程结构中的一种常用构件,它是由两个平行面和垂直于它们的柱面所围成的物体,几何特征是其高度远小于底面尺寸,简称板 薄板的弯曲变形属于弹性力学空间问题,由于数学求解的复杂性,因此,需要首先建立应力和变形分布的基本假设。 薄板的上下两个平行面称为板面,垂直于平行面的柱面称为板边,如图所示。两个平行面之间的距离称为板厚,用δ 表示。平分板厚的平面称为板的中面。 设薄板宽度为a、b,假如板的最小特征尺寸为b,如果δ/b≥1/5,称为厚板;
第9章弯曲应力与弯曲变形习题解答
第9章 弯曲应力与弯曲变形 习题解答 题9 – 1 试计算下列各截面图形对z 轴的惯性矩I z (单位为mm )。 解:(a )mm 317400 250500350200 400250250500350≈?-???-??= c y ()()4 932 3mm 107314002502003171240025050035025031712500350?≈??? ? ????-+?-??? ? ????-+?=.I Z (b )mm 431550 400800500375 550400400800500≈?-???-??= c y ()()4 1032 3mm 1054615504003754311255040080050040043112800500?≈??? ? ????-+?-??? ? ????-+?=.I Z (c )()mm 306020206050 6020102060=?+???+??= c y ()()4 63 2 3mm 103616020503012602020601030122060?=??? ? ????-+?+? ?? ? ????-+?=.Z I (a) (b) (c) 题9-1图
题9–2 悬臂梁受力及截面尺寸如图所示。设q = 60kN/m ,F = 100kN 。试求(1)梁1 – 1截面上A 、B 两点的正应力。(2)整个梁横截面上的最大正应力和最大切应力。 解:(1)求支反力 kN 220100260=+?=A F (↑) m kN 32021001260?=?+??=A M ( ) (2)画F S 、M 图 (3)求1-1截面上A 、B 两点的正应力 m kN 1305016011001?=??+?=.M F M
第9章 弯曲应力与弯曲变形综述
Engineering Mechanics (第3版) 普通高等教育“十一五”国家级规划教材 高等教育出版社
第9章弯曲应力与弯曲变形 9.1 纯弯曲时梁横截面上的正应力 9.2 横力弯曲时梁横截面上的正应力 9.3 弯曲切应力简介 9.4 弯曲变形的概念 9.5 梁的挠曲线近似微分方程 9.6 用积分法求弯曲变形 9.7 用叠加法求弯曲变形 9.8 梁的刚度校核 9.9 提高梁强度和刚度的措施 小结 思考题
第9章 弯 曲 应 力 与 弯 曲 变 形 9.1 纯弯曲时梁横截面上的正应力 9.1.1 梁的纯弯曲 前一章讨论了梁弯曲时梁横截面上的内力——剪力和弯矩。但要解决梁的强度问题,必须进一步了解横截面上应力的分布规律。剪力和弯矩是横截面上分布内力的 合成结果。切应力对应的内力为剪力,正应力对应的内力为弯矩。 梁(或某段梁)的各个横截面上仅有弯矩而无剪力,从而仅有正应力而无切应力的弯曲,称为纯弯曲。而横截面上同时存在弯矩和剪力,即既有正应力又有切应力的弯曲称为横力弯曲或剪切弯曲。 例如,图9 - 1a 所示简支梁。由图可知梁的CD 段为纯弯曲,AC 和DB 段为横力弯曲。 图9 – 1 y a a F F B x z A C (a) D x F S F F (c) a a F F B C D (b) A F A F B (d) Fa M x
9.1.2 纯弯曲时梁横截面上的正应力 研究纯弯曲时梁横截面上的正应力,需从几何、物理和静力关系等三方面考虑。 由以上试验结果可作如下假设:原为平面的横截面变形后仍保持为平面,且仍垂直于变形后梁的轴线,只是绕横截面内某一轴旋转一角度。这就是弯曲变形的平面假设。 1. 变形几何关系 取截面具有纵向对称轴(例如矩形截面)的等直梁,在其侧面画两条横向直线mm 及nn ,并在横向线间靠近顶面和底面画两条纵向线段aa 与 bb (图9 – 2a )。然后在梁的纵向对称面内两端施加一对等值、 反向的力偶,作梁的纯弯曲变形试验(图9 – 2b )。 a a b b m m n n (a) (b) m m n n y ρ M e M e O' O' b' b' a' a' d θy y z b' 中性轴 中性层 对称轴 (c) 图9 – 2 b' a a '' b b ''可观察到: (1)横向直线变形后仍为直线,且仍然垂直于已经变成弧线的 和 ,只是相对旋转了一个角度。 (2)靠近顶面的纵向线段aa 缩短,靠近底面的纵向线段bb 伸长。
案例-弯曲变形与强度.
台湾丰原高中礼堂坍塌事故原因分析 建筑物坍毁是工程事故发展的最终阶段,因此所有坍塌事故均属于恶性事故。按照《建筑结构设计统一标准》(GB 68—84、GB 50068—2001)和结构抗震设计“小震不坏,中震可修,大震不倒”三准则的要求,所有坍塌事故,包括地震灾后的坍塌事故,都属于责任事故,应该追究当事人责任。只有经过分析鉴定,确认事故原因存在设计安全水准以外的意外因素时,才能界定为天灾,豁免当事人责仟。下面列举的坍塌事故都是近年来发生在国内外的引起全社会关注的恶性事故,并且都是人为过失事故。说明在所有工程事故中,人为过失事故占了很大比例,值得警惕! 1.案例背景 该礼堂位于一栋19.5m×49.5m的两层长方形建筑的第2层(底层为教室),层高6m,平面如图1所示。屋顶结构由跨度19.5m、中心间距4.5m的钢桁架承重。桁架端部高125cm,跨中高135cm,次桁架起纵向支撑的作用,并与主桁架相连接构成整体,由40cm×60cm的钢筋混凝土柱与纵向连系梁组成纵向排架支承,并在⑤~⑧轴处从联系梁则面悬挑出一很大的钢筋混凝土雨篷。屋盖系统如图2所示。 图1 中学礼堂平面图图2 礼堂顶层结构简图 施工过程中,由于某种原因,在底层教室完工后,曾有10个月的停工间隙期,因而在第2层楼面以上的钢筋混凝土立柱中,存在施工缝的处理问题。 该建筑于1975年1月竣工。由于出现严重的屋面渗漏现象,在1983年6月对屋面进行返修。返修时,为了改善屋面的保温隔热性能,在屋顶上增加了一个蓄水保温系统。 1983年8月24日,该礼堂屋顶结构发生坍塌。虽然事故的前一天曾经下过雨,但在事故发生的时候,并未在结构上施加任何临时额外荷载,坍毁前也没有出现异兆。 2.可用于事故原因分析的线索 (1)节点连接的施工质量问题 台湾技术学院的C.Y.林教授经过现场考察认为,结构系统的坍毁很可能是始于下弦拉杆的某一焊接头断裂,或者是由于垂直杆与斜撑杆的螺栓接头松
工程力学课后习题答案第十二章 组合变形
第十二章 组合变形 习 题 12.1 矩形截面杆受力如图所示。已知kN 8.01=F ,kN 65.12=F ,mm 90=b , mm 180=h ,材料的许用应力[]MPa 10=σ,试校核此梁的强度。 题12.1图 解:危险点在固定端 max y z z y M M W W σ= + max 6.69[]10MPa MPa σσ=<= 12.2 受集度为q 的均布载荷作用的矩形截面简支梁,其载荷作用面与梁的纵向对称面间的夹角为0 30=α,如图所示。已知该梁材料的弹性模量GPa 10=E ;梁的尺寸为 m 4=l , mm 160=h ,mm 120=b ;许用应力[]M Pa 12=σ;许可挠度[]150 l w = 。试校核梁的强度和刚度。 题12.2图 22zmax 11 cos3088y M q l q l ==?解: 22ymax 11 sin 3088 z M q l q l ==?
22 ymax zmax 2 211 cos30sin 308866 z y q l q l M M bh bh W W σ??= +=+ 26cos30sin 30 ()8ql bh h b =+ 3 2 616210422 ( )8120160100.1600.120 -???=+??? []6 11.971012.0,Pa MPa σ=?==强度安全 44 z 3 5512sin 30384384z y q l q l W EI Ehb ?== 4 4 3 5512cos30384384y y z q l q l W EI Ehb ?== max W == = []4 0.0202150 m w m =<=刚度安全。 12.3 简支于屋架上的檩条承受均布载荷kN/m 14=q , 30=?,如图所示。檩条跨长 m 4=l ,采用工字钢制造,其许用应力[]M Pa 160=σ,试选择工字钢型号。 14 kN/m q = 题12.3图 解: cos ,sin y z q q q q ??== 22 max max ,8 8 y z z y q l q l M M = = max max max []y z z y M M W W σσ=+≤
材料力学讲稿:第8章 弯曲变形
第八章弯曲变形 一、教学目标 掌握求梁变形的两种方法:积分法和叠加法,明确叠加原理的使用条件,掌握用变形比较法求解静不定梁。 二、教学内容 弯曲变形的量度及符号规定; 挠曲线近似微分方程及其积分; 计算弯曲变形的两种方法; 用变形比较法解简单的超静定梁 三、重点难点 梁的变形分析。 挠曲线近似微分方程。 积分法求梁的变形。 叠加法求梁的变形。 用变形比较法解简单超静定梁。 四、教学方式 采用启发式教学,通过提问,引导学生思考,让学生回答问题。 五、计划学时 4 学时
六、实施学时 七、讲课提纲 回顾: 弯曲内力——在外力作用下,梁的内力沿轴线的变化规律。 弯曲应力——在外力作用下,梁内应力沿横截面高度的分布规律。 本章 弯曲变形——在外力作用下,梁在空间位置的变化规律。 研究弯曲变形的目的 ★刚度计算; ★解简单的超静定梁。 本章的基本内容 ★弯曲变形的量度及符号规定; ★挠曲线近似微分方程及其积分; ★计算弯曲变形的两种方法; ★用变形比较法解简单的超静定梁。 (一)、弯曲变形的量度及其符号规定 1、度量弯曲变形的两个量: ⑴挠度:梁轴线上的点在垂直于梁轴线方向的所发生的线位移ω称为挠
度。(工程上的一般忽略水平线位移) 图8-1 ⑵转角:梁变形后的横截面相对于原来横截面绕中性轴所转过的角位移θ称为转角。 2、符号规定: ⑴坐标系的建立:坐标原点一般设在梁的左端,并规定:以变形前的梁 轴线为x轴,向右为正;以y轴代表曲线的纵坐标(挠 度),向上为正。 ⑵挠度的符号规定:向上为正,向下为负。 ⑶转角的符号规定:逆时针转向的转角为正; 顺时针转向的转角为负。 (二)、挠曲线近似微分方程及其积分 1、挠曲线 在平面弯曲的情况下,梁变形后的轴线在弯曲平面内成为一条曲线,这
10弯形矫正讲解
钳工工艺一体化授课计划
讲授新课:(工艺知识) 定义:将坯料弯成所需要形状的加工方法,称为弯形。 一、弯形 1.弯形概述 弯形是使材料产生塑性变形,因此只有塑性好的材料才能进行弯形。钢板弯形后它的外层材料伸长,内层材料缩短,而中间有一层材料弯形后长度不 变,则称为中性层。 弯形虽然是塑性变形,但也有弹性变形,为抵消材料的弹性变形,弯形过程中应多弯一些。 2.弯形坯料长度的计算 坯料经弯形后,只有中性层的长度不变,因此计算弯形工件坯料长度时,可按中性层的长度进行计算。但当材料弯形后,中性层并不在材料的正中,而是偏向内层材料一边。实验证明,中性层的实际位置与材料的弯曲半径r和枋料的厚度t有关。 钢板弯曲前后 a)弯曲前 b)弯曲后弯形时中性层位置当材料厚度不变时.弯形半径越大,变形越小,中性层的位置就越接近材料厚度的几何中心。弯形的情况不同时,中性层的位置也不同。 表为中性层系数x0的值。从表中r/t的比值中可以看出,当弯形半径r≥16t 时,中性层在材料的中间(即中性层与几何中心重合)。在一般情况下,为简化计算,当r/t≥8时,可取x0=0.5进行计算。
弯形的形式有多种,图中a 、b 、c 为内面带圆弧的制件,d 是内为直角的制件。 内面带圆弧制件的坯料长度等于直线部分(不变形部分)与圆弧中性层长度(弯形部分)之和。圆弧部分中性层长度的计算式为: A=π(r+ x0t )?180a 式中A ——圆弧部分中性层长度,mm ; r ——弯形半径,mm ; z 。——中性层位置系数; t ——材料厚度(或坯料直径),mm ; a ——弯形角(即弯形中心角),单位(°)。 内面弯形成不带圆弧的直角制件时,其坯料长度的计算可按弯形前后坯料的体积不变,采用A=0.5t 的经验公式求出。 例1厚度t=4mm 的钢板坯料,弯成图中的制件,若弯形角a=120°,内弯形半径r=16 mm ,边长l 1=60mm 、l 2=120 mm ,求坯料长度L 是多少? 解:r/t=6/4 得x 0=O.41 因为 L= l 1+ l 2+A A=π(r+ x 0t )? 180a =3.14×(16+0.41×4) × ??180120 =36.93mm 所以 L= l 1+ l 2+A
弯曲变形分析
弯曲变形分析 弯曲过程中,当坯料上作用有外弯曲力矩时,坯料的曲率半径发生变化。 图1表示板弯曲变形区(ABCD部分)内切向应力的变化情况。弯曲过程中内区 (靠近曲率中心一侧)切向受压,外区(远离曲率中心一侧)受拉。 根据变形程度,弯曲过程可分为三个阶段: 1)弹性弯曲。在变形开始时变形程度较小,坯料变形区应力最大的内、 外表面的材料没有产生屈服,变形区内材料仅为弹性变形。此时的切向应力 分布如图3-1a所示。 2)弹-塑性弯曲。随着变形的增大,坯料变形区内、外表面材料首 先屈服,进入塑性变形状态。随着变形的进一步增大,塑性变形由表面向中 心逐步扩展。切向应力分布如图3-1b。 3)纯塑性弯曲。变形到一定程度,整个变形区的材料完全处于塑性变形 状态。切向应力分布如图3-11c。 弯曲变形过程 在压力机上采用压弯模具对板料进行压弯是弯曲工艺中运用最多的方法。弯曲变形的过程一般经历弹性弯曲变形、弹-塑性弯曲变形、塑性弯曲变形三个阶段。现以常见的V 形件弯曲为例,如图1 所示。板料从平面弯曲成一定角度和形状,其变形过程是围绕着弯曲圆角区域展开的,弯曲圆角区域为主要变形 区。 弯曲开始时,模具的凸、凹模分别与板料在 A 、B 处相接触。设凸模在 A 处施加的弯曲力为 2F (见图 1 a )。这时在 B 处(凹模与板料的接触支点则产生反作用力并与弯曲力构成弯曲力矩M = F·(L 1 /2),使板料产生弯曲。在弯曲的开始阶段,弯曲圆角半径r 很大,弯曲力矩很小,仅引起材料的弹性弯曲变形。
图1 弯曲过程 随着凸模进入凹模深度的增大,凹模与板料的接触处位置发生变化,支点 B 沿凹模斜面不断下移,弯曲力臂 L 逐渐减小,即 L n < L 3 < L 2 < L 1 。同时弯曲圆角半径 r 亦逐渐减小,即 r n < r 3 < r 2 < r 1 ,板料的弯曲变形程度进一步加大。 弯曲变形程度可以用相对弯曲半径 r/t表示,t为板料的厚度。 r/t越小,表明弯曲变形程度越大。一般认为当相对弯曲半径r/t>200时,弯曲区材料即开始进入弹-塑性弯曲阶段,毛坯变形区内(弯曲半径发生变化的部分)料厚的内外表面首先开始出现塑性变形,随后塑性变形向毛坯内部扩展。在弹-塑性弯曲变形过程中,促使材料变形的弯曲力矩逐渐增大,弯曲力臂L继续减小,弯曲力则不断加大。 凸模继续下行,当相对弯曲半径 r/t<200时,变形由弹 -塑性弯曲逐渐过渡到塑性变形。这时弯曲圆角变形区内弹性变形部分所占比例已经很小,可以忽略不计,视板料截面都已进入塑性变形状态。最终,B 点以上部分在与凸模的V形斜面接触后被反向弯曲,再与凹模斜面逐渐靠紧,直至板料与凸、凹模完全贴紧。 若弯曲终了时,凸模与板料、凹模三者贴合后凸模不再下压,称为自由弯曲。若凸模再下压,对板料再增加一定的压力,则称为校正弯曲,这时弯曲力将急剧上升。校正弯曲与自由弯曲的凸模下止点位置是不同的,校正弯曲使弯曲件在下止点受到刚性镦压,减小了工件的回弹(进一步论述见本章第 3.2.2节)。
材料力学的习地的题目册标准详解-第6章弯曲变形
第六章弯曲变形 一、是非判断题 1.梁的挠曲线近似微分方程为EIy’’=M(x)。(√)2.梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角为零。(×)3.两根几何尺寸、支撑条件完全相同的静定梁,只要所受载荷相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是 否相同无关。(×)4.等截面直梁在弯曲变形时,挠曲线的曲率最大值发生在转角等于零的截面处。(×)5.若梁上中间铰链处无集中力偶作用,则中间铰链左右两侧截面的挠度相等,转角不等。(√)6.简支梁的抗弯刚度EI相同,在梁中间受载荷F相同,当梁的跨度增大一倍后,其最大挠度增加四倍。(×)7.当一个梁同时受几个力作用时,某截面的挠度和转角就等于每一个单独作用下该截面的挠度和转角的代数和。(√)8.弯矩突变的截面转角也有突变。(×) 二、选择题 1. 梁的挠度是(D) A 横截面上任一点沿梁轴线方向的位移 B 横截面形心沿梁轴方向的位移 C横截面形心沿梁轴方向的线位移
D 横截面形心的位移 2. 在下列关于挠度、转角正负号的概念中,(B)是正确的。 A 转角的正负号与坐标系有关,挠度的正负号与坐标系无关 B 转角的正负号与坐标系无关,挠度的正负号与坐标系有关 C 转角和挠度的正负号均与坐标系有关 D 转角和挠度的正负号均与坐标系无关 3. 挠曲线近似微分方程在(D)条件下成立。 A 梁的变形属于小变形 B 材料服从胡克定律 C 挠曲线在xoy平面内 D 同时满足A、B、C 4. 等截面直梁在弯曲变形时,挠曲线的最大曲率发生在(D)处。 A 挠度最大 B 转角最大 C 剪力最大 D 弯矩最大 5. 两简支梁,一根为刚,一根为铜,已知它们的抗弯刚度相同。跨中作用有相同的力F,二者的(B)不同。 A支反力 B 最大正应力 C 最大挠度 D最大转角6. 某悬臂梁其刚度为EI,跨度为l,自由端作用有力F。为减小最大挠度,则下列方案中最佳方案是(B) A 梁长改为l /2,惯性矩改为I/8 B 梁长改为3 l /4,惯性矩改为I/2 C 梁长改为5 l /4,惯性矩改为3I/2 D 梁长改为3 l /2,惯性矩改为I/4 7. 已知等截面直梁在某一段上的挠曲线方程为: y(x)=Ax2(4lx - 6l2-x2),则该段梁上(B)
