分式的大小比较
分式数学知识点归纳总结

分式数学知识点归纳总结一、分式的定义和基本性质1. 分式是由分子和分母组成的数,分子和分母都是整数,并且分母不为零。
2. 分式可以表示有理数,有理数包括整数和分数。
3. 分式可以看作是代数式的特殊形式,其中分母不为零。
4. 分式的分子和分母可以约分,即分子和分母同时除以一个相同的非零数。
5. 分式可以相加、相减、相乘和相除,也可以化简和合并。
6. 分式的大小比较可以用分式的加减乘除性质进行比较。
二、分式的化简和合并1. 化简分式:化简分式是指对分式的分子和分母进行约分,使分数的值保持不变的基础上,得到最简分数。
2. 合并分式:合并分式是指将两个分式相加或者相减,得到一个最简分式。
三、分式的加减乘除性质1. 分式的加法性质:分式相加时,首先要找到它们的公分母,然后将分子相加,分母保持不变。
2. 分式的减法性质:分式相减时,首先要找到它们的公分母,然后将分子相减,分母保持不变。
3. 分式的乘法性质:分式相乘时,分子相乘,分母相乘。
4. 分式的除法性质:分式相除时,将除数分子分母互换,再将所得的分式作为乘数分式进行运算。
四、分式的大小比较1. 分式的大小比较:分式大小的比较可以用分式的加减乘除性质进行比较。
对于两个分式a/b和c/d来说,若a/b<c/d,则ad<bc;若a/b>c/d,则ad>bc。
2. 分式的大小比较练习:比较分式大小时,可以将分式通分进行比较,也可以将分式转化为小数进行比较。
五、分式方程的解法1. 分式方程的定义:分式方程是含有分式的代数方程。
2. 分式方程的解法:对于分式方程的解法,首先要通过分式的化简和合并,将分式方程化为最简分式方程,然后可以通过分式方程的乘法性质和除法性质进行求解。
六、分式在实际应用中的问题求解1. 分式在应用问题中的运用:分式在实际生活中有着广泛的应用,包括比例、百分数、利率、比率、工程问题等。
2. 分式应用问题求解:在实际应用问题中,我们可以将问题中的条件转化为分式形式,然后通过分式的运算法则进行求解。
有理数的比较方法

有理数的比较方法
有理数的比较方法
有理数比较方法,是一种比较数值大小的方法,可以用来判断两个有理数之间的大小关系。
一、分式比较法
分式比较法是比较两个分式的有效方法。
当两个分式具有相同的分母时,只需比较两个分式的分子大小,谁的分子大就是大数,谁的分子小就是小数。
而当两个分式具有不同分母时,可以把它们分别乘以分母中较小的那个数,使得分母相等,然后再进行比较,谁的分子大就是大数,谁的分子小就是小数。
二、整数比较法
整数比较法是比较整数的有效方法。
比较两个整数A和B的大小时,可以用A 减去B的结果,即A-B的结果,如果结果大于零,则A大于B,结果小于零,则A 小于B;如果结果等于零,则A等于B。
三、分数比较法
分数比较法是一种专门比较分数之间关系的有效方法,它通过比较两个分数的分母和分子之间的值来判断哪个分数更大,当两个分数具有相同的分母时,只需比较两个分数的分子大小,谁的分子大就是大数,谁的分子小就是小数;而当两个分数具有不同的分母时,可以将它们都乘以分母中较小的那个数,使得它们的分母相等,然后再比较大小。
总之,比较有理数大小有分式比较法,整数比较法和分数比较法等多种方法,根据具体情况选择合适的方法即可。
分式基本性质练习题

分式基本性质练习题分式是数学中重要的概念之一,它在实际生活中有着广泛的应用。
本文将为大家提供一些分式基本性质的练习题,帮助读者巩固和深入理解分式的概念和运算规则。
练习题一:分式的乘法和除法1. 计算:$\frac{2}{3} \times \frac{4}{5}$2. 简化:$\frac{16}{24}$3. 计算:$\frac{5}{6} \div \frac{2}{3}$4. 简化:$\frac{12}{36}$练习题二:分式的加法和减法1. 计算:$\frac{1}{4} + \frac{3}{8}$2. 计算:$\frac{5}{6} - \frac{2}{3}$3. 计算:$\frac{2}{5} + \frac{3}{10}$4. 计算:$\frac{3}{4} - \frac{1}{6}$练习题三:分式的化简和换算1. 化简:$\frac{4x^2}{8x}$2. 化简:$\frac{10ab^2}{5a^2b}$3. 将小数$\frac{0.6}{1.2}$化成分数的形式。
4. 将百分数$75\%$化成分数的形式。
练习题四:分式的比较和大小关系1. 比较大小:$\frac{3}{4}$和$\frac{5}{8}$2. 比较大小:$\frac{2}{3}$和$\frac{4}{5}$3. 将分数$\frac{2}{9}$改写成百分数。
4. 将百分数$25\%$改写成分数。
练习题五:分式的应用1. 假设小明每小时工作5小时,小红每小时工作4小时,他们一起工作的效率是多少?2. 某项工程由甲、乙两人合作完成,甲单独完成需要10天,乙单独完成需要15天,他们一起工作多少天可以完成该项目?3. 假设一块土地上有甲、乙两家农场,甲家的土地面积是乙家的2倍,甲家每年产量为1000千克,乙家每年产量为800千克,问两家农场每年的平均产量是多少千克?以上是分式基本性质的练习题,希望读者朋友们通过这些练习能够提高对分式的理解和运用能力。
2017国家公务员考试行测技巧:巧解资料分析分式比较大小

2017国家公务员考试行测技巧:巧解资料分析分式比较大小众所周知,资料分析是公考行测考试中必考的一类题型,而分式比较大小的题目是资料分析中考察的重要题型。
那么怎样能快速准确的解决这样的题目呢,中公教育专家来具体分析一下。
既然是分式比较大小,那么就要熟悉分数的一些性质:对于一些简单的分式比较大小可以利用上述三个分数的基本性质进行比较。
但是如果遇到两个分数比较大小,不具备上述三种情况,而是分子分母同大小如和,第一个分数的分子、分母比第二个分数的分子、分母都小,中公教育总结有三种好用的方法。
一、首数法这种方法对于商的第一位不同的分数比较好用,比如比较大小,两个分数都是两位数除以三位数,都是0.XXX的数,此时就可以考虑用首数法,第一个数结果是0.2XXX,第二个数是0.3XXX,所以。
二、同位比较法同位比较法即相同位置上的数进行比较,找分子和分子的倍数关系,分母和分母的倍数关系。
如为了方便描述,命名分子分母都小的分数为小分数,分子分母都大的分数为大分数(注意:小分数不一定就小,大分数不一定就大,只是一个称呼)分别找倍数关系:分子:54是28的接近2倍;分母:157是135的1倍多点显然分子的倍数大于分母的倍数,相当于小分数乘以一个大于1的数,得到大分数,所以大分数大于小分数,即。
至此,我们可以得到一个结论:分子的倍数>分母的倍数,推出大分数>小分数;分子的倍数<分母的倍数,推出大分数<小分数。
三、差分法用同位比较法,发现分子分母的倍数关系比较接近时,可以考虑利用差分法,即利用差分数比较的一种方法。
如为了方便描述,命名分子分母都小的分数为小分数,分子分母都大的分数为大分数(注意:小分数不一定就小,大分数不一定就大,只是一个称呼)求出差分数,即 = 接下来用差分数代替大分数与小分数作比较,可得到,所以大分数小于小分数,即。
至此,我们可以得到一个结论:差分数>小分数,推出大分数>小分数;差分数<小分数,推出大分数<小分数。
分式不等式

分式不等式
本文将介绍分式不等式的概念及其在解决实际问题中的应用。
分式不等式是一种数学不等式,它涉及分式的大小比较。
例如,当我们在数学课本中
看到下面这个算术题时:
计算
1/2 > 1/4
我们可以很容易地看出,此题是一个分式不等式。
这里,我们要比较两个分式的大小。
比较相同分母的两个分式时,只需要看分子的大小,即:
1/2 > 1/4 <=> 2>4 => False
因此,这个题的答案是“否”。
除了比较分式的大小,分式不等式还可以用来求解实际问题中给定的分式的取值范围。
例如,我们在论文中需要得到一个式子的解析解,并且希望求出解的取值范围。
根据数学
中的等式性,我们可以用分式不等式来求解这个问题,例如:
计算 x/2+3>2 时 x 的取值范围
令 x/2+3=2,则有 x/2=−1 => x = -2,
因此,解的取值范围是x<-2.
另外,分式不等式还可以用来研究分数的分层性质,从而改进分数的基本算法。
例如,当我们想要在给定的范围内确定最优的分数的时候,可以使用分式不等式来实现。
分式的约分与通分技巧

分式的约分与通分技巧在数学中,分式是由分子和分母组成的表达式,分式可以通过约分和通分来进行简化或合并。
约分是指分式的分子与分母同时除以它们的公约数,使分子和分母尽可能小。
通分则是将两个分式的分母统一为相同的数,以便进行比较或运算。
在本文中,我们将介绍分式的约分与通分的一些技巧。
一、分式的约分技巧当一个分式的分子和分母有公约数时,可以进行约分。
约分的目的是使得分子和分母尽可能地简化,这样可以方便计算和比较。
1. 找出分子和分母的公约数:公约数是指能够同时整除两个或多个数的数。
例如,对于分式4/8,公约数有1、2和4。
2. 除去公约数:将分子和分母分别除以它们的公约数。
对于分式4/8,我们可以除以公约数2,得到最简分式1/2。
3. 化简分式:如果分式的分子和分母仍然有公约数,可以继续进行约分操作,直到无法再约分为止。
例如,对于分式12/24,我们可以先找出它们的最大公约数为12,然后进行除法操作,得到最简分式1/2。
二、分式的通分技巧在进行分式的比较或运算时,往往需要将分式的分母统一为相同的数,这就是通分操作。
1. 找出分式的最小公倍数:最小公倍数是指两个或多个数的公倍数中最小的一个数。
例如,对于分式1/2和3/4,我们可以找出它们的最小公倍数为4。
2. 乘以适当的倍数:将分子和分母同时乘以适当的倍数,使得分母变为最小公倍数。
对于分式1/2,我们乘以2/2得到2/4;对于分式3/4,我们乘以1/1得到3/4。
3. 进行比较或运算:通分后的分式可以进行比较或运算。
例如,对于分式1/2和3/4,通分后分别为2/4和3/4,可以直接比较它们的大小。
三、约分与通分的应用约分与通分技巧在数学中的应用非常广泛,特别是在分数的计算、比较和运算中。
1. 分数的加减运算:当进行分数的加减运算时,需要先找到它们的最小公倍数,然后进行通分操作,最后进行相应的运算。
例如,对于分式1/2和1/3的相加,我们可以找到它们的最小公倍数为6,然后分别将它们通分为3/6和2/6,再进行加法运算得到5/6。
初二数学分式的综合运算、化简及比较大小
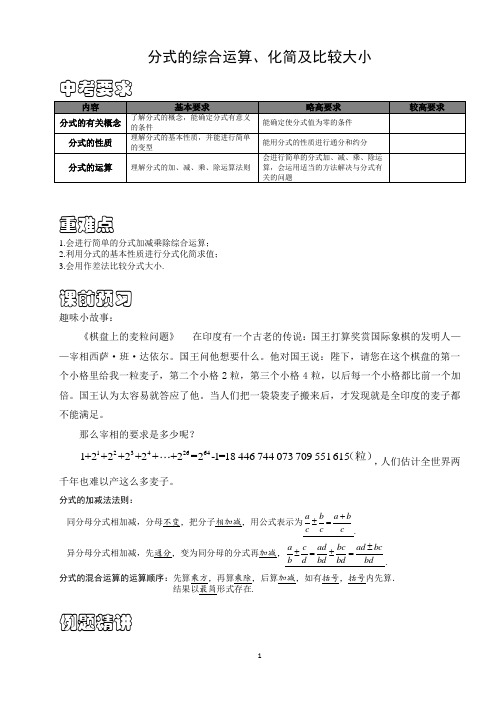
分式的综合运算、化简及比较大小中考要求重难点1.会进行简单的分式加减乘除综合运算;2.利用分式的基本性质进行分式化简求值;3.会用作差法比较分式大小.课前预习趣味小故事:《棋盘上的麦粒问题》在印度有一个古老的传说:国王打算奖赏国际象棋的发明人——宰相西萨·班·达依尔。
国王问他想要什么。
他对国王说:陛下,请您在这个棋盘的第一个小格里给我一粒麦子,第二个小格2粒,第三个小格4粒,以后每一个小格都比前一个加倍。
国王认为太容易就答应了他。
当人们把一袋袋麦子搬来后,才发现就是全印度的麦子都不能满足。
那么宰相的要求是多少呢?123426641+2+2+2+2++2=2-1=18446744073709551615(粒),人们估计全世界两千年也难以产这么多麦子。
分式的加减法法则:同分母分式相加减,分母不变,把分子相加减,用公式表示为a b a b c c c+±=.异分母分式相加减,先通分,变为同分母的分式再加减,a c ad bc ad bcb d bd bd bd±±=±=.分式的混合运算的运算顺序:先算乘方,再算乘除,后算加减,如有括号,括号内先算.结果以最简形式存在.例题精讲模块一 分式的加减运算☞分式分母相同或互为相反数 【例1】 (2010福建泉州)计算:111a a a +=++ .【难度】1星【解析】根据分式的加减运算法则可知,分式的分母相同,分子相加减,即11+1111a a a a a +==+++ 【答案】1【巩固】计算:9333a b a bab ab++-【难度】1星【解析】9393623333a b a b a b a b b ab ab ab ab a +++---===【答案】2a【巩固】计算:2222135333x x x x xx x x +--+-++++ 【难度】2星【解析】22221352623333x x x x x x x x x x +--++-+==++++【答案】2【巩固】计算:22222621616x x x x x +-++-- 【难度】2星【解析】22222262282(4)2=161616(4)(44x x x x x x x x x x x +-+--+==----++)【答案】24x +☞分式分母不相同【例2】 (2010延庆一模)计算:21211x x --- 【难度】2星【解析】分母不同,能分解因式先分解因式再通分。
资料分析之比较大小

资料分析之分式比较大小
古语有云“工欲善其事,必先利其器”,对于参加公务员考试的考生而言,考生的“器”不仅仅指夯实基础,更重要的是要掌握做题时的一些技巧,才能提高效率,在公务员考试的千军万马中脱颖而出。
在行测资料分析中,几乎每年都会涉及一类题目——比较大小,为此,很多考生感到头疼。
在这里,中公教育专家为各位考生总结了一些方法,希望能助广大考生一臂之力!
第三,当分子和分母同向变化,且分子分母相差较小时,利用差分法进行比较。
所谓差分法,就是将分子分母较小的分式称为小分数,将分子分母较大的分式称为大分数,再用大分数减去小分数(注意:是用大分数的分子减去小分数的分子,用大分数的分母减去小分数的分母)得到差分数,再将小分数和差分数做比较,去掉差分数后大小依然成立。
以上就是分式比较大小的常用方法,题目千差万别,但是万变不离其宗。
中公教育专家希望考生能掌握基本的方法以及技巧,勤于练习,在练习的过程中进一步加深理解,融会贯通,争取在这一部分做到不失分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内容 基本要求略高要求较高要求分式的概念 了解分式的概念,能确定分式有意义的条件能确定使分式的值为零的条件分式的性质理解分式的基本性质,并能进行简单的变型能用分式的性质进行通分和约分分式的运算 理解分式的加、减、乘、除运算法则 会进行简单的分式加、减、乘、除运算,会运用适当的方法解决与分式有关的问题【例1】 语句“若x y <,则22x y <”显然是不正确的。
试分别按照下列要求,将它改为正确的语句:(1)增加条件,使结论不变;(2)条件不变,改变结论。
【考点】整式的大小比较 【难度】2星 【题型】解答 【关键词】 【解析】答案不唯一【答案】(1)可增加条件:x y ,都是正数,或0x =,或||||x y <等(2)可改变结论:33x y <,也可改变22x y<等。
【例2】 若实数1a <,则实数22133a a M a N P ++===,,的大小关系为( ) A .P N M >> B .M N P >> C .N P M >> D .M P N >> 【考点】整式的大小比较 【难度】4星 【题型】选择 【关键词】作差法【解析】本题主要考查代数式大小的比较有两种方法:其一,由于选项是确定的,我们可以用特值法,取1a >内的任意值即可;其二,•用作差法和不等式的传递性可得M N P ,,的关系. 中考要求分式的大小比较例题精讲方法一:取2a =,则45233M N P ===,,,由此知M P N >>,应选D .方法二:由1a >知10a ->.又211033a a M P a +--=-=>,∴M P >;21210333a a a P N ++--=-=>,∴P N >.∴M P N >>,应选D .【答案】D【例3】 比较下列各题中的两个式子的大小:⑴a b +与a b -; ⑵221(2)2a b -+与221(21)3a b -+. 【考点】整式的大小比较 【难度】3星 【题型】解答 【关键词】作差法【解析】比较两个代数式的大小一般用求差法,即:若0A B ->,则A B >;若0A B -<,则A B <;若0A B -=,则A B =,在比较的过程中,常常需借助非负数的性质来判断差的符号,当差的符号无法确定时,应分情况进行讨论. ⑴()()2a b a b a b a b b +--=+-+= 当0b >时,20b >,∴a b a b +>-; 当0b <时,20b <,∴a b a b +<-;当0b =时,20b =,∴a b a b +=-; ⑵222222111(2)(21)(4)236a b a b a b -+--+=++ ∵20a ≥,20b ≥∴2240a b ++>即221(4)06a b ++>∴222211(2)(21)23a b a b -+>-+ 当所比较的两个代数式“同号”时,也可用求商法,看其商与1的大小关系是什么,进而判断代断式的大小.【答案】(1)当0b >时,a b a b +>-;当0b <时,a b a b +<-;当0b =时,a b a b +=-;(2)222211(2)(21)23a b a b -+>-+【例4】 已知x ,y ,z 是三个互不相同的非零实数,设222a x y z =++,b xy yz zx =++,222111c x y z =++,111d xy yz zx=++.则a 与b 的大小关系是 ;c 与d 的大小关系是 . 【考点】分式的大小比较 【难度】4星 【题型】填空【关键词】作差法,第15届,希望杯,第1试【解析】∵,,x y z 是三个互不相同的非零实数,∴222()a b x y z xy yz zx -=++-++2221()()()02x y y z z x ⎡⎤=-+-+->⎣⎦.∴a b >. 又∵222111111c d x y z xy yz zx ⎛⎫-=++-++ ⎪⎝⎭222111111102x y y z z x ⎡⎤⎛⎫⎛⎫⎛⎫=-+-+->⎢⎥ ⎪ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎝⎭⎣⎦, ∴.c d > 【答案】a b >,.c d >【例5】 已知a ,b ,c 为正数,且a b ≠,若111x a b c =++,y =,则x 与y 的大小关系是( ).A .x y >B .x y <C .x y -D .随a ,b ,c 的取值而变化【考点】根式的大小比较 【难度】4星 【题型】选择【关键词】第10届,希望杯,第2试,作差法【解析】由题意有22222x y a b c -=++1111()()a b b c =+++11()c a +--+222=++又∵a b =/,∴20->,20≥,20≥.∴0x y ->,x y >.选A .【答案】A【例6】 已知正实数a b c d 、、、满足a b c d <<<且1ac =,且S abcd =,'S a a a =+,'S b b b =+,'Sc c c=+,'sd d d=+,求''''a b c d 、、、的大小关系. 【考点】分式的大小比较【难度】5星 【题型】解答【关键词】河北省,初中数学竞赛【解析】由''()(1)0a b b a cd -=-->,所以''a b >,由''()(1)0d c d c ab -=-->,所以''c d <, 由''()(1)0b d d b ac -=--=,所以''b d =, 所以''''c d b a <=<.【答案】''''c d b a <=<【例7】 已知a b m ,,都是正数,且a b >,试证明分式a m b m ++的值总小于ab的值。
【考点】分式的大小比较 【难度】4星 【题型】解答 【关键词】作差法 【解析】略 【答案】方法1:求出两个分式的差:()()()m b a a m a ab mb ab ma b m b b b m b b m -++---==+++。
根据条件,这个差总小于0,∴a mb m ++的值总小于ab 的值。
方法2:1a m b m a b a b b m b m b m +++--==++++,1a a b b b -=+,∵a b m ,,都是正数,且a b >,所以a b a bb m b --<+ 故a m b m ++的值总小于a b的值。
【例8】 已知a b c ,,是ABC ∆中三边长,试比较ca b +和()22c a b +的大小。
【考点】分式的大小比较 【难度】4星 【题型】解答 【关键词】作差法 【解析】略 【答案】方法一求出这两个分式的差()()()()()22222c a b c c a b c c c a b a b a b a b +-+--==++++。
∵000a b c a b c >>>+>,,,∴()220c c a b a b ->++,即()22c c a b a b >++。
方法二因为a b c ,,是三角形三边长,所以0c a b <<+,所以01ca b<<+∴()22c c a b a b >++【例9】 加以两位采购员同去一家饮料公司购买两次饲料。
两次的价格有变化,两位采购员的购买方式也不同,其中甲每次购买1000千克,乙每次都用800元。
问: (1)甲、乙所购买饲料的平均单价各是多少? (2)谁的购买方式更合算? 【考点】分式的大小比较 【难度】4星 【题型】解答 【关键词】作差法【解析】(1)设两次购买饲料的平均单价分别为a 元/千克和b 元/千克,(a b ,为正数,且a b ≠)甲所购平均单价为1000100020002a b a b++=(元/千克) 乙所购平均单价为8008002800800aba ba b+=++(元/千克)(2)甲、乙所购饲料的平均单价之差是:()()()()2242222a b ab a b a b ab a b a b a b +--+-==+++。
由于a b ,均为整数,且a b ≠,∴()()22a b a b -+也是正数 ∴22a b aba b+>+。
故乙的购买方式更合算。
【答案】(1)甲所购平均单价为2a b+(元/千克)乙所购平均单价为2aba b+(元/千克)(2)乙的购买方式更合算1.设a b c ,,的平均数为M ,a b ,的平均数为N ,N c ,的平均数为P ,若a b c >>,则M 与P 的大小关系是( )A .M P =B .M P >C .M P <D .不确定【考点】整式的大小比较 【难度】4星 【题型】选择【关键词】2000,全国初中数学竞赛,做差法【解析】23224a b c a b N c a b c M N P ++++++====,,,212a b cM P +--=. 因为a b c >>,所以220a b c a c c+-+->=.即0M P ->,所以M P >.课后作业【答案】B2.证明:对于任意两个不等的正数a b ,,不等式a b +>【考点】分式的大小比较 【难度】4星 【题型】解答 【关键词】作差法【解析】略【答案】∵a b ,是不等的正数,∴2220a b +-=+-=>∴a b +>3.设,,a b c 均为正数,若c a ba b b c c a<<+++,则a b c ,,三个数的大小关系是( ) A. c a b << B. b c a << C. a b c << D. c b a << 【考点】分式的大小比较 【难度】4星 【题型】选择【关键词】第11届,希望杯,倒数法【解析】由c a b a b b c c a <<+++,a b c ,,均为正数,可知c a b c a b b a c +++<<,故可知1a cb ++11b c a b a c ++<+<+,即a b c a b c a b cb ac ++++++<<,故有c a b <<,选A . 点评:本题是对已知条件作“倒数”变形. 【答案】A。
