拉伸法测钢丝的杨氏模量(已批阅)教学文案
拉伸法测钢丝的杨氏模量教案

中国地质大学长城学院教案首页中国地质大学长城学院教案正文2、用光杠杆测微小长度L ∆微小长度L ∆测量,需要光杠杆与望远镜标尺组配合使用如上图所示,从望远镜标尺R 发出的物光经过远处光杠杆的镜面反射后到达望远镜,被观察者在望远镜中看到。
开始时,光杠杆的镜面处于垂直状态,从望远镜中看到的标尺R 上的刻度读数为R 。
实验中如果光杠杆的前足固定,而后足的支撑点(金属丝夹)有与外力砝码作用向下改变了L ∆微小长度,则光杠杆就会改变一个角度α,使镜面偏转α角度,而镜面上的反射光会相应地改变2α的角度,此时观察到的标尺R 的刻度变化到了1R 的位置。
根据上图中的几何关系可知tan Lb α∆=10tan 2R R D α-= 式中b 为光杠杆后足尖到两前足尖连线的垂直距离,D 为光杠杆镜面与直尺之间的距离。
由于角α很小,tan αα≈,tan 22αα≈,所以Lb α∆=102R R RD D α-∆==,消去α,得R D bL ∆=∆2 (3)将(3)式代入(2)式得0R1R2ααL ∆Dbα金属丝砝码金属丝夹图1 光杠杆的测量原理光数据处理规范,表格完整,过程,单位明确。
1.数据测量记录:单位:cmL= =L σD= =D σ b= =b σ测钢丝直径数据表(单位:mm ) 螺旋测微计零点0d = 序号i1 2 3 4 5 6 d= ∑2diε= i d (mm )0d d d -'=i ε=测加外力后标尺的读数序号i1 2 3 4 5 6 7 8 9 10 kgm /0.001.002.003.004.005.006.007.008.009.00加砝码时cmn i /减砝码时i n '/cmcmn i /161n n C -= =272n n C -==383n n C -==494n n C -= =5105n n C -= =C==i ε∑2iC ε=。
用拉伸法测金属丝的杨氏弹性模量课件

ቤተ መጻሕፍቲ ባይዱ 实验结果总结
实验数据记录
在实验过程中,我们记录了金属 丝在不同拉伸长度下的应力-应 变数据。通过这些数据,我们可 以分析金属丝的弹性行为并计算
杨氏弹性模量。
数据分析方法
采用线性拟合的方法处理实验数 据,通过最小二乘法得到应力与 应变之间的线性关系,从而求得
斜率,即杨氏弹性模量。
结果准确性评估
为了验证实验结果的准确性,我 们采用了多种方法进行数据分析 和处理,包括手动计算和软件分 析,确保结果的可靠性和一致性
用拉伸法测金属丝的杨 氏弹性模量课件
CONTENTS 目录
• 实验目的 • 实验原理 • 实验步骤 • 数据处理与分析 • 实验总结与思考
CHAPTER 01
实验目的
掌握拉伸法测量金属丝杨氏弹性模量的原理
了解杨氏弹性模量的 定义和物理意义。
理解金属丝在拉伸过 程中的形变和应力变 化。
掌握拉伸法测量金属 丝杨氏弹性模量的基 本原理和方法。
温度影响问题
实验过程中,温度的波动可能对金属丝的弹性模量产生影响。为了减小 温度影响,我们在恒温条件下进行实验,并尽量缩短实验时间。
对实验的改进建议和展望
01
改进实验设备
02
加强数据处理能力
为了提高实验的准确性和可重复性, 建议升级实验设备,如使用高精度测 力计和拉伸装置。
建议采用更先进的数据处理和分析方 法,如使用计算机软件进行自动化处 理和误差分析。
最小二乘法
通过最小化误差的平方和,找到数 据的最佳函数匹配,用于线性回归 分析。
数据误差分析
01
02
03
系统误差
由测量设备、环境因素等 引起的误差,具有重复性 和规律性。
实验6拉伸法测定金属的杨氏模量实验指导书

拉伸法测定金属的杨氏模量实验指导书1.实验仪器杨氏模量仪、光杠杆、尺读望 远镜、游标卡尺、千分尺、钢卷尺、砝码2.教学内容与要求2.1掌握拉伸法测定金属杨氏模量的方法:本实验利用钢丝在外力拉伸时产生形变,使得钢丝伸长。
根据胡克定律,在钢丝的弹性限度内,钢丝的应力与应变成正比:LLYS F ∆=。
只要测出在一定的受力状态下,钢丝的伸长量ΔL 就能求出钢丝的杨氏模量了。
2.2学习用光杠杆放大测量微小长度变化量的方法:钢丝伸长量的变化是一个微小量,用普通的方法难以测量,必须使这个微小量放大后才能测量。
本实验用光杠杆法放大微小量,放大方法如下图所示:从图1中我们可以看到,当钢丝拉力变化ΔF 时长度的变化为ΔL ,此时刻度尺的读数就变化了ΔN ,而要读出ΔN 是一件轻而易举的事。
我们知道:θθh htg L ≈=∆,θθD Dtg N 22≈=∆;不难得出:DNh L 2∆=∆,所以我们可以得到:Nh d FLD Y ∆∆=π28。
又因为F=Mg ,所以有Nh MgLD Y d∆∆=π282.3学习用最小二乘法处理数据。
本实验不直接计算ΔF 和ΔN ,而是将实验中测到的N i 和F i 直接代入最小二乘法公式中计算b 及其不确定度,参看课本27页公式(9)、(10)与(12),令N y M x ==,,之后再求出杨氏模量Y 和它的不确定度。
注意此时hbLDgY dπ28=。
3.重点与难点掌握用光杠杆放大测量微小长度变化量的方法,必需做到能把原理和实际的仪器状态相对应。
学会如何把杨氏模量仪、光杠杆和尺读望远镜三者之间的相对位置调整好。
4.难点指导4.1装置的调节关键在于明确每一调节步骤的目的,而不是盲目地调节。
首先杨氏模量的平台要水平,就需调节水准仪气泡至中央。
然后光杠杆的后足和前足的放置要能达到可以真实地反映钢丝长度的变化,光杠杆的镜面要垂直于杨氏模量的平台。
之后就是尺读望远镜的调节了。
尺读望远镜的调节要达到几个目标:(a )尺读望远镜距离光杠杆约1.5m (实际操作中以实验平台前端不超出地面标志线为准); (b )尺读望远镜要保持水平并与光杠杆的镜面等高;(c )望远镜和它旁边的刻度尺必须要相对于光杠杆镜面的法线成互为对称的关系;图1 光杠杆放大原理图(d )望远镜里面必须能看到光杠杆的整个镜面。
大学物理实验-拉伸法测钢丝的杨氏模量(已批阅)

大学物理实验-拉伸法测钢丝的杨氏模量(已批阅)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN实验题目:用拉伸法测钢丝的杨氏模量 13+39+33=85实验目的:采用拉伸法测定杨氏模量,掌握利用光杠杆测定微小形变地方法。
在数据处理中,掌握逐差法和作图法两种数据处理的方法实验仪器: 杨氏模量测量仪(包括光杠杆,砝码,望远镜,标尺),米尺,螺旋测微计。
实验原理:在胡克定律成立的范围内,应力F/S 和应变ΔL/L 之比满足 E=(F/S )/(ΔL/L )=FL/(S ΔL )其中E 为一常量,称为杨氏模量,其大小标志了材料的刚性。
根据上式,只要测量出F 、ΔL/L 、S 就可以得到物体的杨氏模量,又因为ΔL 很小,直接测量困难,故采用光杠杆将其放大,从而得到ΔL 。
实验原理图如右图:当θ很小时,l L /tan ∆=≈θθ,其中l 是光杠杆的臂长。
由光的反射定律可以知道,镜面转过θ,反射光线转过2θ,而且有:Db =≈θθ22tan故:)2(D b lL =∆,即是)2(D bl L =∆那么SlbDLFE 2=,最终也就可以用这个表达式来确定杨氏模量E 。
实验内容: 1.调节仪器(1) 调节放置光杠杆的平台F 与望远镜的相对位置,使光杠杆镜面法线与望远镜轴线大体重合。
(2) 调节支架底脚螺丝,确保平台水平,调平台的上下位置,使管制器顶部与平台的上表面共面。
(3) 光杠杆的调节,光杠杆和镜尺组是测量金属丝伸长量ΔL 的关键部件。
光杠杆的镜面(1)和刀口(3)应平行。
使用时刀口放在平台的槽内,支脚放在管制器的槽内,刀口和支脚尖应共面。
(4) 镜尺组的调节,调节望远镜、直尺和光杠杆三者之间的相对位置,使望远镜和反射镜处于同等高度,调节望远镜目镜视度圈(4),使目镜内分划板刻线(叉丝)清晰,用手轮(5)调焦,使标尺像清晰。
2.测量(1) 砝码托的质量为m 0,记录望远镜中标尺的读数r 0作为钢丝的起始长度。
实验六用拉伸法测定钢丝的杨氏模量
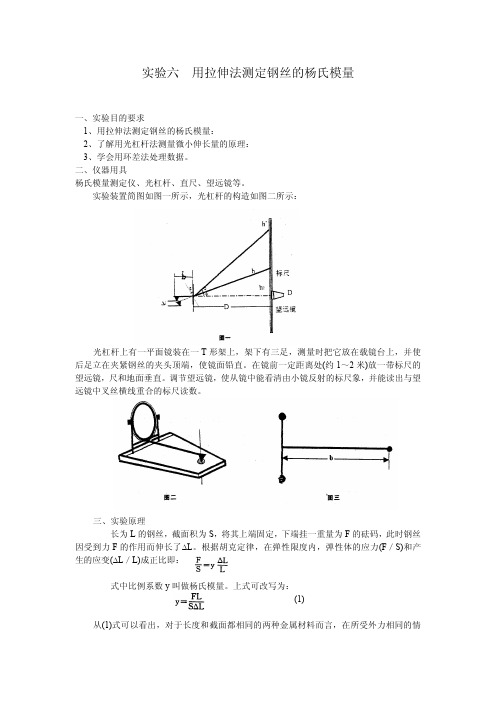
实验六用拉伸法测定钢丝的杨氏模量一、实验目的要求1、用拉伸法测定钢丝的杨氏模量:2、了解用光杠杆法测量微小伸长量的原理:3、学会用环差法处理数据。
二、仪器用具杨氏模量测定仪、光杠杆、直尺、望远镜等。
实验装置简图如图一所示,光杠杆的构造如图二所示:光杠杆上有一平面镜装在一T形架上,架下有三足,测量时把它放在载镜台上,并使后足立在夹紧钢丝的夹头顶端,使镜面铅直。
在镜前一定距离处(约1~2米)放一带标尺的望远镜,尺和地面垂直。
调节望远镜,使从镜中能看清由小镜反射的标尺象,并能读出与望远镜中叉丝横线重合的标尺读数。
三、实验原理长为L的钢丝,截面积为S,将其上端固定,下端挂一重量为F的砝码,此时钢丝因受到力F的作用而伸长了∆L。
根据胡克定律,在弹性限度内,弹性体的应力(F/S)和产生的应变(∆L/L)成正比即:式中比例系数y叫做杨氏模量。
上式可改写为:(1)从(1)式可以看出,对于长度和截面都相同的两种金属材料而言,在所受外力相同的情况下,杨氏模量大的一种材料变形∆L就小,杨氏模量小的变形就大,因此杨氏模量表示了材料抵抗形变的能力。
本实验是通过对L、S、及∆L的测量(F给定),按(1)式计算,从而测定钢丝的杨氏模量。
但由于∆L是一微小的长度变化量,不易直接测准,为此我们借助于光学放大的方法——光杠杆来测量。
在钢丝已被拉直的情况下,假定初始读数为h0,当在砝码盘上再加若干砝码时,钢丝由悬点到夹头一般将伸长∆L,同时光杠杆的后足也要随之向下移动∆L,因而使镜面向后抑了一微小角度φ,此时望远镜中标尺的读数也相应地变为h'(见图一)。
由光的反射定律知,设光杠杆两前足连线到后足的距离为b(见图),镜面到标尺的垂直距离为D,h'与h0间的距离为h,当长度变化量∆L很小时,由此可得:(2)可见通过光杠杆,∆L被放大了倍,将(2)式代人(1)式得:(3)若钢丝的直径为d,则(3)式可写成(4)在上述实验装置中,(4)式中L、D、d和b各量都是定值,唯有h随悬挂砝码重量F的增减作相应的改变。
拉伸法测量金属杨氏模量-讲义

实验七拉伸法测量金属杨氏模量杨氏模量是描述固体材料抵抗形变能力的物理量。
当一条长度为L、截面积为S的金属丝在力F作用下伸长ΔL(为微小变化量)时,F/S叫应力,即金属丝单位截面积所受到的力;ΔL/L叫应变,即金属丝单位长度所对应的伸长量;应力与应变的比叫弹性模量。
杨氏模量(Young's modulus),又称拉伸模量(tensile modulus)是沿纵向的弹性模量(elastic modulus or modulus of elasticity)。
除了杨氏模量以外,弹性模量还包括体积模量(bulk modulus)和剪切模量(shear modulus)等。
杨氏模量是工程设计上选用材料时常需涉及的重要参数之一,一般只与材料的性质和温度有关,与其几何形状无关。
杨氏模量的大小标志了材料的刚性,杨氏模量越大,越不容易发生形变。
实验测定杨氏模量的方法很多,如拉伸法、弯曲法和振动法(前两种方法属静态法,后一种属动态法)。
本实验是用拉伸法测定金属丝的杨氏模量,它提供了测量微小长度的方法,既有光杠杆法,也有显微镜法。
显微镜测量基本分2种:目镜分化测量和软件测量。
实验仪器兼具光杠杆法和显微镜法两种功能,后者采用软件测量方式,两种方法相互独立,实验时既可只采用其中一种方法,也可两种方法同时采用。
实验目的1. 学会用拉伸法测量金属丝的杨氏模量2. 理解光杠杆法测量微小伸长量的原理实验仪器ZKY-YM-3双法杨氏模量测量仪,主要包括实验架、光杠杆组件(含望远镜)、数码显微组件,以及数字拉力计、长度测量工具(包括卷尺、游标卡尺、螺旋测微器)、安装有专业测量软件的计算机,如图1所示。
1. 实验架实验架是待测金属丝杨氏模量测量的主要平台。
金属丝一端穿过横梁被上夹头夹紧,另一端被下夹头夹紧,并与拉力传感器相连,拉力传感器再经螺栓穿过下台板与施力螺母相连。
施力螺母通过旋转方式加力。
拉力传感器输出拉力信号通过数字拉力计显示金属丝受到的拉力值。
最新-拉伸法测钢丝的杨氏弹性模量1 精品

拉伸法测钢丝的杨氏弹性模量篇一:用拉伸法测金属丝的杨氏弹性模量实验报告示范实验名称:用拉伸法测金属丝的杨氏弹性模量一.实验目的学习用拉伸法测定钢丝的杨氏模量;掌握光杠杆法测量微小变化量的原理;学习用逐差法处理数据。
二.实验原理长为,截面积为的金属丝,在外力的作用下伸长了?,称?丝直径为,即截面积??24,则?为杨氏模量(如图1)。
设钢?4。
??2伸长量?比较小不易测准,因此,利用光杠杆放大原理,设计装置去测伸长量?(如图2)。
由几何光学的原理可知,??8。
(?0)???,??222??图1图2三.主要仪器设备杨氏模量测定仪;光杠杆;望远镜及直尺;千分卡;游标卡尺;米尺;待测钢丝;砝码;水准器等。
四.实验步骤1调整杨氏模量测定仪2.测量钢丝直径3.调整光杠杆光学系统4.测量钢丝负荷后的伸长量(1)砝码盘上预加2个砝码。
记录此时望远镜十字叉丝水平线对准标尺的刻度值0。
'''(2)依次增加1个砝码,记录相应的望远镜读数1。
,2,?,7''''''''(3)再加1个砝码,但不必读数,待稳定后,逐个取下砝码,记录相应的望远镜读数7。
,6,?,1,0(4)计算同一负荷下两次标尺读数('和'')的平均值?('?'')2。
(5)用隔项逐差法计算?。
5用钢卷尺单次测量标尺到平面镜距离和钢丝长度;用压脚印法单次测量光杠杆后足到两前足尖连线的垂直距离。
6.进行数据分析和不确定度评定,报道杨氏模量值。
五.数据记录及处理1.多次测量钢丝直径表1用千分卡测量钢丝直径(仪器误差取0004)钢丝直径的:类不确定度()?112(?)?(?)2?1)??(?1)?0278?10?4(6?1)?00024类不确定度()???0004?00023总不确定度()?22()?()?00034相对不确定度()?()00034??048%0710测量结果???(0710?0004)?()?048%2.单次测量:用米尺单次测量钢丝长、平面镜与标尺间距,用游标卡尺测量光杠杆长(都取最小刻度。
用拉伸法测钢丝杨氏模量——实验报告

用拉伸法测钢丝杨氏模量——实验报告实验报告:用拉伸法测钢丝杨氏模量引言:拉伸试验是一种重要的材料力学测试方法,用于测量物体的杨氏模量。
钢丝作为一种常用的结构材料,其强度和刚度是工业应用的关键指标。
本实验旨在采用拉伸法来测量钢丝的杨氏模量,并通过实验结果来验证钢丝的力学性能。
实验原理:拉伸试验是通过对材料施加拉力,观察其应变与应力之间的关系来测量杨氏模量。
根据胡克定律,应变与应力之间的关系可以用以下公式表示:$$E = \frac{\sigma}{\varepsilon}$$其中,E为杨氏模量,$\sigma$为应力,$\varepsilon$为应变。
实验步骤:1. 准备工作:清洁并标识钢丝样品,准备拉力计、卡尺、示波器等实验设备。
2. 固定材料:将钢丝夹紧在拉力计上,确保钢丝受力均匀且垂直于拉力计。
3. 测量初始长度:使用卡尺测量钢丝的初始长度$L_0$,并记录。
4. 施加拉力:逐渐增加拉力施加在钢丝上,保持拉力保持稳定后记录下拉力计示数。
5. 测量应变:通过示波器等设备,测量钢丝的伸长量$\Delta L$。
6. 计算应变率:根据公式$\varepsilon = \frac{\Delta L}{L_0}$,计算出钢丝的应变率。
7. 计算应力:根据公式$\sigma = \frac{F}{A}$,计算出钢丝的应力,其中$F$为施加在钢丝上的拉力,$A$为钢丝的横截面积。
8. 绘制应力-应变曲线:将应变作为横坐标,应力作为纵坐标,绘制出钢丝的应力-应变曲线。
9. 计算杨氏模量:根据公式$E = \frac{\sigma}{\varepsilon}$,通过应力-应变曲线确定杨氏模量。
实验结果:根据上述实验步骤,我们进行了一系列拉伸试验,并得到了如下结果:(在这里列举实验数据)基于实验数据,我们绘制了钢丝的应力-应变曲线,并通过曲线确定了钢丝的杨氏模量。
讨论与结论:通过本实验,我们成功应用拉伸法测量了钢丝的杨氏模量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拉伸法测钢丝的杨氏模量(已批阅)
实验题目:用拉伸法测钢丝的杨氏模量5-
实验目的:掌握利用光杠杆测定微小形变的方法,在数据处理中,掌握逐差法和作图法两种
数据处理的方法
实验原理:在胡克定律成立的范围内,应力F/S 和应变ΔL/L 之比满足 E=(F/S )/(ΔL/L )=FL/(S ΔL )
其中E 为一常量,称为杨氏模量,其大小标志了材料的刚性。
根据上式,只要测量出F 、ΔL/L 、S 就可以得到物体的杨氏模量,又因为ΔL 很小,直
接测量困难,故采用光杠杆将其放大,从而得到ΔL 。
实验原理图如右图:
当θ很小时,l L /tan ∆=≈θθ,其中l 是光杠杆的臂
长。
由光的反射定律可以知道,镜面转过θ,反射光
线转过2θ,而且有:
故:)
2(D b l
L =∆,即是)
2(D bl L =∆
那么Slb
DLF
E 2=,最终也就可以用这个表达式来确定杨氏模量E 。
实验内容: 1.
调节仪器
(1) 调节放置光杠杆的平台F 与望远镜的相对位置,使光杠杆镜面法线与望远镜轴线大体
重合。
(2) 调节支架底脚螺丝,确保平台水平,调平台的上下位置,使管制器顶部与平台的上表
面共面。
(3) 光杠杆的调节,光杠杆和镜尺组是测量金属丝伸长量ΔL 的关键部件。
光杠杆的镜面
(1)和刀口(3)应平行。
使用时刀口放在平台的槽内,支脚放在管制器的槽内,刀口和支脚尖应共面。
(4) 镜尺组的调节,调节望远镜、直尺和光杠杆三者之间的相对位置,使望远镜和反射镜
处于同等高度,调节望远镜目镜视度圈(4),使目镜内分划板刻线(叉丝)清晰,用手轮(5)调焦,使标尺像清晰。
2.
测量
(1) 砝码托的质量为m 0,记录望远镜中标尺的读数r 0作为钢丝的起始长度。
(2) 在砝码托上逐次加500g 砝码(可加到3500g ),观察每增加500g 时望远镜中标尺上
的读数r i ,然后再将砝码逐次减去,记下对应的读数r ’i ,取两组对应数据的平均值
i r 。
(3) 用米尺测量金属丝的长度L 和平面镜与标尺之间的距离D ,以及光杠杆的臂长l 。
3.
数据处理
(1) 逐差法
用螺旋测微计测金属丝直径d ,上、中、下各测2次,共6次,然后取平均值。
将i r 每隔四项相减,得到相当于每次加2000g 的四次测量数据,如设040r r b -=,151r r b -=,
262r r b -=和373r r b -=并求出平均值和误差。
将测得的各量代入式(5)计算E ,并求出其误差(ΔE/E 和ΔE ),正确表述E 的测量结果。
(2) 作图法
把式(5)改写为
i i i MF SlE DLF r ==)/(2 (6)
其中)/(2SlE DL M =,在一定的实验条件下,M 是一个常量,若以i r 为纵坐标,F i 为横坐标作图应得一直线,其斜率为M 。
由图上得到M 的数据后可由式(7)计算杨氏模量 )/(2SlM DL E = (7) 4.
注意事项
(1) 调整好光杠杆和镜尺组之后,整个实验过程都要防止光杠杆的刀口和望远镜及竖尺的
位置有任何变动,特别在加减砝码时要格外小心,轻放轻取。
(2) 按先粗调后细调的原则,通过望远镜筒上的准星看反射镜,应能看到标尺,然后再细
调望远镜。
调目镜可以看清叉丝,调聚焦旋钮可以看清标尺。
实验数据:
实验中给定的基本数据如下:
一个砝码的质量m=(500±5)g ,Δm=5g ,ΔD=2mm ,ΔL=2mm ,Δl=0.2mm 实验中测量得到的数据如下:
钢丝直径d (六次测量结果):0.290mm ,0.291mm ,0.296mm ,0.296mm ,0.297mm ,
0.292mm
钢丝原长L=1005.0mm ,光杠杆的臂长l=72.0mm ,标尺到平面镜的距离D=1280.0mm
表一:增减砝码过程中刻度指示的变化
数据处理:
金属丝直径的平均值mm mm d 2937.06
292
.0297.0296.0296.0291.0290.0=+++++=
金属丝直径的标准差
那么它的展伸不确定度为 先考虑逐差法处理刻度:
b 0=r 0-r 4=5.205cm ,b 1=r 1-r 5=5.160cm ,b 2=r 2-r 6=5.135cm ,b 3=r 3-r 7=5.125cm 其平均值cm cm b 156.54
125
.5135.5160.5205.5=+++=
其标准差
那么b 的展伸不确定度为: 根据杨氏模量的表达式2
82lbd DLF
Slb DLF E π=
=
,那么可以求得 又根据不确定度的传递公式,那么有 不是用这个公式
所以ΔE=0.1943×107N/cm 2 最终结果写成 再考虑用图象法处理:
r
F/N
图一:r-F 图
利用ORIGIN 读出斜率为M=0.26294(取绝对值后),那么根据公式计算得 误差分析和上述类似。
实验小结:实验过程中最困难的就是实验中光学仪器的调整,但是我在实验过程中比较顺利,很快就找到了标尺的像并且调整清晰,然后在比较短的时间内顺利完成了实
验。
这个实验的数据处理比较麻烦,从测量所得结果和误差分析结果来看,实验
是比较成功的,在一定误差范围内测得了钢丝的杨氏模量。
其中用逐差法和作图
法所得到的结果基本一致,可以认为结果是可靠的。
思考题:
利用光杠杆把测微小长度ΔL变成测b,光杠杆的放大率为2D/l,根据此式能否以增加D减小l来提高放大率,这样做有无好处?有无限度?应怎样考虑这个问题?
Sol:理论上讲,增加D减小l是可以提高放大率的,但是在实际的操作过程中,在大多数情况下,一定的放大率已经能够保证人的观测和实验精确度,况且若增大D,那么在调整仪器过程中找到标尺的像会更加困难,若减小l,那么对l的测量的误差会变得更大,同时,放大率如果过大,刻度变化太大,会造成到砝码加到一定数量后就已经超过标尺量程,实验无法完成。
综合来看,应该使放大率保持在一个合适的数值,过小会造成放大效果不佳,过小会造成实际操作的困难。
