多机电力系统电磁转矩分析方法
永磁同步电机的转矩直接控制

永磁同步电机的转矩直接控制一、本文概述本文旨在探讨永磁同步电机(PMSM)的转矩直接控制策略。
永磁同步电机作为现代电力传动系统中的核心组件,具有高效率、高功率密度和优良的控制性能。
转矩直接控制作为一种先进的电机控制技术,能够实现对电机转矩的快速、精确控制,从而提高电机系统的动态响应性能和稳定性。
本文首先将对永磁同步电机的基本结构和原理进行简要介绍,为后续转矩直接控制策略的研究奠定基础。
随后,将详细阐述转矩直接控制的基本原理和实现方法,包括转矩计算、控制器设计和优化等方面。
在此基础上,本文将重点分析转矩直接控制在永磁同步电机中的应用,探讨其在实际运行中的优势和局限性。
本文还将对转矩直接控制策略的性能进行仿真和实验研究,评估其在不同工况下的控制效果。
通过对比分析,本文将提出改进和优化转矩直接控制策略的方法,以提高永磁同步电机的控制性能和运行效率。
本文将对转矩直接控制在永磁同步电机中的应用前景进行展望,探讨其在新能源汽车、工业自动化等领域的发展潜力。
本文的研究成果将为永磁同步电机的转矩直接控制提供理论支持和实践指导,推动其在现代电力传动系统中的广泛应用。
二、永磁同步电机的基本原理永磁同步电机(PMSM)是一种特殊的同步电机,其磁场源由永磁体提供,无需外部电源供电。
PMSM利用磁场相互作用产生转矩,从而实现电机的旋转运动。
PMSM的定子部分与常规电机相似,由三相绕组构成,用于产生电磁场。
而转子部分则装有永磁体,这些永磁体产生的磁场与定子绕组的电磁场相互作用,产生转矩。
PMSM的转矩大小和方向取决于定子电流的大小、方向以及永磁体与定子绕组磁场之间的相对位置。
PMSM的控制主要依赖于对定子电流的控制。
通过改变定子电流的大小、频率和相位,可以实现对PMSM转矩和转速的精确控制。
与传统的感应电机相比,PMSM具有更高的转矩密度和效率,以及更低的维护成本。
PMSM的工作原理基于法拉第电磁感应定律和安培环路定律。
当定子绕组通电时,会产生一个旋转磁场,这个磁场与转子上的永磁体磁场相互作用,产生转矩。
电力拖动系统的运动方程与负载转矩特性
实际生产中,单一类型的负载并不多见,通常是几种 不同类型负载的相近或综合,既要全面考虑,又要抓 住重点。
5、起重机提升机构的负载情况示例
起重机提升机构的工作示意图
起重机在提升重物时,负载转矩TL是重物的重力矩和系统的 摩擦转矩之和。重力矩是位能性恒转矩负载,摩擦转矩是反 抗性恒转矩负载,二者的转矩特性不同。 由于提升重物时,重力转矩比摩擦转矩大得多,所以分析其 运行状态时,要以重力转矩为主,适当考虑摩擦转矩,或者 干脆将摩擦转矩忽略不计。
T为制动转矩, TL为驱动转矩。
T和TL都为驱动 转矩。
5.运动方程中各参数的方向
转速n:规定某一旋转方向为正,反之为负。 电磁转矩T:与n的正方向同向为正,反向为负。 负载转矩TL:与n的正方向反向为正,同向为负。
6.电力拖动系统的运动状态
当T=TL时, 电动机静止或匀速运动,系统处于静态或稳态。 当T>TL时, 系统处于加速状态,比如:电动机的启动过程。
一、电力拖动系统简介
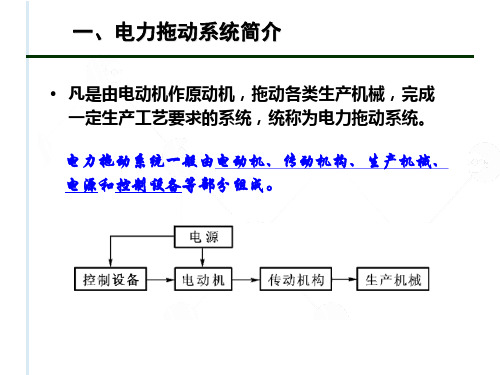
• 凡是由电动机作原动机,拖动各类生产机械,完成 一定生产工艺要求的系统,统称为电力拖动系统。 电力拖动系统一般由电动机、传动机构、生产机械、 电源和控制设备等部分组成。
一、电力拖动系统简介
• 电力拖动系统的起源要追溯到19世纪末期,其标志 是电动机逐渐取代蒸汽机。
蒸汽机
电动机
旋转运动方程:
T
轴
TL n
:作用在旋转运动部件上的拖动转矩(N·m) :负载转矩(N·m) :转动系统的转动惯量(kg·m2) :转动系统的机械角速度(rad/s) :转动系统的机械角加速度(rad/s2)
2.单轴系统的旋转运动方程
● 用转速n代替机械角速度表示系统的速度, 用飞轮矩GD2代替转动惯量J表示系统的机械惯性。
电力系统稳定性问题概述和各元件的机电特性

§ 9电力系统稳定性问题概述和各元件的机电特性1、概述电磁暂态:i(t),u(t)(假设们=肌) 机电暂态:P(t,(t),o(t)的变化)稳定性概念:刀、干扰一如正常运行时的负荷波动一电力系统静态稳定干扰丿打干扰一如重要元件的投切,故障等一电力系统暂态稳定静态稳定:受到任意小干扰后能否回到原来的(或与原来的很接近)运行状态的能力。
不发生非周期性失步。
分析方法:系统状态变量变化小,可将状态方程线性化暂态稳定:受大干扰后戶时性、能否回复原来运行状态第一、第二震荡永久性、能否保持同步运行周期不失步。
分析方法:不能线性化。
等面积定则动态稳定:在自动装置作用下,保持长过程运行稳定性的能力。
电压稳定:2、各元件的机电特性2.1、同步发电机转子运动方程:-M =M T-M E =J- - J (1)T E dt:—转子机械角加速度rad s2; f 1—转子机械角速度rad s ;J—转子的转动惯量kg.m ;M T—原动机机械转矩;M E—发电机电磁转矩。
另外:转子在额定转速(门。
)时的动能W k J「02= J二理(2)2°0将(2)代入(1)式,得:翌d M站dt上式中转矩用标幺值表示( M B = S B0)考虑到机械角速度和电角速度之间的关系: -- Pl 】P —极对数由上式dt J 贡物理意义:在发电机组转子上加额定转矩后, 转子从停顿状态 到额定转速(门..-1)时所经过的时间。
一般机械角速度1的变化不大,则有: 匚 M ..二 P T - P E注: t ,T J ,- '0为有名值,其余均为标幺值。
2WkSB ; 0d'J~dt则:2W k S B 二x —dt 別L —m 丄 (3)S B 0 dt 0 dtT J= 2W k —发电机组的惯性时间常数SB(W)转并且有将( 4) dt^.-.0dt{ 2代入(3 )得也M 厂P“—P E 厂d 、_ d dt 2 一 dt式写成状态方程形式,并且略去下标( *),有--0(Pr -P E )T J"-1^0 dtd 2、(4)并略去*)22、同步发电机的功角方程 (P--J 1、简化条件1) 只计及发电机定子电流中正序基频交流分量产生的电磁转矩 2) 发电机励磁系统的简化a 、U f ,l f 不变,则空载电动势 E q 为常数;c 、励磁装置能够保持发电机端电压 U G 不变。
电力系统分析第七章(1)

′ EqU
& jX qΣ I d
& jX dΣ I d
&& Pe = PU = Re(UI * ) = U d I d + U q I q
&′ Eq
& E′
& U Gq
& Uq & Iq
& jX qΣ I q
& UG
& U
& I
δ
δ′
ϕ
& Ud
& Id
当发电机为隐极机时xd=xq
′ ′ Pe ( Eq ) = PU ( Eq ) =
&& S U = PU + jQU = UI * = U (sin δ + j cos δ )( I d − jI q ) = U d I d + U q I q + j (U q I d − U d I q )
U d = I q X qΣ
U q = Eq − I d X dΣ
选q轴为虚轴
X dΣ = X qΣ = X d + X TL , X TL = X T1 + X L1 // X L2 + X T2
EqU
电机向外输出(系统接收)的有功功率最大(极限)值
QU = U q I d − U d I q = U q
Eq − U q X dΣ
EqU Ud U2 −Ud = cos δ − X dΣ X dΣ X dΣ
3)QU 随发电机功角δ的增大而减小,并在 δ=180度时达到最小值。其原因在于,随着 δ数值的增大,支路电流不断增加,各电气 设备消耗的无功功率不断增加。 在电力系统稳定分析中,主要关心发电 机的有功输出Pe,因此在后面章节中, 将主要讨论Pe与δ的关系。
(完整word版)高等电力系统分析

1. 对极坐标牛顿拉夫逊法简化,可以得到快速解耦潮流。
给出简化步骤,说明后者的优、缺点。
答:(1)简化步骤:快速解耦法是基于两个基本假设: R<<X 以及线路两端相角差比较小(小于10度-20度)。
反映在电力系统中的特性是:有功功率的变化主要决定于电压相位角的变化;无功功率的变化则主要决定于电压模值的变化。
反映在牛顿法修正方程式雅克比矩阵的元素上,是N 和M 两个子块元素的数值相对于H 、L 两个子块的元素要小得多。
⎥⎦⎤⎢⎣⎡∆∆⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡∆∆U U L M N H Q P /θ是一个2n-m-2阶方程组。
略去N 和M ,得到:⎩⎨⎧∆-=∆∆-=∆)/(U U L Q H P θ将原来2n-m-2阶方程组化为一个n-1及一个n-m-1阶方程组。
假设:线路两端的相角差不大(小于10度-20度),而且ij ij B G <<;与节点无功功率相对应的导纳2/i i U Q 通常远小于节点的自导纳ii B ,即ii i ij B U Q 2<<。
⎩⎨⎧==ij j i ijij j i ij B U U L B U U H 即⎩⎨⎧==U UB L U UB H '''得,⎩⎨⎧∆-=∆∆-=∆U B U Q U B U P ''/)('/θ 系数矩阵'B 及''B 由节点导纳矩阵的虚部所组成,从而是一个常数矩阵。
对'B 及''B 的构成进行进一步修改得:⎩⎨⎧∆=∆∆=∆UB U Q B U P ''/'/θ 其中,ij ij X B 1'-=,∑∑=-=jwi jwi ijij ii X B B 1'',ij ij ij ij ij B X R X B -=+-=22'',ii jwi ij ij iji ii B X R X B B -=++-=∑220''。
电力系统电磁转矩系数的性质及其计算方法

电力系统电磁转矩系数的性质及其计算方法郝正航;王映康;李健波;樊容;魏猛【摘要】为了揭示电磁转矩系数的实质,证明了用电磁转矩系数表达电磁转矩只是某种近似,还证明了将单机系统的电磁转矩定义推广于多机系统,其前提条件是所研究的机组相对于惯性中心COI(center of inertia)只有1个运动模式;基于状态空间模型,提出了单机、2机和2机群的电磁转矩系数的定义,给出了理论计算方法.在多机情形下,针对某一模式将系统视为2个机群,通过广域测量系统得到局部系统COI 的转速和功角、各发电机电磁功率,从而不需等值运算而转化为等值2机,并测辨其电磁转矩系数.算例分析表明,所提出的电磁转矩系数的理论计算和辨识方法是有效的,二者能够相互印证.%In order to investigate the essence of electrical torque coefficients, it is proved that the equation between active power and electric torque based on two coefficients is not satisfied completely and electric torque method lead to a simplified path of accurate power system model essentially. If the electric torque definition of single machine is applied to multi-machine system, the given machine must be dominated by only one oscillation mode on the center of inertia(COD. This paper also presents electric toque definition and calculating method which can be used for single machine system, two-machine system, and two-area system. In large power system, a two-area system is defined in term of certain mode and its electric torque coefficient can be computed with measured signals (e. g. speed, angle based on partial COI and active power) from wide area measurement system(WAMS). A four-machine system caseshowed that the methodology proposed can be utilized to identify the coefficient of electric torques.【期刊名称】《电力系统及其自动化学报》【年(卷),期】2011(023)001【总页数】6页(P86-91)【关键词】电力系统;电磁转矩;在线辨识;广域测量系统;小扰动稳定【作者】郝正航;王映康;李健波;樊容;魏猛【作者单位】天津大学电气与自动化学院,天津300072;贵州大学电气工程学院,贵阳550003;重庆渝电信息通信有限公司,重庆400014;重庆铜梁县供电有限责任公司,重庆402500;重庆渝电信息通信有限公司,重庆400014;重庆铜梁县供电有限责任公司,重庆402500【正文语种】中文【中图分类】TM743电力系统机电振荡分析有两种基本方法[3]:其一是根据线性化状态空间模型进行特征分析,即计算系统矩阵的特征值和特征向量,从而得到振荡频率、阻尼和振型;其二是基于物理意义的电磁转矩分析方法,将作用在转子上的电磁转矩分解为阻尼转矩和同步转矩,根据两种转矩的数值大小判断同步发电机的小扰动稳定性。
《电力系统分析》第九章 机组的机电特性

Eq j( X d X q )Id
EQ
jIX q
jId X d
Eq
E jIX d
Uq
U
Iq I
jIq X d
Id Ud
d
第九章 机组的机电特性
由相量图,可得
EQ jEQ U jIX q
Eq jEq EQ j(X d X q )Id U jIX q j(X d X q )Id
j 1
j i
设
Yij Gij jBij Yij e jij
Gij Yij cosij
Bij Yij sin ij
ij
tan1 Bij Gij
通过推演,可得
m
Pi Ei2Gii Ei E j Yij sin(ij ij ) j 1 ji
其中 ij 90 ij ,为导纳角的余角。
第九章 机组的机电特性
上式表明,任一发电机发出的有功功率是该发电机电 动势相对于其它发电机电动势相量的相角差函数。
在系统含有三台及以上发电机的情况下,不能再用曲 线作出发电机的功角特性。
对于系统有两台机的情形,其功率表达式为: PE1 E12G11 E1E2 (G12 cos12 B12 sin 12 )
由回转力矩求单位机组的惯性时间常数的计算公式为
TJ
2.74GD2nN2 1000SN
式中,GD2为包括原动机在内的机组转子的回转力矩;nN 为机组的额定转速;SN为机组的额定功率。
第九章 机组的机电特性
同步发电机基本结构
dc
x
a y
f a
cq b
b z
第九章 机组的机电特性
《电机与拖动基础(第2版)》(习题解答)

电机与拖动基础第一章电机的基本原理 (1)第二章电力拖动系统的动力学基础 (6)第三章直流电机原理 (12)第四章直流电机拖动基础 (14)第五章变压器 (29)第六章交流电机的旋转磁场理论 (43)第七章异步电机原理 (44)第八章同步电机原理 (51)第九章交流电机拖动基础 (61)第十章电力拖动系统电动机的选择 (73)第一章 电机的基本原理1-1 请说明电与磁存在哪些基本关系,并列出其基本物理规律与数学公式。
答:电与磁存在三个基本关系,分别是(1)电磁感应定律:如果在闭合磁路中磁通随时间而变化,那么将在线圈中感应出电动势。
感应电动势的大小与磁通的变化率成正比,即tΦN e d d -= 感应电动势的方向由右手螺旋定则确定,式中的负号表示感应电动势试图阻止闭合磁路中磁通的变化。
(2)导体在磁场中的感应电动势:如果磁场固定不变,而让导体在磁场中运动,这时相对于导体来说,磁场仍是变化的,同样会在导体中产生感应电动势。
这种导体在磁场中运动产生的感应电动势的大小由下式给出Blv e =而感应电动势的方向由右手定则确定。
(3)载流导体在磁场中的电磁力:如果在固定磁场中放置一个通有电流的导体,则会在载流导体上产生一个电磁力。
载流导体受力的大小与导体在磁场中的位置有关,当导体与磁力线方向垂直时,所受的力最大,这时电磁力F 与磁通密度B 、导体长度l以及通电电流i 成正比,即Bli F =电磁力的方向可由左手定则确定。
1-2 通过电路与磁路的比较,总结两者之间哪些物理量具有相似的对应关系(如电阻与磁阻),请列表说明。
答:磁路是指在电工设备中,用磁性材料做成一定形状的铁心,铁心的磁导率比其他物质的磁导率高得多,铁心线圈中的电流所产生的磁通绝大部分将经过铁心闭合,这种人为造成的磁通闭合路径就称为磁路。
而电路是由金属导线和电气或电子部件组成的导电回路,也可以说电路是电流所流经的路径。
磁路与电路之间有许多相似性,两者所遵循的基本定律相似,即KCL:在任一节点处都遵守基尔霍夫第一定律约束;KVL:在任一回路中都遵守基尔霍夫第二定律;另外,磁路与电路都有各自的欧姆定律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( 特征值为 Kk) 下的 N ×N 维的同步转矩系数矩阵
和电磁阻尼转矩系数矩阵; K sij 、D ij 称为机组之间 的同步转矩系数和电磁阻尼转矩系数。由于 Kr 、Ki
每行元素之和为 0, 易知 KS 、K D 每行元 素之和也 为 0。
$TkS
、$T
k D
分别称 为机电 振荡模 式(
特征值 为
2 区间振荡的电磁转矩分析
电力系统区间振荡是指系统中 1 个区域的 1 组 发电机对另 1 个区域的 1 组发电机发生的振荡, 振 荡频率一般在 0. 1~0. 7 Hz 之间[ 6] 。由于区间振荡 表现为 2 群发电机之间的相对摇摆, 同 1 群内发电 机基本同调, 相对振荡的发电机基本反调, 为简化分 析, 这里区间振荡用 1 个由 2 台等值发电机互联构 成的系统来等效研究, 等值系统的机间振荡对应着 原系统的区间振荡。
( 10)
王 青, 等: 多机电力系统电磁转矩分析方法
其中
AS =
0
X0 I
- M- 1 KS - M- 1( K D + Dm ) .
式( 10) 中 $Dk 、$Xk 存在非零解要求
ûAS - Kk Iû = 0,
也就是说, 机电振荡模式( 特征值为 Kk) 下发电机的 同步转矩系数矩阵、电磁阻尼转矩系数矩阵将对应 1 个实数矩阵 AS , 它必然有 1 个特征值等于 Kk 。这 样, 得到了采用机电振荡复特征值定义的多机系统 发电机电磁转矩系数与该特征值之间确切的数学联 系, 从而为多机系统电磁转矩分析方法理论基础的 最终确立创造了有利条件。
低频振荡是严重威胁电力系统安全稳定的重要
问题, 电磁转矩分析方法是研究低频振荡的经典方 法, 该方法源于单机无穷大系统线性化模型。1969 年, Demello 和 Conco rdia[ 1] 对含有快速励磁调压器
收稿日期: 2006-11-10 基金项目: 国家自然科学基金重点资助项目 ( 50323002) ;
( 2)
由式( 2) 可推得
$ E′q = ( T′ d0s + K 3 + ( TA s + I) - 1KA K6 ) - 1 ×
( - K 4 - ( TA s + I ) - 1 KA K5 ) $ D.
( 3)
发电机的电磁转矩为[ 5]
$ TE = K1 $ D+ K2 $ E′ q .
( 4)
电磁转矩分析方法对多机系统的研究较少, 20 世纪 60 年代有前苏联学者提出多机系统阻尼转矩 系数矩阵的概念[ 4, 5] 。文[ 5] 首先取 L aplace 算子 s= j X 定义多机系统电磁转矩系数矩阵, 随后将每台发 电机的电磁转矩增量转换为发电机自身转子角增量 和转速增量的线性函数的形式, 并提出基于 P rony 分析的测算各台机的电磁转矩系数的方法。对多机 系统应用电磁转矩来判定系统的机电振荡稳定性, 其理论依据方面目前还未见到有深入研究的报道。
征值为 Kk ) 相对应的分量记为 $ TkE , 有
$ TkE = KE ( Kk ) $ Dk.
其中
K E( Kk) = K 1 + K2 ( T′d0Kk + K 3 +
( TA Kk + I ) - 1 KA K6 ) - 1( - K 4 -
( TA Kk + I ) - 1 KA K5 ) .
多机电力系统电磁转矩分析方法
王 青, 闵 勇, 张毅威
( 清华大学 电机工程与应用电子技术系, 电力系统及大型发电设备安全控制和仿真国家重点实验室, 北京 100084)
摘 要: 为了将电磁转矩 分析方法应用于多 机系统, 采 用系 统机 电振荡复特 征值定义 多机系统发 电机电磁转 矩和电 磁 转矩系数矩阵, 推导了电磁转矩系数与机电振荡特征值 之间 的函数关系, 为多机系统电磁转矩分析方法理论基础的 最终 确立创造了有利条件。将电磁转矩分析方法应 用于区间振荡 的研 究, 通过 算例验证 了理论分析 的正确性, 并分 析了发 电 机电 磁阻尼转矩 系数受自 动励磁调压 器放大倍数 高低的 影 响规律, 获得了对区间振荡新的深刻认识。
放大倍数、机械阻尼系数对角阵; K 1 至 K6 为系数 矩阵; 以上各列向量均为 N 维, 矩阵均为 N ×N 维。K1 、K4 、K5 矩阵每行元素之和等于 0, 这是由于 采用转子绝对角所致。
令式( 1) 的系统矩阵为 A0, 状态向量为 X , 式 ( 1) 经 L aplace 变换可得
( A0 - sI) X = 0.
将式( 3) 代入式( 4) 可得
$TE = K E( s) $ D.
其中:
K E( s) = K1 + K 2( Td′0 s + K 3 +
( TA s + I ) - 1 KA K6 ) - 1 ( - K4 -
( TA s + I) - 1KA K 5) .
因此有
$D
$D
s $ X = A1 ( s) $ X =
有
$TkE = K r $Dk + jK i$ Dk .
( 7)
其中:
Kr = Re( K E( Kk) ) , K i = Im ( KE( Kk ) ) .
由 K1 、K 4、K5 矩阵每行元素之和等于 0, 容易
推知: Kr 、Ki 每行元素之和必为 0。
式( 6) 中有( R+ jX) $ Dk = X0 $ Xk, 故
Kk) 下的发电机同步转矩、电磁阻尼转矩, 有:
N
∑ $ TkSi =
K sij $Dij , i = 1, …, N ,
j= 1
j ≠i
N
∑ $T
k 1, …, N .
j= 1 j ≠i
将式( 9) 代入式( 6) , 经整理可得
$ Dk
[ AS - Kk I] $ Xk = 0.
ISSN 1000-0054 CN 11-2223/ N
清华大学学报 ( 自然科学版) J T singh ua U n iv ( Sci & Tech ) ,
2008 年 第 2008, V o l.
48 卷 第 1 期 48, N o . 1
w3 http: / / qhx bw . chinajo urnal. net. cn
j$ Dk =
-
R$ Dk + X
X0 $ Xk .
( 8)
式( 8) 代入式( 7) , 可得
$ TkE =
$ TkS +
$T
k D
=
KS $ Dk +
KD $ Xk .
( 9)
其中:
KS =
Kr -
Ki
R X
,
K
D
=
Ki
X0 X
.
KS = { K sij } 、KD = { D ij } 分别称为机电振荡模式
本文将从理论基础和应用 2 方面对多机系统电 磁转矩分析方法展开讨论, 通过严格的数学推导为 多机系统电磁转矩分析方法理论基础的最终确立创 造条件, 同时将电磁转矩分析方法应用于电力系统 区间振荡 的研究之 中, 加 深对区 间振荡 的认识 和 理解。
1 多机系统电磁转矩分析的理论基础
设系统共有 N 台发电机, 装有快速晶闸管型自 动励磁调压器( AVR) , 发电机采用 3 阶模型, 系统
0
- T-A 1K A K6 - T-A 1
$D
$X
$ E′ q .
( 1)
$ Efd 其中: $ D、$ X、$E′ q 、$Efd 分别为发电机的转子绝 对角、转速、暂态电势、励磁电 压列向 量; M、T′ d0、 TA 、KA 、Dm 分别为发电机的惯性时间常数、励磁绕 组时间常数、励磁调压器的时间常数、励磁调压器的
Abstract: T raditi on al elect rical t orque anal yses are limit ed t o sin gle machin e w it h an inf init e bus. T his paper pr esent s a t or qu e anal ysis meth od to m ult i-machin e pow er s yst ems based on t he ut ilizat ion of t he compl ex eigen valu es corresponding t o th e elect romechanical oscillat ions. T he eigenval ues t o elect romech anical oscillat ions are relat ed to t he elect rical t orque coef ficient mat rixes in mult i-m ach ine pow er sys tems . Th e elect rical t orque an al ys is m et hod is t hen app lied t o t he s t udy of int er-area oscil lat ion s in pow er syst ems. A n exam ple ill ust rates t he validit y of t he t heoret ical analys is and th e infl uen ce of t he au tomat ic vol t age regulat or gain on t h e d ampin g t orque coeff icient to f urt her un ders t andin g of i nt er-area os cil lat ions .
