重庆理工大学(10-11)高等数学AⅡ(a)
2011级重庆理工大学化工学院 化学与工艺培养计划

(化学工程与工艺)专业培养方案专业代码:学科二级类:化工与制药类授予学位:工学学士一、有关说明(一)业务培养目标本专业培养具备化学工程与化学工艺方面的知识,有较强工程实践能力,毕业后能在化工、炼油、新材料、制药、能源、环保等领域从事工程设计、技术开发、生产技术管理、科学研究等方面的高素质应用型高级专门人才。
(二)基本规格和要求本专业学生主要学习化学工程与化学工艺学等方面的基本理论和基本知识,受到化学与化工实验技能、工程实践、计算机应用、科学研究与工程设计方法的基本训练,具有对化工企业的生产过程进行模拟优化、革新改造,对新过程进行开发设计和对新产品进行研制的基本能力。
本专业毕业生应获得以下几方面的知识和能力:其一,掌握化学工程、化工工艺、精细化工等学科的基本理论、基本知识;其二,熟悉国家对于化工生产、设计、研究与开发、环境保护等方面的方针、政策和法规;其三,了解化学工程与工艺的理论前沿,了解新工艺、新技术与新设备的发展动态;其四,掌握精细化工,材料化工、生物化工等专业方向基础知识,具有化工产品性能检测、产品质量控制和技术管理的基本知识和初步能力;其五,具有对新产品、新工艺、新技术和新设备进行研究、开发和设计的初步能力;其六,掌握文献检索、资料查询的基本方法,具有一定的科学研究和实际工作能力;其七,具有创新意识和独立获取新知识的能力。
(三)主干学科化学、化学工程与技术。
(四)主要课程无机化学、分析化学、有机化学、物理化学、化工原理、化工热力学、化学反应工程、分离工程、化工工艺学、化工设计。
(五)主要实践环节主要实践教学环节:包括军训、工程训练、课程设计、认识实习、生产实习、毕业设计(论文)等。
主要专业实验:包括无机化学实验、分析化学实验、有机化学实验、物理化学实验、化工原理实验、化工专业基础和专业综合实验等。
(六)专业特色和方向本专业立足重庆,面向企业,制定“厚基础、宽口径、重实践、强能力、高素质”的复合型工程技术人才培养模式;设立精细化工、材料化工、生物化工三个专业方向;强化实践教学环节,加强校企联合办学和产学研的合作,建立实习基地,培养适应地方经济发展应用型人才。
2022年重庆理工大学考研真题812高等代数(A卷)

重庆理工大学2022年硕士研究生招生考试试题学院名称:理学院学科、专业名称:数学考试科目(代码):高等代数812(A 卷)(试题共2页)注意:1.所有试题的答案均写在专用的答题纸上,写在试题纸上一律无效。
2.试题与答卷一并随原信封交回。
一、填空题(本题25分,每小题5分)1.有理数域Q 上的多项式5432()221f x x x x x x =--++-的典型分解式是_______________;2.设A 是5阶矩阵,若线性方程组0Ax =的基础解系中有1个向量,则A 的伴随矩阵*A 的秩*()R A =_______________;3.设A ,B 均为n 阶正定矩阵,则AB 为正定矩阵是AB BA =的__________条件(填充分、必要、充分必要,或既不充分也不必要);4.已知线性方程组12312112323120x a x a x ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪+= ⎪⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭无解,则____________a =;5.设二次型22123121323(,,)24f x x x x x ax x x x =-++的负惯性指数是1,则a 的取值范围是_______________。
二、(本题15分)证明多项式12()1p p f x x x x --=++++ 在有理数域Q 上是不可约的,其中p 是一个素数。
三、(本题10分)求n 阶行列式n x x x y xx y x D x y x x yx xx=的值。
四、(本题15分)设矩阵A 的伴随矩阵*1000010010100308A ⎛⎫⎪ ⎪=⎪⎪-⎝⎭,且113ABA BA I --=+,其中I 为4阶单位矩阵,求矩阵B 。
五、(本题15分)设A 是n 阶矩阵,证明:A 的秩()1R A =的充分必要条件是存在两个n 维非零列向量α和β,使得TA αβ=。
六、(本题15分)设非齐次线性方程组为123123123(1)0(1)3(1)x x x x x x x x x λλλλ+++=⎧⎪+++=⎨⎪+++=⎩。
重庆理工大学继续教育学院课表
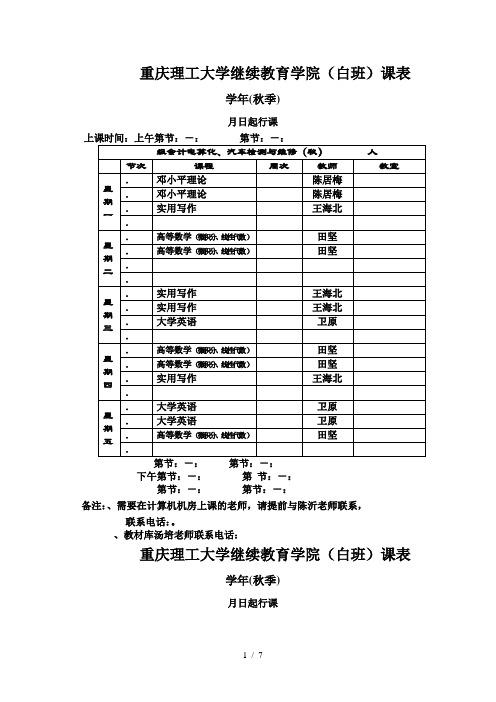
重庆理工大学继续教育学院(白班)课表学年(秋季)月日起行课下午第节:-:第节:-:第节:-:第节:-:备注:、需要在计算机机房上课的老师,请提前与陈沂老师联系,联系电话:。
、教材库汤培老师联系电话:重庆理工大学继续教育学院(白班)课表学年(秋季)月日起行课下午第节:-:第节:-:第节:-:第节:-:备注:、需要在计算机机房上课的老师,请提前与陈沂老师联系,联系电话:。
、教材库汤培老师联系电话:重庆理工大学继续教育学院(白班)课表学年(秋季)月日起行课下午第节:-:第节:-:第节:-:第节:-:备注:、需要在计算机机房上课的老师,请提前与陈沂老师联系,联系电话:。
、教材库汤培老师联系电话:重庆理工大学继续教育学院(周末班)课表学年(秋季)第节:-:第节:-:下午第节:-:第节:-:第节:-:第节:-:重庆理工大学继续教育学院(周末班)课表学年(秋季)第节:-:第节:-:下午第节:-:第节:-:第节:-:第节:-:重庆理工大学继续教育学院(周末班)课表学年(秋季)第节:-:第节:-:下午第节:-:第节:-:第节:-:第节:-:重庆理工大学继续教育学院(周末班)课表学年(秋季)第节:-:第节:-:下午第节:-:第节:-:第节:-:第节:-:重庆理工大学继续教育学院(周末班)课表学年(秋季)第节:-:第节:-:下午第节:-:第节:-:第节:-:第节:-:重庆理工大学继续教育学院(夜大班)课表学年(秋季)月日起行课重庆理工大学继续教育学院毕业论文、毕业实习学年(秋季)7 / 7。
重庆理工大学概率论与数理统计期末试卷答案10年12月(A)

重庆理工大学考试试卷2010~ 2011 学年第 1学期班级 学号 姓名 考试科目 概率与数理统计(理工) A 卷 闭卷 共 3 页 ···································· 密························封························线································学生答题不得超过此线一、 单项选择题(每小题2分,共22分)1、()0.5,()0.6,()0.8,P A P B P B A ===则 ()P A B 的值是( ) A 、0.6B 、0.7C 、0.8D 、0.92、设12),)F x F x ((分别为两随机变量的分布函数,若12)))F x aF x bF x =-(((为某一随机变量的分布函数,则( )A 、32,55a b ==-B 、22,33a b ==C 、13,22a b =-=D 、13,22a b ==-3、设随机变量X 的分布函数为()⎪⎩⎪⎨⎧>≤≤<=111003x x x x x F ,则()E X =( ) A 、⎰+∞04dx x B 、+⎰14dx x ⎰+∞1xdx C 、⎰133dx x D 、⎰+∞33dx x4、线路由A ,B 两元件并联组成(如图),A ,B 元件独立工作,A 正常工作的概率为pB 正常工作的概率为q ,则此线路正常工作的概率为( )A 、pqB 、p q +C 、p q pq +-D 、1pq -5、每张彩票中奖的概率为0.1,某人购买了20张号码杂乱的彩票,设中奖的张数为X ,则X 服从( )分布。
重庆理工大学2014高数C2A

班级学号姓名考试科目高等数学[经管2] A 卷闭卷共3 页································································································密························封························线··································································································学生答题不得超过此线班级学号姓名考试科目高等数学[经管2] A 卷闭卷共3 页································································································密························封························线··································································································学生答题不得超过此线重庆理工大学考试试卷2013 ~ 2014 学年第 二 学期班级 学号 姓名 考试科目 高等数学 [经管2] A 卷 闭卷 共 3 页 ································································································ 密························封························线··································································································学生答题不得超过此线 5、计算二重积分3(e )d d x Dy x y +⎰⎰,其中积分区域D 是由x y =和1x =所围成。
2019年重庆理工大学高等代数考研真题A卷

2019年重庆理工大学高等代数考研真题A 卷一、填空题(每题4分,共20分)1. 设A 为n 阶方阵,Ax =0 有非零解, 则A 必有一个特征值是______.2. 设3维列向量 1α,2α,3α 线性无关,A 是3阶方阵,且 112323A αααα=++,23223A ααα=+,23334A ααα=-,则 ||A =_______.3. 已知3阶方阵A 的特征值为1,2,2-,则A 的伴随矩阵*A 的迹(主对角线元素之和)为________.4. 在3R 中, 若线性变换T 关于基1α,2α,3α的矩阵为123103215A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭,则T 关于基1α,12αα+,123ααα++ 的矩阵为________.5. 设n 阶方阵1111a a a aa a A aa a a a a ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭的秩为1, 则a =__________.二、(15分)(1)(7分) 证明:3(1)5f x x x -=+在有理数域上不可约;(2)(8分) 求432()3552x x x x x f +++-=的全部有理根.三、(15分) 设1013211000120032A -⎛⎫ ⎪- ⎪= ⎪ ⎪⎝⎭,(1)(7分) 计算13233343A A A A +-+的值, 其中ij A 是||A 中元素ij a 的代数余子式;(2)(8分) 问A 是否可逆? 若A 可逆,求1*1(5)4A A --,其中*A 为A 的伴随矩阵.四、(20分)设有向量组 ()A :213312,1,1333a a a a a a a ααα+⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪==-=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭及向量20a a β⎛⎫ ⎪= ⎪ ⎪⎝⎭, 问a 为何值时(1)(6分) 向量β可由向量组()A 线性表示,且表示式唯一;(2)(7分) 向量β可由向量组()A 线性表示,但表示式不唯一;(3)(7分) 向量β不能由向量组()A 线性表示.五、(20分) 设非齐次线性方程组 ()Ax b b =≠0,秩A r =,(1)(10分) 若Ax b =有一个解 *η, 12,,,n r ξξξ-⋯是其导出组Ax =0的一个基础解系, 证明: *12,,,,n r ηξξξ-⋯线性无关;(2)(10分) 若 12,,,s ηηη⋯为Ax b =的解,证明:1122s s k k k x ηηη=+++也是Ax b =的解,其中 12,,,s k k k ⋯为实数, 且121s k k k +++=.六、(20分) 已知A 、B 为n 阶方阵,2n A B AB E --=,2A A =,其中n E 为n 阶单位矩阵,(1)(10分) 证明:A B -可逆, 并求其逆(用A 或B 表示);(2)(10分) 若 100031062A ⎛⎫ ⎪=- ⎪ ⎪-⎝⎭, 求矩阵B .七、(20分) 已知二次型 22212312313,,)2(2T f x x x x Ax x x x bx x ==++-,且()1,1,1T-是矩阵A 的一个特征向量,(1)(6分) 求b 的值;(2)(7分) 求正交变换x Py =, 将二次型123,,)(T x x f x x x A =化为标准形;(3)(7分) 当2T x x =时, 求123,,)(T x x f x x x A =的最大值.八、(20分) 设1302A ⎛⎫=⎪⎝⎭,22K ⨯是数域K 上所有2阶方阵构成的集合,(1)(8分) 证明:{}22,W B AB BA B K ⨯∈==是22K ⨯的子空间;(2)(12分) 求W 的一般形式、基和维数.。
重庆理工大学大一高数A1,B1答案(修改)(理,上册)

习题一一、 1. × 2. \/ 3. × 4. × 5. × 6. × 7. ×二、 1. A 2. D3. B4. A三、1. 直线y x =2. [ -1,3 )3. 1[,0]2- 4.奇5. 2log 1x y x =- 6.3,,sin u y e u v v x ===四、1(2)3f x x+=+,221()1f x x=+,11(())1211x f f x xx+==+++,11()()2f f x x=+习题二一、 1. ∨ 2. × 3. × 4.∨5. ∨6. × 二、 1. B 2. B3. A4. C三、 (1)22110nnε-=<取1N =即可(3)sin 10n n nε-≤<取1[]N ε=即可四、根据条件,0ε∀>,N ∃,当n N >时,有0n n x y M ε-≤即证。
习 题 三一、 1. × 2. × 3. × 二、 1. C2. D3. C4. C四、(1)证明:0ε∀>,要32832x x ε+-=-< 取3εδ=即可(2)0ε∀>,要242x x ε+-=-< 取δε=即可 (3)0ε∀>,要213211x x x ε---=<++只要31x ε>+即可五、 1)lim 1x x x-→=-,0lim 1x x x+→=limx x x→不存在2)1lim ()2x f x +→=,1lim ()2x f x -→=1lim ()2x f x →=2lim ()5, lim ()0x x f x f x →→==习题四一、 1. ∨ 2. × 3.∨4. ∨5. ×6. ×7. × 8. ∨ 9. ×10. × 11. ∨ 12. ×二、 1. D 2. C 3. B 4. D5. D三、 (1) 2131lim11x x x →-+=-+(2) 2211112limlim21213x x x x x x x →→-+==--+(3) 22lim 2h hx hI x h→+==(4) 23I =(5) 0I =(6) 422lim13x x I x →-==-(7) 11133lim1213n n I +→∞-==-(8) 111lim(1)2212n n →∞-=+(9) 23211132limlim111x x x x x I xx x→→++-+==-=--++(10) 15I =(11) I =+∞ (12) 0I =(13) 由于2lim 1lim1x x x→+∞→-∞==-,故原极限不存在。
重庆理工大学高等数学试卷

一、单项选择题(每小题3分,共计15分)1.=-+→113lim )0,0(),(xy xy y x ( )A 、3B 、6C 、∞D 、不存在2.函数⎪⎩⎪⎨⎧=+≠++=000),(222222y x y x y x xy y x f 在点(0,0)处( B )A 、连续但不存在偏导数B 、存在偏导数但不连续C 、既不连续又不存在偏导数D 、既连续又存在偏导数3.D 为圆122≤+y x ,则dxdy y x D⎰⎰--221=( D )A 、 πB 、3π C 、32π D 、2π 4.下面四个函数中,函数( D )在点(0,0)处不取得极值但点(0,0)是它的驻点。
A 、xy y x f =),( B 、22),(y x y x f += C 、)(),(22y x y x f +-= D 、22),(y x y x f +=5.设平面闭区域D ={}222),(R y x y x ≤+,1D ={}0,0,),(222≥≥≤+y x R y x y x ,则下列等式中正确的是( D )A 、σσd x xd D D ⎰⎰⎰⎰=14 B 、σσd y yd D D ⎰⎰⎰⎰=14 C 、σσd xy xyd D D ⎰⎰⎰⎰=14 D 、σσd x d x D D ⎰⎰⎰⎰=1224二、填空题(每小题3分,共计24分)1.微分方程1sin cos =+'x y x y 的通解为 ;2.函数xy z arctan =,则x z ∂∂= ; 3.若曲线L 是圆周122=+y x ,则曲线积分⎰Lds = 2pai ; 4.曲面32=+-xy e z z 在点(1,2,0)处的切平面方程为 2x+y-3=0 ;5.准线C 为⎩⎨⎧=--=++012222222z y x z y x ,母线平行于Z 轴的柱面方程为 ; 6.计算⎰⎰-2202x y dy e dx = ; 7.如曲线积分dy y y x dx xy x L)56()4(4214-++-⎰λλ与路径无关,则λ= 3 ; 8.幂级数∑∞=⋅13n n nn x 的收敛半径是R= 3 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京工程学院(10/11)高等数学AII 试卷
(A)
一、单项选择题 (本大题共5小题, 每题3分, 共15分)
1. 已知两点M 12M 2 (1, 3, 0), 则向量12M M
与x , y , z 轴三个方向余弦依次为
( )
A -1/2, -1/2, 2;
B -1/2, 1/2, 2;
C 1/2, -1/2, 2;
D 1/2, -1/2, 2.
2. 设f (x , y ) 在点 (x 0, y 0) 处的偏导数存在, 则00000(2,)(,)
lim h f x h y f x h y h
→+--= ( )
A f x (x 0, y 0);
B 2 f x (x 0, y 0);
C 2 f y (x 0, y 0);
D 3 f x (x 0, y 0) . 3. 设f (x , y ) 在D : x 2 + (y -2)2 ≤ 4上连续, 则二重积分表示成极坐标系下的二次积分的形式为 ( )
A.4sin 0
0d (cos ,sin )d f r r r r πθ
θθθ⎰⎰
; B.
24sin 00d (cos ,sin )d f r r r r π
θ
θθθ⎰⎰
; C.4cos 0
d (cos ,sin )d f r r r r π
θ
θθθ⎰⎰
; D. 24cos 0
d (cos ,sin )d f r r r r π
θ
θθθ⎰⎰
.
4. 级数1
1
sin
n n n
∞=∑的敛散性是
( )
A 绝对收敛; B. 条件收敛; C 发散;
D 无法判断.
5. 设∑是锥面22z x y +x 2 + y 2 = 2所割下的有限部分, 则2()xy yz z dS ∑
++=⎰⎰
( )
A. 2 ; 2 ; 2 ; 2.
二、填空题 (本大题共7小题, 每小题3分, 共21分)
1. 两平面x -ky +2z -6 = 0与2 x +y +4z -6 = 0相互垂直,则k = .
2. 已知曲面x = y 2 + z 2, 则在点 (2,-1, 1) 处的法线方程为 .
3. 已知方程x 2 + y 2 + z 2 -4 = 0,则z
y ∂=∂ . 4. 幂级数21(1)5
n n
n n x ∞
=-∑的收敛半径R = .
5. 设 Γ 为曲线x = t , y = t 2 , z = t 3从点A (0, 0, 0)到B (1, 1, 1)的一段弧,则d d y x z y Γ
-=⎰ __________ .
6. 设 Ω 是由 |x | = 1, |y | = 1/2, |z | = 1/3所围的闭区域,则(1)d d d x x y z Ω
+⎰⎰⎰= .
7. 设函数,01
()1,1x x f x x π
≤<⎧=⎨≤≤⎩的正弦级数展开式为1sin n n b nx ∞=∑,1sin n n b nx ∞
=∑的和函数为s (x ), 则 ()2s π
-= ______________.
三、解答题 (本大题共5小题, 每小题8分, 共40分)
1. 设(,)y
z f x x =,求d z 和2z x y ∂∂∂.
2. 求过点M (1, 2, 1)且与直线L 1: 20
0x y z x y z -+=⎧⎨-+=⎩
和L 2:
210
10x y z x y z +-+=⎧⎨
-+-=⎩
平行的平面方程. 3. 确定常数A , 使得sin()d d 1D
A x y x y +=⎰⎰,其中D 是由直线y = x , y = 2x , x = π/2所围的闭区域.
4. 将函数()2x x
e e
f x --=展开成x 的幂级数,并求11(21)!
n n ∞
=+∑的值.
5. 计算2222(2)d (2)d L
x xy y x x xy y y +-+--⎰,其中L 是由点O 沿曲线y=sin x 到点A (π, 0)的弧段.
四、综合应用题(本大题共3小题, 满分24分)
1. (8分) 求二元函数2249z x y =++在区域224x y +≤上的最大值、最小值.
2. (10分) 计算2d d d d d d I y y z x z x z x y ∑
=-+⎰⎰, 其中∑为锥面22z x y +z = 1, 2z =所截部分的外侧.
3. (6分) 设正项级数1
n n u ∞
=∑收敛, 证明级数11n
n n
u u ∞
=+∑
收敛.。
