惠更斯原理可以说明波的衍射现象
6-4 惠更斯原理和波的应用
6 – 4 惠更斯原理和波的应用 波的应用(简介) 三 波的应用(简介) 音响技术:音乐的空间感、环绕感,音乐厅设计. 音响技术:音乐的空间感、环绕感,音乐厅设计 超声技术: 超声诊断、无创治疗. 超声技术 超声诊断、无创治疗 通信技术: 卫星通信、光纤通信、网络世界. 通信技术 卫星通信、光纤通信、网络世界 1. 驻波
第六章 机械波
6 – 4 惠更斯原理和波的应用
物理学教程 第二版) (第二版)
驻 波 的 形 成
第六章 机械波
6 – 4 惠更斯原理和波的应用 2. 声强级 超声波和次声波
物理学教程 第二版) (第二版)
在弹性介质中传播的机械纵波,一般统称为声波 在弹性介质中传播的机械纵波,一般统称为声波. 可闻声波 可闻声波 20 ~ 20000 Hz 次声波 低于20 低于 Hz 超声波 高于20000 Hz 高于 声强: 声强: 声波的能流 密度. 密度
波衍射1.swf
第六章 机械波
6 – 4 惠更斯原理和波的应用 利用惠更斯原理可解释波的衍射。 利用惠更斯原理可解释波的衍射。 波在传播过程中,遇到障 波在传播过程中, 碍物时其传播方向发生改变, 碍物时其传播方向发生改变, 绕过障碍物的边缘继续传播。 绕过障碍物的边缘继续传播。 波达到狭缝处, 波达到狭缝处,缝上各点都可 看作子波源,作出子波包络, 看作子波源,作出子波包络,得到 新的波前。在缝的边缘处, 新的波前。在缝的边缘处,波的传 播方向发生改变。 播方向发生改变。 此时波阵面不再是平面, 此时波阵面不再是平面,在靠 近边缘处,波阵面进入了阴影区域, 近边缘处,波阵面进入了阴影区域, 表示波已绕过障碍物的边缘处, 表示波已绕过障碍物的边缘处,波 阵面进入了阴影区域, 阵面进入了阴影区域,表示波已绕 过障碍物的边缘传播。 过障碍物的边缘传播。
【高中物理】人教版选修3-4 12.6 惠更斯原理 教案 Word版含答案

课时12.6惠更斯原理1.知道什么是波面和波线,了解惠更斯原理。
2.认识波的反射现象,并能用惠更斯原理进行解释。
3.认识波的折射现象,并能用惠更斯原理进行解释。
重点难点:波面、波线的概念和惠更斯原理。
以及用惠更斯原理对波的反射规律和折射规律进行解释。
教学建议:本节在已学过的光的反射、折射及回声等知识的基础上,进一步加深对波的特性的理解。
要理解波面、波线等概念及惠更斯原理,并能用惠更斯原理对波的反射规律和折射规律进行解释。
由于这些概念比较抽象,应通过实验演示和日常生活经验来辅助教学。
波的反射和折射是常见的现象,从对现象的研究中概括出规律,再用来解释现象和指导实践,使学生提高学习的兴趣,感受知识的力量。
导入新课:北京天坛的回音壁为圆形,直径为61.5米,周长为193.2米,是用磨砖对缝砌成的,墙面极其光滑整齐。
两个人分东、西方向贴墙而立,一个人靠墙向北说话,无论说话声音多小,也可以使另一人听得清清楚楚,而且声音悠长,堪称奇趣,给人造成一种“天人感应”的神秘气氛。
为什么声音能够传播这么远呢?1.波面和波线任何振动状态①相同的点都组成一个个圆,这些圆叫作②波面,与波面垂直的线代表了波的③传播方向,叫作④波线。
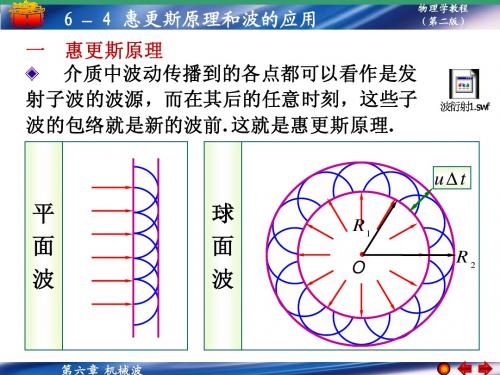
2.惠更斯原理(1)内容:介质中任一波面上的各点,都可以看作可以发射⑤子波的波源,其后任意时刻,这些⑥子波在波前进方向的⑦包络面就是新的波面。
这就是惠更斯原理。
(2)应用:如果知道某时刻一列波的某个⑧波面的位置,还知道⑨波速,利用惠更斯原理可以得到下一时刻这个⑩波面的位置,从而确定波的传播方向。
还可以利用惠更斯原理说明平面波的传播,解释波的衍射。
(3)局限性:惠更斯原理只能解释波的传播方向,不能解释波的强度,所以无法说明衍射现象与狭缝或障碍物的大小的关系。
3.波的反射和折射(1)回声是声波的反射,利用惠更斯原理可以确定反射波的传播方向。
(2)波从一种介质进入另一种介质后传播方向发生偏折的现象叫作波的折射。
大学物理期末练习题

一、力学1.一个质点在做匀速圆周运动,则有( C )A.质点的动量守恒,切向加速度为零,法向加速度不为零B.质点的动量守恒,切向加速度不为零,法向加速度为零C.质点的动能守恒,切向加速度为零,法向加速度不为零D.质点的动能守恒,切向加速度不为零,法向加速度不零 2.下列说法哪种正确(D )A.如果物体的动能不变,则动量也一定不变B.如果物体的动能变化,则动量不一定变化C.如果物体的动量变化,则动能也一定变化D.如果物体的动量不变,则动能也一定不变3.均匀细棒OA 可绕一定轴转动,该轴为通过O 点与纸面垂直的光滑水平轴,如图1所示。
今使棒从水平位置开始自由摆下,在棒转动的过程中,正确的结论是(C ) A.角速度增大,角加速度增大B.角速度增大,角加速度不变C.角速度增大,角加速度减小D.角速度减小,角加速度增大4. 质点在平面内运动,矢径 速度 ,试指出下列四种情况中描述质点速度的是: ( B )A.dr dt B .dr dt C .dv dt D .dv dt5. 试指出下列哪一种说法是错误的:( A ) A .在圆周运动中,加速度的方向一定指向圆心 B .圆周运动的速度大小变化快慢用切向加速度衡量C .物体作曲线运动时,速度方向一定在运动轨道的切线方向D .物体作曲线运动时,加速度必不等零6. 人造地球卫星,绕地球作椭圆轨道运动,地球在椭圆的一个焦点上,则卫星的( C ) A. 动量不守恒,动能守恒 B. 动量守恒,动能不守恒 C. 对地心的角动量守恒,动能不守恒D. 对地心的角动量不守恒,动能守恒7. 有两个力作用在一个有固定转轴的刚体上,则有( A )A.这两个力都平行于轴作用时,它们对轴的合力矩一定为零B.这两个力都垂直于轴作用时,它们对轴的合力矩一定不为零C.当这两个力的合力为零时,它们对轴的合力矩也一定是零D.当这两个力的合力矩为零时,它们对轴的合力也一定是零 8. 刚体的转动惯量的大小与以下哪个物理量无关( C )A. 刚体的密度B. 刚体的几何形状C. 刚体转动的角速度D. 转轴的位置 9. 一运动质点某瞬时位于r处,其速度大小为( C )A.dr dtB.d rdtC.drdt D. dr dt()r r t =()v v t =10. 地球绕太阳做轨道为椭圆的运动,对地球的描述正确的是( C ) A. 动量不守恒,动能守恒 B. 动量守恒,动能不守恒 C. 对太阳的角动量守恒,机械能守恒D. 对太阳的角动量不守恒,机械能不守恒11. 一质点沿x 轴运动,其运动方程为2353x t t =-,式中时间t 以s 为单位。
惠更斯原理、衍射现象讲解

对此类现象进行大量的总结后,荷兰物理学家惠更斯在1679年指出,介质中传播的 波传播到各个点时,每个点都可以看成是发射子波的波源,所有子波形成的包络面 就是新的波前,这就是惠更斯原理;不管是机械波还是电磁波,惠更斯原理都是适 用的;
图2所示的平面波中,根据惠更斯原理,波面S1上的各个点都可以看作是新的波源, 所有波源的包络面S2就是新的波前,当然S1与S2之间的距离就要由波长决定。
比如人在室内时能够听到室外的声音,就是声波绕过门、窗或者缝继续传播的现象。 生活中不只是机械波才存在衍射现象,电磁波 也会存在衍射现象,衍射现象是波动的一个特征之一。
下一章《大型交响乐队演奏中的物理学原理,波的干涉现象》讲解波的干涉现象。
当波在向前传播时,难免会遇到障碍物,于是把波遇到障碍物时,绕过障碍物边缘 继续向前传播的现象叫做衍射;解释衍射现象最好的理论就是惠更斯原理,
图3所示的三幅图中,小孔的尺寸分别是1/10λ、λ、10λ,可以看出小孔的尺寸越 小,小孔处子波的包络面越接近于圆形,也就是说进入图中阴影部分的波前越多, 绕过障碍物传播的现象越明显,当小孔的直径很大时,大部分的波前保持原来的方 向,只有很小一部分波前进入阴影部分。
《从惠更斯原理看,我们知道了波在介质中传播时,实际上就是每个质 点重复上一个质点的运动状态,于是介质中的每个质点都可以看作是一个新的波源, 因为它包含了起始波源的所有信息,
比如图1所示的水面波在传播时,当小孔的大小和波长差不多时,其他位置的质点 在振动时被障碍物挡住,不能继续向前传播,而处于小孔位置的质点就可以以自身 为波源,带动周围的质点继续振动,于是就出现了圆形波。
惠更斯原理与波的衍射

非相干叠加.swf
例 如图所示, A、B两点为同一介质的两相干波源,其
振幅皆为A=5 cm, 频率皆为100 Hz, 但当点A为波峰时,
点B适为波谷。设波速为10 m/s, (A、B两波源的振动垂
直于平面),试写出由A、B发出的两列波传到P点时干涉
的结果。
图示两列振动方向相同得同方向传播得波动得叠加:
同频率不同振幅的两个波的叠加
频率比为2:1的两个等幅波的叠加
一个高频波和一个低频波的叠加
频率相近的两列等幅波的叠加
叠加原理在物理上得重要性还在于可将一列复杂得 波分解为简谐波得组合。
二、波得干涉
干涉现象就是波动形式所独具得重要特征之 讨一论。两列频率相同,振动方向相同,相位相同或相位 差恒定得简谐波得叠加———一种最简单也就是最重 要得波得叠加情况。这两列波叠加后得图像稳定,不 随时间而变化。
Q
解:(1)取坐标如图所示,由题知:= 2 m
两波在S 1 左侧得任一点P得相位差:
P
2
1
2
r2
r1
2 20.5 21
2
2
Ⅰ区处处干涉相消
Ⅰ
Ⅱ
Ⅲ
S1
S2
x
P 0R
Q
两波在S 2 右侧得任一点Q得相位差:
Q
2
1
2
r2
r1
2
2
20.5 2
20
Ⅱ区处处干涉加强
Q
2 [
2
(20.5 x)
o
Hale Waihona Puke xu驻波有一定得波形,此波形不移动,各点以各自确定得 振幅在各自得平衡位置附近振动,没有振动状态或相位得 传播、因此驻波就是一种特殊得振动状态,不就是波,她 不具备波得特性。
惠更斯菲涅尔原理基尔霍夫衍射理论

若取 G~ 也满足亥姆霍兹方程,则
由
22GE~~
kk22GE~~
§5-1惠更斯-菲涅尔原理
波动具有两个基本性质,一方面,它是扰动 的传播,一点的扰动能够引起其它点的扰动, 各点相互之间是有联系的。另一方面,它具有 时空周期性,能够相干迭加。
惠更斯原理中的“次波概念反映了上述前一 基本性质,这是其成功的地方。但“时空周期 性”并没有反映。
利用惠更斯原理,可以说明衍射的存在,但 不能确定光波通过衍射屏后沿不同方向传播的 振幅,因而也就无法确定衍射图样中的光强分 布。
§5-1惠更斯-菲涅尔原理
二、惠更斯-菲涅耳原理 此是研究衍射现象的理论基础: 波动具有两个基本性质: 1、波动是扰动的传播,一点的扰动能够引 起其它点的扰动,各点的扰动相互之间是有 联系的; 2、波动具有时空周期性,能够相干叠加。
§5-1惠更斯-菲涅尔原理
在惠更斯原理中,由于缺少对时空周期性 的反映,从而对各次波如何叠加问题就不 能给出令人满意的回答。
1818年,在巴黎科学院举行的以解释衍射现 象为内容的有奖竞赛会上,年青的菲涅耳 出人意料地取得了优胜,他吸收了惠更斯 提出的次波概念,用“次波相干迭加”的 思想将所有衍射情况引到统一的原理中来, 这个原理就是惠更斯菲涅耳原理。
§5-1惠更斯-菲涅尔原理
惠更斯--菲涅耳原理
Z RQθ
其内容如下:
P
~ EQ
A expikR
R
Σ' Z'
§5-1惠更斯-Z菲涅尔原理
~ EQ
A expikR
R
RQθ
Σ
r
S
P
Σ' Z'
式中,A是离点光源单位距离处的振幅,
大学物理惠更斯原理波的衍射

6.5 波的干涉
6.5.1 波的叠加原理 1. 波传播的独立性原理
几列波在空间某点相遇后,每一列波都能独立地 保持自己的原有特性(频率、波长、振动方向等) 传播,就像在各自路程中,并没有遇到其它波一样.
例如: 管弦乐队合奏;
几个人同时讲话;
天空中多个无线电波.
2. 波的叠加原理
几列波在某点相遇时,该处质点的振动为各列波 单独在该点引起的振动的合振动.
水
波
通
波
过
的
狭
衍
缝
射
后
的
衍
射
讨论
1. 波的衍射现象是否明显,取决于障碍物的线度与波长的关系
小孔的直径远小于 波长时的衍射现象
小孔的直径大于 波长时的衍射现象
2. 室温下,声速为340m/s,频率20-20000Hz,波长范围:
u 0.017 ~ 17m
与障碍物尺度相当,所以声波的衍射现象较显著.
相遇前
相遇时
相遇后
6.5.2 波的干涉条件和公式
频率相同、振动 方向平行、相位 相同或相位差恒 定的两列波相遇 时,某些地方振 动始终加强,另 一些地方振动始 终减弱的现象, 称波的干涉现象.
波的相干条件:
(1) 频率相同;
S1
(2) 振动方向平行;
(3) 相位相同或相位差恒定. S2
r1
*P
r2
当(2 1) 2k 时
A = A1+ A2 —合振幅最大,同相
当(2 1) (2k 1) 时 A = |A1A2 | —合振幅最小,反相
波函数的求解:
上次课内容小结
1. 先求出某点O的振动方程: yO Acos(t )
由初始条件求振幅和初相位:
波的衍射

【波的衍射】亦称波的“绕射”,是波的重要特性之一。
是指波在传播过程中,遇到障碍物或缝隙时传播方向发生变化的现象。
水波、声波、光波都能发生衍射现象。
障碍物或缝隙的宽度越小,而波长越大,则衍射现象就越明显。
波绕过障碍物或通过小孔绕到障碍物的背后。
这种波能绕过障碍物继续传播的现象,叫“波的衍射”。
室内发出声波可以绕过门、窗而到达室外的各角落。
如果障碍物或缝隙的宽度远远超过波长时,波的衍射现象就不明显。
波的衍射现象可用惠更斯原理来解释。
【波的干涉】由两个或两个以上的波源发出的具有相同频率,相同振动方向和恒定的相位差的波在空间迭加时,在交迭区的不同地方振动加强或减弱的现象,称为“波的干涉”。
符合上列条件的波源叫做“相干波源”,它们发出的波叫做“相干波”。
这是波的迭加中最简单的情况。
二相干波迭加后,在迭加区内每一位置有确定的振幅。
在有的位置上,振幅等于二波分别引起的振动的振幅之和,这些位置的合振动最强。
称为“相长干涉”;而有些位置的振幅等于二波分别引起的振动的振幅之差,这些位置上的合振动最弱,称为“相消干涉”。
它是波的一个重要特性。
【波的反射】波由一种媒质达到与另一种媒质的分界面时,返回原媒质的现象。
例如声波遇障碍物时的反射,它遵从反射定律。
在同类媒质中由于媒质不均匀亦会使波返回到原来密度的介质中,即产生反射。
【波的折射】波在传播过程中,由一种媒质进入另一种媒质时,传播方向发生偏折的现象,称波的折射。
在同类媒质中,由于媒质本身不均匀,亦会使波的传播方向改变。
此种现象也叫波的折射。
它也遵从波的折射定律。
【声学】物理学的一个分支,是研究声波的产生、传播、接收和作用等问题的学科。
根据研究的方法、对象和频率范围的不同,它与许多其他学科交叉在一起,形成了很多独特的边缘学科,例如,大气声学、水声学、电声学、生物声学、心理声学、语言声学、建筑声学、环境声学、几何声学、物理声学、生理声学、分子声学、声能学、超声学、次声学、微观声学、音乐声学、振动与波动声学、噪声控制学等部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
惠更斯原理可以说明波的衍射现象
1弗里德曼-赫伯特-惠更斯原理介绍
弗里德曼-赫伯特-惠更斯(Friedmann-Herbert-Huygens)原理是描述波、振动、传播等自由空间中的现象并产生具有哲学意义的一种物理学原理。
它把波描述为传播的小尺寸的圆形或椭圆形的包含着有限的能量的圆波,它们在自由空间中向各个方向传播。
这样就渐渐产生了空间中分布的波,这便是波的扩散或衍射。
2弗里德曼-赫伯特-惠更斯原理的定义
弗里德曼-赫伯特-惠更斯原理可定义为:在每个点,波源发射出的波在任意方向上都能同时传播,前面传播的不受后面新传播的波方向的影响,从而形成扩散或者说发散的波。
3弗里德曼-赫伯特-惠更斯原理的运用
弗里德曼-赫伯特-惠更斯原理可以用来解释一些物理现象,如声波的扩散现象。
当声波源发射出声波时,声波在扩散向它周围的自由空间中,就同时发散投射出去,这与弗里德曼-赫伯特-惠更斯原理是一致的。
此外,同样可以用弗里德曼-赫伯特-惠更斯原理来解释光波的衍射,即当光源发出光线时,光线是同时投射沿着入射面上各个方向,就会发生衍射现象,而这种衍射现象也是由弗里德曼-赫伯特-惠更斯原理得出的结果。
4结论
从上面可以看出,弗里德曼-赫伯特-惠更斯原理不仅可以用来解释声音的扩散现象,还可以用来解释光波的衍射现象,从而帮助我们了解自由空间中的波的传播行为。
同时,也可以作为物理学上一种比较重要的原理,用于研究波的传播、振动及其他相关现象。
总之,弗里德曼-赫伯特-惠更斯原理给我们带来了诸多具有指导意义的理论,在物理学上有其深奥而重要的意义。
