三角函数公式大全表格初中数学
三角函数公式表(免费)

鄙视下载资料还要财富值的!
一:指数函数
二:对数函数
三:指数函数与对数函数有什么关系?(关于y=x 对称)
x
y 2=x
y 3=x
y ⎪⎭
⎫ ⎝⎛=21x
y ⎪⎭
⎫ ⎝⎛=31x
y 2log =x
y 2
1log =x
y 3log =x
y 3
1log =x
y 2=x
y =x
y 2log =
二、基本初等函数及其图像
1
2
3
,奇函数
无界,周期为余割函数
,偶函数无界,周期为正割函数,奇函数无界,周期为余切函数,奇函数无界,周期为正切函数,偶函数有界,周期为余弦函数,奇函数有界,周期为正弦函数性质
表达式名称ππππππ2csc 2sec cot tan 2cos 2sin x
y x y x y x y x y x y ======)
R (sin ∈=x x y 的图象)
R (cos ∈=x x y 的图象tan (π0.5π)
y x x k =≠+的图像
4
cot (π)
y x x k =≠的图像)
0()
(cot arc 22)(arctan ]0[]11[arccos 22]11[arcsin ππππππ,,反余切函数
,,反正切函数,,反余弦函数,,反正弦函数值域定义域表达式名称∞+-∞=⎪⎭⎫ ⎝⎛-∞+-∞=-=⎥⎦⎤
⎢⎣⎡--=x
y x y x y x y。
(完整版)三角函数三角函数公式表

(完整版)三角函数公式表1. 正弦函数 (sin):定义:正弦函数是直角三角形中对边与斜边的比值。
公式:sin(θ) = 对边 / 斜边范围:1 ≤ sin(θ) ≤ 1特殊值:sin(0°) = 0, sin(30°) = 1/2, sin(45°) = √2/2, sin(60°) = √3/2, sin(90°) = 12. 余弦函数 (cos):定义:余弦函数是直角三角形中邻边与斜边的比值。
公式:cos(θ) = 邻边 / 斜边范围:1 ≤ cos(θ) ≤ 1特殊值:cos(0°) = 1, cos(30°) = √3/2, cos(45°) = √2/2, cos(60°) = 1/2, cos(90°) = 03. 正切函数 (tan):定义:正切函数是直角三角形中对边与邻边的比值。
公式:tan(θ) = 对边 / 邻边范围:tan(θ) 可以取任意实数值特殊值:tan(0°) = 0, tan(30°) = 1/√3, tan(45°) = 1, tan(60°)= √3, tan(90°) 不存在(无穷大)4. 余切函数 (cot):定义:余切函数是直角三角形中邻边与对边的比值。
公式:cot(θ) = 邻边 / 对边范围:cot(θ) 可以取任意实数值特殊值:cot(0°) 不存在(无穷大), cot(30°) = √3, cot(45°) = 1, cot(60°) = 1/√3, cot(90°) = 05. 正割函数 (sec):定义:正割函数是直角三角形中斜边与邻边的比值。
公式:sec(θ)= 1 / cos(θ)范围:sec(θ) 可以取任意实数值特殊值:sec(0°) = 1, sec(30°) = 2, sec(45°) = √2, sec(60°) = 2/√3, sec(90°) 不存在(无穷大)6. 余割函数 (csc):定义:余割函数是直角三角形中斜边与对边的比值。
初中三角函数值表

初中三角函数值表2初中三角函数值表特殊角三角函数值sin0=0 sin30=0.5 sin45=0.7071=22 sin60=23=0.866sin90=1 cos0=1 cos30=23=0.866 cos45=22=0.70cos60=0.5 cos90=0 tan0=0 tan30=33=0.577 tan45=1 tan60=3=1.732 tan90=无 cot0=无cot30=3=1.732 cot45=1 cot60=33=0.577 cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(见下)(3)锐角三角函数值的变化情况(i )锐角三角函数值都是正值(ii )当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时,tanα>0, cotα>0.附:三角函数值表sin0=0,sin15=(√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/23sin150=1/2sin165=(√6-√2)/4sin180=0sin270=-1sin360=04sin1=0.01745 sin2=0.034899 sin3=0.052335sin4=0.069756sin5=0.087155sin6=0.104528sin7=0.121869sin8=0.139173sin9=0.156434sin10=0.17364sin11=0.19080sin12=0.20791sin13=0.22495sin14=0.24192sin15=0.25881sin16=0.27563sin17=0.29237sin18=0.30901sin19=0.32556sin20=0.34202sin21=0.35836sin22=0.374605sin24=0.40673sin25=0.42261sin26=0.43837 sin27=0.45399sin28=0.46947 sin29=0.48480sin30=0.49999sin31=0.51503sin32=0.52991sin33=0.54463sin34=0.55919sin35=0.57357sin36=0.58778sin37=0.60181sin38=0.61566sin39=0.62932sin40=0.64278sin41=0.65605sin42=0.66913sin43=0.68199sin44=0.69465sin45=0.70710sin46=0.71933 sin47=0.73135sin48=0.74314sin49=0.75470sin50=0.76604sin51=0.77714sin52=0.788016sin54=0.80901sin55=0.81915sin56=0.82903sin57=0.83867sin58=0.84804sin59=0.85716sin60=0.86602sin61=0.87461sin62=0.88294sin63=0.89100sin64=0.89879sin65=0.90630sin66=0.91354sin67=0.92050sin68=0.92718sin69=0.93358sin70=0.93969sin71=0.94551sin72=0.95105sin73=0.95630sin74=0.96126sin75=0.96592sin76=0.970297sin78=0.97814sin79=0.98162sin80=0.98480sin81=0.98768sin82=0.99026sin83=0.99254sin84=0.99452sin85=0.99619sin86=0.99756sin87=0.99862sin88=0.99939sin89=0.99984sin90=1cos1=0.99984cos2=0.99939cos3=0.99862cos4=0.99756cos5=0.99619cos6=0.99452cos7=0.99254cos8=0.99026cos9=0.98768cos10=0.9848cos11=0.98168cos12=0.97814cos13=0.9743cos14=0.9702cos15=0.9659cos16=0.9612cos17=0.9563cos18=0.9510cos19=0.9455cos20=0.9396cos21=0.9335cos22=0.9271cos23=0.9205cos24=0.9135cos25=0.9063cos26=0.8987cos27=0.8910cos28=0.8829cos29=0.8746cos30=0.8660cos31=0.8571cos32=0.8480cos33=0.8386cos34=0.8290cos35=0.8191cos36=0.8090cos37=0.7986cos38=0.78809cos39=0.7771cos40=0.7660cos41=0.7547cos42=0.7431cos43=0.7313cos44=0.7193cos45=0.7071cos46=0.6946cos47=0.6819cos48=0.6691cos49=0.6560cos50=0.6427cos51=0.6293 cos52=0.6156 cos53=0.6018 cos54=0.5877 cos55=0.5735cos56=0.5592 cos57=0.5446cos58=0.5299cos59=0.5150cos60=0.5000cos61=0.4848cos62=0.4694cos63=0.4539cos64=0.438310cos65=0.4226cos66=0.4067cos67=0.3907cos68=0.3746cos69=0.3583cos70=0.3420cos71=0.3255cos72=0.3090cos73=0.2923cos74=0.2756cos75=0.2588cos76=0.2419cos77=0.2249cos78=0.2079cos79=0.1908cos80=0.1736cos81=0.1564cos82=0.1391cos83=0.1218 cos84=0.1045cos85=0.0871cos86=0.0697311cos87=0.052cos88=0.0348cos89=0.0174cos90=0tan1=0.017455tan2=0.034920tan3=0.052407tan4=0.069926tan5=0.087488tan6=0.105104tan7=0.122784tan8=0.140540tan9=0.158384tan10=0.17632tan11=0.19438tan12=0.21255tan13=0.23086 tan14=0.24932tan15=0.26794tan16=0.28674tan17=0.30573 tan18=0.32491tan19=0.34432tan20=0.36397tan21=0.38386tan22=0.40402tan23=0.42447tan24=0.44522tan25=0.46630tan26=0.48773an27=0.50952tan28=0.5317012tan29=0.55430tan30=0.57735tan31=0.60086tan32=0.62486 tan33=0.64940tan34=0.67450tan35=0.70020tan36=0.72654tan37=0.75355tan38=0.78128tan39=0.80978tan40=0.83909tan41=0.86928tan42=0.90040tan43=0.93251tan44=0.96568tan45=0.99999tan46=1.03553tan47=1.07236tan48=1.11061tan49=1.15036tan50=1.19175tan51=1.23489tan52=1.27994tan53=1.3270413tan54=1.3763tan55=1.42814 tan56=1.48256tan57=1.53986tan58=1.60033tan59=1.66427 tan60=1.73205tan61=1.80404tan62=1.88072tan63=1.96261tan64=2.05030tan65=2.14450tan66=2.24603tan67=2.35585tan68=2.47508tan69=2.60508tan70=2.74747tan71=2.90421tan72=3.07768tan73=3.27085tan74=3.48741tan75=3.73205tan76=4.01078tan77=4.33147tan78=4.70463tan79=5.14455tan80=5.6712814tan81=6.31375tan82=7.11536tan83=8.14434tan84=9.51436tan85=11.4300tan86=14.3006tan87=19.0811tan88=28.6362tan89=57.2899tan90=无取值15。
三角函数公式表(初中)

三角函数公式(最全)
tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)÷(1tanα·tanβ-tanβ·tanγ-tanγ·tanα)
5、幂级数
c0+c1x+c2x2+...+cnxn+...=∑cnxn (n=0..∞) c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n (n=0..∞)
cosh x = 1+x2/2!+x^4/4!+…+x2k/(2k)!+…, x∈R
arcsinh x =x - x3/(2*3) + (1*3)x5/(2*4*5) -(1*3*5)x7/(2*4* 6*7)…, x∈(-1,1)
arctanh x = x + x3/3 + x5/5 + …, x∈(-1,1)
上述两式相比可得: tan3a=tana·tan(60°-a) ·tan(60°+a)
6、四倍角公式
sin4a=-4*[cosa*sina*(2*sina^2-1)] cos4a=1+(-8*cosa^2+8*cosa^4) tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)
7、五倍角公式
5
应用欧拉公式
8、n倍角公式
上式用于求n倍角的三角函数时,可变形为: 所以
其中,Re表示取实数部分,Im表示取虚数部分.而
初中数学三角函数值公式表大全

初中数学三角函数值公式表大全正弦函数值公式表$\\sin 0 = 0$$\\sin \\frac{\\pi}{6} = \\frac{1}{2}$$\\sin \\frac{\\pi}{4} = \\frac{\\sqrt{2}}{2}$ $\\sin \\frac{\\pi}{3} = \\frac{\\sqrt{3}}{2}$ $\\sin \\frac{\\pi}{2} = 1$$\\sin \\pi = 0$$\\sin \\frac{3\\pi}{2} = -1$$\\sin 2\\pi = 0$余弦函数值公式表$\\cos 0 = 1$$\\cos \\frac{\\pi}{6} = \\frac{\\sqrt{3}}{2}$ $\\cos \\frac{\\pi}{4} = \\frac{\\sqrt{2}}{2}$ $\\cos \\frac{\\pi}{3} = \\frac{1}{2}$$\\cos \\frac{\\pi}{2} = 0$$\\cos \\pi = -1$$\\cos \\frac{3\\pi}{2} = 0$$\\cos 2\\pi = 1$正切函数值公式表$\\tan 0 = 0$$\\tan \\frac{\\pi}{6} = \\frac{\\sqrt{3}}{3}$$\\tan \\frac{\\pi}{4} = 1$$\\tan \\frac{\\pi}{3} = \\sqrt{3}$$\\tan \\frac{\\pi}{2}$ 不存在$\\tan \\pi = 0$$\\tan \\frac{3\\pi}{2} = 0$$\\tan 2\\pi = 0$余切函数值公式表$\\cot 0$ 不存在$\\cot \\frac{\\pi}{6} = \\sqrt{3}$$\\cot \\frac{\\pi}{4} = 1$$\\cot \\frac{\\pi}{3} = \\frac{\\sqrt{3}}{3}$ $\\cot \\frac{\\pi}{2} = 0$$\\cot \\pi$ 不存在$\\cot \\frac{3\\pi}{2} = 0$$\\cot 2\\pi = 0$正割函数值公式表$\\sec 0 = 1$$\\sec \\frac{\\pi}{6} = \\frac{2}{\\sqrt{3}}$ $\\sec \\frac{\\pi}{4} = \\sqrt{2}$$\\sec \\frac{\\pi}{3} = 2$$\\sec \\frac{\\pi}{2} = \\infty$$\\sec \\pi = -1$$\\sec \\frac{3\\pi}{2} = \\infty$$\\sec 2\\pi = 1$余割函数值公式表$\\csc 0 = \\infty$$\\csc \\frac{\\pi}{6} = 2$$\\csc \\frac{\\pi}{4} = \\sqrt{2}$$\\csc \\frac{\\pi}{3} = \\frac{2}{\\sqrt{3}}$$\\csc \\frac{\\pi}{2} = 1$$\\csc \\pi = \\infty$$\\csc \\frac{3\\pi}{2} = -\\infty$$\\csc 2\\pi = \\infty$以上是初中数学中常见的三角函数值公式表,通过这些公式可以快速计算各角度下的三角函数值,希望可以帮助大家更好地理解三角函数的性质和应用。
(完整版)三角函数公式大全

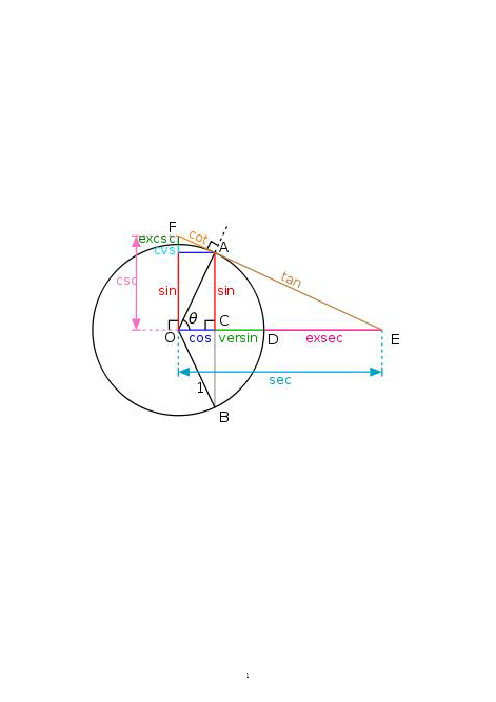
三角函数公式一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦函数:ry=αsin 余弦函数:r x =αcos 正切函数:x y =αtan余切函数:y x =αcot 正割函数:xr=αsec 余割函数:yr=αcsc 二、同角三角函数的基本关系式六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”倒数关系:1csc sin =⋅x x ,1sec cos =⋅x x ,1cot tan =⋅x x 。
商数关系:x x x cos sin tan =,xxx sin cos cot =。
平方关系:1cos sin 22=+x x ,x x 22sec tan 1=+,x x 22csc cot 1=+。
积的关系:sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)=sinα cos(2kπ+α)=cosαtan (2kπ+α)=tanα cot(2kπ+α)=cotα (其中k ∈Z) 公式二:设α为任意角,π+α的三角函数的值与α的三角函数值之间的关系: sin (π+α)=-sinα cos(π+α)=-cosα tan (π+α)=tanα cot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系: sin (-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)=sinα cos(π-α)=-cosα tan (π-α)=-tanα cot(π-α)=-cotα 公式五:απ-2与α的三角函数值之间的关系:sin (απ-2)=cosα cos(απ-2)=sinα tan (απ-2)=cotα cot(απ-2)=tanα公式六:απ+2与α的三角函数值之间的关系:sin (απ+2)=cosα cos(απ+2)=-sinαtan(απ+2)=-cotα cot(απ+2)=-tanα公式七:απ-23与α的三角函数值之间的关系: sin(απ-23)=-cosα cos(απ-23)=-sinαtan (απ-23)=cotα cot(απ-23)=tanα公式八:απ+23与α的三角函数值之间的关系:sin(απ+23)=-cosα cos(απ+23)=sinαtan (απ+23)=-cotα cot(απ+23)=-tanα公式九:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)=-sinα cos(2π-α)=cosα tan (2π-α)=-tanα cot(2π-α)=-cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
三角函数公式表

三角函数公式表三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα ·cotα=1sinα ·cscα=1cosα ·secα=1 sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα sin2α+cos2α=11+tan2α=sec2α1+cot2α=csc2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosα tan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=——————1-tanα ·tanβtanα-tanβtan(α-β)=——————1+tanα ·tanβ2tan(α/2)sinα=——————1+tan2(α/2)1-tan2(α/2)cosα=——————1+tan2(α/2)2tan(α/2)tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin———·cos———2 2α+βα-βsinα-sinβ=2cos———·sin———2 2α+βα-βcosα+cosβ=2cos———·cos———2 2α+βα-βcosα-cosβ=-2sin———·sin———2 2 1sinα ·cosβ=-[sin(α+β)+sin(α-β)]21cosα ·sinβ=-[sin(α+β)-sin(α-β)]21cosα ·cosβ=-[cos(α+β)+cos(α-β)]21sinα ·sinβ=— -[cos(α+β)-cos(α-β)]2化asinα±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式集合、函数集合简单逻辑任一x∈A x∈B,记作A BA B,B A A=BA B={x|x∈A,且x∈B}A B={x|x∈A,或x∈B}c ard(A B)=card(A)+card(B)-card(A B)(1)命题原命题若p则q逆命题若q则p否命题若 p则 q逆否命题若 q,则 p(2)四种命题的关系(3)A B,A是B成立的充分条件B A,A是B成立的必要条件A B,A是B成立的充要条件函数的性质指数和对数(1)定义域、值域、对应法则(2)单调性对于任意x1,x2∈D若x1<x2 f(x1)<f(x2),称f(x)在D上是增函数若x1<x2 f(x1)>f(x2),称f(x)在D上是减函数(3)奇偶性对于函数f(x)的定义域内的任一x,若f(-x)=f(x),称f (x)是偶函数若f(-x)=-f(x),称f(x)是奇函数(4)周期性对于函数f(x)的定义域内的任一x,若存在常数T,使得f(x+T)=f(x),则称f(x)是周期函数(1)分数指数幂正分数指数幂的意义是负分数指数幂的意义是(2)对数的性质和运算法则loga(MN)=logaM+logaNlogaMn=nlogaM(n∈R)指数函数对数函数(1)y=ax(a>0,a≠1)叫指数函数(2)x∈R,y>0图象经过(0,1)a>1时,x>0,y>1;x<0,0<y<10<a<1时,x>0,0<y<1;x<0,y>1a> 1时,y=ax是增函数0<a<1时,y=ax是减函数(1)y=logax(a>0,a≠1)叫对数函数(2)x>0,y∈R图象经过(1,0)a>1时,x>1,y>0;0<x<1,y<00<a<1时,x>1,y<0;0<x<1,y>0a>1时,y=logax是增函数0<a<1时,y=logax是减函数指数方程和对数方程基本型logaf(x)=b f(x)=ab(a>0,a≠1)同底型logaf(x)=logag(x) f(x)=g(x)>0(a>0,a≠1)换元型 f(ax)=0或f (logax)=0数列数列的基本概念等差数列(1)数列的通项公式an=f(n)(2)数列的递推公式(3)数列的通项公式与前n项和的关系an+1-an=dan=a1+(n-1)da,A,b成等差 2A=a+bm+n=k+l am+an=ak+al等比数列常用求和公式an=a1qn_1a,G,b成等比 G2=abm+n=k+l aman=akal不等式不等式的基本性质重要不等式a>b b<aa>b,b>c a>ca>b a+c>b+ca+b>c a>c-ba>b,c>d a+c>b+da>b,c>0 ac>bca>b,c<0 ac<bca>b>0,c>d>0 ac<bda>b>0 dn>bn(n∈Z,n>1)a>b>0 >(n∈Z,n>1)(a-b)2≥0a,b∈R a2+b2≥2ab|a|-|b|≤|a±b|≤|a|+|b|证明不等式的基本方法比较法(1)要证明不等式a>b(或a<b),只需证明a-b>0(或a-b<0=即可(2)若b>0,要证a>b,只需证明,要证a<b,只需证明综合法综合法就是从已知或已证明过的不等式出发,根据不等式的性质推导出欲证的不等式(由因导果)的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数公式大全表格初中数学三角函数公式大全
1.正弦函数的定义:
sinθ=a/b
2.余弦定义:
cosθ=b/a
3.正切公式:
tanθ=a/b
4.反正弦公式:
sin-1θ = c/d
5.反余弦公式:
cos-1θ = d/c
6.反正切公式:
tan-1θ = c/d
7.正弦双曲线:
y=a/b*sinθ
8.余弦双曲线:
y=b/a*cosθ
9.正弦型应用:
y=a+b*sin(c*x+d)
10.余弦型应用:
y=a+b*cos(c*x+d)
11.正弦型的解析解:x=(b/c)*sin(θ-d)+A
y=(a/c)*sin(θ-d)+B
12.余弦型的解析解:x=(b/c)*cos(θ-d)+A y=(a/c)*cos(θ-d)+B
13.正弦函数的导数:y'=a*b*cosθ
14.余弦函数的导数:y'=-a*b*sinθ
15.正弦函数的倒数:y'=a/b
16.余弦函数的倒数:y'=b/a
17.正弦三角关系:sin2θ + cos2θ = 1
18.正弦函数的积分:∫sinθdθ = -cosθ+C
19.余弦函数的积分:∫cosθdθ = sinθ+C
20.正切函数的导数:y'=a*b*sec2θ
21.正切函数的倒数:y'=b/a*secθ
22.正切函数的积分:∫tanθdθ = -ln|cosθ|+C
23.正弦函数的复值:sin2θ = 2*sinθ*cosθ
24.余弦函数的复值:
cos2θ =cos2θ-sin2θ
25.正切函数复值:tan2θ =2*tanθ/(1-tan2θ)。
