图解法求理论板数
理论板层数的计算
1、图解法
2021/10/24
2、解析法求理论板层数
1）理论板数的解析表达式
当吸收涉及的浓度区间内平衡关系为直线Y * mX b 时
在 I ~ II 层板间任一截面到塔顶范围内作组分A的衡算
VYII LX 0 LX1 VYI
YII
L V
(
X
1
X 0 ) YI
若相平衡关系可采用 Y * mX b 表示
2021/10/24
XI
YI
m
b
,
X
0
Y0* b m
YII
L V
(YI
Y0* m
)
YI
L A mV YII A(YI Y0*) YI
YII ( A 1)YI AY0*
2021/10/24
在 II ~ III 板间任一截面到塔顶范围内作组分A的衡算
VYIII LX 0 LX II VYI
A
N 1
A
1
1
(YI
Y0*)
Y2 Y0* YN1 Y0*
A 1 AN1 1
YI Y0* YN1 Y0*
1
A A N 1
1
1
1
YN 1 YI AN 1 A YN 1 Y0* AN 1 1
2021/10/24
——克列姆塞尔方程
YN1 Y1,YI Y2 Y0* mX2 b Y2*
Y1 Y2 Y1 Y2*
ANT 1 A ANT 1 1
相对吸收率 溶质的吸收率与理论最大吸收率的比值
Y1 Y2
Y1 Y2*
分析相对吸收率与吸收率的区别与联系
2021/10/24
ANT 1 A ANT 1 1
第五节 理论板数的求法
第五节 理论板数的求法所谓求理论塔板数，就是利用前面讨论的平衡关系，()n n x f y =和操作关系，()()m n n x f y x f y ''='=+或1计算达到指定分离要求所须的汽化-冷凝次数。
（1）逐板计算法每利用一次平衡关系和一次操作关系，即为一块理论板。
提馏段也是一样。
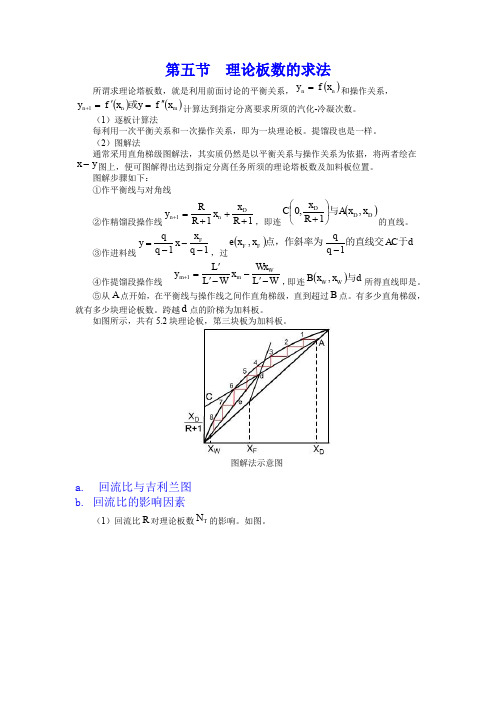
（2）图解法通常采用直角梯级图解法，其实质仍然是以平衡关系与操作关系为依据，将两者绘在y x -图上，便可图解得出达到指定分离任务所须的理论塔板数及加料板位置。
图解步骤如下： ①作平衡线与对角线②作精馏段操作线111+++=+R x x R R y D n n ，即连()D D D x x A R x C ,1,0与⎪⎭⎫ ⎝⎛+的直线。
③作进料线11---=q x x q qy F，过()d AC q q x x e F F 于的直线交点，作斜率为1,- ④作提馏段操作线W L Wx x W L L y W m m -'--''=+1，即连()d x x B W W 与,所得直线即是。
⑤从A 点开始，在平衡线与操作线之间作直角梯级，直到超过B 点。
有多少直角梯级，就有多少块理论板数。
跨越d 点的阶梯为加料板。
如图所示，共有5.2块理论板，第三块板为加料板。
图解法示意图a. 回流比与吉利兰图b. 回流比的影响因素（1）回流比R 对理论板数T N 的影响。
如图。
回流比对T N 的影响↑+↓1R x R D ，，操作线靠近平衡线，↑T N 反之，↓+↑1R x R D ，，操作线远离平衡线，↓T N 即 T N 正比于R 1（2）回流比对设备费与操作费的影响 ()D R D L V 1+=+=↑↑V R ,，塔直径↑，冷凝器↑，蒸馏釜↑ 设备费↑↓↑T N R ,，塔高下降，设备费↓↑↑V R ,，冷却水量↑，加热蒸汽量↑， 操作费↑须选一个合适回流比R ，使总费用最省。
化工原理实验--精馏实验
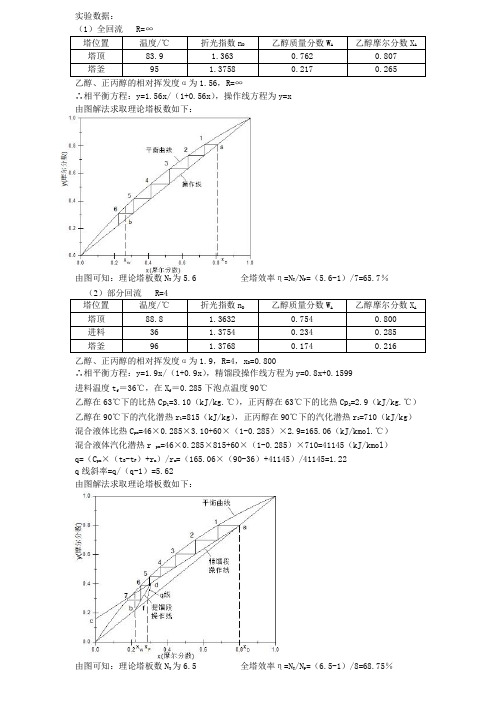
实验数据：
（1）全回流 R=∞
乙醇、正丙醇的相对挥发度α为1.56，R=∞
∴相平衡方程：y=1.56x/（1+0.56x），操作线方程为y=x
由图解法求取理论塔板数如下：
由图可知：理论塔板数N T为5.6 全塔效率η=N T/N P=（5.6-1）/7=65.7％
乙醇、正丙醇的相对挥发度α为1.9，R=4，x D=0.800
∴相平衡方程：y=1.9x/（1+0.9x），精馏段操作线方程为y=0.8x+0.1599
进料温度t f＝36℃，在X f＝0.285下泡点温度90℃
乙醇在63℃下的比热Cp1=3.10（kJ/kg.℃），正丙醇在63℃下的比热Cp2=2.9（kJ/kg.℃）乙醇在90℃下的汽化潜热r1=815（kJ/kg），正丙醇在90℃下的汽化潜热r2=710（kJ/kg）混合液体比热C pm=46×0.285×3.10+60×（1-0.285）×2.9=165.06（kJ/kmol.℃）
混合液体汽化潜热r pm=46×0.285×815+60×（1-0.285）×710=41145（kJ/kmol）
q=（C pm×（t B-t F）+r m）/r m=（165.06×（90-36）+41145）/41145=1.22
q线斜率=q/（q-1）=5.62
由图解法求取理论塔板数如下：
由图可知：理论塔板数N T为6.5 全塔效率η=N T/N P=（6.5-1）/8=68.75％。
理论板数的计算
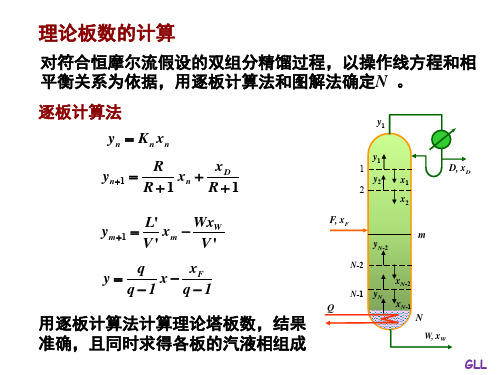
Rmin 1 x D (1 x D ) 1 0.98 2.5( 1 0.98 ) 1.237 1 xF 1 x F 2.5 1 0 . 501 1 0 . 501
R-Rmin 4 1.237 0.553 R1 41
对第二层理论板： y2 K 2 x2
1 2 F, xF
y1 L, xD y1 y2 x1 x2
全凝器
D, xD
R x 第二与第三层之间的气液相 y3 x2 D R1 R1 浓度满足操作关系：
……直至xn≤xq，换操作线方程
yN-2
N-2
m
平衡 作线 平衡 作现 x D y1 相 x1 操 y2 相 x2 操 y2 xn
双组分溶液 略去下标A、B N min
x D 1 xW lg 1 x x D W lg
芬斯克方程
理论板数的简捷算法 在精馏塔设计中，利用 Rmin 和Nmin 估算所需的理论塔板数。 吉利兰 (Gilliland) 关联图 用8个物系，由逐板计算 结果绘制。 精馏条件： 组分数目=2~11
yA xA y x B n1 B n
xA xA yA 离开第 1 块板的汽液平衡为： y 1 x x B 1 B 1 B D yA yA y 1 y B 1 B 2 yA xA 1 2 y x B 1 B 2 yA yA y 1 2 y B B 1 3
yN-2
N-2
理论塔板数求取
全回流时的回流比为：
斜率
2020/4/7
13
2.最少理论板层数
Nmin也可以从芬斯克（Fenske）方程式计算得到：
对双组分溶液 略去下标 A. B
2020/4/7
全回流的理论塔板数
14
(二)最小回流比 Rmin
对于一定的分离任务（即F. xF. q. xW. xD一定）而言, 应选 择适宜的回流比。
浮阀塔,板上开有若干大孔（标准孔 径为39 mm），每孔装有一个可以上、 下浮动的阀片。由孔上升的气流，经过 阀片与塔板的间隙而与板上横流的液体 接触，进行传质和传热过程。
（二）全塔效率（总效率）
为完成一定分离任务所需的理论塔板数与实际所需的实际塔板数之比。
2020/4/7
E NT
NP
12
十、回流比的影响及其选择
从上块塔板流到下一块塔板的液体，塔顶第一块板上的回流液是由塔 顶上升蒸汽经冷凝后回流至塔内的液体称为回流液。
（一）全回流及最少理论板层数
1、全回流
若塔顶上升蒸气经冷凝后，全部回流至塔内，这种方式称为全回流。 此时，塔顶产品为零，通常F 及W 也均为零--既不向塔内进料，亦不从 塔内取出产品。全塔也就无精馏段和提馏段之区分，两段的操作线合二 为一。
（二）恒沸剂（或挟带剂）（溶剂）
第三组分与原溶液中的一个组分形成恒沸物，原有组分间的相对 挥发度增大，使该溶液能用一般精馏方法分离。第三组分称为恒沸剂 或挟带剂。
（三）恒沸精馏中合适挟带剂的选用：
（1）恒沸物恒沸点与溶液中纯组分沸点有相当差值，一般不小于10℃ （2）恒沸物易分离，以便回收挟带剂，挟带剂含量越少操作费用越省 （3）热稳定性、腐蚀性、毒性、价格等因素
循环糠醛 苯
化工原理下1.4 理论板计算(逐板、图解ppt课件
yB
xB
(
x x
A B
)
D
(
yA yB
)1
1(
xA xB
)1
1(
yA yB
)2
1
2(
xA xB
)2
1 1
2( 2
yyBA3)(3xxBA
)3
1 1
2 3( 2 3
yA yB
)4
W
(
xA xB
)W
(
yA yB
)n1
22
2. 最小回流一比、全回流和最小回流比
g
斜率
Rm in Rmin 1
yq
夹 紧 区
夹
R2
紧
点
R1
xW
xF xq
xD
23
一、全回流和最小回流比
(1)最小回流比的概念
对于一定分离任务，减小操作回流比，两操作 线向平衡线靠近，所需理论板层数增多。当回流比 减小到某一数值，两操作线的交点d落到平衡线上 时，若在平衡线与操作线之间绘阶梯，将需要无穷 多阶梯才能到达点d，相应的回流比即为最小回流 比，以Rmin表示。
(
xA xB
)n
N 1 m
(
xA xB
)W
(xA / xB )D (xA / xB )W
mN1
m N1 12 N+1
(N
1) lgm
lg
(xA (xA
/ /
xB )D xB )W
lg (xA / xB )D
Nmin
(xA / xB )W 1
理论塔板数的计算 (2)
' 1
（加料板下流液相组成）
平衡 ' 2
x y x
' 2
xm xW
提馏段：m块板，提馏段内不包括再沸器，而 xW是再沸器内的浓度，所以m块板中包括再沸 器，再沸器相当一个理论板，所以塔内提馏段 为（m-1）块板。
讨论： 1） 逐板计算法很重要，用计算机编程计算很 快就计算出结果。 2）以上理论板数是用泡点进料的情况所得，则 xq=xF，如果不是泡点进料，这时xq≠xF，我们要 把两条操作线交点q坐标求出，当x≤xq，即为加 料板。 3）塔顶采用分凝器： 塔顶分凝器相当于第一块理论板（进一个 气相，出一个气相和一个液相）；塔内第一块 板就成为第二块板。
f
加料过早
e
图6-38 理论板数图解法示意图
2、精馏段操作线：
y n 1
R 1 xn xD R 1 R 1
（6-39）
3、提馏段操作线：
L qF W ym1 xm xW L qF W L qF W
（6-59）
4、画直角梯级： 从a点开始，在精馏段操作线与平衡线之间 作水平线及垂直线，当梯级跨过q点时，则改在 提馏段操作线与平衡线之间作直角梯级，直至 梯级的水平线达到或跨过b点为止。 其中过q点的梯级为加料板，最后一个梯级 为再沸器。 塔内总共需要（m+n-2）块理论板。 作梯级时跨q点换线，用提馏段操作线。
NP
式中：
NT
（5-61）
NP——实际塔板数； NT——理论板数；
η——全塔效率；
根据：
1、平衡关系： ①用某一温度下纯组分的饱和蒸汽压表示； ② t-x-y图； ③ x-y图； ④用相对挥发度表示；
精馏过程工艺参数的确定(理论塔板数计算)最新实用版
（三）实际塔板数确定 全塔效率 在指定的分离条件 下，所需的理论塔板 数NT（不包括塔釜） 与实际塔板数N之比 称为全塔效率，用符
号ET表E示T 。N即NT
实际塔板数：
N NT ET
L
泡罩塔塔板效率关系曲线
❖ 课后思考题
❖ 逐板计算法和图解法求算理论塔板数都是基于恒摩尔流假 定，而假定的主要条件是组分的摩尔汽化潜热相等。对组 分的摩尔汽化潜热相差较大物系，就不能用基于恒摩尔假 定的方法求取理论塔板数。
感谢观看
如此重复计算直至x m xW为止。
理论塔板数与哪些参数有关？ 试用（1）逐板计算法，（2）图解法分别求出所需的理论板层数及进料板位置。 理论塔板数常见的确定方法有逐板计算法和图解法 全回流和最少理论塔板数
Rmin
xD yq
yq xq
二、回流比计算
3. 适宜回流比
分析回流比大小对精馏设备费用和操作费用的 影响。以精馏过程的设备费用与操作费用之和最 小为原则来确定适宜回流比。一般取最小回流比 的1.1~2.0倍。
❖ 应该采用什么方法求理论塔板数？请查阅有关书籍。
二、回流比计算
1. 全回流和最少理论塔板数
回流比的最大极限，此时操作过程没有产品， 操作线斜率为1，对应的塔板数为最少，仅用于 精馏开车阶段和科研工作。
二、回流比计算
2. 最小回流比
用图解法求回理论流塔板比层数的最具体小步骤极如下：限，对应的塔板数为无穷多，确
（1）绘相平衡曲线 （2）绘操作线 绘出精馏段 操作线和提馏段操作线
（3）绘直角梯级 从（xD,xD）点开始，在精馏段操作线 与平衡线之间绘水平线与垂直线构成直角梯级，当梯级跨
过两段操作线交点d时，则改在提馏段操作线与平衡线之间
化工单元操作：理论塔板数计算
1
2
a
3
f4
5d
6
e
7
b8 c
xW
xF
xD
理论塔板数
实际塔板数的确定
全塔效率 ：在指定的分离条件下，所需的理论塔板数NT（不包括塔釜）与 实际塔板数N之比，用符号ET表示。即
ET
NT N
则实际塔板数：
N NT ET
L
泡罩塔塔板效率关系曲线
（2）画出三条操作线
（3）画直角梯级：从塔顶a点 开始，跨越d点，到达c点结束
每一个梯级顶点代表一层 理论板，过d点为进料板， 末级为再沸器
1
2
a
3
f4
5d
6
e
7
b8 c
xW
xF
xD
理论塔板数
图解法
最适宜的进料位置 一般应在塔内液相或气相组成
与进料组成相同或相近的塔板上 ，分离效果好或一定的分离要求 所需理论板较少。
yn1
R R
1
xn
1 R
1
xD
ym1
L qF L qF W
xm
L
W qF
W
理论塔板数
逐板计算法
精馏段 从塔顶开始 ：塔顶采用全凝器，泡点回流
y1 xD (已知）
y1
1
x1 ( 1)x1
y1 x1(平衡关系)
x1
y1
1
y1
x1 y2（操作关系）
y2
R R 1
x1
xD R 1
理论塔板数
逐板计算法
精馏段
x
y
1
y
7-6 最小回流比、理论板数的确定、精馏塔操作问题
☼ F=D+W， D↓→ W↑ ☼ R↑→（L/V）↑精馏段分离能力提高， xD↑ ☼ L’↑，V’不变→（L’/V’）↑；提馏段分离能力↓，xW↑ 。
☼ 结论： V’不变，R↑， xD↑ ， D↓ 。
化工原理----精馏
☼ ②塔顶产品量不变
问题：R↑，F、xF、q、D不变，L、V、 L’、V’、W、xD、xW如何变化？
化工原理----精馏
R = Rmin时，对平衡线不正常（有明显下凹）的情况， 不能采用解析法，只能采用图解法求最小回流比。而正常的
平衡线也可采用图解法。
1
e
d xD R min1
0 xW xF
1
d
xD
e
R min1
xD 1
0 xW
xF
xD 1
化工原理----精馏
☼3、适宜回流比
R → Rmin时，N→∞；R→∞， N → Nmin R 对分离过程有显著的影响，确定回流比的方法有 两种：
影响-20
化工原理----精馏
化工原理----精馏
七、理论板数的简捷计算法
☼吉利兰关联图
用于初步估算 适用范围
化工原理----精馏
练习
☼121 习题 7-21
化工原理----精馏
八、理论板当量高度与填料层高度
☼填料层高度=理论塔板数X等板高度
化工原理----精馏
九、精馏装置的热量衡算
☼1、冷凝器、再沸器的热量衡算（自学） ☼2、 精馏过程的节能措施
（2）减小塔顶与塔釜间温差
温差越大，则有效能损失越大，缩小塔顶与塔釜 温差主要方法有：①降低塔板压降；②设置中间 再沸器或冷凝器。
精馏过程工艺参数的确定(理论塔板数计算)讲解
x D = y1
x 根据 x y 根据 y x 根据 x y
相平衡方程求
1
1
精馏段操作线方程
相平衡方程求
2
2
2
精馏段操作线方程
2
3
xn-1
yn
精馏段操作线方程
相平衡方程求
yn
x n≤ x d
直到xn xd（xd为两段操作线交点坐标x数值）时，说明第n 层板为加 料板，该板应属于提馏段。因此精馏段所需理论板数为n -1块。
理论塔板数与哪些参数有关？ 与物料量的多少是否有关？
NT f xF , xD , xW , q, R,
与进料位置也有关，提前进料和推迟进料都会使理论塔板数增多
某理想混合液用常压精馏塔进行分离。进料组成含 A81.5％，含B18.5％（摩尔百分数，下同），饱和 液体进料，塔顶为全凝器，塔釜为间接蒸气加热。 要求塔顶产品为含A95％，塔釜为含B95％，此物系 的相对挥发度为2.0，回流比为4.0。 试用（1）逐板计算法，（2）图解法分别求出所需 的理论板层数及进料板位置。
根据 y2 xm-1 ym
相平衡方程求
提馏段操作线方程
相平衡方程求
如此重复计算直至xm xW为止。由于离开塔釜的汽液两相组成达到平 衡，故塔釜相当于一块理论板，提馏段所需的理论塔板数为m-1块。
WxW L y m1 xm L W L W
x A yA 1 ( 1) x A
全塔所需的理论塔板数NT为
N n m 2
T
（不包括塔釜） （包括塔釜）
N n m 1
T
2、图解法 图解法求理论塔板数的基本原 理与逐板计算法相同，所不同的 是用相平衡曲线和操作线分别代 替相平衡方程和操作线方程。用 图解法求理论塔板层数的具体步 骤如下： （1）绘相平衡曲线 （2）绘操作线 绘出精馏段 操作线和提馏段操作线
化工原理下1.4 理论板计算(逐板、图解
yn1 xn
17
(2)最少理论板层数
一、全回流和最小回流比
R 越大 NT 越少
R1 R2
R3
xW
xF
xD
回流比与理论板层数的关系
一、全回流和最小回流比
回流比愈大，完成一定的分离任务所需的理 论板层数愈少。当回流比为无限大，两操作线与 对角线重合，此时，操作线距平衡线最远，气液 两相间的传质推动力最大，因此所需理论板层数
1.5.4 理论板数的求法
• 逐板计算法 • 图解法 • 简捷法
1
1.逐板计算法
yn1
R R1
xn
xD R1
(1)
y1 y2
x1
x2
F xF
L D xD
y
/ 2
xn (x1/ )
y m1
L' L'W
xm
W L'W
xW
(2)
y x
(3)
1 ( 1)x
xD y1 (3)
采用分凝器有什么作用？
一是为了得到气相产品（在生产流程中常 作为下一个设备的气相进料）；
二是为了除去比塔顶产品沸点低的组分， 此时塔顶产品就应是经分凝器后的液相产品。
此外，采用分凝器还可合理利用热能。
4
2.图解法 二、梯级图解法
梯级图解法又称麦克布—蒂利法，简称M—T法。
1）操作线的作法
5
❖ 精馏段操作线方程特点
芬斯克公式
lg (xA / xB )D
Nmin
(xA / xB )W 1
lg m
芬斯克公式的使用范围: 1. 全回流 2. 全凝器 3.相对挥发度变化不大
图解法求理论板数
一、图解法求理论板数图解法计算精馏塔的理论板数与逐板计算法一样,也就是利用汽液平衡关系与操作关系,只就是把气液平衡关系与操作线方程式描绘在y x -相图上,使繁琐数学运算简化为图解过程。
两者并无本质区别,只就是形式不同而己。
(1)精馏段操作线的作法 由精馏段操作线方程式可知精馏段操作线为直线,只要在x y -图上找到该线上的两点,就可标绘出来。
若略去精馏段操作线方程中变量的下标, 11+++=R x x R R y D 上式中截距为1+R x D ,在图7－12中以c 点表示。
当D x x =时,代入上式得D x y =,即在对角线上以a 点表示。
a 点代表了全凝器的状态。
联ac 即为精馏段操作线。
(2)提馏段操作线的作法 由q 线ef,即可求得它与精馏段操作线的交点,而q 线就是两操作线交点的轨迹,故这一交点必然也就是两操作线的交点d,联接bd 即得提馏段操作线。
(3)图解法求理论板数的步骤①在直角坐标纸上绘出待分离的双组分混合物在操作压强下的y x -平衡曲线,并作出对角线。
如图7-14所示。
②依照前面介绍的方法作精馏段的操作线ac,q 线ef,提馏段操作线bd 。
③从a 点开始,在精馏段操作线与平衡线之间作水平线及垂直线构成直角梯级,当梯级跨过d 点时,则改在提馏段与平衡线之间作直角梯级,直至梯级的水平线达到或跨过b 点为止。
④梯级数目减一即为所需理论板数。
每一个直角梯级代表一块理论板,这结合逐板计算法分析不难理解。
其中过d 点的梯级为加料板,最后一级为再沸器。
因再沸器相当于一块理论板,故所需理论板数应减一。
在图7-14中梯级总数为７。
第四层跨过d 点,即第４层为加料板,精馏段共3层,在提馏段中,除去再沸器相当的一块理论板,则提馏段的理论板数为4-1=3。
该分离过程共需6块理论板(不包括再沸器)。
图解法较为简单,且直观形象,有利于对问题的了解与分析,目前在双组分连续精馏计算中仍广为采用。
理论塔板数求取-61页文档资料
由
Vs
4
D2u
得 D 4V s
u 20
十二、连续精馏装置的热量衡算 (一)全塔的热量衡算
原料液所带入的热量:
QFGF.CF.tF
再沸器所带入的热量:
QGG.R
回流液所带入的热量:
QLGL.CL.tL
21
馏出液所带走的热量: 残液所带走的热量: 热损失:
Q D G D R 1 .IV
简单、造价低、安装维修方便等。
30
二、板式塔结构
板式塔结构如右图所示， 主要由塔体、塔板、裙座、接 口等部分组成。
31
三、板式塔的类型 塔板：有降液管式塔板和无降液管式塔板。
32
（一）泡罩塔
主要元件：升气管及泡罩 泡罩安装在升气管的顶部， 泡罩的下部周边有很多齿 缝，泡罩在塔板上按一定 规律排列。
y x 1( 1)x
代入
得
yq
xq 1(1)xq
Rmi n
xD yq
yq xq
18
（三）适宜回流比的选择
最适宜回流比应通过经济衡算来决定，即按照操作费用与 设备折旧费用之和为最小的原则来确定，它是介于全回流与最 小回流比之间的某个值。通常适宜回流比可取最小回流比的 （1.1－2.0）倍，即
8
2.求N 的步骤 自对角线上a点始, 在平衡线与
精馏段操作线间绘出水平线及铅垂 线组成的梯级. 如右图所示。
当梯级跨过两操作线交点d 时, 则改在平衡线与提馏操作线间作梯 级, 直至某梯级的垂直线达到或小 于xW为止。
每一个梯级代表一层理论板。 梯级总数即为所需理论板数。
9
八、适宜的进料位置
如前所述，图 解过程中当某梯级 跨过两操作线交点 时，应更换操作线。 跨过交点的梯级即 代表适宜的加料板 (逐板计算时也相同), 这是因为对一定的 分离任务而言, 如此 作图所需的理论板 层数为最少。
第五节理论板数的求法
第五节理论板数的求法所谓求理论塔板数，就是利用前面讨论的平衡关系，和操作关系，计算达到指定分离要求所须的汽化-冷凝次数。
（1）逐板计算法每利用一次平衡关系和一次操作关系，即为一块理论板。
提馏段也是一样。
（2）图解法通常采用直角梯级图解法，其实质仍然是以平衡关系与操作关系为依据，将两者绘在图上，便可图解得出达到指定分离任务所须的理论塔板数及加料板位置。
图解步骤如下：①作平衡线与对角线②作精馏段操作线，即连的直线。
③作进料线，过④作提馏段操作线，即连所得直线即是。
⑤从点开始，在平衡线与操作线之间作直角梯级，直到超过点。
有多少直角梯级，就有多少块理论板数。
跨越点的阶梯为加料板。
如图所示，共有5.2块理论板，第三块板为加料板。
图解法示意图a. 回流比与吉利兰图b. 回流比的影响因素（1）回流比对理论板数的影响。
如图。
回流比对的影响，操作线靠近平衡线，反之，，操作线远离平衡线，即正比于（2）回流比对设备费与操作费的影响，塔直径，冷凝器，蒸馏釜设备费，塔高下降，设备费，冷却水量，加热蒸汽量，操作费须选一个合适回流比，使总费用最省。
如图所示。
费用示意图１线为“设备费～Ｒ”的关系式２线为“操作费～Ｒ”的关系式３线为“总费用～Ｒ”的关系式。
c. 全回流与最小回流比全回流——当时，则，此时称为全回流。
这时精馏段与提馏段操作线方程均与对角线重合，此时理论板数最少。
最小回流比——当减小时，，当减至两操作线交点逼近平衡线时，此时，此时Ｒ称为最小回流比。
最小回流比推导图解之得，………………与是平衡线与进料线之交点。
最小回流比是指对于一定分离要求的最小回流比，分离要求变动了（例如变了），对应的亦要改变。
d. 吉利兰图法求理论板数吉利兰图是一种经验关联图，它总结了八种不同的物系，个组分，操作压力由真空个大气压，进料由过冷液体过热蒸汽。
它如何归纳得到，本章并不关心，重点是如何应用它？下面是吉利兰图法应用举例。
【例】某二元理想混合液其平均相对挥发度为。
图解法求理论板数(图文运用)
一、图解法求理论板数图解法计算精馏塔的理论板数和逐板计算法一样，也是利用汽液平衡关系和操作关系，只是把气液平衡关系和操作线方程式描绘在y x -相图上，使繁琐数学运算简化为图解过程。
两者并无本质区别，只是形式不同而己。
（1）精馏段操作线的作法 由精馏段操作线方程式可知精馏段操作线为直线，只要在x y -图上找到该线上的两点，就可标绘出来。
若略去精馏段操作线方程中变量的下标， 11+++=R x x R R y D 上式中截距为1+R x D ，在图7－12中以c 点表示。
当D x x =时，代入上式得D x y =，即在对角线上以a 点表示。
a 点代表了全凝器的状态。
联ac 即为精馏段操作线。
（2）提馏段操作线的作法 由q 线ef ，即可求得它和精馏段操作线的交点，而q 线是两操作线交点的轨迹，故这一交点必然也是两操作线的交点d,联接bd 即得提馏段操作线。
（3）图解法求理论板数的步骤①在直角坐标纸上绘出待分离的双组分混合物在操作压强下的y x -平衡曲线，并作出对角线。
如图7-14所示。
②依照前面介绍的方法作精馏段的操作线ac ，q 线ef ，提馏段操作线bd 。
③从a 点开始，在精馏段操作线与平衡线之间作水平线及垂直线构成直角梯级，当梯级跨过d 点时，则改在提馏段与平衡线之间作直角梯级，直至梯级的水平线达到或跨过b 点为止。
④梯级数目减一即为所需理论板数。
每一个直角梯级代表一块理论板，这结合逐板计算法分析不难理解。
其中过d 点的梯级为加料板，最后一级为再沸器。
因再沸器相当于一块理论板，故所需理论板数应减一。
在图7-14中梯级总数为７。
第四层跨过d 点，即第４层为加料板，精馏段共3层，在提馏段中，除去再沸器相当的一块理论板，则提馏段的理论板数为4-1=3。
该分离过程共需6块理论板（不包括再沸器）。
图解法较为简单，且直观形象，有利于对问题的了解和分析，目前在双组分连续精馏计算中仍广为采用。
但对于相对挥发度较小而所需理论塔板数较多的物系，结果准确性较差。
6-2 理论塔板数的计算(简版)
逐 板 法 图 解 法 捷 算 法
23:29:19
6-2 理论塔板数计算 （48）
2
双组分连续精馏塔的计算
理论板 理论板是指离开塔板的蒸汽和液体呈平 衡的塔板，它是人为的理想化的塔板。 理论板可以作为衡量实际塔板分离效果 的一个标准。
23:29:19
6-2 理论塔板数计算 （48）
3
例1 环己烷 80.8℃ 苯 80.1℃ 常压下沸点 糠醛 161.7℃ 苯酚 180℃
环己烷-苯恒沸物 77℃
糠醛能显著降低苯的饱和蒸汽压，而对环己烷影响不明 显，使苯从易挥发组分变为难挥发组分，而且使环己烷-苯的 增大至2以上。
23:29:19
6-2 理论塔板数计算 （48）
22
萃取剂的选择原则：
6-2 理论塔板数计算 （48）
23:29:19
说明： （1）EmV(n)和 EmL(n)不 一定相等， （2）一般情况单板效率 小于 1， 特殊情况它们会 大于 1， 通常出现在塔径 较大的精馏塔中。
16
2．全塔效率E0
又称总板效率，其定义为：
D, xD
理论板数 N E0 实际板数 N e
恒 沸 精 馏 特殊精馏 萃 取 精 馏
23:29:19
6-2 理论塔板数计算 （48）
x
19
1．恒沸精馏
加入的第三组分与原溶液中的一个或者两个组分形成 最低恒沸物，从而形成了“恒沸物－纯组分”的精馏体系， 恒沸物从塔顶蒸出，纯组分从塔底蒸出，这种形式的精馏称 为恒沸精馏，其中所添加的第三组分称为 恒沸剂或者夹带 剂。
ym+1 xm yN-1 xm+1
x N1 1 y N1 2 x N1 2 y N1 3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、图解法求理论板数
图解法计算精馏塔的理论板数和逐板计算法一样，也是利用汽液平衡关系和操作关系，只是把气液平衡关系和操作线方
程式描绘在y x -相图上，使繁琐数学运算
简化为图解过程。
两者并无本质区别，只是
形式不同而己。
（1）精馏段操作线的作法 由精馏段
操作线方程式可知精馏段操作线为直线，只
要在x y -图上找到该线上的两点，就可标
绘出来。
若略去精馏段操作线方程中变量的
下标， 1
1+++=R x x R R y D 上式中截距为
1+R x D ，在图7－12中以c 点表示。
当D x x =时，代入上式得
D x y =，即在对角线上以a 点表示。
a 点代
表了全凝器的状态。
联ac 即为精馏段操作线。
（2）提馏段操作线的作法 由q 线ef ，即可求得它和精馏段操作线的交点，而q 线是两操作线交点的轨迹，故这一交点必然也是两操作线的交点d,联接bd 即得提馏段操作线。
（3）图解法求理论板数的步骤
①在直角坐标纸上绘出待分离的双组分混合物在操作压强下的y x -平衡曲线，并作出对角线。
如图7-14所示。
②依照前面介绍的方法作精馏段的操作线ac ，q 线ef ，提馏段操作线bd 。
③从a 点开始，在精馏段操作线与平衡线之间作水平线及垂直线构成直角梯级，当梯级跨过d 点时，则改在提馏段与平衡线之间作直角梯级，直至梯级的水平线达到或跨过b 点为止。
④梯级数目减一即为所需理论板数。
每一个直角梯级代表一块理论板，这结合逐板计算法分析不难理解。
其中过d 点的梯级为加料板，最后一级为再沸器。
因再沸器相当于一块理论板，故所需理论板数应减一。
在图7-14中梯级总数为７。
第四层跨过d 点，即第４层为加料板，精馏段共3层，在提馏段中，除去再沸器相当的一块理论板，则提馏段的理论板数为4-1=3。
该分离过程共需6块理论板（不包括再沸器）。
图解法较为简单，且直观形象，有利于对问题的了解和分析，目前在双组分连续精馏计算中仍广为采用。
但对于相对挥发度较小而所需理论塔板数较多的物
系，结果准确性较差。
二、适宜的进料位置
在设计中确定适宜进料板位置的问题也就是如何选择加料位置可使总理论板数最少。
适宜的进料位置一般应在塔内液相或汽相组成与进料组成相近或相同的塔板上。
当采用图解法计算理论板时，适宜的进料位置应为跨过两操作线交点所对应的阶梯。
对于一定的分离任务，选此位置所需理论板数为最少，跨过两操作线交点后继续在精馏段操作线与平衡线之间作阶梯，或没有跨过交点就更换操作线，都会使所需理论板数增加。
对于已有的精馏装置，在适宜进料位置进料，可获得最佳分离效果。
在实际操作中，进料位置过高，会使馏出液的组成偏低（难挥发组分偏高）；反之，使釜残液中易挥发组分含量增高，从而降低馏出液中易挥发组分的收率。
对于实际的塔，往往难以预先准确确定最佳进料位置，特别是当料液浓度和其他操作条件有变化时，因此通常在相邻的几层塔板上均装有进料管，以便调整操作时选用。