第三章几何光学
第三章几何光学球面反射折射物像公式
例3.4:
一个折射率为1.6的玻璃哑铃,长20cm,两端的曲率半径为 2cm。若在 离哑铃左端5cm处的轴上有一物点,试求像的位置和性质。
[解]:两次折射成像问题。
n
P
O1
n
P’1 n` O 2
1、P为物, 对球面O1折射成像P1’
已知 : s1 5cm , r1 2cm , n 1, n ' 1.6 n n n n 由折射成像公式 ' r1 s1 s1
沿轴线段
A、凡光线与主轴交点在顶点右方者线段长度数值为正; 凡光线与主 轴交点在顶点左方者线段长度数值为负; B、物点或像点至主轴的距离在主轴上方为正,下方为负。 ② 光线的倾角均从主轴或球面法线算起,并取小于900的角度;由主轴 (或法线)转向有关光线时: A、顺时针转动,角度为正;B、逆时针转动,角度为负。 (注意:角度的正负与构成它的线段的正负无关)
2
r
2
s r
'
2
2 r s ' r cos
光程 PAP ' nl nl ' n
r 2 r s 2 2 r r s cos r
2
n
s r
'
2
2 r s r cos
1、高斯公式:
球面反射 : f ' f 1 1 2 ' s s r
六、理想成象的两个普适公式
n' n n' n 将物像公式 ' 变形为 : s s r n' n r r ' ' ' f f n n n n 1 1 ' ' s s s s
第三章几何光学的基本原理-卓士创($5-6)

其中:
(17)——横向放大率
(18)——角度放大率
(16)
推广:对于共轴光具组,理想成像应满足亥——拉定理,即
(19)
小结
一、 近轴物近轴光线条件下的球面反射
(1) 物象公式
(11)
(2) 横向放大率
(12)
二、近轴物近轴光线条件下的球面折射
(1)物象公式
(13)
(2)横向放大率
(14)
倒立象 ;
(2)公式:
(8)
由图知:
所以有:
近轴光线、近轴物物件下!
(9) ——也适用于单个球面
将
、
代入上式有:
说明:
(1)
,表示放大;
,表示等大;
(2) 对实物而言: ,表示像相对物正立;
对虚物而言: ,表示像相对物倒立;
(10)
,表示缩小。 ,表示像倒立。 ,表示像正立。
参图
小结
一、近轴条件下的薄透镜成像公式
已知: f1’= -f1 =2cm, f2’=-f2=2cm , -r =8cm。试求:(1) d12= 5cm, d23= 10cm,-s2 =1cm ,叉丝P经光学系统成像的位置: S1’ (经L1) 、 S2’ (经L2) 、 S3’ (经L3) 、 S4’ (回经L2) 、 S5’ (又经L1) =? (2)当d12= 5cm时,目镜L1能成1个清晰叉丝像, d23=?
令
球
令
——球面折射公式(2)
面
反
射
令焦距
公
式
⑸
——球面折射公式(3)——高斯公式
由
、
——球面折射公式(4)——牛顿公式
例题3.4 一个折射率为1.6的玻璃哑铃,长为20cm,两端的曲 率半径为2.0cm.若在离哑铃左端5.0cm处的轴上有一物点,试 求像的位置和性质。
第三章-几何光学
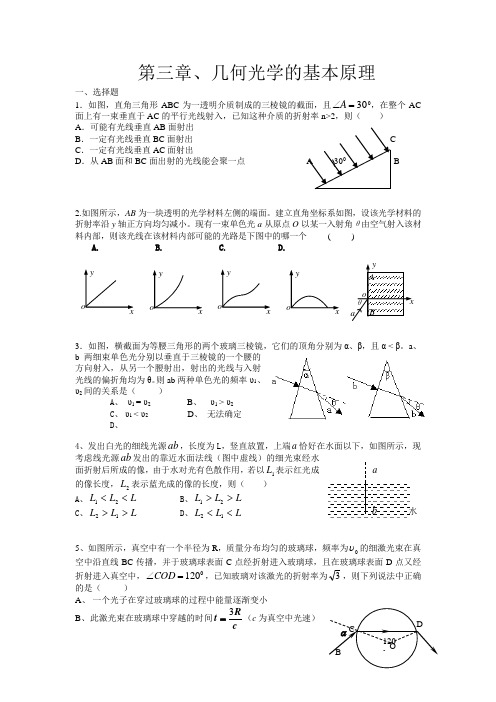
第三章、几何光学的基本原理一、选择题1.如图,直角三角形ABC 为一透明介质制成的三棱镜的截面,且30=∠A 0,在整个AC 面上有一束垂直于AC 的平行光线射入,已知这种介质的折射率n>2,则( ) A .可能有光线垂直AB 面射出 B .一定有光线垂直BC 面射出 CC .一定有光线垂直AC 面射出D .从AB 面和BC 面出射的光线能会聚一点 A 300 B2.如图所示,AB 为一块透明的光学材料左侧的端面。
建立直角坐标系如图,设该光学材料的折射率沿y 轴正方向均匀减小。
现有一束单色光a 从原点O 以某一入射角θ由空气射入该材料内部,则该光线在该材料内部可能的光路是下图中的哪一个 ( )A. B. C. D.3.如图,横截面为等腰三角形的两个玻璃三棱镜,它们的顶角分别为α、β,且α < β。
a 、b 两细束单色光分别以垂直于三棱镜的一个腰的方向射入,从另一个腰射出,射出的光线与入射光线的偏折角均为θ。
则ab 两种单色光的频率υ1、υ2间的关系是( )A 、 υ1 = υ2B 、 υ1 > υ2C 、 υ1 < υ2D 、 无法确定 D 、4、发出白光的细线光源ab ,长度为L ,竖直放置,上端a 恰好在水面以下,如图所示,现考虑线光源ab 发出的靠近水面法线(图中虚线)的细光束经水面折射后所成的像,由于水对光有色散作用,若以1L 表示红光成的像长度,2L 表示蓝光成的像的长度,则( ) A 、L L L <<21B 、L L L >>21C 、L L L >>12D 、L L L <<125、如图所示,真空中有一个半径为R ,质量分布均匀的玻璃球,频率为0υ的细激光束在真空中沿直线BC 传播,并于玻璃球表面C 点经折射进入玻璃球,且在玻璃球表面D 点又经折射进入真空中,0120=∠COD ,已知玻璃对该激光的折射率为3,则下列说法中正确的是( )A 、 一个光子在穿过玻璃球的过程中能量逐渐变小B 、 此激光束在玻璃球中穿越的时间cRt 3=(c 为真空中光速) 水 a b O CDB α1200y a θ xo A ByxoyxoyxoyxoC 、 改变入射角α的大小,细激光可能在玻璃球的内表面发生全反射D 、 图中的激光束的入射角045=α6、如图所示,两束单色光A 、B 自空气射向玻璃,经折射形成复合光束C ,则下列说法中正确的是:( )A 、 A 光子的能量比B 光子的能量大 B 、 在空气中,A 光的波长比B 光的波长短C 、 在玻璃中,A 光的光速小于B 光的光速D 、 玻璃对A 光的临界角大于对B 光的临界角7、如图所示,激光液面控制仪的原理是:固定的一束光AO 以入射角i 照射到液面上,反射光OB 射到水平的光屏上,屏上用一定的装置将光信号转变为电信号,电信号输入控制系统用以控制液面高度,如果发现光点B 在屏上向右移动了Δs 的距离到B ˊ,则可知液面升降的情况是( )A 、 升高了2S ∆·tan i B .降低了2S ∆·tan i D 、 升高了2S ∆·cot i D 、 降低了2S∆·cot i8.人类对光的本性的认识经历了曲折的过程。
光学 第3章 几何光学的基本原理

(1) 偏向角
i1
又
i2
i2
i2 '
i1'i2
A
'
i1 i1' A
(2) 最小偏向角0
当i1改变时 、i1'均随之而改变,当 i1 i1'时,偏向角取最小 0。
0 2i1 A
A
此时在棱镜内传播的光线平行于底边,有:
i2
i2 '
A 2
,i1
i1'
0
2
A
2. 棱镜的折射率
3、折射定律:(1) 折射线在入射线和法线决定的平面内; (2) 折射线、入射线分居法线两侧; (3) 折射角和入射角满足斯涅尔定律:n1sini1=n2sini2
i1 i1'
n1
n2
i2
7 反射和折射定律光路图
3、光的独立传播定律:几个光源发出的光在空间传播并相遇后, 它们将各自保持自己原有的特性(频率、波长、偏振状态)沿原来 的方向继续传播,互不影响。 4、光路可逆原理:当光线的方向反转时,它将逆着同一路径传 播,称为光路可逆原理。
i2 i2
A2 x2,0
i1 i1
B2 n2
x
n1
晰,像的深度由上式确定,y‘ 叫做像似深度 ,y是物的实际深度。
20
(3)像散现象:当i1≠0,即入射光束倾斜入射时,折射光线会发生像散现象。如沿 着倾斜的角度观察水中的物体时,像的清晰度由于像散而被破坏。
例1: 使一束向P点会聚的光在到达P点之前通过一平行玻璃板。如果将玻璃板 垂直于光束的轴竖放,问会聚点将朝哪个方向移动?移动的距离为多少?
A1 A2
P
P'
M
第三章 几何光学的基本原理

第三章几何光学的基本原理干涉和衍射现象揭示了光的波动性。
光既然具有波动性,那么,所有光学现象都应该能用波动概念来解释,包括光的直线传播现象在内。
但是直线传播,尤其是反射,折射成像等问题,如果不用波长、相位等波动的概念,而代之以光线和波面等概念,并用几何学方法来研究将更为方便。
这就是几何光学的研究内容。
由于这只有在波面线度远比波长大时才适用,因此本章所讲述的内容仅以成像的一级近似理论为限,因为这种近似有很大的实用意义。
3.1 光线的概念3.1.1 光线与波面“光线”只能表示光的传播方向,不可以误认为是从实际光束中借助于有孔光阑分出的一个狭窄部分,那么,在极限情况下,选用任意小的孔,就能得到像几何线那样的所谓“光线”,但是由于衍射作用,实际上要分出任意窄的光束是不可能的。
通过半径为R的圆孔的实际光束,其传播范围不可比避免的要扩大,其角宽度由衍射角θ∝λ/R决定[见(2-23)?的情况下,由衍射引起的扩大已不显著,光的传播过程才不用以次波叠式]。
只有在R l加的原理来分析,而只用光线来表示光的传播方向。
我们说“光束由无数光线构成”,不过是说明光沿着无数不同的方向传播罢了。
光波在介质中沿着光线传播时,相位不断地改变,但是同一波面上所有点的相位是相同的。
在各向同性介质中,光的传播方向总是和波面的法向方向相重合。
在许多实际情况中,人们经常考虑的只是光的传播方向问题,而不去考虑相位。
这时波面就只是垂直于光线的几何平面或曲面。
在这种极限情况下,实际上是把光线和波面都看做是抽像的数学概念。
对许多实际问题,特别是光学技术成像和照明工程等问题,借助于上述光线(有时用波面)的概念,并应用某些基本实验定律及几何定律,就可以进行所有必要的计算而不必涉及光的本性问题。
这部分以几何定律和某些基本实验定律为基础的光学称为几何光学(或光线光学)。
反映光的波动性的那部分光学称为波动光学。
在第1、2章波动光学中主要考虑的是波长、振幅和相位;这一章几何光学所考虑的主要将是光线和波面。
光学第三章几何光学

联系光与电磁波
3、λ ——光波长
是否趋近于零 区分几何光学与波动光
学 4、χ ——介质的电极化率
其对光场响应是线性与非线性区分线性 与非线性光学
费马原理
一、费马原理:光在指定的两点间传播时,
实际的光程总是一个极值。其数学表达式为:
B nds 极值(极大值、极小值或恒定值) A
射光束都是单心光束的成像。这也是我们
着重研究的情况。
3、物、像与人眼
问题:
‘
这里的像就是人眼视网膜上所成的
像吗?人眼能否区分物与像?
结论:
对人眼来所,物与像都是进入瞳孔的发
射光束的顶点。物、像、虚像人眼不能分辨。
但对于像,其光束有一定的限制,必须在特定
的范围才能观察到。
光在平面界面上的反射和折射 光学纤维 棱镜
第 三 章 几 何 光 学
三角形孔夫琅禾费衍射图像
本章内容
光线的概念 几何光学的基本定律 费马原理 光束 实象和虚像 平面反射和折射,棱镜的最小偏向角,光
学纤维 光在球面界面上的反射和折射、符号法则 近轴物点近轴光线成像的条件 薄透镜 理想光具组的基点和基面
光线的概念、几何光学的基本定律
B
或: nds 0 A
或:t 1
B
nds 0
ccA
二、几何光学的基本实验定律与费马原理
1、几何光学的基本实验定律或费马原理都可以 作为几何光学出发点,从而建立几何光学内容 体系。 2、由费马原理可以推导几何光学的基本实验 定律。 (1)、光在均匀介质中的直线传播
S
1
l = ([ - r)2 +(r - s)2 + (2 - r)( r - s)cos ] 2
第三章几何光学基本概念与费马原理

2
教学要求
(1)理解光线和光束的概念 (2)理解物和像的概念,掌握物、像虚实的实质 及判断。 (3)掌握几何光学基本定律,并应用它讨论一些 问题。 (4)了解由惠更原理,费马原理导出几何光学基 本定律,了解费马原理在光学中的地位及作用。 (5)掌握几何光学中的符号法则。
3
(6)掌握用物像公式寻找成像规律。 (7)掌握以光线作图法寻找成像规律。 (8)熟练掌握正确运用物像公式和光线 作图法求解单球面、薄透镜及简单光具组 的成像问题。
y A(x1,y1,o) i i’ D(x,0,0) C(x,0,z) z B(x2,y2,0) x
y 由A 经C 到 B 的光程为
A(x1,y1,o) i i’
B(x2,y2,0)
L n AC n CB
n ( x x1 ) y z
2 2 1 2 2 2 2 2
x
D(x,0,0)
波线
波线
在波场中有一线簇,它们每点的切线方向代表该点波的 传播方向,这种线簇——波线。 在各向同性介质中,波线总是与波面垂直的。
二、 基本实验规律 1 、光在均匀介质中沿直线传播
说明:不均匀介质中,光线弯曲
2 、光的独立传播和光路可逆原理
3、 光的反射定律和折射定律
反射、折射线同在入射面内,并与入射线分居 两侧,且 i' i n1 sin i1 n 2 sin i 2
二、几何光学基本定律 1、光的直线传播定律:
光在各向同性的均匀介质中沿直线传播物体的影子、针孔
成像、日蚀、月蚀、日食、月食都是直线传播的实验。
2、光的独立传播定律: 自不同方向或不同物体发出的光线相遇时,对每一光线 的独立传播不发生影响,相遇前后的传播方向和强度都保 持原来的传播方向和强度。 适用于强度不太大,相干性较差的光线传播。
光学教程___第3章_几何光学的基本原理

i2 ic的光线折射出光纤;i2 ic 的光线在两层介质间多次全
反射从一端传到另一端.
内窥镜、光导通讯……
为了使更大范围内的光束能在纤维中传播,应选择n1和n2的差
值较大的材料去制造光学纤维。
/ 77
20
四.棱镜
主截面:垂直于两界面的截面. 偏向角:出射线与入射线间的夹角.
=(i1-i2 )+(i1 -i2 )= i1 +i1 -A
由P点所发出的单心光束经球面反射后,单心性被破坏
/ 77
26
三、近轴光线条件下球面反射的物像公式
当φ很小时,cosφ 1
l r2 r s2 2 rr s r r s2 s
l' r2 s' r 2 2 r s' r r s' r 2 s'
由:
A
d l
n 2rs rsin 0 P
l
l
-u
i
-i′ l '
-u`
C
P` -s` O
化简有:r l
s
s r l'
0
-r -s
即:1 l'
1 l
1 r
s l'
s l
对一定的球面和发光点P(S一定),不同的入射点对应有不同的S‘。
即:同一个物点所发出的不同光线经球面反射后不再交于一点。
第三章 几何光学的基 本原理
/ 77
1
干涉和衍射现象揭示了光的波动性,所有 光学现象都能够用波动概念解释。但是在波面 线度远大于波长时,研究光的反射,折射成象 等问题,如果不用波长、位相等波动概念而代 之以光线和波面等概念,即用几何的方法来研 究,将更为方便。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
再经第一界面折射成像
n n n n s s r
n 1.5, n 1, r r1 5cm, s s3 , s s2
1 1 1.5 1.5 1 1.5 1.5 ( 1 1 )
由物像公式得
s
2s s 40 30(cm )
1 0 .8
1 0 .2
2 r
r
0.53 m
例2.在报纸上放一个平凸透镜,眼睛通过透镜看报纸,当平面在上时,报 纸的虚像在平面下13.3mm处,当凸面在上时,报纸的虚像在凸面下14.6mm 处.若透镜的中央厚度为20mm,求透镜的折射率和凸球面镜的曲率半径。
s3
r1
s2
5
15 1.5s
即:1 0.1 0.1 1 1
解:经第一界面成像
n n n n s s r
n 1.5, n 1, r r1 5cm, s s1
n n n n
s1
r1
s
即:1.5=1.5 1 1
s1
5s
1=1 1 s1 15 1.5s
经第二界面(涂银面)反射成像:
1 12 s s r
ss2,ss1,rr2 15cm
s
s
s
s
利用牛顿公式得
x f
f x
例1. 凹面镜的曲率半径为40cm,(1)物体放在何处成放大两倍的
实像? (2)物与虚像相距为1m,如果物高4倍于像高,求凹面镜的
曲率半径。y
放大倍数:y s
ys
C y -r
-s` O 0 ,实 像 ; 0 ,虚 像
-s
解 : (1) s 2 s
理想光具组的概念(高斯1841年提出):能保持 光束的单心性以及物和像在几何上的相似性,物 方的每一点、每一条直线、每一个平面,像方相 应的有一个共轭点、一条共轭直线、一个共轭平 面。
近轴条件下的共轴光具组可近似于理想光具组来 研究。
从高斯理论可知:只要在光具组的物像空间上建立点与点、线 与线、面与面之间的共轭关系,即可简单地由物获得像。
-s
s′
f
n
f′
P
P/
F
O1 δ O2
F′
-r2 p
r1 p′
厚透镜基点位置(附录3-4):
像方焦点F′的位置(以H′为基点)
1(n1)[11(n1)]
f
r1 r2 nr1r2
物方主点H的位置(以O1为基点)
p
r 1
f(n 1 )
n (r 2 r 1 ) (n 1 )
r 2 n
像方主点H′的位置(以O2为基点)
p
r 2
f(n 1 )
n (r 2 r 1 ) (n 1 )
r 1 n
厚透镜的高斯公式
1 1 1 s s f
2、厚透镜的基点和基面
物方主点H:s、f的参考点 像方主点H´:s´、f´的参考点: 物方主面:过物方主点垂直于主轴的平面 像方主面:过像方主点垂直于主轴的平面 物方焦点、像方焦点、物方焦平面、像方焦平面。
1 1.5 11.5 14.6 20 r
r 76.84mm
例3.将一根40cm长的透明玻璃棒的左端磨平,右端磨成半 径为12cm的凸半球面,有一物点嵌在棒轴上并与棒两端等距, 当从棒左端面看去时,该物的表观深度为12.5cm,试问从棒 右端面看去时它的表观深度为多组的放大率
横向放大率:
f s 1 s
f
f
利用高斯物像公式,可得
s 或 = f
s
f s
利用牛顿公式得
x f
f x
角放大率:
M
M
P
u H
H u P
s
s
定义: tgu
tgu
tg(u) HM , tgu H M , MH M H (两主面共轭)
解 : 由 像 似 深 度 公 式 yn n 1 2y, 且 n21 ,y12.5cm ,y20cm得 玻 璃 的 折 射 率 : nn 1y yn21 2 2 0 .51.6
由 折 射 成 像 公 式 : n n n-n 得 s s r
解:(1)像似深度 y13.3mm,物的实际深度 y20mm
由yn2 y 得透镜的折射率为 n1
n1yyn2
2011.5 13.3
(2)依题意,此时为球面折射成像情况: s 20mm, s 14.6mm
由成像公式 n n n n 得 s s r
1 1.6 1-1.6 s 20 12 s33.3cm
例4.(习题22)折射率为1.5的薄透镜,其凸面的曲率半径为 5cm,凹面的曲率半径为15cm,且镀上银。试证明:当光从凸面入射时, 该透镜的作用相当于一个平面镜。(提示:物经过凸面折射、凸面反射和凹 面再次折射后,s/=-s,β=1.)
第三章 几何光学的 基本原理
本课内容: §3-9理想光具组的基点和基面 §3-10理想光具组的放大率
§3-9 理想光具组的基点和基面
分析:光具组的成像,可以用逐个球面成像法求得。其中要进行 大量复杂的计算。能否把共轴光具组当成一个整体,略去各 镜面间复杂的计算简化求像过程?
关于光具组的理论结果:
实际的光具组:除平面反射外,一般都不能保持 光束的单心性以及物和像在几何上的相似性。
( 2 ) s 1 s 1 s
s4
4
s 2 s 又 s s 1 1 s s 1
由物像公式得
4
s 0 .8 m s 0 .2 m
1 1 2
关键点:求出物与像空间之间共轭的基本点和面,即基点和基 面(焦点、主点、焦平面、主平面)。
利用基点和基面,即可建立起物像空间的共轭关系。 求光具组的基点和基面可以先求各个透镜的基点基面,再
逐个组合求出整个光具组的基点基面。
以最简单的光具组:厚透镜为例,求解基点和基面。
1、厚透镜物像公式的高斯形式
H H′
