基本逻辑运算解读
逻辑代数的三个基本运算

逻辑代数的三个基本运算逻辑代数是一种数学分支,研究命题和命题之间的逻辑关系。
它主要包括命题逻辑和谓词逻辑两个部分。
在逻辑代数中,有三个基本运算,即合取、析取和否定。
接下来,我将一步一步回答有关逻辑代数的这三个基本运算的问题。
一、合取运算(AND)合取运算,也称为与运算,用∧(圆圈上有一个小竖杠)表示。
在逻辑代数中,合取运算指的是将两个或多个命题连接起来,当且仅当这些命题都为真时,合取命题才为真。
1. 合取命题的真值表首先,我们可以通过真值表来表示合取命题。
假设有两个命题P和Q,可以通过以下真值表来表示合取命题:P Q P∧QT T TT F FF T FF F F从上表可以看出,当且仅当P和Q的值均为真时,合取命题才为真。
2. 合取的代数表达式除了使用真值表,我们还可以使用代数表达式来表示合取命题。
例如,我们可以用“P ∧Q”来表示“P和Q的合取”。
在逻辑代数中,合取的代数表达式遵循以下规则:- 合取满足交换律:P ∧Q = Q ∧P- 合取满足结合律:(P ∧Q) ∧R = P ∧(Q ∧R)- 合取满足吸收律:P ∧(P ∨Q) = P二、析取运算(OR)析取运算,也称为或运算,用∨(有一个小竖杠在圆圈顶部)表示。
在逻辑代数中,析取运算是将两个或多个命题连接起来,当且仅当这些命题中至少有一个为真时,析取命题才为真。
1. 析取命题的真值表与合取运算类似,我们可以使用真值表来表示析取命题。
假设有两个命题P和Q,可以通过以下真值表来表示析取命题:P Q P∨QT T TT F TF T TF F F从上表可以看出,只有当P和Q的值至少有一个为真时,析取命题才为真。
2. 析取的代数表达式类似于合取运算,我们可以使用代数表达式来表示析取命题。
例如,我们可以用“P ∨Q”来表示“P或Q的析取”。
在逻辑代数中,析取的代数表达式遵循以下规则:- 析取满足交换律:P ∨Q = Q ∨P- 析取满足结合律:(P ∨Q) ∨R = P ∨(Q ∨R)- 析取满足分配律:P ∨(Q ∧R) = (P ∨Q) ∧(P ∨R)三、否定运算(NOT)否定运算,也称为非运算,用¬表示。
逻辑运算法则

03
非门(NOT Gate)
• 非门是一种一元运算,表示为¬A
• 非门的功能是将输入的真变为假,将假变为真
逻辑门电路的设计与实现:晶体管与二极管电路
晶体管
• 晶体管是一种常用的半导体器件,可以用作开关和放大器
• 晶体管可以实现与门、或门和非门等逻辑门电路
二极管
• 二极管是一种半导体器件,具有单向导电性
• 逻辑门电路是数字电路的基础,广泛应用于电子设备中
逻辑运算在计算机科学中的应用
• 逻辑运算用于处理计算机中的逻辑操作
• 逻辑运算在计算机硬件和软件的设计中都起着重要作用
逻辑运算在编程语言中的应用
• 逻辑运算用于编写条件语句和循环语句
• 逻辑运算在算法和数据处理中有着广泛的应用
逻辑运算的历史发展:从布尔代数到现代逻辑电路
• 二极管可以实现或门和非门等逻辑门电路
逻辑电路的综合与优化:用逻辑代数表示电路设计
逻辑代数
电路综合
• 逻辑代数是一种用代数符号表示逻辑运算的方法
• 电路综合是一种将逻辑代数表达式转化为实际电路设计
• 逻辑代数可以用于分析和设计逻辑电路
的方法
• 电路综合可以用于优化逻辑电路的性能,提高电路的可
靠性
的便利
• 现代逻辑电路在计算机科学、通信技术等领域有着广泛的应用
02
逻辑运算的基本种类与性质
常见的逻辑运算:与、或、非、异或等
01
02
03
04
与运算(AND)
或运算(OR)
非运算(NOT)
异或运算(XOR)
• 与运算的逻辑表达式为:A
• 或运算的逻辑表达式为:A
• 非运算的逻辑表达式为:
1逻辑代数中的三种基本运算

B
“与非”门电路
L=AB=(AB)’
“与非”逻辑真值表
AB L 00 1 01 1 10 1 11 0
15 本继页续完
“逻或辑非”代逻数辑的表三符种号基和本真值运算
二、门电路的表组合
把逻辑运算的“与”、“或”和“非”运算进行组合, 可得出各种各样的逻辑关系。
2.“或非”门
将“或”门和“非”门结合在一起,构成了“或非门” 电路。
结果:灯亮(1);灯不亮(0)
条件:开关闭合(1);开 关断开(0)。
R A
E
L
“非”关系:只要开关闭合(1)灯就灭(0),当开 关断开(0)时,灯才亮(1)。
12 本继页续完
逻⑵“辑非代”数关系的的三三种种基表本示运法算:
一、基本逻辑运算
逻辑运算的三种基本运算:“与”、“或”和“非”。
3.“非”运算(逻辑否定)
以其运算规律与二进制数不同。
负逻辑:与正逻辑表示相反的逻辑称为负逻辑。电路
表示高电平为0,低电平为1。
3 本继页续完
⒈ (逻1“)辑“与与代””数逻的运辑三举算种例((基贷逻本款运辑事例算乘) )
一、基本逻辑运算
逻辑运算的三种基本运算:“与”、“或”和“非”。 ⒈“与”运算(逻辑乘)
⑴“与”逻辑:当几个条件同时具备才能出现某一结 果时,这些条件与结果之间关系称为“与”逻辑。
1 0 11 1 1 01
1 1 11
10 本继页续完
逻③辑“或代”数逻的辑三符种号基表示本法运:算
一、基本逻辑运算
逻辑运算的三种基本运算:“与”、“或”和“非”。
2.“或”运算(逻辑加)
⑵“或”关系的三种表示法: A
≥1
78个逻辑类型及总结

78个逻辑类型及总结在计算机科学中,逻辑类型是指变量或表达式的类型,用于表示真值逻辑运算的结果。
逻辑类型通常只有两个取值:真(True)和假(False)。
在本文中,我们将介绍并总结78种常见的逻辑类型。
逻辑类型的基本运算1.逻辑与 (AND): 当两个表达式都为真时,结果为真;否则为假。
2.逻辑或 (OR): 当两个表达式至少一个为真时,结果为真;否则为假。
3.逻辑非 (NOT): 对单个表达式求反,即真变为假,假变为真。
基本逻辑类型4.布尔型 (Bool): 最基本的逻辑类型,只有真和假两个取值。
数字比较类型5.相等 (Equal): 判断两个数值是否相等。
6.不等 (Not equal): 判断两个数值是否不相等。
7.大于 (Greater than): 判断一个数值是否大于另一个数值。
8.小于 (Less than): 判断一个数值是否小于另一个数值。
9.大于等于 (Greater than or equal to): 判断一个数值是否大于等于另一个数值。
10.小于等于 (Less than or equal to): 判断一个数值是否小于等于另一个数值。
字符串比较类型11.相等 (Equal): 判断两个字符串是否相等。
12.不等 (Not equal): 判断两个字符串是否不相等。
13.大于 (Greater than): 判断一个字符串是否大于另一个字符串。
14.小于 (Less than): 判断一个字符串是否小于另一个字符串。
15.大于等于 (Greater than or equal to): 判断一个字符串是否大于等于另一个字符串。
16.小于等于 (Less than or equal to): 判断一个字符串是否小于等于另一个字符串。
集合比较类型17.集合相等 (Set equal): 判断两个集合是否相等。
18.集合不等 (Set not equal): 判断两个集合是否不相等。
基本逻辑运算有与运算(逻辑乘)、或运算(逻辑加)和非运算(解读
1
1 1 1
1 1 1
10 Y = ABC AC D ABC ACD
11 已知某逻辑函数的卡诺图如下所示,试写出其 最简与或式。
CD AB 00 01 11 10 00 1 1 01 1 1 1 11 1 1 1 10 1 1 1 0 0 方格很少且为相 邻项,故用圈 0 法先求 Y 的最简与或式。
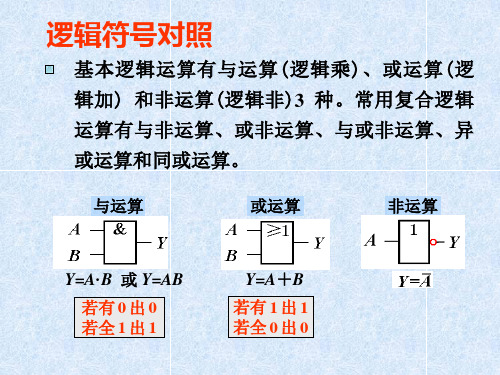
逻辑符号对照
基本逻辑运算有与运算 ( 逻辑乘 ) 、或运算 ( 逻 辑加 ) 和非运算 ( 逻辑非 )3 种。常用复合逻辑 运算有与非运算、或非运算、与或非运算、异 或运算和同或运算。
与运算 或运算 非运算
Y=A· B 或 Y=AB 若有 0 出 0 若全 1 出 1
Y=A+B
若有 1 出 1 若全 0 出 0
4 CMOS门的输入端空接时会发生下面什么 情况? A 输入端为高电位 B 输入端为低电位 C 输入端空接对电路无影响 D 会造成输出不稳定现象 答案:D
判断题 1.TTL与非门的多余输入端可以接固定高电平。 2.当TTL与非门的输入端悬空时相当于输入为逻辑1。 3.普通的逻辑门电路的输出端不可以并联在一起,否则 可能会损坏器件。 4.CMOS或非门与TTL或非门的逻辑功能完全相同。 5.三态门的三种状态分别为:高电平、低电平、不高不 低的电压。 6.TTL集电极开路门输出为1时由外接电源和电阻提供 输出电流。 7.一般TTL门电路的输出端可以直接相连,实现线与。 8.TTL OC门(集电极开路门)的输出端可以直接相连,实 现线与。 错误:5、7
解:
Y=1
Y=0
OC 门输出 端需外接 上拉电阻
RC
7 分别采用与非门和或非门实现与门和或门。
逻辑的运算规则

逻辑的运算规则逻辑是一门研究思维和推理的学科,它通过运用一定的规则和方法来研究思维的合理性和推理的正确性。
逻辑的运算规则是逻辑学中的基础知识,它们是推理过程中必须遵循的规则,用于保证推理的准确性和有效性。
本文将介绍几个常用的逻辑运算规则,包括命题逻辑中的合取、析取、蕴含和等价运算规则,以及谓词逻辑中的全称量词和存在量词运算规则。
一、命题逻辑中的运算规则1. 合取运算规则:合取是指将两个命题同时成立的情况,用符号“∧”表示。
在合取运算中,有以下两个重要的规则:(1)合取交换律:P∧Q与Q∧P是等价的,即合取运算可以交换位置。
(2)合取结合律:(P∧Q)∧R与P∧(Q∧R)是等价的,即合取运算可以按照任意顺序进行。
2. 析取运算规则:析取是指将两个命题中至少有一个成立的情况,用符号“∨”表示。
在析取运算中,有以下两个重要的规则:(1)析取交换律:P∨Q与Q∨P是等价的,即析取运算可以交换位置。
(2)析取结合律:(P∨Q)∨R与P∨(Q∨R)是等价的,即析取运算可以按照任意顺序进行。
3. 蕴含运算规则:蕴含是指从一个命题推导出另一个命题的过程,用符号“→”表示。
在蕴含运算中,有以下两个重要的规则:(1)蕴含的传递性:如果P蕴含Q,Q蕴含R,则P蕴含R。
(2)蕴含的假设消除:如果假设P成立,然后通过推理得出Q成立,那么可以得出P蕴含Q。
4. 等价运算规则:等价是指两个命题具有相同的真值,用符号“↔”表示。
在等价运算中,有以下两个重要的规则:(1)等价交换律:P↔Q与Q↔P是等价的,即等价运算可以交换位置。
(2)等价结合律:(P↔Q)↔R与P↔(Q↔R)是等价的,即等价运算可以按照任意顺序进行。
二、谓词逻辑中的运算规则1. 全称量词运算规则:全称量词是指对于所有的元素都成立,用符号“∀”表示。
在全称量词运算中,有以下两个重要的规则:(1)全称量词的交换律:∀x∀yP(x,y)与∀y∀xP(x,y)是等价的,即全称量词可以交换位置。
逻辑运算

1.6 逻辑运算逻辑运算在我们今后的编程中会经常使用到的。
本节必须掌握的知识点:掌握逻辑运算计算机中所有的数据都是使用二进制保存,但是这些复杂的电路又是如何做运算的呢?1.6.1【逻辑运算】逻辑运算是CPU运算的本质,不管是计算机能处理多么复杂的事情,它最终还是通过电路的开关来实现的。
逻辑是指对某个事物的推理,“真”和“假”是两个对立的逻辑状态,逻辑运算是指用数学符号来表示逻辑状态,以便于用数学方法研究逻辑问题。
我们通常将电路通电状态表示为“真”,用数字“1”表示,不通电表示为“假”,用数字“0”表示。
“或”、“与”、“非”是三种基本逻辑运算,计算机逻辑运算也包含“异或”、“位”。
1、或运算或运算:汇编中用“OR”表示,C语言中用“|”来表示,可以理解为“或者”,即只要有一个条件满足就为“真”,用电路来描述:只要有一条电路通电这条总电路就能通电,原理如图1-6-1:图1-6-1:OR运算等效电路这是一个并联电路图,不管是A为闭合状态、还是B为闭合状态,还是AB都处于闭合状态,电灯泡都能亮。
我们把电路图用符号0和1来表示,或运算表示只要有一个为1,结果就为1。
我们来看一个宽度为8的或运算:1 0 1 1 0 1 0 0or 1 0 0 1 1 1 1 01 0 1 1 1 1 1 0总结:或(or)运算“有1为1”。
2、与运算与运算:汇编中用“and”表示,C语言中用“&”来表示,它表示两个条件都成立才能为真,即两个都为1结果为1,其他为0,电路实现原理如图1-6-2:图1-6-2:AND运算等效电路这是一个串联电路图,A和B都为闭合状态,灯泡才能亮。
如果有一个开关没有闭合,灯泡是不能亮的。
即两个都为1,结果为1,只要有一个为0 ,结果为0。
我们来看一下下面的运算:1 0 1 1 0 1 0 0and 1 0 0 1 1 1 1 01 0 0 1 0 1 0 0总结:与(and)运算的法则:“有0为0”。
逻辑运算原理及计算方法

逻辑运算1.逻辑常量与变量:逻辑常量只有两个,即0和1,用来表示两个对立的逻辑状态。
逻辑变量与普通代数一样,也可以用字母、符号、数字及其组合来表示,但它们之间有着本质区别,因为逻辑常量的取值只有两个,即0和1,而没有中间值。
2.逻辑运算:在逻辑代数中,有与、或、非三种基本逻辑运算。
表示逻辑运算的方法有多种,如语句描述、逻辑代数式、真值表、卡诺图等。
3.表示方法"∨" 表示"或""∨" 表示"与"."┐" 表示"非"."=" 表示"等价".1和0表示"真"和"假"逻辑或对于逻辑或,如果一个操作数或多个操作数为true,则逻辑或运算符返回true;只有全部操作数为false,结果才是false。
在决定一事物的若干条件中,只要有一个条件能满足时,结果就会出现;只有当所有条件都起;只有两个开关都不闭合,电灯EL才不会亮。
亮)。
1 V 1结果就是1,0 V 1结果就是1,0 V 0结果就是0。
逻辑与只有两个操作数都是真,结果才是真。
逻辑与操作属于短路操作,既如果第一个操作数能够决定结果,那么就不会对第二个操作数求值。
对于逻辑与操作而言,如果第一个操作数是假,则无论第二个操作数是什么值,结果都不可能是真,相当于短路了右边。
亮。
一个是0(开关不闭合)那么结果就是0(灯不亮)1^1结果就是1,1^0结果就是0,0^0结果就是0例题101001^000111 →000001从左到右1^0 00^1 01^0 00^0 00^1 01^1 (1)→000001。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
T3 2
0.3V
饱和
(2)输入有低电平0.3V 时。
由于T4和D导通,所以: 该发射结导通, VB1=1V 。 T2 、 T3 都截止。 VO≈VCC-VBE4-VD =5-0.7-0.7=3.6(V) 忽略流过RC2的电流,VB4≈VCC=5V 。 实现了与非门的逻辑 功能的另一方面: 输入有低电平时, 输出为高电平。
_
_
A B
=1
L=A + B
(1)两变量的“异或逻辑”和“同或逻辑”互为反 函数。
A B A ⊙ B A⊙ B A B A B A B A B AB A B AB A B A B
_ _ ___________ _ _ _ _ ___________ _ _
_________
________
A B
=
L=A + B
两变量的“异或逻辑”和“同或逻辑”互为反函 数。
(2) 多变量的“异或”及“同或”逻辑
多变量的“异或”或“同或”运算, 要利用两变量的“异 或门”或“同或门”来实现。
图 2 – 11 多变量的“异或”电路
图 2 – 12 多变量的“同或”电路
A B F F1 C ( A B) C A B C 由图2 - 11(b)得: F A B F C D 1 2 F F1 F2 ( A B) (C D) A B C D Y1 A B 由图2 - 12(a)得:Y Y1 ⊙ C ( A ⊙ B ) ⊙ C A ⊙ B ⊙ C Y1 A ⊙ B Y2 C ⊙ D 由图2 - 12(b)得:Y Y1 ⊙ Y2 ( A ⊙ B ) ⊙ (C ⊙ D ) A ⊙ B ⊙C ⊙ D
+VCC( + 5V ) Rc 4 T4
1 3 2
+VCC( + 5V ) Rc 4 T4
1 3 2
导通
D
截止 充电 Vo
D
导通 T3
1 3 2
截止 T3
1
Vo
3 2
截止
CL
导通
放电
CL
(2)TTL与非门传输延迟时间tpd
Vi
Vo
t PHL
t PLH
导通延迟时间tPHL——从输入波形上升沿的中点到输出波形下降沿的 中点所经历的时间。 截止延迟时间tPLH——从输入波形下降沿的中点到输出波形上升沿的 中点所经历的时间。
A B ≥1 L=A+B
由或运算和
非运算组合 而成。
3.“异或”和“同或”
异或是一种二变量逻辑运算,当两个变量取值相同时,
逻辑函数值为0;当两个变量取值不同时,逻辑函数值为1。
异或的逻辑表达式为:
“异或”真值 表 输 入 输出 A 0 0 1 1 B 0 1 0 1 L 0 1 1 0
F1 A B A B A B
A
非逻辑——某事情发生与否,仅取决于一个条件,而 且是对该条件的否定。即条件具备时事情不发生;条
件不具备时事情才发生。
2.2、常用复合逻辑
1.与非 ——
“与非”真值 表 输 入 输出
由与运算 和非
运算组合而成。
A
0 0 1 1
B
0 1 0 1
L
1 1 1 0
A B
&
L=A· B
2.或非 ——
“或非”真值 表 输 入 输出 A 0 0 1 1 B 0 1 0 1 L 1 0 0 0
L =A+B
输 A 0 0 1 1
入 B 0 1 0 1
输出 L 0 1 1 1
或逻辑表达式: L=A+B
或逻辑——当决定一件事情的几个条件中,只要有一个
或一个以上条件具备,这件事情就发生。
3.非运算
R A
A
闭合
灯L
不亮 亮
V
L
不闭合
非逻辑真值表
A 1 L=A
A
0 1
L
1 0
非逻辑表达式: L
1.输入低电平电流IIL——是指当门电路的输入端接低电平时,从 门电路输入端流出的电流。
可以算出:
I IL
VCC VB1 5 1 1(mA) Rb1 4
产品规定IIL<1.6mA。
2.输入高电平电流IIH ——是指当门电路的输入端接高电平时,流入 输入端的电流。
产品规定:IIH<40uA。
2V
0.4V 0V
“0”
低电平电压 的范围
0.4V 0V
V OL(max)VNL 输出“0”
0.8V
输入“0”
0V
低电平噪声容限 高电平噪声容限
VNL=VOFF-VOL(max)=0.8V-0.4V=0.4V VNH=VOH(min)-VON=2.4V-2.0V=0.4V
(7)输入低电平电流IIL与输入高电平电流IIH
灯亮,L=1
灯不亮,L=0 与逻辑表达式:
A
0 0 1 1
B
0 1 0 1
L
0 0 0 1
闭合 闭合
L A B
件事情才会发生。
与逻辑——只有当决定一件事情的条件全部具备之后,这
2.或运算
A
不闭合 不闭合
B
不闭合 闭合 不闭合 闭合 或逻辑真值表
灯L
不亮 亮 亮 亮
A B
V
L
闭合 闭合
A B
≥1
E(3.6V,0.3V)
Vi (V)
VOFF VON
(6)噪声容限—TTL门电路的输出高低电平是一个范围, 即它的输入信号允许一定的容差。
& Vo
Vo
3.6V
Vi
& G2
Vo
G1
Vi
“1”
2.4V
高电平电压 的范围
3.6V
3.6V
输出“1”
2.4V
VOH(min) V NH VON VOFF
输入“1”
第2章 基本逻辑运算及集成逻辑门
2.1 基本逻辑运算 2.2 常用复合逻辑 2.3 集成逻辑门
2.1
一、基本逻辑运算 1.与运算
设:开关闭合=“1” 开关不闭合=“0”
基本逻辑运算
A B
A & L =A· B B
V
L
灯L 不亮 不亮 不亮 亮
与逻辑真值表 A 不闭合 不闭合 B 不闭合 闭合 不闭合 闭合 输 入 输出
应的输入电压。即输入低电压的最大值。在产品手册中常
称为输入低电平电压,用VIL(max)表示。产品规定VIL(max) =0.8V。(0.8-1V)
Vo (V)
4.0 ( 4 ) 开门电平电压 VON—— 是指输出电压下降到 VOL A B ( max ) 时对 A(0V,3.6V) 3.5 B(0.6V,3.6V) 应的输入电压。即输入高电压的最小值。在产品手册中常 3.0 C(1.3V,2.48V) 称为输入高电平电压,用VIH 表示。产品规定 VIH(min) 2.4V C ( min ) V 2.5 OH( min) D(1.4V,0.3V) =2V。(1.4-1.8V) 2.0 1.5 1.0 0.5 V (V) o 0.4V V OL( max) D E (5)阈值电压Vth——电压传输特性的过渡区所对应的输入电压, Vi (V) 4.0 1.0 0.5 1.5 2.0 2.5 3.0 即决定电路截止和导通的分界线,也是决定输出高、低电 3.5 4.0 A B A(0V,3.6V) VOFF VON 3.5 压的分界线。 B(0.6V,3.6V) 3.0 C(1.3V,2.48V) 近似地:Vth≈ V ≈ VON C 2.4V OFF VOH( 2.5 min) D(1.4V,0.3V) 2.0 即Vi<Vth,与非门关门,输出高电平; E(3.6V,0.3V) 1.5 Vi>Vth,与非门开门,输出低电平。 1.0 0.5 。 0.4V V OL( max) Vth又常被形象化地称为门槛电压 Vth的值为 1.3V D E~1. 4 V。 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
3 主要参数
(1)TTL与非门提高工作速度的原理
a.采用多发射极三极管加快了存储电荷的消散过程。
+VCC Rc 2 i B1 1V R b1 4kΩ
1
1.6kΩ
3.6V A B C 0.3V
3
1.4V
1
3
T1 β iB1 0.7V
T2 2
3 1
Vo T3 2
Re 2 1kΩ
b.采用了推拉式输出级,输出阻抗比较小,可迅速给负载电容充放电。
(8)灌电流负载——当驱动门输出低电平时,电流从负载门 灌入驱动门。
R b1 4kΩ
VO=VCES3≈0.3V
+VCC( + 5V) Rc 2 1.6kΩ Rc 4 130Ω
3 1
1V
3
实现了与非门的逻 辑功能之一:
A 输入全为高电平时, B C
2.1V
截止 T 24
D
1
1.4V 3 1
T1 倒置状态 3.6V
截止 Vo
T2 2
饱和
输出为低电平。
0.7V 1
Re 2 1K
+VCC Rc 2 R b1 4kΩ 3.6V 1.6kΩ Rc 4 130Ω
3 1
5V
3
1
综合上述两种情况 , 该电路满足与非的逻
导通 T 24
1V
4.3V
D 3 1
导通 Vo
辑功能,即:
L A B C
A B C 0.3V
T1 饱和
