重积分部分练习题
重积分典型例题

重积分典型例题
例 1 在下列积分中改变累次积分的次序: (1) 解 (2) 解
ò
b a
dx ò f ( x , y ) dy , ( a < b ) ;
a
x
ò
b a
dx ò f ( x , y ) dy = ò dy ò f ( x , y ) dx .
a a y 2 ax 2 ax - x 2 2 ax 2 ax - x 2
òò ( x - a )( y - b ) dxdy £ òò | x - a | | y - b | dxd y £ òò
D D
| x - a || y - b | dxdy
[ a ,b ]´[ c , d }
= ò | x - a | dx × ò | y - b | dy
a c b =æ - x ) dx + ò ( x - a ) dx ö ç òa (a ÷× a è ø
2 2
f ( x , y ) dx + ò dy ò x , y ) dy . y f (
2
2 a
2 a
a
2 a
例 2 计算下列重积分:
(1)
òò xy dxdy ,D 为抛物线 y
D p 2 òò xy dxdy = ò 2 xdx ò 0 D p 4 p 2 p 2 7 p 5 2 2 = × x 0 = . 3 7 21 2 px - 2 px
解
令 x = ar cos q , y = br sin q ,则 0 £ q £ 2 p , 0 £ r £ 1 ,
¶ ( x, y ) = abr .有 ¶ ( r , q )
重积分练习题

则 I=
(7) 设
∫∫∫ [ y sin x + 2]dV = ________ .
∫∫∫ xyzdxdydz = ______ .
.
是由平面 x = a ( a > 0 ), y = x , z = 0, z = y 所围成
的有界闭域 , 则三重积分 I =
(8) 设
是由曲面 z =
x + y 及 z=
2
( R > 0)
.
)
(B)
(A)
∫
∫ ∫
2R
0
2π
z dz
π 2 0
∫∫ dxdy
x2 + y2 ≤ R2
2 R cos ϕ 0
∫
2R
0
z 2 dz
∫∫ dxdy
x 2 + y 2 ≤ 2 Rz − z 2
(C)
0
dθ ∫ dϕ ∫
R 0
r 4 cos 2 ϕ sin ϕ dr
2π
(D)
0
dθ ∫ ρ dρ ∫
2 2
1 x + y +1
2 2
所围成
的有界闭域 , 则三重积分在柱坐标系 下的三次积分为 :
.
2.选择 选择 (1) 记 I 1 =
(A) I1 ≤ I2
∫∫ | xy | dxdy ,
x 2 + y 2 ≤1
I2 =
| x |+ | y | ≤ 1
∫∫ | xy | dxdy ,
(D) I1 > I2
D
x
则在极坐标下的二次积分为
. (4) 交换二次积分的积分顺序: 交换二次积分的积分顺序:
重积分习题word版

42、设Ω是由x2+y2+z2≤2z+3所确定的有界闭区域,试将 化成柱面坐标下的三次积分式
43、试将 化成柱面坐标下的三次积分式。
44、设Ω是由1≤x2+y2+z2≤2,z≥0及x2+y2≤1所确定的闭区域,试将
35、设Ω是由z=x2+y2,x2+y2=1以及z=0所围的有界闭区域,试将I= 分别化成直角,柱面及球面坐标下的三次积分式。
36、设Ω是由x2+y2+z2≤a2, (a>0)及z≥0所确定的有界闭区域。试将
f(x,y,z)dv分别化成柱面及球面坐标下的三次积分式。
37、试将 化成柱面及球面坐标下的三次积分式。
31、Ω是由曲面2z=x2+y2,(x2+y2)2=x2-y2及z=0所围的有界闭区域,试将I= f(x,y,z)dv化成柱面坐标下的三次积分式。
32、试将 化成柱面坐标下的三次积分式。
33、设Ω是由1≤x2+y2+z2≤4以及 所确定的闭区域,试将I= 化成柱面坐标下的三次积分式。
34、设Ω是由 (0<a<R)及z≥0所确定的闭区域,试将I= 化成球面坐标下的三次积分式。
7、设Ω是由曲面y=x2,y=1,z=y,z=-y所围的有界闭区域。试将I= f(x,y,z)dv化成先对z次对y再对x积分的三次积分式。
8、设Ω是由 所确定的有界闭区域。试将I= f(x,y,z)dv化成先对z次对y再对x积分的三次积分式。
9、设Ω是由x+y≥a,x2+y2≤a2及0≤z≤a-y(a>0)所确定的有界闭区域。试将I= f(x,y,z)dv化成先对z次对y再对x积分的三次积分式。
重积分习题三

重积分习题三1、试求函数f(x,y)=xy2在区域D:0≤x≤1,0≤y≤1上的平均值。
2、计算二次积分3、计算二次积分4、计算二次积分5、计算二次积分6、计算二次积分7、计算二次积分8、计算二次积分9、计算二次积分10、计算二次积分11、计算二次积分12、计算二重积分其中D:|x|≤2,|y|≤1.13、计算二重积分其中D:0≤x≤1,0≤y≤2.14、计算二重积分其中D:0≤x≤a0≤y≤b.15、计算二重积分其中D:0≤x≤1,0≤y≤2.16、计算二重积分其中D:0≤x≤1,0≤y≤1.17、计算二重积分其中D:0≤x≤1,0≤y≤1.18、计算二重积分其中D:-1≤x≤1,0≤y≤2.19、计算二重积分其中D:0≤x≤2,-1≤y≤1.20、计算二重积分其中D:0≤x≤π,0≤y≤.21、计算二重积分其中D:-1≤x≤3,0≤y≤2.22、计算二重积分其中D:0≤x≤1,0≤y≤4.23、计算二重积分其中24、计算二重积分其中D:|x|≤π,|y|≤1.25、计算二重积分其中D:|x|≤3,|y|≤1.26、计算二重积分其中D:|x|≤1,0≤y≤1.27、计算二重积分其中D是以O(0,0)A(1,1)和B(0,1)为顶点的三角形区域。
28、计算二重积分其中D:0≤x≤1,-1≤y≤0.29、计算二重积分其中D:0≤y≤sin x,0≤x≤π.30、计算二重积分其中D是由曲线y=x2,直线y=0,x=2所围成区域。
31、计算二重积分其中D为由y=x,y=2x,x=4所围成的区域。
32、计算二重积分其中D:x≤y≤x,1≤x≤2.33、计算二重积分其中D是由直线x=0,y=π和y=x围成的区域。
34、计算二重积分其中D是由直线y=x,y=x+1,y=1及y=3所围成的区域。
35、计算二重积分其中36、计算二重积分其中D:-1≤x≤1,1≤y≤1.37、计算二重积分其中D:|x|≤π,0≤y≤1.38、计算二重积分其中D为由y=x,x=0,y=1所围成的区域。
(完整版)重积分习题及答案

第九章 重积分(A)1.填空题(1) 设()y x y x P 2,=,()23,y x y x Q =,定义于:D 10<<x ,10<<y ,则()σd y x P D⎰⎰, ()⎰⎰Dd y x Q σ,(2) 设曲顶柱体的顶面是()y x f z ,=,()D y x ∈,,侧面是母线平行于z 轴,准线为D的边界线的柱面,则此曲顶柱体的体积用重积分可表示为=V 。
(3) 在极坐标系中,面积元素为 。
2.利用二重积分的性质,比较下列积分大小(1) ()⎰⎰+Dd y x σ2与()⎰⎰+Dd y x σ3,其中积分区域D 由x 轴,y 轴以及直线1=+y x 所 围成。
(2) ()⎰⎰+D d y x σ2与()⎰⎰+Dd y x σ3,其中积分区域D 是由圆周()()21222=-+-y x 所围成。
3.利用二重积分性质,估计积分()⎰⎰++=Dd y x I σ92222的值,其中D 是圆形闭区域422≤+y x 。
4.交换积分()⎰⎰--a ax ax xa dy y x f dx 2222,的积分次序。
5.交换积分()⎰⎰-2120,ydx y x f dy 的积分次序。
6.交换二次积分()⎰⎰+-aa y y a y x f dy 022,的积分次序。
7.计算()⎰⎰+Dd y x σ23,其中D 是由两坐标轴及直线2=+y x 所围成的闭区域。
8.计算()⎰⎰+Dd y x x σcos ,其中D 是顶点分别为()0,0,()0,π和()ππ,的三角形区域。
9.计算()⎰⎰+Dyd x σsin 1,其中D 是顶点分别为()0,0,()0,1,()2,1和()1,0的梯形闭区域。
10.计算二重积分⎰⎰Ddxdy ,其中区域D 由曲线21x y -=与12-=x y 围成。
11.计算二重积分⎰⎰Dd xy σ2,其中D 是由圆周422=+y x 及y 轴所围成的右半闭区域。
重积分习题及解答

重积分练习一. 填空1.⎰⎰12),(xx dy y x f dx 交换积分次序后为_________________.2.用柱面坐标系化三重积分为三次积分________________),,(=⎰⎰⎰Ωdv z y x f其中2,1,1:22===+Ωz z y x 围成. 3. (化为柱面坐标中的三次积分)__________________),,(22222211111111==⎰⎰⎰--+-------dz z y x f dydxI y x y x x x (化为柱面坐标中的三次积分) 二.选择题1. =+⎰⎰-dy y x dxx x243221( ).A. ⎰⎰302πθrdr d . B.⎰⎰232ππθrdr d C.⎰⎰3022πθdr r d . D.⎰⎰2322ππθdr r d2.若区域D 由1)1(22=+-y x 所围,则⎰⎰Ddxdy y x f ),(化成累次积分为 ( )A.⎰⎰πθθθθ0cos 20)sin ,cos (rdr r r f d . B. ⎰⎰-ππθθθθcos 20)sin ,cos (rdr r r f dC.⎰⎰20cos 20)sin ,cos (2πθθθθrdr r r f d D. ⎰⎰-22cos 20)sin ,cos (ππθθθθrdr r r f d三.计算1.. 计算⎰⎰-+=+-⋅+22)(4122222x a a xady y x a y x dx2. 计算⎰⎰-Ddxdy y x ||,其中D 是由2,0,1,0====y y x x 所围成的区域.3. 求由x e z y 222-=+与平面1,0==x x 所围立体体积.4.D 由直线x y y x ===,2,4所围成,求⎰⎰--Dxdxdy x e 22.5.计算⎰⎰-=Dd y x I σ||,其中0,0,1:22≥≥≤+y x y x D .6.计算⎰⎰⎰Ω+dV z x )(,其中22221,:y x z y x z --=+=Ω所围的空间区域.四.应用题。
高数重积分总习题

重积分总复习题一 判 断1.若(,)f x y 在D 上的二重积分存在,则必定有(,)(,)DDf x y d f x y d σσ≤⎰⎰⎰⎰( )2.111(,)(,)yxdy f x y dx dx f x y dy =⎰⎰⎰⎰. ( )二 填空题1.改换二次积分的积分次序⎰⎰yy dx y x f dy 2202),(= .2.化2220)adx x y dy +⎰为极坐标形式下的二次积分为 .3.将极坐标系下的二重积分化为直角坐标系下的二重积分21(cos ,sin )d f r r rdr πθθθ⋅=⎰⎰ ___________________4.二次积分2xdx f dy ⎰的极坐标形式的二次积分为 .5.交换二次积分201111(,)(,)xxdx f x y dy dx f x y dy --+⎰⎰⎰⎰的积分次序为 .三 选择题1.设区域D :221x y +≤,f 是域D 上的连续函数,则22()Df xy dxdy +=⎰⎰( )A.12()rf r dr π⎰B .104()rf r dr π⎰ C.122()rf r dr π⎰ D.04()rrf r dr π⎰2.设4(,)xI dx f x y dy =⎰⎰,交换积分次序,得( )A.24104(,)y y dy f x y dx ⎰⎰ B.21440(,)y ydy f x y dx -⎰⎰C.44104(,)dy f x y dx ⎰⎰ D.20144(,)y y dy f x y dx ⎰⎰3.设积分区域D 由x 轴,y 轴及直线1x y +=围成,则二重积分(,)Df x y d σ⎰⎰化为累次积分后为( ).A.10dx ⎰1(,)0x f x y dy -⎰. B.10x dy -⎰1(,)0f x y dx ⎰. C.10dx ⎰1(,)0f x y dy ⎰.D.10dy ⎰1(,)0f x y dx ⎰.4.),(z y x f =在有界闭区域D 上连续是二重积分σd ),(D⎰⎰y x f 存在的( )条件。
重积分例题
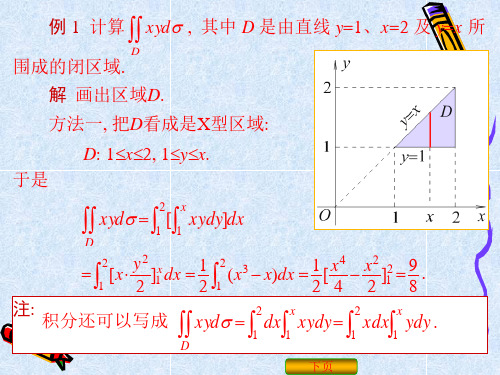
c
下页
例 3 利用柱面坐标计算三重积分 zdxdydz , 其中是
由曲面zx2y2与平面z4所围成的闭区域. 解 闭区域可表示为:
2z4, 02, 02.
于是
zdxdydz zdddz
d d 2 zdz
0 0
x
I d
0
2
/4
0
d
R
0
2 2sin d
2 2 5 R . 5
练习
试用三种坐标系分别计 算三重积分 I zdv, 其中(V ) : x 2 y 2 z 2 2 z.
(V )
z
2
z
解法1
直角坐标系 (切片法)
2 2 2
( z ) : x y 2z z ; 0 z 2.
D
2a cos 2 d 0 0
4a 2 2 d
32 a 2 ( 2 ) . 3 2 3
例 1 计算三重积分 xdxdydz , 其中为三个坐标面及
平面x2yz1所围成的闭区域. 解 区域可表示为:
0z1x2y, 0 y 1 (1 x) , 0x1. 2
V 4 4a 2 x 2 y 2 dxdy ,
D
其中 D 为半圆周 y 2ax x 2 及 x 轴所围成的闭区域. 在极坐标系中D可表示为 02acos , 0 . 2
于是
V 4 4a 2 2 dd 4
32 a 2 2 (1 sin 3 )d 0 3
于是
e
D
x2 y2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其中
(4分)[34]计算二重积分
其中
(5分)[35]计算二重积分
其中
(4分)[36]利用极坐标计算二次积分
(5分)[37]利用极坐标计算二重积分
其中D:1≤x2+y2≤4,y≥0,y≤x.
(4分)[38]利用极坐标计算二重积分
其中D:a2≤x2+y2≤1,x≥0,y≥0,a>0,x=0处广义。
其中
(4分)[69]利用极坐标计算二重积分
其中D:x2+y2≤a2,x≥0,y≥0. (a>0)
(3分)[70]利用极坐标计算二重积分
其中D:1≤x2+y2≤8.
(3分)[71]计算二重积分
其中D:x2+y2≤4.
(5分)[72]计算二重积分
其中D:x2+y2≥1,x2+y2≤2x,y≥0.
(5分)[73]计算二重积分 ,其中区域D为x2+y2≤1在第一象限部分。
答( )
(4分)[13]设 其中D是由直线x=0,y=0, 及x+y=1所围成的区域,则I1,I2,I3的大小顺序为
(A)I3<I2<I1; (B)I1<I2<I3;
(C)I1<I3<I2; (D)I3<I1<I2.
答( )
(3分)[14]设有界闭域D1与D2关于oy轴对称,且D1∩D2=,f(x,y)是定义在D1∪D2上的连续函数,则二重积分
(5分)[64]计算二重积分
其中D:x2+y2≥2x,x2+y2≤4x.
(5分)[65]计算二重积分
其中D:x2+y2≤2x.
(4分)[66]利用极坐标计算二重积分
其中D:π2≤x2+y2≤4π2
(4分)[67]计算二重积分
其中D:x2+y2≤1,x≥0,y≥0.
(7分)[68]设区域D:x2+y2≤a2(a>0),计算二重积分
(4分)[24]计算二重积分
其中D是由y=x,y=0,x=1所围成的区域。
(4分)[25]计算二重积分
其中D为 与x=0所围成的区域。
(4分)[26]计算二重积分
其中D是由抛物线 及直线y=x+4所围成的区域。
(4分)[27]计算二重积分
其中D为由y=x,y=0,x=1所围成的区域。
(4分)[28]计算二重积分
其中D是由曲线xy=1,y=x2与直线x=2所围成的区域。
(5分)[29]计算二重积分
其中D是由x=0, ,y=x所围成的区域。
(4分)[30]计算二重积分
其中D:0≤y≤sinx, .
(5分)[31]计算二重积分
其中D: , 0≤y≤2.
(4分)[32]计算二重积分
其中D是由抛物线 及y=x2所围成的区域。
(A)
(B)
(C)
(D)
答( )
(3分)[8]设f(x,y)为连续函数,则积分
可交换积分次序为
(A)
(B)
(C)
(D)
答( )
(4分)[9]若区域D为(x-1)2+y2≤1,则二重积分 化成累次积分为
(A) (B)
(C) (D)
其中F(r,θ)=f(rcosθ,rsinθ)r.
答( )
(3分)[10]若区域D为x2+y2≤2x,则二重积分 化成累次积分为
(2分)[1]
(3分)[2]二重积分 (其中D:0≤y≤x2,0≤x≤1)的值为
(A) (B) (C) (D)
答( )
(3分)[3]若区域D为0≤y≤x2,|x|≤2,则 =
(A)0; (B) (C) (D)256
答( )
(3分)[4]设D1是由ox轴,oy轴及直线x+y=1所圈成的有界闭域,f是区域D:|x|+|y|≤1上的连续函数,则二重积分
(3分)[3][答案]
A.
(3分)[4][答案]
(B).
(3分)[5][答案]
(C).
(3分)[6][答案]
C.
(3分)[7][答案]
B.
(3分)[8][答案]
C
(4分)[9][答案]
C.
(3分)[10][答案]
D.
(4分)[11][答案]
C.
(5分)[12][答案]
A.
(4分)[13][答案]
B.
(A)
(B)
(C)
(D)
答( )
(4分)[11]设 其中D是由x=0,y=0, ,x+y=1所围成的区域,则I1,I2,I3的大小顺序是
(A)I1<I2<I3; (B)I3<I2<I1;
(C)I1<I3<I2; (D)I3<I1<I2.
答( )
(5分)[12]设 ,则I满足
(A) (B)
(C) (D)
(5分)[78]利用极坐标计算二重积分
其中D:1≤x2+y2≤4,x≥0,y≥0.
====================答案====================
答案部分,(卷面共有100题,分,各大题标有题量和总分)
一、选择 (16小题,共分)
(2分)[1][答案]
B.
(3分)[2][答案]
B.
(4分)[10]计算二重积分
其中D是由直线y=x,y=x+1,y=1及y=3所围成的区域。
(3分)[11]计算二重积分
其中
(3分)[12]计算二重积分
其中D为由y=x,x=0,y=1所围成的区域。
(3分)[13]计算二重积分
其中D是由直线y=x,y=5x及x=1所围成的区域。
(3分)[14]计算二重积分
(3分)[6][答案]
三、计算 (78小题,共分)
(3分)[1][答案]
原式=
(3分)[2][答案]
原式=
(3分)[3][答案]
原式=
(3分)[4][答案]
原式=
(4分)[5][答案]
原式
(3分)[6][答案]
原式
(3分)[7][答案]
原式
(3分)[8][答案]
原式
(3分)[9][答案]
原式
(4分)[10][答案]
其中D:0≤y≤sinx,0≤x≤π.
(3分)[6]计算二重积分
其中D是由曲线y=x2,直线y=0,x=2所围成区域。
(3分)[7]计算二重积分
其中D为由y=x,y=2x,x=4所围成的区域。
(3分)[8]计算二重积分
其中D:x≤y≤ x,1≤x≤2.
(3分)[9]计算二重积分
其中D是由直线x=0,y=π和y=x围成的区域。
(5分)[39]试求函数f(x,y)=2x+y在由坐标轴与直线x+y=3所围成三角形内的平均值。
(6分)[40]试求函数f(x,y)=x+6y在由直线y=x,y=5x和x=1所围成三角形内的平均值。
(4分)[41]由二重积分的几何意义,求
(4分)[42]计算二重积分
其中D:x2+y2≤2及x≥y2.
原式
(4分)[22][答案]
原式
(4分)[23][答案]
原式
(4分)[24][答案]
原式
(4分)[25][答案]
原式
(4分)[26][答案]
原式
(4分)[27][答案]
原式
(4分)[28][答案]
交点为
原式
(5分)[29][答案]
(其中入是Δσi(i=1,2,…,n)的最大直径)存在,则称此极限值为______________的二重积分。
(4分)[2]若D是以(0,0),(1,0)及(0,1)为顶点的三角形区域,由二重积分的几何意义知 =___________.
(3分)[3]设 ,由二重积分的几何意义知
___________.
__________
(A)2 (B)4 (C)8 (D)
答( )
(3分)[5]设f(x,y)是连续函数,则二次积分
(A)
(B)
(C)
(D)
答( )
(3分)[6]设函数f(x,y)在区域D:y2≤-x,y≥x2上连续,则二重积分 可化累次积分为
(A) (B)
(C) (D)
答( )
(3分)[7]设f(x,y)为连续函数,则二次积分 可交换积分次序为
三、计算 (78小题,共分)
(3分)[1]设f(x,y)为连续函数,交换二次积分
的积分次序。
(3分)[2]设f(x,y)为连续函数,交换二次积分
的积分次序。
(3分)[3]设f(x,y)为连续函数,交换二次积分
的积分次序。
(3分)[4]设f(x,y)为连续函数,交换二次积分
的积分次序。
(4分)[5]计算二重积分
原式
(3分)[11][答案]
原式
(3分)[12][答案]
原式
或解原式
(3分)[13][答案]
原式
(3分)[14][答案]
原式
(3分)[15][答案]
原式
(3分)[16][答案]
原式
(3分)[17][答案]
原式
(4分)[18][答案]
原式
(4分)[19][答案]
原式
(4分)[20][答案]
原式
(4分)[21][答案]
其中D是由直线y=x,y=x+a,y=a及y=3a(a>0)所围成的区域。
(4分)[20]计算二次积分
(4分)[21]计算二重积分
其中D是由y=x,xy=1,x=3所围成的区域。
(4分)[22]计算二重积分
其中D是由y=2,y=x,y=2x所围成的区域。
