交流绕组的磁动势(2)
合集下载
(完整版)03--2磁动势
磁力线穿过转子铁心，定子铁心和两个气隙。 由于气隙点不论离开线圈圈边A或X是远是近，磁势的大小 都是相等的，所以，此时在其隙的空间分布是一个矩形波。
纵坐标的正负表示极性。
铁心磁导率极大,相对于气隙而言，铁芯消耗的磁压降可以 忽略不计，就可认为磁压全部降落在气隙上。
若，励磁线圈电流为ic、匝数为Nc 。 则：fc= Ncic/2
本章研究的是交流绕组有交流电流流通后所建立的磁动 势。其特点是：
交流绕组是分布绕组，绕组上的电流又随时间变化，所 以，磁动势既是时间的函数，又是空间的函数。
二、研究交流绕组磁动势的步骤：
同研究电动势的步骤
单个线圈磁动势 线圈组磁动势 相绕组磁动势 三相绕组合成磁动势
三、方法： 1、简化次要因素的影响，假定： 绕组中的电流随时间按正弦规律变化，不考虑高次
⑴ 分析：q=3，α=20
把各矩形波逐点相加， 便得到线圈组的磁动势波， 它是一个阶梯波 。
分解每个矩形波，可得到各 自的基波分量和一系列高次 谐波分量。
图中曲线1，2，3分布代 表三个矩形磁动势波的三个基 波磁动势分量，它们振幅相等， 空间相差20° 电角度，把三 个正弦波曲线相加，得到线圈 组的磁动势基波如曲线4，
如果通过线圈的电流为正弦波，
ic 2Ic sin t 则，矩形波的高度也按正弦变化。
t 2k
2
ic 2Ic
t k
ic 0
t 2k
2
ic 2Ic
可见，通入电流的线 圈所产生的气隙磁动势沿 圆周分布是一个矩形波， 在通电流的线圈处，气隙 磁动势发生突跳。
——脉振磁动势。
磁势波的高度随时间按正 弦规律变化，但空间位置固 定不变（磁轴不变）。
短距角β＝α
交流电机绕组的基本理论
Y.Q.Xiong 2010-06 第4章 交流电机绕组的基本理论
15
相绕组磁动势及 其基波分量动画
基波表达式 f1(t, ) Fm1 sin t cos
基波振幅
Fm1
0.9
NkN1I p
串联匝数
N
2 pqNc a
pqN c a
(双层绕组) (单层绕组)
电机学 Electric Machinery
华中科技大学 电气与电子工程学院
熊永前
2010.06
Y.Q.Xiong 2010-06 第4章 交流电机绕组的基本理论
1
4.3 交流绕组磁动势
1. 单相绕组磁动势
(1) 单层集中相绕组的磁动势
Z=6，p=1，三相单层绕组。q=1，相当于集中绕组，每相只 有1个整距线圈。
磁动势空间矢量的长度代 表幅值的大小，矢量的位 置代表幅值所处的空间位 置。
将各线圈的基波磁动势矢
量相加得到分布相绕组磁
动势基波矢量。
Y.Q.Xiong 2010-06 第4章 交流电机绕组的基本理论
8
考虑到一般情况，对于q个线 圈，合成磁动势基波是q个依 次位移α1度的正弦波叠加而成 。
采用磁动势迭加原理，三个线圈分别产生矩形波磁动势。
将三个矩形波叠加起来，得到阶梯波脉振磁动势。
Y.Q.Xiong 2010-06 第4章 交流电机绕组的基本理论
7
用迭加原理求合成磁动势
三个线圈分别产生矩形波 磁动势。磁动势波形一样 ，依次位移槽距电角α1度 。
各线圈磁动势的基波分量 为空间分布正弦波，和时 间相量相似，可以用空间 矢量来表示。
f y (t, ) Fy cos 1,3,5,
第七章 交流绕组的磁动势
第七章交流绕组的磁动势目录第一节概述 (1)第二节单相绕组的磁动势 (1)第三节对称三相电流流过对称三相绕组的基波磁动势 (6)第四节不对称三相电流流过对称三相绕组的基波磁动势 (9)第五节三相绕组磁动势的空间谐波分量和时间谐波分量 (11)小结 (14)思考题 (14)习题 (15)第一节概述在第六章介绍旋转电机基本作用原理的基础时，电机类别不同则电机磁场的建立方式和特性也不同，气隙磁场对电机的机电能量转换和运行特性具有重要影响。
气隙磁场的建立是很复杂的，它可以由电流励磁产生，也可以由永磁体产生。
电流励磁也可以分直流励磁和交流励磁。
图6－1中的三相同步电机转子电流流过直流电建立空载磁场，当同步发电机接上负载后，定子绕组里就有了交流电流，它同样也会产生磁动势，这个磁动势必然会对转子磁动势产生影响。
在介绍异步电机作用原理时，当定子三相绕组通流入交流电，也会产生一个与同步电机气隙磁场类同的旋转磁场，这个磁场与交流电流的参数、绕组的构成之间的关系密切，这些内容将在本章内进行认真的分析。
根据由简入繁的原则，按下列层次逐项讨论：线圈、线圈组、单相绕组的磁动势；三相绕组的基波磁动势；三相电流不对称的基波磁动势以及磁动势空间谐波的分析等。
为了简化分析，本章对交流绕组磁动势分析时，作如下几点假定：（1）绕组的电流随时间按正弦规律变化，不考虑高次谐波电流；（2）槽内电流集中于槽中心处，齿槽的影响忽略不计，定转子间的气隙是均匀的，气隙磁阻是常数；（3）铁心不饱和，略去定转子铁芯的磁压降。
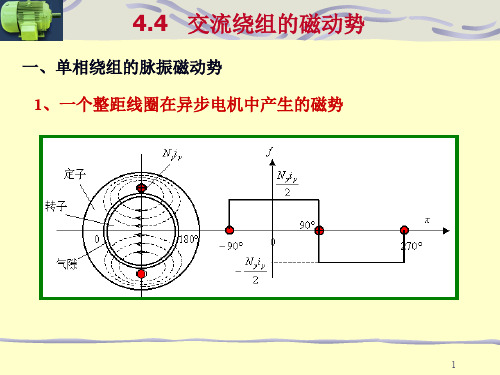
第二节单相绕组的磁动势一、线圈的磁动势图7－1（a）表示任一个整距线圈通以电流后的磁场分布情况，气隙磁场为一对磁极，由于是整距线圈，气隙的磁通密度均相同，按照全电流定律，在磁场中沿任一磁力线的磁位降等于该磁力线所包围的全部电流。
如线圈的匝数为，电流为，则作用在磁路上的磁势为。
由于铁心中磁压降不考虑，所以线圈的磁动势降落在两个均匀的气隙中，则气隙各处的磁压降均等于线圈磁动势的一半，即。
第七章 交流绕组的磁动势
•磁势的v次谐波振幅：
F m 2 F q k p 0 .9 2 qc N k p k d I c 0 .9 2 qc N k N I c
单相脉振磁势的幅值表达式
• 为了统一表示相绕组的磁势，引入每相电 流I1，每相串联匝数N1等概念。
Iy
I1 a
Fp10.9(2qNy)Iykqky
对双层绕组：
2．振幅 合成磁势的振幅为每相脉动磁势振幅的3/2倍。
3．转速 角速度ω=2πf（电弧度/s）
n1=f/p（r/s）=60f/p (r/min)同步转速，基波转速。 4．幅值位置合成磁势的振幅的位置随时间而变化，出现在
ωt-x＝0处。当某相电流达到最大值时，旋转磁势的波 幅刚好转到该线绕组的轴线上
5．旋转方向 由超前电流的相转向பைடு நூலகம்后电流的相
之间相差电角度
也相当于分布
sin q
kd1
q sin
2
2
•相当于单层绕组的分布情况
kp1 cos 2
分析：
• 双层绕组磁势的基波振幅：
F m 1 2 F q 1 k p 1 0 . 9 2 q c k p 1 k N d 1 I c 0 . 9 2 q c k N 1 N I c
脉动磁势分解成两个旋转磁势
脉动磁势波的节点和幅值的位置是固定不变的。
基波分量
F m 1 s t s i x n 1 2 i F m 1 c n t o x 1 2 F m 1 c s t o x s
• 在空间按正弦规律分布随时间按正弦规律变化的 脉动磁势可以分解为两个旋转磁势分量
改变旋转磁场转向的方法：调换任意两相电源线（改变 相序）
问题：
1、若额定负载的星形旋转电机突然断了一相，电机会发生什么变化？
F m 2 F q k p 0 .9 2 qc N k p k d I c 0 .9 2 qc N k N I c
单相脉振磁势的幅值表达式
• 为了统一表示相绕组的磁势，引入每相电 流I1，每相串联匝数N1等概念。
Iy
I1 a
Fp10.9(2qNy)Iykqky
对双层绕组：
2．振幅 合成磁势的振幅为每相脉动磁势振幅的3/2倍。
3．转速 角速度ω=2πf（电弧度/s）
n1=f/p（r/s）=60f/p (r/min)同步转速，基波转速。 4．幅值位置合成磁势的振幅的位置随时间而变化，出现在
ωt-x＝0处。当某相电流达到最大值时，旋转磁势的波 幅刚好转到该线绕组的轴线上
5．旋转方向 由超前电流的相转向பைடு நூலகம்后电流的相
之间相差电角度
也相当于分布
sin q
kd1
q sin
2
2
•相当于单层绕组的分布情况
kp1 cos 2
分析：
• 双层绕组磁势的基波振幅：
F m 1 2 F q 1 k p 1 0 . 9 2 q c k p 1 k N d 1 I c 0 . 9 2 q c k N 1 N I c
脉动磁势分解成两个旋转磁势
脉动磁势波的节点和幅值的位置是固定不变的。
基波分量
F m 1 s t s i x n 1 2 i F m 1 c n t o x 1 2 F m 1 c s t o x s
• 在空间按正弦规律分布随时间按正弦规律变化的 脉动磁势可以分解为两个旋转磁势分量
改变旋转磁场转向的方法：调换任意两相电源线（改变 相序）
问题：
1、若额定负载的星形旋转电机突然断了一相，电机会发生什么变化？
交流电机绕组磁动势(2)解读
2. 三相谐波磁动势
1）三相的3次谐波磁动势
fA3 FK 3 cost cos 3
fB3
FK3 cos(t 120
) cos 3( 120
) FK3 cos(t 120
) cos 3
fC3
FK 3
cos(t
240
) cos 3(
240
)
FK 3
cos(t
240
)
cos
3
式中
FK 3
1 3
FK1
1 0.9 5
N1I p
将上式三式相加，可得三相绕组5次谐波合成磁动势为:
f5
f A5
fB5
fC5
3 2
FK 5
cos(5a t)
F5 cos(5a t)
F5
3 2
FK 5
3 2
1 5
0.9N1I p
是三相合成的5次谐波磁动势的幅值
可见，三相绕组的5次谐波合成磁动势也是一个余弦分 布，幅值恒定的旋转磁动势，但由于磁动势的极对数 为基波的5倍，故其转速为基波的1/5，转向与基波相 反。
1.35
N1I p
三相绕组合成基波磁动势的特点
（1）每一相绕组产生脉振磁动势，但在三相对 称分布的绕组中，通入三相对称的交流电流时， 所产生的合成基波磁动势是一个空间按正弦规律 分布、波幅恒定的旋转磁动势。
链接基波磁场分布动画
（2）三相合成基波磁动势的波长和单相的一样， 即极对数一样。
（3）每相的脉振磁动势，它们的振幅大小随着 时间的不同是变化的，而三相合成基波磁动势幅 值不变，是基波脉振磁动势最大振幅的3/2倍。
2）空间矢量图法
用空间矢量法来分析三相绕组合成磁动势，即用 空间矢量把一个脉振磁动势分解为两个旋转磁动 势，然后进行矢量相加，这个方法比前面的数学 分析法更直观。
8交流电机电枢绕组的电动势和磁动势
电机与拖动
2、线圈中的感应电势 ：
（1）整距线匝中 的感应电势（线匝 首尾两端相距一个 整极矩） 两导体感应电动势 分别为Ea1和Ea2
线匝基波电动势向量ET
E T E a1 E a 2
整矩线匝基波电 E 2 E 2 2 . 22 f 4 . 44 f A 动势（有效值） T
E AB 3 E A 3 E B 3 0 三相采用△接法：
三次谐波感应电动势会在绕组回路中产生三次 谐波环流，整个闭合绕组三次谐波感应电动势恰好 与环流在三次谐波阻抗上产生压降相等，因此线电 压中也没有三次谐波分量。
同理：适合于3k次谐波
思考题：三相交流发电机定子绕组一般接成什 么形式？
E 4 . 44 fqW y k q p 4 . 44 f pqW a 4 . 44 fWk q
W pqW a
y
1 a
y
kq
是一相绕组串连的总匝数
（3） 三 相 双 层 叠 绕 组
电机与拖动
一交流机：Z=24，2P=4，m=3，y1=5,画出 双层叠绕组展开图。
1、画出结构图，标出槽号 B2 21 1817 22 2、标出AZBXCY的位置 Y2 16 Z 23 2 15 24 Z 24 S1 q 2 14 2 pm 223 1 n N N2 A1 1 13A2 2 Z 24 S2 12 6 3 2p 4 Z1 4 11 Y1 56 10 y1=5 B1 7 8 9 C 1 X1 上下 C2
三相交流电机中线电压的三次谐波 三相交流电机三相绕组在空间上互隔120 度空间电角度，他们的基波感应电动势时间 相位互隔120度。三次谐波感应电动势相位互 隔360度；并且三次谐波感应电动势幅值大小 相等。
交流绕组的磁动势
定、转子旋转磁场：
A Z
旋转方向相同
X
转速相等
定、转子旋转磁场在空间保 持相对静止——同步
B
• 3、在产生一定大小的电动势和磁动势，且 保证绝缘性能和机械强度可靠的条件下，尽 量减少用铜量。
• 4、制造工艺简单、检修方便。
C X
B
转子绕组又称励磁绕组，
Y
C
A
X
起励电源
图1.18 自并励系统原理电路图
Z
B
励磁绕组中流过直流电流，产生的磁场称励磁磁场或主极磁场，
相对于转子静止，随转子一起转动，相对于定子转速为转子转速n，
在随转子一起转动的过程中，定子三相绕组感应对称的电动势， 电动势的相序由转子的转向决定， 频率由转速决定， f pn
60
• 1、导体电动势
• 2 、整距线匝电动势 y1= τ
Ec1 2.22 f 1 Et1 4.44 f 1
3、短距线匝电动势有效值y1< τ Et1( y1 ) 4.44k y1 f 1
对于三相绕组，当流过对称的三相电流，将产生一个旋转磁动势
Y A
Z
C X
B
定、转子磁动势之间的关系
转子磁场旋转，
定子三相绕组感应对称的电动势， 电动势的相序由转子的转向决定，
定子三相合成旋转磁场
Y
C
频率由转速决定，
f
pn 60
转向由三相电流的相序和绕组的空
间排列决定，
转速由频率决定，
n
60 f p
对于单相绕组，将产生一个脉振磁动势，
因为采用了短距和分布绕组，其各高 次谐波已被极大的削弱，
该脉振磁动势为，在时间上随电
流同频率脉振，在空间上每一时
交流电机绕组的基本理论3
三相合成的三次谐波磁动势
f3 fa3 fb3 fc3 0
三相合成的三次谐波磁动势为零
这个结论可推广到＝6k－3的谐波次数
21
五次谐波磁势
（2）五次谐波磁动势的极对数是基波的五倍， 三相绕组各 自建立的五次谐波磁动势表达式
fa5 F5 cos 5 cos t
1 2
F 5
k y1
cos
2
sin( y1
900 )
7
3、 单相绕组磁势的统一表达式
• 为了统一表示相绕组的磁势，引入每相电流I、每相串联
匝数N 等概念
I Ic a ;
N 2 pqNc (双层绕组); a
N pqNc (单层绕组） a
将单层绕组磁势公式 F1 0.9Ic (qNc )kq1ky1
cos(
t
480 0
)
14
• 三相合成磁势为
f1 fa fb fc 3 F1 cos( t )
2
• 三相对称交流绕组通过三相 对称电流时将产生旋转磁势
15
关于旋转磁势的进一步讨论
• 三相对称交流绕组通过三相对称交流电流时，三个反向旋 转磁势在空间错开120电角度相互抵消，三个正向旋转磁势 在空间同相位，合成一个圆形旋转磁势
26
sinq 2
q sin
2
5
（2）双层短距绕组的磁势
• 双层整距绕组可以等 效为两个整距单层绕组
• 双层短距绕组的磁势可 以等效为两个错开的单层 整距绕组的磁势在空间的 叠加，错开的角度等于短 距角
6
• 双层短距绕组的磁势振幅为
f3 fa3 fb3 fc3 0
三相合成的三次谐波磁动势为零
这个结论可推广到＝6k－3的谐波次数
21
五次谐波磁势
（2）五次谐波磁动势的极对数是基波的五倍， 三相绕组各 自建立的五次谐波磁动势表达式
fa5 F5 cos 5 cos t
1 2
F 5
k y1
cos
2
sin( y1
900 )
7
3、 单相绕组磁势的统一表达式
• 为了统一表示相绕组的磁势，引入每相电流I、每相串联
匝数N 等概念
I Ic a ;
N 2 pqNc (双层绕组); a
N pqNc (单层绕组） a
将单层绕组磁势公式 F1 0.9Ic (qNc )kq1ky1
cos(
t
480 0
)
14
• 三相合成磁势为
f1 fa fb fc 3 F1 cos( t )
2
• 三相对称交流绕组通过三相 对称电流时将产生旋转磁势
15
关于旋转磁势的进一步讨论
• 三相对称交流绕组通过三相对称交流电流时，三个反向旋 转磁势在空间错开120电角度相互抵消，三个正向旋转磁势 在空间同相位，合成一个圆形旋转磁势
26
sinq 2
q sin
2
5
（2）双层短距绕组的磁势
• 双层整距绕组可以等 效为两个整距单层绕组
• 双层短距绕组的磁势可 以等效为两个错开的单层 整距绕组的磁势在空间的 叠加，错开的角度等于短 距角
6
• 双层短距绕组的磁势振幅为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A
X
A相绕组展开图
注意到：磁动势的大小及分布仅与导体中的电流大小及导 体在空间的位置有关，而与导体连接的先后顺序无关。 所以可将双层短距线圈组产生的磁动势看成：由上层边构 成的整距线圈组产生的磁动势，与由下层边构成的整距线圈 组产生的磁动势二者的合成；但须考虑其空间上的相位差。
9.2.3 双层短距线圈组的磁动势
等效绕组：在p=1且产生磁动势
相等的前提下，以一个单层整距线
A
圈代替一相短距、分布绕组。
等效的单层整距线圈平面中法
W kW1 线即为相绕组轴线，且基波脉振磁
A
X
动势空间矢量位于相绕组轴线上。
三相绕组可简化成空间上互差
B
C
120度的三个单层整距线圈。
9.2.4 一相绕组的磁动势
(1) 分析
上述单、双层线圈组的分析结果，即为一对极电机 一相绕组产生的磁动势。
电机可以是多对极的，但每 对极磁路均对称且相互独立，不 同极对下的磁动势并不叠加（此 特点与电动势不同）。
由于多对极磁路的对称性，故 一相绕组的磁动势即为每对极中每 极的安匝数。
9.2.4 一相绕组的磁动势
9.2.2 单层整距线圈组的磁动势
(1) 线圈组的特征
① 每个线圈组是由q个线圈串联而成。 ② 每个线圈匝数相等，并且电流相同， 所以各个线圈产生的磁动势大小相等。 ③ 每个线圈在空间上依次互差α空间电 角度，使各线圈产生的磁动势幅值在空 间也依次互差α空间电角度。
Fc1
Fc1
Fc1
(2) 合成方法（以q=3为例）
cos
其中： kw ky kq
k y
sin
2
特别是当： 1
sin q
kq
2
q sin
2
得： fq1( ) Fq1 cos (qFc1kw1) cos [q(0.9IcWc cost)kw1]cos
9.2.3 双层短距线圈组的磁动势
例： m 3
p 1
Z 18
q3
9
y 8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 2
y)180 2
2Fq1上
cos(90
y
90)
y
2Fq1上 sin 90 2Fq1上ky1
Fq1
所以： fq1( ) 2[q(0.9IcWc cost)kq1]ky1 cos
2q(0.9IcWc cost)kw1 cos
Fq1下
Fq1上
同理：
fq
(
)
2q(0.9IcWc
1
cos
t
)kw
cos
完全仿照线圈组电动势的求和方法，但须特别注意 磁动势为空间矢量，而电动势为时间相量。
9.2.2 单层整距线圈组的磁动势
(3) 合成结果
fq ( ) Fq cos (qFc kq ) cos
Fc1
[q(0.9IcWc
1
sin
2
cos t )kq
]cos
Fc1 Fc1
q(0.9IcWc
1
cos t )kw
0.9 1
I
W p
kw
为最Байду номын сангаас幅值
特别是当： 1
得： f1( ) F1m cost cos
而： f ( ) f1( ) f3 ( ) f5 ( )
9.2.4 一相绕组的磁动势
(2) 结论
f
( )
(0.9 1
I
W p
kw
) cost
cos
① 单相绕组通入单相交流电流产生的磁动势即是空间
的函数，又是时间的函数。
② 谐波磁动势是指磁动势在空间上的谐波分布。
③ 基波与谐波磁动势的幅值均以通入电流的频率随时
间在空间脉振。
④ 基波磁动势仍可用空间矢量表示，为此需引入等效
绕组及相绕组轴线的概念。
9.2.4 一相绕组的磁动势
(3) 等效绕组及相绕组轴线
A
f1
(0.9
I
W p
kw1) cost cos
W kW1
A
X
(1) 分析
单层绕组：
fq
( )
q(0.9IcWc
1
cos t )kw
cos
双层绕组：
fq
( )
2q(0.9IcWc
1
cos t )kw
cos
但其中是以线圈匝数和线圈电流有效值表示，工程应用不便。
注意到： 每相绕组每条支路串联匝数
W
2
pqWc pqWc
（a 单层） （a 双层）
每相电流有效值 I aIc
得： I
W
2pqpIqcIWcWc c
(单层) (双层)
即：
IcWc
I I
W W
pq （单层） 2 pq （双层）
9.2.4 一相绕组的磁动势
(1) 分析
结果得： f
( )
(0.9 1
I
W p
kw
cost) cos
F
cos
其中：
F
(0.9 1
I W p
kw ) cost
F m cost
为幅值
再其中：F m
以基波为例： 因为：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 2
y
A
180
y
X
Fq1
所以：
18 1 2 3
y 180
F 9 10 11 12
q1下
Fq1上
9.2.3 双层短距线圈组的磁动势
由矢量图：
Fq1
2Fq1上 cos 2
(
2Fq1上 cos