15-2第十五讲:有介质存在时磁场的规律,电介质典型例题,介质的击穿及接触起电
合集下载
高二物理竞赛磁场中的磁介质 课件

i
I M dl
L
14
介质表面磁化电流密度:
Mt
M
选
dl ∥Mt
dIs M dl
M tdl
磁化面电流密度考虑到方向来自jdIs dl
Mt
若M
平行于表面,则j′=M
j M nˆ
15
与磁介质内任意闭合路径L铰链的总束缚电流
I '
dI '
M • dr
L
L
3. 磁化规律(实验规律) 各向同性线性磁介质
的磁矩的总和,叫分子磁矩。 m mi
某些分子在正常情况下,其磁矩的矢量和 一定,称为分子的固有磁矩。
抗磁质 m 0 无外场作用时,对外不显磁性。
顺磁质 m 0
无外场作用时,由于热
运动,对外也不显磁性
8
5. 磁场对磁介质分子的作用
(1) 分子磁矩方向变化 磁矩将转向外场方向。
(2) 分子磁矩大小变化 • 外场与分子磁矩 m 同向
M
r
1
B
m
B
0r
0r
m
介质的磁化率
对比 电介质
P e0E
0 r 1E
e 极化率
16
磁化强度
pmi
M lim i
ΔV 0 ΔV
磁化强度与磁化电流的关系
j M nˆ
I M dl
L
对比电介质
极化强度
pei
P lim i
ΔV 0 ΔV
q
P
nˆ P
ds
S
17
•各向同性线性磁介质
M
r
1
B
r 0
B
为介质中磁场 的磁感应强度
15-3 有磁介质存在时磁场的基本定理
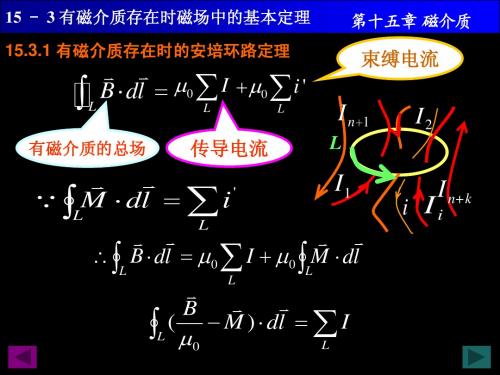
(
L
B
0
L
L
M ) dl I
L
15 - 3 有磁介质存在时磁场中的基本定理
第十五章 磁介质
定义磁场强度 H
B
物理意义
H dl I
L L
0
M 则有:
沿任一闭合路径磁场强度的环流等于该 闭合路径所包围的自由电流的代数和。
磁场强度H的单位:安培/米(A/m)
S
H dl I
L
0
M
D dS e dV
S V
D 0E P
def
S
15 - 3 有磁介质存在时磁场中的基本定理
第十五章 磁介质
B, H , M 之间的关系 P、D、E 之间的关系: 各向同性电介质 各向同性磁介质 实验规律
M mH def B H M
B 0 (1 m ) H
0
def D 0E P
P e 0 E
D (1 e ) 0 E
D r 0 E E
或相对介电常量。
r (1 m ) B 0 r H H
S
S
L
B dl 0 I 0 M dl
(
L
B
0
L
L
1 E dS
S
0
q
0
1
0
P dS
S
M ) dl I
def H
L
B
L
( 0 E P) dS q0
高二物理竞赛课件:介质的电磁性

介质的电磁性
通过薄层进入介质2的正电荷为 P2 ds, 由介 质1通过薄层下侧面进入薄层的正电荷为 P1 ds 因此薄层出现的净余电荷为
dQp (P2 P1) ds
以 p为极化电荷面密度,则有
pds (P2 P1) ds (P2 P1) nˆds
得到
p nˆ (P2 P1)
总电流有贡献,但这种情形只能发生在边界上。当
然,在S面外的电流环8,对总电流同样无贡献。
每一个环形电流贡献为i 或-i,在S面上一共有多
少这种电流呢?
在边界线L上取一线元 ,dl设环
a
形电流圈 的面积为 a,则由图可见 ,
若分子中心位于体积元
的a柱d体l 内,
dl
则该环形电流就被 所穿过。因dl 此,
jp
P t
④ 介质中的电场
称为极化电流密度
E Es Ei Ep , Ep是有源无旋场
考虑到极化电荷产生电场,
E f p 0
由于 p P,上式变为: (0 E P) f
令D 0 E p --电位移矢量.
D
f
,
E
B t
对各向同性的线性介质:
P e0 E, D E
0r 0 (1 e )
由于磁化,引起介质内部环形电流有规则取向,
呈现宏观电流效应,这种由磁化引起的电流称为磁
化电流。
设S为介质内部的一个曲
8
L6
1
4
面,其边界线为L,环形电流 7 通过S面有两种情况:
S3
2
5
一种是在S面中间通过两次的环形电流,为1、2、
3,这种电流环对总电流没有贡献;而另一种是在S
面中间通过一次的环流,如4、5、7,这种电流环对
通过薄层进入介质2的正电荷为 P2 ds, 由介 质1通过薄层下侧面进入薄层的正电荷为 P1 ds 因此薄层出现的净余电荷为
dQp (P2 P1) ds
以 p为极化电荷面密度,则有
pds (P2 P1) ds (P2 P1) nˆds
得到
p nˆ (P2 P1)
总电流有贡献,但这种情形只能发生在边界上。当
然,在S面外的电流环8,对总电流同样无贡献。
每一个环形电流贡献为i 或-i,在S面上一共有多
少这种电流呢?
在边界线L上取一线元 ,dl设环
a
形电流圈 的面积为 a,则由图可见 ,
若分子中心位于体积元
的a柱d体l 内,
dl
则该环形电流就被 所穿过。因dl 此,
jp
P t
④ 介质中的电场
称为极化电流密度
E Es Ei Ep , Ep是有源无旋场
考虑到极化电荷产生电场,
E f p 0
由于 p P,上式变为: (0 E P) f
令D 0 E p --电位移矢量.
D
f
,
E
B t
对各向同性的线性介质:
P e0 E, D E
0r 0 (1 e )
由于磁化,引起介质内部环形电流有规则取向,
呈现宏观电流效应,这种由磁化引起的电流称为磁
化电流。
设S为介质内部的一个曲
8
L6
1
4
面,其边界线为L,环形电流 7 通过S面有两种情况:
S3
2
5
一种是在S面中间通过两次的环形电流,为1、2、
3,这种电流环对总电流没有贡献;而另一种是在S
面中间通过一次的环流,如4、5、7,这种电流环对
高二物理竞赛有磁介质时磁场的计算PPT(课件)

m
0
1
496
例 一细螺绕环,它由表面绝缘的导线在铁环上
12
密绕而成,每厘米绕10匝。I=2A时,测得环内
B为1.0T,则铁环的相对磁导率r为
(A)796 增加的角速度和磁矩为: (B)398 (C)199 (D)63.3
选取合适的积分环路,使H从积分号提出来;
(A)796 (B)398 (C)199 (D)63. 磁化强度与磁化电流的关系 根据B与H的关系求B。 磁化强度 M 沿闭合回路的线积分等于该回路包围的磁化电流代数和。 分析:H→B→Φ→μ→ 例 同轴电缆由一导体圆柱(半径为a)和同轴导体园管(内外半径为b、c)构成,二者之间充满 磁介质,电流I从导体圆柱流去,从导体管流回,求磁感应强度分布。 恰好可以由库仑力和洛伦兹力的合力提供,故电子维持原有轨道,但速率增加。 磁化强度与磁化电流的关系 匀速缓慢增加与原角动量同向的磁场,产生的感生电场加速电子: 分析:H→B→Φ→μ→ --有介质时的高斯定律 恰好可以由库仑力和洛伦兹力的合力提供,故电子维持原有轨道,但速率增加。 例 同轴电缆由一导体圆柱(半径为a)和同轴导体园管(内外半径为b、c)构成,二者之间充满 磁介质,电流I从导体圆柱流去,从导体管流回,求磁感应强度分布。
r
r
r
FC e v0 v B
FC FL
恰好可以由库仑力和洛伦兹力的合力提供,
故电子维持原有轨道,但速率增加。
4
增加的角速度和磁矩为:
e B
当磁化强度与介质表面不平行时 根据B与H的关系求B。
2m
选取合适的积分环路,使H从积分号提出来; 增加的角速度和磁矩为:
2
er 磁化强度 M 沿闭合回路的线积分等于该回路包围的磁化电流代数和。
高二物理竞赛有磁介质的稳恒磁场课件

鱼跳龙门往上游。
立志是事业的大门,工作是登门入室的旅程。
经典励志短句(二) 鱼跳龙门往上游。 有志者能使石头长出青草来。
Bh Bh 0ih
鸟不展翅膀难高飞。
远大的希望造就伟大的人物。
B
1 2
0i
让自己的内心藏着一条巨龙,既是一种苦刑,也是一种乐趣。
雄心壮志是茫茫黑夜中的北斗星。
天才是由于对事业的热爱感而发展起来的,简直可以说天才。
轨道和自旋磁矩的贡献), 解 设 i为载流平面的面电流密度 , 为载流平面的磁感应强度,作安培环路abcda,由安培环路定理得:
磁介质-与磁场有相互作用的物质(所有物质)。
轨道和自旋磁矩的贡献),
轨道和自旋磁矩的贡献),
面元在B0中所受的安培力为:
电子轨道磁矩与轨道角动量的关系:
电流单位“安培”的定义
解 设 i为载流平面的面电流密度 , 为载流平面的磁感应强度,作安培环路abcda,由安培环路定理得: 安培-载有等量电流,相距1米的两根平行长直导线,当每米长度所受安培力为2 10-7N时,每根导线中的电流为1安培。
距1米的两根平行长直导 B>>B0 (纯铁、硅钢)
显然,顺磁性受温度影响较大
磁介质对磁场的影响来源于其内部机制。
电子轨道磁矩与轨道角动量的关系:
例 将一无限大均匀载流平面放入均匀磁场 中(设均匀磁场方向沿 X 轴正方向),且其电流方向与磁场方向垂直指向纸内。
显然,顺磁性受温度影响较大
电子自旋磁矩和自旋角动量 S 的关系:
例 将一无限大均匀载流平面放入均匀磁场 B中0
5
(设均匀磁场方向沿 X 轴正方向),且其电流方
f 2 a f a
I
o
大学物理第11章磁场中的磁介质ppt课件

第三篇 电磁学
无损耗输电。传统输电过程中总要产生一部分焦耳热损耗,一般在 10%~20%,如果采用超导体输电,几乎没有电能损失,而且不需要 升压,可以不用变压器设备,也不必架设高压线,可以在地下管道中。 甚至可以直接传输直流电。
产生强磁场。因超导体无热损耗,可通过很大电流,如用超导芯线为 Nb3Sn。其最大电流密度为 109 A/m2, 在承受相同电流的情况下,超 导芯线可以细得多,超导磁铁不仅效率高,而且可以做得很轻便。例 如,一个能产生 5T 的中型电磁铁的重量可达 20 吨,而超导磁铁的重
量不过几公斤。 美国在 磁谱仪中,将采用超导磁铁产生强磁场,
2003 年再次送入地球轨道,观察暗物质和反物质。
第三篇第三篇电磁学电磁学在无外磁场时抗磁质中分子的轨道和自旋磁矩均不为零但其和分子磁矩为零m0物质不显磁抗磁质的磁化机理抗磁性电子进动有外场时外磁场使分子中作轨道运动的电子的角速度变化当电子轨道运动角速度与外磁场同向时角速度增加
第三篇 电磁学
第十一章 磁场中的磁介质
上章我们学习了真空中稳恒电流激发的磁场及其规律。当 空间有介质(导体、绝缘体)存在时,磁场将与介质发生相互 作用,我们把磁场中的介质称为磁介质。磁介质在外加磁场 作用下自身产生附加磁场的过程称为磁化。
分子电流——分子磁矩产生的磁效应可 以用一等效的圆电流的磁效应来表示。
这就是安培提出的分子电流假设。
第三篇 电磁学
顺磁质和抗磁质的磁化可用安培分子电流假说解释,而铁磁质的磁化很 复杂,后面我们将用磁畴的概念解释。
1. 顺磁质的磁化机理——顺磁性
无外磁场时,顺磁质中的每个分子虽然具有磁矩m≠0,但由于分子热 运动而使其取向无规则,物质分子的总分子磁矩m=0,物质对外不 显磁性。
高中物理竞赛-第三篇 电磁学:磁介质(共19张PPT)

说明:
1º当全部磁畴都沿外磁场方向时,铁磁质的磁化就 达到饱和状态。饱和磁化强度MS等于每个磁畴中 原来的磁化强度,该值很大。
——这就是铁磁质磁性 r大的原因。
2º磁滞 现象是由于材料有杂质和内应力等的作用, 当撤掉外磁场时,磁畴的畴壁很难恢复到原来的 形状而表现出来。
3º当温度升高时,热运动会瓦解磁畴内磁矩的规则 排列。在临界温度(相变温度Tc )时,铁磁质完 全变成了顺磁质。居里点 Tc (Curie Point)
16
解:因管外磁场为零,取图示的回路
根据:
L H dl
Ii
L
B
ab H n ab I
B
I
...
a
b
× × × ×M
则:H nI 又:M
B
mH
or
H
nI
d
c nˆ
M
mH
(r 1)nI
i M nˆ
顺磁质 r 1,i || I
i (r 1)nI 抗磁质 r 1, i I
铁磁性主要来源于电子的自旋磁矩。
★ 交换力:电子之间的交换作用使其在自旋平行排列 时能量较低,这是一种量子效应。
★ 磁畴:原子间电子交换耦合作用
B
很强,使其自旋磁矩平行
排列形成磁畴
——自发的磁化区域。
★ 磁畴的变化可用金相显微镜观测
H =0
H
H↑
H↑↑
H H↑↑↑
自 0 自 0 自↑ (自)↗ 自 13
电磁元件的磁芯、磁棒。
B
(2) 硬磁材料:钨钢,碳钢,铝镍钴合金
矫顽力(Hc)大,剩磁Br大
HC
磁滞回线的面积大,损耗大。
适用于做永磁铁。
有介质存在时磁场的规律,电介质典型例题,介质的击穿及接触起电

Qo
4
01
R
2 1
Q0 4 01R21E1
对于外层介质,当r=R处场强达到E2,则 击穿
E2
EC
|rR
Qo
4 0 2R2
R2 1R12E1 R 2E2
1E1 2E2
R1
2013/4/15
气泡问题
平行板电容器,原来充满均匀 介质,A、B、C等处的场强是 均匀场 ,现在A处挖一个球形 小空腔,问A、B两电场强比 增大还是减小?
e DA DB 0EA 0rEB
EA rEB
未挖空腔前
e0 D0 0rE0
E0 EB
e 0rEB 0,B对应处的电荷量减少
2013/4/15
电荷守恒,且导体板等电势, 所以C点对应处电荷增加
c DC D EC E0
因为C点离空穴较远,电荷迁移的 影响不会太大,故
2013/4/15
类似地可以得到两种电介质相接触时的偶 电层电荷面密度的大小为
电子由功 函数小的 一侧转移 至功函数 大的一侧。
20 1 2 )
e
1 r1
2 r2
1、2、r1、r2、1、 2
依次为两侧电介质功函数、 相对介电常数和空间电荷 的厚度
接触起电虽然是静电现象,但是有时也会造 成严重的不良后果
若 出qD0已,知但,由只于要不场知分道布P,有仍一然定无对法称求性出,E可以求
2013/4/15
需要补充D和E的关系式,并且需要已知描
述介质极化性质的极化率e
对于各向同性线性介质,有
介 电
P e0 E
常
数
D 0 E P 0(1 e )E 0 E
1 e 相对介电常数(与真空相对)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析气泡:
极化电荷出现在界面,削弱介质 内场强,加强了气泡内场强
A、B两点的场强会因为气泡边
缘介质极化电荷而改变。
2013/4/15
北京大学物理学院王稼军编
EA E0 E'A EB E0 E'B
加强 削弱
EA E0 EB E0
过A、B路径 EBd1 EAd2 ECd 空腔中线处,D法向连续
2013/4/15
北京大学物理学院王稼军编
小结:
静电荷 (自由、极化)
自由 电荷
真空
有介质
1
EdS
q
S
0 S内
D d S q0
S
S内
E dl 0
L
E dl 0
L
各向同性线性介质D 正比于 E
普遍情况下,两者关系不简单,不一定成正比关系
2013/4/15
北京大学物理学院王稼军编
1
0
S内
q0
S
P d S
S
EdS
S
P
0
dS
1
0
q0
S内
S面内包 围的自 由电荷
D 0 E P
(0 E P) d S q0
S
S内
电位移矢量
2013/4/15
电位移矢量 通量
D d S q0
S
S内
北京大学物理学院王稼军编
电位移矢量 D 0 E P 辅助矢量
D d S q0
2013/4/15
北京大学物理学院王稼军编
D d S q0
S
S内
有介质时D的通量与闭 合面内自由电荷的关系
理论地位:描述场的性质,有源无旋场 可以用来计算某些场分布(由对称性决定)
利用D- Gauss定理按以下路径求
D E P q'( ') E'
利用电容定义和串并联公式按以下路径求
击穿场强Em:电介质发生击穿时的临界场强 击穿电压Vm: 电介质发生击穿时的临界电压
2013/4/15
北京大学物理学院王稼军编
例 球形电容器内外半径分别为R1与R2其间充以相 题 对介电常数为1和2的均匀介质,两介质界面
半径为R。求:1)容器的电容;2)若内外两 层电介质的击穿场强分别为E1和E2,且E1< E2, 为合理使用材料,最好使两种介质内的电场强 度同时达到其击穿值,求此时R的大小。
m
e
0
E介
dl
0 r
0
xdx
0
dx
0 r
1 2
2
2
2 2 0 r
2 0 r e
(m
)
m 0 0 m 0
介质表面积累了导体转移过来的负电荷, 而导体表面因失去电子而出现正电荷。
2013/4/15
北京大学物理学院王稼军编
类似地可以得到两种电介质相接触时的偶 电层电荷面密度的大小为
C0
介质内场强削弱了
1
倍
电容增加了 倍
2013/4/15
北京大学物理学院王稼军编
特殊情况下,特别是在各向同性线性介 质中 D 与E之间关系简单
从理论上可以证明
当均匀介质充满整个电场空间,或均匀介质 是等势面时有介质部分内,下述关系式成立
D 0E0,
E E0
这种情况下可以把有介质部 等势面 分与真空部分看成两个电容的 串、并联
实际对应:高压变压器用油做介质,油的击
穿场强比空气大,E油=4.5E空气,油中忌带进 气泡杂质,若有气泡,气泡中场强大,耐压
低,先被击穿,则气泡处短路。如10mm厚
的油可承受10万伏电压的加载,有气泡,只
相当于8mm,耐压降低。
2013/4/15
北京大学物理学院王稼军编
导体球和电介质
导体球外部半无限大区域充以电
在接触面两侧电荷转移达到平衡时,偶电层产生的电势 差恰好抵消了两侧功函数之差
此时如果迅速分离两物体,则偶电层两边的电荷来不及 完全消失,而使A面带负电,B面带正电——接触起电
接触面上所带电荷面密度取决于两物体的功函数差
2013/4/15
北京大学物理学院王稼军编
例题
作高斯面 S
如图金属与电介质的接触面,均为无 限大平面,设金属上的空间电荷面密
电子由功 函数小的 一侧转移 至功函数 大的一侧。
20 1 2 )
e
1 r1
2 r2
1、2、r1、r2、1、 2
依次为两侧电介质功函数、 相对介电常数和空间电荷 的厚度
接触起电虽然是静电现象,但是有时也会造 成严重的不良后果
2013/4/15
北京大学物理学院王稼军编
接触起电的危害和应用
人体放电
北京大学物理学院王稼军编
需要补充D和E的关系式,并且需要已知描
述介质极化性质的极化率e
对于各向同性线性介质,有
介 电
P e0 E
常
数
D 0 E P 0(1 e )E 0 E
1 e 相对介电常数(与真空相对)
真空中
1, D 0 E
有介质的问题总体上说,比较复杂 但就各向同性线性介质来说,比较简单。
介质,相对介电常数为 ,
试分析导体球上的电荷分布
求导体球以外各处的场强、极化 强度矢量和电位移矢量。
解:分析电荷分布: 1)导体球球对称;2)为了保证导体球是等势体, 3)猜测平衡以后:有效电荷密度 分布依然对称; 否则不满足等势体
(有效电荷=自由电荷+极化电荷)
2013/4/15
北京大学物理学院王稼军编
2013/4/15
北京大学物理学院王稼军编
E1
EB
|rR1
Qo
4
01R
2 1
Q0
4
0
1R
2 1
E1
对于外层介质,当r=R处场强达到E2,则 击穿
E2
EC
|rR
Qo
4 0 2R2
R2 1R12E1 R 2E2
1E1 2E2
R1
2013/4/15
北京大学物理学院王稼军编
气泡问题
平行板电容器,原来充满均匀 介质,A、B、C等处的场强是 均匀场 ,现在A处挖一个球形 小空腔,问A、B两电场强比 增大还是减小?
有介质时,场和真空中的场有何异、同? 库仑定律+叠加原理 仍成立 静电场性质(有源、无旋)?——不变
为什么?因为极化电荷也是静电荷(只是不能动)
2013/4/15
北京大学物理学院王稼军编
考虑关系 P d S q'
S
S内
把静电场Gauss定理变换一下
S
EdS
1
0
S内
q0
1
0
S内
q'
求电容:求D——E——U——C
r R1 R1 r R
R r R2
DA 0, EA o
DB
Q
4r 2
,
EB
Q
4 01r 2
DC
Q
4r 2
, EC
4 0 2r 2
2013/4/15
北京大学物理学院王稼军编
U AD
R2
E
dl
R1
R E R1 B dl
R2 R
EC
dl
由于有效电荷对称分布,所以在导体球外各处
的电场强度是球对称分布
E
1
4 0
Qe r2
4R2 e 4 0r 2
2 0 R2 0 (1 )r 2
有介质部分
P
e 0 E
2( 1)0R2 (1 )r2
rˆ
无介质部分P=0,界面上无极化电荷 D 0E
有介质部分 D
2 0R2 (1 )r 2
无介质部分
Q 1 1 1 1 1 1
4
0
1
R1
R
2
R
R2
Q
4
0
R1R2
(1
2 ) ( 2R2 1 2R1R2R
1R1
)
R
C Q
4 01 2R1R2R
U AB R1R2 (1 2 ) ( 2R2 1R1)R
求 R:要求两种介质内的电场强度同时达到其击穿 值,且E1< E2;由于r越小E越大,所以内层最先达到 击穿值,只要取r=R1处的场强为该层介质的击穿场 强E1,则可以确定加在电容器两极的最大电量Q0
2013/4/15
北京大学物理学院王稼军编
起电 机制
当两物体表面距离25m时,有电子从一个物体转移到 另一物体
若余的A>负空B 间,电则荷B (内不的是电极子化容,易而向是A由转对移方,转则移A表而面来形的成)多
B表面层将因失去电子而出现等量的正空间电荷;于是两 接触面之间产生一个偶电层,其厚度为
电场依然维持辐射状球对称
介质/空气界面有无极化电荷?
' ( ) 0, 为什么?
P
n, '()
Pn
0
先求电荷分布
两边有效电荷相等 1e 2e ?
在有介质的一半界面处,作小扁平高斯面, 可得导体球表面附近场强和高斯面包围的自 由电荷和极化电荷面密度
2013/4/15
北京大学物理学院王稼军编
E
1
0
( 10
')
'
P
e 0 E
e 0 0
( 10
')
解得
'
1
10
1
10
10
有效电荷1e
10
'
10
又1e
10
=
2e
20
