(精品)社会统计学公式总结及要点
(完整版)统计学公式大全
(完整版)统计学公式大全统计学公式大全本文档旨在提供统计学领域常用的公式大全，便于大家在研究和实践中进行参考和应用。
描述统计学公式中心趋势度量1. 平均数（Mean）：$\bar{x} =\frac{{\sum_{i=1}^{n}x_i}}{n}$2. 中位数（Median）：若数据个数为奇数，中位数为排序后的中间值；若数据个数为偶数，中位数为排序后的中间两个值的平均值。
3. 众数（Mode）：出现频率最高的数值。
离散趋势度量1. 方差（Variance）：$Var(x) = \frac{{\sum_{i=1}^{n}(x_i - \bar{x})^2}}{n}$2. 标准差（Standard Deviation）：$SD(x) = \sqrt{Var(x)}$3. 极差（Range）：$Range(x) = \max(x) - \min(x)$分布形状度量1. 偏度（Skewness）：$\text{Skewness} =\frac{{\sum_{i=1}^{n}(x_i - \bar{x})^3}}{n \cdot SD(x)^3}$2. 峰度（Kurtosis）：$\text{Kurtosis} =\frac{{\sum_{i=1}^{n}(x_i - \bar{x})^4}}{n \cdot SD(x)^4}$ 推断统计学公式参数估计1. 样本均值的抽样分布标准差（Standard Error of the Mean）：$SE(\bar{x}) = \frac{{SD(x)}}{\sqrt{n}}$2. 双侧置信区间公式（Confidence Interval）：$\bar{x} \pm Z\cdot SE(\bar{x})$3. 样本比例的抽样分布标准差（Standard Error of Proportion）：$SE(p) = \sqrt{\frac{{p(1-p)}}{n}}$4. 双侧置信区间公式（Confidence Interval）：$p \pm Z \cdotSE(p)$假设检验1. 样本均值和总体均值的差异（t检验）：$t = \frac{{\bar{x} -\mu}}{{SE(\bar{x})}}$2. 双侧拒绝域临界值（t分布）：$t_{\text{critical}} = \pmt_{\alpha/2, df}$3. 样本比例和总体比例的差异（z检验）：$z = \frac{{\hat{p} - p}}{{SE(p)}}$4. 双侧拒绝域临界值（z分布）：$z_{\text{critical}} = \pmz_{\alpha/2}$回归分析公式简单线性回归模型1. 回归方程（Simple Linear Regression）：$y = \beta_0 +\beta_1x + \epsilon$2. 线性预测公式（Simple Linear Regression）：$\hat{y} =\hat{\beta}_0 + \hat{\beta}_1x$3. 斯皮尔曼秩相关系数（Spearman's Rank Correlation Coefficient）：$r_s = 1 - \frac{6\sum d_i^2}{n(n^2 - 1)}$4. 相关系数的显著性检验（t检验）：$t = \frac{r}{\sqrt{\frac{1 - r^2}{n-2}}}$结论本文档列举了统计学领域常用的公式，包括描述统计学中的中心趋势度量、离散趋势度量和分布形状度量，推断统计学中的参数估计和假设检验，以及回归分析中的简单线性回归模型等相关公式。
统计学公式总结
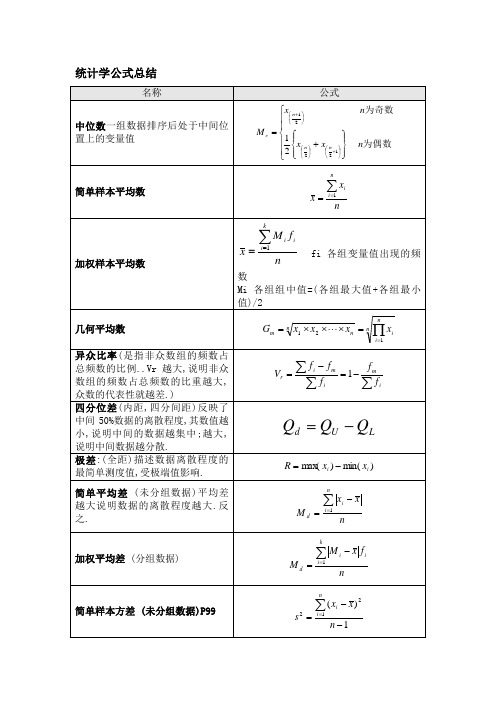
标准分数 （变量值与其平均数的离 差除以标准差后的值。）
离散系数(变异系数)是一组数据的 标准差与其相应的平均数之比..离 散系数大,数据的离散程度大.反 之..它们是成正比的. （二）抽样分布主要公式
zi
xi
s
x
vs
s x
( s 标准差,x 平均数)
总体均值的置信区间（正态总体， 已知）P183 注意 P184 例题
总体比例的检验 (检验方法的总结)
假设
双侧检验
假设形式
H0：= H1：
左侧检验 H0： H1 ：<
右侧检验 H0 ： H1 ：>
统计量
z
p 0 0 (1 0 )
n
拒绝域 P 值决策
z z / 2
z z
P 拒绝 H0
z z
M d i1 n
简单样本方差 (未分组数据)P99
n
(xi x)2
s 2 i1 n 1
加权样本方差 (分组数据)
k
(Mi x)2 fi
s 2 i1 n 1
简单样本标准方差 (未分组数据)
n
(xi x)2
s i1 n 1
加权样本标准差 (分组数据)
k
(Mi x)2 fi
s i1 n 1
异众比率(是指非众数组的频数占 总频数的比例..Vr 越大,说明非众 数组的频数占总频数的比重越大, 众数的代表性就越差.) 四分位差(内距,四分间距)反映了 中间 50%数据的离散程度,其数值越 小,说明中间的数据越集中;越大, 说明中间数据越分散. 极 差 :( 全 距 ) 描 述 数 据 离 散 程 度 的 最简单测度值,受极端值影响.
n
Gm n x1 x2 xn n xi i 1
社会统计学公式总结及要点
3．一个变项，1个样本 ：
①(n≥100)：
②(n≤30)： , df=b-1
4．1个变项，2个样本 1 2
n=n1+n2＞100 →
五、归类总结之五：有关消减误差比例
1.
有消减误差比例意义，且对称
、G、Q拉系数、rs2、r2、rxy.12、、Ry.122= Ry.x1x22
2.有无自由度的表达
G、r、F、x2结果解释加上“其显著度水平达到或没有达到……水平”
3.有关r净相关系数
（两个定距变项）
r=rxy.1——引入第三个变项时对X、Y变项产生共同影响。
rx（y-1）——引入第三个变项时，只对Y产生影响，无消减误差意义。
ry（x-1）——引入第三个变项时，只对X产生影响，无消减误差意义。
Q= Q3- Q1
有单个数（n为偶数时会出现偏离）、区间之分。
（有几种Q，就有几种S计算法）
当为区间表格时(n/4)
①计算向上累加数cf；②Q1位置= ，Q3位置= ；
③Q1=L1+ W1，Q3= L3+ W3；④Q= Q3- Q1P57
5.标准差
①单个数：S= ，②区间：S= P60
对S的解释：如以均值来估计各个个案的数值，所犯的错误 平均是S。用均值作估计变项数值时所犯错误的大小。
社会统计学公式汇总及要点2011.09.09-09.10
(仅供参考,如不能显示公式，请安装Microsoft公式3.0)
一、归类总结之一
测量层次
特质
数学特质
单变项：X
定类变项
只分类
Mo、V
比例、比率、对比值、
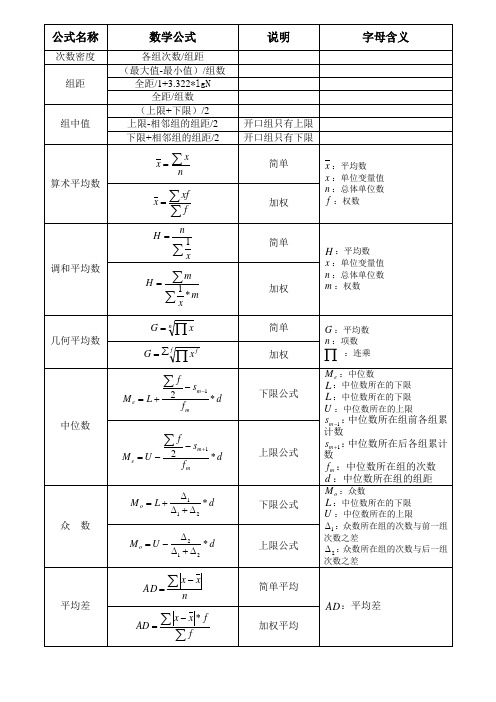
社会统计学常用公式及说明
b
b
i 1
n
i
n
yn y0
平均发展速度-1
回归方程
公式名称
数学公式
yt a bt （方程式）
说明
说明
当 t 0 时：
b
N tY t Y N t 2 ( t ) 2
Y b t N
直线回归
b
N tY t Y N t 2 ( t ) 2
H
调和平均数
H
x
1
简单
H ：平均数
m 1 x *m
x x
f
加权
x ：单位变量值 n ：总体单位数 m ：权数
Gn
简单 加权
G ：平均数
几何平均数
f G
n ：项数
：连乘
f
Me L 2
sm 1 fm
*d
下限公式
中位数
Me U
f
2
sm 1 fm
*d
上限公式
环比
Ai
增长速度
Bi
yi y0 (i 1,2,....n) y0
yi yi 1 (i 1,2,....n) yi 1
n
定基
环比
环比发展速度-1 1、等 于 各 环 比 发 展 速度连乘开 n 次方 根 2、等于 n 次方根下报 告期水平 / 基期水 平
平均发展 速度 平均增长 速度
a
a
Y
N
回归方程
a
yt a bt ct 2 （方程式）
t Y t t Y N t ( t )
4 2 2 4 2 2
b
统计学常用公式汇总
《统计学原理》常用公式汇总（一）第三章统计整理a) 组距＝上限－下限b) 组中值＝（上限+下限）÷2c) 缺下限开口组组中值＝上限－1/2邻组组距d) 缺上限开口组组中值＝下限+1/2邻组组距第四章综合指标i. 相对指标1.结构相对指标＝各组（或部分）总量/总体总量2.比例相对指标＝总体中某一部分数值/总体中另一部分数值3.比较相对指标＝甲单位某指标值/乙单位同类指标值4.强度相对指标＝某种现象总量指标/另一个有联系而性质不同的现象总量指标5.计划完成程度相对指标＝实际数/计划数＝实际完成程度（%）/计划规定的完成程度（%）ii.平均指标1.简单算术平均数：2.加权算术平均数或iii.变异指标1.全距＝最大标志值－最小标志值2.差: 简单σ= ；加权σ=3.差系数:第五章抽样估计1.平均误差：重复抽样：不重复抽样：2.抽样极限误差3.重复抽样条件下：平均数抽样时必要的样本数目成数抽样时必要的样本数目4.不重复抽样条件下：平均数抽样时必要的样本数目第七章相关分析1.相关系数2.配合回归方程ｙ＝ａ＋ｂｘ3.估计误：第八章指数分数一、综合指数的计算与分析(1)数量指标指数此公式的计算结果说明复杂现象总体数量指标综合变动的方向和程度。
( - )此差额说明由于数量指标的变动对价值量指标影响的绝对额。
(2)质量指标指数此公式的计算结果说明复杂现象总体质量指标综合变动的方向和程度。
（ -）此差额说明由于质量指标的变动对价值量指标影响的绝对额。
加权算术平均数指数=加权调和平均数指数=(3)复杂现象总体总量指标变动的因素分析相对数变动分析：= ×绝对值变动分析：- = ( - )×（ -）第九章动态数列分析一、平均发展水平的计算方法：(1)由总量指标动态数列计算序时平均数①由时期数列计算②由时点数列计算在间断时点数列的条件下计算：a.若间断的间隔相等，则采用“首末折半法”计算。
公式为：b.若间断的间隔不等，则应以间隔数为权数进行加权平均计算。
社会统计学公式总结LIJUN
社会统计学考试必备公式
学院：人文学院
姓名：李军
学号：2011014737
专业：社会学
班级：社会111
时间：2013年6月20日
社会统计学考试必备公式
第二章单变量统计描述分析
直方图：频次密度=频次/组距（条宽）
相对频次密度（频率密度）=相对频次（频率）/组距（条宽）
频次=频率密度*组距
A、集中趋势测量法
众值：m0
B、离散趋势测量法
极值R：观察的最大值-观察的最小值
四分互差Q=Q75-Q25
第三章概率
一、概率的运算
1.当事件A与事件B互不相容时，
P(A+B)=P(A)+P(B)
2. 当事件A与事件B不满足互不相容时，
P(A+B)=P(A)+P(B)-P(AB)
3.A、B相互独立
P(AB)=P(A)P(B)
4. A、B不相互独立
P(AB)=P(A)P(B/A)或P(B)(A/B)
第五章正态分布
第六章参数估计
第七章假设检验的基本概念
1.统计假设
2.原假设与备择假设
3.假设检验的基本原理
4.双边检验与单边检验
第十四章非参数检验。
统计学常用公式汇总
《统计学原理》常用公式汇总第三章统计整理a) 组距＝上限－下限 b) 组中值＝（上限+下限）÷2c) 缺下限开口组组中值＝上限－1/2邻组组距d) 缺上限开口组组中值＝下限+1/2邻组组距第四章综合指标i. 相对指标1.结构相对指标＝各组（或部分）总量/总体总量2.比例相对指标＝总体中某一部分数值/总体中另一部分数值3.比较相对指标＝甲单位某指标值/乙单位同类指标值4.强度相对指标＝某种现象总量指标/另一个有联系而性质不同的现象总量指标5.计划完成程度相对指标＝实际数/计划数＝实际完成程度（%）/计划规定的完成程度（%）ii.平均指标1.简单算术平均数：2.加权算术平均数或iii.变异指标1.全距＝最大标志值－最小标志值2.标准差: 简单σ= ；加权σ=3.标准差系数:第五章抽样估计1.平均误差：重复抽样：不重复抽样：2.抽样极限误差3.重复抽样条件下：平均数抽样时必要的样本数目成数抽样时必要的样本数目4.不重复抽样条件下：平均数抽样时必要的样本数目第七章相关分析1.相关系数2.配合回归方程ｙ＝ａ＋ｂｘ3.估计标准误：第八章指数分数一、综合指数的计算与分析(1)数量指标指数此公式的计算结果说明复杂现象总体数量指标综合变动的方向和程度。
( - )此差额说明由于数量指标的变动对价值量指标影响的绝对额。
(2)质量指标指数此公式的计算结果说明复杂现象总体质量指标综合变动的方向和程度。
（ -）此差额说明由于质量指标的变动对价值量指标影响的绝对额。
加权算术平均数指数=加权调和平均数指数=(3)复杂现象总体总量指标变动的因素分析相对数变动分析：= ×绝对值变动分析：- = ( - )×（ -）第九章动态数列分析一、平均发展水平的计算方法：(1)由总量指标动态数列计算序时平均数①由时期数列计算②由时点数列计算在间断时点数列的条件下计算：a.若间断的间隔相等，则采用“首末折半法”计算。
社会统计学笔记
第一章科学方法与社会研究历程1·社会学研究：就是运用科学的方法来搜集和分析社会事实，以理解社会现象之间的关系。
2·科学研究：就是运用客观的、逻辑的和系统的方法来搜集事实及分析事实。
3·社会学研究的整个历程，大致上可以分为三个阶段：（1)筹划，（2)执行,（3）总结。
4·初步探索步骤:（1）收集有关的文献,（2）咨询那些对研究的题目有经验、有知识的人，进行了解，（3）观察个案.5·假设：就是根据我们对问题的了解,假定现象与现象之间的关系。
就是假定某一现象的变化与另一种现象的变化具有某种关系.假设的方式：函数式（要求变项之数值有高低之分)、差异式(不存在高低之分）6·较为常用的研究方式：实验法、社会调查法.（皆可验证假设)①实验法的逻辑：有意的改变A变项,然后看看B变项是否随着变化;如果B变项显然是随着A变项的变化而变化，就说明A变项对B变项有影响。
②社会调查法特点：在研究过程中不改变社会现状,只求就地取材，然后以统计方法推算变项与变项之间的关系。
7·能够有效地验证假设的实验法称为典型或理想实验法8·社会调查法可以分为两大类：一是叙述性调查(重点是报道社会事实,较少分析社会事实(即变项）之间的因果关系)，一是解释性调查（目的是要证明不同的变项之间是否有因果关系）。
9·全体调查:就是从所有研究对象中搜集资料。
抽样调查：就是从全体的研究对象中科学的抽出一个数目较少的样本，然后据此样本的资料推论全体的情况。
10·个案研究:就是选择一个或几个个案（即研究对象），作深入的接触和观察,目的是对所研究的问题作深入的了解.11·横剖研究：指的是在同一时期搜集资料，目的是理解各种社会现象（即变项）在某时期的相关情况的研究.纵贯研究:是指在不同时期搜集的，目的在了解社会现象(即变项)在不同时期中的变动情况的研究.12·纵贯研究分为两种:趋势研究、同组研究（指的是在不同时期调查相同的样本).同组分析的问题：遗失个案的问题。
统计知识点公式总结
统计知识点公式总结一、总体与样本1. 总体：总体是指我们想要研究的全部个体或者事物的总体。
通常情况下，总体是非常大的，难以直接观察和研究。
比如全国人口、某一批产品的质量等等。
2. 样本：样本是总体的一个子集，是总体的一部分。
通常情况下，我们是通过对样本的研究来推断总体的特征。
样本的选择应该具有代表性，这样才能保证我们得出的结论是有说服力的。
3. 样本量：样本量是指研究中所使用的样本的大小。
通常情况下，样本量越大，研究的结果越可靠。
但是，样本量过大也会增加研究的成本，因此需要在可接受的范围内选择合适的样本量。
二、描述统计1. 中心趋势指标：中心趋势指标是用来描述数据集中趋势的指标，主要包括均值、中位数和众数。
- 均值（Mean）：均值是指所有数据之和除以数据的个数。
均值的计算公式为：μ = ΣXi/ n，其中，μ为均值，Xi为第i个数据，n为数据的总个数。
- 中位数（Median）：中位数是指将数据集中的数据按照大小排序，处于中间位置的值。
如果数据的个数为奇数，那么中位数就是中间位置的值；如果数据的个数为偶数，那么中位数就是中间两个值的平均值。
- 众数（Mode）：众数是指数据集中出现次数最多的值。
有时候，一个数据集可以有多个众数。
2. 离散程度指标：离散程度指标是用来描述数据的分散程度的指标，主要包括极差、方差和标准差。
- 极差（Range）：极差是指数据的最大值和最小值之间的差异。
极差的计算公式为：Range = Max - Min，其中，Range为极差，Max为数据的最大值，Min为数据的最小值。
- 方差（Variance）：方差是描述数据分布的离散程度的指标，它是每个数据与均值之差的平方的平均值。
方差的计算公式为：σ^2 = Σ(Xi - μ)^2 / n，其中，σ^2为方差，Xi为第i个数据，μ为均值，n为数据的总个数。
- 标准差（Standard Deviation）：标准差是方差的平方根，它的计算公式为：σ = √σ^2，其中，σ为标准差，σ^2为方差。
社会统计学知识点总结
第一章数据与统计学数据分析所使用的方法大体上可分为描述统计和推论统计（推断统计），描述统计主要是利用图表形式对数据进行展示，或通过计算一些简单的统计量（诸如:比例、比率、平均数、标准差等）对数据进行分析。
推断统计主要研究如何根据样本信息来推断总体的特征，内容包括参数估计和假设检验两大类。
变量：是描述观察对象某种特征的概念，其特点是从一次观察到下一次观察可能会出现不同的结果（具有一个以上取值的概念）1、下列哪一个选项不是变量?( )A. 民族B. 智商C. 衣服的尺寸D. 女性答案：C2、下列变量属于数值型变量的是( )A. 工资收入B. 产品等级C. 学生对考试改革的态度D. 企业的类型答案：A解析：3、社会统计学的数据分析方法主要包括统计描述和( )A. 统计描述B. 统计推导C. 统计推论D. 统计分析答案：C4、能计算均值和标准差的必须是哪种变量( )A. 自变量B. 因变量C. 数值型变量D. 字符串型变量答案：C5、在SPSS中最多可以设置几个独立的缺失值?( )A. 3B. 4C. 5D. 8答案：A6、描述统计可以最恰当地表述为( )A.数据作概括性的表达B.对总体所作的结论C.测量操作的应用D.原始数据到标准分的转变答案：A解析：描述统计主要是利用图表形式对数据进行展示，或通过计算一些简单的统计量（诸如:比例、比率、平均数、标准差等）对数据进行分析。
第二章数据的描述性分析：图表展示1、欲以图形显示两变量X和Y的关系,最好创建( )。
A. 直方图B. 圆形图C. 柱形图D. 散点图答案：D第三章数据的描述性分析：概括性度量1、下列统计指标中,对极端值的变化最不敏感的是( )。
A. 众值B. 中位值C. 四分位差D. 均值答案：A2、经验法则表明,当一组数据正态分布时,在平均数加减1个标准差的范围之内大约有 ( )A. 50%的数据B. 68%的数据C. 95%的数据D. 99%的数据答案：B解析：根据标准得分可以判断一组数据中是否存在离群点。
社会统计学社会学测量尺度复习资料大纲总结
1、四种测量尺度：（1）定类尺度：按现象性质差异进行的辨别与区分。
测量结果形成定类变量或指标。
定类变量或指标确切的值是以文字表述的，可用数值标识，但仅起标签作用。
各类别间是平等的，没有高低、大小、优劣之分。
分类的原则：穷尽性或无遗性；互不重叠或互斥性属性：对称性；传递性（2）定序尺度：按现象顺序差异进行的辨别与区分。
测量结果形成定序变量或指标。
定类变量或指标确切的值是以文字表述的，可用数值标识，但仅起标签作用。
定序变量或指标各类别间有高低优劣之分，不能随意排列。
（3）定距尺度：按现象绝对数量差异进行的辨别与区分。
测量结果形成定距变量或指标。
定居变量或指标的值以数字表述，有计量单位可进行加减运算，不能进行乘除运算。
各类别间有大小之分，但没有绝对零点。
（4）定比尺度：按现象绝对差异与相对差异进行的辨别与区分。
测量结果形成定比变量或指标。
定比变量或指标确切的值以数字表述，有计量单位，可加减。
有绝对意义上的零点，可乘除。
2、测量尺度的作用：（1）决定数据的整理、显示方法。
（2）决定数据的分析方法。
（3）决定计算机的处理方法。
3、对测量尺度的判断：测量精度、计算方法、信息数量4、条形图和直方图的区别：条形图：是以长方形的长度(宽度相同)来表示次数或百分率的多少，为求清楚长方形之间可以分开(当然也可以不分)，宽度没有意义。
直方图：又称矩形图，以一个矩形的面积()表示每组数值的次数或百分率的多少。
与条形图的不同。
条形图的宽度没有意义，直方图的长度与宽度均有意义；直方图各个矩形要相连排列，条形图可以分开。
5、累加次数：累加次数就是把次数逐级相加起来，分为两种；一种是向上累加(cf↑)，一种是向下累加(cf ↓)，其作用是使我们容易知道某值以下(或以上)之次数总和。
向上累积表示由低层向高层累加。
向下累积表示由高层向低层累加。
6、众值：众值(Mo)就是次数最多之值。
对于定类变项，以众值作预测所犯的错误是最小的。
众值适合于分析定类变项，也可以用来分析定序、定距变项的资料。
社会统计学-社会统计学知识点(仅供参考)
第7章住户活动统计
第一节住户活动及其统计内容
1、住户的概念
2、住户活动统计应该包括的内容
3、住户的分类
第二节居民收入统计
1、居民收入、居民消费、居民投资、居民财产的含义
2、居民总收入和居民可支配收入的概念
3、工资性收入、经营性收入、财产性收入、转移性收入
4、居民收入需要明确的两点
5、住户收入总量统计：
1）住户总收入：城镇住户总收入、农村住户总收入
2）住户可支配收入：城镇住户可支配收入、农村住户纯收入（可支配收入）、农村住户现金收入
6、居民收入水平及其变动统计：
1）总体人均收入
2）户人均收入
3）实际收入
7、居民收入结构统计：
第三节居民消费统计
1、居民消费含义
2、居民消费统计需注意的六点
3、居民消费总量及其水平统计：
1）住户主要消费品消费量和人均消费量：居民人均消费品消费量；户人均消费品消费量
2）居民消费支出总额与人均消费支出：人均年消费支出；户人均年消费支出4、居民消费倾向与消费结构统计：
1）居民消费倾向统计：居民平均消费倾向；居民边际消费倾向
2）居民消费结构统计：消费内容结构；消费方式结构；消费目的结构
5、恩格尔系数及其应用：恩格尔定律；恩格尔系数定义及计算公式
第四节居民收入、消费分布差异的统计与分析。
社会经济统计学原理复习要点
一、统计的涵义:一是指统计活动（统计工作);二是指统计资料；三是指统计科学。
二、社会经济统计:它是从数量方面入手研究社会经济现象的现状及发展规律的一种手段.社会经济统计的性质：它是社会认识的最有力的武器之一。
三、社会经济统计认识社会的特点：A、数量性是它的基本特点；B、总体性是统计的另一重要特点。
四、社会经济统计学的研究对象：是社会经济统计活动的过程。
1、统计总体：是指根据统计任务的要求，由客观存在的，在同一性质基础上结合起来的许多个别事物的集合。
2、总体单位:构成统计总体的个别事物叫总体单位。
3、标志:是指总体单位的特征或属性的的名称。
4、标志按其表现形式不同,分为数量标志和品质标志。
数量标志表现为数量上不同的标志,如职工的年龄、工资、工龄等;品质标志是指不能用数量表现的标志，如性别、隶属关系等。
5、变量：统计中的变量是指可变的数量标志.6、变量的数值叫变量值,即可变数量标志的数值,也称标志值。
7、变量值按其数值是否连续分为离散变量和连续变量.离散变量是指变量的值只能是整数而不出现小数;如职工人数、机器设备台数.连续变量是指其数值在整数之间可以有无限的数值；如人的身高、体重。
8、统计指标：表明总体特征的概念及其数量表现.标志：是指总体单位的特征或属性的的名称。
9、简答统计指标的设置的要求。
A、指标所反映的总体特征，概念要有理论依据；B、指标要有明确的计算口径范围；C、指标要有科学的计算方法。
10、指标的分类：A、按反映的时间特点不同，有时点指标和时期指标；时点指标是反映总体特征在某一时点上的数量表现，常用的是期末数字；时期指标是反映总体特征在某一时期的数量表现。
B、按其计量单位的特点，有实物指标和价值指标；实物指标是以实物单位计量的指标；价值指标是以货币单位计量，反映情况事物价值量的指标C、按其反映总体特征的性质不同分为数量指标和质量指标；数量指标反映情况总体某一特征的绝对数量，这类指标主要说明总体的规模、工作总量和小平,一般用绝对数表示；质量指标反映总体的强度、密度、效果、工作量等.这类指标用平均数、相对数表示。
统计学常用公式知识讲解
公式一1. 众数【MODE 】（1） 未分组数据或单变量值分组数据众数的计算未分组数据或单变量值分组数据的众数就是出现次数最多的变量值。
（2） 组距分组数据众数的计算对于组距分组数据，先找出出现次数最多的变量值所在组，即为众数所在组，再根据下面的公式计算计算众数的近似值。
下限公式： 1012M =L++i ∆⨯∆∆ 式中：0M 表示众数；L 表示众数的下线；1∆表示众数组次数与上一组次数之差；2∆表示众数组次数与下一组次数之差；i 表示众数组的组距。
上限公式：2012M =U-+i ∆⨯∆∆ 式中：U 表示众数组的上限。
2．中位数【MEDIAN 】（1）未分组数据中中位数的计算根据未分组数据计算中位数时，要先对数据进行排序，然后确定中位数的位置。
设一组数据按从小到大排序后为12N X X X ，，…，，中位数e M ，为则有：e N+M =X1（）2当N 为奇数e N N +1221M =X +X 2⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭当N 为偶数（2）分组数据中位数的计算分组数据中位数的计算时，要先根据公式N / 2 确定中位数的位置，并确定中位数所在的组，然后采用下面的公式计算中位数的近似值：N=1m-1e m-S 2M =L+ii fd f ⨯∑式中：e M 表示中位数；L 表示中位数所在组的下限；m-1S 表示中位数所在组以下各组的累计次数；m f 表示中位数所在组的次数；d 表示中位数所在组的组距。
3．均值的计算【A VERAGE 】（1）未经分组均值的计算未经分组数据均值的计算公式为： 112n ++==nii x x x x x n n=∑…（2）分组数据均值计算分组数据均值的计算公式为： 11221121+++==+ki ik k i k kii x f xf x f x f xf f f f==+∑∑+4．几何平均数【GEOMEAN 】几何平均数是N 个变量值乘积的N 次方根，计算公式为：式中：G 表示几何平均数；∏表示连乘符号。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
①
两个定类
定类
定类
、 、tau-y
x2
②
定类+定序
定类
定序
同上
③
两个定序
定序
定序
G、dy
Z(n≥100)、t(n≤30)
④
两个定距
定距
定距
r、b，即r=rxy,b=bxy
F、r (n≤30)
⑤
定类+定距
定类
定距
E
只能用F检定
⑥
定序+定距
定序
定距
E
只能用F检定
四、归类总结之四：有关计算题
1．第二章、第四或第六章、第七八章
计算公式表（一）⑥①②③④⑤⑥（红色字体为特别关注的公式）
1.众值
Mo=次数最多之值。
2.中位项
Md位置= ，Md=L+ W，Md=L+ W
有三种情况：单个数奇、偶、区间。fm：原始次数；cfm-1：累加次数P48
3.均值
= P49
4.离异比率
V= = P52
5.四分位差
由低到高排列，分四个等分计算Q1、Q3位置，Q1位置= ，Q3位置= ，
2.两个
定序变项
G=
Ns是同序对数，Nd是异序对数对G检定，只有两种检定法：Z、t。
dy=
Ns是同序对数，Nd是异序对数,
Ty是只在依变项Y上同分的对数。因为dy系数是以X预测Y，如果两个个案在X上有高低之分，就要预测或估计他们在Y上的相对等级。因上分母要加上Ty。
rs=
斯皮尔曼rho系数。常出现在填空选择，一般不考计算题。
2．相关系数→第四章；定类、定序、定距→第四章；假设、推论→检定→第七、八章
3．一个变项，1个样本 ：
①(n≥100)：
②(n≤30)： , df=b-1
4．1个变项，2个样本 1 2
n=n1+n2＞100→
五、归类总结之五：有关消减误差比例
1.
有消减误差比例意义，且对称
、G、Q拉系数、rs2、r2、rxy.12、、Ry.122= Ry.x1x22
④已知：可信度，p,
P or e，求n。
计算公式表（三）假设的检定：两个变项之相关Z（5个）、t（4）、F（2个）
Z检定法（大样本）、t检定法（小样本）：定矩变项、随机抽样、总体正态分布。
1、Z检定法
2、t检定法
①（大样本）
n≥100(单均值)
①（小样本）n≤30
以t值来表示样本的均值在标准化抽样中分布中的位置。
2.有无自由度的表达
G、r、F、x2结果解释加上“其显著度水平达到或没有达到……水平”
3.有关r净相关系数
（两个定距变项）
r=rxy.1——引入第三个变项时对X、Y变项产生共同影响。
rx（y-1）——引入第三个变项时，只对Y产生影响，无消减误差意义。
ry（x-1）——引入第三个变项时，只对X产生影响，无消减误差意义。
2．
有消减误差比例意义，且不对称
dy、 、tau-y、E2、CR2（特征值）
3.
无消减误差比例意义，且对称
、V系数、C系数、tau-a、tau-b、tau-c、Vs、r
4.
无消减误差比例意义，且不对称
b、E
六、其他细节
1．显著度的表达
①两端检定： ；②一端检定： ；③ ；④F(df1,df2)；⑤x2(df)
6.定序+定距
因此社会学家常改用相关比率——即将定序变项看做是定类变项。E
参数值的估计：的均值M
①已知：n， （样本的均值），可信度为95%，求M。
（S是样本的标准差）
③已知：n，可信度95%，样本比率p，求总体比率P。
（百分率（或比例）的间距估计）
②已知： ，可信度，M或e，求n。（决定样本的大小）
S2方差：就是标准的平方值，其意义与标准差相同。
计算公式表（二）二个变项
1.两个
定类变项
①
②
My=Y变项的众值次数，Mx=X变项的众值次数，n=全部个案数目。
my=X变项的每个值（类别）之下Y变项的众值次数，mx=Y变项的每个值之下X变项的众值次数，
③tau-y= (E1= ，E2= )
n=全部个案数目，f=某条件次数，Fy=Y变项的某个边缘次数，Fx=X变项的某个边缘次数。
3.两个
定距变项
Y’=bX+a, a= —b = 简单线性回归分析
X是自变项数值，自变项数值，b是回归系数，表示回归张的斜率，a是截距，即回归线与Y轴的交点，Y’是根据回归方程式所预测的Y变项的值。
r=rxy=
积矩相关测量法
r系数与简单线性回归分析都是假定X与Y的关系具有直线的性质。
4.
定类+定项
，ni是每个自变项Xi的个案数目。 =每类的平均值， 每个竖列平方的和。E值无负值，因为是定类变项。
4.参数检定：Z、t、F
非参数检定：x2、U、H、K-S、走动检定P201
②2个定序
G、dy
③2个定距
R、b，即r=rxy,b=bxy
④定类+定距
E
⑤定类+定序
同①： 、 、tau-y大多数社会学者将定序看作定类，即2个定类。
三、归类总结之三：理解如下：（红色字体为特别关注的公式）
变项X
变项Y
可计算
累加次数、累加百分率
定距变项
不仅分类，有大小、高低、程度，还可加减
Mo、V、Md、Q、 、S（S2）
同上
定比变项
最高测量层次
加减乘除
二、归类总结之二
①2个定类
、 、tau-y
1.集中趋势测量法：Mo、Md、
2.离散趋势测量法：V、Q、S
2.有下标，表示不对称
3.具有消减误差比例意义的有：r2、E2、G、dy、 、 、tau-y、rs2(rs斯皮尔曼系数)
社会统计学公式汇总及要点2011.09.09-09.10
(仅供参考,如不能显示公式，请安装Microsoft公式3.0)
一、归类总结之一
测量层次
特质
数学特质
单变项：X
定类变项
只分类
Mo、V
比例、比率、对比值、
次数分布、长作图、圆瓣
双变项：
X、Y
定序变项
不仅分类，有大小、高低、程度等
Mo、V、Md、Q
相关比率与非线性相关
又称为eta平方系数（E2），是以一个定类变项X为自变项，以一个定距变项Y为依变项。是根据自变项的每一个值来预测或估计依变项的均值。
E是假定X是非线性关系。E值从0-1，其E2具有消减误差的意义。
5.定类+定序
=两个定类，大部分的社会学研究都采用Lambda或tau-y系数来测量
Q= Q3- Q1
有单个数（n为偶数时会出现偏离）、区间之分。
（有几种Q，就有几种S计算法）
当为区间表格时(n/4)
①计算向上累加数cf；②Q1位置= ，Q3位置= ；
③Q1=L1+ W1，Q3= L3+ W3；④Q= Q3- Q1P57
5.标准差
①单个数：S= ，②区间：S= P60
对S的解释：如以均值来估计各个个案的数值，所犯的错误 平均是S。用均值作估计变项数值时所犯错误的大小。