2020届高三一轮复习立体几何大题
高三数学一轮复习【立体几何】练习题
高三数学一轮复习【立体几何】练习题1.空间中，用a，b，c表示三条不同的直线，γ表示平面，则下列说法正确的有()A.若a∥b，b∥c，则a∥cB.若a⊥γ，b⊥γ，则a∥bC.若a∥γ，b∥γ，则a∥bD.若a⊥b，b⊥c，则a⊥c答案AB解析根据空间平行直线的传递性可知A正确；由直线与平面垂直的性质定理知B正确；若a∥γ，b∥γ，则a，b可能平行、相交或异面，故C错误；若a⊥b，b⊥c，则a，c可能相交、平行或异面，故D错误.2.对于两条不同直线m，n和两个不同平面α，β，下列选项正确的为()A.若m⊥α，n⊥β，α⊥β，则m⊥nB.若m∥α，n∥β，α⊥β，则m⊥n或m∥nC.若m∥α，α∥β，则m∥β或m⊂βD.若m⊥α，m⊥n，则n∥α或n⊂α答案ACD解析对A，令m，n分别为直线m，n的方向向量，因为m⊥α，n⊥β，所以m⊥α，n⊥β，又α⊥β，所以m⊥n，即m⊥n，所以选项A正确；对B，如图所示，在正方体ABCD-A1B1C1D1中，令平面ABCD为平面α，平面ABB1A1为平面β，直线A1C1为m，直线C1D为n，满足α⊥β，m∥α，n∥β，但m与n既不平行也不垂直，所以选项B错误；对C，若m⊄β，过m作一平面γ分别与平面α和平面β相交，且交线分别为a，b，则m∥a，a∥b，所以m∥b，所以m∥β；若m⊂β，符合题意，所以选项C 正确；对D，若n⊂α，符合题意；若n⊄α，过直线n作一平面β与平面α相交，设交线为b，因为b⊂α，m⊥α，所以m⊥b，又m⊥n，且n，b在同一平面内，所以n∥b，所以n∥α，所以选项D正确.综上，选ACD.3.如图是一个正方体的平面展开图，则在该正方体中()A.AE∥CDB.CH∥BEC.DG⊥BHD.BG⊥DE答案BCD解析由正方体的平面展开图还原正方体如图，连接AH，DE，BG，BH，DG，HC.由图形可知，AE⊥CD，故A错误；因为HE∥BC，HE＝BC，所以四边形BCHE为平行四边形，所以CH∥BE，故B正确；因为DG⊥HC，DG⊥BC，HC∩BC＝C，HC，BC⊂平面BHC，所以DG⊥平面BHC，又BH⊂平面BHC，所以DG⊥BH，故C正确；因为BG∥AH，而DE⊥AH，所以BG⊥DE，故D正确.故选BCD.4.用一个平面截正方体，所得的截面不可能是()A.锐角三角形B.直角梯形C.有一个内角为75°的菱形D.正五边形答案BCD解析对于A，如图1，截面的形状可能是正三角形，故A可能；图1图2对于B，首先考虑平面截正方体得到的截面为梯形，且QR与AA1不平行，如图2所示，不妨假设PQ⊥QR，因为AA1⊥平面A1B1C1D1，PQ⊂平面A1B1C1D1，所以AA1⊥PQ，从而有PQ⊥平面A1ABB1，这是不可能的，故B不可能；对于C，当平面截正方体得到的截面为菱形(非正方形)时，只有如下情形，如图3，其中P，R为所在棱的中点，易知当菱形为PBRD1时，菱形中的锐角取得最小值，即∠PD1R最小.设正方体的棱长为2，则PD1＝RD1＝5，PR＝22，则由余弦定理，得cos∠PD1R＝PD21＋RD21－PR22PD1·RD1＝5＋5－82×5×5＝15<6－24＝cos 75°，所以∠PD1R>75°，故C不可能；图3对于D，假设截面是正五边形，则截面中的截线必然分别在5个面内，由于正方体有6个面，分成两两平行的三对，故必然有一对平行面中有两条截线，而根据面面平行的性质可知这两条截线互相平行，但正五边形的边中是不可能有平行的边的，故截面的形状不可能是正五边形，故D不可能.综上所述，选BCD.5.已知正方体ABCD-A1B1C1D1的棱长为2，M为AA1的中点，平面α过点D1且与CM垂直，则()A.CM⊥BDB.BD∥平面αC.平面C1BD∥平面αD.平面α截正方体所得的截面图形的面积为9 2答案ABD解析如图，连接AC，则BD⊥AC.因为BD⊥AM，AM∩AC＝A，AM，AC⊂平面AMC，所以BD⊥平面AMC，又CM⊂平面AMC，所以BD⊥CM，故A正确；取AD的中点E，连接D1E，DM，由平面几何知识可得D1E⊥DM，又CD⊥D1E，DM∩CD＝D，DM，CD⊂平面CDM，所以D1E⊥平面CDM，又CM⊂平面CDM，所以D1E⊥CM.连接B1D1，过点E作EF∥BD，交AB于F，连接B1F，所以CM⊥EF，又D1E∩EF＝E，D1E，EF⊂平面D1EFB1，所以CM⊥平面D1EFB1，所以平面α截正方体所得的截面图形即梯形D1EFB1.由EF∥BD，BD⊄平面α，EF⊂平面α，得BD∥平面α，故B正确；连接AB1，AD1，易知平面AB1D1∥平面C1BD，而平面AB1D1∩平面α＝B1D1，所以平面C1BD与平面α不平行，故C不正确；截面图形为等腰梯形D1EFB1，EF＝2，B1D1＝22，D1E＝B1F＝5，所以截面图形的面积S＝12×(2＋22)×（5）2－⎝⎛⎭⎪⎫22－222＝92，故D正确.6.在正方体ABCD-A1B1C1D1中，N为底面ABCD的中心，P为线段A1D1上的动点(不包括两个端点)，M为线段AP的中点，则()A.CM与PN是异面直线B.CM>PNC.平面PAN⊥平面BDD1B1D.过P，A，C三点的正方体的截面一定是等腰梯形答案BCD解析对于选项A，如图，连接NC，PC，则A，N，C三点共线.又M为AP的中点，N为AC的中点，所以CM与PN共面，故A错误；对于选项B，因为P为线段A1D1上的动点(不包括两个端点)，所以AC>AP.在△MAC中，CM2＝AC2＋AM2－2AC·AM cos∠MAC＝AC2＋14AP2－AC·AP·cos∠MAC.在△PAN中，PN2＝AP2＋AN2－2AP·AN cos∠PAN＝AP2＋1 4AC 2－AP ·AC cos ∠PAN ，则CM 2－PN 2＝34(AC 2－AP 2)>0，所以CM >PN ，故B 正确；对于选项C ，在正方体ABCD-A 1B 1C 1D 1中，易知AC ⊥平面BDD 1B 1，即AN ⊥平面BDD 1B 1，又AN ⊂平面PAN ，所以平面PAN ⊥平面BDD 1B 1，故C 正确； 对于选项D ，连接A 1C 1，在平面A 1B 1C 1D 1内作PK ∥A 1C 1，交C 1D 1于K ，连接KC .在正方体中，A 1C 1∥AC ，所以PK ∥AC ，PK ，AC 共面，所以四边形PKCA 就是过P ，A ，C 三点的正方体的截面，AA 1＝CC 1，A 1P ＝C 1K ，所以AP ＝CK ，即梯形PKCA 为等腰梯形，故D 正确.故选BCD.7.如图，在正四棱柱ABCD-A 1B 1C 1D 1中，AA 1＝2AB ＝2，点P 为线段AD 1上一动点，则下列说法正确的是( )A.直线PB 1∥平面BC 1DB.三棱锥P-BC 1D 的体积为13C.三棱锥D 1-BC 1D 外接球的表面积为3π2D.直线PB 1与平面BCC 1B 1所成角的正弦值的最大值为53 答案 ABD解析 对于A 选项，连接B 1D 1，AB 1，根据正四棱柱的性质可知AD 1∥BC 1，BD ∥B 1D 1，因为BC 1⊄平面AB 1D 1，AD 1⊂平面AB 1D 1，所以BC 1∥平面AB 1D 1，同理得BD ∥平面AB 1D 1，又BC 1∩BD ＝B ，所以平面AB 1D 1∥平面BC 1D ，又PB 1⊂平面AB 1D 1，所以PB 1∥平面BC 1D ，所以A 选项正确；对于B 选项，易知AD 1∥平面BC 1D ，所以V P-BC 1D ＝V A-BC 1D ＝V C 1-ABD ＝13×12×1×1×2＝13，所以B 选项正确；对于C 选项，三棱锥D 1-BC 1D 的外接球即正四棱柱ABCD-A 1B 1C 1D 1的外接球.设外接球的半径为R ，则4R 2＝12＋12＋22＝6，所以外接球的表面积为4πR 2＝6π，所以C 选项错误；对于D 选项，过P 作PE ∥AB ，交BC 1于点E ，则PE ⊥平面BCC 1B 1，连接B 1E ，则∠PB 1E 即直线PB 1与平面BCC 1B 1所成的角，当B 1E 最小时，∠PB 1E 最大，此时B 1E ⊥BC 1，由等面积法得S △BB 1C 1＝12BC 1·B 1E ＝12BB 1·B 1C 1，解得B 1E ＝25，在Rt △PB 1E 中，PE ＝AB ＝1，所以PB 1＝12＋⎝ ⎛⎭⎪⎫252＝35，所以∠PB 1E 的正弦值的最大值为PE PB 1＝53，所以D 选项正确.故选ABD.8.如图，已知正方体ABCD-A 1B 1C 1D 1的棱长为2，E ，F ，G 分别为BC ，CC 1，BB 1的中点，则( )A.直线D1D与直线AF垂直B.直线A1G与平面AEF平行C.平面AEF截正方体ABCD-A1B1C1D1所得的截面的面积为9 2D.点A1和点D到平面AEF的距离相等答案BCD解析对于选项A，假设AF与D1D垂直，又D1D⊥AE，AE∩AF＝A，AE，AF⊂平面AEF，所以D1D⊥平面AEF.因为EF⊂平面AEF，所以D1D⊥EF，这显然是错误的，所以假设不成立，故A错误；图1对于选项B，取B1C1的中点N，连接A1N，GN，如图1所示，易知A1N∥AE，又AE⊂平面AEF，A1N⊄平面AEF，所以A1N∥平面AEF.因为GN∥EF，EF⊂平面AEF，GN⊄平面AEF，所以GN∥平面AEF.又A1N，GN⊂平面A1GN，A1N∩GN＝N，所以平面A1GN∥平面AEF.因为A1G⊂平面A1GN，所以A1G∥平面AEF，故B正确；对于选项C，连接AD1，FD1，如图2所示，因为AD1∥EF，所以四边形AD1FE 为平面AEF截正方体ABCD-A1B1C1D1所得的截面，又AD1＝22＋22＝22，图2EF ＝12＋12＝2，D 1F ＝AE ＝12＋22＝5，所以四边形AD 1FE 为等腰梯形， 高为（5）2－⎝ ⎛⎭⎪⎫222＝322，则S 梯形AD 1FE ＝12×(2＋22)×322＝92，故C 正确；对于选项D ，连接A 1D ，如图2所示，由选项C 可知A 1D 与平面AEF 相交且交点为A 1D 的中点，所以点A 1和点D 到平面AEF 的距离相等，故D 正确.综上，选BCD.9.已知棱长为a 的正方体ABCD-A 1B 1C 1D 1中，M 是B 1C 1的中点，点P 在正方体的表面上运动，且总满足MP ⊥MC ，则下列结论中正确的是( ) A.点P 的轨迹中包含AA 1的中点B.点P 在侧面AA 1D 1D 内的轨迹的长为5a4 C.MP 长度的最大值为21a4D.直线CC 1与直线MP 所成角的余弦值的最大值为55 答案 BCD解析 如图，取A 1D 1的中点E ，分别取A 1A ，B 1B 上靠近A 1，B 1的四等分点F ，G ，连接EM ，EF ，FG ，MG ，易知EM ∥FG 且EM ＝FG ，所以E ，M ，F ，G 四点共面.连接GC ，因为MG 2＝⎝ ⎛⎭⎪⎫a 22＋⎝ ⎛⎭⎪⎫a 42＝5a 216，MC 2＝⎝ ⎛⎭⎪⎫a 22＋a 2＝5a 24，GC 2＝⎝ ⎛⎭⎪⎫3a 42＋a 2＝25a 216，因此MG 2＋MC 2＝GC 2，所以MG ⊥MC ，易知ME ⊥MC ，又MG ∩ME ＝M ，MG ，ME ⊂平面MEFG ，所以MC ⊥平面MEFG ，即点P 的轨迹为四边形MEFG (不含点M )，易知点P 在侧面AA 1D 1D 内的轨迹为EF ，且EF ＝MG ＝5a4，所以A 选项错误，B 选项正确；根据点P 的轨迹可知，当P 与F 重合时，MP 最长，易知FG ⊥平面BB 1C 1C ，则FG ⊥MG ，连接MF ，所以MF ＝a 2＋5a 216＝21a4，故C 选项正确；由于点P 的轨迹为四边形MEFG (不含点M )，所以直线CC 1与直线MP 所成的最小角就是直线CC 1与平面MEFG 所成的角，又向量CC 1→与平面MEFG 的法向量CM →的夹角等于∠C 1CM ，且sin ∠C 1CM ＝a25a 2＝55，所以直线CC 1与平面MEFG 所成角的余弦值为55，即直线CC 1与直线MP 所成角的余弦值的最大值等于55，故D 选项正确.10.如图，长方体ABCD-A 1B 1C 1D 1中，AB ＝BC ＝1，AA 1＝2，M 为AA 1的中点，过B 1M 作长方体的截面α交棱CC 1于N ，则( )A.截面α可能为六边形B.存在点N，使得BN⊥截面αC.若截面α为平行四边形，则1≤CN≤2D.当N与C重合时，截面图形的面积为36 4答案CD解析设N0为棱CC1的中点，当N从C1移动到C时，其过程中存在以下几种情况，如图1，当点N在线段C1N0上时，截面α为平行四边形；当点N在线段N0C上(不包括点N0，C)时，截面α为五边形；当点N与点C重合时，截面α为梯形.图1图2由以上分析可知，对于A，截面α不可能为六边形，所以A错误；对于B，假设BN⊥截面α，因为B1M⊂α，所以BN⊥B1M，所以必有点N，C重合，而BC与平面B1CQM不垂直，所以B错误；对于C，当截面α为平行四边形时，点N在线段C1N0上，则1≤CN≤2，所以C 正确；对于D，当点N与点C重合时，截面α为梯形，如图2，过M作MM′⊥B1C，垂足为M′.设梯形的高为h，B1M′＝x，则在Rt△B1MM′中，由勾股定理，得h2＝(2)2－x2，①同理h 2＝⎝ ⎛⎭⎪⎫522－⎝ ⎛⎭⎪⎫52－x 2，② 由①②，解得x ＝255，h ＝65，所以截面α的面积等于12×⎝⎛⎭⎪⎫5＋52·h ＝12×352×65＝364，所以D 正确. 综上可知，选CD.。
高三精选立体几何大题30题(含详细解答)
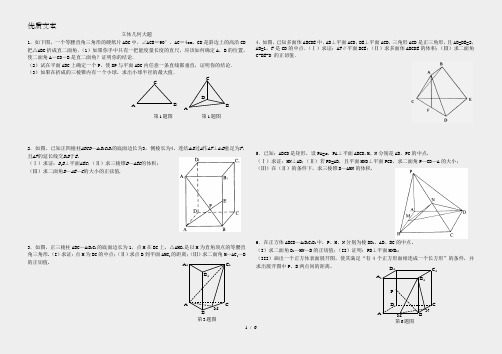
A BC第1题图ABCD第1题图立体几何大题1．如下图，一个等腰直角三角形的硬纸片ABC中，∠ACB＝90°，AC＝4cm，CD是斜边上的高沿CD 把△ABC折成直二面角．（1）如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A－CD－B是直二面角？证明你的结论．（2）试在平面ABC上确定一个P，使DP与平面ABC内任意一条直线都垂直，证明你的结论．（3）如果在折成的三棱锥内有一个小球，求出小球半径的最大值．2．如图，已知正四棱柱ABCD—A1B1C1D1的底面边长为3，侧棱长为4，连结A1B过A作AF⊥A1B垂足为F，且AF的延长线交B1B于E。
（Ⅰ）求证：D1B⊥平面AEC；（Ⅱ）求三棱锥B—AEC的体积；（Ⅲ）求二面角B—AE—C的大小的正弦值.3．如图，正三棱柱ABC—A1B1C1的底面边长为1，点M在BC上，△AMC1是以M为直角顶点的等腰直角三角形.（I）求证：点M为BC的中点；（Ⅱ）求点B到平面AMC1的距离；（Ⅲ）求二面角M—AC1—B 的正切值. 4．如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，三角形ACD是正三角形，且AD=DE=2，AB=1，F是CD的中点．（Ⅰ）求证：AF∥平面BCE；（Ⅱ）求多面体ABCDE的体积；（Ⅲ）求二面角C-BE-D 的正切值．5．已知：ABCD是矩形，设PA=a，PA⊥平面ABCD.M、N分别是AB、PC的中点.（Ⅰ）求证：MN⊥AB；（Ⅱ）若PD=AB，且平面MND⊥平面PCD，求二面角P—CD—A的大小；（Ⅲ）在（Ⅱ）的条件下，求三棱锥D—AMN的体积.6．在正方体ABCD—A1B1C1D1中，P、M、N分别为棱DD1、AB、BC的中点。
（I）求二面角B1—MN—B的正切值；（II）证明：PB⊥平面MNB1；（III）画出一个正方体表面展开图，使其满足“有4个正方形面相连成一个长方形”的条件，并求出展开图中P、B两点间的距离。
2020版高考数学(理)一轮总复习层级快练：第八章 立体几何 作业53 含解析
题组层级快练(五十三)1．(2019·广东五校协作体诊断考试)设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是()A．若α⊥β，m⊂α，n⊂β，则m⊥n B．若m⊥α，m∥n，n∥β，则α⊥βC．若m⊥n，m⊂α，n⊂β，则α⊥βD．若α∥β，m⊂α，n⊂β，则m∥n答案 B解析A项，若α⊥β，m⊂α，n⊂β，则m∥n与m，n与异面直线均有可能，不正确；C项，若m⊥n，m⊂α，n⊂β，则α，β有可能相交但不垂直，不正确；D项，若α∥β，m⊂α，n⊂β，则m，n 有可能是异面直线，不正确，故选B.2．设a，b，c是三条不同的直线，α，β是两个不同的平面，则a⊥b的一个充分不必要条件是() A．a⊥c，b⊥c B．α⊥β，a⊂α，b⊂βC．a⊥α，b∥αD．a⊥α，b⊥α答案 C解析对于C，在平面α内存在c∥b，因为a⊥α，所以a⊥c，故a⊥b；A，B中，直线a，b可能是平行直线，相交直线，也可能是异面直线；D中一定推出a∥b.3．(2019·江西南昌模拟)如图，在四面体ABCD中，已知AB⊥AC，BD⊥AC，那么D在平面ABC内的射影H必在()A．直线AB上B．直线BC上C．直线AC上D．△ABC内部答案 A解析由AB⊥AC，BD⊥AC，又AB∩BD＝B，则AC⊥平面ABD，而AC⊂平面ABC，则平面ABC⊥平面ABD，因此D在平面ABC内的射影H必在平面ABC与平面ABD的交线AB上，故选A.4．(2019·江西临安一中期末)三棱柱ABC－A1B1C1中，侧棱AA1垂直于底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC的中点，则下列叙述正确的是()①CC1与B1E是异面直线；②AE与B1C1是异面直线，且AE⊥B1C1；③AC⊥平面ABB1A1；④A1C1∥平面AB1E.A．②B．①③C．①④D．②④答案 A解析对于①，CC1，B1E都在平面BB1C1C内，故错误；对于②，AE，B1C1为在两个平行平面中且不平行的两条直线，底面三角形ABC是正三角形，E是BC中点，所以AE⊥BC，又B1C1∥BC，故AE⊥B1C1，故正确；对于③，上底面ABC是一个正三角形，不可能存在AC⊥平面ABB1A1，故错误；对于④，A1C1所在的平面与平面AB1E相交，且A1C1与交线有公共点，故错误．故选A. 5．(2019·福建泉州质检)如图，在下列四个正方体ABCD－A1B1C1D1中，E，F，G均为所在棱的中点，过E，F，G作正方体的截面，则在各个正方体中，直线BD1与平面EFG不垂直的是()答案 D解析如图，在正方体中，E，F，G，M，N，Q均为所在棱的中点，且六点共面，直线BD1与平面EFMNQG垂直，并且A项，B，C中的平面与这个平面重合，满足题意．对于D项中图形，由于E，F为AB，A1B1的中点，所以EF∥BB1，故∠B1BD1为异面直线EF与BD1所成的角，且tan∠B1BD1＝2，即∠B1BD1不为直角，故BD1与平面EFG不垂直，故选D.6．(2019·保定模拟)如图，在正四面体P－ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论不成立的是()A．BC∥平面PDFB．DF⊥平面PAEC．平面PDF⊥平面PAED．平面PDE⊥平面ABC答案 D解析因BC∥DF，DF⊂平面PDF，BC⊄平面PDF，所以BC∥平面PDF，A成立；易证BC⊥平面PAE，BC∥DF，所以结论B，C均成立；点P在底面ABC内的射影为△ABC的中心，不在中位线DE上，故结论D不成立．7.已知直线PA垂直于以AB为直径的圆所在的平面，C为圆上异于A，B的任一点，则下列关系中不正确的是()A．PA⊥BC B．BC⊥平面PACC．AC⊥PB D．PC⊥BC答案 C解析AB为直径，C为圆上异于A，B的一点，所以AC⊥BC.因为PA⊥平面ABC，所以PA⊥BC.因为PA∩AC＝A，所以BC⊥平面PAC，从而PC⊥BC.故选C.8.如图，在三棱锥D－ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列命题中正确的是()A．平面ABC⊥平面ABDB．平面ABD⊥平面BCDC．平面ABC⊥平面BDE，且平面ACD⊥平面BDED．平面ABC⊥平面ACD，且平面ACD⊥平面BDE答案 C解析因为AB＝CB，且E是AC的中点，所以BE⊥AC，同理，DE⊥AC，由于DE∩BE＝E，于是AC⊥平面BDE.因为AC⊂平面ABC，所以平面ABC⊥平面BDE.又AC⊂平面ACD，所以平面ACD⊥平面BDE.故选C.9．(2019·沧州七校联考)如图所示，已知六棱锥P－ABCDEF的底面是正六边形，PA⊥平面ABC.则下列结论不正确的是()A．CD∥平面PAF B．DF⊥平面PAFC．CF∥平面PAB D．CF⊥平面PAD答案 D解析A中，∵CD∥AF，AF⊂面PAF，CD⊄面PAF，∴CD∥平面PAF成立；B中，∵六边形ABCDEF 为正六边形，∴DF⊥AF.又∵PA⊥面ABCDEF，∴DF⊥平面PAF成立；C中，CF∥AB，AB⊂平面PAB，CF⊄平面PAB，∴CF∥平面PAB；而D中CF与AD不垂直，故选D.10．(2019·重庆秀山高级中学期中)如图，点E为矩形ABCD边CD上异于点C，D的动点，将△ADE 沿AE翻折成△SAE，使得平面SAE⊥平面ABCE，则下列说法中正确的有()①存在点E使得直线SA⊥平面SBC；②平面SBC内存在直线与SA平行；③平面ABCE内存在直线与平面SAE平行；④存在点E使得SE⊥BA.A．1个B．2个C．3个D．4个答案 A解析①若直线SA⊥平面SBC，则SA⊥SC，又SA⊥SE，SE∩SC＝S，∴SA⊥平面SEC，又平面SEC ∩平面SBC ＝SC ，∴点S ，E ，B ，C 共面，与已知矛盾，故①错误；②∵平面SBC ∩直线SA ＝S ，故平面SBC 内的直线与SA 相交或异面，故②错误；③在平面ABCD 内作CF ∥AE ，交AB 于点F ，由线面平行的判定定理，可得CF ∥平面SAE ，故③正确；④若SE ⊥BA ，过点S 作SF ⊥AE 于点F ，∵平面SAE ⊥平面ABCE ，平面SAE ∩平面ABCE ＝AE ，∴SF ⊥平面ABCE ，∴SF ⊥AB ，又SF ∩SE ＝S ，∴AB ⊥平面SEC ，∴AB ⊥AE ，与∠BAE 是锐角矛盾，故④错误．11．(2019·泉州模拟)点P 在正方体ABCD －A 1B 1C 1D 1的面对角线BC 1上运动，给出下列命题：①三棱锥A －D 1PC 的体积不变； ②A 1P ∥平面ACD 1； ③DB ⊥BC 1；④平面PDB 1⊥平面ACD 1. 其中正确的命题序号是________． 答案 ①②④解析 对于①，V A －D 1PC ＝VP －AD 1C 点P 到面AD 1C 的距离，即为线BC 1与面AD 1C 的距离，为定值故①正确，对于②，因为面A 1C 1B ∥面AD 1C ，所以线A 1P ∥面AD 1C ，故②正确，对于③，DB 与BC 1成60°角，故③错．对于④，由于B 1D ⊥面ACD 1，所以面B 1DP ⊥面ACD 1，故④正确． 12．(2019·山西太原一模)已知在直角梯形ABCD 中，AB ⊥AD ，CD ⊥AD ，AB ＝2AD ＝2CD ＝2，将直角梯形ABCD 沿AC 折叠成三棱锥D －ABC ，当三棱锥D －ABC 的体积取最大值时，其外接球的体积为________． 答案 43π解析 当平面DAC ⊥平面ABC 时，三棱锥D －ABC 的体积取最大值．此时易知BC ⊥平面DAC ，∴BC ⊥AD ，又AD ⊥DC ，∴AD ⊥平面BCD ，∴AD ⊥BD ，取AB 的中点O ，易得OA ＝OB ＝OC ＝OD ＝1，故O 为所求外接球的球心，故半径r ＝1，体积V ＝43πr 3＝43π.13．(2019·辽宁大连双基测试)如图所示，∠ACB ＝90°，DA ⊥平面ABC ，AE ⊥DB 交DB 于E ，AF ⊥DC 交DC 于F ，且AD ＝AB ＝2，则三棱锥D －AEF 体积的最大值为________． 答案26解析 因为DA ⊥平面ABC ，所以DA ⊥BC ，又BC ⊥AC ，DA ∩AC ＝A ，所以BC ⊥平面ADC ，所以BC ⊥AF ，又AF ⊥CD ，BC ∩CD ＝C ，所以AF ⊥平面DCB ，所以AF ⊥EF ，AF ⊥DB ，又DB ⊥AE ，AE ∩AF ＝A ，所以DB ⊥平面AEF ，所以DE 为三棱锥D －AEF 的高．因为AE 为等腰直角三角形ABD 斜边上的高，所以AE ＝2，设AF ＝a ，FE ＝b ，则△AEF 的面积S ＝12ab ≤12·a 2＋b 22＝12×22＝12，所以三棱锥D －AEF 的体积V ≤13×12×2＝26(当且仅当a ＝b ＝1时等号成立)．14．如图所示，在四棱锥P －ABCD 中，PA ⊥底面ABCD ，AB ⊥AD ，AC ⊥CD ，∠ABC ＝60°，PA ＝AB ＝BC ，E 是PC 的中点，求证： (1)CD ⊥AE ； (2)PD ⊥平面ABE. 答案 (1)略 (2)略证明 (1)∵PA ⊥底面ABCD ， ∴CD ⊥PA.又CD ⊥AC ，PA ∩AC ＝A ， 故CD ⊥平面PAC ，AE ⊂平面PAC. 故CD ⊥AE.(2)∵PA ＝AB ＝BC ，∠ABC ＝60°，故PA ＝AC. ∵E 是PC 的中点，故AE ⊥PC. 由(1)知CD ⊥AE ，由于PC ∩CD ＝C ， 从而AE ⊥平面PCD ，故AE ⊥PD. 易知BA ⊥PD ，故PD ⊥平面ABE.15．(2019·安徽马鞍山一模)如图①，在直角梯形ABCD 中，AB ⊥BC ，BC ∥AD ，AD ＝2AB ＝4，BC ＝3，E 为AD 的中点，EF ⊥BC ，垂足为F.沿EF 将四边形ABFE 折起，连接AD ，AC ，BC ，得到如图②所示的六面体ABCDEF.若折起后AB 的中点M 到点D 的距离为3.(1)求证：平面ABFE ⊥平面CDEF ； (2)求六面体ABCDEF 的体积． 答案 (1)略 (2)83解析 (1)如图，取EF 的中点N ，连接MN ，DN ，MD.根据题意可知，四边形ABFE 是边长为2的正方形，∴MN ⊥EF.由题意，得DN ＝DE 2＋EN 2＝5，MD ＝3， ∴MN 2＋DN 2＝22＋(5)2＝9＝MD 2，∴MN ⊥DN ，∵EF ∩DN ＝N ，∴MN ⊥平面CDEF. 又MN ⊂平面ABFE ，∴平面ABFE ⊥平面CDEF. (2)连接CE ，则V 六面体ABCDEF ＝V 四棱锥C －ABFE ＋V 三棱锥A －CDE . 由(1)的结论及CF ⊥EF ，AE ⊥EF ，得 CF ⊥平面ABFE ，AE ⊥平面CDEF ， ∴V 四棱锥C －ABFE ＝13·S 正方形ABFE ·CF ＝43，V 三棱锥A －CDE ＝13·S △CDE ·AE ＝43，∴V 六面体ABCDEF ＝43＋43＝83.16.(2019·潍坊质检)直四棱柱ABCD －A 1B 1C 1D 1中，底面ABCD 是直角梯形，∠BAD ＝∠ADC ＝90°，AB ＝2AD ＝2CD ＝2. (1)求证：AC ⊥平面BB 1C 1C ；(2)在A 1B 1上是否存在一点P ，使得DP 与平面BCB 1和平面ACB 1都平行？证明你的结论． 答案 (1)略(2)P 为A 1B 1的中点时，DP 与平面BCB 1和平面ACB 1都平行．解析 (1)∵直四棱柱ABCD －A 1B 1C 1D 1中，BB 1⊥平面ABCD ，∴BB 1⊥AC. 又∵∠BAD ＝∠ADC ＝90°，AB ＝2AD ＝2CD ＝2， ∴AC ＝2，∠CAB ＝45°.∴BC ＝ 2.∵BC 2＋AC 2＝AB 2，∴BC ⊥AC. 又BB 1∩BC ＝B ，BB 1⊂平面BB 1C 1C ， BC ⊂平面BB 1C 1C ，∴AC ⊥平面BB 1C 1C. (2)存在点P ，P 为A 1B 1的中点．由P 为A 1B 1的中点，有PB 1∥AB ，且PB 1＝12AB.又∵DC ∥AB ，DC ＝12AB ，∴DC ∥PB 1，且DC ＝PB 1.∴四边形DCB 1P 为平行四边形，从而CB 1∥DP. 又CB 1⊂平面ACB 1，DP ⊄平面ACB 1， ∴DP ∥平面ACB 1.同理，DP ∥平面BCB 1.。
(天津专用)2020届高考数学一轮复习单元质检7立体几何(A)(含解析)新人教A版
单元质检七立体几何(A)(时间:45分钟满分:100分)一、选择题(本大题共6小题,每小题7分,共42分)1.已知圆柱的侧面展开图是边长为2和4的矩形,则圆柱的体积是()A. B. C. D.或2.下列命题中,错误的是()A.三角形的两条边平行于一个平面,则第三边也平行于这个平面B.平面α∥平面β,a⊂α,过β内的一点B有唯一的一条直线b,使b∥aC.α∥β,γ∥δ,α,β,γ,δ所成的交线为a,b,c,d,则a∥b∥c∥dD.一条直线与两个平面所成的角相等,则这两个平面平行3.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为()A. B.2C. D.34.已知l1,l2,l3是空间三条不同的直线,则下列命题正确的是()A.若l1⊥l2,l2⊥l3,则l1∥l3B.若l1⊥l2,l2∥l3,则l1⊥l3C.若l1∥l2∥l3,则l1,l2,l3共面D.若l1,l2,l3共点,则l1,l2,l3共面5.一个正方体的表面展开图如图所示,点A,B,C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD所成的角的余弦值为()A. B.C. D.6.我国古代数学名著《九章算术》中有这样一些数学用语,“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,而“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的堑堵,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1的体积最大时,则堑堵ABC-A1B1C1的表面积为()A.4+4B.6+4C.8+4D.10+4二、填空题(本大题共2小题,每小题7分,共14分)7.已知矩形ABCD的边AB=a,BC=3,PA⊥平面ABCD,若BC边上有且只有一点M,使PM⊥DM,则a的值为.8.已知在三棱锥A-BCD中,AB=AC=BC=2,BD=CD=,点E是BC的中点,点A在平面BCD上的射影恰好为DE的中点,则该三棱锥外接球的表面积为.三、解答题(本大题共3小题,共44分)9. (14分)如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1.设AB1的中点为D,B1C∩BC1=E.求证:(1)DE∥平面AA1C1C;(2)BC1⊥AB1.10. (15分)如图,三棱柱ABC-A1B1C1的所有棱长都是2,AA1⊥平面ABC,D,E分别是AC,CC1的中点.(1)求证:AE⊥平面A1BD;(2)求二面角D-BE-B1的余弦值.11.(15分) 如图,三角形PDC所在的平面与矩形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3,点E是CD边的中点,点F,G分别在线段AB,BC上,且AF=2FB,CG=2GB.(1)证明:PE⊥FG;(2)求二面角P-AD-C的正切值;(3)求直线PA与直线FG所成角的余弦值.单元质检七立体几何(A)1.D解析圆柱的侧面展开图是边长为2与4的矩形,当母线为4时,圆柱的底面半径是,此时圆柱体积是π××4=;当母线为2时,圆柱的底面半径是,此时圆柱的体积是π××2=,综上可知,所求圆柱的体积是或.故选D.2.D解析A正确,三角形可以确定一个平面,若三角形两边平行于一个平面,则它所在的平面与这个平面平行,故第三边平行于这个平面;B正确,平面α与平面β平行,则平面α中的直线a必平行于平面β,平面β内的一点与这条线可以确定一个平面,这个平面与平面β交于一条直线,过该点在平面β内只有这条直线与a平行;C正确,利用同一平面内不相交的两条直线一定平行判断即可确定C是正确的;D错误,一条直线与两个平面所成的角相等,这两个平面可能是相交平面,故应选D.3.C解析由计算可得O为B1C与BC1的交点.设BC的中点为M,连接OM,AM,则可知OM⊥平面ABC,连接AO,则AO的长为球半径,可知OM=6,AM=,在Rt△AOM中,由勾股定理得半径OA=.4.B解析从正方体同一个顶点出发的三条棱两两垂直,可知选项A错误;因为l1⊥l2,所以l1与l2所成的角是9 °.又因为l2∥l3,所以l1与l3所成的角是9 °,所以l1⊥l3,故选项B正确;三棱柱中的三条侧棱平行,但不共面,故选项C错误;三棱锥的三条侧棱共点,但不共面,故选项D错误.故选B.5.C解析如图所示,可知∠EGF为AB和CD所成的角,F为正方体棱的中点.设正方体棱长为1,则EF=GF=,EG=.故cos∠EGF=.6.B解析设AC=x,则0<x<2,由题意,得四棱锥B-A1ACC1的体积为V=·2·x·-·x·--,当且仅当x=-,即x= 时,取等号.堑堵ABC-A1B1C1的表面积为S=2S△ABC+2矩形矩形+2×2×+2×2=6+4.7.1.5解析如图,连接AM.因为PA⊥平面ABCD,所以PA⊥DM.若BC边上有且只有一点M,使PM⊥MD,则DM⊥平面PAM,即DM⊥AM,故以AD为直径的圆和BC相切即可.因为AD=BC=3,所以圆的半径为1.5,要使线段BC和半径为1.5的圆相切,则AB=1.5,即a=1.5.8.π解析由题意知,△BCD为等腰直角三角形,点E是△BCD外接圆的圆心,点A在平面BCD上的射影恰好为DE的中点F,则BF=,∴AF=-,设三棱锥A-BCD外接球的球心O到平面BCD的距离为h,则1+h2=-,∴h=,r=(r为球O的半径),∴该三棱锥外接球的表面积为4π×π.9.证明(1)由题意知,E为B1C的中点.因为D为AB1的中点,所以DE∥AC.又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C,所以DE∥平面AA1C1C.(2)因为棱柱ABC-A1B1C1是直三棱柱,所以CC1⊥平面ABC.因为AC⊂平面ABC,所以AC⊥CC1.又因为AC⊥BC,CC1⊂平面BCC1B1,BC⊂平面BCC1B1,BC∩CC1=C,所以AC⊥平面BCC1B1.又因为BC1⊂平面BCC1B1,所以BC1⊥AC.因为BC=CC1,所以矩形BCC1B1是正方形,所以BC1⊥B1C.因为AC,B1C⊂平面B1AC,AC∩B1C=C,所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC,所以BC1⊥AB1.10.(1)证明∵AB=BC=CA,D是AC的中点,∴BD⊥AC.∵AA1⊥平面ABC,∴平面AA1C1C⊥平面ABC,∴BD⊥平面AA1C1C,∴BD⊥AE.又在正方形AA1C1C中,D,E分别是AC,CC1的中点,易证得△A1AD≌△ACE,∴∠A1DA=∠AEC,∵∠AEC+∠CAE=9 °,∴∠A1DA+∠CAE=9 °,即A1D⊥AE.又A1D∩BD=D,∴AE⊥平面A1BD.(2)解取A1C1的中点F,以DF,DA,DB所在直线为x,y,z轴建立空间直角坐标系,则D(0,0,0),E(1,-1,0),B(0,0,),B1(2,0,),=(0,0,),=(1,-1,0),=(2,0,0),=(1,1,).设平面DBE的一个法向量为m=(x,y,z),则· ,·,- ,令x=1,则m=(1,1,0).设平面BB1E的一个法向量为n=(a,b,c),则· ,·,,令c=,则n=(0,-3,).设二面角D-BE-B1的平面角为θ,观察可知θ为钝角,cos<m,n>=·=-,∴cosθ=-.故二面角D-BE-B1的余弦值为-.11.解法一(1)证明:∵PD=PC,且点E为CD边的中点,∴PE⊥DC.又平面PDC⊥平面ABCD,且平面PDC∩平面ABCD=CD,PE⊂平面PDC, ∴PE⊥平面ABCD.∵FG⊂平面ABCD,∴PE⊥FG.(2)∵四边形ABCD是矩形,∴AD⊥DC.又平面PDC⊥平面ABCD,且平面PDC∩平面ABCD=CD,AD⊂平面ABCD, ∴AD⊥平面PDC.∵PD⊂平面PDC,∴AD⊥PD.∴∠PDC即为二面角P-AD-C的平面角.在Rt△PDE中,PD=4,DE=AB=3,PE=-,∴tan∠PDC=,即二面角P-AD-C的正切值为.(3)如图所示,连接AC,∵AF=2FB,CG=2GB,即=2,∴AC∥FG,∴∠PAC即为直线PA与直线FG所成的角或其补角.在△PAC中,PA==5,AC==3.由余弦定理可得cos∠PAC=-·9,∴直线PA与直线FG所成角的余弦值为9.解法二(1)见解法一.(2)取AB的中点M,连接EM,可知EM,EC,EP两两垂直,故以E为原点,EM,EC,EP所在直线为x轴、y 轴、z轴建立如图所示的空间直角坐标系.可得A(3,-3,0),D(0,-3,0),P(0,0,),C(0,3,0),即=(-3,0,0),=(0,-3,-),设平面PAD的法向量为n=(x,y,z),则· ,· ,可得- ,-- ,令y=,可得一个法向量n=(0,,-3).因为平面ADC的一个法向量为=(0,0,),所以二面角P-AD-C的余弦值为|cos<n,>|=.所以二面角P-AD-C的正切值为.(3)由(2)中建立的空间直角坐标系可得=(3,-3,-),F(3,1,0),G(2,3,0),则=(-1,2,0), 故cos<>=-9.所以直线PA与直线FG所成角的余弦值为9.。
2020年高中数学03 立体几何大题解题模板(原卷版)
专题03 立体几何大题解题模板一、证明平行或垂直的主要方法：1、证明线线平行的方法：(1)利用直线平行的传递性：31//l l ，32//l l ⇒21//l l ；(2)利用垂直于同一平面的两条直线平行：α⊥1l ，α⊥2l ⇒21//l l ；(3)中位线法：选中点，连接形成中位线；(4)平行四边形法：构造平行四边形；(5)利用线面平行推线线平行：2l =βα ，β⊂1l ，α//1l ⇒21//l l ；(6)建系：),,(1111z y x l =，),,(2222z y x l =，21l l λ=⇒21//l l 。
2、证明线面平行的方法：(1)利用线面平行的判定定理(主要方法)：α⊄1l ，α⊂2l ，21//l l ⇒α//1l ；(2)利用面面平行的性质定理：βα//，β⊂1l ⇒α//1l ；(3)利用面面平行的性质：βα//，α⊄1l ，β//1l ⇒α//1l 。
(4)建系：),,(1111z y x l =，平面α的法向量),,(222z y x n =，01=⋅n l ⇒α//1l 。
3、证明面面平行的方法：(1)利用面面平行的判定定理(主要方法：证明两个平面内的两组相交直线相互平行)：31//l l ，42//l l ，A l l =21 ，B l l =43 ，α⊂21l l 、，β⊂43l l 、⇒βα//；(2)利用垂直于同一条直线的两平面平行(客观题可用)：α⊥1l ，β⊥1l ⇒βα//；(3)利用平面平行的传递性：γα//，γβ//⇒βα//。
(4)建系：平面α的法向量),,(1111z y x n =，平面α的法向量),,(2222z y x n =，21n n λ=⇒βα//。
4、证明线线垂直的方法：(1)利用平行直线的性质：31l l ⊥，32//l l ⇒21l l ⊥；(2)利用直面垂直的推理：α⊥1l ，α⊂2l ⇒21l l ⊥；(3)中线法：等腰三角形中选中点，三线合一；(4)利用勾股定理的逆定理：若222c b a +=，则ABC ∆是直角三角形；(5)建系：),,(1111z y x l =，),,(2222z y x l =，021=⋅l l ⇒21l l ⊥。
2020届高考数学(理)大一轮复习：专题突破练(5) 立体几何的综合问题
专题突破练(5)立体几何的综合问题2.如图，三棱柱ABC－A1B1C1中，AA1⊥平面ABC，A1A＝AB＝2，BC＝1，AC＝5，若规定正视方向垂直平面ACC1A1，则此三棱柱的侧视图的面积为()45C.5 D．6答案C折成四面体A′－BCD，使平面A′BD⊥平面BCD，则下列结论正确的是()A．A′C⊥BDB.∠BA′C＝90°5.[2018·河南豫东、豫北十校测试]鲁班锁是中国传统的智力玩具，起源于古代汉族建筑中首创的榫卯结构，这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合，十分巧妙，原为木质结构，外观看是严丝合缝的十字立方体，其上下、左右、前后完全对称．从外表上看，六根等长的正四棱柱体分成三组，经90度榫卯起来，若正四棱柱体的高为4，底面正方形的边长为1，则该鲁班锁的表面积为 ( )A.48 B ．60 C ．72 D ．846．如图所示，已知在多面体ABC －DEFG 中，AB ，AC ，AD 两两垂直，平面ABC ∥平面DEFG ，平面BEF ∥平面ADGC ，AB ＝AD ＝DG ＝2，AC ＝EF ＝1，则该多面体的体积为( )A.2 B ．4 C ．6 D ．8答案 B解析 如图所示，将多面体补成棱长为2的正方体，那么显然所求的多面体的体积即为该正方体体积的一半，于是所求几何体的体积为V ＝12×23＝4.选B.7.[2017·湖北黄冈中学二模]一个几何体的三视图如图所示，其中正视图是边长为2的等边三角答案 B解析 由三视图可知，该几何体是半圆锥，其展开图如图所示，则依题意，点A ，M 的最短距离，即为线段AM .∵P A ＝PB ＝2，半圆锥的底面半圆的弧长为π，∴展开图中的∠BPM ＝πPB＝π2， π5π5π答案 B解析 如图所示，为组合体的轴截面，记BO 1的长度为x ，由相似三角形的比例关系，得PO 13R＝x R，则PO 1＝3x ，圆柱的高为3R －3x ，所以圆柱的表面积为S ＝2πx 2＋2πx ·(3R －3x )＝－4πx 2＋6πRx ，则当x ＝34R 时，S 取最大值，S max ＝94πR 2.选B.9．在正方体ABCD －A 1B 1C 1D 1中，P 为正方形A 1B 1C 1D 1四边上的动点，O 为底面正方形ABCD的中心，M ，N 分别为AB ，BC 边的中点，点Q 为平面ABCD 内一点，线段D 1Q 与OP 互相平分，则满足MQ →＝λMN →的实数λ的值有( )A.0个 B ．1个 C ．2个 D ．3个10. [2017·东北三省三校二模]已知三棱柱ABC －A 1B 1C 1，侧棱BB 1⊥平面ABC ，AB ＝2，AC ＝3，AA 1＝14，AC ⊥BC ，将其放入一个水平放置的水槽中，使AA 1在水槽底面内，平面ABB 1A 1与水槽底面垂直，且水面恰好经过棱BB 1，现水槽底面出现一个小洞，水位下降，则在水位下降过程中，几何体露出水面部分的面积S 关于水位下降的高度h 的函数图象大致为( )答案 A1x 时，正四棱锥的体积最大，则x 为 ( )A ．0.5B ．0.8C ．0.2D ．1答案 C二、填空题13．如图，在正方体ABCD－A1B1C1D1中，P为棱DC的中点，则D1P与BC1所在直线所成角的余弦值等于________.10514.如图，已知球O的面上有四点A，B，C，D，DA⊥平面ABC，AB⊥BC，DA＝AB＝BC＝2，则球O的体积等于________.答案6π解析如图，以DA，AB，BC为棱长构造正方体，设正方体的外接球球O的半径为R，则正方体的体对角线长即为球O的直径，所以64πR315．如图，用一个边长为2的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个巢，将半径为1的球体放入其中，则球心与巢底面的距离为__________.3＋12解析 由题意知，折起后原正方形顶点间最远的距离为1，如图中的DC ；折起后原正方形顶点到底面的距离为12，如图中的BC .由图知球心与巢底面的距离OF ＝1－122＋12＝3＋12. 16.[2017·安徽黄山第二次质检]如图所示，正方体ABCD －A ′B ′C ′D ′的棱长为1，E ，F 分别是棱AA ′，CC ′的中点，过直线EF 的平面分别与棱BB ′，DD ′交于点M ，N ，设BM＝x ，x ∈[0,1]．给出以下五个命题：①当且仅当x ＝0时，四边形MENF 的周长最大；17．[2017·河南洛阳月考]如图，在直三棱柱ABC－A1B1C1中，∠ACB＝90°，AA1＝BC＝2AC＝4.(1)若点P为AA的中点，求证：平面B CP⊥平面B C P；值；若不存在，说明理由.解(1)证明：如图，以C为原点，CA，CB，CC1所在直线分别为x轴，y轴，z轴建立空间直角坐标系，则C(0,0,0)，A(2,0,0)，B1(0,4,4)，C1(0,0,4)，P(2，0,2)，B(0,4,0)，→→118.719.[2018·广东韶关调研]已知四棱锥P－ABCD中，P A⊥平面ABCD，底面ABCD为菱形，∠ABC(2)由(1)得AE，AD，AP两两垂直，连接AM，以AE，AD，AP所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系.520.[2017·湖北黄冈期末]如图，在各棱长均为2的三棱柱ABC－A1B1C1中，侧面A1ACC1⊥底面ABC，∠A1AC＝60°.(1)求侧棱AA与平面AB C所成角的正弦值的大小；1故以O为坐标原点，建立如图所示的空间直角坐标系Oxyz，。
立体几何 大题-2023届高三数学一轮复习
立体几何复习1.（多选）如图，四棱锥P ABCD -中，平面PAD ⊥底面ABCD ，PAD △是等边三角形，底面ABCD 是菱形，且60BAD ∠=︒，M 为棱PD 的中点，N 为菱形ABCD 的中心，下列结论正确的有（ ） A ．直线PB 与平面AMC 平行 B ．直线PB 与直线AD 垂直C ．线段AM 与线段CM 长度相等D ．PB 与AM 所成角的余弦值为24 2.（多选）如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝4，BC ＝BB 1＝2，E 、F 分别为棱AB 、A 1D 1的中点，则下列说法中正确的有（ ）A ．DB 1⊥CEB ．三棱锥D —CEF 的体积为83C ．若P 是棱C 1D 1上一点，且D 1P ＝1，则E 、C 、P 、F 四点共面D ．平面CEF 截该长方体所得的截面为五边形3.（多选）已知菱形ABCD 的边长为2, ∠ABC=3π,将ΔDAC 沿着对角线AC 折起至ΔD'AC,连接BD'.设二面角D'-AC-B 的大小为θ,则下列说法正确的是（ ）A.若四面体D'ABC 为正四面体，则θ=3π B.四面体D'ABC 的体积最大值为1 C.四面体D'ABC 的表面积最大值为2(3+2) D.当θ=23π时，四面体D'ABC 的外接球的半径为2134.如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ． （1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．5.如图，点C 是以AB 为直径的圆上的动点（异于,A B ），已知2AB =，2AC =，AE =BEDC 为矩形，平面ABC ⊥平面BEDC .设平面EAD 与平面ABC 的交线为l .（1）证明：l BC ；（2）求平面ADE 与平面ABC 所成的锐二面角的余弦值.6.7. 在如图所示的几何体中，四边形ABCD 为正方形，PA ⊥平面ABCD ，//PA BE ，2BE =，4AB PA ==.（1）求证：//CE 平面PAD ；（2）在棱AB 上是否存在一点F ，使得二面角E PC F --的大小为60︒？如果存在，确定点F 的位置；如果不存在，说明理由.8.如图,四棱锥P -ABCD 中,底面ABCD 是直角梯形,AB ∥DC ,∠BAD =90°,PD =DC =BC =2PA =2AB =2,PD ⊥DC .(1)求证：PA ⊥平面ABCD ；(2)设BM =BD λ(0<λ<1),当二面角A-PM-B 的余弦值为77时,求λ的值.9.如图，四棱锥P ABCD -中，四边形ABCD 是菱形，PA PC =，BD PA ⊥，E 是BC 上一点，且3EC BE =，设AC BD O =.（1）证明：PO ⊥平面ABCD ；（2）若60BAD ∠=︒，PA PE ⊥，求二面角A PE C --的余弦值.10.如图，在四棱锥P ABCD -中，底面ABCD 是菱形，PA ⊥平面ABCD .（1）求证：平面PAC ⊥平面PBD ；（2）若2AP AB ==，60BAD ∠=︒，求二面角A PB D --的余弦值.11.如图，在三棱柱ABC-A 1B 1C 1中，ΔABC 是边长为2的等边三角形，平面ABC ⊥平面AA 1B 1B,A 1A=A 1B,∠A 1AB=60°,O 为AB 的中点，M 为A 1C 1的中点． （1)求证：OM//平面BB 1C 1C;（2)求二面角C 1-BA 1-C 的正弦值．12.如图，在五面体ABCDEF 中，四边形ABEF 为正方形，平面ABEF ⊥平面CDFE ，CD ∥EF ，DF ⊥EF ， EF ＝2CD ＝2．（1）若DF ＝2，求二面角A －CE －F 的正弦值；（2）若平面ACF ⊥平面BCE ，求DF 的长．13.如图，在斜三棱柱111ABC A B C -中，底面是边长为3的等边三角形，12A A =，点1A 在下底面上的射影是ABC ∆的中心O .（1）求证：平面1A AO ⊥平面11BCC B ；（2）求二面角1C AB C --的余弦值.14.如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，AD CD ⊥，//AD BC ，2PA AD CD ===，3BC =．E为PD的中点，点F在PC上，且13 PFPC=．（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）求二面角F AE P--的余弦值；（Ⅲ）设点G在PB上，且23PGPB=．判断直线AG是否在平面AEF内，说明理由．15.如图，在三棱锥A－BCD中，△ABD与△BCD都为等边三角形，平面ABD⊥平面BCD，M，O分别为AB，BD 的中点，AO∩DM＝G，N在棱CD上且满足2CN＝ND，连接MC，GN．（1）证明：GN∥平面ABC；（2）求直线AC和平面GND所成角的正弦值．16.在多面体ABCDE中，平面ACDE⊥平面ABC，四边形ACDE为直角梯形，CD∥AE，AC⊥AE，AB⊥BC，CD＝1，AE＝AC＝2，F为DE的中点，且点E满足EB4EG=．（1）证明：GF∥平面ABC；（2）当多面体ABCDE的体积最大时，求二面角A—BE—D的余弦值．17一副标准的三角板(图1)中,∠ABC为直角,∠A=60°,∠DEF为直角,DE=EF,BC=DF.把BC与DF重合,拼成一个三棱锥(图2)｡设M是AC的中点,N是BC的中点｡(1)求证:平面ABC⊥平面EMN;(2)若AC=4,二面角E-BC-A为直二面角,求直线EM与平面ABE所成的正弦18.如图四边形ABCD为梯形，AD∥BC，BM⊥AD于M，CN⊥AD于N，∠A=45°，AD=4BC=4，AB=2，现沿CN将△CDN折起，使△ADN为正三角形，且平面AND⊥平面ABCN，过BM的平面与线段DN、DC分别交于E、F．(1)求证：EF⊥DA；(2)在棱DN上(不含端点)是否存在点E，使得直线DB与平面BMEF所成角的正弦值为34，若存在，请确定E点的位置；若不存在，说明理由．19.如图，在四棱锥P—ABCD中，底面ABCD为正方形，PD⊥底面ABCD，M为线段PC的中点，PD＝AD，N为线段BC上的动点．（1）证明：平面MND⊥平面PBC；（2）当点N在线段BC的何位置时，平面MND与平面PAB所成锐二面角的大小为30°？指出点N的位置，并说明理由．。
2020版高考数学人教版理科一轮复习第七章 立体几何 (2)
1．(方向 1)(2019·洛阳市第一次统考)某几何体的三视图如图所示，
则该几何体的体积是( B )
15π A. 2
17π C. 2
B．8π D．9π
解析：依题意，题中的几何体是由两个完全相同的圆柱各自 用一个不平行于其轴的平面去截后所得的部分拼接而成的组合 体(各自截后所得的部分也完全相同)，其中一个截后所得的部分 的底面半径为 1，最短母线长为 3、最长母线长为 5，将这两个截 后所得的部分拼接，恰好可以形成一个底面半径为 1，母线长为 5＋3＝8 的圆柱，因此题中的几何体的体积为 π×12×8＝8π，故 选 B.
又平面 B1D1D∩平面 B1EDF＝B1D，
所以 O1H⊥平面 B1EDF，
所以 O1H 等于四棱锥 C1-B1EDF 的高．
因为△B1O1H∽△B1DD1，
Байду номын сангаас
所以
O1H＝B1OB11·DDD1＝
6 6 a.
方向 3 利用体积法求点面距离 【例 4】 如图，在四棱锥 P-ABCD 中，底面 ABCD 是矩形，PD ⊥底面 ABCD，M，N 分别为 AB，PC 的中点，PD＝AD＝2，AB＝4.
如图，连接 AB′，AD′，B′D′，因为三棱锥 A′-AB′D′ 是正三棱锥，所以 A′A，A′B′，A′D′与平面 AB′D′所成 的角都相等．分别取 C′D′，B′C′，BB′，AB，AD，DD′ 的中点 E，F，G，H，I，J，连接 EF，FG，GH，IH，IJ，JE， 易得 E，F，G，H，I，J 六点共面，平面 EFGHIJ 与平面 AB′D′ 平行，且截正方体所得截面的面积最大．又 EF＝FG＝GH＝IH ＝IJ＝JE＝ 22，所以该正六边形的面积为 6× 43×( 22)2＝343， 所以 α 截此正方体所得截面面积的最大值为34 3，故选 A.
2020年(江苏)高考数学(理)大一轮复习检测：专题十七 立体几何
专题十七立体几何一、填空题考向一立体几何中的计算问题1.(2017·苏州、无锡、常州、镇江二模)已知正四棱锥的底面边长是2,侧棱长是,则该正四棱锥的体积为.2.(2018·南通、泰州一模)如图,铜质六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的,已知正六棱柱的底面边长、高都为4 cm,圆柱的底面积为9 cm2.若将该螺帽熔化后铸成一个高为6 cm 的正三棱柱零件,则该正三棱柱的底面边长为cm.(不计损耗)(第2题)(第3题)3.(2018·苏州期初)如图,正四棱锥P-ABCD的底面一边AB的长为2 cm,侧面积为8 cm2,则它的体积为cm3.4.(2017·江苏大联考)已知正四面体P-ABC的棱长为2,若M,N分别是PA,BC的中点,则三棱锥P-BMN 的体积为.(第5题)5.(2018·苏州一模)鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根等长的正四棱柱体分成三组,经90°榫卯起来.若正四棱柱的高为5,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为.(容器壁的厚度忽略不计,结果保留π)6.(2018·无锡一模)在直三棱柱ABC-A1B1C1中,已知AB⊥BC,AB=3,BC=4,AA1=5,若三棱柱的所有顶点都在同一球面上,则该球的表面积为.考向二立体几何中的命题真假的判定问题7.(2017·丹阳高级中学期初)设α,β为两个不重合的平面,m,n为两条不同的直线,给出下列四个命题:①若m⊥n,m⊥α,则n∥α;②若n⊂α,m⊂β,α与β相交且不垂直,则n与m不垂直;③若α⊥β,α∩β=m,n⊂α,n⊥m,则n⊥β;④若m∥n,n⊥α,α∥β,则m⊥β.其中正确的命题是.(填序号)8.(2016·南京三模)已知α,β是两个不重合的平面,l,m是两条不同的直线,l⊥α,m⊂β.给出下列四个命题:①α∥β⇒l⊥m;②α⊥β⇒l∥m;③m∥α⇒l⊥β;④l⊥β⇒m∥α.其中正确的命题是.(填序号)9.(2016·镇江期末)已知b,c表示两条不同的直线,α,β表示两个不重合的平面,给出下列四个命题:①若b⊂α,c∥α,则b∥c;②若b⊂α,b∥c,则c∥α;③若c∥α,α⊥β,则c⊥β;④若c∥α,c⊥β,则α⊥β.其中正确的命题是.(填序号)10.(2017·南京、盐城、连云港二模)已知α,β是两个互不重合的平面,m,n是两条不同的直线,下列命题中正确的是.(填序号)①若α∥β,m⊂α,则m∥β;②若m∥α,n⊂α,则m∥n;③若α⊥β,α∩β=n,m⊥n,则m⊥β;④若n⊥α,n⊥β,m⊥α,则m⊥β.11.(2017·广州模拟)已知α,β是两个不重合的平面,m,n是两条不同的直线,则下列说法中正确的是.(填序号)①若m∥α,α∩β=n,则m∥n;②若m⊥α,n⊥m,则n∥α;③若m⊥α,n⊥β,α⊥β,则m⊥n;④若α⊥β,α∩β=n,m⊥n,则m⊥β.(第12题)12.(2017·咸阳模拟)如图,在棱长均相等的正四棱锥P-ABCD中,O为底面正方形的中心,M,N分别为侧棱PA,PB的中点,有下列结论:①PC∥平面OMN;②平面OMN⊥平面PAB;③OM⊥PA;④平面PCD∥平面OMN.其中正确的结论是.(填序号)考向三立体几何中的综合问题(第13题)13.(2016·无锡期末)如图,在圆锥VO中,O为底面圆的圆心,点A,B在圆O上,且OA⊥OB.若OA=VO=1,则点O到平面VAB的距离为.14.(2016·南通、扬州、淮安、宿迁、泰州二调)在体积为的四面体ABCD中,若AB⊥平面BCD,AB=1,BC=2,BD=3,则CD长度的所有值为.二、解答题15.(2017·常州一模)如图,在三棱柱ABC-A1B1C1中,所有棱长都相等,且∠ABB1=60°,D为AC的中点.(1)求证:B1C∥平面A1BD;(2)求证:AB⊥B1C.(第15题)16.(2017·苏州、无锡、常州、镇江二模)如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1∩A1C=O,E是棱AB上一点,且OE∥平面BCC1B1.(1)求证:E是AB中点;(2)若AC1⊥A1B,求证:AC1⊥BC.(第16题)17.(2017·扬州一模)如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F分别是棱PC和PD的中点.(1)求证:EF∥平面PAB;(2)若AP=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.(第17题)18.(2018·苏州一模)如图,在正方体ABCD-A1B1C1D1中,已知E,F,G,H分别是A1D1,B1C1,D1D,C1C的中点.(1)求证:EF∥平面ABHG;(2)求证:平面ABHG⊥平面CFED.(第18题)19.(2018·苏州期初)如图,在三棱锥P-ABC中,已知平面PBC⊥平面ABC.(1)若AB⊥BC,CP⊥PB,求证:CP⊥PA;(2)若过点A作直线l⊥平面ABC,求证:l∥平面PBC.(第19题)20.(2018·常州一模)如图,四棱锥P-ABCD的底面ABCD是平行四边形,PC⊥平面ABCD,PB=PD,点Q 是棱PC上异于P,C的一点.(1)求证:BD⊥AC;(2)过点Q和AD的平面截四棱锥得到截面ADQF(点F在棱PB上),求证:QF∥BC.(第20题)专题十七立体几何(第1题)1.【解析】如图,在正四棱锥P-ABCD中,PA=,AB=2,故AO=AB=,所以PO==1,所以V=Sh=×22×1=.2. 2【解析】由题知,铜质六角螺帽毛坯的体积V=6××42×sin60°-9×4=60(cm3).设正三棱柱的底面边长为a cm,则×a2×sin60°×6=60,解得a=2,所以正三棱柱的底面边长为2 cm.3. 4【解析】设正四棱锥P-ABCD的高为H,斜高为h,由题意得×2×4h=8,解得h=2,所以H==1,所以该四棱锥的体积V=S·H=×(2)2×1=4(cm3).4.【解析】如图,连接AN,作MD⊥PN,垂足为D.因为正四面体P-ABC的棱长为2,M,N分别是PA,BC 的中点,所以AN⊥BC,PN⊥BC,由此可得MN⊥AP,且AN=PN=.因为AN∩PN=N,AN⊂平面PAN,PN⊂平面PAN,所以BC⊥平面PAN.因为MD⊂平面PNA,所以MD⊥BC.因为MD⊥PN,BC∩PN=N,BC⊂平面PBN,PN⊂平面PBN,所以MD⊥平面PBN.又由题知MN==,因为PN·MD=PM·MN,所以MD===,所以三棱锥P-BMN 的体积==×S△PBN×MD=××1××=.(第4题)5. 30π【解析】由题图知,该鲁班锁外接球的直径与长、宽、高分别为2,1,5的长方体的外接球直径相同.设该球形容器的半径为R,则2R≥,即R≥,所以S=4πR2≥4π×=30π.6. 50π【解析】在直三棱柱ABC-A1B1C1中,因为AB⊥BC,所以可以将该直三棱柱补形成长、宽、高分别为3,4,5的长方体,该长方体的体对角线长即为该直三棱柱的直径,且2R==5,所以S=4πR2=50π.7.③④【解析】因为m⊥α,m⊥n,所以n∥α或n⊂α,故①错误;对于②,当m平行α与β的交线,n垂直于α与β的交线时,m⊥n,故②错误;由面面垂直的性质定理知③正确;因为n⊥α,α∥β,所以n⊥β,又m∥n,所以m⊥β,故④正确.8.①④【解析】对于①,因为l⊥α且α∥β,所以l⊥β,又m⊂β,所以l⊥m,故①正确;对于②,由l⊥α,α⊥β,可知l∥β或l⊂β,则l与m的位置关系不确定,故②不正确;对于③,由m∥α且m⊂β,可知α与β平行或相交,若α与β相交,则l与β不垂直,故③不正确;对于④,由l⊥α且l⊥β,可知α∥β,又m⊂β,所以m∥α,故④正确.9.④【解析】对于①,b与c的位置关系不确定;对于②,可能c⊂α;对于③,c与β的位置关系不确定;只有④是正确的.10.①④【解析】①是面面平行的性质,故①正确;②m,n可能异面,故②错误;③当m⊄α时,m⊥β不成立,故③错误;④由m⊥α,n⊥α,得m∥n,又n⊥β,所以m⊥β,故④正确.(第11题)11.③【解析】对于①,如图,m∥α,α∩β=n,此时m,n异面,故①错误;对于②,若m⊥α,m⊥n,则n∥α或n⊂α,故②错误;对于③,若n⊥β,α⊥β,则n∥α或n⊂α,又m⊥α,所以m⊥n,故③正确;对于④,若α⊥β,α∩β=n,m⊥n,则m也可能与β相交、平行或在β内,故④错误.12.①③④【解析】如图,其中E,F分别为AD,BC的中点,G为OE的中点,平面OMN即平面MNFE.因为PC∥OM,所以PC∥平面OMN,同理PD∥ON,又OM∩ON=O,所以平面PCD∥平面OMN,故①④正确;由于四棱锥的棱长均相等,所以PA2+PC2=AB2+BC2=AC2,所以PC⊥PA,又PC∥OM,所以OM⊥PA,故③正确;因为OM=PC=PD=ME,所以MG⊥OE,又MN∥OE,所以GM⊥MN,假设平面OMN⊥平面PAB,则GM⊥平面PAB,则MG⊥PA,设四棱锥的棱长为4,则MA=2,AG=,MG=,三边长度不满足勾股定理,所以MG不垂直PA,与假设矛盾,故②不正确.(第12题)13.【解析】方法一:设点O到平面VAB的距离为h.由题意知=,所以××1×1×1=××h,解得h=.方法二:取AB的中点M,连接OM,VM.在Rt△VOM中,点O到VM的距离即为点O到平面VAB的距离.因为VO=1,OM=,VM=,所以点O到VM的距离d==,故点O到平面VAB的距离为.14.,【解析】因为四面体ABCD的体积V=××2×3×sin∠CBD×1=,所以sin∠CBD=,所以∠CBD=60°或120°.当∠CBD=60°时,CD2=22+32-2×2×3×cos 60°=7,所以CD=;当∠CBD=120°时,CD2=22+32-2×2×3×cos 120°=19,所以CD=.综上,CD长度的所有值为,.15.(1)连接AB1交A1B于点E,连接DE.因为D,E分别为AC,AB1的中点,所以DE∥B1C.因为DE⊂平面A1BD,B1C⊄平面A1BD,所以B1C∥平面A1BD.(2)取AB的中点O,连接OC,OB1.因为BA=BB1,且∠ABB1=60°,所以△ABB1为正三角形.而O为AB的中点,所以OB1⊥AB.在正三角形ABC中,O为AB的中点,所以OC⊥AB.因为OB1∩OC=O,且OB1⊂平面OB1C,OC⊂平面OB1C,所以AB⊥平面OB1C.又因为B1C⊂平面OB1C,所以AB⊥B1C.16.(1)如图,连接BC1,因为OE∥平面BCC1B1,OE⊂平面ABC1,平面BCC1B1∩平面ABC1=BC1,所以OE∥BC1.因为侧面AA1C1C是菱形,AC1∩A1C=O,所以O是AC1的中点.所以==1,即E是AB的中点.(2)因为侧面AA1C1C是菱形,所以AC1⊥A1C.因为AC1⊥A1B,A1C∩A1B=A1,A1C⊂平面A1BC,A1B⊂平面A1BC,所以AC1⊥平面A1BC.因为BC⊂平面A1BC,所以AC1⊥BC.(第16题)17.(1)因为点E,F分别是棱PC和PD的中点,所以EF∥CD.又在矩形ABCD中,AB∥CD,所以EF∥AB.又AB⊂平面PAB,EF⊄平面PAB,所以EF∥平面PAB.(2)在矩形ABCD中,AD⊥CD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊂平面ABCD,所以CD⊥平面PAD.又AF⊂平面PAD,所以CD⊥AF.因为PA=AD且F是PD的中点,所以AF⊥PD.因为PD⊂平面PCD,CD⊂平面PCD,PD∩CD=D,所以AF⊥平面PCD.18.(1)因为E,F分别是A1D1,B1C1的中点,所以EF∥A1B1.在正方体ABCD-A1B1C1D1中,A1B1∥AB,所以EF∥AB.又EF⊄平面ABHG,AB⊂平面ABHG,所以EF∥平面ABHG.(2)在正方体ABCD-A1B1C1D1中,CD⊥平面BB1C1C.又BH⊂平面BB1C1C,所以BH⊥CD.①如图,设BH∩CF=P,△BCH≌△CC1F,所以∠HBC=∠FCC1.因为∠HBC+∠PHC=90°,所以∠FCC1+∠PHC=90°,所以∠HPC=90°,即BH⊥CF.②由①②,又DC∩CF=C,CF,CD⊂平面CFED,所以BH⊥平面CFED.又因为BH⊂平面ABHG,所以平面ABHG⊥平面CFED.(第18题)(第19题)19.(1)因为平面PBC⊥平面ABC,平面PBC∩平面ABC=BC,AB⊂平面ABC,AB⊥BC,所以AB⊥平面PBC.因为CP⊂平面PBC,所以CP⊥AB.又因为CP⊥PB,且PB∩AB=B,AB,PB⊂平面PAB,所以CP⊥平面PAB,因为PA⊂平面PAB,所以CP⊥PA.(2)如图,在平面PBC内过点P作PD⊥BC,垂足为D.因为平面PBC⊥平面ABC,平面PBC∩平面ABC=BC,PD⊂平面PBC,所以PD⊥平面ABC.又l⊥平面ABC,所以l∥PD.又l⊄平面PBC,PD⊂平面PBC,所以l∥平面PBC.20.(1)因为PC⊥平面ABCD,BD⊂平面ABCD,所以BD⊥PC.如图,记AC,BD的交点为O,连接OP.平行四边形对角线互相平分,则O为BD的中点,又在△PBD中,PB=PD,所以BD⊥OP.又PC∩OP=P,PC,OP⊂平面PAC,所以BD⊥平面PAC.又AC⊂平面PAC,所以BD⊥AC.(2)因为四边形ABCD是平行四边形,所以AD∥BC.又AD⊄平面PBC,BC⊂平面PBC,所以AD∥平面PBC.又AD⊂平面ADQF,平面ADQF∩平面PBC=QF,所以AD∥QF.又AD∥BC,所以QF∥BC.(第20题)。
高三数学一轮复习：1218高考中的立体几何问题
所成角的正弦值的最大值为
6 3
3．二面角的棱上有 A，B 两点，直线 AC，BD 分别在这个二面角的两个半平面内，且都垂 直于 AB.已知 AB＝4，AC＝6，BD＝8，CD＝2 17.则该二面角的大小为________．
5．如图所示，在菱形 ABCD 中，∠ABC＝60°，AC 与 BD 相交于点 O，AE⊥平面 ABCD，CF∥AE，AB＝AE＝2.
例 2 (2020·新高考全国Ⅰ)如图，四棱锥 P－ABCD 的底面为正方形，PD⊥底面 ABCD．设平 面 PAD 与平面 PBC 的交线为 l． (1)证明：l⊥平面 PDC； (2)已知 PD＝AD＝1，Q 为 l 上的点， 求 PB 与平面 QCD 所成角的正弦值的最大值．
例 3 (2020·全国Ⅰ)如图，D 为圆锥的顶点，O 是圆锥底面的圆心，AE 为底面直径，AE＝ AD．△ABC 是底面的内接正三角形，P 为 DO 上一点，PO＝ 66DO． (1)证明：PA⊥平面 PBC； (2)求二面角 B－PC－E 的余弦值．
例 4 (2021·全国高考真题)在正三棱柱 ABC A1B1C1 中， AB AA1 1 ，点 P 满足
BP BC BB1 ，其中 0,1， 0,1 ，则（ ）
A．当 1时， △AB1P 的周长为定值
B．当 1时，三棱锥 P A1BC 的体积为定值
C．当
1 2
时，有且仅有一个点
高考中的立体几何问题
作业讲评 2．(多选)如图，在正方体 ABCD-A1B1C1D1 中，点 P 在线段 B1C 上运动，则( )
A．直线 BD1⊥平面 A1C1D B．三棱锥 P-A1C1D 的体积为定值
C．异面直线 AP 与 A1D 所成角的取值范围是π4 ，π2
2019-2020年高考数学大题专题练习——立体几何(一)
2019-2020年高考数学大题专题练习——立体几何（一）1.如图所示，四棱锥P ABCD 中，底面ABCD 为正方形，⊥PD 平面ABCD ，2PD AB ，点,,E F G 分别为,,PC PD BC 的中点.(1)求证：EF PA ⊥；(2)求二面角D FG E 的余弦值.2.如图所示，该几何体是由一个直角三棱柱ADE BCF 和一个正四棱锥P ABCD 组合而成，AF AD ⊥，2AEAD .(1)证明：平面⊥PAD 平面ABFE ；(2)求正四棱锥P ABCD 的高h ，使得二面角C AF P 的余弦值是223.3.四棱锥P ABCD-中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是面积为ADC∠为锐角，M为PB的中点．（Ⅰ）求证：PD∥面ACM．（Ⅱ）求证：PA⊥CD．（Ⅲ）求三棱锥P ABCD-的体积．4.如图，四棱锥S ABCD-满足SA⊥面ABCD，90DAB ABC∠=∠=︒．SA AB BC a===，2AD a=．（Ⅰ）求证：面SAB⊥面SAD．（Ⅱ）求证：CD⊥面SAC．SB A DMC BAPD5.在四棱锥P ABCD -中，底面ABCD 为矩形，测棱PD ⊥底面ABCD ，PD DC =，点E 是BC 的中点，作EF PB ⊥交PB 于F ． （Ⅰ）求证：平面PCD ⊥平面PBC ． （Ⅱ）求证：PB ⊥平面EFD ．6.在直棱柱111ABC A B C -中，已知AB AC ⊥，设1AB 中点为D ，1A C 中点为E ． （Ⅰ）求证：DE ∥平面11BCC B ． （Ⅱ）求证：平面11ABB A ⊥平面11ACC A ．E DABC C 1B 1A 1DAB CEF P7.在四棱锥P ABCD -中，PA ⊥平面ABCD ，//AB CD ，AB AD ⊥，PA PB =，::2:2:1AB AD CD =.（1）证明BD PC ⊥；（2）求二面角A PC D --的余弦值；（3）设点Q 为线段PD 上一点，且直线AQ 平面PAC 所成角的正弦值为23，求PQ PD的值.8.在正方体1111ABCD A B C D -中，O 是AC 的中点，E 是线段D 1O 上一点，且D 1E ＝λEO . （1）若λ=1，求异面直线DE 与CD 1所成角的余弦值； （2）若λ=2，求证：平面CDE ⊥平面CD 1O .9.如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，135BCD =︒∠，侧面PAB ⊥底面ABCD ，90BAP =︒∠，2AB AC PA ===，E ，F 分别为BC ，AD 的中点，点M 在线段PD 上．（Ⅰ）求证：EF ⊥平面PAC ．（Ⅱ）若M 为PD 的中点，求证：ME ∥平面PAB ． （Ⅲ）如果直线ME 与平面PBC 所成的角和直线ME 与平面ABCD 所在的角相等，求PMPD的值．10.如图，在三棱柱111ABC A B C -，1AA ⊥底面ABC ，AB AC ⊥，1AC AB AA ==，E ，F 分别是棱BC ，1A A 的中点，G 为棱1CC 上的一点，且1C F ∥平面AEG ． （1）求1CGCC 的值． （2）求证：1EG AC ⊥． （3）求二面角1A AG E --的余弦值．A 1B 1C 1G F AB CEM F E CBAPD11.如图，在四棱锥P ABCD -中，PB ⊥底面ABCD ，底面ABCD 为梯形，AD BC ∥，AD AB ⊥，且3PB AB AD ===，1BC =．（Ⅰ）若点F 为PD 上一点且13PF PD =，证明：CF ∥平面PAB ．（Ⅱ）求二面角B PD A --的大小． （Ⅲ）在线段PD 上是否存在一点M ，使得CM PA ⊥？若存在，求出PM 的长；若不存在，说明理由．12.如图，在四棱锥E ABCD -中，平面EAD ⊥平面ABCD ，CD AB ∥，BC CD ⊥，EA ED ⊥，4AB =，2BC CD EA ED ====．Ⅰ证明：BD AE ⊥．Ⅱ求平面ADE 和平面CDE 所成角（锐角）的余弦值．DABCEPF DBCA13.己知四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是菱形，且2PA AB ==．60ABC ∠=︒，BC 、PD 的中点分别为E ，F ．（Ⅰ）求证BC PE ⊥．（Ⅱ）求二面角F AC D --的余弦值．（Ⅲ）在线段AB 上是否存在一点G ，使得AF 平行于平面PCG ？若存在，指出G 在AB 上的位置并给予证明，若不存在，请说明理由．14.如图，ABCD 是边长为3的正方形，DE ⊥平面ABCD ，AF DE ∥，3DE AF =，BE 与平面ABCD 所成角为60︒．（Ⅰ）求证：AC ⊥平面BDE ． （Ⅱ）求二面角F BE D --的余弦值．（Ⅲ）设点M 线段BD 上一个动点，试确定点M 的位置，使得AM ∥平面BEF ，并证明你的结论．DDABCEF15.如图，PA ⊥面ABC ，AB BC ⊥，22AB PA BC ===，M 为PB 的中点． （Ⅰ）求证：AM ⊥平面PBC ． （Ⅱ）求二面角A PC B --的余弦值． （Ⅲ）在线段PC 上是否存在点D ，使得BD AC ⊥，若存在，求出PDPC的值，若不存在，说明理由．16.如图所示，在四棱锥P -ABCD 中，AB ⊥平面,//,PAD AB CD E 是PB 的中点,2,5,3,2AHPD PA AB AD HD===== . （1）证明：PH ⊥平面ABCD ；（2）若F 是CD 上的点，且23FC FD ==，求二面角B EF C --的正弦值.MDABCP17.如图，DC ⊥平面ABC ，//EB DC ，22AC BC EB DC ====，120ACB ∠=︒，Q为AB 的中点．（Ⅰ）证明：CQ ⊥平面ABE ； （Ⅱ）求多面体ACED 的体积； （Ⅲ）求二面角A -DE -B 的正切值．18.如图1 ,在△ABC 中，AB =BC =2, ∠B =90°,D 为BC 边上一点，以边AC 为对角线做平行四边形ADCE ，沿AC 将△ACE 折起，使得平面ACE ⊥平面ABC ,如图2.(1)在图 2中，设M 为AC 的中点，求证:BM 丄AE ； (2)在图2中，当DE 最小时，求二面角A -DE -C 的平面角.19.如图所示，在已知三棱柱ABF -DCE 中，90ADE ∠=︒，60ABC ∠=︒，2AB AD AF ==，平面ABCD ⊥平面ADEF ，点M在线段BE 上，点G 是线段AD 的中点．（1）试确定点M 的位置，使得AF ∥平面GMC ； （2）求直线BG 与平面GCE 所成角的正弦值．20.已知在四棱锥P -ABCD 中，底面ABCD 是菱形，AC =AB ，P A ⊥平面ABCD ，E ，F 分别是AB ，PD 的中点.（Ⅰ）求证：AF ∥平面PCE ；（Ⅱ）若22AB AP ==，求平面P AD 与平面PCE 所成锐二面角的余弦值.21.如图，五面体P ABCD 中，CD ⊥平面P AD ，ABCD 为直角梯形，,2BCD PD BC CD π∠===1,2AD AP PD =⊥. （1）若E 为AP 的中点，求证：BE ∥平面PCD ； （2）求二面角P -AB-C 的余弦值.22.如图（1）所示，已知四边形SBCD 是由Rt △SAB 和直角梯形ABCD 拼接而成的，其中90SAB SDC ∠=∠=︒.且点A 为线段SD 的中点，21AD DC ==，2AB =.现将△SAB沿AB 进行翻折，使得二面角S -AB -C 的大小为90°，得到图形如图（2）所示，连接SC ，点E ，F 分别在线段SB ，SC 上. （Ⅰ）证明：BD AF ⊥；（Ⅱ）若三棱锥B -AEC 的体积为四棱锥S -ABCD 体积的25，求点E 到平面ABCD 的距离.23.四棱锥S-ABCD中，AD∥BC，,BC CD⊥060SDA SDC∠=∠=，AD DC=1122BC SD==，E为SD的中点.（1）求证：平面AEC⊥平面ABCD；（2）求BC与平面CDE所成角的余弦值.24.已知三棱锥P-ABC，底面ABC是以B为直角顶点的等腰直角三角形，P A⊥AC，BA=BC=P A=2，二面角P-AC-B的大小为120°.（1）求直线PC与平面ABC所成角的大小；（2）求二面角P-BC-A的正切值.25.如图，在四棱锥P -ABCD 中，平面P AD ⊥平面ABCD ，090=∠=∠BCD ABC ，AB CB DC PD PA 21====，E 是PB 的中点， （Ⅰ）求证：EC ∥平面APD ；（Ⅱ）求BP 与平面ABCD 所成的角的正切值； （Ⅲ）求二面角P -AB -D 的余弦值.26.四棱锥P ﹣ABCD 的底面ABCD 为边长为2的正方形，P A =2，PB =PD =22，E ，F ，G ，H 分别为棱P A ，PB ，AD ，CD 的中点．（1）求CD 与平面CFG 所成角的正弦值；（2）探究棱PD 上是否存在点M ，使得平面CFG ⊥平面MEH ，若存在，求出PDPM的值；若不存在，请说明理由．试卷答案1以点D 为坐标原点，建立如图所示的空间直角坐标系D xyz ，则 0,0,0D ，0,2,0A ，2,0,0C，0,0,2P ，1,0,1E ，0,0,1F ，2,1,0G .(1)∵0,2,2PA ，1,0,0EF，则0PA EF ，∴PA EF .(2)易知0,0,1DF，2,11FG， 设平面DFG 的法向量111,,m x y z ，则m DF m FG ，即1111020z x yz ，令11x ，则1,2,0m 是平面DFG 的一个法向量，同理可得0,1,1n 是平面EFG 的一个法向量，∴210cos ,552m n m nm n， 由图可知二面角D FG E 为钝角， ∴二面角D FG E 的余弦值为105.2.(1)证明：直三棱柱ADE BCF 中，AB 平面ADE ，所以：AB AD ，又AD AF ，所以：AD平面ABFE ，AD 平面PAD ，所以：平面PAD 平面ABFE .(2)由(1)AD平面ABFE ，以A 为原点，,,AB AE AD 方向为,,x y z 轴建立空间直角坐标系A xyz ，设正四棱锥P ABCD 的高h ，2AE AD ，则0,0,0A ，2,2,0F ，2,0,2C ，1,,1P h . 2,2,0AF，2,0,2AC，1,,1APh .设平面ACF 的一个法向量111,,m x y z ，则：1111220220m AF x y n ACx z ，取11x ，则111y z ，所以：1,1,1m .设平面AFP 的一个法向量222,,n x y z ，则222222200n AF x y n APx hy z ，取21x ，则21y ，21z h ，所以：1,1,1n h ，二面角C AF P 的余弦值是223，所以：211122cos ,3321m n h m n m nh ， 解得：1h .3.E ODPABC M（Ⅰ）证明：连结AC 交BD 于O ，则O 是BD 中点， ∵在PBD △中，O 是BD 的中点，M 是PB 的中点， ∴PD MO ∥，又PD ⊄平面ACM ，MO ⊂平面ACM ，∴PD ∥平面ACM ．（Ⅱ）证明：作PE CD ⊥，则E 为CD 中点，连结AE ， ∵底面ABCD 是菱形，边长为2，面积为，∴11sin 222sin 222S AD DC ADC ADC =⨯⨯⨯∠⨯=⨯⨯∠⨯=∴sin ADC ∠，60ADC ∠=︒， ∴ACD △是等边三角形， ∴CD AE ⊥， 又∵CD PE ⊥， ∴CD ⊥平面PAE ， ∴CD PA ⊥．（Ⅲ）11233P ABCD ABCD V S PE -=⨯=⨯．4.DABCSE（1）证明：∵SA ⊥平面ABCD ，AB ⊂平面ABCD ， ∴AB SA ⊥， 又∵90BAD ∠=︒， ∴AB AD ⊥， ∵SA AD A =， ∴AB ⊥平面SAD ， 又AB ⊂平面SAB ， ∴平面SAB ⊥平面SAD ． （Ⅱ）证明：取AD 中点为E ，∵90DAB ABC ∠=∠=︒，2AD a =，BC a =，E 是AD 中点， ∴ABCE ∠是矩形，CE AB a ==，DE a =，∴CD =，在ACD △中，AC，CD =，2AD a =， ∴222AC CD AD +=， 即CD AC ⊥，又∵SA ⊥平面ABCD ，CD ⊂平面ABCD ， ∴CD SA ⊥， ∴CD ⊥平面PAC ． 5.P F ECB AD（Ⅰ）证明：∵PD ⊥底面ABCD ，BC ⊂平面ABCD ， ∴PD BC ⊥，又∵底面ABCD 为矩形， ∴BC CD ⊥， ∴BC ⊥平面PCD ， ∵BC ⊂平面PBC ， ∴平面PCD ⊥平面PBC ．（Ⅱ）证明：∵PD DC =，E 是PC 中点， ∴DE PC ⊥，又平面PCD ⊥平面PBC ，平面PCD 平面PBC PC =， ∴DE ⊥平面PBC ， ∴DE PB ⊥， 又∵EF PB ⊥，EF DE E =，∴PB ⊥平面EFD ．6.E A 1B 1C 1CBAD（Ⅰ）证明：连结1A B ， ∵D 是1AB 的中点， ∴D 是1A B 的中点，∵在1A BC △中，D 是1A B 的中点，E 是1A C 的中点， ∴DE BC ∥，又DE ⊄平面11BCC B ，BC ⊂平面11BCC B ， ∴DE ∥平面11BCC B ．（Ⅱ）证明：∵111ABC A B C -是直棱柱， ∴1AA ⊥平面ABC ， ∴1AA AB ⊥， 又AB AC ⊥， ∴AB ⊥平面11ACC A ， ∵AB ⊂平面11ABB A ， ∴平面11ABB A ⊥平面11ACC A ．7.以A 为坐标原点，建立空间直角坐标系(2,0,0)B，D ，(0,0,2)P，C（1）(BD =-，(1,2)PC =-， ∵0BD PC •=∴BD PC ⊥（2）(1,AC =，(0,0,2)AP =，平面PAC 的法向量为(2,1,0)m =-(0,2)DP =，(1,0,0)AP =，平面DPC 的法向量为(0,2,1)n =--.2cos ,3m n m n m n•==•，二面角B PC D --的余弦值为3.（3）∵AQ AP PQ AP tPD =+=+，[]0,1t ∈ ∴(0,0,2)(0,2,2)(0,2,22)AQ t t t =+-=- 设θ为直线AQ 与平面PAC 所成的角2sin cos ,3AQ m AQ m AQ mθ•===• 2222223684332(22)tt t t t t =⇒=-++-，解得2t =（舍）或23. 所以，23PQ PD =即为所求.8.解:(1)不妨设正方体的棱长为1，以DA ,DC ,1DD 为单位正交基底建立如图所示的空间直角坐标系D xyz -． 则A (1，0，0)，()11022O ，，，()010C ，，，D 1(0，0，1)， E ()111442，，， 于是，.由cos＝＝.所以异面直线AE 与CD 1所成角的余弦值为36. （2）设平面CD 1O 的向量为m =(x 1，y 1，z 1)，由m ·CO ＝0，m ·1CD ＝0 得 取x 1＝1，得y 1＝z 1＝1，即m =(1，1，1) .由D 1E ＝λEO ，则E ，.又设平面CDE 的法向量为n ＝(x 2，y 2，z 2)，由n ·CD ＝0，n ·DE ＝0. 得取x 2=2，得z 2＝－λ，即n ＝(－2，0，λ) .因为平面CDE ⊥平面CD 1F ，所以m ·n ＝0，得λ＝2．9.（Ⅰ）证明：在平行四边形ABCD 中， ∵AB AC =，135BCD =︒∠，45ABC =︒∠， ∴AB AC ⊥，∵E ，F 分别为BC ，AD 的中点， ∴EF AB ∥，∴EF AC ⊥，∵侧面PAB ⊥底面ABCD ，且90BAP =︒∠， ∴PA ⊥底面ABCD ，∴PA EF ⊥， 又∵PAAC A =，PA ⊂平面PAC ，AC ⊂平面PAC ，∴EF ⊥平面PAC ．（Ⅱ）证明：∵M 为PD 的中点，F 为AD 的中点， ∴MF PA ∥，又∵MF ⊄平面PAB ，PA ⊂平面PAB ， ∴MF ∥平面PAB ，同理，得EF ∥平面PAB ， 又∵MFEF F =，MF ⊂平面M EF ，EF ⊂平面M EF ，∴平面MEF ∥平面PAB ，又∵ME ⊂平面M EF ， ∴ME ∥平面PAB ．（Ⅲ）解：∵PA ⊥底面ABCD ，AB AC ⊥，∴AP ，AB ，AC 两两垂直，故以AB ，AC ，AP 分别为x 轴，y 轴和z 轴建立如图空间直角坐标系，则(0,0,0)A ，(2,0,0)B ，(0,2,0)C ，(0,0,2)P ，(2,2,0)D -，(1,1,0)E ， 所以(2,0,2)PB =-，(2,2,2)PD =--，(2,2,0)BC =-， 设([0,1])PMPDλλ=∈，则(2,2,2)PM λλλ=--， ∴(2,2,22)M λλλ--，(12,12,22)ME λλλ=+--， 易得平面ABCD 的法向量(0,0,1)m =， 设平面PBC 的法向量为(,,z)n x y =，则：n BC n PB ⎧⋅=⎪⎨⋅=⎪⎩，即220220x y x z -+=⎧⎨-=⎩，令1x =，得(1,1,1)n =， ∴直线ME 与平面PBC 所成的角和此直线与平面ABCD 所成的角相等， ∴|cos ,||cos ,|ME m ME n <>=<>，即||||||||||||ME m ME n ME m ME n ⋅⋅=⋅⋅，∴|21|λ-=，解得λ=或λ=（舍去），故PM PD ．D10.（1）∵1C F ∥平面AEG ，又1C F ⊂平面11ACC A ，平面11ACC A 平面AEG AG =，∴1C F AG ∥，∵F 为1AA 的点，且侧面11ACC A 为平行四边形， ∴G 为1CC 中点， ∴112CG CC =． （2）证明：∵1AA ⊥底面ABC ，1AA AB ⊥，1AA AC ⊥， 又AB AC ⊥，如图，以A 为原点建立空间直角坐标系A xyz -，设2AB =，则由1AB AC AA ==可得(2,0,0)C ，(0,2,0)B ，1(2,0,2)C ，1(0,0,2)A ， ∵E ，G 分别是BC ，1CC 的中点，∴(1,1,0)E ，(2,0,1)G ， ∴1(1,1,1)(2,0,2)0EG CA ⋅=-⋅-=， ∴1EG CA ⊥， ∴1EG AC ⊥． （3）设平面AEG 的法向量为(,,)n x y z =，则：0n AE n AG ⎧⋅=⎪⎨⋅=⎪⎩，即020x y x z +=⎧⎨+=⎩，令1x =，则1y =-，2z =-， ∴(1,1,2)n =--，由已知可得平面1A AG 的法向量(0,1,0)m =， ∴6cos ,6||||n m n m n m ⋅<>==-⋅由题意知二面角1A AG E --为钝角， ∴二面角1A AG E --的余弦值为．111.（Ⅰ）证明：过点F 作FH AD ∥， 交PA 于H ，连结BH ，如图所示，∵13PF PD =，∴13HF AD BC ==，又FH AD ∥，AD BC ∥，HF BC ∥， ∴四边形BCFH 为平行四边形， ∴CF BH ∥，又BH ⊄平面PAB ，CF ⊄平面PAB ， ∴CF ∥平面PAB ．z D（Ⅱ）解：∵梯形ABCD 中，AD BC ∥，AD AB ⊥， ∴BC AB ⊥， ∵PB ⊥平面ABCD ， ∴PB AB ⊥，PB BC ⊥，∴如图，以B 为原点，BC ，BA ，BP 所在直线为x ，y ，z 轴建立空间直角坐标系， 则(1,0,0)C ，(3,0,0)D ，(0,3,0)A ，(0,0,3)P ，设平面BPD 的一个法向量为(,,)n x y z =， 平面APD 的一个法向量为(,,)m a b c =， ∵(3,3,3)PD =-，(0,0,3)BP =，∴00PD n BP n ⎧⋅=⎪⎨⋅=⎪⎩，即333030x y z z +-=⎧⎨=⎩，令1x =得(1,1,0)n =-，同理可得(0,1,1)m =， ∴1cos ,2||||n m n m n m ⋅<>==-⋅，∵二面角B PD A --为锐角， ∴二面角B PD A --为π3． （Ⅲ）假设存在点M 满足题意，设(3,3,3)PM PD λλλλ=-， ∴(13,3,33)CM CP PD λλλλ=+=-+-，∵(0,3,3)PA =-，∴93(33)0PA CM λλ⋅=+-=，解得12λ=，∴PD 上存在点M 使得CM PA ⊥，且12PM PD =．12.Ⅰ∵BC CD ⊥，2BC CD ==，∴BD =，同理EA ED ⊥，2EA ED ==，∴AD =，又∵4AB =，∴由勾股定理可知222BD AD AB +=，BD AD ⊥， 又∵平面EAD ⊥平面ABCD ，平面EAD 平面ABCD AD =，BD ⊂平面ABCD ，∴BD ⊥平面AED ， 又∵AE ⊂平面AED ， ∴BD AE ⊥．Ⅱ解：取AD 的中点O ，连结OE ，则OE AD ⊥， ∵平面EAD ⊥平面ABCD ，平面EAD 平面ABCD AD =，∴OE ⊥平面ABCD ，取AB 的中点F ，连结DF BD ∥，以O 为原点，建立如图所示的空间直角坐标系O xyz -，则(D ，(C -，E ，(DC =-，(2,0,DE =， 设平面CDE 的法向量为(,,)n x y z =，则00DC n DE n ⎧⋅=⎪⎨⋅=⎪⎩即00x z x y +=⎧⎨-+=⎩，令1x =，则1z =-，1y =，∴平面CDE 的法向量(1,1,1)n =-， 又平面ADE 的一个法向量为1(0,1,0)n =， 设平面ADE 和平面CDE 所成角（锐角）为θ， 则1113cos |cos ,|3||||nn n n n n θ⋅=<>==⋅，∴平面ADE 和平面CDE． C13.（1）证明：连结AE ，PE ．∵PA ⊥平面ABCD ，BC ⊂平面ABCD ， ∴PA BC ⊥．又∵底面ABCD 是菱形，AB BC =，60ABC ∠=︒， ∴ABC △是正三角形． ∵E 是BC 的中点， ∴AE BC ⊥．又∵PA AE A =，PA ⊂平面PAE ，PE ⊂平面PAE ，∴BC ⊥平面PAE ， ∴BC PE ⊥．（2）由（1）得AE BC ⊥，由BC AD ∥可得AE AD ⊥． 又∵PA ⊥底面ABCD ，∴PA AE ⊥，PA AD ⊥．∴以A 为原点，分别以AE ，AD ，AP 为x 轴，y 轴，z 轴建立空间直角坐标系A xyz -，如图所示，则(0,0,0)A，E ，(0,2,0)D ，(0,0,2)P，1,0)B -，C ，(0,1,1)F ．∵PA ⊥平面ABCD ，∴平面ABCD 的法向量为(0,0,2)AP =． 又∵(3,1,0)AC =，(0,1,1)AF =． 设平面ACF 的一个法向量(,,)n x y z =，则：AC n AF n ⎧⋅=⎪⎨⋅=⎪⎩，即00y y z +==⎪⎩+，令1x =，则y =z ，∴(1,3,n =-． ∴21cos ,7||||AP n AP n AP n ⋅==． ∵二面角F AC D --是锐角， ∴二面角F AC D -- （3）G 是线段AB 上的一点，设(01)AG t AB t =≤≤． ∵(3,1,0)AB =-，∴,,0)G t -． 又∵(3,1,2)PC =-，(3,,2)PG t t =--． 设平面PCG 的一个法向量为(,,)n x y z =，则：1100PC n PGn ⎧⋅=⎪⎨⋅=⎪⎩，即1111112020yz ty z-=--=+，∴1()n t t =-+， ∵AF ∥平面PCG ，∴AF n ⊥，0AF n ⋅=1)0t -=， 解得12t =． 故线段AB 上存在一点G ，使得AF 平行于平面PCG ，G 是AB 中点．14.（1）证明：∵DE ⊥平面ABCD ，AC ⊂平面ABCD ， ∴DE AC ⊥． ∵ABCD 是正方形， ∴AC BD ⊥． 又DEBD D =，∴AC ⊥平面BDE ．（2）∵DA ，DC ，DE 两两重叠，∴建立空间直角坐标系D xyz -如图所示．∵BE 与平面ABCD 所成角为60︒，即60DBE ∠=︒，∴EDDB． 由3AD =，可知DZ =AF ，则(3,0,0)A，F，E ，(3,3,0)B ，(0,3,0)C ．∴(0,BF =-，(3,0,EF =-， 设平面BEF 的法向量为(,,)n x y z =，则00n BF n EF ⎧⋅=⎪⎨⋅=⎪⎩，即3030y x ⎧-=⎪⎨-=⎪⎩，令z (4,2,6)n =． ∵AC ⊥平面BDE ，∴CA 为平面BDE 的一个法向量，(3,3,0)CA =-，∴cos ,||||32n CA n CA n CA ⋅==．∵二面角F BE D --为锐角， ∴二面角F BE D -- （3）点M 线段BD 上一个动点，设(,,0)M t t ，则(3,,0)AM t t =-．∵AM ∥平面BEF ，∴0AM n ⋅=，即4(3)20t t -+=，解得2t =，此时，点M 坐标为(2,2,0)，13BM BD =，符合题意．15.（1）证明：∵PA ⊥平面ABC ，BC ⊂平面ABC ， ∴PA BC ⊥．∵BC AB ⊥，PA AB A =， ∴BC ⊥平面PAB ． 又AM ⊂平面PAB ， ∴AM BC ⊥．∵PA AB =，M 为PB 的中点， ∴AM PB ⊥． 又∵PBBC B =，∴AM ⊥平面PBC ．（2）如图，在平面ABC 内作AZ BC ∥，则AP ，AB ，AZ 两两垂直，建立空间直角坐标系A xyz -．则(0,0,0)A ，(2,0,0)P ，(0,2,0)B ，(0,2,1)C ，(1,1,0)M ． (2,0,0)AP =，(0,2,1)AC =，(1,1,0)AM =．设平面APC 的法向量为(,,)n x y z =，则：0n AP n AC ⎧⋅=⎪⎨⋅=⎪⎩，即020x y z =⎧⎨+=⎩，令1y =，则2z =-． ∴(0,1,2)n =-．由（1）可知(1,1,0)AM =为平面PBC 的一个法向量，∴cos||||5AM nn AMAM n⋅⋅==∵二面角A PC B--为锐角，∴二面角A PC B--．（3）证明：设(,,)D v wμ是线段PC上一点，且PD PCλ=，(01)λ≤≤，即(2,,)(2,2,1)v wμλ-=-，∴22μλ=-，2vλ=，wλ=．∴(22,22,)BDλλλ=--．由0BD AC⋅=，得4[0,1]5λ=∈，∴线段PC上存在点D，使得BD AC⊥，此时45PDPCλ==．16.解：（1）证明：因为AB⊥平面PAD，所以PH AB⊥，因为3,2AHADHD==，所以2,1AH HD==，设PH x=，由余弦定可得，22221cos22x HD PH xPHDx HD x+--∠==⋅22221cos24x HA PH xPHAx HA x+--∠==⋅因为cos cosPHD PHA∠=-∠，故1PH x==，所以PH AD⊥，因为AD AB A=，故PH⊥平面ABCD.（2）以H为原点，以,,HA HP HP所在的直线分别为,,x y z轴，建立空间直角坐标系，则3139(2,3,0),(0,0,1),(1,,),(1,,0),(1,,0)2222B P E F C--，所以可得，3311(3,,0),(1,,),(2,0,),(0,3,0)2222BF BE EF FC=--=--=-=，设平面BEF的法向量(,,)n x y z=，则有：33002(1,2,4)30022x yBF nnzBE n x y⎧--=⎪⎧⋅=⎪⎪⇒⇒=-⎨⎨⋅=⎪⎪⎩--+=⎪⎩，设平面EFC的法向量(,,)m x y z=，则有：020(1,0,4)2030z EF m x m FC m y ⎧⎧⋅=--=⎪⎪⇒⇒=-⎨⎨⋅=⎪⎪⎩=⎩，故17cos ,21n m n m n m⋅===⋅设二面角B EF C --的平面角为θ ，则sin 21θ=.17.解（Ⅰ）证明：∵DC ⊥平面ABC ，//BE DC ∴BE ⊥平面ABC ∴CQ BE ⊥ ①又∵2AC BC ==，点Q 为AB 边中点 ∴CQ AB ⊥ ②AB BE B =故由①②得CQ ⊥平面ABE（Ⅱ）过点A 作AM BC ⊥交BC 延长线于点M ∵,AM BC AM BE ⊥⊥ ∴AM ⊥平面BEDC ∴13A CED CDE V S AM -∆=sin33AM AC π==11212CDE S ∆=⨯⨯= ∴113A CED V -=⨯= （Ⅲ）延长ED 交BC 延长线于S ，过点M 作MQ ES ⊥于Q ，连结AQ 由（Ⅱ）可得：AQM ∠为A DE B --的平面角∵1//2CD BC ∴2SC CB == ∴SE ==1MC MS ==∵SQM ∆∽SBE ∆∴QM SM BE SE=∴1225QM=即55QM=∴3tan1555AMAQMQM∠===18.（1）证明：∵在中，，∴当为的中点时，∵平面平面，平面，平面平面∴平面∵平面∴（2）如图，分别以射线，的方向为，轴的正方向，建立空间直角坐标系设，则，，，∵，，平面平面∴∴当且仅当时，最小，此时，设，平面，则，即∴令，可得，，则有∴∴观察可得二面角的平面角19.（1）取FE 的中点P ，连接CP 交BE 于点M ，M 点即为所求的点． 连接PG ，∵G 是AD 的中点，P 是FE 的中点，∴//PG AF ， 又PG ⊂平面MGC ，AF ⊄平面MGC ，所以直线//AF 平面MGC ， ∵//PE AD ，//AD BC ，∴//PE BC ，∴2BM BCME PE==， 故点M 为线段BE 上靠近点E 的三等分点． （2）不妨设2AD =，由（1）知PG AD ⊥， 又平面ADEF ⊥平面ABCD ，平面ADEF平面ABCD AD =，PG ⊂平面ADEF ，∴PG ⊥平面ABCD ．故PG GD ⊥，PG GC ⊥，以G 为坐标原点，GC ，GD ，GP 分别为x ，y ，z 轴建立空间直角坐标系G xyz -，∵60ABC ∠=︒，2AB AD AF ==，∴ADC ∆为正三角形，3GC =，∴(0,0,0)G ，3,0,0)C ，(0,1,0)D ，(0,1,1)E ，∴(0,1,1)GE =，(3,0,0)GC =，设平面CEG 的一个法向量1(,,)n x y z =，则由10n GE ⋅=，10n GC ⋅=可得0,30,y z x +=⎧⎪⎨=⎪⎩令1y =，则1(0,1,1)n =-，∵(3,1,0)CD =-BA =，且(0,1,0)A -，故3,2,0)B -，故(3,2,0)BG =-， 故直线BG 与平面GCE 所成角的正弦值为11||14sin 7||||n BG n BG θ⋅==⋅．20.（Ⅰ）取PC 中点H ，连接、EH FH .∵E 为AB 的中点，ABCD 是菱形，∴//AE CD ，且12AE CD =，又F 为PD 的中点，H 为PC 的中点，∴//FH CD ，且12FH CD =，∴//AE FH ，且AE FH =，则四边形AEHF 是平行四边形，∴//AF EH .又AF ⊄平面PCE ，EH ⊂面PCE ，∴//AF 平面PCE .（Ⅱ）取BC 的中点为O ，∵ABCD 是菱形，AC AB =，∴AO BC ⊥，以A 为原点，,,AO AD AP 所在直线分别为,,z x y 轴，建立空间直角坐标系A xyz -，则)()()3,1,0,3,1,0,0,2,0BCD -，)()313,0,0,0,0,1,,02OP E ⎫-⎪⎪⎝⎭，∴()333,1,1,,,022PC EC ⎛⎫=-= ⎪ ⎪⎝⎭，()3,0,0AO =，设平面的法向量为()1,,n x y z =，则1100n PC n EC ⎧⋅=⎪⎨⋅=⎪⎩，即3033022x y z x y ⎧+-=⎪+=⎪⎩，令1y =-，则3,2x z ==，∴平面PCE 的一个法向量为)13,1,2n =-，又平面PAD 的一个法向量为()21,0,0n =.∴12121236cos ,|n ||n |4314n n n n ⋅<>===⋅++.即平面PAD 与平面PCE 621.解：（1）证明：取PD 的中点F ，连接,EF CF ， 因为,E F 分别是,PA PD 的中点，所以//EF AD 且12EF AD =， 因为1,//2BC AB BC AD =，所以//EF BC 且EF BC =，所以//BE CF , 又BE ⊄平面,PCD CF ⊂平面PCD ，所以//BE 平面PCD .（2）以P 为坐标原点，,PD PA 所在直线分别为x 轴和y 轴，建立如图所示的空间直角坐标系，不妨设1BC =，则13(0,0,0),3,0),(1,0,0),(1,0,1),(2P A D C B ， 13(0,3,0),(,1),(1,3,0)2PA AB AD ==-=-,设平面PAB 的一个法向量为(,,)n x y z =，则30013002n PA yn AB x z ⎧=⎧⋅=⎪⎪⇒⎨⎨⋅=+=⎪⎪⎩⎩， 令2x =，得(2,0,1)n =-， 同理可求平面ABD 的一个法向量为6(3,3,0)cos ,55n m m n m n m⋅=⇒===⨯，平面ABD 和平面ABC 为同一个平面， 所以二面角P AB C --.22.解：（Ⅰ）证明：因为二面角S AB C --的大小为90°，则SA AD ⊥， 又SA AB ⊥，故SA ⊥平面ABCD ，又BD ⊂平面ABCD ，所以SA BD ⊥； 在直角梯形ABCD 中，90BAD ADC ∠=∠=︒，21AD CD ==，2AB =， 所以1tan tan 2ABD CAD ∠=∠=，又90DAC BAC ∠+∠=︒， 所以90ABD BAC ∠+∠=︒，即AC BD ⊥； 又ACSA A =，故BD ⊥平面SAC ，因为AF ⊂平面SAC ，故BD AF ⊥.（Ⅱ）设点E 到平面ABCD 的距离为h ，因为B ABC E ABC V V --=，且25E ABC S ABCD V V --=，故511215*********ABCD S ABCD E ABCABC S SAV V S h h --∆⨯⋅⨯===⋅⨯⨯⨯梯形，故12h =，做点E 到平面ABCD 的距离为12.23.（1）E 为SD 的中点，01,602AD DC SD SDA SDC ==∠=∠=.ED EC AD DC ∴===设O 为AC 的中点，连接,EO DO 则EO AC ⊥//,AD BC BC CD ⊥ .AD BC ∴⊥又OD OA OC ==EOC EOD ∴∆≅∆ 从而EO OD ⊥AC ABCD = DO ⊂面ABCD 0AC DO =EO ∴⊥面ABCD EO ⊂面AEC∴面EAC ⊥面ABCD ………………6分（2）设F 为CD 的中点,连接OF EF 、,则OF 平行且等于12AD AD ∥BC EF ∴∥BC不难得出CD ⊥面OEF （EO CD ⊥ FO CD ⊥）∴面ECD ⊥面OEFOF 在面ECD 射影为EF ，EFO ∠的大小为BC 与面ECD 改成角的大小设AD a =，则2aOF =32EF a = 3os OF c EFO EF <== 即BC 与ECD 3（亦可以建系完成） ………………12分24.解（Ⅰ）过点P 作PO ⊥底面ABC ，垂足为O ， 连接AO 、CO ，则∠PCO 为所求线面角，,AC PA ⊥,AC PO PA PO P ⊥⋂=且，AC ∴⊥平面PAO .则∠P AO 为二面角P -AC -B 平面角的补角∴∠ 60=PAO ，又23PA =∴，，1sin 2PO PCO CO ∠== 030PCO ∴∠=，直线PC 与面ABC 所成角的大小为30°.（Ⅱ）过O 作OE BC ⊥于点E ,连接PE ，则PEO ∠为二面角P -BC -A 的平面角，AC ⊥平面PAO ,AC OA ⊥045AOE ∠=,设OE 与CA 相交于F 22OE EF FO ∴=+=+在PEO ∆中，3436tan 7222POPEO EO-∠===+则二面角P -BC -A 的正切值为4367-.25.解：（Ⅰ）如图，取PA 中点F ，连接FD EF ,，E 是BP 的中点，AB EF // 且AB EF 21=，又AB DC AB DC 21,//= ∴∴DC EF //四边形EFDC 是平行四边形，故得//EC FD又⊄EC 平面⊂FD PAD ,平面PAD//EC ∴平面ADE（Ⅱ）取AD 中点H ,连接PH ,因为PD PA =，所以AD PH ⊥平面⊥PAD 平面ABCD 于AD ，⊥∴PH 面ABCD ，HB ∴是PB 在平面ABCD 内的射影 PBH ∠∴是PB 与平面ABCD 所成角四边形ABCD 中，090=∠=∠BCD ABC ∴四边形ABCD 是直角梯形AB CB DC 21== 设a AB 2=，则a BD 2=在ABD ∆中，易得a AD DBA 2,450=∴=∠.22212222a a a DH PD PH =-=-=又22224AB a AD BD ==+ABD ∆∴是等腰直角三角形，090=∠ADBa a a DB DH HB 2102212222=+=+=∴ ∴ 在PHB Rt ∆中，5521022tan ===∠a aHB PH PBH（Ⅲ）在平面ABCD 内过点H 作AB 的垂线交AB 于G 点，连接PG ,则HG 是PG 在平面ABCD 上的射影，故AB PG ⊥，所以PGH ∠是二面角D AB P --的平面角， 由a HA a AB 22,2==，又a HG HAB 21450=∴=∠ 在PHG Rt ∆中，22122tan ===∠a aHG PH PGH ∴ 二面角D AB P --的余弦值大小为.3326.（1）∵四棱锥P ﹣ABCD 的底面ABCD 为边长为2的正方形，PA=2，PB=PD=2，∴PA 2+AB 2=PB 2，PA 2+AD 2=PD 2， ∴PA ⊥AB ，PA ⊥AD ，∴以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴， 建立空间直角坐标系，∵E ，F ，G ，H 分别为棱PA ，PB ，AD ，CD 的中点． ∴C （2，2，0），D （0，2，0），B （2，0，0）， P （0，0，2），F （1，0，1），G （0，1，0）， =（﹣2，0，0），=（﹣1，﹣2，1），=（﹣2，﹣1，0），设平面CFG 的法向量=（x ，y ，z ）， 则，取x=1，得=（1，﹣2，﹣3），设CD与平面CFG所成角为θ，则sinθ=|cos＜＞|===．∴CD与平面CFG所成角的正弦值为．（2）假设棱PD上是否存在点M（a，b，c），且，（0≤λ≤1），使得平面CFG⊥平面MEH，则（a，b，c﹣2）=（0，2λ，﹣2λ），∴a=0，b=2λ，c=2﹣2λ，即M（0，2λ，2﹣2λ），E（0，0，1），H（1，2，0），=（1，2，﹣1），=（0，2λ，1﹣2λ），设平面MEH的法向量=（x，y，z），则，取y=1，得=（，1，），平面CFG的法向量=（1，﹣2，﹣3），∵平面CFG⊥平面MEH，∴=﹣2﹣=0，解得∈[0，1]．∴棱PD上存在点M，使得平面CFG⊥平面MEH，此时=．。
2023届高考一轮复习试卷(立体几何)
2023届高考一轮复习试卷（立体几何）一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的。
1.已知圆锥的侧面展开图是一个半径为2的半圆，则该圆锥的体积为A ．3πB ．3π3C ．3πD ．2π2.金刚石的成分为纯碳，是自然界中天然存在的最坚硬物质，它的结构是由8个等边三角形组成的如图所示的正八面体.若某金刚石的棱长为2，则它的表面积为A ．8B ．82C ．83D ．1633.如图，用斜二测画法作水平放置的正三角形111A B C 的直观图，则正确的图形是A ．B ．C ．D ．4.已知两条不同直线,l m 与两个不同平面,αβ，下列命题正确的是A ．若//,l l m α⊥，则m α⊥B ．若,//l l αβ⊥，则αβ⊥C ．若//,//l m αα，则//l m D ．若//,//m αβα，则//m β5.如图，平行六面体1111ABCD A B C D -的体积为482，11A AB A AD ∠=∠，16AA =，底面边长均为4，且π3DAB ∠=，M ，N ，P 分别为AB ，1CC ，11C D 的中点，则A ．//MN APB ．1AC ⊥平面BDN C ．1AP AC ⊥D ．//AP 平面MNC6.如图所示，在正方体1111ABCD A B C D -中，点E 是棱1CC 上的一个动点，平面1BED 交棱1AA 于点.F 则下列结论中错误．．的是A ．存在点E ，使得11//AC 平面1BED FB ．存在点E ，使得1B D ⊥平面1BED FC ．对于任意的点E ，平面11ACD ⊥平面1BED FD ．对于任意的点E ，四棱锥11B BEDF -的体积均不变7.足球运动成为当今世界上开展最广、影响最大、最具魅力、拥有球迷数最多的体育项目之一，2022年卡塔尔世界杯是第22届世界杯足球赛．比赛于2022年11月21日至12月18日在卡塔尔境内7座城市中的12座球场举行．已知某足球的表面上有四个点A ，B ，C ，D 满足2dm AB BC AD BD CD =====，二面角A BD C --的大小为23π，则该足球的体积为A ．3742dm 27πB ．3352dm 27πC ．314dm 27πD ．3322dm 27π8.一个长方体的盒子内装有部分液体（液体未装满盒子），以不同的方向角度倾斜时液体表面会呈现出不同的变化，则下列说法中错误的个数是①当液面是三角形时，其形状可能是钝角三角形②在一定条件下，液面的形状可能是正五边形③当液面形状是三角形时，液体体积与长方体体积之比的范围是150,,166⎛⎤⎡⎫⋃ ⎪⎥⎢⎝⎦⎣⎭④当液面形状是六边形时，液体体积与长方体体积之比的范围是13,44⎛⎫ ⎪⎝⎭A ．1个B ．2个C ．3个D ．4个二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9.下列关于空间向量的命题中，正确的是A ．若空间向量,a b ，满足a b =r r ，则a b= B ．若非零向量,,a b c ，满足,a b b c ⊥⊥ ，则有a c∥ C ．若,,OA OB OC 是空间的一组基底，且111333OD OA OB OC =++ ，则,,,A B C D 四点共面D ．若向量,,a b b c c a +++ 是空间的一组基底，则,,a b c 也是空间的一组基底10.如图，若正方体的棱长为1，点M 是正方体1111ABCD A B C D -的侧面11ADD A上的一个动点（含边界），P 是棱1CC 的中点，则下列结论正确的是A ．沿正方体的表面从点A 到点P 的最短路程为132B ．若保持2PM =，则点M 在侧面内运动路径的长度为π3C ．三棱锥1B C MD -的体积最大值为16D ．若M 在平面11ADD A 内运动，且111MD B B D B ∠=∠，点M 的轨迹为线段11.已知a ，b ，c 为三条不同的直线，α，β，γ为三个不同的平面，则下列说法错误的是A ．若a b ∥，b α⊂，则a αP B ．若a αβ⋂=，b βγ= ，c αγ⋂=，a b ∥，则b c ∥C ．若b β⊂，c β⊂，a b ⊥r r ，a c ⊥，则a β⊥D ．若a α⊂，b β⊂，a b ∥，则αβ∥12.如图，已知二面角l αβ--的棱l 上有A ，B 两点，C α∈，AC l ⊥，D β∈，BD l ⊥，若2AC AB BD ===，22CD =，则A ．直线AB 与CD 所成角的大小为45°B ．二面角l αβ--的大小为60°C ．三棱锥A BCD -的体积为23D ．直线CD 与平面β所成角的正弦值为64三、填空题：本题共4小题，每小题5分，共20分．13.在空间直角坐标系中，已知()3,2,1OA = ，()1,0,5OB = ，()1,2,1OC =-- ，点M 为线段AB 的中点，则CM = ．14.用一个平面将圆柱切割成如图的两部分.将下半部分几何体的侧面展开，平面与圆柱侧面所形成的交线在侧面展开图中对应的函数表达式为 1.52cos y x =+.则平面与圆柱底面所形成的二面角的正弦值是.15.“云南十八怪”描述的是由云南独特的地理位置、民风民俗所产生的一些特有的现象或生活方式，是云南多元民族文化的写照.“云南十八怪”中有一怪“摘下草帽当锅盖”所指的锅盖是用秸秆或山茅草编织成的，因其形状酷似草帽而传为佳话.一种草帽锅盖呈圆锥形，其母线长为6dm ，侧面积为2183dm π，若此圆锥的顶点和底面圆都在同一个球面上，则该球体的表面积等于2dm .16.在直四棱柱1111ABCD A B C D -中，底面ABCD 为正方形，122AA AB ==．点P 在侧面11BCC B 内，满足1A C ⊥平面BDP ，设点P 到平面ABCD 的距离为1h ，到CD 的距离为2h ，则12h h +的最小值为．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17.如图所示，在四棱锥P ABCD -中，底面ABCD 是边长为4的正方形，4,PA PD PB ==，点E 在线段PA 上，3,PE EA BE AD =⊥，点,F G 分别是线段,BC CD 的中点.(1)证明：PA ⊥平面ABCD ；(2)求三棱锥P EFG -的体积.18.三棱锥P ABC -中，PA PB PC BC a ====，且PB 与底面ABC 成60°角.(1)设点P 在底面ABC 的投影为H ，求BH 的长；(2)求证：ABC △是直角三角形；(3)求该三棱锥体积的最大值.19.故宫太和殿是中国形制最高的宫殿，其建筑采用了重檐庑殿顶的屋顶样式，庑殿顶是“四出水”的五脊四坡式，由一条正脊和四条垂脊组成，因此又称五脊殿．由于屋顶有四面斜坡，故又称四阿顶．如图，某几何体ABCDEF 有五个面，其形状与四阿顶相类似．已知底面ABCD 为矩形，AB ＝2AD ＝2EF ＝8，EF ∥底面ABCD ，EA ＝ED ＝FB ＝FC ，M ，N 分别为AD ，BC 的中点．(1)证明：EF ∥AB 且BC ⊥平面EFNM ．(2)若二面角E AD B --为4π，求CF 与平面ABF 所成角的正弦值．20.如图，已知ABCD 和CDEF 都是直角梯形，//AB DC ，//DC EF ，5AB =，3DC =，1EF =，60BAD CDE ∠=∠=︒，二面角F DC B --的平面角为60︒．设M ，N 分别为,AE BC 的中点．(1)证明：FN AD ⊥；(2)求直线BM 与平面ADE 所成角的正弦值．21.《瀑布》（图1）是埃舍尔最为人所知的作品之一，图中的瀑布会源源不断地落下，落下的水又逆流而上，荒唐至极，但又会让你百看不腻.画面下方还有一位饶有兴致的观察者，似乎他没发现什么不对劲.此时，他既是画外的观看者，也是埃舍尔自己.画面两座高塔各有一个几何体，左塔上方是著名的“三立方体合体”由三个正方体构成，右塔上的几何体是首次出现，后称“埃舍尔多面体”（图2）埃舍尔多面体可以用两两垂直且中心重合的三个正方形构造，设边长均为2，定义正方形,1,2,3n n n n A B C D n =的顶点为“框架点”，定义两正方形交线为“极轴”，其端点为“极点”，记为,n n P Q ，将极点11,P Q ，分别与正方形2222A B C D 的顶点连线，取其中点记为,,,1,2,3,4m m E F m =，如（图3）.埃舍尔多面体可视部分是由12个四棱锥构成，这些四棱锥顶点均为“框架点”，底面四边形由两个“极点”与两个“中点”构成，为了便于理解，图4我们构造了其中两个四棱锥11122A PE P E -与22131A P E P F -.(1)求异面直线12P A 与12Q B 成角余弦值(2)求平面111PA E 与平面122AE P 的夹角余弦值(3)若埃舍尔体的表面积与体积（直接写出答案）22.在长方体1111ABCD A B C D -中，(1)已知P ､Q 分别为棱AB ､1CC 的中点（如图1），做出过点1D ，P ，Q 的平面与长方体的截面.保留作图痕迹，不必说明理由；(2)如图2，已知13AB =，5AD =，112AA =，过点A 且与直线CD 平行的平面α将长方体分成两部分.现同时将两个球分别放入这两部分几何体内，则在平面α变化的过程中，求这两个球的半径之和的最大值.。
高三一轮复习 立体几何全章 练习(9套)+易错题+答案
第九章立体几何与空间向量第1节简单几何体的结构、三视图和直观图一、选择题1.如图是由哪个平面图形旋转得到的( A )解析:根据面动成体的原理即可解,一个直角三角形绕直角边旋转一周可以得到一个圆锥.一个直角梯形绕着直角腰旋转一周得到圆台.该几何体的上部分是圆锥,下部分是圆台,圆锥的轴截面是直角三角形,圆台的轴截面是直角梯形,所以这个几何图形是由直角三角形和直角梯形围绕直角边所在的直线为轴旋转一周得到.故选A.2.已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4, AB⊥AC,AA1=12,则球O的半径为( C )(A) (B)2 (C) (D)3解析:构建长方体的棱长分别为3,4,12.体对角线长为=13,外接球的半径为,故选C.3.用长为4,宽为2的矩形做侧面围成一个圆柱,此圆柱轴截面面积为( B )(A)8 (B)(C)(D)解析:若以4作为圆柱的高、2作为底面圆的周长,则圆柱轴截面面积为;若以2作为圆柱的高、4作为底面圆的周长,则圆柱轴截面面积为,所以此圆柱轴截面面积为.故选B.4.正四棱锥S-ABCD的底面边长为4,高SE=8,则过点A,B,C,D,S的球的半径为( C )(A)3 (B)4 (C)5 (D)6解析:由正四棱锥及其外接球的对称性,球心O在正四棱锥的高线SE上,球半径R=OS=OB,EB=BD=4.所以在直角三角形OEB中,由勾股定理得,(8-R)2+42=R2,解得R=5,故选C.5.三棱锥P-ABC中,△ABC是底面,PA⊥PB,PA⊥PC,PB⊥PC,且这四个顶点都在半径为2的球面上,PA=2PB,则这个三棱锥的三个侧棱长的和的最大值为( B )(A)16 (B)(C)(D)32解析:因为PA,PB,PC两两垂直,又因为三棱锥P-ABC的四个顶点均在半径为1的球面上,所以以PA,PB,PC为棱的长方体的对角线即为球的一条直径.所以16=PA2+PB2+PC2,因为PA=2PB,则这个三棱锥的三个侧棱长的和PA+PB+PC=3PB+PC,因为5PB2+PC2=16,设PB=4cos α,PC=4sin α,则3PB+PC=cos α+4sin α=sin(α+φ)≤=. 可知其最大值为,选B.6.已知一个四面体其中五条棱的长分别为1,1,1,1,,则此四面体体积的最大值是( B )(A) (B) (C) (D)解析:设四面体为P-ABC,则设PC=X,AB=,其余的各边为1,那么取AB 的中点D,那么连接PD,因此可知,AB垂直于平面PCD,则棱锥的体积可以运用以PCD为底面,高为AD,BD的两个三棱锥体积的和来表示,因此只要求解底面积的最大值即可.由于PD=CD=,那么可知三角形PDC的面积越大,体积越大,可知S△PDC=××sin θ≤=,也就是当PD垂直于CD时,面积最大,因此可得四面体的体积的最大值为××=,选B.二、填空题7.圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的表面积为.解析:因为圆柱的侧面展开图是边长为6π和4π的矩形,①若6π=2πr,r=3,所以圆柱的表面积为4π×6π+2×πr2=24π2+18π;②若4π=2πr,r=2,所以圆柱的表面积为4π×6π+2×πr2=24π2+8π.答案:24π2+8π或24π2+18π8.一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等,这时圆柱、圆锥、球的体积之比为.解析:设球的半径为r,则V圆柱=πr2×2r=2πr3,V圆锥=πr2×2r=,V球=πr3,所以V圆柱∶V圆锥∶V球=2πr3∶∶πr3=3∶1∶2.答案:3∶1∶29.将4个半径都是R的球体完全装入底面半径是2R的圆柱形桶中,则桶的最小高度是.解析:由题意知,小球要分两层放置且每层两个,令下层两小球的球心分别是A,B,上层两小球的球心分别是C,D.此时,圆柱底面的半径=两小球半径的和,恰好使小球相外切,且与圆柱母线相切.圆柱的高=上层小球的上方半径+AB与CD间的距离+下层小球的下方半径=2R+AB与CD间的距离.令AB,CD的中点分别为E,F.很明显,四面体ABCD每条棱的长都是2R,容易求出:EC=ED,FA=FB,由EC=ED,CF=DF,得EF⊥CD.由FA=FB,AE=BE,得EF⊥AB.所以EF是AB与CD间的距离,所以圆柱的高=2R+EF.由勾股定理,有CE2+AE2=AC2,CE2=EF2+CF2.两式相减,消去CE,得AE2=AC2-EF2-CF2,所以EF2=AC2-AE2-CF2=(2R)2-R2-R2=2R2,所以EF=R.所以圆柱的高=2r+R=(2+)R.答案:(2+)R10.一个圆锥有三条母线两两垂直,则它的侧面展开图的圆心角大小为.解析:设母线长为l,因圆锥有三条母线两两垂直,则这三条母线可以构成以它们为侧棱、以底面边长为l的正三角形的正三棱锥,故由正弦定理得,圆锥的底面直径2R=,解得R=,因此可知侧面展开图的圆心角大小为π.答案:π11.若圆锥的侧面展开图是圆心角为180°,半径为4的扇形,则这个圆锥的表面积是.解析:因为圆锥的侧面展开图是圆心角为180°,母线长等于4,半径为4的扇形,则这个圆锥的表面积是底面积加上侧面积,扇形面积加上底面面积的和为12π.答案:12π12.若长方体的一个顶点上的三条棱的长分别为3,4,5,从长方体的一条对角线的一个端点出发,沿表面运动到另一个端点,其最短路程是.解析:从长方体的一条对角线的一个端点A出发,沿表面运动到另一个端点B,有三种方案,如图是它们的三种部分侧面展开图,AB路程可能是:最短路程是.答案:三、解答题13.某几何体的一条棱长为,在该几何体的正视图中,这条棱的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,求a+b的最大值.解:如图,把几何体放到长方体中,使得长方体的体对角线刚好为几何体的已知棱,则长方体的体对角线A 1C=,则它的正视图投影长为A 1B=,侧视图投影长为A1D=a,俯视图投影长为A1C1=b,则a2+b2+()2=2·()2,即a2+b2=8,又≤,当且仅当“a=b=2”时等号成立.所以a+b≤4,即a+b的最大值为4.14.某几何体的三视图如图所示.(1)判断该几何体是什么几何体?(2)画出该几何体的直观图.解:(1)该几何体是一个正方体切掉两个圆柱后得到的几何体.(2)直观图如图所示.15.已知正三棱锥V-ABC的正视图和俯视图如图所示.(1)画出该正三棱锥的侧视图和直观图;(2)求出侧视图的面积.解:(1)如图.(2)侧视图中V A===2,则S △VBC=×2×2=6.第2节简单几何体的表面积与体积一、选择题1.如图所示是一个几何体的三视图,则该几何体的体积为( B )(A)16+2π(B)8+2π(C)16+π (D)8+π解析:由图可知该几何体是由两个相同的半圆柱与一个长方体拼接而成,因此V=1×2×4+π×12×2=8+2π.故选B.2.一个三条侧棱两两互相垂直并且侧棱长都为a的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( B )(A)πa2(B)3πa2(C)6πa2(D)πa2解析:由题可知该三棱锥为一个棱长a的正方体的一角,则该三棱锥与该正方体有相同的外接球,又正方体的对角线长为a,则球半径为a,则S=4πr2=4π(a)2=3πa2.故选B.3.一个棱长都为a的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( A )(A)πa2(B)2πa2(C)πa2(D)πa2解析:如图,设O1,O2为棱柱两底面的中心,球心O为O1O2的中点.又直三棱柱的棱长为a,可知OO1=a,AO1=a,所以R2=OA2=O+A=,因此该直三棱柱外接球的表面积为S=4πR2=4π×=πa2,故选A.4.某几何体的三视图如图所示,则该几何体的体积为( D )(A) (B)2 (C) (D)解析:由三视图可知,该几何体的直观图为一个竖立的圆锥和一个倒立的圆锥组成,其体积为V=2×π×12×1=,选D.5.某四棱锥的三视图如图所示,则该四棱锥的体积是( C )(A)5 (B)2 (C) (D)解析:由三视图知,该四棱锥的底面是直角梯形,上底长为2,下底长为3,高为,四棱锥的高为h=2,故该四棱锥的底面积S=(2+3)×=,所以该四棱锥的体积V=Sh=××2=.6.已知边长为2的菱形ABCD中,∠A=60°,现沿对角线BD折起,使得二面角A BD C为120°,此时点A,B,C,D在同一个球面上,则该球的表面积为( C )(A)20π(B)24π(C)28π(D)32π解析:如图,分别取BD,AC的中点M,N,连接MN,则容易算得AM=CM=3,MN=,MD=,CN=,由图形的对称性可知球心必在MN的延长线上,设球心为O,半径为R,ON=x,则由题设可得解得x=,则R2=+=7,所以球面面积S=4πR2=28π,故选C.二、填空题7.一个圆柱的轴截面为正方形,则与它同底等高的圆锥的侧面积与该圆柱的侧面积的比为.解析:令正方形的边长为a,则圆柱的侧面积S1=2π××a=πa2,与它同底等高的圆锥的侧面积S2=πrl=π××a=,则与它同底等高的圆锥的侧面积与该圆柱的侧面积的比为.答案:8.球O与直三棱柱ABC-A1B1C1的各个面都相切,若三棱柱的表面积为27,△ABC的周长为6,则球的表面积为.解析:设内切球半径为r,那么直三棱柱的底面内切圆半径为r,棱柱的高为2r,由等面积法,则直三棱柱底面面积S 底=r×6=3r,由等体积法,V三棱柱=S底·2r=r·27,所以9r=6r2,解得r=.其表面积为4π×()2=3π.答案:3π9.已知母线长为6,底面半径为3的圆锥内有一球,球与圆锥的底面及圆锥的所有母线都相切,则球的体积是 .解析:取圆锥的轴截面,则截面是边长为6的正三角形,正三角形的内切圆的圆心即为球心,R=6××,所以R=,所以V=πR3=4π.答案:4π10.棱长为a的正方体ABCD A 1B1C1D1的8个顶点都在球O的表面上,E,F 分别是棱AA1,DD1的中点,则过E,F两点的直线被球O截得的线段长为.解析:设过E,F两点的直线与球O交于M,N,所以△OMN,△OEF均为等腰直角三角形,所以OM=ON=R=a,点O到EF的距离为棱长一半,所以|MN|=2= a.答案: a11.四棱锥P-ABCD的各顶点都在同一球面上,且矩形ABCD的各顶点都在同一个大圆上,球半径为R,则此四棱锥的体积的最大值为.解析:点P到平面ABCD的最大距离为R,设矩形ABCD的长宽分别为x,y,则x2+y2=4R2,四棱锥P ABCD的体积V=xyR≤×=R3,当且仅当x=y=R时,V max=R3.答案:R312.设正四面体ABCD的棱长为a,P是棱AB上的任意一点,且P到平面ACD,BCD的距离分别为d1,d2,则d1+d2= .解析:根据题意,由于正四面体ABCD的棱长为a,各个面的面积为a2,高为a,所以V=×a2×a=×a2×(d1+d2),所以d1+d2= a.答案: a三、解答题13.已知一个几何体的三视图如图所示.(1)求此几何体的表面积;(2)如果点P,Q在正视图中所示位置,P为所在线段中点,Q为顶点,求在几何体表面上,从P点到Q点的最短路径的长.解:(1)由三视图知该几何体是由一个圆锥加一个圆柱组成的,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=(2πa)·(a)=πa2,S圆柱侧=(2πa)·(2a)=4πa2,S圆柱底=πa2,所以S 表=πa2+4πa2+πa2=(+5)πa2.(2)沿P点所在母线剪开圆柱侧面,如图.则PQ===a,所以从P点到Q点在侧面上的最短路径长为a.14.如图,四棱锥P ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面PAB;(2)求四面体NBCM的体积.(1)证明:由已知得AM=AD=2.如图,取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.所以AM=TN,又AD∥BC,故TN AM,所以四边形AMNT为平行四边形,于是MN∥AT.因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.(2)解:因为PA⊥平面ABCD,N为PC的中点,所以N到平面ABCD的距离为PA.取BC的中点E,连接AE.由AB=AC=3得AE⊥BC,AE==.由AM∥BC得M到BC的距离为,故S △BCM=×4×=2.所以四面体NBCM的体积V N-BCM=×S△BCM×=.15.如图所示,在空间几何体ADE BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC,AB=AD=DE=2,EF=4,M是线段AE上的动点.(1)试确定点M的位置,使AC∥平面MDF,并说明理由;(2)在(1)的条件下,平面MDF将几何体ADE-BCF分成两部分,求空间几何体M-DEF与空间几何体ADM BCF的体积之比.解:(1)当M是线段AE的中点时,AC∥平面MDF.理由如下:连接CE交DF于点N,连接MN.因为M,N分别是AE,CE的中点,所以MN∥AC.又因为MN⊂平面MDF,AC⊄平面MDF,所以AC∥平面MDF.(2)将几何体ADE-BCF补成三棱柱ADE-B′CF,如图所示,三棱柱ADE-B′CF的体积为V=S△ADE·CD=×2×2×4=8,则几何体ADE-BCF的体积=-=8-×(×2×2)×2=.因为三棱锥M-DEF的体积=×(×2×4)×1=,所以=-=,所以两几何体的体积之比为∶=1∶4.第3节空间图形的基本关系与公理一、选择题1.设m,n是两条不同的直线,α,β是两个不同的平面( C )(A)若m∥α,n∥α,则m∥n(B)若m∥α,m∥β,则α∥β(C)若m∥n,m⊥α,则n⊥α(D)若m∥α,α⊥β,则m⊥β解析:设直线a⊂α,b⊂α,a∩b=A,因为m⊥α,所以m⊥a,m⊥b.又n∥m,所以n⊥a,n⊥b,所以n⊥α.故选C.2.下列命题中,错误的是( D )(A)平行于同一平面的两个不同平面平行(B)一条直线与两个平行平面中的一个相交,则必与另一个平面相交(C)如果两个平面不垂直,那么其中一个平面内一定不存在直线与另一个平面垂直(D)若直线不平行于平面,则此直线与这个平面内的直线都不平行解析:当直线l在平面α内,即l⊂α时,直线l不平行于平面α,但平面α内存在直线与直线l平行,可知D选项错误,故选D.3.下列四个命题:①若一个平面内的两条直线都与另一个平面平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是( D )(A)①和②(B)②和③(C)③和④(D)②和④解析:①显然错误,因为这两条直线相交才满足条件;②成立;③错误,这两条直线可能平行、相交,也可能异面;④成立,用反证法容易证明.故选D.4.若α,β是两个相交平面,则在下列命题中,真命题的序号为( C )①若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线;②若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直;③若直线m⊂α,则在平面β内,不一定存在与直线m垂直的直线;④若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线.(A)①③(B)②③(C)②④(D)①④解析:若α⊥β且直线m⊥α,则在平面β内,一定存在与直线m平行的直线,所以①错误;若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直,故②正确;若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线,故③错误,④正确,故选C.5.设不在同一条直线上的A,B,C三点到平面α的距离相等,且A∉α,则( B )(A)α∥平面ABC(B)△ABC中至少有一条边平行于α(C)△ABC中至多有两条边平行于α(D)△ABC中只可能有一条边平行于α解析:因为A∉α,所以A,B,C均不在平面α内.当A,B,C三点在平面α的同侧时,α∥平面ABC,此时△ABC的三条边都平行于α,排除C,D;当A,B,C三点不在平面α的同侧时,易知△ABC中只有一条边平行于α,此时平面α和平面ABC相交,故选B.6.若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的( B )(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件解析:因为l⊥m,m⊥α,所以l∥α或l⊂α.故充分性不成立.若l∥α,m⊥α,一定有l⊥m.故必要性成立.选B.二、填空题7.长方体ABCD-A1B1C1D1的底面是边长为1的正方形,点E在侧棱AA1上(不与A,A1重合),满足∠C1EB=90°,则异面直线BE与C1B1所成的角为,侧棱AA1的长的最小值为.解析:在长方体ABCD-A1B1C1D1中,CB⊥平面ABB1A1,所以∠CBE=90°,又C1B1∥BC,所以异面直线BE与C1B1所成的角为90°.连接BC1,设AA1=x,AE=m(m>0),则有BE2=1+m2,C1E2=(x-m)2+2,C1B2=1+x2,因为∠C1EB=90°,所以C1B2=C1E2+BE2,即1+x2=(x-m)2+2+1+m2,即m2-mx+1=0,所以x=m+≥2,当且仅当m=,即m=1时,“=”成立.答案:90° 28.四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A1-BCD,使平面A1BD⊥平面BCD,给出下列结论:(1)A1C⊥BD;(2)∠BA1C=90°;(3)四面体A1-BCD的体积为.其中正确的命题是.(把所有正确命题的序号都填上) 解析:若A1C⊥BD,因为BD⊥CD,A1C∩CD=C,所以BD⊥平面A1CD,所以BD⊥A1D.而由A 1B=AB=1,A1D=AD=1,BD=,得A1B⊥A1D,与BD⊥A1D矛盾,故(1)错.因为CD⊥BD,平面BCD⊥平面A1BD,所以CD⊥平面A1BD,则CD⊥A1B.又A1B⊥A1D,A1D∩CD=D,所以A1B⊥平面A1CD,则A1B⊥A1C,故(2)正确.由(2)知==×·A1D·DC·A1B=,故(3)错.答案:(2)9.在正方体ABCD A 1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线有条.解析:在A1D1上任取一点P,过点P与直线EF作一个平面α,因为CD 与平面α不平行,所以它们相交,设α∩CD=Q,连接PQ,则PQ与EF必然相交.由点P的任意性,知有无数条直线与A1D1,EF,CD都相交.答案:无数10.如图,在直三棱柱ABC-A1B1C1中,底面为直角三角形.∠ACB =90°,AC=6,BC=CC 1=,P是BC1上一动点,则CP+PA1的最小值为.解析:连接A1B,将△A1BC1与△CBC1同时展开形成一个平面四边形A1BCC1,则此时对角线CP+PA1=A1C达到最小,在等腰直角三角形△BCC1中,BC1=2,∠CC1B=45°,在△A 1BC1中,A1B==2,A1C1=6,BC1=2,所以A1+B=A1B2,即∠A1C1B=90°.对于展开形成的四边形A1BCC1,如图,在△A 1C1C中,C1C=,A1C1=6,∠A1C1C=135°,由余弦定理有,CP+PA 1=A1C===5.答案:511. 如图,三棱锥A BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是.解析:如图所示,连接DN,取线段DN的中点K,连接MK,CK.因为M为AD的中点,所以MK∥AN,所以∠KMC为异面直线AN,CM所成的角.因为AB=AC=BD=CD=3,AD=BC=2,N为BC的中点,由勾股定理求得AN=DN=CM=2,所以MK=.在Rt△CKN中,CK==.在△CKM中,由余弦定理,得cos∠KMC===.答案:12.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE 翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中不正确的是.①BM是定值;②点M在某个球面上运动;③存在某个位置,使DE⊥A1C;④存在某个位置,使MB∥平面A1DE.解析:取DC中点F,连接MF,BF,MF∥A1D且MF=A1D,FB∥ED且FB=ED,所以∠MFB=∠A1DE.由余弦定理可得MB2=MF2+FB2-2MF·FB·cos∠MFB 是定值,所以M是在以B为圆心,MB为半径的球上,可得①②正确;由MF∥A1D与FB∥ED可得平面MBF∥平面A1DE,可得④正确;A1C在平面ABCD中的投影与AC重合,AC与DE不垂直,可得③不正确.答案:③三、解答题13.如图所示,等腰直角三角形ABC中,∠A=90°,BC=,DA⊥AC,DA⊥AB,若DA=1,且E为DA的中点.求异面直线BE与CD所成角的余弦值.解:如图所示,取AC的中点F,连接EF,BF,在△ACD中,E,F分别是AD,AC的中点,所以EF∥CD.所以∠BEF或其补角即为异面直线BE与CD所成的角.在Rt△EAB中,AB=AC=1,AE=AD=,所以BE=.在Rt△EAF中,AF=AC=,AE=,所以EF=.在Rt△BAF中,AB=1,AF=,所以BF=.在等腰三角形EBF中,cos∠FEB===.所以异面直线BE与CD所成角的余弦值为.14.已知正方体ABCD-A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D,B,F,E四点共面;(2)若A1C交平面DBFE于R点,则P,Q,R三点共线.证明:(1)如图所示,因为EF是△D1B1C1的中位线,所以EF∥B1D1.在正方体ABCD-A1B1C1D1中,B1D1∥BD,所以EF∥BD.所以EF,BD确定一个平面.即D,B,F,E四点共面.(2)在正方体ABCD-A1B1C1D1中,设平面A1ACC1确定的平面为α,又设平面BDEF为β.因为Q∈A1C1,所以Q∈α.又Q∈EF,所以Q∈β.则Q是α与β的公共点,同理,P点也是α与β的公共点.所以α∩β=PQ.又A1C∩β=R,所以R∈A1C,则R∈α且∈β.则R∈PQ,故P,Q,R三点共线.15.在长方体ABCD A 1B1C1D1的A1C1面上有一点P(如图所示,其中P点不在对角线B1D1)上.(1)过P点在空间内作一条直线l,使l∥直线BD,应该如何作图?并说明理由;(2)过P点在平面A1C1内作一条直线m,使m与直线BD成α角,其中α∈(0°,90°],这样的直线有几条,应该如何作图?解:(1)连接B1D1,BD,在平面A1C1内过P点作直线l,使l∥直线B1D1,则l即为所求作的直线.因为直线B1D1∥直线BD,l∥直线B1D1,所以l∥直线BD.如图(1).(2)在平面A1C1内作直线m,使直线m与B1D1相交成α角,因为BD∥B1D1,所以直线m与直线BD也成α角,即直线m为所求作的直线,如图(2).由图(2)知m与BD是异面直线,且m与BD所成的角α∈(0,90°].当α=90°时,这样的直线m有且只有一条,当α≠90°时,这样的直线m 有两条.第4节直线、平面平行的判定与性质一、选择题1.若直线l∥平面α,直线a⊂平面α,则l与a的位置关系是( D )(A)l∥a (B)l与a异面(C)l与a相交 (D)l与a没有公共点解析:因为直线平行于平面,那么l与平面内的任何一条直线都没有公共点,因此l与a的位置关系是没有公共点,选D.2.下列条件能推出平面α∥平面β的是( D )(A)存在一条直线a,a∥α,a∥β(B)存在一条直线a,a⊂α,a∥β(C)存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥α(D)存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α解析:因为根据面面平行的判定定理可知,如果存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α,则可以利用线线平行得到面面平行,选D.3.已知直线l,m,平面α,β,则下列命题中:①若α∥β,l⊂α,则l∥β②若α⊥β,l⊥α,则l∥β③若l∥α,m⊂α,则l∥m④若α⊥β,α∩β=l,m⊥l,则m⊥β,其中真命题有( B )(A)0个(B)1个(C)2个(D)3个解析:当两个平面平行时,一个平面上的线与另一个平面平行,故①正确;一条直线垂直于两个垂直平面中的一个平面,那么这条直线平行于或包含于另一个平面,故②不正确;④不正确;③中l,m的关系是不相交,故③不正确,故选B.4.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( B )(A)①③(B)①④(C)②③(D)②④解析:对图①,构造AB所在的平面,即对角面,可以证明这个对角面与平面MNP平行,由线面平行的定义可得AB∥平面MNP;对图④,通过证明AB∥PN得到AB∥平面MNP;对于②,证MP中点为K,延长BA,KN则相交,所以BA与平面MNP相交,②错;对于③平面MNP与直线AB相交于点B,③错.故选B.5.类比平面几何中的定理“设a,b,c是三条直线,若a⊥c,b⊥c,则a∥b”,得出如下结论:①设a,b,c是空间的三条直线,若a⊥c,b⊥c,则a∥b;②设a,b是两条直线,α是平面,若a⊥α,b⊥α,则a∥b;③设α,β是两个平面,m是直线,若m⊥α,m⊥β,则α∥β;④设α,β,γ是三个平面,若α⊥γ,β⊥γ,则α∥β.其中正确命题的个数是( B )(A)1 (B)2 (C)3 (D)4解析:①错;②垂直于同一个平面的两条直线平行,正确;③垂直于同一条直线的两个平面平行,正确;④错;两个平面也可能相交.6.在空间中,下列命题正确的是( D )(A)平面α内的一条直线a垂直于平面β内的无数条直线,则α⊥β(B)若直线m与平面α内的一条直线平行,则m∥α(C)若平面α⊥β,且α∩β=l,则过α内一点P与l垂直的直线垂直于平面β(D)若直线a与平面α内的无数条直线都垂直,则不能说一定有a⊥α解析:直线a与平面α内的任意直线都垂直,则有a⊥α,所以D正确.二、填空题7.点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF= .解析:取BC的中点D,连接ED与FD,因为E,F分别是SC和AB的中点,点D为BC的中点所以ED∥SB,FD∥AC,而SB⊥AC,SB=AC=2,则三角形EDF为等腰直角三角形,则ED=FD=1,即EF=.答案:8.正四棱锥S ABCD的底面边长为2,高为2,E是边BC的中点,动点P 在这个棱锥表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为.解析:由题意知,点P的轨迹为如图所示的三角形EFG,其中G,F为其所在棱的中点,所以EF=BD=,GE=GF=SB=,所以轨迹的周长为+.答案:+9.将边长为2,一个内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E,F分别为AC,BD的中点,则下列命题中正确的是.①EF∥AB;②EF⊥BD;③EF有最大值,无最小值;④当四面体ABCD的体积最大时,AC=;⑤AC垂直于截面BDE.解析:因为将边长为2,一个内角为60°的菱形ABCD沿较短对角线BD 折成四面体ABCD,点E,F分别为AC,BD的中点,则可知EF⊥BD,当四面体ABCD的体积最大时,AC=,AC垂直于截面BDE成立.答案:②④⑤10.已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于A,C,过点P的直线n与α,β分别交于B,D且PA=6,AC=9,PD=8,则BD的长为.解析:因为平面α∥平面β,所以AB∥CD,①当P在两平面外时,==,所以=,所以BD=.②当P在两平面之间时,=,所以=,所以BD=24,所以BD的长为或24.答案:或2411.给出下列四个命题:①过平面外一点,作与该平面成θ角的直线一定有无穷多条;②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;③对确定的两条异面直线,过空间任意一点有且只有一个平面与这两条异面直线都平行;④对两条异面的直线,都存在无穷多个平面与这两条直线所成的角相等.其中正确的命题序号为.解析:①中,成90度角的时候,就只有一条,因此错误.②中是线面平行的性质定理,显然成立.③不正确.④中,利用等角定理,可知成立. 答案:②④12.侧棱长为2的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°,过A 作截面AEF,则截面△AEF周长的最小值为.解析:沿着侧棱VA把正三棱锥V ABC展开在一个平面内,则设VA的另一边为VA′,则AA′即为截面△AEF周长的最小值,且∠AVA′=3×40=120°.△VAA′中,由余弦定理可得AA′=6.答案:6三、解答题13.已知长方体ABCD-A1B1C1D1中,底面ABCD为正方形,AB=4,AA1=2,点E 在棱C1D1上,且D1E=3.(1)试在棱CD上确定一点E1,使得直线EE1∥平面D1DB,并证明;(2)若动点F在底面ABCD内,且AF=2,请说明点F的轨迹,并探求EF 长度的最小值.解:(1)取CD的四等分点E1,使得DE1=3,则有EE1∥平面D1DB.证明如下:因为D1E∥DE1且D1E=DE1,所以四边形D1EE1D为平行四边形,则D1D∥EE1,因为DD1⊂平面D1DB,EE1⊄平面D1DB,所以EE1∥平面D1DB.(2)因为AF=2,所以点F在平面ABCD内的轨迹是以A为圆心,半径等于2的四分之一圆弧.因为EE1∥DD1,D1D⊥平面ABCD,所以E1E⊥平面ABCD,故EF==.所以当E1F的长度取最小值时,EF的长度最小,此时点F为线段AE1和四分之一圆弧的交点,即E1F=E1A-AF=5-2=3,所以EF==.即EF长度的最小值为.14.在正方体ABCD-A1B1C1D1中,棱长为2,E是棱CD的中点,P是棱AA1的中点,(1)求证:PD∥平面AB1E;(2)求三棱锥B-AB1E的体积.(1)证明:取AB1中点Q,连接PQ,则PQ为中位线,PQ A1B1,而正方体ABCD-A1B1C1D1,E是棱CD的中点,故DE A1B1,所以PQ DE,所以四边形PQED为平行四边形.所以PD∥QE,而QE⊂平面AB1E,PD⊄平面AB1E,故PD∥平面AB1E.(2)解:正方体ABCD-A1B1C1D1中,BB1⊥平面ABE,故BB1为高,BB1=2,因为CD∥AB,所以S△ABE=S△ABC=AB·BC=×2×2=2.故==BB1·S△ABC=.15.如图,在四面体PABC中,PA=PB,CA=CB,D,E,F,G分别是PA,AC,CB,BP的中点.(1)求证:D,E,F,G四点共面;(2)求证:PC⊥AB;(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,PC=,求四面体PABC的体积.(1)证明:依题意DG∥AB,EF∥AB,所以DG∥EF,DG,EF共面,从而D,E,F,G四点共面.(2)证明:取AB中点为O,连接PO,CO.因为PA=PB,CA=CB,所以PO⊥AB,CO⊥AB,因为PO∩CO=O,所以AB⊥平面POC,PC⊂平面POC,所以AB⊥PC.(3)解:因为△ABC和△PAB是等腰直角三角形,所以PO=CO=AB=1,因为PC=,OP2+OC2=PC2,所以OP⊥OC,又PO⊥AB,且AB∩OC=O,所以PO⊥平面ABC,=PO·S△ABC=×1×2×1×=.第5节直线、平面垂直的判定与性质一、选择题1.已知直线l,m和平面α, 则下列命题正确的是( C )(A)若l∥m,m⊂α,则l∥α(B)若l∥α,m⊂α,则l∥m(C)若l⊥α,m⊂α,则l⊥m(D)若l⊥m,l⊥α,则m∥α解析:A项中直线l与平面α可能平行,可能直线在平面内;B项中直线l,m平行或异面;C项中当直线垂直于平面时,直线垂直于平面内任意直线;D项中直线m与平面α平行或直线在平面内.2.在Rt△ABC中,∠ABC=90°,P为△ABC所在平面外一点,PA⊥平面ABC,则四面体P ABC中共有直角三角形个数为( A )(A)4 (B) 3 (C) 2 (D) 1解析:因为PA⊥平面ABC,AB⊥BC,所以PA⊥AB,PA⊥AC,PB⊥CB,所以△ABC,△PBC, △ABP, △APC都是直角三角形,故选A.3.已知直线m,n和平面α,β满足m⊥n,m⊥α,α⊥β,则( C )(A)n⊥β (B)n∥β,或n⊂β(C)n∥α或n⊂α(D)n⊥α解析:由题意画出图形,容易判断选项.由于直线m⊥n,m⊥α,α⊥β,选项A,中线面可能相交,也可能垂直,选项B中,n与β还可能相交,错误,选项D中,直线不能垂直于平面,故结合图象不难得到选项为C.4.正方体的棱长为1,C,D,M分别为三条棱的中点,A,B是顶点,那么点M到截面ABCD的距离是( B )(A)(B)(C)(D)解析:过M作AB的垂线MN交AB于N,连接CN.由于CM⊥AB,MN⊥AB,则AB⊥平面CMN,所以,M到面ABCD的距离h是直角三角形CMN的斜边CN上的高.由于BM=,CM=1,MN=,CN=,则结合=求得h=.故选B.。
高三精选立体几何大题30题(含详细解答)
1．如下图，一个等腰直角三角形的硬纸片ABC中，∠ACB＝90°，AC＝4cm，CD是斜边上的高沿CD把△ABC折成直二面角．
（1）如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A－CD－B是直二面角？证明你的结论．
（2）试在平面ABC上确定一个P，使DP与平面ABC内任意一条直线都垂直，证明你的结论．
∴ ，∴ ．
∴ ．
5．已知：ABCD是矩形，设PA=a，PA⊥平面ABCD.M、N分别是AB、PC的中点.
（Ⅰ）求证：MN⊥AB；
（Ⅱ）若PD=AB，且平面MND⊥平面PCD，求二面角P—CD—A的大小；
（Ⅲ）在（Ⅱ）的条件下，求三棱锥D—AMN的体积.
（Ⅰ）连结AC，AN.由BC⊥AB，AB是PB在
.
6．如图，正方体ABCD—A1B1C1D1中，P、M、N
分别为棱DD1、AB、BC的中点。
（I）求二面角B1—MN—B的正切值；
（II）证明：PB⊥平面MNB1；
（III）画出一个正方体表面展开图，使其满足
“有4个正方形面相连成一个长方形”的条件，
（Ⅲ）求二面角C-BE-D的正切值．
证：（Ⅰ）取CE中点M，连结FM，BM，则有 ．
∴四边形AFMB是平行四边形．
∴AF//BM，
∵ 平面BCE，
平面BCE，
∴AF//平面BCE．
（Ⅱ）由于DE⊥平面ACD，
则DE⊥AF．
又△ACD是等边三角形，则AF⊥CD．而CD∩DE=D，因此AF⊥平面CDE．
= × ×3×3×
= （10分）
解（Ⅲ）连CF，
∵CB⊥平面A1B1BA，又BF⊥AE，
由三垂线定理知，CF⊥AE.
高三精选立体几何大题(每日一题题目).
1精选立体几何大题1. 如图, 已知正四棱柱 ABCD — A 1B 1C 1D 1的底面边长为 3, 侧棱长为 4, 连结 A 1B , 过 A 作 AF ⊥ A 1B 垂足为 F ,且 AF 的延长线交 B 1B 于 E 。
(Ⅰ求证:D 1B ⊥平面 AEC ; (Ⅱ求三棱锥 B — AEC 的体积; (Ⅲ求二面角 B —AE — C 的大小 .2.如图,正三棱柱 ABC — A 1B 1C 1的底面边长为 1,点M 在 BC 上, △ AMC 1是以 M 为直角顶点的等腰直角三角形 . (I 求证:点 M 为BC 的中点; (Ⅱ求点 B 到平面 AMC 1的距离; (Ⅲ求二面角 M — AC 1— B 的正切值 .3.如图,已知多面体 ABCDE 中, AB ⊥平面 ACD , DE ⊥平面 ACD , 三角形ACD 是正三角形,且 AD=DE=2, AB=1, F 是 CD 的中点.(Ⅰ求证:AF ∥平面 BCE ; (Ⅱ求多面体 ABCDE 的体积; (Ⅲ求二面角 C-BE-D 的正切值.4.已知:ABCD 是矩形,设 PA=a , PA ⊥平面 ABCD.M 、 N 分别是 AB 、 PC 的中点 .(Ⅰ求证:MN ⊥ AB ;(Ⅱ若 PD=AB,且平面 MND ⊥平面 PCD ,求二面角 P — CD — A 的大小; (Ⅲ在(Ⅱ的条件下,求三棱锥 D — AMN 的体积 .A C A 1B 1C 1 第 2题图25.如图,四棱锥 P — ABCD 的底面是正方形 ,PA ⊥底面 ABCD , PA=AD=2,点 M 、分别在棱 PD 、 PC 上,且 PC ⊥平面 AMN. (Ⅰ求证:AM ⊥ PD ;(Ⅱ求二面角 P — AM — N 的大小;(Ⅲ求直线 CD 与平面 AMN 所成角的大小 .6.如图,在直三棱柱 ABC — A 1B 1C 1中,∠ ACB=90°. BC=CC1=a , AC=2a . (I 求证:AB 1⊥ BC 1;(II 求二面角 B — AB 1— C 的大小; (III 求点 A 1到平面 AB 1C 的距离 .7.在长方体 ABCD -A 1B 1C 1D 1中,已知 AB =BC =2, BB 1=3, 连接 BC 1,过 B 1作 B 1E ⊥ BC 1交 CC 1于点 E (Ⅰ求证:AC 1⊥平面 B 1D 1E ; (Ⅱ求三棱锥 C 1-B 1D 1E 1的体积;(Ⅲ求二面角 E -B 1D 1-C 1的平面角大小8.在矩形 ABCD 中, AB =4, BC =3, E 为 DC 的中点,沿 AE 将△ AED 折起,使二面角 D -AE -B 为 60 .(Ⅰ求 DE 与平面 AC 所成角的大小; (Ⅱ求二面角 D -EC -B 的大小.D BC AB C E第 8题图39.直三棱柱 ABC -A 1B 1C 1中, AC =CB =AA 1=2,∠ ACB =90°, E 是 BB 1的中点,D ∈ AB ,∠ A 1DE =90°.(Ⅰ求证:CD ⊥平面 ABB 1A 1; (Ⅱ求二面角 D -A 1C -A 的大小 .10.如图,正三棱柱 AC 1中, AB=2, D 是 AB 的中点, E 是 A 1C 1的中点, F 是 B 1B 中点,异面直线 CF 与 DE 所成的角为 90°. (1求此三棱柱的高;(2求二面角 C — AF — B 的大小 .11. 已知 ABCD 是矩形, PD ⊥平面 ABCD , PD=DC=a, AD ,M 、 N 分别是 AD 、 PB 的中点。
2020版高考文科数学第一轮复习练习：第八章 立体几何 课后跟踪训练47 Word版含解析
课后跟踪训练(四十七) 基础巩固练一、选择题1．(2018·黑龙江大庆月考)有以下三种说法，其中正确的是( )①若直线a与平面α相交，则α内不存在与a平行的直线；②若直线b∥平面α，直线a与直线b垂直，则直线a不可能与α平行；③直线a，b满足a∥b，则a平行于经过b的任何平面．A．①②B．①③C．②③D．①[解析] 对于①，若直线a与平面α相交，则α内不存在与a平行的直线，是真命题，故①正确；对于②，若直线b∥平面α，直线a 与直线b垂直，则直线a可能与α平行，故②错误；对于③，若直线a，b 满足a∥b，则直线a与直线b可能共面，故③错误．故选D.[答案] D2．(2019·辽宁丹东期末)已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是( )A．若α，β垂直于同一平面，则α与β平行B．若m，n平行于同一平面，则m与n平行C．若α，β不平行，则在α内不存在与β平行的直线D．若m，n不平行，则m与n不可能垂直于同一平面[解析] 由于α，β垂直于同一平面，则α与β平行或相交，利用正方体可判断，故A不正确；若m，n平行于同一平面，则m与n 可能平行、相交或异面，故B不正确；利用正方体中的侧面与底面，侧面的上底面的棱与下底面的棱，能够找到平行线，所以C不正确；D 正确．故选D.[答案] D3．(2019·河北石家庄模拟)过三棱柱ABC－A1B1C1的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有( ) A．4条B．6条C．8条D．12条[解析] 如图，H，G，F，I是相应线段的中点，故符合条件的直线只能出现在平面HGFI中，有FI，FG，GH，HI，HF，GI共6条直线，故选B.[答案] B4．(2019·湖南长沙二模)已知m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的是( )A．m∥α，n∥α，则m∥n B．m∥n，m∥α，则n∥αC．m⊥α，m⊥β，则α∥βD．α⊥γ，β⊥γ，则α∥β[解析] 对于A，平行于同一平面的两条直线可能相交，可能平行，也可能异面，故A不正确；对于B，m∥n，m∥α，则n∥α或n⊂α，故B不正确；对于C，利用垂直于同一直线的两个平面平行，可知C正确；对于D，因为垂直于同一平面的两个平面的位置关系是相交或平行，故D不正确．故选C.[答案] C5．(2017·全国卷Ⅰ)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是( )[解析] 解法一：对于选项B，如图所示，连接CD，因为AB∥CD，M，Q分别是所在棱的中点，所以MQ∥CD，所以AB∥MQ，又AB⊄平面MNQ，MQ⊂平面MNQ，所以AB∥平面MNQ.同理可证选项C，D 中均有AB∥平面MNQ.故选A.解法二：对于选项A ，设正方体的底面对角线的交点为O (如图所示)，连接OQ ，则OQ ∥AB ，因为OQ 与平面MNQ 有交点，所以AB 与平面MNQ 有交点，即AB 与平面MNQ 不平行，故选A.[答案] A 二、填空题6．(2019·广东顺德质检)如图所示，四棱锥P －ABCD 的底面是一直角梯形，AB ∥CD ，BA ⊥AD ，CD ＝2AB ，PA ⊥底面ABCD ，E 为PC 的中点，则BE 与平面PAD 的位置关系为________．[解析] 取PD 的中点F ，连接EF 、AF ，在△PCD 中，EF 綊CD .12又∵AB ∥CD 且CD ＝2AB ，∴EF 綊AB ，∴四边形ABEF 是平行四边形，∴EB ∥AF .又∵EB ⊄平面PAD ，AF ⊂平面PAD ，∴BE ∥平面PAD .[答案] 平行7．(2018·湖南株洲调研)如图所示，正方体ABCD －A 1B 1C 1D 1中，AB ＝2，点E 为AD 的中点，点F 为CD 上一点．若EF ∥平面AB 1C ，则线段EF 的长度等于________．[解析] 在正方体ABCD －A 1B 1C 1D 1中，AB ＝2，∴AC ＝2.又E 2为AD 中点，EF ∥平面AB 1C ，EF ⊂平面ADC ，平面ADC ∩平面AB 1C ＝AC ，∴EF ∥AC ，∴F 为DC 中点，∴EF ＝AC ＝.122[答案] 28．棱长为2的正方体ABCD －A 1B 1C 1D 1中，M 是棱AA 1的中点，过C ，M ，D 1作正方体的截面，则截面的面积是________．[解析] 由面面平行的性质知截面与面AB 1的交线MN 是△AA 1B的中位线，所以截面是梯形CD 1MN ，易求其面积为.92[答案] 92三、解答题9.如图所示，四边形ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH.求证：AP∥GH.[证明] 如图所示，连接AC交BD于点O，连接MO，∵四边形ABCD是平行四边形，∴O是AC的中点，又M是PC的中点，∴AP∥OM.又MO⊂平面BMD，PA⊄平面BMD，∴PA∥平面BMD.∵平面PAHG∩平面BMD＝GH，且PA⊂平面PAHG，∴PA∥GH.10.(2019·南通模拟)如图所示，斜三棱柱ABC －A 1B 1C 1中，点D ，D 1分别为AC ，A 1C 1上的点．(1)当等于何值时，BC 1∥平面AB 1D 1?A 1D 1D 1C 1(2)若平面BC 1D ∥平面AB 1D 1，求的值．AD DC[解] (1)如图所示，取D 1为线段A 1C 1的中点，此时＝1.连接A 1B ，A 1D 1D 1C 1交AB 1于点O ，连接OD 1.由棱柱的性质知，四边形A 1ABB 1为平行四边形，∴点O 为A 1B 的中点．在△A 1BC 1中，点O ，D 1分别为A 1B ，A 1C 1的中点，∴OD 1∥BC 1.又∵OD 1⊂平面AB 1D 1，BC 1⊄平面AB 1D 1，∴BC 1∥平面AB 1D 1.∴当＝1时，BC 1∥平面AB 1D 1.A 1D 1D 1C 1(2)由平面BC 1D ∥平面AB 1D 1，且平面A 1BC 1∩平面BC 1D ＝BC 1，平面A 1BC 1∩平面AB 1D 1＝D 1O ，得BC 1∥D 1O ，∴＝，A 1D 1D 1C 1A 1O OB又由题(1)可知＝，＝1，∴＝1，即＝1.A 1D 1D 1C 1DC AD A 1O OB DC AD AD DC能力提升练11．如图，在正方体ABCD －A 1B 1C 1D 1中，棱长为a ，M 、N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝，2a3则MN 与平面BB 1C 1C 的位置关系是( )A ．相交B ．平行C ．垂直D ．不能确定[解析] 连接CD 1、AD 1，在CD 1上取点P ，使D 1P ＝，连接MP 、2a 3NP ，∴MP ∥BC ，PN ∥AD 1∥BC 1，∴MP ∥平面BB 1C 1C ，PN ∥平面BB 1C 1C ，∴平面MNP ∥平面BB 1C 1C ，∴MN ∥平面BB 1C 1C .故选B.[答案] B12．(2018·江西高安期末)三棱柱ABC－A1B1C1中，侧棱AA1垂直于底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC的中点，则下列叙述正确的是( )①CC1与B1E是异面直线；②AE与B1C1是异面直线，且AE⊥B1C1；③AC⊥平面ABB1A1；④A1C1∥平面AB1E.A．②B．①③C．①④D．②④[解析] 对于①，CC1，B1E都在平面BB1C1C内，故错误；对于②，AE，B1C1为在两个平行平面中且不平行的两条直线，底面三角形ABC 是正三角形，E是BC中点，所以AE⊥BC，又B1C1∥BC，故AE与B1C1是异面直线，且AE⊥B1C1，故正确；对于③，上底面ABC是一个正三角形，不可能存在AC ⊥平面ABB 1A 1，故错误；对于④，A 1C 1所在的平面与平面AB 1E 相交，且A 1C 1与交线有公共点，故错误．故选A.[答案] A13．已知正方体ABCD －A 1B 1C 1D 1的棱长为1，点P 是面AA 1D 1D 的中心，点Q 是B 1D 1上一点，且PQ ∥面AB 1，则线段PQ 长为__________．[解析] 连接AB 1、AD 1，∵点P 是平面AA 1D 1D 的中心，∴点P 是AD 1的中点，∵PQ ∥平面AB 1，PQ ⊂平面D 1AB 1，平面D 1AB 1∩平面AB 1＝AB 1，∴PQ ∥AB 1，∴PQ ＝AB 1＝.1222[答案] 2214．如图所示，平面α∥平面β，点A ∈α，点C ∈α，点B ∈β，点D∈β，点E，F分别在线段AB，CD上，且AE∶EB＝CF∶FD.(1)求证：EF∥平面β；(2)若E，F分别是AB，CD的中点，AC＝4，BD＝6，且AC，BD 所成的角为60°，求EF的长．[解] (1)证明：①当AB，CD在同一平面内时，由平面α∥平面β，平面α∩平面ABDC＝AC，平面β∩平面ABDC＝BD知，AC∥BD.∵AE∶EB＝CF∶FD，∴EF∥BD.又EF⊄β，BD⊂β，∴EF∥平面β.②当AB与CD异面时，如图所示，设平面ACD∩平面β＝DH，且DH＝AC，∵平面α∥平面β，平面α∩平面ACDH＝AC，∴AC∥DH，∴四边形ACDH是平行四边形，在AH上取一点G，使AG∶GH＝CF∶FD，连接EG，FG，BH.又∵AE∶EB＝CF∶FD＝AG∶GH，∴GF∥HD，EG∥BH.又EG∩GF＝G，BH∩HD＝H，∴平面EFG∥平面β.又EF⊂平面EFG，∴EF∥平面β.综合①②可知，EF∥平面β.(2)如图所示，连接AD，取AD的中点M，连接ME，MF.∵E，F分别为AB，CD的中点，∴ME∥BD，MF∥AC，且ME ＝BD ＝3，MF ＝AC ＝2.1212∴∠EMF 为AC 与BD 所成的角或其补角，∴∠EMF ＝60°或120°.∴在△EFM 中，由余弦定理得EF ＝ME 2＋MF 2－2ME ·MF ·cos ∠EMF＝ 32＋22±2×3×2×12，13±6即EF ＝或EF ＝.719拓展延伸练15．如图，透明塑料制成的长方体容器ABCD －A 1B 1C 1D 1内灌进一些水，固定容器底面一边BC 于地面上，再将容器倾斜，随着倾斜度的不同，有下面四个命题：①没有水的部分始终呈棱柱形；②水面EFGH 所在四边形的面积为定值；③棱A 1D 1始终与水面所在平面平行；④当容器倾斜如图所示时，BE ·BF 是定值．其中正确的个数是( )A ．1B ．2C ．3D ．4[解析] 由题图，显然①是正确的，②是错的；对于③因为A 1D 1∥BC ，BC ∥FG ，所以A 1D 1∥FG 且A 1D 1⊄平面EFGH ，所以A 1D 1∥平面EFGH (水面)．所以③是正确的；因为水是定量的(定体积V )．所以S △BEF ·BC ＝V ，即BE ·BF ·BC ＝V .12所以BE ·BF ＝(定值)，即④是正确的，故选C.2V BC[答案] C 16.(2019·河北承德模拟)如图所示，在正四棱柱ABCD －A 1B 1C 1D 1中，E ，F ，G ，H 分别是棱CC 1，C 1D 1，D 1D ，DC 的中点，N 是BC 的中点，点M 在四边形EFGH 及其内部运动，则M 只需满足条件________时，就有MN ∥平面B 1BDD 1.(注：请填上你认为正确的一个条件即可，不必考虑全部可能情况)[解析] 连接HN ，FH ，FN ，则FH ∥DD 1，HN ∥BD ，∴FH ∥平面B 1BDD 1，HN ∥平面B 1BDD 1.∴平面FHN ∥平面B 1BDD 1，只需M ∈FH ，则MN ⊂平面FHN ，∴MN ∥平面B 1BDD 1.[答案] 点M 在线段FH 上(或点M 与点H 重合)。
湖南省2020届高三数学理一轮复习典型题专项训练：立体几何
湖南省2020届高三数学理一轮复习典型题专项训练立体几何一、选择、填空题1、（常德市2019届高三上学期检测）如图，网格线上小正方形的边长为1，粗实线画出的是某几何体的三视图，其正视图，侧视图均为等边三角形，则该几何体的体积为 A ．83(1)3π+ B ．43(2)π+ C ．43(2)3π+ D ．83(1)π+2、（衡阳八中2019届高三上学期第二次月考）某几何体的三视图如图所示，其中俯视图中六边形ABCDEF 是边长为1的正六边形，点G 为AF 的中点，则该几何体的外接球的表面积是（ C ）A.316π B. 318π C. 48164πD. 313148π3、（怀化市2019届高三统一模拟（二））某组合体的三视图如图所示.则该组合体的体积为 A. 4 B. 8 C.43 D. 834、（三湘名校教育联盟2019届高三第一次大联考）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为A.8B.16C.24D.485、（邵阳市2019届高三10月大联考）已知三棱锥P ABCA B C在球O的同一个-底面的3个顶点,,大圆上，且ABC-体积的最大值为23，则球△为正三角形，P为该球面上的点，若三棱锥P ABCO的表面积为( )A.12πB.16πC.32πD.64π6、（五市十校教研教改共同体2019届高三12月联考）已知E，F分别是三棱锥P ABC-的棱AP，EF=，则异面直线AB与PC所成的角为（）PC=，33BC的中点，6AB=，6A.120︒B.45︒C.30︒D.60︒7、（湘潭市2019届高三下学期第二次模拟）某几何体的三视图如图所示，则该几何体的体积为（）A. B. C. D.8、（益阳市2019届高三上学期期末考试）如图，—个圆柱从上部挖去半球得到几何体的正视图、侧28，则x =视图都是图1，俯视图是图2，若得到的几何体表面积为A.3B. 4C.5D.69、（永州市2019届高三上学期第二次模拟）如图，在正方体中，点在线段上运动，则下列判断中正确的是（）①平面平面；②直线平面；③异面直线与所成角的取值范围是；④三棱锥的体积不变.A. ① ②B. ①②④C. ③④D. ①④10、（岳阳市2019届高三教学质量检测（一模））个几何体的三视图如右图所示，已知这个几何10，则h为体的体积为3A. 23B.3 C. 33 D. 3511、（长郡中学2019届高三第六次月考）在三棱锥 P —ABC 中，PA 丄平面 ABC ，∠BAC =32π，AP=3，AB =32, Q 是边BC 上的一动点，且直线PQ 与平面ABC 所成角的最大值为3π，则三棱锥P —ABC 的外接球的表面积为A.π45B.π57C. π63D. π8412、（雅礼中学2019届高三第五次月考）如图1所示，是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图，其中DD 1＝1，若此几何体的俯视图如图2所示，则可以作为其正视图的是13、（株洲市2019届高三教学质量统一检测（一））已知正方体1111ABCD A B C D -的棱长为2，M 为CC 1的中点．若AM ⊥平面α，且B ∈平面α，则平面α截正方体所得截面的周长为（ ）A ．32+25B ． 4+42C ． 22+25D ．6214、（湖南师大附中2019届高三月考试卷（六））正四棱锥S －ABCD 的侧棱长与底面边长相等，E 为SC 的中点，则BE 与SA 所成角的余弦值为(C)A.13B.12C.33D.3215、（湖南湖北八市十二校（湖南师范大学附属中学、衡阳八中等）2019届高三第二次调研联考）已知三棱锥的四个顶点都在半径为3的球面上，，则该三棱锥体积的最大值是A ．B ．C ．D ． 6416、（湖南师大附中2019届高三月考试卷（六））已知三棱锥P －ABC 的四个顶点均在某球面上，PC 为该球的直径，△ABC 是边长为4的等边三角形，三棱锥P －ABC 的体积为163，则此三棱锥的外接球的表面积为__80π3__．参考答案：1、C2、C3、D4、B5、B6、D7、A8、B9、B 10、B 11、12、C 13、A 14、【解析】如图，设AC ∩BD ＝O ，连接OE ，因为OE 是△SAC 的中位线，故EO ∥SA ，则∠BEO 为BE 与SA 所成的角．设SA ＝AB ＝2a ，则OE ＝12SA ＝a ，BE ＝32SA ＝3a ，OB ＝22SA ＝2a ，所以△EOB 为直角三角形，所以cos ∠BEO ＝OE BE ＝a 3a ＝33，故选C.15、A 16、【解析】依题意，记三棱锥P －ABC 的外接球的球心为O ，半径为R ，点P 到平面ABC 的距离为h ，则由V P －ABC ＝13S △ABC h ＝13×⎝⎛⎭⎫34×42×h ＝163得h ＝433.又PC 为球O 的直径，因此球心O 到平面ABC 的距离等于12h ＝233.又正△ABC 的外接圆半径为r ＝AB 2sin 60°＝433，因此R 2＝r 2＋⎝⎛⎭⎫2332＝203，所以三棱锥P －ABC 的外接球的表面积为4πR 2＝80π3.二、解答题1、（常德市2019届高三上学期检测）如图，在直三棱柱111C B A ABC -中，21111==C A B A ，321=CC ， ︒=∠120BAC ，O 为线段11C B 的中点，P 为线段1CC 上一动点（异于点1C C 、），Q 为线段BC 上一动点，且OP QP ⊥；（Ⅰ）求证：平面1A PQ ^平面1A OP ；（Ⅱ）若PQ BO //，求直线OP 与平面PQ A 1所成角的正弦值.2、（衡阳八中2019届高三上学期第二次月考）如图，已知AB ⊥平面ACD ，DE ⊥平面ACD ，△ACD 为等边三角形，AD ＝DE ＝2AB ，F 为CD 的中点. (1)求证：AF ∥平面BCE ；(2)求二面角C －BE －D 的余弦值的大小.3、（怀化市2019届高三统一模拟（二））如图，在四棱锥P-ABCD 中，PC ⊥底面A BCD ，底面ABCD 是直角梯形，AB ⊥AD ，AB //CD ，AB=2AD=2CD=4，PC=4. (1)证明：当点E 在PB 上运动时，始终有平面EAC ⊥平面PBC (2)求锐二而角A- PB-C 的余弦值.4、（三湘名校教育联盟2019届高三第一次大联考）如图，四棱锥P-ABCD 中，底面ABCD 为正方形，PA 丄底面ABCD,且PA=2AB ，F 是AB 的中点，点E 在线段PC 上，且PE ＝PC 31. （1）证明：平面DEF 丄平面ABCD; （2）求二面角B-AE-D 的余弦值.5、（邵阳市2019届高三10月大联考）如图，菱形ABCD 的边长为4，60DAB =∠°，矩形BDFE 的面积为8，且平面BDFE ⊥平面ABCD .(1)证明：AC BE ⊥；(2)求二面角E AF D --的正弦值.6、（五市十校教研教改共同体2019届高三12月联考）如图，四棱锥P ABCD -中，PA ⊥底面ABCD ，底面ABCD 为直角梯形，90CDA BAD ∠=∠=︒，222AB AD DC ===E ，F 分别为PD ，PB 的中点.（1）求证：//CF 平面PAD ；（2）若截面CEF 与底面ABCD 所成锐二面角为4，求PA 的长度.7、（湘潭市2019届高三下学期第二次模拟）如图，四棱锥的底面是直角梯形，，，和是两个边长为2的正三角形，，为的中点，为的中点.（1）证明：平面.（2）在线段上是否存在一点，使直线与平面所成角的正弦值为？若存在，求出点的位置；若不存在，说明理由.8、（益阳市2019届高三上学期期末考试）五面体ABCDEF 中，ADEF 是等腰梯形,AD = 2,AB=2,AF=FE = ED=BC = 1，∠SAD=900，平面 BAF 丄平面 ADEF 。
高三立体几何大题线面角练习
高三立体几何大题线面角练习介绍:立体几何是数学中的一个重要分支，主要研究物体的形状和空间位置关系。
高三学生在准备高考时，需要熟练掌握立体几何的相关知识和解题方法。
本文档为高三学生提供一个包含线面角练题的大题集，旨在帮助学生加深对立体几何的理解并提升解题能力。
大题一: 平面与立体的关系题目: 已知一个平面与一个立方体的三个面相交，求证该平面与立方体的其他三个面也相交。
解析:考虑立方体的性质，每个顶点都是三个面的交点。
假设已知的平面与立方体的三个面相交，将其中的三个交点标记为$A$，$B$和$C$。
由于平面与立方体的其他三个面都经过$A$，$B$和$C$，所以可以得出结论：该平面与立方体的其他三个面也相交。
大题二: 线面角的计算题目: 在一个正方体中，一个角所在的三条边分别与三个不同的面平行，已知其中两个面的夹角为$60^\circ$，求该角的大小。
解析:设该角所在的三条边分别为$AB$，$AC$和$AD$，与三个面分别平行。
已知$AC$与$AD$所在的两个面的夹角为$60^\circ$，即$∠CAD=60^\circ$。
由于正方体的每个内角都是$90^\circ$，所以可知$∠BAD=180^\circ - ∠CAD - ∠ACD = 180^\circ - 60^\circ -90^\circ =30^\circ$。
因此，该角的大小为$30^\circ$。
大题三: 空间几何的应用题目: 已知一个球塔高$10\sqrt{3}$，上底半径为$10$，下底半径为$8$，求球与塔的交线的长度。
解析:根据题意，球与塔的交线可以看作是球与一个圆台的交线，而圆台的上下底半径分别为$10$和$8$，高为$10\sqrt{3}$。
通过计算，可以得到圆台的斜高为$2\sqrt{3}$。
根据球和圆台的交线特性，可以计算出交线的长度为$\sqrt{3}$倍的圆台底面周长。
因此，球与塔的交线的长度为$2\sqrt{3}$倍的$\pi \times 10 = 20\pi\sqrt{3}$。
2020届高考数学理一轮(新课标通用)单元质量测试： 第六章 立体几何 Word版含解析
单元质量测试(六)时间：120分钟满分：150分第Ⅰ卷(选择题，共60分)一、选择题(本大题共12小题，每小题5分，共60分)1．某空间几何体的三视图中，有一个是正方形，则该空间几何体不可能是()A．圆柱B．圆锥C．棱锥D．棱柱答案B解析易知仅圆锥的三视图中一定不会出现正方形，故选B．2．(2018·郑州检测)已知一三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一条直角边为2的直角三角形，则该三棱锥的正视图可能为()答案C解析由已知条件得直观图如图所示，正视图是直角三角形，中间的线是看不见的线P A形成的投影，应为虚线．故选C．3．已知各顶点都在一个球面上的正四棱柱的高为2，这个球的表面积为6π，则这个正四棱柱的体积为( )A ．1B ．2C ．3D ．4 答案 B解析 S 表＝4πR 2＝6π，∴R ＝62，设正四棱柱底面边长为x ，则x 2＋x 2＋22＝(2R )2，∴x ＝1．∴V 正四棱柱＝2．故选B ．4．(2018·贵阳模拟)设m ，n 为两条不同的直线，α，β为两个不同的平面，给出下列命题：①若m ⊥α，m ⊥β，则α∥β； ②若m ∥α，m ∥β，则α∥β； ③若m ∥α，n ∥α，则m ∥n ； ④若m ⊥α，n ⊥α，则m ∥n ．上述命题中，所有真命题的序号是( ) A ．①④ B ．②③ C ．①③ D ．②④ 答案 A解析 对于①，垂直于同一条直线的两个平面互相平行，所以①正确；对于②，平行于同一条直线的两个平面的位置关系不确定，所以②错误；对于③，平行于同一个平面的两条直线的位置关系不确定，所以③错误；对于④，垂直于同一个平面的两条直线互相平行，所以④正确．故选A ．5．(2018·太原三模)如图是某几何体的三视图，则这个几何体的体积是( )A ．2＋π2B ．2＋π3C．4＋π3D．4＋π2答案A解析由三视图可知，该几何体由一个半圆柱与三棱柱组成，这个几何体的体积V＝12×π×12×1＋12×(2)2×2＝2＋π2．故选A．6．(2018·江西赣州二模)某几何体的主视图和左视图如图1，它的俯视图的直观图是矩形O1A1B1C1，如图2，其中O1A1＝6，O1C1＝2，则该几何体的侧面积为()A．48 B．64 C．96 D．128答案C解析由题图2及斜二测画法可知原俯视图为如图所示的平行四边形OABC，设CB与y轴的交点为D，则易知CD＝2，OD＝2×22＝42，∴CO＝CD2＋OD2＝6＝OA，∴俯视图是以6为边长的菱形，由三视图知几何体为一个直四棱柱，其高为4，所以该几何体的侧面积为4×6×4＝96．故选C．7．(2018·郑州质检三)已知A，B，C，D四点在半径为5的球面上，且AC＝BD＝4，AD＝BC＝11，AB＝CD，则三棱锥D－ABC的体积是()A．67 B．47 C．27 D．7答案 C解析 如图所示，将三棱锥D －ABC 放在长、宽、高分别为a ，b ，c 的长方体中，则依题意有⎩⎨⎧a 2＋c 2＝AC 2＝16，a 2＋b 2＝BC 2＝11，a 2＋b 2＋c 2＝(2R )2＝20，解得⎩⎨⎧a ＝7，b ＝2，c ＝3，则三棱锥D －ABC 的体积为abc －413·12abc ＝27．选C ． 8．(2018·山西四校联考)如图所示，P 为矩形ABCD 所在平面外一点，矩形对角线交点为O ，M 为PB 的中点，给出下列五个结论：①PD ∥平面AMC ；②OM ∥平面PCD ；③OM ∥平面PDA ；④OM ∥平面PBA ；⑤OM ∥平面PBC ．其中正确的个数是( ) A ．1 B ．2 C ．3 D ．4 答案 C解析 矩形ABCD 的对角线AC 与BD 交于点O ，所以O 为BD 的中点．在△PBD 中，M 是PB 的中点，所以OM 是△PBD 的中位线，OM ∥PD ，则PD ∥平面AMC ，OM ∥平面PCD ，且OM ∥平面PDA ．因为M ∈PB ，所以OM 与平面PBA 、平面PBC 相交．故选C ．9．(2018·大庆质检一)已知一个圆柱的轴截面是边长为a 的正方形．在圆柱内有一个球O ，该球与圆柱的上、下底面及母线均相切，则圆柱内除了球之外的几何体的体积为( )A ．πa 34B ．πa 36C ．πa 38D ．πa 312 答案 D解析 由题意可知，该圆柱底面直径和高都是a ，故其体积为V 1＝πR 2h ＝π×a22×a ＝πa 34．而圆柱体的内切球的直径也为a ，故其体积为V 2＝4π3R 3＝4π3×a 23＝πa 36，所以圆柱体内除球体以外部分的体积为V ＝V 1－V 2＝πa 312．故选D ．10．(2018·湖南长沙四校联考)祖暅是南北朝时代的伟大数学家，5世纪末提出体积计算原理，即祖暅原理：“幂势既同，则积不容异”．意思是：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任何一个平面所截，如果截面面积都相等，那么这两个几何体的体积一定相等．现有以下四个几何体：图①是从圆柱中挖去一个圆锥所得的几何体，图②、图③、图④分别是圆锥、圆台和半球，则满足祖暅原理的两个几何体为( )A ．①②B ．①③C ．②④D ．①④ 答案 D解析 设截面与底面的距离为h ，则①中截面内圆的半径为h ，则截面圆环的面积为π(R 2－h 2)；②中截面圆的半径为R －h ，则截面圆的面积为π(R －h )2；③中截面圆的半径为R －h 2，则截面圆的面积为πR －h 22；④中截面圆的半径为R 2－h 2，则截面圆的面积为π(R 2－h 2)．所以①④中截面的面积相等，故其体积相等，故选D ．11．(2018·浙江高考)已知四棱锥S －ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点(不含端点)．设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S －AB －C 的平面角为θ3，则( )A ．θ1≤θ2≤θ3B ．θ3≤θ2≤θ1C ．θ1≤θ3≤θ2D ．θ2≤θ3≤θ1 答案 D解析 由题意知该四棱锥为正四棱锥，设AB ，AD ，BC 的中点分别为P ，M ，N 连接MN ，过点E 作直线MN 的垂线交MN 于点Q ．设O 为S 在底面ABCD 内的射影，连接SO ，OP ，OE ，SP ，SQ ，则∠SEQ ＝θ1，∠SEO ＝θ2，∠SPO ＝θ3，∴tan θ2＝OS OE ，tan θ3＝OSOP ，∵OP ≤OE ，∴tan θ3≥tan θ2．又EQ ⊥MN ，EQ ⊥SO ，MN ∩SO ＝O ，MN ，SO ⊂平面SOQ ，∴EQ ⊥平面SOQ ，又SQ ⊂平面SOQ ，∴EQ ⊥SQ ．∴tan θ1＝SQEQ ，∵SQ ≥SO ，EQ ＝OP ，∴tan θ1≥tan θ3．故有tan θ1≥tan θ3≥tan θ2．由图可知θ1，θ2，θ3∈0，π2．∴θ1≥θ3≥θ2，故选D ．12．(2018·全国卷Ⅰ)已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为( )A ．334B ．233C ．324D ．32 答案 A解析 根据相互平行的直线与平面所成的角是相等的，所以在正方体ABCD －A 1B 1C 1D 1中，平面AB 1D 1与线AA 1，A 1B 1，A 1D 1所成的角是相等的，所以平面AB 1D 1与正方体的每条棱所在的直线所成角都是相等的，同理平面C 1BD 也满足与正方体的每条棱所在的直线所成的角都是相等的，要求截面面积最大，则截面的位置为夹在两个面AB 1D 1与C 1BD 中间的，且过棱的中点的正六边形，边长为22，所以其面积为S ＝6×34×⎝ ⎛⎭⎪⎫222＝334，故选A ．第Ⅱ卷 (非选择题，共90分)二、填空题(本大题共4小题，每小题5分，共20分)13．如图，一个底面半径为R 的圆柱形量杯中装有适量的水．若放入一个半径为r 的实心铁球，水面高度恰好升高r ，则Rr ＝________．答案 233解析 由水面高度升高r ，得圆柱体积增加πR 2r ，恰好是半径为r 的实心铁球的体积，因此有43πr 3＝πR 2r ．故R r ＝233．14．直三棱柱ABC －A 1B 1C 1的六个顶点都在球O 的球面上．若AB ＝BC ＝2，∠ABC ＝90°，AA 1＝22，则球O 的表面积为________．答案 16π解析 由题设可知，直三棱柱可以补成一个球的内接长方体，所以球的直径为长方体的体对角线长，即22＋22＋(22)2＝4，故球O 的表面积S ＝4πR 2＝16π．15．已知某几何体的三视图如图所示，则其体积为________．答案8π解析由三视图可知该几何体为一个底面半径为1，高为5的圆柱与一个底面半径为1，高为3的圆柱的组合体，其体积为V＝π×12×(5＋3)＝8π．16．(2018·唐山模拟)已知一个几何体由八个面围成，每个面都是正三角形，有四个顶点在同一平面内且为正方形，若该八面体的棱长为2，所有顶点都在球O 上，则球O的表面积为________．答案8π解析依题意，该八面体的各个顶点都在同一球面上，则其中四点所组成的截面在球的大圆面上，因为该八面体的棱长为2，所以这四点组成的正方形的对角线的长为22，故球的半径为2，该球的表面积为4π(2)2＝8π．三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(2018·珠海摸底)(本小题满分10分)中秋节即将到来，为了做好中秋节商场促销活动，某商场打算将进行促销活动的礼品盒重新设计．方案如下：将一块边长为10的正方形纸片ABCD剪去四个全等的等腰三角形(△SEE′，△SFF′，△SGG′，△SHH′)，再将剩下的阴影部分折成一个四棱锥形状的包装盒S－EFGH，其中A，B，C，D重合于点O，E与E′重合，F与F′重合，G与G′重合，H与H′重合(如图所示)．(1)求证：平面SEG⊥平面SFH；(2)已知AE＝52，过O作OM⊥SH于点M，求cos∠EMO的值．解(1)证明：因为折叠后A，B，C，D重合于一点O，所以拼接成底面EFGH的四个直角三角形必为全等的等腰直角三角形，所以底面EFGH是正方形，故EG⊥FH．因为在原平面图形中，△SEE′≌△SGG′，所以SE＝SG，所以EG⊥SO．又FH∩SO＝O，FH⊂平面SFH，SO⊂平面SFH，故EG⊥平面SFH．又因为EG⊂平面SEG，所以平面SEG⊥平面SFH．(2)依题意，当AE＝52时，即OE＝5 2．Rt△SHO中，OH＝52，SH＝552，故SO＝5，所以OM＝SO·OHSH＝5．由(1)知EG⊥平面SFH，且OM⊂平面SFH，故EG⊥OM，从而EO⊥OM，故Rt△EMO中，EM＝EO2＋OM2＝35 2，所以cos∠EMO＝OMEM＝23．18．(2018·安徽江淮十校联考)(本小题满分12分)四棱锥A －BCDE 中，EB ∥DC ，且EB ⊥平面ABC ，EB ＝1，DC ＝BC ＝AB ＝AC ＝2，F 是棱AD 的中点．(1)证明：EF ⊥平面ACD ； (2)求二面角B －AE －D 的余弦值．解 (1)证明：取AC 中点M ，连接FM ，BM ， ∵F 是AD 中点，∴FM ∥DC ，且FM ＝12DC ＝1． 又∵EB ∥DC ，EB ＝1， ∴FM 綊EB ，∴四边形FMBE 是平行四边形． ∴EF ∥BM ，又BC ＝AB ＝AC ， ∴△ABC 是等边三角形，∴BM ⊥AC ， ∵EB ⊥平面ABC ，EB ∥DC ， ∴CD ⊥平面ABC ，∴CD ⊥BM ． 又CD ∩AC ＝C ，∴BM ⊥平面ACD ，∴EF ⊥平面ACD ．(2)取BC 中点N ，连接AN ，则AN ⊥BC ⇒AN ⊥平面BCD ．以N 为原点建立如图所示的空间直角坐标系．则各点坐标为A (0，0，3)，B (0，－1，0)，C (0，1，0)，D (2，1，0)，E (1，－1，0)．可得BA →＝(0，1，3)，BE →＝(1，0，0)，EA →＝(－1，1，3)，ED →＝(1，2，0)， 设平面ABE 的法向量为n 1＝(x 1，y 1，z 1)， 则⎩⎪⎨⎪⎧n 1·BA →＝0，n 1·BE →＝0，得⎩⎨⎧y 1＋3z 1＝0，x 1＝0，可取n 1＝(0，－3，1)，设平面ADE 的法向量为n 2＝(x 2，y 2，z 2)， 则⎩⎪⎨⎪⎧n 2·EA →＝0，n 2·ED →＝0，得⎩⎨⎧－x 2＋y 2＋3z 2＝0，x 2＋2y 2＝0，可取n 2＝(－2，1，－3)，于是cos 〈n 1，n 2〉＝－3－32×8＝－64，注意到二面角B －AE －D 是钝二面角， 因此，所求二面角的余弦值就是－64．19．(2018·湖北重点中学联考二)(本小题满分12分)如图1，等腰直角三角形ABC 的底边AB ＝2，点D 在线段AC 上，DE ⊥AB 于点E ，现将△ADE 沿DE 折起到△PDE 的位置(如图2)．(1)求证：PB ⊥DE ；(2)若PE ⊥BE ，直线PD 与平面PBC 所成的角为30°，求平面PDE 与平面PBC 所成的锐二面角的正弦值．解 (1)证明：由图1，图2可知，DE ⊥PE ，DE ⊥BE ，PE ∩BE ＝E ， ∴DE ⊥平面PBE ，又PB ⊂平面PBE ，∴PB ⊥DE ．(2)由(1)及PE ⊥BE 可知，DE ，BE ，PE 两两互相垂直．分别以ED →，EB →，EP →的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系Exyz ．设|PE |＝a (0<a <1)，则B (0，2－a ，0)，D (a ，0，0)，C (1，1－a ，0)，P (0，0，a )， ∴PB→＝(0，2－a ，－a )，BC →＝(1，－1，0)． 设平面PBC 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧PB →·n ＝0，BC →·n ＝0，∴⎩⎨⎧(2－a )y －az ＝0，x －y ＝0，∴平面PBC 的一个法向量为n ＝(a ，a ，2－a )， ∵直线PD 与平面PBC 所成的角为30°， 且PD→＝(a ，0，－a )， ∴sin30°＝|a 2－a (2－a )|2a 2·a 2＋a 2＋(2－a )2， ∴a ＝2(舍去)或a ＝25．∴平面PBC 的一个法向量为n ＝25，25，85． 易知平面PDE 的一个法向量为m ＝(0，1，0)，设所求的锐二面角为θ，则cosθ＝m·n|m||n|＝26，所以sinθ＝34 6，即平面PDE与平面PBC所成的锐二面角的正弦值为34 6．20．(2018·山东青岛统一质检)(本小题满分12分)如图，圆柱H横放在底面边长为1的正六棱锥P－ABCDEF的顶点P上，O1和O2分别是圆柱左和右两个底面的圆心，正六棱锥P－ABCDEF的底面中心为O，PO＝1，M，N分别是圆柱H的底面圆O1的最高点和最低点，G是圆柱H的底面圆O2的最低点，P为NG的中点，点M，O1，N，A，O，D，G，P共面，O1，P，D共线，四边形ADGN为矩形．(1)证明：MG∥平面PCD；(2)求二面角M－CD－A的大小．注：正棱锥就是底面是一个正多边形，顶点在底面上的正投影为底面的中心的棱锥．解(1)证明：连接PO1(图略)，∵P为NG的中点，O1为MN的中点，∴PO1∥MG，又点O1，P，D共线，∴PD∥MG，∵PD⊂平面PCD，MG⊄平面PCD，∴MG∥平面PCD．(2)∵O为正六棱锥P－ABCDEF的底面中心，∴PO⊥底面ABCDEF，取BC 的中点W (图略)，连接OW ，AD ， 则点O 在AD 上，OW ⊥AD ．分别以OA ，OW ，OP 为x 轴、y 轴、z 轴建立空间直角坐标系Oxyz ． ∵P 为NG 的中点，四边形ADGN 为矩形，O 为AD 的中点，PO ＝1， ∴NA ∥PO ，NA ＝PO ＝1，从而NA ⊥底面ABCDEF ， ∵M ，N 分别是圆柱H 的底面圆O 1的最高点和最低点， ∴O 1N ⊥底面ABCDEF ，从而M ，O 1，N ，A 四点共线， ∵正六棱锥P －ABCDEF 的底面边长为1，∴AD ＝2， ∵四边形ADGN 为矩形，NG ∥AD ，且NG ＝AD ＝2， 又P 为NG 的中点，NP ∥AD ，且NP ＝12AD ＝1， ∴在△O 1AD 中，NP 为△O 1AD 的中位线， 从而N 为O 1A 的中点，∴O 1N ＝AN ＝1， 故M (1，0，3)，C －12，32，0，D (－1，0，0)， DC→＝12，32，0，DM →＝(2，0，3)． 设平面MCD 的法向量为m ＝(x ，y ，z )， 由⎩⎪⎨⎪⎧m ·DC →＝0，m ·DM →＝0⇒⎩⎨⎧x 2＋3y 2＝0，2x ＋3z ＝0.令x ＝1，则y ＝－33，z ＝－23， ∴m ＝1，－33，－23．取平面ABCDEF 的一个法向量为n ＝OP →＝(0，0，1)． 设二面角M －CD －A 的大小为锐角θ， 则cos θ＝|m ·n ||m ||n |＝12，因此θ＝π3，即二面角M －CD －A 的大小为π3．21．(2018·河北衡水中学九模)(本小题满分12分)已知正三棱柱ABC －A 1B 1C 1中，E ，F 分别为BB 1，AB 的中点，设AA 1AB ＝λ．(1)求证：平面A 1CF ⊥平面A 1EF ；(2)若二面角F －EA 1－C 的平面角为π3，求实数λ的值，并判断此时二面角E －CF －A 1是否为直二面角，请说明理由．解 (1)证明：因为三棱柱ABC －A 1B 1C 1是正三棱柱， 所以AA 1⊥平面ABC ，所以AA 1⊥CF ． 又△ABC 是正三角形，F 为AB 的中点， 所以CF ⊥AB ，又AB ∩AA 1＝A ，故CF ⊥平面A 1EF ，又CF ⊂平面A 1CF ，所以平面A 1CF ⊥平面A 1EF ．(2)如图，以F 为坐标原点，FB →，FC →方向分别为x 轴、y 轴的正方向建立如图所示的空间直角坐标系，不妨设底边长AB ＝2，由题意AA 1＝2λ，则F (0，0，0)，A 1(－1，0，2λ)，E (1，0，λ)，C (0，3，0)． EC →＝(－1，3，－λ)，FC →＝(0，3，0)，A 1E →＝(2，0，－λ)， 设平面EA 1C 的法向量为n ＝(x ，y ，z )， 则⎩⎪⎨⎪⎧n ·EC →＝－x ＋3y －λz ＝0，n ·A 1E →＝2x －λz ＝0，令z ＝2，则平面EA 1C 的一个法向量为n ＝(λ，3λ，2)，由(1)可知FC →＝(0，3，0)为平面A 1EF 的一个法向量， 故cos π3＝FC →·n |FC →||n |＝3λ4λ2＋4×3，解得λ＝22， 由(1)可知EF ⊥CF ，A 1F ⊥CF ，由定义可知∠EF A 1为二面角E －CF －A 1的平面角． EF ＝12＋222＝62，A 1F ＝12＋(2)2＝3，A 1E ＝22＋222＝322， 满足EF 2＋A 1F 2＝A 1E 2，则∠EF A 1＝π2， 此时二面角E －CF －A 1为直二面角．22．(2018·江西南昌二模)(本小题满分12分)如图，四棱锥P －ABCD 中，底面ABCD 是直角梯形，AB ∥CD ，AB ⊥AD ，AB ＝2CD ＝2AD ＝4，侧面P AB 是等腰直角三角形，P A ＝PB ，平面P AB ⊥平面ABCD ，点E ，F 分别是棱AB ，PB 上的点，平面CEF ∥平面P AD ．(1)确定点E ，F 的位置，并说明理由； (2)求二面角D －EF －C 的余弦值． 解 (1)因为平面CEF ∥平面P AD ， 平面CEF ∩平面ABCD ＝CE ， 平面P AD ∩平面ABCD ＝AD ， 所以CE ∥AD ，又因为AB ∥DC ， 所以四边形AECD 是平行四边形， 所以DC ＝AE ＝12AB ，即点E 是AB 的中点． 因为平面CEF ∥平面P AD ， 平面CEF ∩平面P AB ＝EF ， 平面P AD ∩平面P AB ＝P A ，所以EF ∥P A ，因为点E 是AB 的中点， 所以点F 是PB 的中点，综上，E ，F 分别是AB ，PB 的中点． (2)连接PE ，因为P A ＝PB ，AE ＝EB ， 所以PE ⊥AB ，又因为平面P AB ⊥平面ABCD ， 平面P AB ∩平面ABCD ＝AB ， 所以PE ⊥平面ABCD ， 又因为AB ⊥AD ， 所以CE ⊥AB ．如图，以点E 为坐标原点，EC ，EB ，EP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，则B (0，2，0)，C (2，0，0)，D (2，－2，0)，E (0，0，0)，P (0，0，2)， 由中点公式得到F (0，1，1)，则EC→＝(2，0，0)，EF →＝(0，1，1)，ED →＝(2，－2，0)， 设平面CEF 、平面DEF 的法向量分别为 m ＝(x 1，y 1，z 1)，n ＝(x 2，y 2，z 2)， 由m ⊥EC→，m ⊥EF →，得⎩⎨⎧2x 1＋0·y 1＋0·z 1＝0，0·x 1＋y 1＋z 1＝0， 令y 1＝1，得m ＝(0，1，－1)， 由n ⊥ED→，n ⊥EF →， 得⎩⎨⎧2x 2－2y 2＋0·z 2＝0，0·x 2＋y 2＋z 2＝0， 令y 2＝1，得n ＝(1，1，－1)，所以cos 〈m ·n 〉＝m ·n |m ||n |＝22×3＝63，因为二面角D －EF －C 是锐角，所以二面角D －EF －C 的余弦值是63．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
P ABCDE1如图，在直三棱柱111ABC A B C -中，190,30,1,o o ACB BAC BC AA ∠=∠===M 是棱1CC 的中点.(1)求证：1A B AM ⊥；(2)求直线AM 与平面11AA BB 所成角的正弦值.2图，三棱柱111ABC A B C -中，侧棱1AA ⊥平面ABC ，ABC ∆为等腰直角三角形，90BAC ∠=，且1,,AB AA E F =分别是1,CC BC 的中点（1）求证：1B F ⊥平面AEF ； （2）求锐二面角1B AE F --的余弦值.3四棱锥P -ABCD 中，直角梯形ABCD 中，AD ⊥CD ，AB ∥CD ，∠APD =60°，PA =CD =2PD =2AB =2，且平面PDA ⊥平面ABCD ，E 为PC 的中点．（Ⅰ）求证：PD ⊥平面ABCD ；（Ⅱ）求直线PD 与平面BDE 所成角的大小．FEC 1B 1A 1C B AEFA BCPD4如图，已知矩形ABCD 所在平面外一点P ，⊥PA 平面ABCD ，F E ,分别是PC AB ,的 中点，121==AD AB ． （1）求证：//EF 平面PAD （2）若4π=∠PDA ，求直线AC 与平面PCD 所成角的正弦值．5如图，在四棱柱ABCD -PGFE 中，底面ABCD 是直角梯形，侧棱垂直于底面，AB //DC ，∠ABC ＝45o，DC ＝1，AB ＝2，PA ＝1．(1)求PD 与BC 所成角的大小； (2)求证：BC ⊥平面PAC ； (3)求二面角A -PC -D 的大小．6如图，在三棱柱111ABC A B C -中，四边形11AA C C 是边长为4的正方形，平面ABC ⊥平面11AA C C ，3,5AB BC ==（Ⅰ）求证：1AA ⊥平面ABC ； （Ⅱ）求二面角111C A B C --的大小；（Ⅲ）若点D 是线段BC 的中点，请问在线段1AB 上是否存在点E ，使得DE ∥面11AA C C ？若 存在，请说明点E 的位置；若不存在，请说 明理由.A B C 11A BFP EDC7如图：在四棱锥ABCD P -中，底面ABCD 为菱形，60=∠DAB ，ABCD PD 平面⊥，1==AD PD ，点F E ,分别为PD AB 和的中点.（Ⅰ）求证：直线AF ∥平面PEC ;（Ⅱ）求PC 与平面PAB 所成角的正弦值.8如图，正方形ABCD 与直角梯形ADEF 所在平面互相垂直，90ADE ∠=，DE AF //，22===AF DA DE . (Ⅰ) 求证：//AC 平面BEF ；(Ⅱ) 求平面BEF 与平面ABCD 所成角的正切值．9直三棱柱111ABC A B C - 中，11AA AB AC ===，E ，F 分别是1CC 、BC 的中点，11AE A B ⊥，D 为棱11A B 上的点. （1）证明：DF AE ⊥;（2）是否存在一点D ，使得平面DEF 与平面ABC 所成锐二面角的余弦值为14?若存在，说明点D 的位置，若不存在，说明理由.ABC DF EB 11(1)因为C1C⊥平面ABC，BC⊥AC，所以以C为原点，射线CA,CB,CC1分别为x轴，y轴，z轴的正半轴建立如图所示的空间直角坐标系，则B(0,1,0),A1,0,0),M(0,0,2),所以1A B(3,1,6),AM(3,0,=--=-,所以1A B AM=3+0-3=0,所以1A B AM⊥，即A1B⊥AM.(2)由(1)知AB1A A),设面AA1B1B的法向量为n=(x,y,z),则3x y0,6z0.-+=⎧⎨-=⎩不妨取设直线AM与平面AA1B1B所成角为θ,则AM6sin|cos<AM,>|||.6|AM|||θ===nnn所以直线AM与平面AA1B1B2(1）连结AF，∵F是等腰直角三角形ABC∆斜边BC的中点，∴AF BC⊥.又 三棱柱111ABC A B C-为直三棱柱，∴面ABC⊥面11BB C C，∴AF⊥面11BB C C，1AF B F⊥. ……… 2分设11AB AA==，则1132B F EF B E===.∴22211B F EF B E+=，∴1B F E F⊥. ………4分又AF EF F=，∴1B F⊥平面AEF. ………6分（2）以F为坐标原点，,FA FB分别为,x y轴建立直角坐标系如图，设11AB AA==，则11(0,0,0),((0,(0,)2222F A B E-，CC1()2AE =-，1(AB =-. ………8分由（Ⅰ）知，1B F ⊥平面AEF ， ∴可取平面AEF的法向量1(0,2m FB ==. 设平面1B AE 的法向量为(,,)n x y z =，由110,0,0,222020,022x y z n AE z n AB z x y z ⎧--+=⎪⎧=+-=⎪⎪⇒⇒⎨⎨=--=⎪⎪⎩-++=⎪⎩ ∴可取(3,1,n =-. ………10分 设锐二面角1B AE F --的大小为θ，则03(1)1cos |cos ,|||||m nmn m n θ⨯-+⨯=<>===∴所求锐二面角1B AE F --的余弦值为6………12分3解：（1）2,1,60,==∠=oQ PA PD PAD2222cos 3∴=+-⋅∠=AD PA PD PA PD PAD ，∴=AD 222∴=+PA AD PD∴⊥PD AD ，又⊂Q PD 平面PDA ，平面PDA I 平面=ABCD AD ，平面PDA ⊥平面ABCD ，∴⊥PD 平面ABCDL L 6‘（2）⊥Q AD CD ，∴以,,DA DC DP 分别为x 轴，y 轴，z 轴，建立空间直角坐标系1(0,0,0),(0,0,1),(0,1,),2D P EB 1(0,1,),2∴==uuu r uu ur DE DB ，设平面BDE 的一个法向量为(,,)=rn x y z ，则1020⎧+=⎪+=y z y ，令1=x ，(1∴=r ncos ,142∴〈〉==⨯uu u r r DP n ，设直线PD 与平面BDE 所成的角为θ，sin 2θ=，∴直线PD 与平面BDE 所成的角为60.o L L 12‘4【解析】：（1）证明：取PD 中点M ，连结FM AM ,1//,2MF CD MF CD =， 1//,2A E C D A E CD = //,MF AE MF AE ∴= ∴四边形AEFM 为平行四边形所以//,AM EF AM ⊂平面PAD ∴//EF 平面PAD （2）连结CM AM ,，由条件知PD AM ⊥，⊥CD 平面PADD CD PD AM CD =⊥∴ , 所以⊥AM 平面PCD ，∴ACM ∠就是直线AC 与平面PCD 所成的角经计算得5,3,2===AC CM AM ∴510sin ==∠AC AM ACM 5（Ⅰ）取的AB 中点H ，连接DH ，易证BH//CD ，且BD=CD ………………………1分 所以四边形BHDC 为平行四边形，所以BC//DH所以∠PDH 为PD 与BC 所成角………………………………2分 因为四边形，ABCD 为直角梯形，且∠ABC=45o， 所以⊥DA ⊥AB又因为AB=2DC=2，所以AD=1， 因为Rt △PAD 、Rt △DAH 、Rt △PAH 都为等腰直角三角形，所以，故∠PDH=60o……………………………………………………………4分 （II ）连接CH ，则四边形ADCH 为矩形， ∴AH=DC 又AB=2，∴BH=1在Rt △BHC 中，∠ABC=45o， ∴CH=BH=1，∴AD=CH=1，∴AC 2+BC 2=AB 2∴BC ⊥AC …………………………………6分 又PA 平面ABCD ∴PA ⊥BC ……………………………………7分 ∵PA ∩AC=A ∴BC ⊥平面PAC …………………………………8分（Ⅲ）如图，分别以AD 、AB 、AP 为x 轴，y 轴，z 轴建立空间直角坐标系，则由题设可知：A(0，0，0)，P(0，0，1)，C(1，1，0)，D(1，0，0)， ∴AP =(0，0，1)，PC =(1，1，-1) …………………………9分设m =(a ，b ，c)为平面PAC 的一个法向量， 则00AP PC ⎧=⎪⎨=⎪⎩m m ，即00c a b c =⎧⎨+-=⎩设1a =，则1b =-，∴m =(1，-1，0) …………………10分同理设n =(x ，y ，z) 为平面PCD 的一个法向量，求得 n =(1，1，1) …………………………………………………11分∴1cos ,2===m n m n m n所以二面角A-PC-D 为60o………………………………… 12分FPD6（Ⅰ）因为四边形11AA C C 是边长为4的正方形，所以1AA AC ⊥， ……1分 因为平面ABC ⊥平面11AA C C 且平面ABC 平面11AAC C AC =，……2分 所以1AA ⊥平面ABC……3分（Ⅱ）解：以A 为坐标原点，以1,,AC AB AA所在直线分别为,,x y z 轴建立空间直角坐标系如图所示：(图略) 则111,,,,,A B C A B C 点坐标分别为：(0,0,0)A ；(0,3,0)B ；(4,0,0)C ；1(0,0,4)A ；1(0,3,4)B ；1(4,0,4)C……5分则3(2,,0)2D 设平面11CA B 的法向量'''(,,)m x y z =所以111,m AC m A B ⊥⊥且 ，所以'''44030x z y ⎧-=⎪⎨=⎪⎩ ……6分令'1x =，所以(1,0,1)m =，又易知平面111A B C 的法向量为(0,0,1)n = ……7分所以2cos ||||m n m n θ⋅==所以二面角111C A B C --的大小为45︒……8分（Ⅲ）设111(,,)E x y z ；平面11AA C C 的法向量(,,)u x y z =．因为点E 在线段1AB 上，所以假设1AE AB λ=，所以111034x y z λλ=⎧⎪=⎨⎪=⎩ (01)λ<≤即(0,3,4)E λλ，所以3(2,3,4)2DE λλ=--． ……10分又因为平面11AA C C 的法向量易知(0,3,0)u =． 而//DE 面11AA C C ，所以0DE u ⋅=，所以12λ= ……11分 所以点E 是线段1AB 的中点．……12分 若采用常规方法并且准确，也给分。
7证明：（Ⅰ）取PC 上的中点H ，则//,FH AE FH AE = ∴//,,AF EH AF PEC EH PEC ⊄⊂面面 ∴//AF PEC 平面．．．．．．．．．．．．．．．．．．5分（Ⅱ）连接DE ，知DE DC ⊥所以以D 为坐标原点，分别以,DE DC DP ，为x y z 轴，轴，轴建立坐标系．．．．6分∴11(0,0,1),,0),,0),(0,1,0)22P A B C - 设平面PAB 的法向量为=,,)n x y （1则有00n PA n PB ⎧⋅=⎪⎨⋅=⎪⎩⇒12102x y x y -=+-=⇒=,0,2n （1．．．．．．．．．．．．．10分 则有42sin cos 14PC n PC nθα⋅===⋅．．．．．．．．．．．．．12分8解：(Ⅰ) 证明：方法一：设AC BD O =I ，取BE 中点G ，连结OG FG 、， 则OG ∥DE 且OG ＝12DE ， ∵DE AF //，AF DE 2=， ∴AF ∥OG 且AF ＝OG ，∴AFGO 是平行四边形，∴AO FG //.∵FG ⊂平面BEF ，AO ⊄平面BEF ，∴//AO 平面BEF ，即//AC 平面BEF . 方法二：∵90ADE ∠=，∴DE AD ⊥∵正方形ABCD 与直角梯形ADEF 所在平面互相垂直，平面ABCD I 平面ADEF AD =，DE ⊂平面ADEF ，∴DE ⊥平面ABCD以点D 为坐标原点，DA 、DC 、DE 所在的直线为x 轴、y 轴、z轴建立空间直角坐标系，设平面BEF 的一个法向量为(,,)n x y z =r，则00n FE n FB ⎧⋅=⎪⎨⋅=⎪⎩r uur r uu r ，而(2,0,1)(0,2,1)FE FB ⎧=-⎪⎨=-⎪⎩uur uu r ，∴2020x z y z -+=⎧⎨-=⎩，令1x =，则1y =，2z =，(1,1,2)n =r. ∵(2,2,0)AC =-uu u r ， ∴0n AC ⋅=r uuu r ，∴n AC ⊥r u u u r，而AC ⊄平面BEF ，∴//AC 平面BEF .(Ⅱ) 设平面ABCD 与平面BEF 所成二面角的平面角为α，由条件知α是锐角由 (Ⅰ) 知平面BEF 的法向量为( 1,1,2)n =r，又平面ABCD与z轴垂直，所以平面ABCD的法向量可取为1(0,0,1)n= u r所以111cos|cos,|||3||||n nn nn nα⋅=<>===⋅u r ru r ru r r，所以tan2α=即为所求.。