基础知识天天练数学5-3

53天天练五年级上册答案数学

53天天练五年级上册答案数学第一单元：自然数的认识1.1 自然数集合在本单元中，我们将学习自然数的概念和性质。

自然数是一种基本的数学概念，它由0和大于0的整数组成。

自然数集合用N表示，即N = {0, 1, 2, 3, 4, …}。

问题1求出自然数集合N的前10个数。

答案1N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}问题2自然数有哪些性质？答案2自然数具有以下性质： - 自然数是无限的，即没有最大的自然数。

- 任意两个自然数之和仍然是自然数。

- 任意两个自然数之差可能是自然数，也可能是负整数。

- 任意两个自然数之积仍然是自然数。

- 任意两个自然数之商可能是自然数，也可能是分数或小数。

- 自然数是整数的子集。

1.2 相邻数和进位在本节中，我们将学习相邻数的概念和进位的计算方法。

问题3什么是相邻数？答案3相邻数是指自然数集合N中相邻排列的两个数。

例如，2和3是相邻数，5和6是相邻数。

问题4怎样计算相邻数之和？答案4计算相邻数之和的方法是将这两个数相加。

例如，2和3的和是5，5和6的和是11。

问题5什么是进位？答案5进位是指在相加时某一位上的和大于9时，向前一位进1。

例如，7和5相加时，个位上的和是12，需要向十位进1。

如何计算进位？答案6计算进位的方法是将相邻数相加，如果需要进位，则向前一位进1。

例如，7和5相加时，个位上的和是12，需要向十位进1。

第二单元：分数的认识2.1 分数的定义本单元中，我们将学习分数的概念和分数的表示方法。

问题7什么是分数？答案7分数是指将一个整体分成若干等分，其中一份为单位的数。

分数由分子和分母组成，分子表示被分成的等分中的份数，分母表示整体被分成的总份数。

例如，1/2、3/4、5/8都是分数。

问题8如何表示分数？分数可以用如下形式表示：分子/分母。

例如，1/2表示将整体分成两份中的一份。

2.2 分数的运算在本节中，我们将学习分数的加法、减法、乘法和除法。

部编人教版小学数学三年级上册《第五单元达标作业》5·3天天练

一、填一填。 1.圈一圈，填一填。
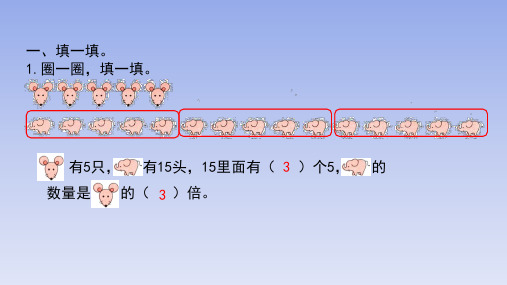
有5只，有15头，15里面有（ 3 ）个5，的数量是的（ 3 ）倍。
一、填一填。 2.在横线上画○，画的○的数量是的4倍。
画（ 4 ）组5个的○才是我们的4倍。
○○○○○ ○○○○○ ○○○○○ ○○○○○
二、说一说。
的只数是
的（ 5 ）倍。
的数量是
的（ 3 ）倍。
4.萍萍今年8岁，明年爸爸的年龄是她的5倍，爸爸今年多少岁？
8＋1＝9（岁） 9×5－1＝44（岁）答：爸爸今年44岁。
3.（1）丽丽有8个五角星，千纸鹤的数量比五角星的5倍少5个。千纸鹤有多少个？
8×5＝40（个） 40－5＝35（个）答：千纸鹤有35个。
（2）丽丽想把这些五角星和千纸鹤串起来。千纸鹤的数量不变，要使千纸鹤的数量是五角星的5倍，需要减少几个五角星？
35÷5＝7（个） 8－7＝1（个）答：需要减少1个五角星。
三、填一填，算一算。 1.
的数量是的7倍，
4 × 7 ＝ 28 （只）有（ 28 ）只。
2.
ቤተ መጻሕፍቲ ባይዱ有32辆，
有8辆。
的数量是
的（ 4 ）倍。
32 ÷ 8 ＝ 4
3.
4.1只 8只
？个
吃5根胡萝卜，吃（ 40 ）根胡萝卜。
4 × 3 ＝ 12 （个） 5 × 8 ＝ 40 （根）
四、生活中的数学。 1.学校购买体育用品，买了8个足球，又买了48个篮球。购买的篮球的个数是足球的多少倍？
48÷8＝6 答：购买的篮球的个数是足球的6倍。
2.（1）爸爸做了多少个南瓜灯？
5×5＝25（个）答：爸爸做了25个南瓜灯。

小学一年级5 3天天练数学期末综合复习一电子版

小学一年级5 3天天练数学期末综合复习一电子版一、填空(第5小题3分，其余每题2分，共17分)1、0.37×4.9的积是( )位小数，数确到个位是( )。

2、1里面有( )个十分之一，2.7里面有( )个十分之一。

3、6.64÷3.3的商是( )，保留两位小数约是( )。

4、把34.65÷0.25转化成除数是整数的除法算式是( )，根据是( )。

6、9a+6a=(_____+_____ )•7、一堆煤有x吨，已经烧了5天，烧了a吨，平均每天烧( )吨煤，还剩( )吨煤。

(用含有字母的式子表示)8、小明晨跑2分钟跑了400米，平均每分钟跑( )米，跑1米需要( )分钟。

二、判断，对的在括号里打“√”，错的打“×”(每题2分，共16分)。

1、循环小数一定是无限小数，所以无限小数也一定是循环小数。

( )2、一个数的2.5倍，比原数大。

( )3、近似数5和5.0比较，5.0比5精确。

( )4、a+a=a2 。

( )5、X=3是方程。

( )6、36.9÷0.25×4=36.9÷(0.25×4)。

( )7、观察一个物体时，最多能看到两个面。

( )8、0.244444可以记作0.24。

( )三、选择，把正确答案前的字母填在本题的括号里。

(每题2分，共10分。

)1、在计算0.8÷0.24时，被除数和除数都要同时( )。

A、不扩大B、扩大10倍C、扩大100倍2、下面各式的结果大于1的算式是( )。

A、1÷0.44B、0.44÷1C、0.44×13、计算2.5×3.7+2.5×0.3的结果时，可用( )使计算简便。

A、乘法交换律B、乘法分配律C、乘法结合律4、小红的妈妈将5千克香油分装在一些玻璃瓶里，每个瓶最多可装0.8千克，妈妈需要准备( )个瓶。

A、6B、6.25C、75、下面的数最小的是( )。

二年级数学北师大版上册《期末测试》5·3天天练

4.9的3倍是（ 27 ），9是3的（ 3 ）倍。
答案不唯一
5.买5块蛋糕需要（ 35 ）元。
36元可以买（ 9 ）个面包。7元Fra bibliotek4元6.
（ 8 ）厘米
（ 5 ）厘米
期末测试
7.括号里最大能填几？
（ 7 ）×4＜32
9×（ 8 ）＜74 （ 8 ）×6＜49
8.如果把24个气球平均分给4个小朋友，每个小朋友分到（ 6 ）个。若
C.①③④
D.①②③④
期末测试
三、算一算。 1.口算。 15÷3＝ 5 6×3＝18 8×2＝ 16 48÷6＝ 8
14÷2＝ 7 54÷9＝ 6
32÷4＝ 8 7×5＝ 35
期末测试
2.用竖式计算。
34＋26＋29＝ 89
34 ＋26
60 ＋29
89
72－15－18＝ 39
72 －15
57 －18
5×3＝15（元）或3×5＝15（元）答：全家人坐小火车需要15元。（答案不唯一）
20－16＝4（元）答：应找回4元。（3）坐小火车时，小明排在第20个座位上，他坐第几节车厢？
20÷4＝5（节）
答：他坐第5节车厢。
期末测试
3.小明和爸爸、妈妈去公园游玩。
划船碰碰车
每人3元每人8元
小火车每人5元（有6节车厢，每节车厢限坐4人）
（4）请你再提出一个用乘法或除法解决的问题，并尝试解答。全家人坐小火车需要多少元？
小刚
小冰
小林
（1）小冰有多少本故事书？（2）小林的故事书本数是小刚的几倍？
6×2＝12（本）
24÷6＝4
或2×6＝12（本）
答：小林的故事书本数是小刚的4倍。

五年级五三天天练数学答案

五年级五三天天练答案五年级上册数学答案一．算术1.整数的认识1）认识正整数和负整数答案：正整数：1，2，3，4，5，……负整数：-1，-2，-3，-4，-5，……2）数轴上的正负整数答案：数轴上正方向表示正数，负方向表示负数。

3）连续进行加减运算答案：答案不唯一，因为可以改变运算的顺序。

2.小数的初步认识1）小数的含义答案：小数是整数和分数的一种表示方法，包括有限小数和无限循环小数。

2）小数和分数相互转化答案：将分数化成小数，分子除以分母即可；将小数化成分数，小数位数作为分母，去掉小数点作为分子，约分得到最简分数。

3）连续进行加减运算答案：答案需要按照加减运算的顺序计算，注意小数点位置对齐。

3.分数的初步认识1）正分数和零的认识答案：正分数是大于零的分数，零是没有大小的分数。

2）分数的大小比较答案：当分数的分母相同时，分子越大，分数越大；当分数的分子相同时，分母越小，分数越大。

3）连续进行加减运算答案：需要通分之后按照加减运算的顺序计算。

4.加减法1）两个整数的加法答案：将两个整数的绝对值相加，符号和大的整数相同。

2）两个整数的减法答案：将减数取相反数，然后按照加法运算进行。

3）两个小数的加减法答案：需要按照小数点位置对齐，补齐小数位后进行加减运算。

4）两个分数的加减法答案：需要通分后按照加减法运算进行。

5.乘除法1）两个整数的乘法答案：将两个整数的绝对值相乘，符号根据规律确定。

2）两个小数的乘法答案：将小数转化成带分数，然后进行乘法运算，最后把结果化成小数。

3）两个分数的乘法答案：分母乘以分母，分子乘以分子，最后化成最简分数。

4）两个整数的除法答案：将除数和被除数的绝对值相除，符号根据规律确定。

5）两个小数的除法答案：将小数化成带分数，然后进行除法运算，最后把结果化成小数。

6）两个分数的除法答案：将除数倒数乘以被除数，然后化成最简分数。

二．数学思维1.分组1）利用分组解决问题答案：分组是将一组数据按照某种规律进行分类，然后分别进行统计，可以更清晰地了解数据的特点。

高三基础知识天天练数学5-3人教版

第5模块第3节[知能演练]一、选择题1．若数列{a n }的前n 项和S n ＝3n －a ，数列{a n }为等比数列，则实数a 的值是( )A ．3B ．1C ．0D ．－1解析：可用特殊值法，由S n 得a 1＝3－a ，a 2＝6，a 3＝18，由等比数列的性质可知a ＝1.答案：B2．设a 1，a 2，a 3，a 4 成等比数列，其公比为2，则2a 1＋a 22a 3＋a 4的值为( )A.14B.12C.18D ．1解析：由题意得a 2＝2a 1，a 3＝4a 1，a 4＝8a 1. ∴2a 1＋a 22a 3＋a 4＝2a 1＋2a 18a 1＋8a 1＝14.答案：A3．等比数列{a n }前n 项的积为T n ，若a 3a 6a 18是一个确定的常数，那么数列T 10，T 13，T 17，T 25中也是常数的项是( )A ．T 10B ．T 13C ．T 17D ．T 25解析：a 3a 6a 18＝a 31q 2＋5＋17＝(a 1q 8)3＝a 39，即a 9为定值，所以下标和为9的倍数的两项积为定值，可知T 17为定值．答案：C4．已知等比数列{a n }中，a 1＋a 2＝30，a 3＋a 4＝120，则a 5＋a 6等于( )A ．240B ．±240C ．480D ．±480解析：∵{a n }为等比数列，∴数列a 1＋a 2，a 3＋a 4，a 5＋a 6也成等比数列，∴(a 3＋a 4)2＝(a 1＋a 2)(a 5＋a 6)，∴a 5＋a 6＝120230＝480.答案：C 二、填空题5．等比数列{a n }中，a 1＋a 3＝10，a 4＋a 6＝54，则数列{a n }的通项公式为________．解析：由a 4＝a 1q 3，a 6＝a 3q 3得 a 4＋a 6a 1＋a 3＝q 3＝54×110＝18，∴q ＝12，又a 1(1＋q 2)＝10，∴a 1＝8.∴a n ＝a 1q n －1＝8×(12)n －1＝24－n .答案：a n ＝24－n6．在等差数列{a n }中，a 1＝1，a 7＝4，数列{b n }是等比数列，已知b 2＝a 3，b 3＝1a 2，则满足b n <1a 80的最小自然数n 是________．解析：{a n }为等差数列a 1＝1，a 7＝4,6d ＝3，d ＝12.∴a n ＝n ＋12，{b n }为等比数列，b 2＝2，b 3＝23，q ＝13.∴b n ＝6×(13)n －1，b n <1a 80＝281，∴81<26×⎝⎛⎭⎫13n －1，即3n －2>81＝34.∴n >6，从而可得n min ＝7. 答案：7 三、解答题7．设数列{a n }的前n 项和S n ＝2a n －2n . (1)求a 3，a 4；(2)证明：{a n ＋1－2a n }是等比数列； (3)求{a n }的通项公式． (1)解：因为a 1＝S 1,2a 1＝S 1＋2，所以a 1＝2，S 1＝2. 由2a n ＝S n ＋2n 知2a n ＋1＝S n ＋1＋2n ＋1＝a n ＋1＋S n ＋2n ＋1，得a n ＋1＝S n ＋2n ＋1，①所以a 2＝S 1＋22＝2＋22＝6，S 2＝8， a 3＝S 2＋23＝8＋23＝16，S 3＝24. a 4＝S 3＋24＝40.(2)证明：由题设和①式知a n ＋1－2a n ＝(S n ＋2n ＋1)－(S n ＋2n )＝2n ＋1－2n ＝2n .所以{a n ＋1－2a n }是首项为2，公比为2的等比数列．(3)a n ＝(a n －2a n －1)＋2(a n －1－2a n －2)＋…＋2n －2(a 2－2a 1)＋2n －1a 1＝(n ＋1)·2n －1.8．设各项均为正数的数列{a n }和{b n }满足5a n ，5b n ，5a n ＋1成等比数列，lg b n ，lg a n ＋1，lg b n ＋1成等差数列，且a 1＝1，b 1＝2，a 2＝3，求通项a n 、b n .解：∵5a n ，5b n ，5a n ＋1成等比数列， ∴(5b n )2＝5a n ·5a n ＋1，即2b n ＝a n ＋a n ＋1.① 又∵lg b n ，lg a n ＋1，lg b n ＋1成等差数列， ∴2lg a n ＋1＝lg b n ＋lg b n ＋1，即a 2n ＋1＝b n ·b n ＋1.② 由②及a i >0，b j >0(i 、j ∈N *)可得 a n ＋1＝b n b n ＋1.③ ∴a n ＝b n －1b n (n ≥2)．④将③④代入①可得2b n ＝b n －1b n ＋b n b n ＋1(n ≥2)， ∴2b n ＝b n －1＋b n ＋1(n ≥2)． ∴数列{b n }为等差数列．∵b 1＝2，a 2＝3，a 22＝b 1b 2，∴b 2＝92. ∴b n ＝2＋(n －1)( 92－2) ＝12(n ＋1)(n ＝1也成立)． ∴b n ＝(n ＋1)22.∴a n ＝b n －1·b n ＝n 22·(n ＋1)22＝n (n ＋1)2(n ≥2)．又当n ＝1时，a 1＝1也成立．∴a n ＝n (n ＋1)2.[高考·模拟·预测]1．已知等比数列{a n }的公比为正数，且a 3·a 9＝2a 25，a 2＝1，则a 1＝( )A.12B.22C. 2 D ．2解析：因为a 3·a 9＝2a 25，则由等比数列的性质有：a 3·a 9＝a 26＝2a 25，所以a 26a 25＝2，即(a 6a 5)2＝q 2＝2，因为公比为正数，故q ＝ 2.又因为a 2＝1，所以a 1＝a 2q ＝12＝22.答案：B2．已知等比数列{a n }满足a n >0，n ＝1,2，…，且a 5·a 2n －5＝22n (n ≥3)，则当n ≥1时，log 2a 1＋log 2a 3＋…＋log 2a 2n －1＝( )A ．n (2n －1)B ．(n ＋1)2C ．n 2D ．(n －1)2解析：设等比数列{a n }的首项为a 1公比为q ，∵a 5·a 2n －5＝a 1q 4·a 1q 2n －6＝22n ，即a 21·q 2n －2＝22n ⇒(a 1·q n －1)2＝22n ⇒(a n )2＝(2n )2，∵a n >0，∴a n ＝2n ，∴a 2n －1＝22n －1，∴log 2a 1＋log 2a 3＋…＋log 2a 2n －1＝log 22＋log 223＋…＋log 222n －1＝1＋3＋…＋(2n －1)＝1＋(2n －1)2·n ＝n 2，故选C.答案：C3．已知数列{a n }共有m 项，定义{a n }的所有项和为S (1)，第二项及以后所有项和为S (2)，第三项及以后所有项和为S (3)，…，第n 项及以后所有项和为S (n )．若S (n )是首项为2，公比为12的等比数列的前n 项和，则当n <m 时，a n 等于( )A ．－12n －2B.12n －2 C ．－12n －1D.12n －1 解析：∵n <m ，∴m ≥n ＋1.又S (n )＝2(1－12n )1－12＝4－12n －2，∴S (n ＋1)＝4－12n －1，故a n ＝S (n )－S (n ＋1)＝12n －1－12n －2＝－12n －1.答案：C4．设{a n }是公比为q 的等比数列，|q |>1，令b n ＝a n ＋1(n ＝1,2，…)，若数列{b n }有连续四项在集合{－53，－23,19,37,82}中，则6q ＝________.解析：由a n ＝b n －1，且数列{b n }有连续四项在集合{－53，－23,19,37,82}中，则{a n }有连续四项在集合{－54，－24,18,36,81}中．经分析判断知{a n }的四项应为－24,36，－54,81.又|q |>1，所以数列{a n }的公比为q ＝－32，则6q ＝－9.答案：－95．等比数列{a n }的前n 项和为S n ，已知对任意的n ∈N *，点(n ，S n )均在函数y ＝b x ＋r (b >0且b ≠1，b ，r 均为常数)的图象上．(Ⅰ)求r 的值；(Ⅱ)当b ＝2时，记b n ＝n ＋14a n (n ∈N *)，求数列{b n }的前n 项和T n .解：(Ⅰ)由题意，S n ＝b n ＋r ，当n ≥2时，S n －1＝b n －1＋r ，所以a n ＝S n －S n －1＝b n －1(b －1)，由于b >0且b ≠1，所以当n ≥2时，{a n }是以b 为公比的等比数列，又a 1＝b ＋r ，a 2＝b (b －1)， a 2a 1＝b ，即b (b －1)b ＋r＝b ，解得r ＝－1. (Ⅱ)由(Ⅰ)知，n ∈N *，a n ＝(b －1)b n －1，当b ＝2时，a n ＝2n －1，所以b n ＝n ＋14×2n －1＝n ＋12n ＋1. T n ＝222＋323＋424＋…＋n ＋12n ＋1.12T n ＝223＋324＋…＋n2n ＋1＋n ＋12n ＋2，两式相减得12T n ＝222＋123＋124＋…＋12n ＋1－n ＋12n ＋2＝12＋123×(1－12n －1)1－12－n ＋12n ＋2 ＝34－12n ＋1－n ＋12n ＋2，故T n ＝32－12n －n ＋12n ＋1＝32－n ＋32n ＋1. [备选精题]6．已知数列{a n }满足a 1＝a (a ≠0且a ≠1)，前n 项和为S n ，且S n ＝a1－a (1－a n )．(1)求证：{a n }是等比数列；(2)记b n ＝a n lg|a n |(n ∈N *)，当a ＝－73时，是否存在正整数m ，使得对于任意正整数n ，都有b n ≥b m ？如果存在，求出m 的值；如果不存在，说明理由．解：(1)当n ≥2时，S n ＝a 1－a (1－a n )，S n －1＝a 1－a(1－a n －1)， a n ＝S n －S n －1＝a 1－a [(1－a n )－(1－a n －1)]＝a1－a (a n －1－a n )，即a n ＝aa n －1.又a 1＝a ≠0，所以a na n －1＝a ，所以{a n }是首项和公比都为a 的等比数列． (2)由(1)知，a n ＝a n ，则b n ＝a n lg|a n |＝na n lg|a |. 又a ＝－73∈(－1,0)，则lg|a |<0. 所以当n 为偶数时，b n ＝na n lg|a |<0；当n 为奇数时，b n >0. 可见，若存在满足条件的正整数m ，则m 为偶数． b 2k ＋2－b 2k ＝[(2k ＋2)a 2k＋2－2ka 2k ]lg|a |＝2a 2k [(k ＋1)a 2－k ]lg|a |＝2a 2k [k (a 2－1)＋a 2·a 2－1a 2－1]lg|a |＝2a 2k (a 2－1)(k －a 21－a2)lg|a |(k ∈N *)．当a ＝－73时，a 2－1＝－29，∴2a 2k (a 2－1)lg|a |>0.又a 21－a 2＝72，当k >72时，b 2k ＋2>b 2k ，即b 8<b 10<b 12<…；当k <72时，b 2k ＋2<b 2k ，即b 8<b 6<b 4<b 2.故存在正整数m ＝8使得对于任意正整数n ，都有b n ≥b m .。

部编人教版小学数学四年级上册《选择策略》5·3天天练

1.小冬和小春各有“团长”“营长”“连长”三枚军棋，级别高的“吃掉” 级别低的。每人每次出一枚棋，各出三次，赢两次者胜。如果小冬先出，那么小春怎样出棋才能赢？（军棋级别从高到低：军师旅团营连排）
（1）第1次第2次第3次小冬连长团长营长
（2）第1次第2次第3次小冬团长营长连长
小春营长连长团长
小春连长团长营长
（3）第1次第2次第3次小冬营长团长连长
小春团长连长营长
2.五（1）班和五（2）班举行象棋比赛，每班选出5名选手，采取五局三胜制。每班选手按实力从强到弱分5个等级：1级、2级、3级、4级和5级。两个班级各等级的选手的实力相近。为增大五（1）班获胜把握，可以采取什么样的对阵策略？
把小东的牌换小一些，还可以获胜。小东获胜的最小的三张牌应该是8、5、1。
3
9
5
4.盒子里有20个球，笑笑和乐乐玩拿球游戏，两人轮流拿走1个或 2个球，谁拿到最后一个球谁获胜。如果笑笑先拿，那么她怎样能确保获胜？
笑笑先拿2个球，然后乐乐拿，乐乐如果拿1个球，笑笑就拿2个球；乐乐如果拿2个球，笑笑就拿1个球，以此类推，笑笑就可以拿到第20个球。
场次第1场第2场第3场第4场第5场
五（1）班 5级 1级 2级 3级 4级
五（2）班）班五（1）班五（1）班五（1）班
3.小明有10、7、4三张扑克牌，小东有3、5、9三张扑克牌，规定每人每次出一张牌，数字大的赢，各出三次，赢两次者胜。如果小明先出（顺序如下图），那么小东应该怎样应对才能获胜？把小东的牌换小一些，还可以获胜吗？小东获胜的最小的三张牌应该是哪三张？

二年级人教版数学下册《第一单元达标作业》5·3天天练

茄子和西红柿共有多少个？ 7＋12＝19（个）
答：茄子和西红共有19个。答案不唯一
第一单元达标作业
二、二（1）班四个同学进行投沙包比赛，每人投20个。下面是四个同学
投中个数的统计结果。
姓名投中个数
文文 16
丽丽 10
明明 17
兰兰 12
1.根据上面的结果，获得投沙包比赛第一名的是（明明）。
2.如果每人再接着投2个沙包，文文有可能获得第一名吗？请在□18
套圈 4
踢毽子 10
季节）
季节春
夏
秋
冬
人数 16
9
12
7
1.喜欢（春）季的人最多，喜欢（冬）季的人数最少。 2.这个班一共有多少人？
16＋9＝25（人） 25＋12＝37（人） 37＋7＝44（人）
答：这个班一共有44人。
第一单元达标作业
四、下面是二（3）班同学最喜欢的季节的调查情况。（每人只能选一个
季节）
“√”。
可能√□
不可能□
第一单元达标作业
三、课外实践小组统计了一个停车场停放车辆的情况。
小轿车正正正丅
面包车正一
大客车正
1.这个停车场停放的小轿车比面包车多（ 11 ）辆。 2.这个停车场一共停放了（ 28 ）辆车。
第一单元达标作业
四、下面是二（3）班同学最喜欢的季节的调查情况。（每人只能选一个
第一单元达标作业
人教版二年级下学期
第一单元达标作业
一、绿色蔬菜。
1.用自己喜欢的方法统计出每种蔬菜的数量。
√√√√ √√√
正正
正正丅
○○○○ ○○
第一单元达标作业
一、绿色蔬菜。
2.（西红柿）的数量最多，（豌豆）的数量最少。 3.西红柿比茄子多（ 5 ）个。 4.你还能提出其他数学问题并解答吗？

冀教版数学五年级下册_《第七单元达标检测》5 3天天练

第七单元达标检测一、填空。

（每空2分，共28分）1.王叔叔想了解自家超市每周收入增减变化情况，决定把每周收入绘成统计图，他应该绘制（）统计图。

2.我们要了解第31届夏季奥林匹克运动会时中国、美国、英国、俄罗斯、法国、德国、日本7个国家获得金牌、银牌情况，应绘制（）统计图。

要了解中国在近6届奥运会上获得金牌和银牌数目的变化情况，应该绘制（）统计图。

3.在一幅统计图的纵轴上，用3厘米表示15万吨煤。

那么40万吨煤用（）厘米表示，6厘米表示（）万吨煤。

4.小丽和小红进行了400米跑步测试，测试情况如下图。

（1）在本次测试中，（）先到达终点，（）后到达终点，后者比前者晚图到（）秒。

（2）在测试过程中小红的速度是先（）后（）。

（在括号里填“快”或“慢”）（3）在老师发出指令后，最初（）领先，（）秒钟后（）领先，测试中两人最远相距（）米。

二、选择。

（共15分）1.右图是一辆摩托车和一辆汽车的行程图，路程（千米）汽车摩托车下面说法正确的是（）。

A.摩托车的平均速度是每分钟0.6千米B.汽车中途停留了5分钟C.摩托车比汽车晚到5分钟D.摩托车的速度与汽车的相比先快后慢2.用折线统计图表示实验小学近五年新生入学人数情况，横轴上这5个数据应该（）。

A.按年份顺序排列B.按数据的大小从大到小排列C.按先平年后闰年的顺序排列D.随意排列3.甲、乙两人住在同一栋楼，两人分别骑自个路程（千米）一x×－－一资迷行车沿同一条路线到距家18千米远的植18物园去玩，已知甲比乙早出发，他们所行的路程和时间关系如图所示，下面说法正确的是（）。

A.他们都骑行了18千米B.两人同时到达植物园C.甲在中途停留了1小时D.相遇后甲的速度比乙的速度快4.右图是2018年某商场7月至12月T恤和羽绒服销售量情况统计图。

根据统计图判断下面说法不正确的是（）。

A.虚线表示的是T恤销售情况B.实线表示的是羽绒服销售情况C.11月份羽绒服销售量最高D.7－11月T恤销售量逐月增长5.学校教学楼一共有4层，某天上午，明明第一节课在三楼上语文课，第二节课在四楼上形体课，第三节课在二楼科学实验室上科学课，第四节课在一楼上烹饪课。

五年级上册五三天天练2022年秋季答案数学

五年级上册五三天天练2022年秋季答案数学第一页一、3， 1.2， 8.7， 1.26， 12，417，0.4， 0.24， 3 ， 0.06，15二、4.14，0.，2.04 ，28三、16.25，.5 ，0.,42 ，0.42 ， 0.42四、15.6，27.72第二页四、2.25，4.16 ，25.75，82五、4.8×3.2÷2 2.8×1.6=15.36÷2 =4.48(平方厘米)=7.68(平方厘米)(2.4+4.6)×3.2÷2(8.4+11.8)×7.5÷2=7×3.2÷2=20.2×7.5÷2=11.2(平方厘米) =75.75(平方厘米)第三页六、解决问题。

1、÷4×3.2=×3.2=(千米)2、① .8÷15= 36.12(米)② .8÷7= 77.4 (米)③ 77.4-36.12=41.28 (米)3、×5.4= (千米)4、0.8×24×18=19.2×18=.6(元)第四页5、×1.2+48=.8+48=.8(元)提升篇：1、282、.6×-×0..5×23+31×2.5=.6×-.6×92=2.5×(3×23)+31×2.5=.6×(-92)=2.5×(69+31)=.6× =2.5×==3、0.79×0.46+7.9×0.24+11.4×0.=0.79×0.46+0.79×2.4+1.14×0.79=0.79×(0.46+2.4+1.14)=0.79×4=3.16第五页1、>，<，<，<，>，>2、32.37.73、0..464、0.56× =0.56×+0.56×1=56+0.56=56.562.37×0.5×4=2.37×(0.5×4)=2.37×2=4.743.7×2.5+6.3×2.5=(3.7+6.3)×2.5=10×2.5=251.2×0.25=4×0.25×0.3=1×0.3=0.30.25×6.9×0.4=0.25×0.4×6.9=0.1×6.9=0.690.25×32×1.25=0.25×4×(8×1.25)=1×10=10第六页5、周长(4.8+3.2)×2=8×2=16(厘米)面积4.8×3=14.4(平方厘米)6、1) 4.75×1.2=5.7(元)2) 短6×1.5=9(米)9×6=54(平方米)或6×1.5×6=9×6=54(平方米)3) (35.7+24.3)×25=60×25=(元)第七页4) 15×0.45=6.75(千米)6×0.9=5.4(千米)6.75>5.4请问:李老师家离学校存有6.75千米,用0.9小时无法至学校.5) 2.94×23=67.62(米)≈68(米)6) 6.5×4÷2÷×=0.13×=14.56(元) (必须把平方分米切换为平方米)第八页7)24×18.5=(平方厘米)8)4.8×1.5÷2=7.2÷2=3.6 (平方厘米)(2.7+6.3)×5÷2=45÷2=22.5(平方分米)9)10×20+(12-10)×(20-14)÷2=+6=(平方厘米)(方法多种)提升篇:1、甲数的小数点向右移动一位就等于乙数，说明乙数是甲数的10倍。

部编人教版小学数学五年级上册《实际问题与方程(1)》5·3天天练

解：设每千克苹果x元。方程： 2.8x＝22.4
2.列方程解决下面的问题。
（1）人造地球卫星脱离地球环绕太阳运行的速度是每秒11.2km，比
人造地球卫星环绕地球运行的速度每秒多3.3km。人造地球卫星环绕
地球运行的速度是每秒多少千米？
解：设人造地球卫星环绕地球运行的速度是每秒xkm。 11.2－x＝3.3
x＝7.9 答：人造地球卫星环绕地球运行的速度是每秒7.9km。
（2）北美洲的面积约是2422.8万平方千米，是南极洲面积的1.73倍。南极洲的面积约是多少万平方千米？（结果保留整数）
解：设南极洲的面积约是x万平方千米。 1.73x＝2422.8
x≈1400 答：南极洲的面积约是1400万平方千米。
（3）整理图书。
96本童话书全部放在这个书柜里。平均每层放多少本？
解：设平均每层放x本。 4x＝96
x＝24
答：平均每层放24本。
3.小松鼠储藏了一些松果过冬，它原计划每天吃6个松果，实际每天比
原计划多吃2个，结果提前5天吃完松果。小松鼠一共储藏了多少个松
Байду номын сангаас果？
解：设原计划吃x天。（6＋2）（x－5）－6x＝0
1.（易错题）先补充用一步算式解答的问题，再根据题意写出等量关
系式，并列出方程。
（1）钢琴的白键有52个，比黑键多16个，黑键有多少个
？
白键个数
－黑键个数
＝ 16
解：设黑键有x个。方程： 52－x＝16
（2）买2.8kg苹果花了22.4元，每千克苹果多少钱
？
苹果的单价 × 苹果的质量＝苹果的总价
x＝20 6×20＝120（个）答：小松鼠一共储藏了120个松果。

三年级人教版数学下册《练习课(第1～3课时)》5·3天天练

3.根据小朋友的描述，把花园小学附近建筑的示意图填完整。北
书店礼品店邮局
银行花园小学
超市
服装城公交公司
少年宫
花园小学的南面是超市，北面是银行，东面是公交公司，东南方向是少年宫，西南方向是邮局，东北方向是服装城。
练习课（第1～3课时）
4.怎样才能不重复地参观到所有的景点呢？用箭头标出路线，并说一说。
风雨桥
北
入口
望江亭
长廊
荷花池
出口
石台
鹤舞园
从入口先向东走到望江亭，向南走到石台；再向东北走到荷花池，向北走
到风雨桥；然后向东南走到长廊，向南走到鹤舞园；最后向东北走到出口。（答案不唯一）
练习课（第1～3课时）
人教版三年级下学期
练习课（第1～3课时）
1.看图辨方向。（1）药店在理发店的（东）面，面馆的东面有（鞋店）和（书店），服装店
理发店
药店
北鲜花店
在面馆的（东北）方向，书店在鲜花店的（南）面，（理发店）在（面包房）的（西北）方向。
冰点屋面馆
面包房鞋店
服装店书店
（2）从书店出来去理发店，可以先向（西）走，再向（北）走，走
到十字路口的（西北）角就是理发店。
练习课（第1பைடு நூலகம்3课时）
2.圣诞老人先向（西北）走，给玲玲送礼物；再向（西南）走，给波波
送礼物；然后向（西北）走，给晶晶送礼物；最后向（东北）走，给帅帅
送礼物。
北
晶晶
帅帅波波
玲玲
练习课（第1～3课时）

部编人教版小学数学五年级上册《实际问题与方程(5)》5·3天天练

6km，乙每小时行4km。甲带着一只狗，狗每小时跑10km。这只狗同甲
一道出发，碰到乙时它就掉头跑向甲，碰到甲时又掉头跑向乙，直到
两人相遇时才停止。这只狗一共跑了多少千米？
解：设甲、乙经过x小时相遇。（6＋4）ห้องสมุดไป่ตู้＝40
x＝4 10×4＝40（km）答：这只狗一共跑了40km。
摩托车同时由乙城开往甲城。汽车每小时行驶60km，3小时后两车相距
15km。摩托车每小时行驶多少千米？解：设摩托车每小时行驶xkm。 3（60＋x）＝315－15 x＝40 3（60＋x）＝315＋15 x＝50 答：摩托车每小时行驶40km或50km。
6.甲、乙两人同时从两地出发，相向而行，距离是40km。甲每小时行
1.先根据示意图把等量关系补充完整，再列出方程。
已知两人同时从家出发，x分钟后相遇。（小红走的路程）＋（小军走的路程）＝总路程方程： 60x＋65x＝1600
2.杭州到上海全程约长180km。快车和慢车分别从两地同时相向开出， 1.5小时后两车相遇。慢车每小时行48km，快车每小时行多少千米？
解：设快车每小时行xkm。 1.5（x＋48）＝180
x＝72 答：快车每小时行72km。
3.甲、乙两地相距270km。一辆客车与一辆货车同时从两地相向开出
，2小时后相遇。已知客车的速度是货车的2倍，客车与货车的速度分
别是多少？
解：设货车每小时行驶xkm，则客车每小时行驶2xkm。 2（x＋2x）＝270
x＝45 2x＝90 答：货车每小时行驶45km，客车每小时行驶90km。
4.A、B两艘货轮同时从天津港开往上海港，经过4小时，A船落后B船 24.8km。A船每小时行45km，B船每小时行多少千米？