反比例函数中“K”与面积专题4
2024年中考数学一轮复习-反比例函数K值与几何面积综合(解析版)
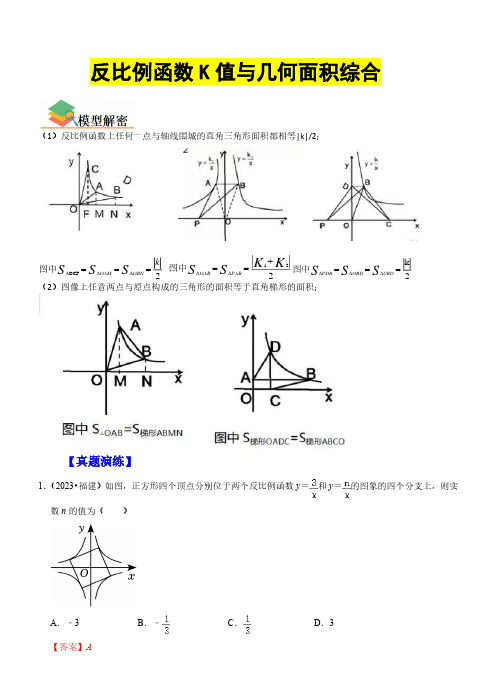
反比例函数K 值与几何面积综合（1）反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2；2OCF k S S S OBN OAM ===∆∆∆图中 221K K S S PAB OAB +==∆∆图中2k ===∆∆∆S S S CBD OBD PDB 图中（2）图像上任意两点与原点构成的三角形的面积等于直角梯形的面积；【真题演练】 1．（2023•福建）如图，正方形四个顶点分别位于两个反比例函数y ＝和y ＝的图象的四个分支上，则实数n 的值为（ ）A ．﹣3B ．﹣C ．D ．3【答案】A【解答】解：连接正方形的对角线，由正方形的性质知对角线交于原点O，过点A，B分别作x轴的垂线．垂足分别为C、D，点B在函数y＝上，如图：∵四边形是正方形，∴AO＝BO，∠AOB＝∠BDO＝∠ACO＝90°，∴∠CAO＝90°﹣∠AOC＝∠BOD，∴△AOC≌△BOD（AAS），∴S△AOC＝S△OBD＝＝，∵点A在第二象限，∴n＝﹣3，故选：A．2．（2023•张家界）如图，矩形OABC的顶点A，C分别在y轴、x轴的正半轴上，点D在AB上，且AD＝AB，反比例函数y＝（k＞0）的图象经过点D及矩形OABC的对称中心M，连接OD，OM，DM．若△ODM的面积为3，则k的值为（）A．2B．3C．4D．5【答案】C【解答】解：解法一：∵四边形OCBA是矩形，∴AB＝OC，OA＝BC，设B点的坐标为（a，b），∵矩形OABC的对称中心M，∴延长OM恰好经过点B，M（，），∵点D在AB上，且AD＝AB，∴D（，b），∴BD＝a，∴S△BDM＝BD•h＝×a×（b﹣）＝ab，∵D在反比例函数的图象上，∴ab＝k，∵S△ODM＝S△AOB﹣S△AOD﹣S△BDM＝ab﹣k﹣ab＝3，∴ab＝16，∴k＝ab＝4，解法二：连接BM，因为点M是矩形的对称中心，∴三角形DMO的面积＝三角形DMB的面积，则三角形DBO的面积为6，∵AD＝1/4AB，∴AD：DB＝1：3，∴三角形ADO的面积：三角形DBO的面积为1：3，即三角形ADO的面积为2，∴K＝4．故选：C．3．（2023•黑龙江）如图，△ABC是等腰三角形，AB过原点O，底边BC∥x轴，双曲线y＝过A，B两点，过点C作CD∥y轴交双曲线于点D．若S△BCD＝12，则k的值是（）A．﹣6B．﹣12C．﹣D．﹣9【答案】C【解答】解：设BC与y轴的交点为F，B（b，），则A（﹣b，﹣），b＞0，由题意知，AO＝BO，即O是线段AB的中点，过A作AE⊥BC于点E，∵AC＝AB，AE⊥BC，∴BE＝CE，AE∥y轴，∴CF＝3BF＝3b，∴C（﹣3b，），∴D（﹣3b，），∴CD＝，BC＝4b，∴S△BCD＝，∴k＝﹣．故选：C．4．（2023•宜宾）如图，在平面直角坐标系xOy中，点A、B分别在y、x轴上，BC⊥x轴，点M、N分别在线段BC、AC上，BM＝CM，NC＝2AN，反比例函数y＝（x＞0）的图象经过M、N两点，P为x轴正半轴上一点，且OP：BP＝1：4，△APN的面积为3，则k的值为（）A．B．C．D．【答案】B【解答】解：如图，过点N作NQ⊥x轴于点Q，过C作CT⊥y轴交y轴于T，交NQ于K，设OA＝a，OP＝b，BM＝c，N（m，n），∵OP：BP＝1：4，BM＝CM，∴A（0，a），B（5b，0），M（5b，c），C（5b，2c），∵∠NCK＝∠ACT，∠NKC＝90°＝∠ATC，∴△NKC∽△ATC，∴＝＝，∵NC＝2AN，∴CK＝2TK，NK＝AT，∴，解得，∴，∴，，∴，∵△APN的面积为3，∴S梯形OANQ﹣S△AOP﹣S△NPQ＝3，∴，∴2ab+bc＝9，将点M（5b，c），代入得：，整理得：2a＝7c，将2a＝7c代入2ab+bc＝9得：7bc+bc＝9，∴，∴，故选：B．5．（2022•日照）如图，矩形OABC与反比例函数y1＝（k1是非零常数，x＞0）的图象交于点M，N，与反比例函数y2＝（k2是非零常数，x＞0）的图象交于点B，连接OM，ON．若四边形OMBN的面积为3，则k1﹣k2＝（）A．3B．﹣3C．D．【答案】B【解答】解：∵y1、y2的图象均在第一象限，∴k1＞0，k2＞0，∵点M、N均在反比例函数y1＝（k1是非零常数，x＞0）的图象上，∴S△OAM＝S△OCN＝k1，∵矩形OABC的顶点B在反比例函数y2＝（k2是非零常数，x＞0）的图象上，∴S矩形OABC＝k2，∴S四边形OMBN＝S矩形OABC﹣S△OAM﹣S△OCN＝3，∴k2﹣k1＝3，∴k1﹣k2＝﹣3，故选：B．6．（2022•郴州）如图，在函数y＝（x＞0）的图象上任取一点A，过点A作y轴的垂线交函数y＝﹣（x ＜0）的图象于点B，连接OA，OB，则△AOB的面积是（）A．3B．5C．6D．10【答案】B【解答】解：∵点A在函数y＝（x＞0）的图象上，∴S△AOC＝×2＝1，又∵点B在反比例函数y＝﹣（x＜0）的图象上，∴S△BOC＝×8＝4，∴S△AOB＝S△AOC+S△BOC＝1+4＝5，故选：B．7．（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（）A．36B．18C．12D．9【答案】B【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：∵四边形ABCD是正方形，∴AE＝BE＝CE＝DE，设AE＝BE＝CE＝DE＝m，D（3，a），∵BD∥y轴，∴B（3，a+2m），A（3+m，a+m），∵A，B都在反比例函数y＝（k1＞0）的图象上，∴k1＝3（a+2m）＝（3+m）（a+m），∵m≠0，∴m＝3﹣a，∴B（3，6﹣a），∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图象上，D（3，a）在y＝（k2＞0）的图象上，∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，∴k1+k2＝18﹣3a+3a＝18；故选：B．8．（2022•黑龙江）如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是（）A．2B．1C．﹣1D．﹣2【答案】D【解答】解：设B（a，），∵四边形OBAD是平行四边形，∴AB∥DO，∴A（，），∴AB＝a﹣，∵平行四边形OBAD的面积是5，∴（a﹣）＝5，解得k＝﹣2，故选：D．9．（2023•连云港）如图，矩形OABC的顶点A在反比例函数y＝（x＜0）的图象上，顶点B、C在第一象限，对角线AC∥x轴，交y轴于点D．若矩形OABC的面积是6，cos∠OAC＝，则k＝﹣．【答案】﹣．【解答】解：作AE⊥x轴于E，∵矩形OABC的面积是6，∴△AOC的面积是3，∵∠AOC＝90°，cos∠OAC＝，∴，∵对角线AC∥x轴，∴∠AOE＝∠OAC，∵∠OEA＝∠AOC＝90°，∴△OEA∽△AOC，∴，∴，∴S△OEA＝，∵S△OEA＝|k|，k＜0，∴k＝﹣．故答案为：﹣．10．（2023•枣庄）如图，在反比例函数（x＞0）的图象上有P1，P2，P3，…P2024等点，它们的横坐标依次为1，2，3，…，2024，分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3，…，S2023，则S1+S2+S3+…+S2023＝．【答案】．【解答】解：∵P1，P2，P3，...P2024的横坐标依次为1，2，3， (2024)∴阴影矩形的一边长都为1，将除第一个矩形外的所有矩形向左平移至y轴，∴S 1+S2+S3+…+S2023＝，把x＝2024代入关系式得，y＝，即OA＝，∴S矩形OABC＝OA•OC＝，由几何意义得，＝8，∴＝8﹣＝．故答案为：．11．（2023•朝阳）如图，点A是反比例函数y＝（k≠0，x＞0）的图象上一点，过点A作AB⊥x轴于点B，点P是y轴上任意一点，连接P A，PB．若△ABP的面积等于3，则k的值为．【答案】6．【解答】解：设反比例函数的解析式为y＝，∵△AOB的面积＝△ABP的面积＝3，△AOB的面积＝|k|，∴|k|＝3，∴k＝±6；又∵反比例函数的图象的一支位于第一象限，∴k＞0．∴k＝6．故答案为：6．12．（2023•衢州）如图，点A，B在x轴上，分别以OA，AB为边，在x轴上方作正方形OACD，ABEF，反比例函数y＝（k＞0）的图象分别交边CD，BE于点P，Q．作PM⊥x轴于点M，QN⊥y轴于点N．若OA＝2AB，Q为BE的中点，且阴影部分面积等于6，则k的值为．【答案】见试题解答内容【解答】解：设OA＝4a，∵AO＝2AB，∴AB＝2a，∴OB＝AB+OA＝6a，则B（6a，0），由于在正方形ABEF中，AB＝BE＝2a，∵Q为BE中点，∴BQ＝AB＝a，∴Q（6a，a），∵Q在反比例函数y＝（k＞0））上，∴k＝6a×a＝6a2，∵四边形OACD是正方形，∴C（4a，4a），∵P在CD上，∴P点纵坐标为4a，∵P在反比例函数y＝（k＞0）上，∴P点横坐标为：x＝，∴P（，4a），∵作PM⊥x轴于点M，QN⊥y轴于点N，∴四边形OMNH是矩形，∴NH＝，MH＝a，∴S矩形OMHN＝NH×MH＝×a＝6，则k＝24，故答案为：24．13．（2023•锦州）如图，在平面直角坐标系中，△AOC的边OA在y轴上，点C在第一象限内，点B为AC 的中点，反比例函数y＝（x＞0）的图象经过B，C两点．若△AOC的面积是6，则k的值为．【答案】4．【解答】解：过点C作CD⊥y轴于点D，如图：设点C的坐标为（a，b），点A的坐标为（0，c），∴CD＝a，OA＝c，∵△AOC的面积是6，∴，∴ac＝12，∵点C（a，b）在反比例函数（x＞0）的图象上，∴k＝ab，∵点B为AC的中点，∴点，∵点B在反比例函数（x＞0）的图象上，∴，即：4k＝a（b+c），∴4k＝ab+ac，将ab＝k，ac＝12代入上式得：k＝4．故答案为：4．14．（2023•黄石）如图，点A（a，）和B（b，）在反比例函数y＝（k＞0）的图象上，其中a＞b＞0．过点A作AC⊥x轴于点C，则△AOC的面积为；若△AOB的面积为，则＝．【答案】，2．【解答】解：因为点A（a，）在反比例函数y＝的图象上，则，又a＞0，解得k＝5．根据k的几何意义可知，．过点B作x轴的垂线，垂足为D，则S△OBD+S梯形ACDB＝S△AOC+S△AOB，又根据k的几何意义可知，S△OBD＝S△AOC，则S梯形ACDB＝S△AOB．又△AOB的面积为，且A（a，），B（b，），所以，即．解得．又a＞b＞0，所以．故答案为：，2．15．（2023•辽宁）如图，矩形ABCD的边AB平行于x轴，反比例函数y＝（x＞0）的图象经过点B，D，对角线CA的延长线经过原点O，且AC＝2AO，若矩形ABCD的面积是8，则k的值为6．【答案】6．【解答】解：如图，延长CD交y轴于E，连接OD，∵矩形ABCD的面积是8，∴S△ADC＝4，∵AC＝2AO，∴S△ADO＝2，∵AD∥OE，∴△ACD∽△OCE，∴AD：OE＝AC：OC＝2：3，∴S△ODE＝3，由几何意义得，＝3，∵k＞0，∴k＝6，故答案为：6．16．（2023•绍兴）如图，在平面直角坐标系xOy中，函数（k为大于0的常数，x＞0）图象上的两点A （x1，y1），B（x2，y2），满足x2＝2x1，△ABC的边AC∥x轴，边BC∥y轴，若△OAB的面积为6，则△ABC的面积是．【答案】2．【解答】解：如图，延长CA交y轴于E，延长CB交x轴于点F，∴CE⊥y轴，CF⊥x轴，∴四边形OECF为矩形，∵x2＝2x1，∴点A为CE的中点，由几何意义得，S△OAE＝S△OBF，∴点B为CF的中点，∴S△OAB＝S矩形OECF＝6，∴S矩形OECF＝16，∴S△ABC＝×16＝2．故答案为：2．217．（2022•烟台）如图，A，B是双曲线y＝（x＞0）上的两点，连接OA，OB．过点A作AC⊥x轴于点C，交OB于点D．若D为AC的中点，△AOD的面积为3，点B的坐标为（m，2），则m的值为．【答案】见试题解答内容【解答】解：因为D为AC的中点，△AOD的面积为3，所以△AOC的面积为6，所以k＝12＝2m．解得：m＝6．故答案为：6．18．（2022•黄石）如图，反比例函数y＝的图象经过矩形ABCD对角线的交点E和点A，点B、C在x轴上，△OCE的面积为6，则k＝．【答案】8．【解答】解：如图，过点E作EH⊥BC于H，设点A（a，），C（c，0），∵点E是矩形ABCD的对角线的交点，∴E（，），∵点E在反比例函数y＝的图象上，∴＝k，∴c＝3a，∵△OCE的面积为6，∴OC•EH＝c•＝×3a•＝6，∴k＝8，故答案为：8．19．（2022•衢州）如图，在△ABC中，边AB在x轴上，边AC交y轴于点E．反比例函数y＝（x＞0）的图象恰好经过点C，与边BC交于点D．若AE＝CE，CD＝2BD，S△ABC＝6，则k＝．【答案】．【解答】解：如图，作CM⊥AB于点M，DN⊥AB于点N，设C（m，），则OM＝m，CM＝，∵OE∥CM，AE＝CE，∴＝＝1，∴AO＝m，∵DN∥CM，CD＝2BD，∴＝＝＝，∴DN＝，∴D的纵坐标为，∴＝，∴x＝3m，即ON＝3m，∴MN＝2m，∴BN＝m，∴AB＝5m，∵S△ABC＝6，∴5m•＝6，∴k＝．故答案为：．20．（2022•宜宾）如图，△OMN是边长为10的等边三角形，反比例函数y＝（x＞0）的图象与边MN、OM分别交于点A、B（点B不与点M重合）．若AB⊥OM于点B，则k的值为．【答案】9．【解答】解：过点B作BC⊥x轴于点C，过点A作AD⊥x轴于点D，如图，∵△OMN是边长为10的等边三角形，∴OM＝ON＝MN＝10，∠MON＝∠M＝∠MNO＝60°设OC＝b，则BC＝，OB＝2b，∴BM＝OM﹣OB＝10﹣2b，B（b，b），∵∠M＝60°，AB⊥OM，∴AM＝2BM＝20﹣4b，∴AN＝MN﹣AM＝10﹣（20﹣4b）＝4b﹣10，∵∠AND＝60°，∴DN＝＝2b﹣5，AD＝AN＝2b﹣5，∴OD＝ON﹣DN＝15﹣2b，∴A（15﹣2b，2b﹣5），∵A、B两点都在反比例函数y＝（x＞0）的图象上，∴k＝（15﹣2b）（2b﹣5）＝b•b，解得b＝3或5，当b＝5时，OB＝2b＝10，此时B与M重合，不符题意，舍去，∴b＝3，∴k＝b•b＝9，故答案为：9．21．（2022•鄂尔多斯）如图，正方形OABC的顶点A、C分别在x轴和y轴上，E、F分别是边AB、OA上的点，且∠ECF＝45°，将△ECF沿着CF翻折，点E落在x轴上的点D处．已知反比例函数y1＝和y2＝分别经过点B、点E，若S△COD＝5，则k1﹣k2＝．【答案】见试题解答内容【解答】解：作EH⊥y轴于点H，则四边形BCHE、AEHO都为矩形，∵∠ECF＝45°，∴∠OCD+∠OCF＝45°，∵∠DOC+∠OCF＝45°，∴∠BCE＝∠OCD，∵BC＝OC，∠B＝∠COD，∴△BCE≌△OCD（ASA），∴S△BCE＝S△COD＝5，∴S△CEH＝5，S矩形BCHE＝10，∴根据反比例函数系数k的几何意义得：k1﹣k2＝S矩形BCHE＝10，故答案为：10．22．（2022•东营）如图，△OAB是等腰直角三角形，直角顶点与坐标原点重合，若点B在反比例函数y＝（x＞0）的图象上，则经过点A的函数图象表达式为．【答案】y＝﹣．【解答】解：如图，作AD⊥x轴于D，BC⊥x轴于C，∴∠ADO＝∠BCO＝90°，∵∠AOB＝90°，∴∠AOD+∠BOC＝90°，∴∠AOD+∠DAO＝90°，∴∠BOC＝∠DAO，∵OB＝OA，∴△BOC≌△OAD（AAS），∵点B在反比例函数y＝（x＞0）的图象上，∴S△OBC＝，∴S△OAD＝，∴k＝﹣1，∴经过点A的反比例函数解析式为y＝﹣．故答案为：y＝﹣．23．（2022•绍兴）如图，在平面直角坐标系xOy中，点A（0，4），B（3，4），将△ABO向右平移到△CDE 位置，A的对应点是C，O的对应点是E，函数y＝（k≠0）的图象经过点C和DE的中点F，则k的值是．【答案】6．【解答】解：过点F作FG⊥x轴于点G，FH⊥y轴于点H，过点D作DQ⊥x轴于点Q，如图所示，根据题意可知，AC＝OE＝BD，设AC＝OE＝BD＝a，∴四边形ACEO的面积为4a，∵F为DE的中点，FG⊥x轴，DQ⊥x轴，∴FG为△EDQ的中位线，∴FG＝DQ＝2，EG＝EQ＝，∴四边形HFGO的面积为2（a+），∴k＝4a＝2（a+），解得：a＝，∴k＝6．故答案为：6．24．（2022•内蒙古）如图，在平面直角坐标系中，Rt△OAB的直角顶点B在x轴的正半轴上，点O与原点重合，点A在第一象限，反比例函数y＝（x＞0）的图象经过OA的中点C，交AB于点D，连接CD．若△ACD的面积是1，则k的值是．【答案】．【解答】解：连接OD，过C作CE∥AB，交x轴于E，∵∠ABO＝90°，反比例函数y＝（x＞0）的图象经过OA的中点C，∴S△COE＝S△BOD＝k，S△ACD＝S△OCD＝1，∵CE∥AB，∴△OCE∽△OAB，∴△OCE与△OAB得到面积比为1：4，∴4S△OCE＝S△OAB，∴4×k＝1+1+k，∴k＝．故答案为：．。
《用反比例函数比例系数k的几何意义解与面积相关的应用》PPT课件
(3)若 M(x1，y1)，N(x2，y2)是反比例函数 y＝mx 图 象上的两点，当 x1＜x2＜0 时，比较 y1 与 y2 的大小关系．
解：∵M(x1，y1)，N(x2，y2)是反比例函数 y＝ －2x图象上的两点，且 x1＜x2＜0，∴y1＜y2.
6．如图是由四条曲线围成的广告标志，建立平面直角坐 标系，双曲线对应的函数表达式分别为 y＝－6x，y＝6x. 现用四根钢条固定这四条曲线，这种钢条加工成矩形 产品按面积计算，每单位面积 25 元，请你帮助工人 师傅计算一下，所需钢条一共花多少钱？
(3)在x轴正半轴上是否存在点M，使得△MAB 为等腰三角形？若存在，请直接写出M点的 坐标；若不存在，说明理由．
解:M(－1＋ 23，0)或(3＋ 31，0)．
3．【2019·东营】如图，在平面直角坐标系中，直线 y＝mx 与双曲线 y＝nx相交于 A(－2，a)，B 两点， BC⊥x 轴，垂足为 C，△ AOC 的面积是 2. (1)求 m，n 的值；
(2)求两函数图象的交点A，C的坐标；
解:由yy＝ ＝－ －3xx＋，2，解得xy11＝＝3－，1，xy22＝＝－3，1. ∴点 A，C 的坐标分别为(－1，3)，(3，－1)．
(3)若点P是y轴上一动点，且S△APC＝5，求点P的坐标．
解：设点 P 的坐标为(0，m)，直线 y＝－x＋2 与 y 轴 的交点为 M，则 M 的坐标为(0，2)． ∵S△ APC＝S△ AMP＋S△ CMP＝12×PM×(|－1|＋|3|)＝5， ∴PM＝52，即|m－2|＝52.∴m＝92或 m＝－12. ∴点 P 的坐标为0，92或0，－12.
2021年九年级数学中考复习专题：反比例函数综合(考察坐标、取值范围、面积等)(四)
2021年九年级数学中考复习专题：反比例函数综合（考察坐标、取值范围、面积等）（四）1．如图1，在平面直角坐标系中，已知△ABC，∠ABC＝90°，∠ACB＝30°，顶点A 在第二象限，B，C两点在x轴的负半轴上（点C在点B的右侧），BC＝2，△ACD与△ABC关于AC所在的直线对称．（1）当OC＝2时，求点D的坐标；（2）若点A和点D在同一个反比例函数的图象上，求OC的长；（3）如图2，将第（2）题中的四边形ABCD向左平移，记平移后的四边形为A1B1C1D1，过点D1的反比例函数y＝（k≠0）的图象与BA的延长线交于点P，问：在平移过程中，是否存在这样的k，使得以点P，A1，D为顶点的三角形是直角三角形？若存在，请直接写出所有符合题意的k的值；若不存在，请说明理由．2．如图1，A（1，0）、B（0，2），双曲线y＝（x＞0）（1）若将线段AB绕A点顺时针旋转90°后B的对应点恰好落在双曲线y＝（x＞0）上①则k的值为；②将直线AB平移与双曲线y＝（x＞0）交于E、F，EF的中点为M（a，b），求的值；（2）将直线AB平移与双曲线y＝（x＞0）交于E、F，连接AE．若AB⊥AE，且EF ＝2AB，如图2，直接写出k的值．3．如图1，在平面直角坐标系xOy中，函数y＝（m为常数，m＞1，x＞0）的图象经过点P（m，1）和Q（1，m），直线PQ与x轴，y轴分别交于C，D两点．（1）求∠OCD的度数；（2）如图2，连接OQ、OP，当∠DOQ＝∠OCD﹣∠POC时，求此时m的值；（3）如图3，点A，点B分别在x轴和y轴正半轴上的动点．再以OA、OB为邻边作矩形OAMB．若点M恰好在函数y＝（m为常数，m＞1，x＞0）的图象上，且四边形BAPQ为平行四边形，求此时OA、OB的长度．4．如图，在四边形ABCD中，AB＝BC＝5，AD＝DC＝8，对角线BD＝3+4，点B在y轴上，BD与x轴平行，点C在x轴上．（1）求∠ADC的度数．（2）点P在对角线BD上，点Q在四边形ABCD内且在点P的右边，连接AP、PQ、QC，已知AP＝AQ，∠APQ＝60°，设BP＝m．①求CQ的长（用含m的代数式表示）；②若某一反比例函数图象同时经过点A、Q，求m的值．5．已知一次函数y1＝kx+n（n＜0）和反比例函数y2＝（m＞0，x＞0）．（1）如图1，若n＝﹣2，且函数y1、y2的图象都经过点A（3，4）．①求m，k的值；②直接写出当y1＞y2时x的范围；（2）如图2，过点P（1，0）作y轴的平行线l与函数y2的图象相交于点B，与反比例函数y3＝（x＞0）的图象相交于点C．①若k＝2，直线l与函数y1的图象相交点D．当点B、C、D中的一点到另外两点的距离相等时，求m﹣n的值；②过点B作x轴的平行线与函数y1的图象相交于点E．当m﹣n的值取不大于1的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．6．如图，四边形OABC为矩形，点B坐标为（4，2），A，C分别在x轴，y轴上，点F 在第一象限内，OF的长度不变，且反比例函数y＝经过点F．（1）如图1，当F在直线y＝x上时，函数图象过点B，求线段OF的长．（2）如图2，若OF从（1）中位置绕点O逆时针旋转，反比例函数图象与BC，AB相交，交点分别为D，E，连结OD，DE，OE．①求证：CD＝2AE．②若AE+CD＝DE，求k．③设点F的坐标为（a，b），当△ODE为等腰三角形时，求（a+b）2的值．7．如图，二次函数与反比例函数的图象有公共点A（﹣2，5），▱ABCD的顶点B（﹣5，p）在双曲线上，C、D两点在抛物线上（点C在y轴负半轴，点D在x轴正半轴）（1）求直线AB的表达式及C、D两点的坐标；（2）第四象限的抛物线上是否存在点E，使得四边形ACED的面积最大，若存在，求出点E的坐标和面积的最大值，不存在，说明理由．8．如图，在平面直角坐标系中，四边形ABCD为正方形，已知点A（﹣6，0）、D（﹣7，3），点B、C在第二象限内．（1）点B的坐标；（2）将正方形ABCD以每秒2个单位的速度沿x轴向右平移t秒，若存在某一时刻t，使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式；（3）在（2）的情况下，问是否存在y轴上的点P和反比例函数图象上的点Q，使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点P、Q的坐标；若不存在，请说明理由．9．如图所示，在平面直角坐标系Oxy中，等腰△OAB的边OB与反比例函数y＝（m ＞0）的图象相交于点C，其中OB＝AB，点A在x轴的正半轴上，点B的坐标为（2，4），过点C作CH⊥x轴于点H．（1）已知一次函数的图象过点O，B，求该一次函数的表达式；（2）若点P是线段AB上的一点，满足OC＝AP，过点P作PQ⊥x轴于点Q，连结OP，记△OPQ的面积为S△OPQ，设AQ＝t，T＝OH2﹣S△OPQ①用t表示T（不需要写出t的取值范围）；②当T取最小值时，求m的值．10．如图，点P在曲线上，PA⊥x轴于点A，点B在y轴正半轴上，PA＝PB，OA、OB的长是方程t2﹣8t+12＝0的两个实数根，且OA＞OB，点C是线段PB延长线上的一个动点，△ABC的外接圆⊙M与y轴的另一个交点是D．（1）填空：OA＝；OB＝；k＝；（2）设点Q是⊙M上一动点，若圆心M在y轴上且点P、Q之间的距离达到最大值，则点Q的坐标是；（3）试问：在点C运动的过程中，BD﹣BC的值是否为定值？若是，请求出该定值；若不是，请给出合理的解释．参考答案1．解：（1）∵△ADC与△ABC关于AC所在的直线对称，∴CD＝BC＝2，∠ACD＝∠ACB＝30°，如图1，过点D作DE⊥BC于点E，∵∠DCE＝60°，∴，∵OC＝2，∴OE＝3，∴；（2）设OC＝m，则OE＝m+1，OB＝m+2在Rt△ABC中，∠ACB＝30°，BC＝2，∴，∴，∵A，D在同一反比例函数上，∴，解得：m＝1，∴OC＝1；（3）由（2）得：∴，∵四边形A1B1C1D1由四边形ABCD平移得到，∴，∵D1在反比例函数上，∴同理：，，∴，∴，∵x P＝x A＝﹣3，P在反比例函数上，∴，①若P为直角顶点，则A1P⊥DP，过点P作l1⊥y轴，过点A1作A1F⊥l1，过点D作DG⊥l1，则△A1PF∽△PDG，，解得：；②若D为直角顶点，则A1D⊥DP，过点D作l2⊥x轴，过点A1作A1H⊥l2，则△A1DH∽△DPG，，，解得：k＝0（舍），综上：存在．2．解：（1）设旋转后点B的对应点为点C，过点C作CD⊥x轴于点D，如图所示∵∠BAC＝90°，∴∠BAO+∠CAD＝90°，∵∠BAO+∠ABO＝90°，∴∠ABO＝∠CAD，在△OAB和△DCA中，，∴△OAB≌△DCA（AAS），∴CD＝OA＝1，AD＝OB＝2，∴OD＝OA+AD＝3，∴C（3，1），把C（3，1）代入y＝中，得k＝3，故答案为：3；（2）直线AB表达式中的k值为﹣2，AB∥EF，则直线EF表达式中的k值为﹣2，设点E（m，n），mn＝3，直线EF的表达式为：y＝﹣2x+t，将点E坐标代入上式并解得，直线EF的表达式为y＝﹣2x+2m+n，将直线EF表达式与反比例函数表达式联立并整理得：2x2﹣（2m+n）x+3＝0，x1+x2＝，x1x2＝，则点F（n，），则a＝（），b＝（n+），＝＝＝2；（3）故点E作EH⊥x轴交于点H，由（1）知：△ABO∽△EHA，∴，设EH＝m，则AH＝2m，则点E（2m+1，m），且k＝m（2m+1）＝2m2+m，直线AB表达式中的k值为﹣2，AB∥EF，则直线EF表达式中的k值为﹣2，设直线EF的表达式为：y＝﹣2x+b，将点E坐标代入并求解得：b＝5m+2，故直线EF的表达式为：y＝﹣2x+5m+2，将上式与反比例函数表达式联立并整理得：2x2﹣（5m+2）x+3＝0，用韦达定理解得：x F+x E＝，则x F＝，则点F（m，4m+2），则EF＝＝2AB＝2×，整理得：3m2+4m﹣4＝0，解得：m＝或﹣2（舍去负值），k＝m（2m+1）＝2m2+m＝．3．解：（1）设直线PQ的解析式为y＝kx+b，则有，解得，∴y＝﹣x+m+1，令x＝0，得到y＝m+1，∴D（0，m+1），令y＝0，得到x＝m+1，∴C（m+1，0），∴OC＝OD，∵∠COD＝90°，∴∠OCD＝45°．（2）如图2，过Q作QM⊥y轴于M，过P作PN⊥OC于N，过O作OH⊥CD于H，∵P（m，1）和Q（1，m），∴MQ＝PN＝1，OM＝ON＝m，∵∠OMQ＝∠ONP＝90°，∴△OMQ≌△ONP（SAS），∴OQ＝OP，∠DOQ＝∠POC，∵∠DOQ＝∠OCD﹣∠POC，∠OCD＝45°，∴∠DOQ＝∠POC＝∠QOH＝∠POH＝22.5°，∴MQ＝QH＝PH＝PN＝1，∵∠OCD＝∠ODC＝45°，∴△DMQ和△CNP都是等腰直角三角形，∴DQ＝PC＝，∵OC＝OD＝m+1，∴CD＝OC＝，∵CD＝DQ+PQ+PC，∴＝2+2，∴m＝+1；（3）如图3，∵四边形BAPQ为平行四边形，∴AB∥PQ，AB＝PQ，∴∠OAB＝45°，∵∠AOB＝90°，∴OA＝OB，∴矩形OAMB是正方形，∵点M恰好在函数y＝（m为常数，m＞1，x＞0）的图象上，∴M（，），即OA＝OB＝，∵AB＝PQ，∴，解得：m＝或（舍），∴OA＝OB＝＝＝＝．4．解：（1）连接AC交BD于点H，∵AB＝BC，AD＝DC，BD＝BD，∴△ABD≌△CBD（SSS），∴∠ABD＝∠CBD，∴BH是等腰三角形ABC的高，即BH⊥AC，即BD是AC的中垂线，设HD＝x，则BH＝4+3﹣x，AH2＝AB2﹣BH2＝AD2﹣DH2，即82﹣x2＝52﹣（3+4﹣x）2，解得：x＝，cos∠ADB＝＝＝，故∠ADB＝30°BD是AC的中垂线，则∠ADB＝30°＝∠CDB，故∠ADC＝2∠ADB＝60°；（2）①连接AQ、QD、PC，∵∠APQ＝60°，AP＝AQ，∴△APQ为等边三角形，故∠PAQ＝60°＝∠PAC+∠HAQ，同理△ACD是边长为8的等边三角形，∴∠CAD＝60°＝∠HAQ+∠QAD，∴∠PAC＝∠QAD，而AP＝AQ，AD＝AC，∴△ACP≌△ADQ（SAS），∵BD是AC的中垂线，故PA＝PC，则△ACP为等腰三角形，∴△AQD也为等腰三角形，即AQ＝QD，而AC＝CD（△ACD为等边三角形），CQ＝CQ，∴△ACQ≌△DCQ（SSS），故∠ACQ＝∠DCQ，在△CAD中，延长CQ交AD于点K，∵AC＝CD，则CK⊥AD，∴∠AKQ＝90°∵∠AKQ＝90°＝∠AHP，∠QAK＝∠PAH，PA＝AQ，∴△AKQ≌△QHP（AAS），∴QK＝PH，过点D作DR⊥x轴交于点R，BD∥x轴，故∠BDC＝∠DCR＝30°，DR＝CD＝8×＝4＝CH＝OB，而BC＝5，故OC＝3＝BH，故点C（3，0），PH＝BH＝BP＝3﹣m＝QK，在等边三角形ACD中，AD边上的高CK＝CD sin∠CDA＝8×sin60°＝4，则CQ＝CK﹣QK＝4﹣3+m；②过点Q分别作x、y轴的垂线，垂足为M、N，∵AK是等边三角形CDA的高，则∠KCD＝30°，而∠DCR＝30°，故∠QCR＝60°，QM＝CQ sin∠QCM＝CQ sin60°＝CQ，CM＝CQ，故点Q（3+CQ，CQ），点C（3，0），CH＝4，故点A（3，8），反比例函数图象同时经过点A、Q，则3×8＝（3+CQ）×CQ，而CQ＝4﹣3+m，即m2+24m+39﹣96＝0，解得：m＝﹣4（不合题意值已舍去）．5．解：（1）①将点A的坐标代入一次函数表达式并解得：k＝2，将点A的坐标代入反比例函数得：m＝3×4＝12；②由图象可以看出x＞3时，y1＞y2；（2）①当x＝1时，点D、B、C的坐标分别为（1，2+n）、（1，m）、（1，n），则BD＝|2+n﹣m|，BC＝m﹣n，DC＝2+n﹣n＝2则BD＝BC或BD＝DC或BC＝CD，即：|2+n﹣m|＝m﹣n或|2+n﹣m|＝2或m﹣n＝2，即：m﹣n＝1或0或2或4，当m﹣n＝0时，m＝n与题意不符，点D不能在C的下方，即BC＝CD也不存在，n+2＞n，当B、D重合时，m﹣n＝2成立，故m﹣n＝1或4或2；②点E的横坐标为：，当点E在点B左侧时，d＝BC+BE＝m﹣n+（1﹣）＝1+（m﹣n）（1﹣），m﹣n的值取不大于1的任意数时，d始终是一个定值，当1﹣＝0时，此时k＝1，从而d＝1．当点E在点B右侧时，同理BC+BE＝（m﹣n）（1+）﹣1，当1+＝0，k＝﹣1时，（不合题意舍去）故k＝1，d＝1．6．解：（1）∵F在直线y＝x上∴设F（m，m）∵y＝经过点B（2，4）．∴k＝8．∵F（m，m）在反比例函数的图象上，∴m2＝8∴m＝2（负值已舍去）．∴由两点间的距离公式可知：OF＝＝4．（2）①∵函数y＝的图象经过点D，E∴OC•CD＝OA•AE＝k．∵OC＝2，OA＝4，∴CD＝2AE．②由①得：CD＝2AE∴可设：CD＝2n，AE＝n∴DE＝CD+AE＝3n，BD＝4﹣2n，BE＝2﹣n在Rt△EBD，由勾股定理得：DE2＝BD2+BE2，∴9n2＝（4﹣2n）2+（2﹣n）2．解得n＝，∴k＝4n＝6﹣10．③CD＝2c，AE＝c当OD＝DE时，22+4c2＝（4﹣2c）2+（2﹣c）2，∴c＝10﹣2，∴k＝4c＝40﹣8．（a+b）2＝a2+b2+2ab＝16+2k＝96﹣16．当若OE＝DE时，16+c2＝（4﹣2c）2+（2﹣c）2，∴c＝．∴k＝4c＝10﹣2．∴（a+b）2＝a2+b2+2ab＝16+2k＝36﹣4．当OE＝OD时，4+4c2＝16+c2，解得c＝2．此时点D与点E重合，故此种情况不存在．综上所述，（a+b）2的值为96﹣16或36﹣4．7．解：（1）设反比例函数的解析式为y＝．∵它图象经过点A（﹣2，5）和点B（﹣5，p），∴5＝，∴k＝﹣10，∴反比例函数的解析式为y＝﹣，∴P＝﹣＝2，∴点B的坐标为（﹣5，2），设直线AB的表达式为y＝mx+n，则，∴，∴直线AB的表达式为y＝x+7．由▱ABCD中，AB∥CD，设CD的表达式为y＝x+c，∴C（0，c），D（﹣c，0），∵CD＝AB，∴CD2＝AB2，∴c2+c2＝（﹣5+2）2+（2﹣5）2，∴c＝﹣3，∴点C、D的坐标分别是（0，﹣3）、（3，0）．（2）设二次函数的解析式为y＝ax2+bx﹣3，，∴，∴二次函数的解析式为y＝x2﹣2x﹣3，假设第四象限的抛物线上存在点E，使得△CDE的面积最大．设E（k，k2﹣2k﹣3），则F（k，k﹣3），过点E作x轴的垂线交CD于点F，则S△CDE＝S△EFC+S△EFD＝•EF•OD＝•[（k﹣3）﹣（k2﹣2k﹣3）]＝﹣（k2﹣3k）＝﹣（k﹣）2+，所以，当k＝时，△CDE的面积最大值为，此时点E的坐标为（，﹣）．∵A（﹣2，5），C（0，﹣3），D（3，0），∴△ACD的面积为定值，∵直线AD的解析式为y＝﹣x+3，∴直线AD交y轴于K（0，3），∴S△ACD＝S△ACK+S△CKD＝×6×2+×6×3＝15，∴四边形ACED的面积的最大值为15+＝．8．解：（1）过点B、D分别作BE⊥x轴、DF⊥x轴交于点E、F，∵∠DAF+∠BAE＝90°，∠DAF+∠FDA＝90°，∴∠FDA＝∠BAE，又∠DFA＝∠AEB＝90°，AD＝AB，∴△DFA≌△AEB（AAS），∴DF＝AE＝3，BE＝AF＝1，∴点B坐标为（﹣3，1），故答案为（﹣3，1）；（2）t秒后，点D′（﹣7+2t，3）、B′（﹣3+2t，1），则k＝（﹣7+2t）×3＝（﹣3+2t）×1，解得：t＝，则k＝6，则点D′（2，3）、B′（6，1）；（3）存在，理由：设：点Q（m，n），点P（0，s），mn＝6，①当BD为平行四边形一条边时，图示平行四边形B′D′QP，点B′向左平移4个单位、向上平移2个单位得到点D′，同理点Q（m，n）向左平移4个单位、向上平移2个单位为（m﹣4，n+2）得到点P （0，s），即：m﹣4＝0，n+2＝s，mn＝6，解得：m＝4，n＝，s＝，故点Q（4，）、点P（0，）；②当BD为平行四边形对角线时，图示平行四边形D′Q′B′P′，B′、D′中点坐标为（4，2），该中点也是P′Q′的中点，即：4＝，＝2，mm＝6，解得：m＝8，n＝，s＝，故点Q′（8，）、P′（0，）；故点Q的坐标为：Q（4，）或（8，），点P的坐标为P（0，）（0，）．9．解：（1）将点O、B的坐标代入一次函数表达式：y＝kx得：4＝2k，解得：k＝2，故一次函数表达式为：y＝2x，（2）①过点B作BM⊥OA，则∠OCH＝∠QPA＝∠OAB＝∠ABM＝α，则tanα＝，sinα＝，∵OB＝AB，则OM＝AM＝2，则点A（4，0），设：AP＝a，则OC＝a，在△APQ中，sin∠APQ＝＝＝sinα＝，同理PQ＝＝2t，则PA＝a＝t，OC＝t，则点C（t，2t），T＝OH2﹣S△OPQ＝（OC•sinα）2﹣×（4﹣t）×2t＝4t2﹣4t，②∵4＞0，∴T有最小值，当t＝时，T取得最小值，而点C（t，2t），故：m＝t×2t＝．10．解：（1）t2﹣8t+12＝0，解得：t＝2或6，∵OA、OB的长是方程t2﹣8t+12＝0的两个实数根，且OA＞OB，即OA＝6，OB＝2，即点A、B的坐标为（﹣6，0）、（0，2），设点P（﹣6，），由PA＝PB得：36+（2+）2＝（）2，解得：k＝﹣60，故点P（﹣6，10），故答案为：6，2，﹣60；（2）当PQ过圆心M时，点P、Q之间的距离达到最大值，tan∠ACO＝，线段AB中点的坐标为（﹣3，1），则过AB的中点与直线AB垂直的直线PQ的表达式为：y＝mx+n＝﹣3x+n，将点（﹣3，1）的坐标代入上式并解得：n＝﹣8，即点M的坐标为（0，﹣8），则圆的半径r＝MB＝2+8＝10＝MQ，过点Q作QG⊥y轴于点G，tan∠QMG＝tan∠HMP＝＝＝，则sin∠QMG＝故GQ＝MQ sin∠QMG＝，MG＝3，故点Q（，﹣8﹣3）；故答案为：（，﹣8﹣3）．（3）是定值，理由：延长PA交圆M于E，过点E作EH⊥BD于H，连接CE，DE，∵PA＝PB，∴∠PAB＝∠PBA，∵四边形ABCE是圆的内接四边形，∴∠PAB＝∠PCE，∠PBA＝∠PEC，∴∠PEC＝∠PCE，∴PE＝PC，∴AE＝BC，∵AO⊥BD，EH⊥BD，PA⊥OA，∴四边形AOHE是矩形，∴AO＝EH，AE＝OH＝BC，∵PA∥BD，∴＝，∴，∴∠ABD＝∠BDE，且∠AOB＝∠EHD＝90°，AO＝EH，∴△AOB≌△EHD（AAS）∴OB＝DH＝2，∴BD﹣BC＝BD﹣OH＝OB+DH＝4．。
反比例函数_---动点、面积专题(附详解)
转135°得到△OA′B′，写出A′B′的中点P的坐标，试判断点P是否在此双曲线上，并说明理由；（3）若该反比例函数图象上有一点F（m，错误！未找到引用源。
）（其中m＞0），在线段OF上任取一点E，设E点的纵坐标为n，过F点作FM⊥x轴于点M，连接EM，使△OEM的面积是错误！未找到引用源。
，求代数式错误！未找到引用源。
的值．3、如图，M点是正比例函数y=kx和反比例函数错误！未找到引用源。
的图象的一个交点．（1）求这两个函数的解析式；（2）在反比例函数错误！未找到引用源。
的图象上取一点P，过点P做PA垂直于x轴，垂足为A，点Q是直线MO上一点，QB垂直于y轴，垂足为B，直线MO 上是否存在这样的点Q，使得△OBQ的面积是△OPA的面积的2倍？如果存在，请求出点Q的坐标，如果不存在，请说明理由．4、如图，已知：一次函数：y=﹣x+4的图象与反比例函数：错误！未找到引用源。
（x＞0）的图象分别交于A、B两点，点M是一次函数图象在第一象限部分上的任意一点，过M分别向x轴、y轴作垂线，垂足分别为M1、M2，设矩形MM1OM2的面积为S1；点N为反比例函数图象上任意一点，过N分别向x轴、y轴作垂线，垂足分别为N1、N2，设矩形NN1ON2的面积为S2；（1）若设点M的坐标为（x，y），请写出S1关于x的函数表达式，并求x取何值时，S1的最大值；（2）观察图形，通过确定x的取值，试比较S1、S2的大小．5、如图，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P （﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB 垂直于y轴，垂足分别是A、B．（1）写出正比例函数和反比例函数的关系式；（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ 与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由．6、如图1，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P （﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB 垂直于y轴，垂足分别是A、B．（1）写出正比例函数和反比例函数的关系式；（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ 与△OAP面积相等如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．。
1.2反比例函数k的几何意义(第4课时)ppt课件
o
A
x
o
A
x
18
2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面 积为1,则这个反比例函数的关系式是 .
y 2 y
x
y
P
P
C oO D
xx
y k (k 0) 的面积不变性
x
y P（ x, y） S K k ( k 0 )
22
0
Q
x
y
P（ x , y）
x 0
3
1
平面直. 角坐标系内任意一点P(x,y)
P到x轴的距离是这点纵坐标的绝对值即是
P到y轴的距离是6这点横坐的绝对值即0是.5
y
y
x
y
p
N
M
ox
4
1.如图，点P(3，2)在反比例
函数 y k 图像上 则K=( 6 ),过xP作PA⊥x轴，
PB⊥y轴,则OA=( 3), PA=( 2),S矩形OAPB=（ ）6
如图s矩形oapbsoap10反比例函数上一点px0y0过点p分别作pay轴pbx轴垂足分别为ab则矩形aobp的面积为且saopsbop1112则有面积分别为轴引垂线经过三点分别向的图像上有三点occobboaaocoboas2s3b1c1s1s3s213已知点p是反比例函数14谢谢大家再见15九年级数学组16垂足分别为轴的垂线apoa过反比例函数图象上任一点p分别作x轴y轴的垂线垂足分别为ab它们与坐标轴形成的矩形面积是不变的
oA
x
y
CE B F
x
O
A
16
过反比例函数图象上任一点P分别作x轴、y轴的垂线，垂足分别为A,B，它们与
坐标(轴2形)过 成的P 矩分 形面积是别 不变x轴 的。作 ,y轴 的,垂 足 线分 A,B别 ,
反比例函数中的面积问题
解得 k=2 评注：第①小题中由图形所在象限可确定k>0，应用结论可直接求k值。 第②小题首先应用三角形面积的计算方法分析得出四个三角形面积相 等，列出含k的方程求k值。
例2（2008贵州省黔南州）如图，矩形ABOD的顶点A是函数 与函数 在第二象限的交点， 轴于B， 轴于D，且矩形ABOD的பைடு நூலகம்积为3． （1）求两函数的解析式． （2）求两函数的交点A、C的坐标．
图象上，∴
解得x=1从而所求面积为π 评注：对于较复杂的图形面积计算问题，先应观察图形的特征，若具有 对称特征，则应用对称关系可以简化解题过程。
四、 讨论与面积有关的综合问题 例8．（2008山东省）（1）探究新知：
如图1，已知△ABC与△ABD的面积相等， 试判断AB与CD的位置关系，并说明理由． （2）结论应用：
与x轴交于点C，其中点A的坐标为（－2，4），点B的横坐标为－4. （1）试确定反比例函数的关系式； （2）求△AOC的面积.
.解：（1）∵点A（-2，4）在反比例函数图象上 ∴k=-8 ∴反比例函数解析式为y=
（2）∵B点的横坐标为-4， ∴纵坐标为y=2 ∴B(-4，2) ∵点A（-2，4）、 点B（-4，2）在直线y=kx+b上 ∴ 4=-2k+b 且2=-4k+b 解得 k=1 b=6 ∴直线AB为y=x+6 与x轴的交点坐标C（-6，0）
（3）若点P是y轴上一动点，且 ， 求点P的坐标．
解：（1）由图象知k<0，由结论及已知条件得 -k=3 ∴
∴反比例函数的解析式为 ，一次函数的解析式为 （2）由 ，解得 ，
∴点A、C的坐标分别为（
，3），（3， ） （3）设点P的坐标为（0，m） 直线 与y轴的交点坐标为M（0，2） ∵
反比例函数面积问题专题
反比率函数面积问题专题【围矩形】1．以下图，点 P 是反比率函数图象上一点，过点 P 分别作 x 轴、 y 轴的垂线，假如构成的矩形面积是4，那么反比率函数的分析式是（）A. B.C..D.2．反比率函数的图象以下图，则k 的值可能是（）A.-1B.C.1D. 23．如图， A、 B 是双曲线上的点，分别过A、 B 两点作 x 轴、 y 轴的垂线段．S1，S2，S3分别表示图中三个矩形的面积，若S3 =1，且 S1+S2=4，则 k 值为（）A.1B.2C. 3D. 44．如图，在反比率函数y= （x＞0）的图象上，有点P1、P2、P3、 P4，它们的横坐标挨次为1，2，3，4．分别过这些点作x 轴与 y 轴的垂线，图中所构成的暗影部分的面积从左到右挨次为S1、S2、S3，则 S1+S2+S3=（）A. 1B.C. 2D.没法确立5．如图，两个反比率函数y=和y=（此中k1＞0＞k2）在第一象限内的图象是C1，第二、四象限内的图象是C2，设点 P 在 C1上， PC⊥x轴于点 M，交 C2于点 C，PA⊥y轴于点 N，交 C2于点 A，AB∥PC，CB∥AP 订交于点 B，则四边形 ODBE的面积为（）A. |k 1﹣ k2| B. C. |k 1? k2| D.【围三角形】6．如图，A、 C 是函数y=的图象上的随意两点，过 A 作 x轴的垂线，垂足为B，过C作y 轴的垂线，垂足为D，记 Rt△AOB的面积为S1，Rt△COD的面积为S2，则（）A. S 1＞S2B. S 1＜S2C. S 1=S2D. 关系不可以确立7．如图，过y 轴上随意一点p，作x 轴的平行线，与反比率函数的图象交于 A 点，若 B 为 x 轴上随意一点，连结8．如图， A 是反比率函数AB，PB则△ APB的面积为（）A. 1 B. 2 C. 3 D. 4图象上一点，过点 A 作 AB⊥x轴于点 B，点 P 在 y 轴上，△ABP的面积为9．反比率函数1，则y=与k 的值为（）A. 1 B. 2 C. -1 D. -2y= 在第一象限的图象以下图，作一条平行于x 轴的直线分别交双曲线于A、B 两点，连结OA、 OB，则△ AOB的面积为（）A. B.2 C. 3 D. 110．如图，过 x 轴正半轴上的随意一点P，作 y 轴的平行线，分别与反比率函数y=﹣和 y= 的图象交于 A、 B 两点．若点 C 是 y 轴上随意一点，连结AC、BC，则△ ABC的面积为（） A.3 B.4 C. 5 D. 1011．双曲线y1=与y2=在第一象限内的图象如图．作一条平行于x 轴的直线交y1，y2于B、A，连 OA，过 B 作 BC∥OA，交x 轴于C，若四边形OABC的面积为3，则k=（）A.2B.4C.3D.512．如图，直线 l 和双曲线交于A、B两点，P是线段AB上的点（不与A、B重合），过点 A、 B、 P 分别向 x 轴作垂线，垂足分别为C、D、E，连结 OA、 OB、0P，设△ AOC的面积为 S1、△BOD的面积为 S2、△ POE的面积为 S3，则（）A. S 1＜S2＜S3B. S 1＞S2＞S3C. S 1=S2＞S3D. S 1=S2＜ S313．如图是反比率函数和在第一象限内的图象，在上取点M分别作两坐标轴的垂线交于点 A、 B，连结 OA、OB，则图中暗影部分的面积为．【对称点】14．如图，直线 y=kx（k＞0）与双曲线 y= 交于 A，B 两点， BC⊥x轴于 C，连结 AC交 y 轴于 D，下列结论：① A、 B 对于原点对称；②△ ABC的面积为定值；③D 是 AC的中点；④S△AOD= ．此中正确结论的个数为（）个 A.1 B.2 C.3 D. 415．如图，直 y=mx与双曲线 y= 交于点 A，B．过点 A 作 AM⊥x轴，垂足为点 M，连结 BM．若 S△ABM=1，则 k 的值是（）A. 1 B. m﹣1C. 2 D. m16．正比率函数 y=x 与反比率函数 y= 的图象订交于 A、C两点． AB⊥x轴于 B，CD⊥y轴于 D，如图，则四边形ABCD的面积为（）A. 1B.C.2D.17．如图， A，C 是函数 y= （k≠0）的图象上对于原点对称的随意两点，AB， CD垂直于 x 轴，垂足分别为 B， D，那么四边形 ABCD的面积 S 是（）A. B. 2k C. 4k D. k18．如图，反比率函数y=﹣的图象与直线 y=﹣x 的交点为 A，B，过点 A 作 y 轴的平行线与过点 B 作 x 轴的平行线订交于点C，则△ ABC的面积为（）A.8B.6C.4D.2【三角形叠梯形】19．如图，点 A 和 B 是反比率函数 y= （x＞0）图象上随意两点，过A，B 分别作 y 轴的垂线，垂足为 C和 D，连结 AB，AO，BO，△ ABO的面积为 8，则梯形 CABD的面积为（）A.6B.7C.8D.1020．如图，△ ABO的极点 A 和 AB边的中点 C 都在双曲线 y=（x＞0）的一个分支上，点 B 在 x 轴上， CD⊥OB于 D，若△ AOC的面积为 3，则 k=（）A. 2B. 3 C.4 D.21．如图， A、B 是双曲线上随意两点，过 A、B 两点分别作 y 轴的垂线，垂足分别为 C、D，连结 AB，直线 OB、 OA分别交双曲线于点 E、F，设梯形 ABCD的面积和△ EOF的面积分别为 S、S ，则 S 与 S 的大小关系是（）A. S1=S S ＞S S ＜S不可以确立1212 2 B.1 2 C.1 2 D.【截矩形】22．如图，过点 P（2，3）分别作 PC⊥x轴于点 C，PD⊥y轴于点 D，PC、 PD分别交反比率函数y=（x＞0）的图象于点 A、B，则四边形 BOAP的面积为（）A. 3 B. C. 4 D. 523．如图，双曲线y= （k＞0）经过矩形 OABC的边 BC的中点 E，交 AB于点 D．若梯形 ODBC的面积为 3，则 k=．24．函数 y= 和 y= 在第一象限内的图象如图，点 P 是 y= 的图象上一动点， PC⊥x轴于点 C，交 y=的图象于点 B．给出以下结论：①△ ODB与△ OCA的面积相等；② PA与 PB一直相等；③四边形 PAOB的面积大小不会发生变化；④CA= AP．此中全部正确结论的序号是（）A. ①②③B.②③④C.①③④D.①②④25．两个反比率函数和（k1＞k2＞0）在第一象限内的图象如图，P 在 C1上，作 PC、PD 垂直于坐标轴，垂线与C2交点为 A、B，则以下结论：①△ ODB与△ OCA的面积相等；②四边形PAOB的面积等于 k1﹣k2③PA与 PB一直相等；④当点 A 是 PC的中点时，点B必定是 PD的中点．此中正确的选项是（）.①② B.①②④ C.①④ D.①③④【截直角三角形】26．如图，已知双曲线经过直角三角形OAB斜边 OA的中点 D，且与直角边 AB订交于点 C．若点 A 的坐标为（﹣ 8， 6），则△ AOC的面积为（）A. 20B. 18C. 16D. 1227．如图，双曲线经过Rt△OAB斜边OA的中点D，且与直角边AB订交于点C．则△ AOC的面积为（）A. 9 B. 6 C. D. 328．如图，已知矩形ABCO的一边 OC在 x 轴上，一边 OA在 y 轴上，双曲线交OB的中点于D，交 BC边于 E，若△ OBC的面积等于 4，则 CE：BE的值为（）A.1：2B.1：3C.1：4D.没法确立29．如图，已知梯形ABCO的底边 AO在 x 轴上， BC∥AO，AB⊥AO，过点 C的双曲线交OB于D，且OD：DB=1：2，若△ OBC的面积等于3，则k的值（）A. 2 B. C. D. 没法确立30．如图，反比率函数的图象经过矩形OABC对角线的交点 M，分别与 AB、 BC订交于点 D、E．若四边形 ODBE的面积为 6，则 k 的值为（）反比率函数【围矩形】1．解：由题意得：矩形面积等于|k| ，∴ |k|=4又∵反比率函数图象在二、四象限．∴k＜0∴k=﹣4∴反比率函数的分析式是y=﹣．应选 C．2．解：∵反比率函数在第一象限，∴ k＞ 0，∵当图象上的点的横坐标为 1 时，纵坐标小于 1，∴k ＜ 1，应选 B．3．解：∵S1 +S2=4，∴S1=S2═2，∵S3=1，∴S1+S3=1+2=3，∴ k=3 应选 C．4．解：由题意可知点P1、P2、P3、P4坐标分别为：（1，2），（2，1），（ 3，），（4，）．∴由反比率函数的几何意义可知：S1+S2+S3 =2﹣1×= =．应选 B．5．解：∵ AB∥PC，CB∥AP，∠ APC=90°，∴四边形APCB是矩形．设 P（x，），则A（，），C（x，），∴S矩形 APCB=AP?P C=（x﹣）（﹣）=，∴四边形ODBE的面积 =S 矩形APCB﹣S 矩形PNOM﹣S 矩形MCDP﹣S 矩形AEON=﹣k1﹣|k2|﹣|k2|=．应选D．【围三角形】6．解：联合题意可得：A、 C 都在双曲线y=上，反比率函数系数k 的几何意义有S1 =S2；应选C．7．解：依题意得：△ APB的面积 S= |k|=×|4|=2．应选B8．解：如图，连 OA，∵ AB⊥x轴，∴ AB∥OP，∴S△OAB=S△PAB=1，∴ |k|=2×1=2，∵反比率函数图象过第二象限，∴ k=﹣ 2．应选 D．9．解：分别过A、 B 作 x 轴的垂线，垂足分别为D、 E，过 B 作 BC⊥y轴，点 C 为垂足，∵由反比率函数系数k 的几何意义可知， S 四边形OEAC=6，S△AOE=3，S△BOC= ，∴S△AOB=S四边形 OEAC﹣S△AOE﹣S△BOC=6﹣3﹣= ．应选A．10．解：设 P（ a， 0），a＞0，则 A 和 B 的横坐标都为 a，将 x=a 代入反比率函数 y=﹣中得： y=﹣，故 A（a，﹣）；将 x=a 代入反比率函数 y= 中得： y= ，故 B（a，），∴AB=AP+BP=+ =，则S△ABC= AB? x P的横坐标 =××a=5．应选C11．解：由题意得：S 四边形OABC=|k 1| ﹣|k 2 |=|6|﹣|k|=3；又因为反比率函数位于第一象限，k＞0；k=3．故选 C．12．解：联合题意可得： AB都在双曲线 y= 上，则有 S1=S2；而 AB之间，直线在双曲线上方；故 S1=S2＜S3应选 D．13．解：∵在上取点M分别作两坐标轴的垂线交于点A、 B，∴S△AOC=×5=，S△BOD= ×5= S 矩形MDOC=3∴S暗影 =S△AOC+S△BOD﹣S 矩形MDOC=5﹣3=2 故答案为 2．【对称点】14．解：①反比率函数与正比率函数如有交点，必定是两个，且对于原点对称，因此正确；②依据 A、B 对于原点对称， S△ABC为即 A 点横纵坐标的乘积，为定值 1，因此正确；③因为 AO=BO，OD∥BC，因此 OD为△ ABC的中位线，即 D是 AC中点，因此正确；④在△A DO中，因为 AD和 y 轴其实不垂直，因此面积不等于k 的一半，不等于，错误．应选C．15．解：由图象上的点A、B、M构成的三角形由△ AMO和△ BMO的构成，点 A 与点 B 对于原点中心对称，∴点 A，B 的纵横坐标的绝对值相等，∴△ AMO和△ BMO的面积相等，且为，∴点 A 的横纵坐标的乘积绝对值为 1，又因为点 A 在第一象限内，因此可知反比率函数的系数 k 为 1．应选 A．16．解：依据反比率函数的对称性可知： OB=OD，AB=CD，∴四边形 ABCD的面积 =S△AOB+S△ODA+S△ODC+S△OBC=1×2=2．应选 C．17．解：∵ A， C 是函数 y= （k≠0）的图象上对于原点对称的随意两点，∴若假定 A 点坐标为（ x，y），则 C点坐标为（﹣ x，﹣ y）．∴ BD=2x， AB=CD=y，∴S四边形 ABCD=S△ABD+S△CBD=BD? AB+ BD? CD=2xy=2k．故四边形 ABCD的面积 S 是 2k．应选 B．18．解：因为点 A、B 在反比率函数图象上对于原点对称，则△ABC的面积 =2|k|=2 ×4=8．应选 A．【三角形叠梯形】19．解：过点 B 向 x 轴作垂线，垂足是 G．由题意得：矩形 BDOG的面积是 |k|=3 ，∴S△ACO=S△BOG= ．所以△ AOB的面积 =S矩形BDOG+S 梯形ABDC﹣ S△ACO﹣S△BOG=8，则梯形 CABD的面积 =8﹣ 3+3=8．应选 C20．解：过点 A 作 AM⊥OB于 M，设点 A 坐标为（ x， y），∵极点 A 在双曲线 y= （x＞0）图象上，∴ xy=k，∴S△AMO= OM? AM= xy= k，设 B 的坐标为（ a，0），∵中点 C在双曲线 y= （x＞ 0）图象上， CD⊥OB于 D，∴点 C坐标为（，），∴S△CDO= OD? CD= ?? = k，∴ ay=3k，∵S△A OB=S△AOM+S△AMB=k+ ? （a﹣x）y = k+ ay﹣ xy= k+ ×3k﹣k = k，又∵C为 AB中点，∴△ AOC的面积为×k=3，∴ k=4，应选 C．21．解：∵直线 OB、 OA分别交双曲线于点E、F，∴S2=S△AOB，∵S1=S△AOC+S△AOB﹣S△BOD，而S△AOC=S△BOD= k，∴S1=S△AOB，∴S1=S2．应选 A．【截矩形】22．解：∵ B、 A 两点在反比率函数y= （ x＞0）的图象上，∴S△DBO=S△AOC= ×2=1，∵P（ 2，3），∴四边形 DPCO的面积为 2×3=6，∴四边形 BOAP的面积为 6﹣1﹣1=4，应选： C．23．解：连结 OE，设此反比率函数的分析式为y= （k≠0）， C（ c， 0），则 B（c，b），E（c，），设 D（x，y），∵D和 E 都在反比率函数图象上，∴xy=k，=k，即 S△AOD=S△OEC= ×c×，∵梯形 ODBC的面积为 3，∴ bc﹣×c×=3，∴bc=3，∴ bc=4，∴S△AOD=S△OEC=1，∵k＞ 0，∴k=1，解得 k=2，故答案为： 2．24．解：∵ A、 B 是反比函数 y= 上的点，∴S△OBD=S△OAC= ，故①正确；当P 的横纵坐标相等时PA=PB，故②错误；∵P是 y= 的图象上一动点，∴S矩形PDOC=4，∴S四边形 PAOB=S矩形 PDOC﹣S△ODB﹣﹣S△OAC=4﹣﹣=3，故③正确；连结 OP，= = =4，∴ AC= PC，PA= PC，∴=3，∴AC= AP；故④正确；综上所述，正确的结论有①③④．应选C．25．解：①∵ A、 B 两点都在 y=上，∴△ ODB与△ OCA的面积都都等于，故①正确；②S矩形 OCPB﹣S△AOC﹣S△DBO=|k 2|﹣2×|k1|÷2=k2﹣k1 ，故②正确；③只有当 P 的横纵坐标相等时， PA=PB，错误；④当点 A 是 PC的中点时，点B必定是 PD的中点，正确．应选B．【截直角三角形】26．解：∵点 A 的坐标为（﹣ 8，6），O点坐标为（ 0， 0），∴斜边 OA的中点 D的坐标为（﹣ 4， 3），把 D（﹣ 4， 3）代入 y= 得 k=﹣4×3=﹣ 12，∴反比率函数的分析式为y=﹣，∵AB⊥x轴，∴C点和横坐标为点 A 同样，都为﹣ 8，把 x=﹣8 代入 y=﹣得 y= ，∴C点坐标为（﹣ 8，），∴ AC=6﹣ = ，∴△ AOC的面积 = AC? OB= × ×8=18．应选 B．27．解：∵ OA的中点是 D，双曲线 y=﹣经过点 D，∴ k=xy=﹣ 3，D 点坐标为：（x，y），则 A 点坐标为：（2x，2y），∴△ BOC的面积 = |k|=3 ．又∵△ AOB的面积 = ×2x×2y=12，∴△ AOC的面积 =△AOB的面积﹣△ BOC的面积 =12﹣3=9．应选： A．28．解：设D点的坐标是（x，y）．∵点D是线段OB的中点，∴B 点的坐标是（2x，2y）；∵△ OBC的面积等于 4，∴×2x×2y=4，即 xy=﹣2，∴ k=﹣ 2；又∵点 E 在双曲线上，∴点E的坐标为（2x，）；∴CE： BE= ：（2y﹣）=：（2×﹣）=1：3；应选B．29．解：方法 1：设 B 点坐标为（ a，b），∵ OD： DB=1： 2，∴D点坐标为（a， b），依据反比率函数的几何意义，∴a?b=k，∴ ab=9k①，∵BC∥AO，AB⊥AO， C 在反比率函数 y= 的图象上，∴设 C 点横坐标为 m，则 C点坐标为（ m，b）将（ m，b）代入 y= 得， m= ， BC=a﹣，又因为△ OBC的高为 AB，因此 S△OBC= （a﹣）? b=3，因此（ a﹣） ? b=3，（a﹣）b=6，ab﹣k=6②，把①代入②得， 9k﹣ k=6，解得 k= ．方法 2：延伸 BC交 y 轴于 E，过 D作 x 轴的垂线，垂足为 F．由△OAB的面积=△OBE的面积，△ODF的面积=△OCE的面积，可知，△ ODF的面积 = 梯形 DFAB= △BOC的面积 = ，即k= ， k= ．应选 B．30．解：由题意得：E、 M、 D 位于反比率函数图象上，则S△OCE=，S△OAD=，过点M作MG⊥y轴于点G，作MN⊥x轴于点N，则S□ONMG=|k| ，又∵M为矩形 ABCO对角线的交点，则S 矩形 ABCO=4S□O NMG=4|k|，因为函数图象在第一象限，k＞0，则+ +6=4k， k=2．应选B．。
专题：反比例函数中的面积问题
微专题 反比例函数中的面积问题
模型一 一点一垂线
反比例函数图象上一点与坐标轴垂线、另一坐标轴上一点(含原点)围成的三 角形面积＝ |k|.
1
S△ABC＝ 2 |k|
S△ABC＝12 |k|
1
S△AOC＝ 2 |k|
1. 如图，点A在反比例函数y＝－ 4 的图象上，AM⊥y轴于点M，点P是x轴上的一
方法一：S△EOF＝S△EOD－S△FOD. 方法二：作EM⊥x轴于点M，交OF于点B，FA⊥x轴于点A，则S△OEB＝S四边形 BMAF(划归到模型一)，则S△EOF＝S直角梯形EMAF.
类型一 两交点在反比例函数同一支上
Байду номын сангаас
方法一：当
BE CE
或
BFFA＝m时，则S四边形OFBE＝m|k|.
方法二：作EM⊥x轴于点M，
A. 1
B. m－1
C. 2
D. m
第3题图
模型四 两点两垂线
反比例函数与正比例函数的交点及由交点向坐标轴所作两条垂线围成的图形 面积＝2|k|.
SABC 2 | k |
易得四边形ANBM是平行四边形， ∴S四边形ANBM＝AM·NM＝AM·2OM＝2|k|
模型四 两点两垂线 反比例函数与正比例函数的交点及由交点向坐标轴所作两条垂线围成的图形
＝ ＝
1
2
1
OM·AM＋12 OM·BC |k|＋1 |k|＝|k|
22
S△ABM＝S△ADM＋S△MDB
＝
1 2
MD·|yB－yA|
S△ABM＝S△BMO＋S△AMO
＝
1 2
MO·|xB－xA|
3. 如图，直线y＝mx与双曲线y＝k (k≠0)交于点A，B，过点A作
反比例函数背景下的面积问题(解析版)-2023年中考数学重难点解题大招复习讲义-函数
模型介绍一、反比例函数k 的几何意义1.反比例函数k 的几何意义：如图，在反比例函数图象上任选一点，向两坐标轴作垂线，垂线与坐标轴所围成矩形的面积为k 。
如图二，所围成三角形的面积为2k二、利用k 的几何意义进行面积转化1.如图，直线AB 与反比例函数k y x=（0k ≠）交于A 、B 两点，与x 、y 轴的交点分别为C 、D ，那么OAB OCD OBD OAC S S S S ∆∆∆∆=--，此方法是绝大部分学生选用的方法。
但是，从效率来讲，就比较低2.如图，过点A 、B 作x 轴的垂线，垂足分别为E 、F ，则根据k 的几何意义可得，OBF OAE S S ∆∆=，而OBF OAB OAE ABFE S S S S ∆∆∆+=+梯形，所以OAB ABFE S S ∆=梯形，此方法的好处，在于方便，快捷，不易出错。
【例1】．如图，反比例函数y＝在第一象限的图象上有两点A，B，它们的横坐标分别是2，6，则△AOB的面积是8．过点A作AC⊥y轴于点C，过点B作BD⊥x轴于点D，∴x＝2时，y＝3；x＝6时，y＝1，＝S△OBD＝3，故S△ACOS四边形AODB＝×（3+1）×4+3＝11，故△AOB的面积是：11﹣3＝8．故答案为：8．变式训练【变1-1】．如图，点A在反比例函数（x＞0）的图象上，点B在x轴负半轴上，直线AB交y轴于点C，若，△AOB的面积为12，则k的值为（）A．4B．6C．10D．12解：如图，过点A作AD⊥x轴，垂足为D，∵OC∥AD，，∴，∴，k＞0，∴k＝12，故选：D．【变1-2】．如图，反比例函数y＝（k＞0）的图象与矩形ABCO的两边相交于E，F两点，＝4，则k的值为16．若E是AB的中点，S△BEF解：设E（a，），则B纵坐标也为，∵E是AB中点，∴F点坐标为（2a，），∴BF＝BC﹣FC＝﹣＝，＝4，∵S△BEF∴a•＝4，∴k＝16．故答案是：16．【例2】．如图，平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为6，4，反比例函数y＝（x＞0）的图象经过A，B两点，若菱形ABCD的面积为2，则k的值为12．解：解法一：过点A作x轴的垂线，交CB的延长线于点E，∵BC∥x轴，∴AE⊥BC，∵A，B两点在反比例函数y＝（x＞0）的图象，且纵坐标分别为6，4，∴A（，6），B（，4），∴AE＝2，BE＝﹣＝，∵菱形ABCD的面积为2，∴BC×AE＝2，即BC＝，∴AB＝BC＝，在Rt△AEB中，BE＝＝＝1，∴k＝1，∴k＝12．解法二：同理知：BE＝1，设A（a，6），则B（a+1，4），∴6a＝4（a+1），∴a＝2，∴k＝2×6＝12．故答案为12．变式训练【变2-1】．如图，点A、B在反比例函数y＝的图象上，A、B的纵坐标分别是3和6，连接OA、OB，则△OAB的面积是（）A．9B．8C．7D．6解：∵点A、B在反比例函数y＝的图象上，A、B的纵坐标分别是3和6，∴A（4，3），B（2，6），作AD⊥y轴于D，BE⊥y轴于E，＝S△BOE＝×12＝6，∴S△AOD＝S△AOD+S梯形ABED﹣S△BOE＝S梯形ABED，∵S△OAB＝（4+2）×（6﹣3）＝9，∴S△AOB故选：A．【变2-2】．如图，在直角坐标系中，O为坐标原点，函数y＝与y＝（a＞b＞0）在第一象限的图象分别为曲线C1，C2，点P为曲线C1上的任意一点，过点P作y轴的垂线交C2于点A，作x轴的垂线交C2于点B，则阴影部分的面积S△AOB＝a﹣．（结果用a，b表示）解：设B（m，），A（，n），则P（m，n），∵点P为曲线C1上的任意一点，∴mn＝a，＝mn﹣b﹣b﹣（m﹣）（n﹣）∴阴影部分的面积S△AOB＝mn﹣b﹣（mn﹣b﹣b+）＝mn﹣b﹣mn+b﹣＝a﹣．故答案为：a﹣．1．如图，在△ABC中，AB＝AC，点A在反比例函数y＝（k＞0，x＞0）的图象上，点B，C在x轴上，OC＝OB，延长AC交y轴于点D，连接BD，若△BCD的面积等于1，则k的值为（）A．3B．2C．D．4解：作AE⊥BC于E，连接OA，∵AB＝AC，∴CE＝BE，∵OC＝OB，∴OC＝BC＝×2CE＝CE，∵AE∥OD，∴△COD∽△CEA，∴＝（）2＝4，∵△BCD的面积等于1，OC＝OB，＝S△BCD＝，∴S△COD＝4×＝1，∴S△CEA∵OC＝CE，＝S△CEA＝，∴S△AOC＝+1＝，∴S△AOE＝k（k＞0），∵S△AOE∴k＝3，故选：A．2．如图，OC交双曲线y＝于点A，且OC：OA＝5：3，若矩形ABCD的面积是8，且AB ∥x轴，则k的值是（）A．18B．50C．12D．解：延长DA、交x轴于E，∵四边形ABCD是矩形，且AB∥x轴，∴∠CAB＝∠AOE，∴DE⊥x轴，CB⊥x轴，∴∠AEO＝∠ABC∴△AOE∽△CAB，∴＝（）2，∵矩形ABCD的面积是8，OC：OA＝5：3，∴△ABC的面积为4，AC：OA＝2：3，∴＝（）2＝，＝9，∴S△AOE∵双曲线y＝经过点A，＝|k|＝9，∴S△AOE∵k＞0，∴k＝18，故选：A．3．如图，已知点A，B分别在反比例函数y1＝﹣和y2＝的图象上，若点A是线段OB 的中点，则k的值为（）A．﹣8B．8C．﹣2D．﹣4解：设A（a，b），则B（2a，2b），∵点A在反比例函数y1＝﹣的图象上，∴ab＝﹣2；∵B点在反比例函数y2＝的图象上，∴k＝2a•2b＝4ab＝﹣8．故选：A．4．如图，点A（m，n），B（4，）在双曲线y＝上，且0＜m＜n．若△AOB的面积为，则m+n＝（）A．7B．C．D．3解：∵点A（m，n），B（4，）在双曲线y＝上，∴mn＝4×＝k，∴mn＝k＝6，∴双曲线为y＝，∴n＝，作AD⊥x轴于D，BE⊥x轴于E，＝S△AOD+S梯形ADEB﹣S△BOE＝S梯形ADEB，∵S△AOB∴（+）（4﹣m）＝，解得m1＝1，m2＝﹣16，∵0＜m＜n．∴m＝1，∴n＝6，∴m+n＝7，故选：A．5．如图，点A，B是反比例函数y＝（x＞0）图象上的两点，过点A，B分别作AC⊥x轴＝3，则S△于点C，BD⊥x轴于点D，连接OA、BC，已知点C（2，0），BD＝3，S△BCDAOC为（）A．2B．3C．4D．6解：在Rt△BCD中，∵×CD×BD＝3，∴×CD×3＝3，∴CD＝2，∵C（2，0），∴OC＝2，∴OD＝4，∴B（4，3），∵点B是反比例函数y＝（x＞0）图象上的点，∴k＝12，∵AC⊥x轴，＝＝6，∴S△AOC故选：D．6．如图，平行于y轴的直线分别交y＝与y＝的图象（部分）于点A、B，点C是y 轴上的动点，则△ABC的面积为（）A．k1﹣k2B．（k1﹣k2）C．k2﹣k1D．（k2﹣k1）解：由题意可知，AB＝﹣，AB边上的高为x，＝×（﹣）•x＝（k1﹣k2），∴S△ABC故选：B．7．已知四边形OABC是矩形，边OA在x轴上，边OC在y轴上，双曲线y＝与边BC交于点D、与对角线OB交于中点E，若△OBD的面积为10，则k的值是（）A．10B．5C．D．解：设E点的坐标是（x，y），∵E是OB的中点，∴B点的坐标是（2x，2y），则D点的坐标是（，2y），∵△OBD的面积为10，∴×（2x﹣）×2y＝10，解得，k＝，故选：D．8．如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数（x＞0）与AB相交于点D，与BC相交于点E，若BD＝3AD，且△ODE的面积是12，则k＝（）A．6B．9C．D．解：∵四边形OCBA是矩形，∴AB＝OC，OA＝BC，设B点的坐标为（a，b），∵BD＝3AD，∴D（，b）∵D、E在反比例函数的图象上，∴＝k，设E的坐标为（a，y），∴ay＝k∴E（a，），＝S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE＝ab﹣k﹣k﹣••（b﹣）＝12，∵S△ODE∴4k﹣k﹣+＝12k＝故选：D．9．如图，一直线经过原点O，且与反比例函数y＝（k＞0）相交于点A、点B，过点A作AC⊥y轴，垂足为C，连接BC．若△ABC面积为8，则k＝8．解：∵反比例函数与正比例函数的图象相交于A、B两点，∴A、B两点关于原点对称，∴OA＝OB，∴△BOC的面积＝△AOC的面积＝8÷2＝4，又∵A是反比例函数y＝图象上的点，且AC⊥y轴于点C，∴△AOC的面积＝|k|，∴|k|＝4，∵k＞0，∴k＝8．故答案为8．10．如图，若反比例函数y＝的图象经过等边三角形POQ的顶点P，则△POQ的边长为2．解：如图，过点P作x轴的垂线于M，∵△POQ为等边三角形，∴OP＝OQ，OM＝QM＝OQ，∵反比例函数的图象经过点P，∴设P（a，）（a＞0），则OM＝a，OQ＝OP＝2a，PM＝，在Rt△OPM中，PM＝＝＝a，∴＝a，∴a＝1（负值舍去），∴OQ＝2a＝2，故答案为：2．11．如图，A（4，3）是反比例函数y＝在第一象限图象上一点，连接OA，过A作AB∥x 轴，截取AB＝OA（B在A右侧），连接OB，交反比例函数y＝的图象于点P．则△OAP 的面积为5．解：过P作MN⊥x轴于M，交AB于N，过A作AD⊥x轴于D，∵A（4，3），∴AD＝3，OD＝4，∴AO＝＝5，∵AB＝AO，∴AB＝5，∵AB∥x轴，点B的横坐标是4+5＝9，纵坐标是3，即点B的坐标是（9，3），设直线OB的解析式是y＝ax，把B点的坐标（9，3）代入得：3＝9a，解得：a＝，即y＝x，∵AB∥x轴，∴MN⊥AB，把A（4，3）代入y＝，得k＝12，即y＝，解方程组得：或，∵点P在第一象限，∴点P的坐标是（6，2），∵A（4，3），AB∥x轴，P（6，2），∴MN＝AD＝3，PN＝3﹣2＝1，﹣S△APB＝3﹣＝5，∴△OAP的面积是S△ABO故答案为：5．12．如图，直线y＝x+m与双曲线y＝相交于A，B两点，BC∥x轴，AC∥y轴，则△ABC 面积的最小值为6．解：方法一：设A（a，），B（b，），则C（a，）．将y＝x+m代入y＝，得x+m＝，整理，得x2+mx﹣3＝0，则a+b＝﹣m，ab＝﹣3，∴（a﹣b）2＝（a+b）2﹣4ab＝m2+12．＝AC•BC∵S△ABC＝（﹣）（a﹣b）＝••（a﹣b）＝（a﹣b）2＝（m2+12）＝m2+6，∴当m＝0时，△ABC的面积有最小值6．故答案为6．方法二：因为y＝x+m斜率为1，且BC∥x轴，AC∥y轴，∴∠ABC＝∠BAC＝45°，∴△ABC为等腰直角三角形，∴AC＝BC＝AB，＝AC•BC＝AB2，∴S△ABC当AB最小时，m＝0，直线为y＝x，联立方程，解得或，∴A（，），B（﹣，﹣），AB＝×2＝2，＝×4×6＝6．∴S△ABC最小故答案为：6．13．如图，在平面直角坐标系中，△OAB的边OA在x轴正半轴上，其中∠OAB＝90°，AO ＝AB，点C为斜边OB的中点，反比例函数y＝（k＞0，x＞0）的图象过点C，且交线＝6，则k的值为8．段AB于点D，连接CD，OD．若S△OCD解：根据题意设B（m，m），则A（m，0），∵点C为斜边OB的中点，∴C（，），∵反比例函数y＝（k＞0，x＞0）的图象过点C，∴k＝•＝，∵∠OAB＝90°，∴D的横坐标为m，∵反比例函数y＝（k＞0，x＞0）的图象过点D，∴D的纵坐标为，作CE⊥x轴于E，＝S△AOD，∵S△COES△OCD＝S△COE+S梯形ADCE﹣S△AOD＝S梯形ADCE，S△OCD＝6，∴（AD+CE）•AE＝6，即（+）•（m﹣m）＝6，∴m2＝32，∴k＝＝8，故答案为：8．解法二：作CE⊥OA于E，∵C为AB的中点，OA＝AB，∠OAB＝90°，＝S△AOD＝k，S△AOB＝2k，∴S△OEC＝k，∴S△BOD∵C为斜边OB的中点，＝S△BCD＝S△BOD＝6，∴S△OCD∴×k＝6，∴k＝8．故答案为：8．14．如图，在平面直角坐标系中，▱OABC的顶点A，B在第一象限内，顶点C在y轴上，经过点A的反比例函数y＝（x＞0）的图象交BC于点D．若CD＝2BD，▱OABC的面积为15，则k的值为18．解：过点D作DN⊥y轴于N，过点B作BM⊥y轴于M，设OC＝a，CN＝2b，MN＝b，∵▱OABC的面积为15，∴BM＝，∴ND＝BM＝，∴A，D点坐标分别为（，3b），（，a+2b），∴•3b＝（a+2b），∴b＝a，∴k＝•3b＝•3×a＝18，故答案为：18．15．如图，点A在双曲线y＝的第一象限的那一支上，AB垂直于y轴于点B，点C在x 轴正半轴上，且OC＝2AB，点E在线段AC上，且AE＝3EC，点D为OB的中点，若△ADE的面积为3，则k的值为．解：连DC，如图，∵AE＝3EC，△ADE的面积为3，∴△CDE的面积为1，∴△ADC的面积为4，设A点坐标为（a，b），则AB＝a，OC＝2AB＝2a，而点D为OB的中点，∴BD＝OD＝b，＝S△ABD+S△ADC+S△ODC，∵S梯形OBAC∴（a+2a）×b＝a×b+4+×2a×b，∴ab＝，把A（a，b）代入双曲线y＝，∴k＝ab＝．故答案为：．16．如图，已知反比例函数y1＝与一次函数y2＝k2x+b的图象交于点A（1，8），B（﹣4，m）两点．（1）求k1，k2，b的值；（2）求△AOB的面积；（3）请直接写出不等式x+b的解．解：（1）∵反比例函数y1＝与一次函数y2＝k2x+b的图象交于点A（1，8）、B（﹣4，m），∴k1＝8，B（﹣4，﹣2），解方程组，解得；（2）由（1）知一次函数y＝k2x+b的图象与y轴的交点坐标为（0，6），＝×6×4+×6×1＝15；∴S△AOB（3）﹣4≤x＜0或x≥1．17．如图，在平面直角坐标系中，A点的坐标为（a，6），AB⊥x轴于点B，cos∠OAB＝，反比例函数y＝的图象的一支分别交AO、AB于点C、D．延长AO交反比例函数的图象的另一支于点E．已知点D的纵坐标为．（1）求反比例函数的解析式；（2）求直线EB的解析式；．（3）求S△OEB解：（1）∵A点的坐标为（a，6），AB⊥x轴，∴AB＝6，∵cos∠OAB＝＝，∴，∴OA＝10，由勾股定理得：OB＝8，∴A（8，6），∴D（8，），∵点D在反比例函数的图象上，∴k＝8×＝12，∴反比例函数的解析式为：y＝；（2）设直线OA的解析式为：y＝bx，∵A（8，6），∴8b＝6，b＝，∴直线OA的解析式为：y＝x，则，x＝±4，∴E（﹣4，﹣3），设直线BE的解式为：y＝mx+n，把B（8，0），E（﹣4，﹣3）代入得：，解得：，∴直线BE的解式为：y＝x﹣2；＝OB•|y E|＝×8×3＝12．（3）S△OEB18．如图，直线y＝x与反比例函数的图象交于点A（3，a），第一象限内的点B在这个反比例函数图象上，OB与x轴正半轴的夹角为α，且tanα＝．（1）求反比例函数的解析式；（2）求点B的坐标；．（3）求S△OAB解：（1）∵直线y＝x与反比例函数的图象交于点A（3，a），∴a＝×3＝4，∴点A的坐标为（3，4），∴k＝3×4＝12，∴反比例函数解析式y＝．（2）∵点B在这个反比例函数图象上，设点B坐标为（x，），∵tanα＝，∴＝，解得：x＝±6，∵点B在第一象限，∴x＝6，∴点B的坐标为（6，2）．（3）设直线OB为y＝kx，（k≠0），将点B（6，2）代入得：2＝6k，解得：k＝，∴OB直线解析式为：y＝x．过A点做AC⊥x轴，交OB于点C，如图所示：则点C坐标为（3，1），∴AC＝3．S△OAB的面积＝S△OAC的面积+S△ACB的面积＝×|AC|×6＝9．∴△OAB的面积为9．19．已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A（﹣2，0），与反比＝4．例函数在第一象限内的图象的交于点B（2，n），连接BO，若S△AOB （1）求该反比例函数的解析式和直线AB的解析式；（2）若直线AB与双曲线的另一交点为D点，求△ODB的面积．＝•|x A|•y B，解：（1）由题意得：S△AOB即×2×y B＝4，y B＝4，∴B（2，4），设反比例函数的解析式为：y＝，把点B的坐标代入得：k＝2×4＝8，∴y＝，设直线AB的解析式为：y＝ax+b，把A（﹣2，0）、B（2，4）代入得：，解得：，∴y＝x+2；（2）由题意得：x+2＝，解得：x1＝﹣4，x2＝2，∴D（﹣4，﹣2），＝S△OAD+S△OAB＝×2×2+4＝6．∴S△ODB20．如图，在平行四边形OABC中，，点A在x轴上，点D是AB 的中点，反比例函数的图象经过C，D两点．（1）求k的值；（2）求四边形OABC的面积．解：（1）过点C作CE⊥x轴于E，∵∠AOC＝45°，∴OE＝CE，∴OE2+CE2＝OC2∵OC＝2，∴OE＝CE＝2，∴C（2，2），∵反比例函数的图象经过点C点，∴k＝2×2＝4；（2）过点D作DF⊥x轴于F，∵四边形OABC是平行四边形，∴AB＝OC＝2，∠DAF＝∠AOC＝45°，又∵点D是AB的中点，∴AD＝，AF＝DF，∴AF2+DF2＝AD2，∴AF＝DF＝1，∴D点的纵坐标为1，∵反比例函数的图象过点D点，∴D（4，1），∴OF＝4，OA＝OF﹣AF＝4﹣1＝3，∴平行四边形OABC的面积S＝OA•CE＝3×2＝6．21．如图，直线y＝6x与双曲线y＝（k≠0，且x＞0）交于点A，点A的横坐标为2．（1）求点A的坐标及双曲线的解析式；（2）点B是双曲线上的点，且点B的纵坐标是6，连接OB，AB，求△AOB的面积．解：（1）将x＝2代入y＝6x，得：y＝12，∴点A的坐标为（2，12），将A（2，12）代入y＝，得：k＝24，∴反比例函数的解析式为y＝；（2）在y＝中y＝6时，x＝4，∴点B（4，6），而A（2，12），如图，过A作AC⊥y轴，BD⊥x轴，交于点E，则OD＝4，OC＝12，BD＝6，AC＝2，AE＝2，BE＝6，＝S矩形OCED﹣S△AOC﹣S△BOD﹣S△ABE∴S△AOB＝4×12﹣×2×12﹣×4×6﹣×2×6＝48﹣12﹣12﹣6＝18．22．如图，已知A（﹣4，n），B（2，﹣4）是一次函数y＝kx+b的图象和反比例函数的图象的两个交点．（1）求反比例函数和一次函数的表达式；（2）求△AOB的面积；（3）若D（x，0）是x轴上原点左侧的一点，且满足，求x的取值范围．解：（1）∵B（2，﹣4）在反比例函数y＝的图象上，∴m＝﹣8，∴反比例函数的表达式为y＝﹣．∵A（﹣4，n）在y＝﹣的图象上，∴n＝2，∴A（﹣4，2）．∵y＝kx+b经过A（﹣4，2）和B（2，﹣4），∴，解得∴一次函数的表达式为y＝﹣x﹣2．（2）当y＝﹣x﹣2＝0时，解得x＝﹣2．∴点C（﹣2，0），∴OC＝2，＝S△AOC+S△COB∴S△AOB＝×2×2+×2×4＝6．（3）根据函数的图象可知：若D（x，0）是x轴上原点左侧的一点，当﹣4＜x＜0时，满足kx+b﹣＜0．23．如图，一次函数y＝k1x+b的图象与反比例函数y＝（x＜0）的图象相交于点A（﹣1，2）、点B（﹣4，n）．（1）求此一次函数和反比例函数的表达式；（2）求△AOB的面积；（3）在x轴上存在一点P，使△PAB的周长最小，求点P的坐标．解：（1）∵反比例函数y＝（x＜0）的图象经过点A（﹣1，2），∴k2＝﹣1×2＝﹣2，∴反比例函数表达式为：y＝﹣，∵反比例y＝﹣的图象经过点B（﹣4，n），∴﹣4n＝﹣2，解得n＝，∴B点坐标为（﹣4，），∵直线y＝k1x+b经过点A（﹣1，2），点B（﹣4，），∴，解得：，∴一次函数表达式为：y＝+．（2）设直线AB与x轴的交点为C，如图1，当y＝0时，x+＝0，x＝﹣5；∴C点坐标（﹣5，0），∴OC＝5．S△AOC＝•OC•|y A|＝×5×2＝5．S△BOC＝•OC•|y B|＝×5×＝．S△AOB＝S△AOC﹣S△BOC＝5﹣＝；（3）如图2，作点A关于x轴的对称点A′，连接A′B，交x轴于点P，此时△PAB的周长最小，∵点A′和A（﹣1，2）关于x轴对称，∴点A′的坐标为（﹣1，﹣2），设直线A′B的表达式为y＝ax+c，∵经过点A′（﹣1，﹣2），点B（﹣4，）∴，解得：，∴直线A′B的表达式为：y＝﹣x﹣，当y＝0时，则x＝﹣，∴P点坐标为（﹣，0）．24．如图，在平面直角坐标系xOy中，已知四边形DOBC是矩形，且D（0，4），B（6，0）．若反比例函数y＝（x＞0）的图象经过线段OC的中点A（3，2），交DC于点E，交BC于点F．设直线EF的解析式为y＝k2x+b．（1）求反比例函数和直线EF的解析式；（2）求△OEF的面积；（3）请结合图象直接写出不等式k2x+b＞0的解集．解：（1）∵四边形DOBC是矩形，且D（0，4），B（6，0），∴C点坐标为（6，4），∵A点坐标为（3，2），∴k1＝3×2＝6，∴反比例函数解析式为y＝；把x＝6代入y＝得x＝1，则F点的坐标为（6，1）；把y＝4代入y＝得x＝，则E点坐标为（，4），把F（6，1）、E（，4）代入y＝k2x+b，得，解得，，∴直线EF的解析式为y＝﹣x+5；﹣S△ODE﹣S△OBF﹣S△CEF（2）△OEF的面积＝S矩形BCDO＝4×6﹣×4×﹣×6×1﹣×（6﹣）×（4﹣1）＝；（3）由图象得：不等式k2x+b﹣＞0的解集为＜x＜6．25．如图，已知反比例函数y＝（m≠0）的图象经过点（1，4），一次函数y＝﹣x+b的图象经过反比例函数图象上的点Q（﹣4，n）．（1）求反比例函数与一次函数的表达式；（2）一次函数的图象分别与x轴、y轴交于A、B两点，与反比例函数图象的另一个交点为P，连结OP、OQ．求△OPQ的面积．解：（1）反比例函数y＝（m≠0）的图象经过点（1，4），解得m＝4，故反比例函数的表达式为y＝．一次函数y＝﹣x+b的图象与反比例函数的图象相交于点Q（﹣4，n），所以，解得n＝﹣1，b＝﹣5．∴一次函数的表达式y＝﹣x﹣5；（2）由，解得或．∴点P（﹣1，﹣4），在一次函数y＝﹣x﹣5中，令y＝0，得﹣x﹣5＝0，解得x＝﹣5，故点A（﹣5，0），S△OPQ＝S△OP A﹣S△OAQ＝×5×4−×5×1＝7.5．26．如图，在平面直角坐标系中，边长为4的等边△OAB的边OB在x轴的负半轴上，反比例函数y＝（x＜0）的图象经过AB边的中点C，且与OA边交于点D．（1）求k的值；（2）连接OC，CD，求△OCD的面积；（3）若直线y＝mx+n与直线CD平行，且与△OAB的边有交点，直接写出n的取值范围．解：（1）∵等边△OAB，∴AB＝BO＝AO＝4，∠ABO＝∠BOA＝∠OAB＝60°，∵点C是AB的中点，∴BC＝AC＝2，过点C作CM⊥OB，垂足为M，在Rt△BCM中，∠BCM＝90°﹣60°＝30°，BC＝2，∴BM＝1，CM＝，∴OM＝4﹣1＝3，∴点C 的坐标为（﹣3，），代入y ＝得：k ＝﹣3答：k 的值为﹣3；（2）过点A 作AN ⊥OB ，垂足为N ，由题意得：AN ＝2CM ＝2，ON ＝OB ＝2，∴A （﹣2，2），设直线OA 的关系式为y ＝kx ，将A 的坐标代入得：k ＝﹣，∴直线OA 的关系式为：y ＝﹣x ，由题意得：，解得：舍去，，∴D （﹣，3）过D 作DE ⊥OB ，垂足为E ，S △OCD ＝S CMED +S △DOE ﹣S △COM ＝S CMED ＝（+3）×（3﹣）＝3，答：△OCD 的面积为3．（3）①当与直线CD 平行的直线y ＝mx +n 过点O 时，此时y ＝mx +n 的n ＝0，②当与直线CD 平行的直线y ＝mx +n 经过点A 时，设直线CD 的关系式为y ＝ax +b ，把C 、D 坐标代入得：，解得：a ＝1，b ＝3+∴直线CD 的关系式为y ＝x +3+，∵y ＝mx +n 与直线y ＝x +3+平行，∴m ＝1，把A （﹣2，2）代入y ＝x +n 得：n ＝2+2因此：0≤n ≤2+2且n ．答：n 的取值范围为：0≤n ≤2+2且n ≠3+．。
专题07 反比例函数K值与几何面积综合中考数学专题复习
专题07 反比例函数K 值与几何面积综合（1）反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2；2OCF k S S S OBN OAM ===∆∆∆图中 221K K S S PAB OAB +==∆∆图中2k ===∆∆∆S S S CBD OBD PDB 图中（2）图像上任意两点与原点构成的三角形的面积等于直角梯形的面积；【真题演练】1．（2023•福建）如图，正方形四个顶点分别位于两个反比例函数y ＝和y ＝的图象的四个分支上，则实数n 的值为（ ）A ．﹣3B ．﹣C ．D ．32．（2023•张家界）如图，矩形OABC 的顶点A ，C 分别在y 轴、x 轴的正半轴上，点D 在AB 上，且AD ＝AB ，反比例函数y ＝（k ＞0）的图象经过点D 及矩形OABC 的对称中心M ，连接OD ，OM ，DM ．若△ODM的面积为3，则k的值为（ ）A．2B．3C．4D．53．（2023•黑龙江）如图，△ABC是等腰三角形，AB过原点O，底边BC∥x轴，双曲线y＝过A，B两点，过点C作CD∥y轴交双曲线于点D．若S△BCD＝12，则k的值是（ ）A．﹣6B．﹣12C．﹣D．﹣94．（2023•宜宾）如图，在平面直角坐标系xOy中，点A、B分别在y、x轴上，BC⊥x轴，点M、N分别在线段BC、AC上，BM＝CM，NC＝2AN，反比例函数y＝（x＞0）的图象经过M、N两点，P为x轴正半轴上一点，且OP：BP＝1：4，△APN的面积为3，则k的值为（ ）A．B．C．D．5．（2022•日照）如图，矩形OABC与反比例函数y1＝（k1是非零常数，x＞0）的图象交于点M，N，与反比例函数y2＝（k2是非零常数，x＞0）的图象交于点B，连接OM，ON．若四边形OMBN的面积为3，则k1﹣k2＝（ ）A．3B．﹣3C．D．6．（2022•郴州）如图，在函数y＝（x＞0）的图象上任取一点A，过点A作y轴的垂线交函数y＝﹣（x＜0）的图象于点B，连接OA，OB，则△AOB的面积是（ ）A．3B．5C．6D．107．（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（ ）A．36B．18C．12D．98．（2022•黑龙江）如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是（ ）A．2B．1C．﹣1D．﹣29．（2023•连云港）如图，矩形OABC的顶点A在反比例函数y＝（x＜0）的图象上，顶点B、C在第一象限，对角线AC∥x轴，交y轴于点D．若矩形OABC的面积是6，cos∠OAC＝，则k＝ ．10．（2023•枣庄）如图，在反比例函数（x＞0）的图象上有P1，P2，P3，…P2024等点，它们的横坐标依次为1，2，3，…，2024，分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3，…，S2023，则S1+S2+S3+…+S2023＝ ．11．（2023•朝阳）如图，点A是反比例函数y＝（k≠0，x＞0）的图象上一点，过点A作AB⊥x轴于点B，点P是y轴上任意一点，连接PA，PB．若△ABP的面积等于3，则k的值为 ．12．（2023•衢州）如图，点A，B在x轴上，分别以OA，AB为边，在x轴上方作正方形OACD，ABEF，反比例函数y＝（k＞0）的图象分别交边CD，BE于点P，Q．作PM⊥x轴于点M，QN⊥y轴于点N．若OA＝2AB，Q为BE的中点，且阴影部分面积等于6，则k的值为 ．13．（2023•锦州）如图，在平面直角坐标系中，△AOC的边OA在y轴上，点C在第一象限内，点B为AC 的中点，反比例函数y＝（x＞0）的图象经过B，C两点．若△AOC的面积是6，则k的值为 ．14．（2023•黄石）如图，点A（a，）和B（b，）在反比例函数y＝（k＞0）的图象上，其中a＞b＞0．过点A作AC⊥x轴于点C，则△AOC的面积为 ；若△AOB的面积为，则＝ ．15．（2023•辽宁）如图，矩形ABCD的边AB平行于x轴，反比例函数y＝（x＞0）的图象经过点B，D，对角线CA的延长线经过原点O，且AC＝2AO，若矩形ABCD的面积是8，则k的值为 6 ．16．（2023•绍兴）如图，在平面直角坐标系xOy中，函数（k为大于0的常数，x＞0）图象上的两点A （x1，y1），B（x2，y2），满足x2＝2x1，△ABC的边AC∥x轴，边BC∥y轴，若△OAB的面积为6，则△ABC的面积是 ．17．（2022•烟台）如图，A，B是双曲线y＝（x＞0）上的两点，连接OA，OB．过点A作AC⊥x轴于点C，交OB于点D．若D为AC的中点，△AOD的面积为3，点B的坐标为（m，2），则m的值为 ．18．（2022•黄石）如图，反比例函数y＝的图象经过矩形ABCD对角线的交点E和点A，点B、C在x轴上，△OCE的面积为6，则k＝ ．19．（2022•衢州）如图，在△ABC中，边AB在x轴上，边AC交y轴于点E．反比例函数y＝（x＞0）的图象恰好经过点C，与边BC交于点D．若AE＝CE，CD＝2BD，S△ABC＝6，则k＝ ．20．（2022•宜宾）如图，△OMN是边长为10的等边三角形，反比例函数y＝（x＞0）的图象与边MN、OM 分别交于点A、B（点B不与点M重合）．若AB⊥OM于点B，则k的值为 ．21．（2022•鄂尔多斯）如图，正方形OABC的顶点A、C分别在x轴和y轴上，E、F分别是边AB、OA上的点，且∠ECF＝45°，将△ECF沿着CF翻折，点E落在x轴上的点D处．已知反比例函数y1＝和y2＝分别经过点B、点E，若S△COD＝5，则k1﹣k2＝ ．22．（2022•东营）如图，△OAB是等腰直角三角形，直角顶点与坐标原点重合，若点B在反比例函数y＝（x＞0）的图象上，则经过点A的函数图象表达式为 ．23．（2022•绍兴）如图，在平面直角坐标系xOy 中，点A （0，4），B （3，4），将△ABO 向右平移到△CDE 位置，A 的对应点是C ，O 的对应点是E ，函数y ＝（k ≠0）的图象经过点C 和DE 的中点F ，则k 的值是 ．24．（2022•内蒙古）如图，在平面直角坐标系中，Rt △OAB 的直角顶点B 在x 轴的正半轴上，点O 与原点重合，点A 在第一象限，反比例函数y ＝（x ＞0）的图象经过OA 的中点C ，交AB 于点D ，连接CD ．若△ACD 的面积是1，则k 的值是 ．专题07 反比例函数K 值与几何面积综合（1）反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2；2OCF k S S S OBN OAM ===∆∆∆图中 221K K S S PAB OAB +==∆∆图中2k ===∆∆∆S S S CBD OBD PDB 图中（2）图像上任意两点与原点构成的三角形的面积等于直角梯形的面积；【真题演练】1．（2023•福建）如图，正方形四个顶点分别位于两个反比例函数y＝和y＝的图象的四个分支上，则实数n的值为（ ）A．﹣3B．﹣C．D．3【答案】A【解答】解：连接正方形的对角线，由正方形的性质知对角线交于原点O，过点A，B分别作x轴的垂线．垂足分别为C、D，点B在函数y＝上，如图：∵四边形是正方形，∴AO＝BO，∠AOB＝∠BDO＝∠ACO＝90°，∴∠CAO＝90°﹣∠AOC＝∠BOD，∴△AOC≌△BOD（AAS），∴S△AOC＝S△OBD＝＝，∵点A在第二象限，∴n＝﹣3，故选：A．2．（2023•张家界）如图，矩形OABC的顶点A，C分别在y轴、x轴的正半轴上，点D在AB上，且AD＝AB，反比例函数y＝（k＞0）的图象经过点D及矩形OABC的对称中心M，连接OD，OM，DM．若△ODM的面积为3，则k的值为（ ）A．2B．3C．4D．5【答案】C【解答】解：解法一：∵四边形OCBA是矩形，∴AB＝OC，OA＝BC，设B点的坐标为（a，b），∵矩形OABC的对称中心M，∴延长OM恰好经过点B，M（，），∵点D在AB上，且AD＝AB，∴D（，b），∴BD＝a，∴S△BDM＝BD•h＝×a×（b﹣）＝ab，∵D在反比例函数的图象上，∴ab＝k，∵S△ODM＝S△AOB﹣S△AOD﹣S△BDM＝ab﹣k﹣ab＝3，∴ab＝16，∴k＝ab＝4，解法二：连接BM，因为点M是矩形的对称中心，∴三角形DMO的面积＝三角形DMB的面积，则三角形DBO的面积为6，∵AD＝1/4AB，∴AD：DB＝1：3，∴三角形ADO的面积：三角形DBO的面积为1：3，即三角形ADO的面积为2，∴K＝4．故选：C．3．（2023•黑龙江）如图，△ABC是等腰三角形，AB过原点O，底边BC∥x轴，双曲线y＝过A，B两点，过点C作CD∥y轴交双曲线于点D．若S△BCD＝12，则k的值是（ ）A．﹣6B．﹣12C．﹣D．﹣9【答案】C【解答】解：设BC与y轴的交点为F，B（b，），则A（﹣b，﹣），b＞0，由题意知，AO＝BO，即O是线段AB的中点，过A作AE⊥BC于点E，∵AC＝AB，AE⊥BC，∴BE＝CE，AE∥y轴，∴CF＝3BF＝3b，∴C（﹣3b，），∴D（﹣3b，），∴CD＝，BC＝4b，∴S△BCD＝，∴k＝﹣．故选：C．4．（2023•宜宾）如图，在平面直角坐标系xOy中，点A、B分别在y、x轴上，BC⊥x轴，点M、N分别在线段BC、AC上，BM＝CM，NC＝2AN，反比例函数y＝（x＞0）的图象经过M、N两点，P为x轴正半轴上一点，且OP：BP＝1：4，△APN的面积为3，则k的值为（ ）A．B．C．D．【答案】B【解答】解：如图，过点N作NQ⊥x轴于点Q，过C作CT⊥y轴交y轴于T，交NQ于K，设OA＝a，OP＝b，BM＝c，N（m，n），∵OP：BP＝1：4，BM＝CM，∴A（0，a），B（5b，0），M（5b，c），C（5b，2c），∵∠NCK＝∠ACT，∠NKC＝90°＝∠ATC，∴△NKC∽△ATC，∴＝＝，∵NC＝2AN，∴CK＝2TK，NK＝AT，∴，解得，∴，∴，，∴，∵△APN的面积为3，∴S梯形OANQ﹣S△AOP﹣S△NPQ＝3，∴，∴2ab+bc＝9，将点M（5b，c），代入得：，整理得：2a＝7c，将2a＝7c代入2ab+bc＝9得：7bc+bc＝9，∴，∴，故选：B．5．（2022•日照）如图，矩形OABC与反比例函数y1＝（k1是非零常数，x＞0）的图象交于点M，N，与反比例函数y2＝（k2是非零常数，x＞0）的图象交于点B，连接OM，ON．若四边形OMBN的面积为3，则k1﹣k2＝（ ）A．3B．﹣3C．D．【答案】B【解答】解：∵y1、y2的图象均在第一象限，∴k1＞0，k2＞0，∵点M、N均在反比例函数y1＝（k1是非零常数，x＞0）的图象上，∴S△OAM＝S△OCN＝k1，∵矩形OABC的顶点B在反比例函数y2＝（k2是非零常数，x＞0）的图象上，∴S矩形OABC＝k2，∴S四边形OMBN＝S矩形OABC﹣S△OAM﹣S△OCN＝3，∴k2﹣k1＝3，∴k1﹣k2＝﹣3，故选：B．6．（2022•郴州）如图，在函数y＝（x＞0）的图象上任取一点A，过点A作y轴的垂线交函数y＝﹣（x＜0）的图象于点B，连接OA，OB，则△AOB的面积是（ ）A．3B．5C．6D．10【答案】B【解答】解：∵点A在函数y＝（x＞0）的图象上，∴S△AOC＝×2＝1，又∵点B在反比例函数y＝﹣（x＜0）的图象上，∴S△BOC＝×8＝4，∴S△AOB＝S△AOC+S△BOC＝1+4＝5，故选：B．7．（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（ ）A．36B．18C．12D．9【答案】B【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：∵四边形ABCD是正方形，∴AE＝BE＝CE＝DE，设AE＝BE＝CE＝DE＝m，D a），∵BD∥y轴，∴B（3，a+2m），A（3+m，a+m），∵A，B都在反比例函数y＝（k1＞0）的图象上，∴k1＝3（a+2m）＝（3+m）（a+m），∵m≠0，∴m＝3﹣a，∴B（3，6﹣a），∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图象上，D（3，a）在y＝（k2＞0）的图象上，∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，∴k1+k2＝18﹣3a+3a＝18；故选：B．8．（2022•黑龙江）如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD 的面积是5，则k的值是（ ）A．2B．1C．﹣1D．﹣2【答案】D【解答】解：设B（a，），∵四边形OBAD是平行四边形，∴AB∥DO，∴A（，），∴AB＝a﹣，∵平行四边形OBAD的面积是5，∴（a﹣）＝5，解得k＝﹣2，故选：D．9．（2023•连云港）如图，矩形OABC的顶点A在反比例函数y＝（x＜0）的图象上，顶点B、C在第一象限，对角线AC∥x轴，交y轴于点D．若矩形OABC的面积是6，cos∠OAC＝，则k＝ ﹣ ．【答案】﹣．【解答】解：作AE⊥x轴于E，∵矩形OABC的面积是6，∴△AOC的面积是3，∵∠AOC＝90°，cos∠OAC＝，∴，∵对角线AC∥x轴，∴∠AOE＝∠OAC，∵∠OEA＝∠AOC＝90°，∴△OEA∽△AOC，∴，∴，∴S△OEA＝，∵S△OEA＝|k|，k＜0，∴k＝﹣．故答案为：﹣．10．（2023•枣庄）如图，在反比例函数（x＞0）的图象上有P1，P2，P3，…P2024等点，它们的横坐标依次为1，2，3，…，2024，分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3，…，S2023，则S1+S2+S3+…+S2023＝ ．【答案】．【解答】解：∵P1，P2，P3，...P2024的横坐标依次为1，2，3， (2024)∴阴影矩形的一边长都为1，将除第一个矩形外的所有矩形向左平移至y轴，∴S 1+S2+S3+…+S2023＝，把x＝2024代入关系式得，y＝，即OA＝，∴S矩形OABC＝OA•OC＝，由几何意义得，＝8，∴＝8﹣＝．故答案为：．11．（2023•朝阳）如图，点A是反比例函数y＝（k≠0，x＞0）的图象上一点，过点A作AB⊥x轴于点B，点P是y轴上任意一点，连接PA，PB．若△ABP的面积等于3，则k的值为 6 ．【答案】6．【解答】解：设反比例函数的解析式为y＝，∵△AOB的面积＝△ABP的面积＝3，△AOB的面积＝|k|，∴|k|＝3，∴k＝±6；又∵反比例函数的图象的一支位于第一象限，∴k＞0．∴k＝6．故答案为：6．12．（2023•衢州）如图，点A，B在x轴上，分别以OA，AB为边，在x轴上方作正方形OACD，ABEF，反比例函数y＝（k＞0）的图象分别交边CD，BE于点P，Q．作PM⊥x轴于点M，QN⊥y轴于点N．若OA＝2AB，Q为BE的中点，且阴影部分面积等于6，则k的值为 24 ．【答案】见试题解答内容【解答】解：设OA＝4a，∵AO＝2AB，∴AB＝2a，∴OB＝AB+OA＝6a，则B（6a，0），由于在正方形ABEF中，AB＝BE＝2a，∵Q为BE中点，∴BQ＝AB＝a，∴Q（6a，a），∵Q在反比例函数y＝（k＞0））上，∴k＝6a×a＝6a2，∵四边形OACD是正方形，∴C（4a，4a），∵P在CD上，∴P点纵坐标为4a，∵P在反比例函数y＝（k＞0）上，∴P点横坐标为：x＝，∴P（，4a），∵作PM⊥x轴于点M，QN⊥y轴于点N，∴四边形OMNH是矩形，∴NH＝，MH＝a，∴S矩形OMHN＝NH×MH＝×a＝6，则k＝24，故答案为：24．13．（2023•锦州）如图，在平面直角坐标系中，△AOC的边OA在y轴上，点C在第一象限内，点B为AC的中点，反比例函数y＝（x＞0）的图象经过B，C两点．若△AOC的面积是6，则k的值为 4 ．【答案】4．【解答】解：过点C作CD⊥y轴于点D，如图：设点C的坐标为（a，b），点A的坐标为（0，c），∴CD＝a，OA＝c，∵△AOC的面积是6，∴，∴ac＝12，∵点C（a，b）在反比例函数（x＞0）的图象上，∴k＝ab，∵点B为AC的中点，∴点，∵点B在反比例函数（x＞0）的图象上，∴，即：4k＝a（b+c），∴4k＝ab+ac，将ab＝k，ac＝12代入上式得：k＝4．故答案为：4．14．（2023•黄石）如图，点A（a，）和B（b，）在反比例函数y＝（k＞0）的图象上，其中a＞b＞0．过点A作AC⊥x轴于点C，则△AOC的面积为 ；若△AOB的面积为，则＝ 2 ．【答案】，2．【解答】解：因为点A（a，）在反比例函数y＝的图象上，则，又a＞0，解得k＝5．根据k的几何意义可知，．过点B作x轴的垂线，垂足为D，则S△OBD+S梯形ACDB＝S△AOC+S△AOB，又根据k的几何意义可知，S△OBD＝S△AOC，则S梯形ACDB＝S△AOB．又△AOB的面积为，且A（a，），B（b，），所以，即．解得．又a＞b＞0，所以．故答案为：，2．15．（2023•辽宁）如图，矩形ABCD的边AB平行于x轴，反比例函数y＝（x＞0）的图象经过点B，D，对角线CA的延长线经过原点O，且AC＝2AO，若矩形ABCD的面积是8，则k的值为 6 ．【答案】6．【解答】解：如图，延长CD交y轴于E，连接OD，∵矩形ABCD的面积是8，∴S△ADC＝4，∵AC＝2AO，∴S△ADO＝2，∵AD∥OE，∴△ACD∽△OCE，∴AD：OE＝AC：OC＝2：3，∴S△ODE＝3，由几何意义得，＝3，∵k＞0，∴k＝6，故答案为：6．16．（2023•绍兴）如图，在平面直角坐标系xOy中，函数（k为大于0的常数，x＞0）图象上的两点A （x1，y1），B（x2，y2），满足x2＝2x1，△ABC的边AC∥x轴，边BC∥y轴，若△OAB的面积为6，则△ABC的面积是 2 ．【答案】2．【解答】解：如图，延长CA交y轴于E，延长CB交x轴于点F，∴CE⊥y轴，CF⊥x轴，∴四边形OECF为矩形，∵x2＝2x1，∴点A为CE的中点，由几何意义得，S△OAE＝S△OBF，∴点B为CF的中点，∴S△OAB＝S矩形OECF＝6，∴S矩形OECF＝16，∴S△ABC＝×16＝2．故答案为：2．217．（2022•烟台）如图，A，B是双曲线y＝（x＞0）上的两点，连接OA，OB．过点A作AC⊥x轴于点C，交OB于点D．若D为AC的中点，△AOD的面积为3，点B的坐标为（m，2），则m的值为 6 ．【答案】见试题解答内容【解答】解：因为D为AC的中点，△AOD的面积为3，所以△AOC的面积为6，所以k＝12＝2m．解得：m＝6．故答案为：6．18．（2022•黄石）如图，反比例函数y＝的图象经过矩形ABCD对角线的交点E和点A，点B、C在x轴上，△OCE的面积为6，则k＝ 8 ．【答案】8．【解答】解：如图，过点E作EH⊥BC于H，设点A（a，），C（c，0），∵点E是矩形ABCD的对角线的交点，∴E（，），∵点E在反比例函数y＝的图象上，∴＝k，∴c＝3a，∵△OCE的面积为6，∴OC•EH＝c•＝×3a•＝6，∴k＝8，故答案为：8．19．（2022•衢州）如图，在△ABC中，边AB在x轴上，边AC交y轴于点E．反比例函数y＝（x＞0）的图象恰好经过点C，与边BC交于点D．若AE＝CE，CD＝2BD，S△ABC＝6，则k＝ ．【答案】．【解答】解：如图，作CM⊥AB于点M，DN⊥AB于点N，设C（m，），则OM＝m，CM＝，∵OE∥CM，AE＝CE，∴＝＝1，∴AO＝m，∵DN∥CM，CD＝2BD，∴＝＝＝，∴DN＝，∴D的纵坐标为，∴＝，∴x＝3m，即ON＝3m，∴MN＝2m，∴BN＝m，∴AB＝5m，∵S△ABC＝6，∴5m•＝6，∴k＝．故答案为：．20．（2022•宜宾）如图，△OMN是边长为10的等边三角形，反比例函数y＝（x＞0）的图象与边MN、OM分别交于点A、B（点B不与点M重合）．若AB⊥OM于点B，则k的值为 9 ．【答案】9．【解答】解：过点B作BC⊥x轴于点C，过点A作AD⊥x轴于点D，如图，∵△OMN是边长为10的等边三角形，∴OM＝ON＝MN＝10，∠MON＝∠M＝∠MNO＝60°设OC＝b，则BC＝，OB＝2b，∴BM＝OM﹣OB＝10﹣2b，B（b，b），∵∠M＝60°，AB⊥OM，∴AM＝2BM＝20﹣4b，∴AN＝MN﹣AM＝10﹣（20﹣4b）＝4b﹣10，∵∠AND＝60°，∴DN＝＝2b﹣5，AD＝AN＝2b﹣5，∴OD＝ON﹣DN＝15﹣2b，∴A（15﹣2b，2b﹣5），∵A、B两点都在反比例函数y＝（x＞0）的图象上，∴k＝（15﹣2b）（2b﹣5）＝b•b，解得b＝3或5，当b＝5时，OB＝2b＝10，此时B与M重合，不符题意，舍去，∴b＝3，∴k＝b•b＝9，故答案为：9．21．（2022•鄂尔多斯）如图，正方形OABC的顶点A、C分别在x轴和y轴上，E、F分别是边AB、OA上的点，且∠ECF＝45°，将△ECF沿着CF翻折，点E落在x轴上的点D处．已知反比例函数y1＝和y2＝分别经过点B、点E，若S△COD＝5，则k1﹣k2＝ 10 ．【答案】见试题解答内容【解答】解：作EH⊥y轴于点H则四边形BCHE、AEHO都为矩形，∵∠ECF＝45°，∴∠OCD+∠OCF＝45°，∵∠DOC+∠OCF＝45°，∴∠BCE＝∠OCD，∵BC＝OC，∠B＝∠COD，∴△BCE≌△OCD（ASA），∴S△BCE＝S△COD＝5，∴S△CEH＝5，S矩形BCHE＝10，∴根据反比例函数系数k的几何意义得：k1﹣k2＝S矩形BCHE＝10，故答案为：10．22．（2022•东营）如图，△OAB是等腰直角三角形，直角顶点与坐标原点重合，若点B在反比例函数y＝（x＞0）的图象上，则经过点A的函数图象表达式为 y＝﹣ ．【答案】y＝﹣．【解答】解：如图，作AD⊥x轴于D，BC⊥x轴于C，∴∠ADO＝∠BCO＝90°，∵∠AOB＝90°，∴∠AOD+∠BOC＝90°，∴∠AOD+∠DAO＝90°，∴∠BOC＝∠DAO，∵OB＝OA，∴△BOC≌△OAD（AAS），∵点B在反比例函数y＝（x＞0）的图象上，∴S△OBC＝，∴S△OAD＝，∴k＝﹣1，∴经过点A的反比例函数解析式为y＝﹣．故答案为：y＝﹣．23．（2022•绍兴）如图，在平面直角坐标系xOy中，点A（0，4），B（3，4），将△ABO向右平移到△CDE位置，A的对应点是C，O的对应点是E，函数y＝（k≠0）的图象经过点C和DE的中点F，则k的值是 6 ．【答案】6．【解答】解：过点F作FG⊥x轴于点G，FH⊥y轴于点H，过点D作DQ⊥x轴于点Q，如图所示，根据题意可知，AC＝OE＝BD，设AC＝OE＝BD＝a，∴四边形ACEO的面积为4a，∵F为DE的中点，FG⊥x轴，DQ⊥x轴，∴FG为△EDQ的中位线，∴FG＝DQ＝2，EG＝EQ＝，∴四边形HFGO的面积为2（a+），∴k＝4a＝2（a+），解得：a＝，∴k＝6．故答案为：6．24．（2022•内蒙古）如图，在平面直角坐标系中，Rt△OAB的直角顶点B在x轴的正半轴上，点O与原点重合，点A在第一象限，反比例函数y＝（x＞0）的图象经过OA的中点C，交AB于点D，连接CD．若△ACD的面积是1，则k的值是 ．【答案】．【解答】解：连接OD，过C作CE∥AB，交x轴于E，∵∠ABO＝90°，反比例函数y＝（x＞0）的图象经过OA的中点C，∴S△COE＝S△BOD＝k，S△ACD＝S△OCD＝1，∵CE∥AB，∴△OCE∽△OAB，∴△OCE与△OAB得到面积比为1：4，∴4S△OCE＝S△OAB，∴4×k＝1+1+k，∴k＝．故答案为：．。
第26章.反比例函数——专题4.用反比例函数系数k的几何意义解与面积相关的问题
4．如图，函数y＝－x与函数y＝－4x的图象相交于A，B两点，过点分别作y轴的垂线，垂足分别为点C则四边形ACBD的面积为A．2 B．4 C．65.如图,点P是反比例函数y=2x图象上的一点积为 .6.如图，在第一象限内,点P,M(2,a 点,PA⊥x轴于点MB⊥x轴于点B,PA7.如图，A，C是函数＝1x的图象上任意两点，过点A作y轴的垂线，垂足为B，过点C作△AOB的面积为S1，COD的面积为S2，则A．S1＞S2C．S1＝S28.如图，点A是反比例函数点C是x轴上的动点，则△A．1 B．2 C9.直线y=kx与反比例函数于y轴于点C，则10.如图，正比例函数x与反比例函数y＝的图象相交于A，B两点，BC⊥x轴于点C，则△ABC的面积为( )A．1 B．2 C．3 D．411.如图，Rt△AOB的一条直角边的中点C，与另一直角边交于点12.如图，A，B是双曲线于点D，垂足为C.若△A.43B.8313．如图，过x轴正半轴上的任意一点P作y轴的平行线交反比例函数＝2x(x＞0)和y＝－4x(x＞0)的图象于A，B两点，是y轴上任意一点，则△ABC的面积为________．14．如图，在平面直角坐标系中，点P(1，4)Q(m，n)在函数y＝kx(x>0)的图象上，当m>1时，过点P分别作x轴、y轴的垂线，垂足为点A、过点Q分别作x轴、 y轴的垂线，垂足为点C D. QD交PA于点E，随着m的增大，四边形ACQE 的面积( )A．减小 B．增大 C．先减小后增大 D．先增大后减小15.如图所示，反比例函数y＝kx(x＞0)的图象经过矩形OABC的对角线的中点D，若矩形OABC的面积为8，则k的值为．16．如图，反比例函数y＝2x的图象经过矩形OABC的边AB的中点D，则矩形OABC的面积为17.如图，已知点P(6，过点P作PM⊥x轴于点M，PN⊥y轴于点N.比例函数y＝kx的图象交，若四边形OAPB的面积为12，则k＝．19．如图，在平面直角坐标系与反比例函数在第一象限内的图象交于点(1)求该反比例函数的解析式和直线(2)若直线AB与y轴的交点为题型2：已知四边形面积求解析式20．如图，矩形ABOD在第二象限的图象的交点，3.(1)求两函数的解析式；(2)求两函数图象的交点(3)若点P是y轴上一动点，且22．如图，点A在双曲线D两点在x轴上，若矩形解析式．考查形式三.已知反比例函数解析式求图形的面积题型1：利用解析式求面积23．如图，已知反比例函数8)，B(－4，m)．(1)求k1，k2，b的值；(2)求△AOB的面积；(3)若M(x1，y1)，N(xy1<y2，指出点M，N各位于哪个象限，并简要说明理由．题型2：利用对称性求面积25．如图，是由四条曲线围成的广告标志，建立平面直角坐标系，双曲线对应的函数解析式分别为这种钢条加工成矩形产品按面积计算，每单位面积师傅计算一下，所需钢条一共花多少钱？题型3：利用点的坐标及面积公式求面积26．如图，直线y＝k1xB，与x轴交于点C，其中点(1)试确定反比例函数的解析式；(2)求△AOC的面积．。
第六章反比例函数及反比例函数k的几何意义专题训练北师大版2024—2025学年九年级上册
第六章反比例函数及反比例函数k的几何意义专题训练北师大版2024—2025学年九年级上册反比例函数比例系数k的几何意义（1）意义：从反比例函数y＝(k≠0)图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|.（2）常见的面积类型：例1.如图，点P是反比例函数y＝（k≠0）的图象上任意一点，过点P作PM⊥x轴，垂足为M，若△POM的面积等于3，则k的值等于（）A．﹣6B．6C．﹣3D．3变式1.如图，在▱AOBC中，对角线AB、OC交于点E，双曲线经过A、E两点，若▱AOBC的面积为18，则k的值是（）A．5B．6C．7D．8变式2.如图，平行于x轴的直线与函数y＝（k1＞0，x＞0），y＝（k2＞0，x＞0）的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点．若△ABC的面积为4，则k1﹣k2的值为（）A．8B．﹣8C．4D．﹣4变式3.如图，点P是反比例函数图象上的一点，PF⊥x轴于F点，且Rt△POF面积为4．则k的值为（）A．8B．﹣8C．﹣4D．4变式4.如图，点M是反比例函数y＝（x＜0）图象上一点，MN⊥y 轴于点N．若P为x轴上的一个动点，则△MNP的面积为（）A．2B．4C．6D．无法确定变式5.如图，点P是双曲线C：y＝（x＞0）上的一点，过点P作x轴的垂线交直线AB：y＝x﹣2于点Q，连接OP，OQ，当点P在曲线C上运动，且点P在Q上方时，△POQ面积的最大值为（）A．2B．3C．4D．6变式6．如图，已知点A为反比例函数y＝（x＜0）的图象上一点，过点A作AB⊥y轴，垂足为B，若△OAB的面积为3，则k的值为（）A．3B．﹣3C．6D．﹣6变式7.关于x的反比例函数y＝的图象如图，A、P为该图象上的点，且关于原点成中心对称．△P AB中，PB∥y轴，AB∥x轴，PB 与AB相交于点B．若△P AB的面积大于12，则关于x的方程（a ﹣1）x2﹣x+＝0的根的情况是（）A．2个不相等的实数根B．2个相等的实数根C．1个实数根D．无实数根变式8.如图，两个反比例函数y1＝和y2＝在第一象限内的图象分别是C1和C2，设点P在C1上，P A⊥x轴于点A，交C2于点B，则△POB的面积为（）A．4B．2C．1D．6变式9.如图，若反比例函数的图象经过点A，AB⊥x轴于点B，C点是y轴上一点，且△ABC的面积4，则k的值为（）A．﹣8B．﹣4C．4D．8变式10.如图，反比例函数的图象经过矩形OABC的边AB的中点D，若矩形OABC的面积为6，则k的值为（）A．﹣3B．3C．﹣6D．6变式11.如图，点A是反比例函数的图象上的一点，过点A作AB ⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC 的面积为3，则k的值是（）A．3B．﹣6C．6D．﹣3变式12.下面四个图中反比例函数的表达式均为，则阴影部分的图形的面积为3的有（）A．1个B．2个C．3个D．4个变式13.如图，将一块含30°角的三角板AOB按如图所示摆放在平面直角坐标系中，∠B＝60°，∠BAO＝90°，△AOB的面积为4，BO与x轴的夹角为30°，若反比例函数的图象经过点A，则k的值为（）A．3B．C．6D．9变式14.如图1，在△OAB中，∠AOB＝45°，点B的坐标为，点A在反比例函数的图象上，设△OAB的面积为S1；如图2，在△ABC中，AB＝AC，BC在x轴上，且OB：BC＝1：2，点A在反比例函数的图象上，设△ABC的面积为S2，则S1+S2的值为（）A．B．5C．D．变式15.如图，已知四边形OABC是矩形，边OA在x轴上，边OC在y轴上，双曲线过OB的中点E，且与边BC交于点D，若△DOE的面积为7.5，则k的值是（）A．5B．10C．15D．变式16.如图，点A是反比例函数y＝（x＞0）图象上的一点，AB垂直于x轴，垂足为B，△OAB的面积为8．若点P（a，4）也在此函数的图象上，则a的值是（）A．2B．﹣2C．4D．﹣4变式17.如图，在平面直角坐标系xOy中，点A、B分别在y、x 轴上，BC⊥x轴，点M、N分别在线段BC、AC上，BM＝CM，NC＝2AN，反比例函数y＝（x＞0）的图象经过M、N两点，P为x轴正半轴上一点，且OP：BP＝1：4，△APN的面积为3，则k的值为（）A．B．C．D．变式18.如图，在平面直角坐标系中，平行四边形ABCD与y轴分别交于E、F两点，对角线BD在x轴上，反比例函数的图象过点A并交AD于点G，连接DF．若BE：AE＝1：2，AG：GD＝3：2，且△FCD的面积为，则k的值是（）A．B．3C．D．5变式19.如图，平面直角坐标系中，矩形OABC的边与函数y＝（x＞0）图象交于E，F两点，且F是BC的中点，则四边形ACFE的面积等于（）A．4B．6C．8D．不能确定例2.如图，矩形OABC的顶点A，C分别在x轴、y轴的正半轴上，它的对角线OB与函数的图象相交于点D，且，若矩形OABC的面积为24，则k的值是．变式1.如图，已知在平面直角坐标系xOy中，点P是▱ABCO对角线OB的中点，反比例函数的图象经过点A，点P．若▱ABCO的面积为30，且y轴将▱ABCO的面积分为1：3，则k的值为．变式2.如图，在平面直角坐标系xOy中，点A，B都在反比例函数y＝（x＞0）的图象上，延长AB交y轴于点C，过点A作AD⊥y轴于点D，连接BD并延长，交x轴于点E，连接CE．若AB＝2BC，△BCE的面积是4.5，则k的值为．变式3.如图，在平面直角坐标系xOy中，等腰Rt△OAB，∠B＝90°，点A在x轴正半轴上，点B在第一象限内，反比例函数y＝的图象与AB交于点C，连接OC，若BC＝2AC，△OBC的面积为6，则k的值为．变式4.如图，在平面直角坐标系中，C，A分别为x轴、y轴正半轴上的点，以OA，OC为边，在第一象限内作矩形OABC，且S矩形OABC＝8，将矩形OABC翻折，使点B与原点O重合，折痕为MN，点C的对应点C'落在第四象限，过M点的反比例函数y＝（k ≠0）的图象恰好过MN的中点，则点C'的坐标为．变式5.如图，在平面直角坐标系中，点A、C在y轴上，且，点B（﹣2，0）在x轴上，将△ABC绕点A逆时针旋转90°后得到△AB'C′，线段AB′与双曲线交于点D，连接B′C、C′C，当点D为AB′中点，且S△B'CC′＝6时，则k的值是．变式6.如图，在△AOB中，OC平分∠AOB，＝，反比例函数y＝（k＜0）图象经过点A、C两点，点B在x轴上，若△AOB的面积为9，则k的值为．变式7.如图，点A，B，C，D是菱形的四个顶点，其中点A，D在反比例函数y＝（m＞0，x＞0）的图象上，点B，C在反比例函数y＝（n＜0）的图象上，且点B，C关于原点成中心对称，点A，C的横坐标相等，则的值为；过点A作AE∥x轴交反比例函数y＝（n＜0）的图象于点E，连结ED并延长交x轴于点F，连结OD．若S△DOF＝7，则m的值为．变式8.如图，A（a，b）、B（﹣a，﹣b）是反比例函数y＝的图象上的两点，分别过点A、B作y轴的平行线，与反比例函数y＝的图象交于点C、D，若四边形ACBD的面积是8，则m、n之间的关系是．变式9.如图，平面直角坐标系xOy中，Rt△ABO的斜边BO在x轴正半轴上，OB＝5，反比例函数y＝（x＞0）的图象过点A，与AB边交于点C，且AC＝3BC，则a的值为，射线OA，射线OC分别交反比例函数y＝（b＞a＞0）的图象于点D，E，连接DE，DC，若△DEC的面积为45，则b的值为．变式10.如图，点A、B在反比例函数y＝（x＞0）的图象上，延长AB交x轴于C点，若△AOC的面积是12，且点B是AC的中点，则k＝．变式11.如图，菱形ABCD中，∠ABC＝120°，顶点A，C在双曲线上，顶点B，D在双曲线上，且BD经过点O．若k1+k2＝2，则菱形ABCD面积的最小值是．变式12.如图，在平面直角坐标系xOy中，正方形ABCD的顶点A、C恰好落在双曲线上，且点O在AC上，AD交x轴于点E．①当A点坐标为（1，m）时，D点的坐标为；②当CE平分∠ACD时，正方形ABCD的面积为．例3.如图，O为坐标原点，点A（﹣1，5）和点B（m，﹣1）均在反比例函数图象上（1）求m，k的值；（2）当x满足什么条件时，﹣x+4＞﹣；（3）P为y轴上一点，若△ABP的面积是△ABO面积的2倍，直接写出点P的坐标．变式1.已知点A（a，ma+2）、B（b，mb+2）是反比例函数y＝图象上的两个点，且a＞0，b＜0，m＞0．（1）求证：a+b＝﹣；（2）若OA2+OB2＝2a2+2b2，求m的值；（3）若S△OAB＝3S△OCD，求km的值．变式2.如图，双曲线y＝上的一点A（m，n），其中n＞m＞0，过点A作AB⊥x轴于点B，连接OA．（1）已知△AOB的面积是3，求k的值；（2）将△AOB绕点A逆时针旋转90°得到△ACD，且点O的对应点C恰好落在该双曲线上，求的值．。
反比例函数中“K”与面积专题
专题四反比例函数中“K”与面积一:问题背景反比例函数y＝kx中，比例系数k有一个很重要的几何意义，那就是：过反比例函数y＝kx图象上任一点P作x轴、y轴的垂线PM、PN，垂足为M、N（如图1所示），则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以，对双曲线上任意一点作x轴、y轴的垂线，它们与x轴、y轴所围成的矩形面积为常数|k|,由此基本图形带来的衍生图形也很多，他们与K都有固定的结论。
在解有关反比例函数的问题时，若能灵活运用这些基本图形，会给解题带来很多方便。
二：基本图形S四边形PEOF =|K|S△ABO=|K|S△ABM=|K|S△ABC=2|K|S四边形ABCD=2|K|S△AOC=S四边形ACEF基础题型1、如图,直线y=mx与双曲线y＝kx交于点A,B、过点A作AM⊥x轴,垂足为点M,连接BM.若△ABM的面积为1,则k的值是________2、如图A,B是函数y=的图象上关于O原点对称的任意两点,AC∥Y 轴,BC∥X轴,△ABC的面积记为S,则S=_________3、如图，点A、B是双曲线y=上的点，分别经过A、B两点向X轴、Y轴作垂线段，若S阴影=1，则S1+S2=________4、如图，点A是反比例函数y＝kx图象上的一点，过点A作AB⊥x轴，垂足为点B，点C为y轴上的一点，连接AC，BC.若△ABC的面积为3，则k的值是。
5、如图,点A在函数y=的图象上,点B在函数y＝kx(x﹥0)的图象上,连接AB,AB垂直x轴于点M,且AM︰MB=1︰2,则k=。
6、如图，点A在双曲线y=上，点B在双曲线y=上，且AB∥x 轴，C、D在x轴上，若四边形ABCD为矩形，则S ABCD=。
7、双曲线y1、y2在第一象限的图象如图，y1=，过y1上的任意一点A，作x轴的平行线交y2于B，交y轴于C，若S△AOB=1，则y2的解析式是_____。
反比例函数中“K”与面积专题4
专题四反比例函数中“K”与面积一:问题背景反比例函数y＝kx中，比例系数k有一个很重要的几何意义，那就是：过反比例函数y＝kx图象上任一点P作x轴、y轴的垂线PM、PN，垂足为M、N（如图1所示），则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以，对双曲线上任意一点作x轴、y轴的垂线，它们与x轴、y轴所围成的矩形面积为常数|k|,由此基本图形带来的衍生图形也很多，他们与K都有固定的结论。
在解有关反比例函数的问题时，若能灵活运用这些基本图形，会给解题带来很多方便。
二：基本图形S四边形PEOF =|K|*********************************************************************S△ABO=|K|S△ABM=|K|S △ABC=2|K|S四边形ABCD=2|K|******************************************************************************************************************************************S △AOC=S 四边形ACEF基础题型1、如图,直线y=mx 与双曲线y ＝kx 交于点A,B 、过点A 作AM ⊥x 轴,垂足为点M,连接BM .若△ABM 的面积为1,则k 的值是________2、如图A,B 是函数y =的图象上关于O 原点对称的任意两点,AC ∥Y 轴,BC ∥X 轴,△ABC 的面积记为S,则S=_________*********************************************************************3、如图，点A 、B 是双曲线y =上的点，分别经过A 、B 两点向X 轴、Y 轴作垂线段，若S 阴影=1，则S 1+S 2=________4、如图，点A 是反比例函数y ＝k x图象上的一点，过点A 作AB ⊥x 轴，垂足为y 轴上的一点，连接AC ，BC.若△ABC 的面积为3，则k 的值是 。
反比例函数专题一、k的几何意义解与面积相关问题
∴点A，C的坐标分别为(－1，3)，(3，－1)．
专题训练
(3)若点P是y轴上一动点，且S△APC＝5，求点P的坐标． 解：设点P的坐标为(0，m)，直线y＝－x＋2与y轴的交点
为M，则M的坐标为(0，2)．
∵S△APC＝S△AMP＋S△CMP＝
1 2
×PM×(|－1|＋|3|)＝5，
∴PM＝ 5 ，即|m－2|＝ 5 .∴m＝ 9 或m＝－ 1 .
解：
由
ìïïïíïïïî
y y
= =
- x+ 6， x
7,
得
祆 镲 镲 眄 镲 镲 铑xy11
= =
1, x2 6，y2
= =
6, 1.
∴点D的坐标为(6，1)．
当x＝2时，反比例函数图象上的点为(2，3)，
直线上的点为(2，5)，此时可得整点为(2，4)；
当x＝3时，反比例函数图象上的点为(3，2)，
a 的图象上， x
∴a＝3×2＝6，∴反比例函数的表达式为y＝
6
.
x
∵B(3，2)，∴EF＝2.∵BD⊥y轴，OC＝CA，
∴AE＝EF＝ 1 AF，∴AF＝4，∴点A的纵坐标为4.
2 ∵点A在反比例函数y＝
6 的图象上，
∴点将AA的( 横3 坐, 4标)，为B(332，，2∴)的xA坐( 32标,代4)入. y＝kx＋b，得
专题训练
题型2 利用对称性求面积 7．如图是由四条曲线围成的广告标志，建立平面直角坐
标＝系6x ，.现双用曲四线根对钢应条的固函定数这解四析条式曲分线别，为这y＝种－钢条6x ，加y工 成矩形产品按面积计算，每单位面积25元，请你帮助 工人师傅计算一下，所需钢条一共花多少钱？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
专题四反比例函数中“K”与面积一:问题背景
反比例函数y＝k
x
中，比例系数k有一个很重要的几何意义，那就是：过
反比例函数y＝k
x
图象上任一点P作x轴、y轴的垂线PM、PN，垂足为M、N（如
图1所示），则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以，对双曲线上任意一点作x轴、y轴的垂线，它们与x轴、y轴所围成的矩形面积为常数|k|,由此基本图形带来的衍生图形也很多，他们与K都有固定的结论。
在解有关反比例函数的问题时，若能灵活运用这些基本图形，会给解题带来很多方便。
二：基本图形
S四边形PEOF =|K|
S△ABO=|K|
S△ABM=|K|
S△ABC=2|K|
S四边形ABCD=2|K|
S△AOC=S四边形ACEF
2、如图A,B是函数y=的图象上关于O原点对称的任意两点,AC∥Y 轴,BC∥X轴,△ABC的面积记为S,则S=_________
3、如图，点A、B是双曲线y=上的点，分别经过A、B两点向X轴、Y
轴作垂线段，若S
阴影=1，则S
1
+S
2
=________
4、如图，点A是反比例函数y＝k
x
图象上的一点，过点A作AB⊥x轴，垂足为
点B，点C为y轴上的一点，连接AC，BC.若△ABC的面积为3，则k的值
5、如图,点A在函数y=的图象上,点B在函数y＝k
x
(x﹥0)的图象上,连
接AB,AB垂直x轴于点M,且AM︰MB=1︰2,则
6、如图，点A在双曲线y=上，点B在双曲线y=上，且AB∥x轴，
C、D在x轴上，若四边形ABCD为矩形，则
S ABCD
7、双曲线y1、y2在第一象限的图象如图，y1=，过y1上的任意一点A，作x轴的平行线交y2于B，交y轴于C，若S△AOB=1，则y2的解析式是
_____。
8、(陕西2011中考)如图所示，过y轴正半轴上的任意一点P，作x轴的平行
线，分别与反比例函数y=和y=的图象交于点A和点B，若点C 是x轴上任意一点，连接AC、BC，则S△ABC=____ 。
9、如图，等边三角形OAB的顶点A在反比例函数y=的图象上，点B在y轴上，若将△OAB沿x轴正方向平移，当点B落在反比例函数的图象上时，点A 的坐标为_____。
10、如图所示，在平面直角坐标系中，点A 和点C 分别在y 轴和x 轴正半轴上，以OA 、OC 为边作矩形OABC ，双曲线y= (x>0)交AB 于点E ，AE:EB=1:3，则矩形OABC 的面积是_____。
11、如图,已知矩形OABC 的面积为
,它的对角线OB 与双曲线y ＝k x
相交于点D,且OB:OD=5:3,则k=_____。
△AOC 的面积为6，则
13、(陕西2017中考)如图，在平面直角坐标系中，过点M(－3，2)分别作x
轴，y 轴的垂线与反比例函数y ＝4x
的图象交于A ，B 两点，则四边形MAOB 的面积为________．
14、如图，在Rt △OAB 中，∠OBA=90°，点B 在x 轴上，点A 在第二象限，已
知双曲线y ＝k x
（k ＜0）经过Rt △OAB 斜边OA 的中点D ，且与直角边AB 相交于点C ．若点A 的坐标为（-6，4），△AOC 的面积为________．
15、如图,点A 是反比例函数y=的图象上任意一点,AB ∥x 轴交反比例函数y=的图象于点B,以AB 为边作平行四边形ABCD,其中C 、D 在x 轴上,则四边形ABCD 的面积为_____ 。
16、反比例函数y=与y=的图像在同一坐标戏中如图所示，P
为y=上任意一点，过P作PQ平行于y轴，交y=于点Q,M为y轴上一点，则S△PMQ是_____ 。
17、如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标
轴，点C在反比例函数y＝k
x
（k≠0）的图象上。
若点A的坐标为(-2,-2)，则k
的值为_____ 。
提高型
1、如图，反比例函数y=在第二象限的图象上有两点A、B，它们的
横坐标分别为-1，-3，直线AB与x轴交于点C，则△AOC的面积为
_____ 。
2、如图,反比例函数y＝k
x
(x＞0)的图象经过平行四边形ABCO的顶点A和对
角线的交点E,点A的横坐标为3,对角线AC所在的直线交y轴于(0,6)点,
则函数y＝k
x
的表达式为_____ 。
.
4、如图,点A在反比例函数y=图象上,点B在反比
例函数y=的图象上,且∠AOB=90°,则tan∠OAB的值为_____ 。
5、如图，已知双曲线y＝k
x
(K＞0)经过直角三角形OAB斜边OB的中点D，与
直角边AB相交于点C。
若△OBC的面积为3，则k=_____ 。
6、如图，点A在双曲线y=上，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于点B，当OA=4时，则△ABC周长为_____ 。
-与反比例函数＜0)的图象交于点A,与x轴相交
AB=AC,则k的值为_____ 。
9
y
，∠
（
12、如图,点E,F在函数y=的图象上,直线EF分别与x轴、y轴交于点
A、B,且BE:BF=1:3,则△EOF的面积是_____ 。
13、如图，已知第一象限内的图象是反比例函数y=图象的一个分支，
第二象限内的图象是反比例函数y=图象的一个分支，在x轴的上方有一条平行于x轴的直线m与它们分别交于点A、B，过点A、B作x轴的垂线，垂足分别为C、D。
若四边形ABCD的周长为8，且AB＜AC，则点A的坐标为__ ___ 。