《信息论与编码》习题解答-第三章
信息论与编码（第3版）第3章部分习题答案
3.1设信源()12345670.20.190.180.170.150.10.01X a a a a a a a P X ⎛⎫⎧⎫=⎨⎬ ⎪⎩⎭⎝⎭ (1) 求信源熵()H X (2) 编二进制香农码(3) 计算平均码长及编码效率。
答：(1)根据信源熵公式()()()()21log 2.6087bit/symbol i i i H X p a p a ==−=∑(2)利用到3个关键公式：①根据()()()100,0i a i k k p a p a p a −===∑计算累加概率；②根据()()*22log 1log ,i i i i p a k p a k N −≤<−∈计算码长；③根据()a i p a 不断地乘m 取整（m 表示编码的进制），依次得到的i k 个整数就是i a 对应的码字根据①②③可得香农编码为(3)平均码长公式为()13.14i i i K p a k ===∑单符号信源L =1，以及二进制m =2, 根据信息率公式()2log bit/symbol m KR K L==编码效率()83.08%H X Rη==3.2对习题3.1的信源编二进制费诺码，计算其编码效率答：将概率从大到小排列，且进制m=2,因此，分成2组（每一组概率必须满足最接近相等）。
根据平均码长公式为()12.74i iiK p a k===∑单符号信源L=1，以及二进制m=2, 根据信息率公式()2log bit/symbolmKR KL==编码效率（信源熵看题3.1）()95.21%H XRη==3.3对习题3.1的信源编二进制赫夫曼码，计算平均码长和编码效率答：将n个信源符号的概率从大到小排列，且进制m=2。
从m个最小概率的“0”各自分配一个“0”和“1”，将其合成1个新的符号，与其余剩余的符号组成具有n-1个符号的新信源。
排列规则和继续分配码元的规则如上，直到分配完所有信源符号。
必须保证两点：(1)当合成后的信源符号与剩余的信源符号概率相等时，将合并后的新符号放在靠前的位置来分配码元【注：“0”位表示在前，“1”表示在后】，这样码长方差更小；(2)读取码字时是从后向前读取，确保码字是即时码。
信息论与编码理论_第3章信道容量_习题解答_071102
.. ..... . .第3章 信道容量习题解答3-1 设二进制对称信道的转移概率矩阵为2/31/31/32/3⎡⎤⎢⎥⎣⎦解: (1) 若12()3/4,()1/4P a P a ==，求(),(),(|),(|)H X H Y H X Y H Y X 和(;)I X Y 。
i i 2i=13311H(X)=p(a )log p(a )log()log()0.8113(/)4444bit -=-⨯-=∑符号111121*********j j j=132117p(b )=p(a )p(b |a )+p(a )p(b |a )=43431231125p(b )=p(a )p(b |a )+p(a )p(b |a )=4343127755H(Y)=p(b )log(b )=log()log()0.9799(/)12121212bit ⨯+⨯=⨯+⨯=---=∑符号 22i j j i j i j i ,H(Y|X)=p(a ,b )logp(b |a )p(b |a )logp(b |a )2211log()log()0.9183(/)3333i jjbit -=-=-⨯-⨯=∑∑符号I(X;Y)=H(Y)H(Y|X)=0.97990.91830.0616(/)bit --=符号 H(X|Y)=H(X)I(X;Y)=0.81130.06160.7497(/bit --=符号)(2)求该信道的信道容量及其达到信道容量时的输入概率分布。
二进制对称信息的信道容量H(P)=-plog(p)-(1-p)log(1-p)1122C =1-H(P)=1+log()+log()=0.0817(bit/)3333符 BSC 信道达到信道容量时，输入为等概率分布，即：{0.5，0.5} 注意单位3-4 设BSC 信道的转移概率矩阵为112211Q εεεε-⎡⎤=⎢⎥-⎣⎦1）写出信息熵()H Y 和条件熵(|)H Y X 的关于1()H ε和2()H ε表达式，其中()log (1)log(1)H εεεεε=----。
信息论与编码第3版第3章习题解答
第3章 无失真离散信源编码习题3.1 设信源1234567()0.20.190.180.170.150.10.01X a a a a a a a P X(1) 求信源熵H (X )； (2) 编二进制香农码；(3) 计算其平均码长及编码效率。
解： (1)()()log ()(.log ..log ..log ..log ..log ..log ..log .).7212222222=-020201901901801801701701501501010010012609 i i i H X p a p a bit symbol(2)a i p (a i ) p a (a i ) k i 码字 a 1 0.2 0 3 000 a 2 0.19 0.2 3 001 a 3 0.18 0.39 3 011 a 4 0.17 0.57 3 100 a 5 0.15 0.74 3 101 a 6 0.1 0.89 4 1110 a 70.010.9971111110(3)()3(0.2+0.19+0.18+0.17+0.15)+40.1+70.01=3.1471i i i K k p a()() 2.609=83.1%3.14H X H X R K3.2 对习题3.1的信源编二进制费诺码，计算其编码效率。
解：a i p (a i ) 编 码 码字 k i a 1 0.2 000 2 a 2 0.19 1 0 010 3 a 3 0.18 1 011 3 a 4 0.17 110 2 a 5 0.15 10 110 3 a 6 0.1 10 1110 4 a 70.011 11114()2(0.2+0.17)+3(0.19+0.18+0.15)+4(0.1+0.01)=2.7471i i i K k p a()() 2.609=95.2%2.74H X H X R K3.3 对习题3.1的信源分别编二进制和三进制赫夫曼码，计算各自的平均码长及编码效率。
信息论与编码习题与答案第三章
(1)若P(0)= 3/4,P(1)= 1/4，求H(X), H(X/Y), H(Y/X)和I(X;Y)；
(2)求该信道的信道容量及其达到信道容量时的输入概率分布；
解：1)
（2)
其最佳输入分布为
3.3在有扰离散信道上传输符号0和1，在传输过程中每100个符号发生一个错误，已知P(0)=P(1)=1/2，信源每秒内发出1000个符号，求此信道的信道容量。
解：由题意可知该二元信道的转移概率矩阵为： 为一个BSC信道所以由BSC信道的信道容量计算公式得到：
3-6设有扰离散信道的传输情况分别如图3－17所示。求出该信道的信道容量。
解：信道转移概率矩阵为P= 该信道为离散对称信道DMC
3-7发送端有三种等概率符号 ， ,接收端收到三种符号 ，信道转移概率矩阵为
（7） bit/symbol
H(X/Y)=
i
bit/symbol
3-10一个平均功率受限制的连续信道，其通频带为1MHZ，信道上存在白色高斯噪声。
（1）已知信道上的信号与噪声的平均功率比值为10，求该信道的信道容量；
（2）信道上的信号与噪声的平均功率比值降至5，要达到相同的信道容量，信道通频带应为多大？
=
bit/symbol
（3）当接收为 ，发为 时正确，如果发的是 则为错误，各自的概率为：
则错误概率为：
（4）
从接收端看平均错误概率为
（5）从发送端看的平均错误概率为：
（6）能看出此信道不好。原因是信源等概率分布，从转移信道来看正确发送的概率x1→y1的概率0.5有一半失真；x2→y2的概率0.3有严重失真；x3→y3的概率0完全失真。
(1)接收端收到一个符号后得到的信息量H(Y);
信息论与编码习题参考答案(全)
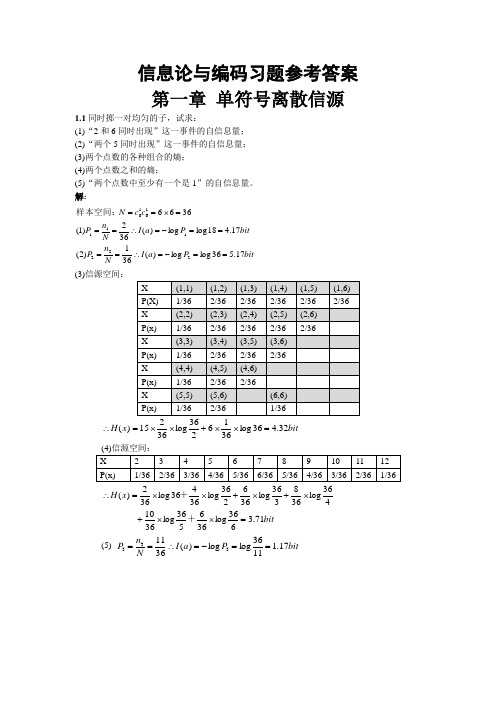
信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。
解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：(3)信源空间：bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格。
（1） 若仅有质点A ，求A 落入任一方格的平均信息量； （2） 若已知A 已落入，求B 落入的平均信息量； （3） 若A ，B 是可辨认的，求A ，B 落入的平均信息量。
解：bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士：“你是否是红绿色盲？”他的回答可能是：“是”，也可能“不是”。
信息论与编码习题解答
信息论与编码习题解答信息论与编码习题解答第⼀章1.⼀位朋友很不赞成“通信的⽬的是传送信息”及“消息中未知的成分才算是信息”这些说法。
他举例说：我多遍地欣赏梅兰芳⼤师的同⼀段表演，百看不厌，⼤师正在唱的正在表演的使我愉快，将要唱的和表演的我都知道，照你们的说法电视⾥没给我任何信息，怎么能让我接受呢？请从信息论的⾓度对此做出解释。
（主要从狭义信息论与⼴义信息论研究的内容去理解和解释）答：从狭义信息论⾓度，虽然将要表演的内容观众已知，但是每⼀次演出不可能完全相同。
⽽观众在欣赏的同时也在接受着新的感官和视听享受。
从这⼀⾓度来说，观众还是可以得到新的信息的。
另⼀种解释可以从⼴义信息论的⾓度来分析，它涉及了信息的社会性、实⽤性等主观因素，同时受知识⽔平、⽂化素质的影响。
京剧朋友们在欣赏京剧时也因为主观因素⽽获得了享受，因此属于⼴义信息论的范畴。
2．利⽤下图（图1.2）所⽰的通信系统分别传送同样时间（例如⼗分钟）的重⼤新闻公告和轻⾳乐，它们在接收端各⽅框的输⼊中所含的信息是否相同，为什么？图1.2 通信系统的⼀般框图答：重⼤新闻是语⾔，频率为300~3400Hz，⽽轻⾳乐的频率为20~20000Hz。
同样的时间内轻⾳乐的采样编码的数据要⽐语⾳的数据量⼤，按码元熵值，⾳乐的信息量要⽐新闻⼤。
但是在信宿端，按信息的不确定度，信息量就应分别对待，对于新闻与⾳乐的信息量⼤⼩在⼴义上说，因⼈⽽异。
第⼆章1．⼀珍珠养殖场收获240颗外观及重量完全相同的特⼤珍珠，但不幸被⼈⽤外观相同但重量仅有微⼩差异的假珠换掉1颗。
（1）⼀⼈随⼿取出3颗，经测量恰好找出了假珠，问这⼀事件⼤约给出了多少⽐特的信息量；（2）不巧假珠⼜滑落进去，那⼈找了许久却未找到，但另⼀⼈说他⽤天平最多6次能找出，结果确是如此，问后⼀事件给出多少信息量；（3）对上述结果作出解释。
解：（1）从240颗珍珠中取3颗，其中恰好有1颗假珠的概率为：22393240239!2!237!240!3!237!11/80240/3C P C====所以，此事件给出的信息量为：I = – log 2P = log 280=6.32 (bit)（2）240颗中含1颗假珠，⽤天平等分法最多6次即可找到假珠，这是⼀个必然事件，因此信息量为0。
信息论与编码习题参考答案(全)
信息论与编码习题参考答案 第一章 单符号离散信源同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。
解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：(3)信源空间：bit x H 32.436log 3616236log 36215)(=⨯⨯+⨯⨯=∴ (4)信源空间：bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格内，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格内。
（1） 若仅有质点A ，求A 落入任一方格的平均信息量； （2） 若已知A 已落入，求B 落入的平均信息量； （3） 若A ，B 是可辨认的，求A ，B 落入的平均信息量。
解：bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为%.如果你问一位男士：“你是否是红绿色盲”他的回答可能是：“是”，也可能“不是”。
信息论与编码习题答案-曹雪虹
3-14
信源 符号 xi x1 x2 x3 x4 x5 x6 x7
符号概 率 pi 1/3 1/3 1/9 1/9 1/27 1/27 1/27 1/3 1/3 1/9 1/9 2/27 1/27 1/3 1/3 1/9 1/9 1/9
编码过程
编码 1/3 1/3 1/3 2/3 1/3 00 01 100 101 111 1100 1101
得p0p1p223当p0或p1时信源熵为0第三章无失真信源编码31321因为abcd四个字母每个字母用两个码每个码为05ms所以每个字母用10ms当信源等概率分布时信源熵为hxlog42平均信息传递速率为2信源熵为hx0198bitms198bitsbitms200bits33与上题相同351hu12log2?14log4?18log8?116log16?132log32?164log64?1128log128?1128log128?1984111111112481632641281282每个信源使用3个二进制符号出现0的次数为出现1的次数为p0p134相应的香农编码信源符号xix1x2x3x4x5x6x7x8符号概率pi12141811613216411281128累加概率pi00507508750938096909840992logpxi12345677码长ki12345677码字010110111011110111110111111011111110相应的费诺码信源符号概符号xi率pix1x2x3x4x5x6x7x812141811613216411281128111第一次分组0第二次分组0第三次分组0第四次分组0第五次分组011第六次分组01第七次分组01二元码0101101110111101111101111110111111105香农码和费诺码相同平均码长为编码效率为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 信道容量-习题答案3.1 设二元对称信道的传递矩阵为⎥⎦⎤⎢⎣⎡3/23/13/13/2 (1) 若P(0) = 3/4, P(1) = 1/4，求H(X), H(X/Y), H(Y/X)和I(X;Y)； (2) 求该信道的信道容量及其达到信道容量时的输入概率分布；解： 1)symbolbit Y X H X H Y X I symbol bit X Y H Y H X H Y X H X Y H Y H Y X H X H Y X I symbol bit y p Y H x y p x p x y p x p y x p y x p y p x y p x p x y p x p y x p y x p y p symbolbit x y p x y p x p X Y H symbolbit x p X H jj iji j i j i i i / 062.0749.0811.0)/()();(/ 749.0918.0980.0811.0)/()()()/()/()()/()();(/ 980.0)4167.0log 4167.05833.0log 5833.0()()(4167.032413143)/()()/()()()()(5833.031413243)/()()/()()()()(/ 918.0 10log )32lg 324131lg 314131lg 314332lg 3243( )/(log )/()()/(/ 811.0)41log 4143log 43()()(222221212221221211112111222=-==-==+-=+-=-=-==⨯+⨯-=-==⨯+⨯=+=+==⨯+⨯=+=+==⨯⨯+⨯+⨯+⨯-=-==⨯+⨯-=-=∑∑∑∑2)21)(/ 082.010log )32lg 3231lg 31(2log log );(max 222==⨯++=-==i mi x p symbolbit H m Y X I C3.2 解：(1)αα-==1)(,)(21x p x p⎥⎦⎤⎢⎣⎡=4/14/12/102/12/1P ，⎥⎦⎤⎢⎣⎡---=4/)1(4/)1(2/)1(02/12/1)(αααααj i y x P 4/)1()(,4/14/)(,2/1)(321αα-=+==y p y p y p接收端的不确定度：))1(41log()1(41)4141log()4141()2log(21)(αααα---++-=Y H)1log(41)1log(4123αααα---++-= (2))4log()1(41)4log()1(41)2log()1(210)2log(21)2log(21)|(ααααα-+-+-+++=X Y H α2123-= (3))|()();(X Y H Y H Y X I -=);(max )()(Y X C i x p =α,0)(=ααC d d,得到5/3=α 161.0)5/3();max(===C Y X C 3.3∑==⨯++=+=21919.001.0log 01.099.0log 99.02log log )log(j ij ij p p m C0.919*1000=919bit/s 3.4⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=εεεε-10-10001ij p2/1)()(0)(321===a p a p a p 0)(1=b p2/12/1)1(2/100)|()(),()(222=⨯+-⨯+⨯===∑∑εεi ii ii a b p a p b a p b p2/1-12/12/100)|()(),()(333=⨯+⨯+⨯===∑∑）（εεi ii ii a b p a p b a p b p)()|(log)|();(j i j ji j i b p a b p a b p Y a I ∑=0);(1=Y a Iεεεε2log )1(2log )1(0)()|(log)|();(222+--+==∑j j jj b p a b p a b p Y a I )1(2log )1(2log 0)()|(log)|();(333εεεε--++==∑j j jj b p a b p a b p Y a I当0=ε，1=C 当2/1=ε，0=C 3.5两个信道均为准对称DMC 信道设输入符号概率αα-==1)(,)(21a p a p ， （1） 对于第一种信道的联合概率的矩阵为：⎥⎦⎤⎢⎣⎡---------)1(2)1)(1()1)((2)()1(αεαεαεεααεαεp p p p⎥⎦⎤⎢⎣⎡---)()1(εαεp p 3.6⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2/1002/12/12/10002/12/10002/12/1P 121log 2121log 214log log )log(41=++=+=∑=ij j ij p p m C3.7解：(1)从已知条件可知：3,2,1,3/1)(==i x p i ，且转移概率⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0109101103103525110321)|(i j x y p ，则联合概率⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡==010330110110115215110161)()|(i i j ij x p x y p p ，因为：),()(∑=ij i j y x p y p ，可计算得到31)(1=y p ，21)(2=y p ，61)(3=y p499.16log 612log 213log 31)(=++=Y H(2)175.1910log 10310log 301310log 101310log10125log 1525log 151310log 1012log 61)|(log )()|(=+++++++=-=∑iji j j i x y p y x p X Y H (3)当接收为2y ，发送为2x 时正确，如果发送为1x 和3x 为错误，各自的概率为： 5/1)|(21=y x p ，5/1)|(22=y x p ，5/3)|(23=y x p 它的错误概率为：5/4)|()|(2321=+=y x p y x p p e(4)从接收端看到的平均错误概率为：===∑∑≠≠ji ij ji j i j e p y x p y p p )|()(收733.010/115/110/310/130/115/2=+++++(5)从发送端看到的平均错误概率为：===∑∑≠≠ji ij ji i j i e p x y p x p p )|()(发733.010/115/110/310/130/115/2=+++++(6)此信道不好，因为信源等概率分布，从转移信道来看，正确发送的概率11y x >-为0.5，有一半失真；22y x >-为0.3，严重失真；33y x >-为0，完全失真。
(7)585.13log )(==X H301.1)35log(103)10log(301)35log(101)5log(101)25log(151)5log(101)2log(61)|(log )()|(=+++++++=-=∑ijj i j i y x p y x p Y X H3.8s Mb WN p W C av /5.19)5.65.451log(5.6)1log(0=+=+=3.9每秒传递的信息速率：10log 3010304⨯⨯⨯=R信道的信噪功率比：dB P P N s 30log 10=，310=N s P P ，R P PW C N s t =+=)1log(所以：MHz W 3=3.10(1) s Mb P P W C N s t /46.3)101log(1)1log(111=+⨯=+= (2) )1log()1log(222111N s N s P P W P P W +=+，已知MHz W 11=，1011=N s P P ，522=N s P P， 所以MHz W 34.12=(3) )1log()1log(333111N s N s P P W P P W +=+，已知MHz W 11=，MHz W 5.02=，1011=N s P P， 所以可求得12022=N s P P ，课外习题： 设二进制对称信道是无记忆信道，信道矩阵为⎥⎥⎦⎤⎢⎢⎣⎡__p pp p ，其中：p > 0，_p < 1，p + _p = 1，_p >> p 。
试写出N = 3次扩展无记忆信道的信道矩阵[P]。
解：[]⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=3222232222322223222322322322322222232232232232223222232222322223111110101100011010001000 111110 101 100 011 010 001 000 p pp pp pp p p pp p p p p p p p pp p p p p p p p ppp pp pp p p p p p ppp p p pp p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p p pp p p p p p p p pp p p p p p p p ppp p p p p p p p P课外习题：在图片传输中，每帧约有2.25 106个像素，为了能很好地重现图像，能分16个亮度电平，并假设亮度电平等概分布。
试计算每分钟传送一帧图片所需信道的带宽（信噪功率比为30dB ）。
解：sbit t I C bit NH I symbol bit n H t / 101.5601091010941025.2/ 416log log 566622⨯=⨯===⨯=⨯⨯=====z15049)10001(log 105.11log 1log 25H P P C W P P W C N X tN X t =+⨯=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫⎝⎛+=课外习题：设电话信号的信息率 5.6 104比特/秒，在一个噪声功率谱为N 0= 5 10-6 mW/Hz 、限频F 、限输入功率P 的高斯信道中传送，若F=4kHz ，问无差错传输所需的最小功率P 是多少瓦？若F →∞，则P 是多少瓦？解：We N C P eN PC F WWN P WN P W C t X X t W C X X t t 1094.171828.2log 105106.5log log 328.0121054000121log 429420204000106.59004--⨯-⨯=⨯⨯⨯===∞→=⎪⎪⎭⎫ ⎝⎛-⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛+=3.12 有一个二元对称信道，其信道矩阵为⎥⎦⎤⎢⎣⎡98.002.002.098.0。