8601最大长方体问题
与长方体有关的最值问题

与长方体有关的最值问题长方体是一种常见的几何形状,具有六个面、八个顶点和十二条边。
在与长方体有关的问题中,我们经常需要寻找最大值或最小值,以满足特定的条件。
1. 长方体的体积最大值问题长方体的体积由其三个边长决定,假设边长分别为a、b、c。
我们想要找到在给定的约束条件下,长方体体积的最大值。
如果只有一个约束条件,我们可以使用微积分的方法求解。
将体积函数V(a,b,c)表示为三个变量的函数,然后计算其对应约束条件的梯度。
最大体积对应于梯度为零的点。
解出梯度为零的方程组,然后通过求解方程组找到边长a、b、c的值。
如果有多个约束条件,可以应用拉格朗日乘数法。
在这种情况下,我们需要将约束条件转化为等式约束,然后构造拉格朗日函数并求解。
2. 长方体的表面积最小值问题长方体的表面积由其三个边长决定。
我们希望找到在给定的体积约束下,长方体表面积的最小值。
与体积最大值问题类似,如果只有一个约束条件,可以使用微积分的方法求解。
将表面积函数A(a,b,c)表示为三个变量的函数,并计算其对应约束条件的梯度。
最小表面积对应于梯度为零的点。
解出梯度为零的方程组,并通过求解方程组找到边长a、b、c的值。
如果有多个约束条件,我们可以再次应用拉格朗日乘数法。
3. 长方体对角线长度最大值问题长方体的对角线长度是其三个边长的函数。
我们希望找到长方体对角线长度的最大值。
与前两种问题不同的是,长方体对角线的函数是一个复杂的非线性函数。
解决这个问题可以使用数值优化方法,如牛顿法、梯度下降法等。
综上所述,与长方体有关的最值问题可以通过微积分方法、拉格朗日乘数法以及数值优化方法来解决。
具体的求解步骤根据具体的约束条件和目标函数而定。
五年级数学长方体和正方体试题答案及解析

五年级数学长方体和正方体试题答案及解析1.一个长方体长12厘米,宽8厘米,高5厘米,这个长方体六个面中最大的面面积是平方厘米,最小的面面积是平方厘米,它的表面积是平方厘米。
【答案】96,40,392【解析】分析:由题意可知:最大的面,即上面(或下面),用12×8进行解答即可;最小的面,即侧面:用5×8计算即可;再据长方体的表面积公式即可求出其表面积。
解答:解:最大:12×8=96(平方厘米);最小:5×8=40(平方厘米);表面积:(12×8+12×5+8×5)×2,=(96+60+40)×2,=196×2,=392(平方厘米);【考点】长方体和正方体的表面积。
2.从面看到的图形是;从面看到的图形是;从面看到的图形是.【答案】右;左;正面或上.【解析】观察图形可知,从上面、正面看到的都是一个长方形和圆形;从左面看到的是一个正方形;从右面看到的是正方形和内切圆形的组合图形,由此即可选择填空.解答:解:根据题干分析可得:从右面看到的图形是;从左面看到的图形是;从正面或上面看到的图形是.故答案为:右;左;正面或上.点评:本题是考查从不同方向观察物体和几何,是训练学生的观察能力和分析能力.3.画一画.在方格纸里分别画出从正面、左面和上面看到的图形.【答案】【解析】从正面看到的有三层,最下面一层是3个正方形,第二层和第三层靠左侧分别是1个正方形:从左面看到有三层,最下面一层有2个正方形,第二层和第三层靠左侧分别是1个正方形:从上面看到的有两层,上面一层有4个正方形,下面靠左侧一个正方形:,由此即可解答.解答:解:答案如图,点评:此题考查了从不同的方向观察到的几何体的形状,做此类题时,应认真审题,根据看到的形状画出即可.4.焊接一个长7cm、宽2cm、高1cm的长方体框架,至少要用 cm的铁丝.【答案】40【解析】需要铁丝的长度等于这个长方体的棱长总和,长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答.解:(7+2+1)×4,=10×4,=40(厘米),答:至少要用40厘米铁丝.故答案为:40.【点评】此题主要考查长方体的棱长总和公式的灵活运用.5.挖一个长和宽都是5米的长方体菜窖,要使菜窖的容积是50立方米,应该挖米深.【答案】2.【解析】根据长方体的体积计算公式v=sh,已知长方体的体积(容积)和底面积,求高.h=v÷s,由此列式解答.解:50÷(5×5),=50÷25,=2(米);答:应该挖2米深.故答案为:2.【点评】此题主要考查根据长方体的体积计算方法,解决有关的实际问题.6.我们在画长方体时一般只画出三个面,这是因为长方体()A.只有三个面B.只能看到三个面C.最多只能看到三个面【答案】C【解析】长方体的特征是:6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相同.再根据观察物体的方法,从某个角度观察一个长方体最多能看到它的3个面.由此解答.解:根据长方体的特征和观察物体的角度及观察的范围,最多能看长方体的3个面.答:这是因为长方体最多只能看到它的3个面.故选:C.【点评】此题主要考查长方体的特征和观察物体的角度及观察的范围.7.一个正方体的棱长总和是60厘米,它的表面积是()A.21600平方厘米B.150平方厘米C.125立方厘米【答案】B【解析】根据一个正方体的棱长总和是60厘米,可求出棱长的长度,进一步用棱长乘棱长乘6求得表面积.解:棱长:60÷12=5(厘米),表面积是:5×5×6=150(平方厘米);答:它的表面积是150平方厘米.故选:B.【点评】此题考查正方体表面积的计算方法.8.长方体或正方体(),叫做它们的表面积。
北师大版小学数学五年级下册长方体(一)难题练习题带答案
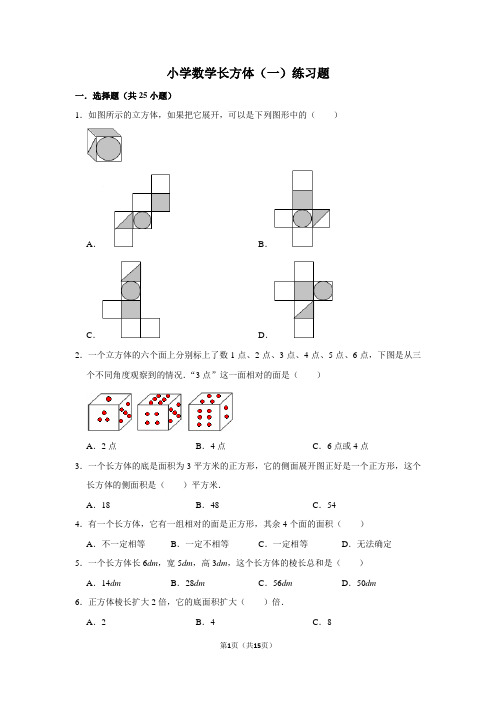
小学数学长方体(一)练习题一.选择题(共25小题)1.如图所示的立方体,如果把它展开,可以是下列图形中的()A.B.C.D.2.一个立方体的六个面上分别标上了数1点、2点、3点、4点、5点、6点,下图是从三个不同角度观察到的情况.“3点”这一面相对的面是()A.2点B.4点C.6点或4点3.一个长方体的底是面积为3平方米的正方形,它的侧面展开图正好是一个正方形,这个长方体的侧面积是()平方米.A.18B.48C.544.有一个长方体,它有一组相对的面是正方形,其余4个面的面积()A.不一定相等B.一定不相等C.一定相等D.无法确定5.一个长方体长6dm,宽5dm,高3dm,这个长方体的棱长总和是()A.14dm B.28dm C.56dm D.50dm6.正方体棱长扩大2倍,它的底面积扩大()倍.A.2B.4C.87.下面图形不是正方体展开图的是()A.B.C.D.8.把一个棱长为4厘米的正方体,分割成两个长方体,这两个长方体表面积总和是()平方厘米.A.64B.128C.80D.969.如图能围成正方体的是()A.B.C.D.10.要把7本长20厘米,宽10厘米,高1厘米的数学课本包装在一起,下面组合方法最节省包装纸的是()A.B.C.11.一个长方体的底面是面积为4平方米的正方形,它的侧面展开图正好也是一个正方形,这个长方体的侧面积是()平方米.A.16B.64C.48D.2412.把6个棱长为2厘米的正方体排成一排拼成一个长方体,这个长方体的表面积是()平方厘米.A.96B.26C.50D.10413.从由8个棱长是1厘米的小正方体拼成的大正方体中拿去1个小正方体(如图),这时它的表面积是()平方厘米。
A.24B.18C.2814.如图是一个长方体的展开图,围成长方体时,点A将与点()重合。
A.G B.B C.C D.E15.用相同的方式包装两个大小不同的正方体礼盒(打结处不计),大礼盒的棱长是小礼盒棱长的2倍,包装大礼盒与小礼盒用去彩带的长度比、用去包装纸的面积比分别是()A.2:1;8:1B.4:1;6:1C.2:1;4:116.一个长方体的底面周长是20厘米,左面面积是20平方厘米,前面面积是30平方厘米,则下面面积是()平方厘米。
8601最大长方体问题

8601 最大长方体问题时间限制:1000MS 内存限制:1000K提交次数:0 通过次数:0题型: 编程题语言: 无限制Description一个长,宽,高分别是m,n,p的长方体被分割成m*n*p个小立方体。
每个小立方体内含一个整数。
试着设计一个算法,计算所给长方体的最大子长方体。
子长方体的大小由它内部所含所有整数之和确定。
约定:当该长方体所有元素均为负数时,输出最大子长方体为0。
Input第一行3个正整数m,n,p,其中1<=m,n,p<=50接下来的m*n行中每行p个整数,表示小立方体中的数。
Output第一行中的数是计算出的最大子长方体的大小。
Sample Input3 3 30 -1 21 2 21 1 -2-2 -1 -1-3 3 -2-2 -3 1-2 3 30 1 32 1 -3Sample Output14Hint1,先编写一维的“最大字段和”的解法。
2,基于“最大字段和”,编写二维的“最大子矩阵和”的解法。
3,基于“最大子矩阵和”,编写三维的“最大子长方体和”的解法。
ProviderzhengchanSource Code#include <iostream>#include <cstring>using namespace std;const int N = 55;int num[N][N][N];//函数声明void input(int m,int n,int k);int check(int m,int n,int k);int maxSum(int a[], int n);int maxSum2(int a[N][N],int m,int n);int maxSum3(int a[N][N][N],int m,int n,int k);int main(){int m, n, k;cin >> m >> n >> k;if(m>=1 && m<=50 && n>=1 && n<=50 && k>= 1 && k<=50){input(m, n, k);int sum = maxSum3(num, m, n, k);if(check(m,n,k) == 1)cout << sum;else cout << 0;}return 0;}void input(int m,int n,int k){int flag = 0; //检测是否全为负数int i, j, l;for(i = 0 ; i < m ; i++)for(j = 0 ; j < n ; j++)for(l = 0 ; l < k ; l++){cin >> num[i][j][l];if(num[i][j][l]>=0)flag = 1;}}int check(int m,int n,int k){int flag = 0; //检测是否全为负数int i, j, l;for(i = 0 ; i < m ; i++)for(j = 0 ; j < n ; j++)for(l = 0 ; l < k ; l++){if(num[i][j][l]>=0)flag = 1;}return flag;}int maxSum(int a[],int n){int sum = a[0], b = 0;for(int i = 0 ; i < n ; i++){if(b > 0)b += a[i];elseb = a[i];if(sum < b)sum = b;}return sum;}int maxSum2(int a[N][N],int m,int n){int sum = a[0][0];int b[N], i, j, k;for(i = 0 ; i < m ; i++){memset(b, 0, sizeof(b));for(j = i ; j < m ; j++) {for(k = 0 ; k < n ; k++)b[k] += a[j][k];int max = maxSum(b, n);if(max > sum)sum = max;}}return sum;}int maxSum3(int a[N][N][N],int m,int n,int k){int b[N][N];int i, j, l;int sum = a[0][0][0], max = 0;for(i = 0 ; i < m ; i++) {memset(b, 0, sizeof(b));for(j = i ; j < m ; j++) {for(l = 0 ; l < n ; l++)for(int t = 0 ; t < k ; t++)b[l][t] += a[j][l][t];max = maxSum2(b, n, k);if(max > sum)sum = max;}}return sum;}。
适用于新教材2023版高中数学阶段复习课第三课立体几何初步探究导学课件新人教A版必修第二册

【易错分析】错解1:如图(1)所示,若沿C1D1剪开,使面ABB1A1与面A1B1C1D1在同 一个平面内,可求得AC1= 42+(5+3)2 = 80 (m), 故蚂蚁爬行的最短路线长为 80 m. 错解2:如图(2)所示,沿AD剪开,使面ADCB与面BCC1B1在同一个平面内,可求得 AC1= 32+(5+4)2 = 90 (m).故蚂蚁爬行的最短路线长为 90 m.
2 ,求原梯形的面积.
【解析】如图由斜二测画法原理知,原梯形与直观图中的梯形上下底边的长度是一 样的,不一样的是两个梯形的高,原梯形的高OC是直观图中OC′长度的2倍,OC′的 长度是直观图中梯形的高的 2 倍,
由此知原梯形的高OC的长度是直观图中梯形高的2 2 倍,故其面积是梯形OA′B′C′ 面积的2 2 倍,梯形OA′B′C′的面积为 2 ,所以原梯形的面积是4.
【易错分析】解答本题时,往往仅凭直观感觉,盲目地认为E,B,F,D1四点共 面,同时条件AE=C1F也没有用到,从而导致错误. 【避错警示】在证明问题中,结论成立与否要有严格的推理过程,不能凭直观感 觉,同时当解决完问题时,发现条件还有没用到的,则需要考虑自己的证明过程是 否有误.
易错七 考虑问题不全面,推理过程不严密致误 【案例7】如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1, AA1=2,∠B1A1C1=90°,D为BB1的中点.
(2)如图(2)所示,沿AD剪开,使面ADCB与面BCC1B1在同一个平面内,可求得AC1 = 32+(5+4)2 = 90 (m). (3)如图(3)所示,沿CC1剪开,使面BCC1B1与面ABB1A1在同一个平面内,可求得AC1 = 52+(4+3)2 = 74 (m).故蚂蚁爬行的最短路线长为 74 m.
人教版五年级下册期末考试易出现易错题

人教版五年级期末考试易出现易错题 华龙区石化路第一小学:彭军波1、将两个长宽高分别是6厘米、7厘米、8厘米的长方体拼成一个大长方体,这个大长方体的表面积最大是( )平方厘米。
A 、876B 、762C 、581D 、5002、已知一组数据5、15、75、45、25、75、45、35、45、35,那么40是这组数据的( )。
A 、众数B 、平均数但不是中位数C 、平均数也是中位数D 、中位数但不是平均数3、一个长方体它的底面是一个正方形,如果把它的侧面展开也是一个正方形,那么这个长方体的底面边长是它的高的( )。
A 、21B 、41 C 、2倍 D 、4倍4、用两个棱长3厘米的正方体拼成一个长方体,这个长方体的表面积是( ),体积是( ),棱长总和是( )厘米。
5、一箱饮料共有12瓶,平均分给24个同学,每瓶饮料是这箱饮料的( ),每人分得的饮料是这箱饮料的( ),每人分得( )6、a 24(a 是大于0的自然数),当a ( )时,a24是真分数;当a ( )时,a 24是假分数;当a 是( )时,a 24是自然数。
7、一 个正方体的棱长是a 分米,这个正方体的棱长总和是( )分米;如果把它截成两个大小相等的长方体,一个长方体的体积是( )立方分米,表面积是( )平方分米。
8、林英家到学校的路程是180米,林英3分钟走完。
平均每分钟走全程的(),平均每走1米要()分钟。
9、一个两位数,其中十位上的数字比个位上的数字大2,且同时是2和3的倍数,这个数是()。
10、用钢筋焊接一个长12分米,宽10分米,高5分米的长方体框架,需要钢筋()分米,如果用三合板包装成木箱,需要三合板()平方分米,这个木箱可容纳物品()立方分米。
11、两个相邻偶数的和是30,这两个数的最大公因数是(),最小公倍数是()。
12、一批水泥共10吨,用去4吨,还剩下这批水泥的(),如果用1,还剩这批水泥的()。
去513、把两个棱长为5厘米的正方体拼成一个长方体,长方体的表面积与两个正方体的表面积之和相比,减少了()。
三年级数学下册长方体练习题
三年级数学下册长方体练习题本文为三年级数学下册长方体练习题解析。
一、填空题1. 长方体共有——个面,它们是_______。
答案:六个面,它们是上下面、前后面、左右面。
2. 一个长方体共有多少个顶点?答案:一个长方体共有8个顶点。
3. 一个长方体共有多少条边?答案:一个长方体共有12条边。
4. 一个长方体的三个平面图分别是:答案:长方体的三个平面图分别是俯视图、正视图和侧视图。
5. 一个长方体的俯视图、正视图和侧视图如图所示,请你填上相应的字母。
答案:由学生自行根据图形填写。
二、判断题判断下列说法是否正确,正确的打“√”,错误的打“×”。
1. 长方体的六个面是相等的。
(√)2. 长方体的四个侧面是相等的。
(×)3. 长方体的体积等于长、宽、高相乘。
(√)4. 长方体的表面积等于长、宽、高相乘。
(×)三、选择题请你从每题的四个选项中选择一个正确的答案。
1. 下列哪个不是长方体的特点?a) 有六个面b) 六个面相等c) 四个侧面相等d) 有八个顶点答案:b) 六个面相等2. 一个长方体的长、宽、高分别是6厘米、4厘米和3厘米,它的体积是多少?a) 72立方厘米b) 48立方厘米c) 36立方厘米d) 24立方厘米答案:a) 72立方厘米表面积是多少?a) 30平方厘米b) 40平方厘米c) 50平方厘米d) 60平方厘米答案:b) 40平方厘米四、计算题请你根据题目计算出正确的答案。
1. 两个长方体的长、宽、高分别是4厘米、3厘米和5厘米,它们的体积之和是多少?答案:第一个长方体的体积为4厘米 * 3厘米 * 5厘米 = 60立方厘米,第二个长方体的体积也是60立方厘米,所以它们的体积之和是60立方厘米 + 60立方厘米 = 120立方厘米。
2. 一个长方体的长度是7厘米,宽度是3厘米,高度是2厘米,求它的表面积。
答案:长方体的表面积等于2 * (7厘米 * 3厘米 + 7厘米 * 2厘米 + 3厘米 * 2厘米) = 98平方厘米。
五年级下册数学长方体和六面体应用题(考试)
五年级下册数学长方体和六面体应用题(考试)题目一某学校的教室由一个长方体和一个六面体组成,长方体的长、宽和高分别为10米、4米和3米,六面体的边长为2米。
请计算教室的总体积。
解答一首先,我们需要计算长方体的体积。
长方体的体积公式为:体积 = 长 ×宽 ×高。
根据题目给出的数据,可以计算出长方体的体积为:10米 × 4米 × 3米 = 120立方米。
其次,我们需要计算六面体的体积。
六面体的体积公式为:体积 = 边长 ×边长 ×边长。
根据题目给出的数据,可以计算出六面体的体积为:2米 × 2米 × 2米 = 8立方米。
最后,将长方体和六面体的体积相加,即可得到教室的总体积:120立方米 + 8立方米 = 128立方米。
教室的总体积为128立方米。
题目二某储物柜的形状是一个长方体和一个六面体的组合,长方体的长、宽和高分别为6米、3米和4米,六面体的边长为2米。
某学生想将一些书放入储物柜,请计算储物柜剩余的可用空间。
解答二首先,我们需要计算长方体的体积。
长方体的体积公式为:体积 = 长 ×宽 ×高。
根据题目给出的数据,可以计算出长方体的体积为:6米 × 3米 × 4米 = 72立方米。
其次,我们需要计算六面体的体积。
六面体的体积公式为:体积 = 边长 ×边长 ×边长。
根据题目给出的数据,可以计算出六面体的体积为:2米 × 2米 × 2米 = 8立方米。
然后,将长方体的体积减去放入的书的体积,即可得到剩余的可用空间:72立方米 - (放入的书的体积)。
最后,根据实际情况计算放入的书的体积,将其代入公式中计算。
请注意,具体的放入书的体积需要根据实际情况进行计算,以上只是一个示例。
结论通过解答一和解答二,我们可以看到长方体和六面体在数学中的应用。
通过计算这些几何图形的体积,我们可以解决实际生活中与空间和容量相关的问题,如计算房间的容量、物品的储存空间等。
五年级数学长方体一试题
五年级数学长方体一试题1.一个长方体展开后,只能得到一种展开图..(判断对错)【答案】×【解析】根据长方体的特征可知,沿着长方体的长、宽、高展开长方体,得到的图形是不同的,据此解答即可.解:沿着长方体的长、宽、高把长方体展开,会得到不同的展开图,所以原题说法错误.故答案为:×.【点评】本题考查的是长方体特征的运用.2.一根长方体的木料,正好可以锯成两个同样的正方体,这时表面积增加了50平方厘米,这根长方体木料原来的表面积是()平方厘米。
【答案】250【解析】略3.下面各图中,()不是长方体表面的展开图。
A、 B、 C、【答案】A【解析】略4.棱长是6厘米的正方体,它的表面积和体积相等。
()【答案】×【解析】略5.把两个棱长10厘米的正方体拼成一个长方体后,表面积减少了()A.100平方米 B.200平方米 C.80平方米【答案】B【解析】略6.求下面图形的表面积。
(单位:cm)【答案】(6×2+4×2+6×4)×2=88平方厘米 4×4×6=96平方厘米【解析】略7.一个正方体的棱长总和是的1.2米,表面积是________,体积是________.【答案】0.06平方米;0.001立方米【解析】解:1.2÷12=0.1(米)0.1×0.1×6=0.06(平方米)0.1×0.1×0.1=0.001(立方米)答:表面积是0.06平方米,体积是0.001立方米.故答案为:0.06平方米,0.001立方米.【分析】首先用棱长总和除以12 求出棱长,再根据正方体的表面积公式:s=6a2,体积公式:v=a3,把数据分别代入公式解答.此题这条考查正方体的棱长总和公式、表面积公式、体积公式的灵活运用,关键是熟记公式.8.一个长方体礼品盒,长20厘米,宽12厘米,高6厘米.如果把2个这样的礼品盒包成一包.准备用包装纸包成一包.估一估,右面两种包装方法哪种方法更节省包装纸?需要多少平方厘米包装纸?【解析】【分析】把这2个这样的礼品盒包成一包,要想使表面积最小,那么应该把它们的最大的面相粘合,由此拼成的新长方体的长、宽、高分别是:20厘米、12厘米、12厘米,根据长方体的表面积公式:s=(ab+ah+bh)×2,把数据代入公式解答.此题主要考查长方体的表面积公式的灵活运用.解答关键是理解:把它们的最大的面相粘合,包装最省纸.9.用纸皮做一个长1.2米,宽50分米,高40分米无盖的长方体箱子,用来堆放同学们收集的矿泉水的空瓶.(1)至少要用多少平方分米的纸皮?(2)这个箱子最多能装多少立方分米的东西?【答案】(1)解:1.2米=12分米12×50+12×40×2+50×40×2=600+960+4000=5560(平方分米);答:至少要用5560平方分米的纸皮(2)解:12×50×40=600×40=24000(立方分米);答:这个箱子最多能装24000立方分米的东西【解析】【分析】解答有关长方体计算的实际问题,一定要搞清所求的是什么(体积、表面积还是几个面的面积),再进一步选择合理的计算方法进行计算解答问题.(1)求要用多少平方分米的纸皮就是求这个长方体的表面积,根据表面积公式求解;(2)这个箱子最多能装多少立方分米的东西,这是求这个长方体的容积,纸皮的厚度不计,10.某养鱼专户的一鱼池,长16米,宽13米,深3.5米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8601 最大长方体问题
时间限制:1000MS 内存限制:1000K
提交次数:0 通过次数:0
题型: 编程题语言: 无限制
Description
一个长,宽,高分别是m,n,p的长方体被分割成m*n*p个小立方体。
每个小立方体内含一个整数。
试着设计一个算法,计算所给长方体的最大子长方体。
子长方体的大小由它内部所含所有整数之和确定。
约定:当该长方体所有元素均为负数时,输出最大子长方体为0。
Input
第一行3个正整数m,n,p,其中1<=m,n,p<=50
接下来的m*n行中每行p个整数,表示小立方体中的数。
Output
第一行中的数是计算出的最大子长方体的大小。
Sample Input
3 3 3
0 -1 2
1 2 2
1 1 -2
-2 -1 -1
-3 3 -2
-2 -3 1
-2 3 3
0 1 3
2 1 -3
Sample Output
14
Hint
1,先编写一维的“最大字段和”的解法。
2,基于“最大字段和”,编写二维的“最大子矩阵和”的解法。
3,基于“最大子矩阵和”,编写三维的“最大子长方体和”的解法。
Provider
zhengchan
Source Code
#include <iostream>
#include <cstring>
using namespace std;
const int N = 55;
int num[N][N][N];
//函数声明
void input(int m,int n,int k);
int check(int m,int n,int k);
int maxSum(int a[], int n);
int maxSum2(int a[N][N],int m,int n);
int maxSum3(int a[N][N][N],int m,int n,int k);
int main()
{
int m, n, k;
cin >> m >> n >> k;
if(m>=1 && m<=50 && n>=1 && n<=50 && k>= 1 && k<=50)
{
input(m, n, k);
int sum = maxSum3(num, m, n, k);
if(check(m,n,k) == 1)
cout << sum;
else cout << 0;
}
return 0;
}
void input(int m,int n,int k)
{
int flag = 0; //检测是否全为负数
int i, j, l;
for(i = 0 ; i < m ; i++)
for(j = 0 ; j < n ; j++)
for(l = 0 ; l < k ; l++)
{
cin >> num[i][j][l];
if(num[i][j][l]>=0)
flag = 1;
}
}
int check(int m,int n,int k)
{
int flag = 0; //检测是否全为负数
int i, j, l;
for(i = 0 ; i < m ; i++)
for(j = 0 ; j < n ; j++)
for(l = 0 ; l < k ; l++)
{
if(num[i][j][l]>=0)
flag = 1;
}
return flag;
}
int maxSum(int a[],int n)
{
int sum = a[0], b = 0;
for(int i = 0 ; i < n ; i++)
{
if(b > 0)
b += a[i];
else
b = a[i];
if(sum < b)
sum = b;
}
return sum;
}
int maxSum2(int a[N][N],int m,int n)
{
int sum = a[0][0];
int b[N], i, j, k;
for(i = 0 ; i < m ; i++)
{
memset(b, 0, sizeof(b));
for(j = i ; j < m ; j++) {
for(k = 0 ; k < n ; k++)
b[k] += a[j][k];
int max = maxSum(b, n);
if(max > sum)
sum = max;
}
}
return sum;
}
int maxSum3(int a[N][N][N],int m,int n,int k)
{
int b[N][N];
int i, j, l;
int sum = a[0][0][0], max = 0;
for(i = 0 ; i < m ; i++) {
memset(b, 0, sizeof(b));
for(j = i ; j < m ; j++) {
for(l = 0 ; l < n ; l++)
for(int t = 0 ; t < k ; t++)
b[l][t] += a[j][l][t];
max = maxSum2(b, n, k);
if(max > sum)
sum = max;
}
}
return sum;
}。
