参考补充例题
补充例题-企业合并

企业合并【例2.1】A公司取得B公司100% 的股权比例,形成同一控制下的控股合并。
合并日B公司的资产、负债以及所有者权益情况如下表所示:【例】A、B公司分别为P公司控制下的两家子公司。
A公司于20×6年3月10日自母公司P处取得B公司l00%的股权,合并后B公司仍维持其独立法人资格继续经营。
为进行该项企业合并,A公司发行了1 500万股本公司普通股〔每股面值l元〕作为对价。
假定A、B公司采用的会计政策相同。
合并日,A公司及B公司的所有者权益构成如下:表1 单位:万元A公司在合并日应进行的会计处理为:【拓展】①在合并工作底稿中,应编制以下调整分录:借:资本公积30 000 000贷:盈余公积l0 000 000未分配利润20 000 000②在编制合并日合并资产负债表时编制的抵销分录:借:股本 1 500资本公积500盈余公积 1 000未分配利润 2 000贷:长期股权投资 5 000【例2.3】20X7年6月30日,P公司向S公司的股东定向增发1 000万股普通股〔每股面值为1元,市价为10.85元〕对S公司进行吸收合并,并于当日取得S公司净资产。
当日,P公司、S公司资产、负债情况如表2-1所示。
表2-1 资产负债表〔简表〕【例2.4】A公司取得B公司100% 的股权比例,形成非同一控制下的控股合并。
购买日B【例2.5】20X7年1月1日,P公司收购了S公司的全部资产,并承担S公司的全部负债。
假定P公司和S公司的合并属于非同一控制下的企业合并。
S公司20X7年1月1日的资产和负债的账面价值和公允价值见下表。
S公司的资产和负债的账面价值和公允价值〔1〕假定P公司以支付现金800 000元、发行普通股100 000股的方式换取S公司的净资产,P公司普通股每股账面价值为10元,每股市价为20元。
P公司以现金支付发行股票发生的手续费、佣金100 000元,合并过程中发生审计费用100 000元,法律服务费50 000元。
工程问题补充

工程问题在下面例题的讲述中,不完全采用通常教科书中“把工作量设为整体1”的做法,而偏重于“整数化”或“从比例角度出发”,也许会使我们的解题思路更灵活一些.一、两个人的问题标题上说的“两个人”,也可以是两个组、两个队等等的两个集体.●例1 一件工作,甲做9天可以完成,乙做6天可以完成。
现在甲先做了3天,余下的工作由乙继续完成,乙需要做几天可以完成全部工作?解一:把这件工作看作1,甲每天可完成这件工作的九分之一,做3天完成的1/3。
乙每天可完成这件工作的六分之一,(1-1/3)÷1/6=4(天)答:乙需要做4天可完成全部工作.解二:9与6的最小公倍数是18.设全部工作量是18份.甲每天完成2份,乙每天完成3份.乙完成余下工作所需时间是(18- 2 × 3)÷ 3= 4(天).解三:甲与乙的工作效率之比是6∶ 9= 2∶ 3.甲做了3天,相当于乙做了2天.乙完成余下工作所需时间是6-2=4(天).工程问题.当知道了两者工作效率之比,从比例角度考虑问题,也需时间是因此,在下面例题的讲述中,不完全采用通常教科书中“把工作量设为整体1”的做法,而偏重于“整数化”或“从比例角度出发”,也许会使我们的解题思路更灵活一些.一、两个人的问题标题上说的“两个人”,也可以是两个组、两个队等等的两个集体.●例1 一件工作,甲做9天可以完成,乙做6天可以完成。
现在甲先做了3天,余下的工作由乙继续完成,乙需要做几天可以完成全部工作?解一:把这件工作看作1,甲每天可完成这件工作的九分之一,做3天完成的1/3。
乙每天可完成这件工作的六分之一,(1-1/3)÷1/6=4(天)答:乙需要做4天可完成全部工作.解二:9与6的最小公倍数是18.设全部工作量是18份.甲每天完成2份,乙每天完成3份.乙完成余下工作所需时间是(18- 2 × 3)÷ 3= 4(天).解三:甲与乙的工作效率之比是6∶ 9= 2∶ 3.甲做了3天,相当于乙做了2天.乙完成余下工作所需时间是6-2=4(天).●例4一件工程,甲队单独做10天完成,乙队单独做30天完成.现在两队合作,其间甲队休息了2天,乙队休息了8天(不存在两队同一天休息).问开始到完工共用了多少天时间?解一:甲队单独做8天,乙队单独做2天,共完成工作量余下的工作量是两队共同合作的,需要的天数是2+8+ 1= 11(天).答:从开始到完工共用了11天.解二:设全部工作量为30份.甲每天完成3份,乙每天完成1份.在甲队单独做8天,乙队单独做2天之后,还需两队合作(30- 3 × 8- 1× 2)÷(3+1)= 1(天).解三:甲队做1天相当于乙队做3天.在甲队单独做8天后,还余下(甲队)10-8= 2(天)工作量.相当于乙队要做2×3=6(天).乙队单独做2天后,还余下(乙队)6-2=4(天)工作量.4=3+1,其中3天可由甲队1天完成,因此两队只需再合作1天.解四:方法:分休合想(题中说甲乙两队没有在一起休息,我们就假设他们在一起休息.)甲队每天工作量为1/10,乙为1/30,因为甲休息了2天,而乙休息了8天,因为8>2,所以我们假设甲休息两天时,乙也在休息。
补充例题
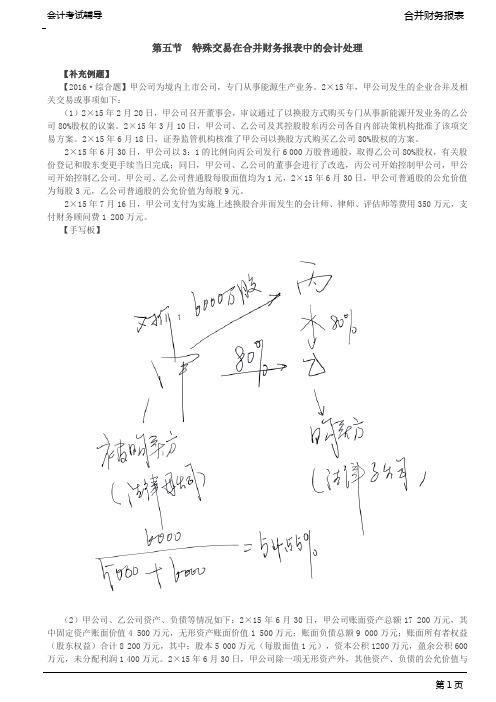
第五节特殊交易在合并财务报表中的会计处理【补充例题】【2016·综合题】甲公司为境内上市公司,专门从事能源生产业务。
2×15年,甲公司发生的企业合并及相关交易或事项如下:(1)2×15年2月20日,甲公司召开董事会,审议通过了以换股方式购买专门从事新能源开发业务的乙公司80%股权的议案。
2×15年3月10日,甲公司、乙公司及其控股股东丙公司各自内部决策机构批准了该项交易方案。
2×15年6月18日,证券监管机构核准了甲公司以换股方式购买乙公司80%股权的方案。
2×15年6月30日,甲公司以3:1的比例向丙公司发行6 000万股普通股,取得乙公司80%股权,有关股份登记和股东变更手续当日完成;同日,甲公司、乙公司的董事会进行了改选,丙公司开始控制甲公司,甲公司开始控制乙公司。
甲公司、乙公司普通股每股面值均为1元,2×15年6月30日,甲公司普通股的公允价值为每股3元,乙公司普通股的公允价值为每股9元。
2×15年7月16日,甲公司支付为实施上述换股合并而发生的会计师、律师、评估师等费用350万元,支付财务顾问费1 200万元。
【手写板】(2)甲公司、乙公司资产、负债等情况如下:2×15年6月30日,甲公司账面资产总额17 200万元,其中固定资产账面价值4 500万元,无形资产账面价值1 500万元;账面负债总额9 000万元;账面所有者权益(股东权益)合计8 200万元,其中:股本5 000万元(每股面值1元),资本公积1200万元,盈余公积600万元,未分配利润1 400万元。
2×15年6月30日,甲公司除一项无形资产外,其他资产、负债的公允价值与其账面价值相同,该无形资产为一项商标权,账面价值1 000万元,公允价值3 000万元,按直线法摊销,预计尚可使用5年,预计净残值为零。
2×15年6月30日,乙公司账面资产总额34 400万元,其中固定资产账面价值8 000万元,无形资产账面价值3 500万元;账面负债总额13 400万元;账面所有者权益(股东权益)合计21 000万元,其中,股本2 500万元(每股面值1元),资本公积500万元,盈余公积1 800万元,未分配利润16 200万元。
统计学统计综合指标补充例题

第四章统计综合指标(五)计算题例1、某集团公司所属各拖拉机厂某月生产情况如下表所示:厂别类型每台马力数产量(台)第1厂履带式36 75履带式18 105轮式28 400 第2厂履带式75 85轮式15 94轮式12 150 第3厂履带式45 40履带式75 25轮式24 50 要求按产品类型和功率核算有关总量指标。
解:【分析】通常总量指标中首选核算实物量。
这里可以核算自然实物量、双重单位实物量和标志单位实物量。
从下面两表看出核算的过程及结果:(1)按自然单位和双重单位核算:产品类型产量(台)产量(台/马力)履带式330 330/14640轮式694 694/15610合计1024 1024/30250 (2)按标准单位核算(以15马力拖拉机为标准单位):产品类型与功率产量(台)换算系数标准台数(1)(2)(3)=(1)÷15 (4)=(2)×(3)履带式18马力105 12636马力75 18045马力40 12075马力110 550小计330 —976轮式12马力150 12015马力94 9424马力50 8028马力400 747小计694 —1041合计1024 —2017例2、下面是某市年末户籍人口和土地面积的资料:单位:人户籍人口数2001年 2002年 人口总数男 女1343599 682524 6610751371588 695762 675826已知该土地面积1565平方公里,试计算全部可能计算的相对指标,并指出它们属于哪一种相对数。
解:计算结果列表如下:2001年 2002年 人口总数男 女(1)男性人口占总人口比重(%) (2)女性人口占总人口比重(%) (3)性别比例(%)男:女 (4)人口密度(人/平方公里)(5)人口增长速度(%) 1343599 682524 661075103 858 —1371588 695762 675826102 876在所计算的相对指标中:(1)、(2)为结构相对数,(3)为比例相对数,(4)为强度相对数,(5)为动态相对数。
《高等数学》(一)(2)补充例题及练习题

第八章 空间解析几何与向量代数(6学时)§8.1 向 量 及 其 线 性 运 算一、补充例题例1 已知向量)1,5,3(-=a ,)3,2,2(=b ,)3,1,4(--c,求c b a 432+-。
例2 在yOz 面上,求与三点)2,1,3(A 、)2,2,4(--B 和)1,5,0(C 等距离的点。
例3 已知两点)1,3,2(-A 和)0,2,1(-B ,求与方向相同的单位向量e。
例4 已知两点)2,1,1(-A 和)3,1,0(B ,计算向量的模、方向余弦和方向角。
例5 一向量的终点在点)7,1,2(-B ,它在x 轴、y 轴和z 轴上的投影依次为4,4-和7。
求这向量的起点A 的坐标。
二、练习1312-p 习题8-1 4,5,15,17§8.2 向量的数量积与向量积一、补充例题例1 已知j i a += ,k i b += ,求b a ⋅,∧),(cos b a 及a j bPr 。
例2 已知四点)1,2,2(A 、)2,1,0(B 、)1,1,1(C 、)2,3,3(D ,求AB j CDPr ,∧),(cos 。
例3 记)0,1,3(-=a,)1,2,1(-=b,求b a⨯。
例4 已知ABC ∆的三个顶点为)2,0,3(A ,)1,3,5(B ,)3,1,0(-C ,(1)求垂直于这个三角形所在平面的单位向量;(2)求ABC ∆的面积。
解 (1)因为a ⨯= 垂直于向量与,所以a是一个垂直于三角形ABC 所在平面的向量。
而)1,3,2(-=,)1,1,3(--=,所以k j i kj i a72113132++=---=⨯=。
63712222=++=a ,)7,1,2(631=a e。
所以垂直于三角形ABC 所在平面的单位向量为)7,1,2(631±。
(2)因为ABC ∆的面积S 是以AB ,AC 为邻边的平行四边形面积的一半,所以6237122121222=++===a S 。
理论力学参考补充例题2

CD杆:
mC (F) 0, FDy 2a FDx 2a F a 0 (1)
例:正方体各边长均为a,作用有 F1 , F2 , F3 ,如图所示。 且三力大小均为F,求此力系向O点简化的结果。
解:
F1x F1y
3 3
F1
3F 3
3
3
F1z 3 F1 3 F,
F2x 0
F2 y F2z
2 F, 2
x
z
F1
o
F3
y
F2
2 F3x F3z 2 F ,
2 2
FR, i FR, j 45o
主矩:
y
F2 450
FR
F1
1 2
(2,2)
x
(-3,0) O
(0,-3)
M
F3
Mo
M
F1
2 5
2
F1
1 5
2
F3
3
F2
cos
450
3
100 200 300 300 100N m
解:(1)将平面力系向O点简化
主矢: FRx ' Fx F2 F1 cos600 250N C F2
FRy ' Fy F1 sin 600 F3
100 3 400 486.6N 2
F1
A
O
M
F3
x B
FR ' FRx ' FRy ' 2502 486.62 512.23N
《数论》第一章补充例题

整除理论补充例题∗彭道意†September 27,2013整除性理论是初等数论的基础.本章要介绍带余数除法,辗转相除法,最大公约数,最小公倍数,算术基本定理以及它们的一些应用.1整数的整除性例1设A ={d 1,d 2,···,d k }是n 的所有约数的集合,则B ={n d 1,n d 2,···,n d k}也是n 的所有约数的集合.解由以下三点理由可以证得结论:(i)A 和B 的元素个数相同;(ii)若d i ∈A ,即d i |n,则n d i |n,反之亦然;(iii)若d i =d j ,则n d i =n d j .例2以d (n )表示n 的正约数的个数,例如:d (1)=1,d (2)=2,d (3)=2,d (4)=3,···.问:d (1)+d (2)+···+d (1997)是否为偶数?解对于n 的每个约数d ,有n =d ·n d ,因此,n 的正约数d 与n d 是成对地出现的.只有当d =n d ,即d =n 2时,d 和n d 才是同一个数.故当且仅当n 是完全平方数时,d (n )是奇数.因为442<1997<452,所以在d (1),d (2),···,d (1997)中恰有44个奇数,故d (1)+d (2)+···+d (1997)是偶数.问题d 2(1)+d 2(2)+···+d 2(1997)被4除的余数是多少?例3证明:存在无穷多个正整数a ,使得n 4+a (n =1,2,3,···)都是合数.∗例题中引用的定理或推论可以在教材相应处找到.本文仅供参考,不足与错误难免,请同学们批评指正!†Email:daoyi123@解取a=4k4,对任意的n∈N,有n4+4k4=(n2+2k2)2−4n2k2=(n2+2k2+2nk)(n2+2k2−2nk).由n2+2k2−2nk=(n−k)2+k2 k2,所以,对于任意的k=2,3,···以及任意的n∈N,n4+a是合数.例4设a1,a2,···,a n是整数,且n∑k=1a k=0,n∏k=1a k=n,则4|n.解如果2 n,则n,a1,a2,···,a n都是奇数.于是a1+a2+···+a n是奇数个奇数之和,不可能等于零,这与题设矛盾,所以2|n,即在a1,a2,···,a n中至少有一个偶数.如果只有一个偶数,不妨设为a1,那么2 a i(2 k n).此时有等式a2+···+a n=−a1,在上式中,左端是(n−1)个奇数之和,右端是偶数,这是不可能的,因此,在a1,a2,···,a n中至少有两个偶数,即4|n.例5若n是奇数,则8|n2−1.解设n=2k+1,则n2−1=(2k+1)2−1=4k(k+1),在k与k+1中有一个偶数,所以8|n2−1.2带余数除法例1设a,b,x,y是整数,k和m是正整数,并且a=a1m+r1,0 r1<m,b=b1m+r2,0 r2<m,则ax+by和ab被m除的余数分别与r1x+r2y和r1r2被m除的余数相同.特别地,a k与r k1被m除的余数相同.解由ax+by=(a1m+r1)x+(b1m+r2)y=(a1x+b1y)m+r1x+r2y可知,若r1x+r2y被m除的余数是r,即r1x+r2y=qm+r,0 r<m,则ax+by=(a1x+b1y+q)m+r,0 r<m,即ax+by被m除的余数也是r.例2设a1,a2,···,a n为不全为零的整数,以y0表示集合A={y|y=a1x1+···+a n x n,x i∈Z,1 i n}中的最小正数,则对任何的y∈A,y0|y;特别地,y0|a i,1 i n.解设y0=a1x′1+···+a n x′n,∀y∈A,由带余除法,∃q,r0∈Z,使得y=qy0+r0,0 r0<y0.因此r0=y−qy0=a1(x1−qx′1)+···+a n(x n−qx′n)∈A.如果r0=0,那么,因为0<r0<y0,所以r0是A中比y0还小的正数,这与y0的定义矛盾.所以r0=0,即y0|y.显然a i∈A(1 i n),所以y0整除每个a i(1 i n).例3任意给出的五个整数中,必有三个数之和被3整除.解设这五个数是a i,i=1,2,3,4,5,记a i=3q i+r i,0 r i<3,i=1,2,3,4,5.分别考虑以下两种情形:(i)若r1,r2,···,r5中数0,1,2都出现,不妨设r1=0,r2=1,r3=2,此时a1+a2+a3=3(q1+q2+q3)+3可以被3整除;(ii)若r1,r2,···,r5中数0,1,2至少有一个不出现,这样至少有三个r i要取相同的值,不妨设r1,r2,r3=r(r=0,1或2),此时a1+a2+a3=3(q1+q2+q3)+3r可以被3整除.例4设a0,a1,···,a n∈Z,f(x)=a n x n+···+a1x+a0,已知f(0)与f(1)都不是3的倍数,证明:若方程f(x)=0有整数解,则3|f(−1)=a0−a1+a2−···+(−1)n a n.证对任意整数x,都有x=3q+r,r=0,1或2,q∈Z.(i)若r=0,即x=3q,q∈Z,则f(x)=f(3q)=a n(3q)n+···+a1(3q)+a0=3Q1+a0=3Q1+f(0),其中Q1∈Z,由于f(0)不是3的倍数,所以f(x)=0;(ii)若r=1,即x=3q+1,q∈Z,则f(x)=f(3q+1)=a n(3q+1)n+···+a1(3q+1)+a0=3Q2+a n+···+a1+a0=3Q2+f(1),其中Q2∈Z.由于f(1)不是3的倍数,所以f(x)=0.因此若f(x)=0有整数解x,则必是x=3q+2=3q′−1,q′∈Z,于是0=f(x)=f(3q′−1)=a n(3q′−1)n+···+a1(3q′−1)+a0=3Q3+a0−a1+a2−···+(−1)n a n.其中Q3∈Z.所以3|f(−1)=a0−a1+a2−···+(−1)n a n.例5设n是奇数,则16|n4+4n2+11.证我们有n4+4n2+11=(n2−1)(n2+5)+16.由上节例题知道,8|n2−1,由此及2|n2+5得到16|(n2−1)(n2+5).例6证明:若a被9除的余数是3,4,5或6,则方程x3+y3=a没有整数解.证∀x,y∈Z,记x=3q1+r1,y=3q2+r2,0 r1,r2<3.则存在Q1,R1,Q2,R2∈Z,使得x3=9Q1+R1,y3=9Q2+R2,其中R1和R2被9除的余数分别与r31和r32被9除的余数相同,即R1=0,1或8,R2=0,1或8.因此x3+y3=9(Q1+Q2)+R1+R2.(2.1)又由式(2.1)可知,R1+R2被9除的余数只可能是0,1,2,7或8,所以,x3+y3不可能等于a.例7证明:方程a21+a22+a23=1999(2.2)无整数解.证若a1,a2,a3都是奇数,则存在整数A1,A2,A3,使得a21=8A1+1,a22=8A2+1,a23=8A3+1,于是a21+a22+a23=8(A1+A2+A3)+3.由于1999被8除的余数是7,所以a1为奇数.由式(2.2),a1,a2,a3中只有一个奇数,设a1为奇数,a2,a3为偶数,则存在整数A1,A2,A3,使得a21=8A1+1,a22=8A2+r,a23=8A3+s,于是a21+a22+a23=8(A1+A2+A3)+1+r+s,其中r和s是整数,而且只能取值0或4.这样a21+a22+a23被8除的余数只可能是1或5,但1999被8除的余数是7,所以这样的a1,a2,a3也不能使式(2.2)成立.3最大公约数例1(105,140,350)=(105,(140,350))=(105,70)=35.例2证明:若n是正整数,则21n+414n+3是既约分数.证由辗转相除法得到(21n+4,14n+3)=(7n+1,14n+3)=(7n+1,1)=1. 4辗转相除法例1用辗转相除法求(125,17),以及x,y,使得125x+17y=(125,17).解作辗转相除法:125=7×17+6,q1=7,r1=6,17=2×6+5,q2=2,r2=5,6=1×5+1,q3=1,r3=1,5=5×1,q4=5.由推论1.1,(125,17)=r3=1.利用定理1计算(这里n=3)P0=1,P1=7,P2=2·7+1=15,P3=1·15+7=22,Q0=0,Q1=1,Q2=2·1+0=2,Q3=1·2+1=3,取x=(−1)3−1Q3=3,y=(−1)3P3=−22,则125·3+17·(−22)=(125,17)=1.例2在m个盒子中放若干个硬币,然后以下述方式往这些盒子里继续放硬币:每一次在n(n<m)个盒子中各放一个硬币.证明:若(m,n)=1,那么无论开始时每个盒子中有多少个硬币,经过若干次放硬币后,总可使所有盒子含有同样数量的硬币.证由于(m,n)=1,所以存在整数x,y,使得mx+ny=1.因此对于任意的自然数k,有1+m(−x+kn)=n(km+y),这样,当k充分大时,总可找出正整数x0,y0,使得1+mx0=ny0.上式说明,如果放y0次(每次放n个),那么在使m个盒子中各放x0个后,还多出一个硬币.把这个硬币放入含硬币最少的盒子中(这是可以做到的),就使它与含有最多硬币的盒子所含硬币数量之差减少1.因此经过若干次放硬币后,必可使所有盒子中的硬币数量相同.5素数与算术基本定理例1写出51480的标准分解式.解我们有51480=2·25740=22·12870=23·6435=23·5·1287=23·5·3·429=23·5·32·143=23·32·5·11·13.例2设a,b,c是整数,证明:(i)(a,b)[a,b]=ab;(ii)(a,[b,c])=[(a,b),(a,c)].证为了叙述方便,不妨假定a,b,c是正整数.(i)设a=pα11pα22···pαk k,b=pβ11pβ22···pβk k,其中p1,p2,···,p k是互不相同的素数,αi,βi(1 i k)都是非负整数.由推论3.3,有(a,b)=pλ11pλ22···pλk k,λi=min{αi,βi},1 i k,[a,b]=pµ11pµ22···pµk k,µi=max{αi,βi},1 i k.由此知(a,b)[a,b]=k∏i=1pλi+µii=k∏i=1p min{αi,βi}+max{αi,βi}i=k∏i=1pαi+βii=ab;(ii)设a=k∏i=1pαii,b=k∏i=1pβii,c=k∏i=1pγii,其中p1,p2,···,p k是互不相同的素数,αi,βi,γi(1 i k)都是非负整数.由推论3.3,有(a,[b,c])=k∏i=1pλii,[(a,b),(a,c)]=k∏i=1pµii,其中,对于1 i k,有λi=min{αi,max{βi,γi}},µi=max{min{αi,βi},min{αi,γi}},不妨设βi γi,则min{αi,βi} min{αi,γi},所以µi=min{αi,γi}=λi,即(a,[b,c])=[(a,b),(a,c)].。
财务管理第二章课后补充习题及课堂例题及答案(学生版)

第二章财务管理的价值观念课后补充计算题:1、某人希望以8%的年利率,按每半年付款一次的方式,在3年内等额偿还现有的6 000元债务,问每次应偿还多少?2、一农户购置了一台新收割机,他估计新机器头两年不需要维修,从第3年末开始的10年中,每年需支付200元维修费,若折现率为3%,问10年维修费的现值为多少?3、某人在2000年1月1日存入银行1000元,年利率为10%。
要求计算:(1)每年复利一次,2003年1月1日存款账户余额是多少?(2)每季度复利一次,2003年1月1日存款账户余额是多少?(3)若1000元,分别在2000年、2001年、2002年和2003年1月1日存入250元,仍按10%利率,每年复利一次,求2003年1月1日余额?(4)假定分4年存入相等金额,为了达到第一问所得到的账户余额,每期应存入多少金额?(5)假定第三问为每季度复利一次,2003年1月1日余额是多少?(6)假定第四问改为每季度复利一次,每年应存入多少金额?4、某人拟明年年初借款42000元,从明年年末开始,每年年末还本付息6000元,连续10年还清,设预定最低借款利率为8%,问此人是否能按计划借到款项?5、有人在今后五年中每年末借给你2 500元,要求你在随后的10年中,每年末归还2 500元于他,若年利率为5%,问你是否接受这笔借款?6、某工商管理研究生计划从银行借款10 000元,利率12%,半年计息一次。
这笔借款在四年内分期等额摊还,每半年还款一次。
第一次还款是从今天起的6个月后,问:(1)贷款的实际年利率是多少?(2)计算每半年应付的偿还额。
(3)计算第二个半年所付的本金和利息。
7、某公司准备投资开发新产品,现有三个方案可供选择。
根据市场预测,三种不同市场状况的预计年报酬率如下表:试计算投资开发各种新产品的风险大小。
8、某公司去年支付的股利为每股1元,一位投资者预计公司股利按固定比率5%增长,该公司股票的β系数为 1.5,无风险利率为8% ,所有股票的平均报酬率为15%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FBx θ FBy
B
1 1 FBx Rc sin qL sin 2 P sin 2 2 4
F
y
0 :Rc cos FBy q 2L 0
1 2 FBy q 2 L Rc cos P(1 cos ) 2
再分析AC悬臂梁:
M F Ax F Ay
杆件内力为正,表示杆件受拉;负号表示杆件受压。
补例 多跨静定梁的平衡。图示多跨静定梁,由主梁 AB和次梁BC铰接而成。已知 qD 9kN / m,m 4kN m 试求A,B,C,D处的约束反力。
m
m
m
解:受力图如图:
1.取次梁BC为研究 对象,B处的线荷载 集度为 :4 列出平衡方程 :
解出:
P YF 1.5kN () 2
代入前式求得:
X F qa 2.5kN()
2. 再研究基本部分ABC三铰刚架,受力图如图(d)
(d)
(e)
列平衡方程:
m (F ) 0 :
A i
YB 4a X F '2a 0
解得:
X F ' qa YB 1.25kN () 2 2
Qmin
如果先求出ND,则可由
m
B
(F ) 0
求出:
Qmin
(a)
1. 先研究两球组成的附属部分,画出其受力图, 如图(b)所示。
(b)
列出平衡方程:
Y
2.
i
0,N D P P 0
N D 2 P()
再研究系统整体,其受力图如图(b),
列出平衡方程,并利用不倾翻的条件:
RC q=P/2L
M=PL C
A L D L 2L θ B
q=P/2L
首先研究斜梁BC:
m
FBx θ FBy
B
B
(F ) 0 :
Rc 2 L q 2 L L cos 0 1 Rc qL cos P cos 2
RC
q=P/2L
F
x
0:
Rc sin FBx 0
1 mA ( Fi ) 0 : P cos(600 ) 2 P[l cos l cos(600 )] 0 2
2 cos 2.5(cos 60 cos sin 60 sin ) 0
0 0
3 tg 0.346 5
19 16
补例11:平面机构ABCD中的AB=0.1m,CD=0.22m,杆AB
及CD上各作用一力偶,在图示位置平衡,已知
m1 0.4 N m
杆重不计,求A、D两铰处的约束力及力偶矩 m2
C B m1 A 60
0
30
0
m2 45
0
D
解:观察AB杆平衡,受力如图(a):
S BC
B m1 600 300
N A 0,Q Qmin
m
B
( Fi ) 0 : P r ( P N D ) (2 R r ) Qmin R 0
解得:
Qmin
2( R r ) P R
()
显然,筒不可能绕A边倾翻。
补例:图示结构自重与摩擦不计,已知:L、θ、M、 q。试求支座A、B的约束反力。 解:分别取斜梁和悬臂梁为 研究对象,受力分析如图:
A i B
3m
3m
4m
解得:
F
4m 3m 3m 4m
F
FB 80kN()
3m
2. 从C和E处拆开,取BCE部分为研究对象,画出 受力图如图(b),列平衡方程:
m (F ) 0 :
C i
FB 7 70 3 FN 3 3 0
解得:
F F F 70kN F
FN 3 116.7kN()
FA FA FD
m m m
q B q D 6kN / m 6
0 : Fx B 0 ( Fi ) 0 :
FC
F m
FB FB FC
xi B
1 4 FC 4 qB 4 0, FC 4kN () 2 3 1 Fyi 0 : Fy B FC 2 qB 4 0, Fy B 8kN ()
Q
E
W
C
解:从BC取开,受力分析如图:
x A
a o
FBY
B
,
Q , FBx FBY RC
C E
Fox FoY W
FBx
首先考虑BCE:
y 0,F
m1 ,m2 ,m 均在x,y平面内如图所示。
m1 20 0.25 5N m m2 30 0.2 6 N m
4 mx m cos m1 cos m2 (1 5) 6 9.2 N m 5 3 m y m sin m1 sin (1 5) 3.6 N m 5 mz 0
倾翻问题. 进行受力分析时,应利用欲倾翻时,有些约束被解脱 的特点。 分析系统整体,当球太重,筒太轻时,圆通由可能绕 B翻倒。刚要翻倒时,A处约束已解脱,其约束反力NA为 零,画出其受力图,如图(a)所示。
系统受已知力P及三个未知力 :
R
R
Qmin N D,N B
是平面平行力系的平衡问题, 只有两个平衡方程, 无法直接求出
F1 20 N,F2 30 N,F3 50 N
m=1N· 求力偶与三个力合成的结果。 m
解:将 F 3 分解为 F 1 F 2,见图(a) F1 20 N,F2 30 N 与
这样三个力与力偶m的合成可看成为力偶 ( F 1, 1 )、 2,F2 ) F (F 与力偶m的合成。以上三力偶用矩矢表示 m1 ,m2 ,m
2.取整体为研究对象, F A 列平衡方程:
FA
FX i 0 : FX A 0
FD
m m m
FC
1 6 mD ( Fi ) 0 : FC 6 m 2 qD 6 3 FY A 4 0 FY A 6.5kN ()
Y 0 :
i
1 FY A FD FC qD 6 0 2 FD 29.5kN ()
SBC C
m2 45
0
RA
A
D
RD
(a) (b)
S AB 与 R A 组成力偶与 m1 平衡,由
m
0
i
0
S AB d m1 0
d AB sin 30 0.05m
S AB
m1 0.4 8N d 0.05
其次观察杆CD,受力如图(b)所示,由
m
i
0 m2 S d 0 AB
2
补例 混合结构的平衡厂房组合桁架的荷载及尺寸 如图(a)所示,长度单位为m。若不计各构件重量, 试求1、2、3杆的内力。 解:
3m 3m 4m
1.先研究组合
3m
4m 3m 3m 4m
桁架整体,
画出受力图,
如图(a)所示,
列出平衡方程:
m (F ) 0: F 14 60 3 40 6 70 10 0
S S AB AB
CD sin 750 0.22 0.9659 0.2125m d
m2 S d 8 0.2125 1.70 Nm AB
RD S S AB 8N AB
补例12:
沿正六面体的三棱边作用着三个力,在平面OABC 内作用一个力偶。已知
q 1kN / m,P 3kN,a 2.5m
试求铰链G、I和B的约束反力。
(a) a a 2a 2a 2a
2a
2a
解:这是一个由基本部分三铰刚架ABC和两个附属的
三铰刚架DEF和GHI所组成的系统。
受力分析如图: 首先分析HC部分,HI为二力杆,
m (F ) 0 : R x 0: X 0 y 0: Y 0
m
A
0 : M A Rc cos 2 L M 0 M A 2 Rc L cos PL PL(1 cos 2 )
x 0:
y 0:
1 FAX Rc sin 0 FAx P sin 2 4 1 FAy Rc cos 0 FAy P cos 2 2
G i
HI
0
G
G
再分析DEFHC部分,
选二未知力的交点D为矩心, 列出平衡方程:
2a
m
D
( Fi ) 0 :
(b)
YF 2a X F 2a P a q 2a a 0
2a
然后研究EF,受力图如图,
列出平衡方程:
m
E
( Fi ) 0 :
YF 2a P a 0
0
补例4
在水平单伸梁上作用有集中力偶和梯形线
荷载,如图,已知m=60kN· m,
q A 4kN / m,qB 2kN / m,l 2m, 300
试求B,C支座反力。
3
4
解:
研究AC梁,画出其受力图,如图5—7所示。在列
平衡方程时,梯形线荷可视为荷载集度为qB的匀布荷载
上,叠加一三角形荷载组成,分别求得这两个线荷载的
补例3
匀质杆AB和BC在B端刚结, A端用绳悬挂,
如图。已知: BC
水平面的倾角θ 。
2 AB
求当刚杆ABC平衡时,BC与
解:研究刚杆ABC的平衡,设杆 AB重P,长L,则杆BC重2P,长 2L。画出杆的受力图,如图所示。 这是平面平行力系的平衡问题,
