最新流体力学题解
(完整版)流体力学习题解析
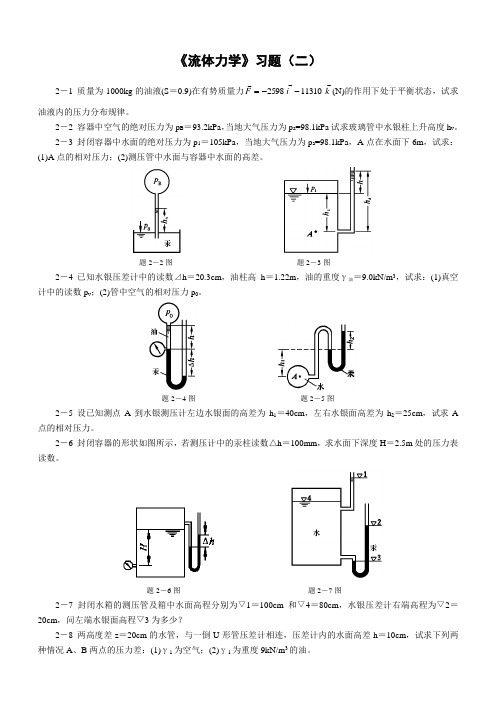
《流体力学》习题(二)2-1 质量为1000kg 的油液(S =0.9)在有势质量力k i F 113102598--=(N)的作用下处于平衡状态,试求油液内的压力分布规律。
2-2 容器中空气的绝对压力为p B =93.2kPa ,当地大气压力为p a =98.1kPa 试求玻璃管中水银柱上升高度h v 。
2-3 封闭容器中水面的绝对压力为p 1=105kPa ,当地大气压力为p a =98.1kPa ,A 点在水面下6m ,试求:(1)A 点的相对压力;(2)测压管中水面与容器中水面的高差。
题2-2图 题2-3图 2-4 已知水银压差计中的读数⊿h =20.3cm ,油柱高h =1.22m ,油的重度γ油=9.0kN/m 3,试求:(1)真空计中的读数p v ;(2)管中空气的相对压力p 0。
题2-4图 题2-5图 2-5 设已知测点A 到水银测压计左边水银面的高差为h 1=40cm ,左右水银面高差为h 2=25cm ,试求A 点的相对压力。
2-6 封闭容器的形状如图所示,若测压计中的汞柱读数△h =100mm ,求水面下深度H =2.5m 处的压力表读数。
题2-6图 题2-7图 2-7 封闭水箱的测压管及箱中水面高程分别为▽1=100cm 和▽4=80cm ,水银压差计右端高程为▽2=20cm ,问左端水银面高程▽3为多少?2-8 两高度差z =20cm 的水管,与一倒U 形管压差计相连,压差计内的水面高差h =10cm ,试求下列两种情况A 、B 两点的压力差:(1)γ1为空气;(2)γ1为重度9kN/m 3的油。
题2-8图题2-9图2-9 有一半封闭容器,左边三格为水,右边一格为油(比重为0.9)。
试求A、B、C、D四点的相对压力。
2-10 一小封闭容器放在大封闭容器中,后者充满压缩空气。
测压表A、B的读数分别为8.28kPa和13.80kPa,已知当地大气压为100kPa,试求小容器内的绝对压力。
流体力学计算题及问题详解

第二章例1:用复式水银压差计测量密封容器内水面的相对压强,如下列图。
:水面高程z 0=3m,压差计各水银面的高程分别为z 1=, z 2=, z 3=m, z 4=m, 水银密度 3/13600m kg ρ=',水的密度3/1000m kg ρ= 。
试求水面的相对压强p 0。
解:ap z z γz z γz z γp =-----+)(')(')(3412100)()('1034120z z γz z z z γp ---+-=∴例2:用如下列图的倾斜微压计测量两条同高程水管的压差。
该微压计是一个水平倾角为θ的Π形管。
测压计两侧斜液柱读数的差值为L=30mm ,倾角θ=30∘,试求压强差p 1 – p 2 。
解: 224131)()(p z z γz z γp =-+-- θL γz z γp p sin )(4321=-=-∴例3:用复式压差计测量两条气体管道的压差〔如下列图〕。
两个U 形管的工作液体为水银,密度为ρ2 ,其连接收充以酒精,密度为ρ1 。
如果水银面的高度读数为z 1 、 z 2 、 z 3、z 4 ,试求压强差p A – p B 。
解: 点1 的压强 :p A )(21222z z γp p A --=的压强:点)()(33211223z z γz z γp p A -+--=的压强:点 B A p z z γz z γz z γp p =---+--=)()()(3423211224 )()(32134122z z γz z z z γp p B A ---+-=-∴例4:用离心铸造机铸造车轮。
求A-A 面上的液体总压力。
解: C gz r p +⎪⎭⎫ ⎝⎛-=2221ωρ a p gz r p +⎪⎭⎫ ⎝⎛-=∴2221ωρ在界面A-A 上:Z = - ha p gh r p +⎪⎭⎫⎝⎛+=∴2221ωρ⎪⎭⎫⎝⎛+=-=∴⎰2420218122)(ghR R rdr p p F a Rωπρπ例5:在一直径d= 300mm ,而高度H=500mm 的园柱形容器中注水至高度h 1 = 300mm ,使容器绕垂直轴作等角速度旋转。
《流体力学》课后习题答案详解

习题【1】1-1 解:已知:120t =℃,1395p kPa '=,250t =℃ 120273293T K =+=,250273323T K =+= 据p RT ρ=,有:11p RT ρ'=,22p RT ρ'= 得:2211p T p T '=',则2211323395435293T p p kPa T ''=⋅=⨯=1-2 解:受到的质量力有两个,一个是重力,一个是惯性力。
重力方向竖直向下,大小为mg ;惯性力方向和重力加速度方向相反为竖直向上,大小为mg ,其合力为0,受到的单位质量力为01-3 解:已知:V=10m 3,50T ∆=℃,0.0005V α=℃-1根据1V V V Tα∆=⋅∆,得:30.000510VVV Tα∆=⋅⋅∆=⨯⨯1-4 解:已知:419.806710Pa p '=⨯,52 5.884010Pa p '=⨯,150t =℃,278t =℃得:1127350273323T t K=+=+=,G =mg自由落体: 加速度a =g2227378273351T t K =+=+=根据mRTp V=,有:111mRT p V '=,222mRT p V '=得:421251219.8067103510.185.884010323V p T V p T '⨯=⋅=⨯='⨯,即210.18V V = 体积减小了()10.18100%82%-⨯=1-5 解:已知:40mm δ=,0.7Pa s μ=⋅,a =60mm ,u =15m/s ,h =10mm根据牛顿内摩擦力定律:uT Ayμ∆=∆ 设平板宽度为b ,则平板面积0.06A a b b =⋅=上表面单位宽度受到的内摩擦力:1100.70.06150210.040.01T A u b N b b h b μτδ-⨯-==⋅=⨯=--/m ,方向水平向左下表面单位宽度受到的内摩擦力: 2200.70.061506300.010T A u b N b b h b μτ-⨯-==⋅=⨯=--/m ,方向水平向左平板单位宽度上受到的阻力:12216384N τττ=+=+=,方向水平向左。
流体力学考试题及答案

流体力学考试题及答案一、选择题(每题2分,共20分)1. 流体力学中,流体的基本假设是什么?A. 流体是不可压缩的B. 流体是完全弹性体C. 流体是完全塑性体D. 流体是连续介质答案:D2. 流体静力学中,压力的分布规律是什么?A. 与深度成正比B. 与深度成反比C. 与深度无关D. 与深度的平方成正比答案:A3. 流体的粘性是由什么决定的?A. 温度B. 压力C. 密度D. 以上都是答案:A4. 伯努利方程描述了什么?A. 流体的静压和动压关系B. 流体的压缩性C. 流体的粘性D. 流体的热力学性质答案:A5. 流体的雷诺数是用来描述什么的?A. 流体的密度B. 流体的粘性C. 流体的惯性力与粘性力的比值D. 流体的压缩性答案:C6. 什么是流体的不可压缩性条件?A. 密度不变B. 温度不变C. 压力不变D. 速度不变答案:A7. 流体的连续性方程描述了什么?A. 流体的动量守恒B. 流体的动能守恒C. 流体的质量守恒D. 流体的热能守恒答案:C8. 流体的湍流与层流的区别是什么?A. 湍流有粘性,层流没有B. 湍流是有序的流动,层流是无序的C. 湍流是无序的流动,层流是有序的D. 湍流和层流都是有序的流动答案:C9. 流体的边界层厚度与什么有关?A. 流体的密度B. 流体的速度C. 流体的粘性D. 流体的压缩性答案:C10. 什么是流体的临界雷诺数?A. 流体开始流动的雷诺数B. 流体从层流转变为湍流的雷诺数C. 流体达到最大速度的雷诺数D. 流体达到最大压力的雷诺数答案:B二、简答题(每题10分,共30分)1. 简述流体力学中的纳维-斯托克斯方程及其物理意义。
答案:纳维-斯托克斯方程是描述流体运动的基本方程,它将流体的动量守恒定律与流体的粘性联系起来。
方程表明,流体的加速度不仅与压力梯度有关,还与粘性力有关。
物理意义上,它描述了流体内部的动量传递过程。
2. 描述流体的粘性对流动的影响。
答案:流体的粘性对流动有显著影响。
流体力学答案解析

流体力学答案解析题目:一不可压缩流体在水平管道内作稳定流动,管道截面由圆形逐渐扩大为方形,入口直径为d,出口边长为a。
已知入口流速为v1,入口处的压力为p1,求出口处的流速v2和压力p2。
解析:首先,根据连续性方程,流体在管道内的流速和截面积之间存在以下关系:A1v1 = A2v2其中,A1和A2分别为入口和出口的截面积。
由于管道截面由圆形变为方形,我们可以分别计算两个截面的面积。
入口截面积A1 = π(d/2)^2出口截面积 A2 = a^2将上述面积代入连续性方程,得到:π(d/2)^2 v1 = a^2 v2解得:v2 = (π(d/2)^2 v1) / a^2接下来,我们应用伯努利方程,该方程描述了流体在流动过程中速度、压力和高度之间的关系。
在水平管道中,高度不变,因此伯努利方程简化为:p1/ρ + v1^2/2 = p2/ρ + v2^2/2其中,ρ为流体的密度。
将v2的表达式代入伯努利方程,得到:p1/ρ + v1^2/2 = p2/ρ + (π(d/2)^2 v1)^2 /(2a^2ρ)化简得到:p2 = p1 + ρ(v1^2 - v2^2)/2将v2的表达式代入上式,得到:p2 = p1 + ρ(v1^2 - (π(d/2)^2 v1)^2 /(2a^2ρ))/2化简得到:p2 = p1 + (ρ/2)(v1^2 - (π(d/2)^4 v1^2) / (2a^2))进一步化简得到:p2 = p1 + (ρ/2)(v1^2(1 - (π(d/2)^4) / (2a^2)))至此,我们已经求得了出口处的流速v2和压力p2。
以下是对解题过程的详细解析:1. 连续性方程的应用:连续性方程是流体力学中的一个基本原理,描述了流体在流动过程中质量守恒的关系。
在本题中,由于流体是不可压缩的,因此在流动过程中质量守恒。
根据连续性方程,我们可以求出出口处的流速v2。
2. 伯努利方程的应用:伯努利方程是流体力学中的一个重要方程,描述了流体在流动过程中速度、压力和高度之间的关系。
流体力学考试试题(附答案)剖析

可编辑修改精选全文完整版流体力学考试试题(附答案)1、如图所示,有一直径=d 12cm 的圆柱体,其质量=m 5kg ,在力=F 100N 的作用下,当淹深=h 0.5m 时,处于静止状态,求测压管中水柱的高度H 。
解: 圆柱体底面上各点所受的表压力为:3.131844/12.014.3806.951004/22=⨯⨯+=+=d mg F p g π(Pa )由测压管可得:)(h H g p g +=ρ则:84.05.0806.910003.13184=-⨯=-=h gp H gρ(m )2、为测定90º弯头的局部阻力系数,在A 、B 两断面接测压管,流体由A 流至B 。
已知管径d =50 mm ,AB 段长度L AB = 0.8 m ,流量q = 15 m 3/h ,沿程阻力系数λ=0.0285,两测压管中的水柱高度差Δh = 20 mm ,已知水银的密度为13600kg/m 3,求弯头的局部阻力系数ξ。
解:)/(12.2405.0360015422s m d q v v v v B A =⨯⨯====ππ 对A 、B 列伯努利方程:f BB B A A A h gv z g P g v z g P +++=++2222水水ρρ 2211z gPz g P z g Pz g P B B A A +=++=+水水水水ρρρρf BA h gv z g P g v z g P +++=++∴22222211水水ρρ vv v B A == 又64.005.08.00285.0)1100013600(12.202.08.92)(2)2(222)(22222221212211=--⨯⨯⨯=-∆-∆=-=∴+=+=∆-∆=-+-=+-+=∴d l h h v g g v d l h v g gv g v d l h h h h gh g z z g P P z gP z gP h f f f λρρλξξλρρρρρξλ水汞水汞水水水又3、一变直径管段AB ,内径d A =0.2m ,d B =0.4m ,高度差Δh =1m ,压强表指示p A =40kPa ,p B =70kPa ,已知管中通过的流量q v =0.2m 3/s ,水的密度ρ=1000kg/m 3,试判断管中水流的方向。
流体力学试题及答案4

流体力学试题及答案4一、选择题(每题2分,共10分)1. 流体力学中,描述流体运动的基本概念是()。
A. 质量B. 密度C. 速度D. 压力答案:C2. 流体静力学基本方程中,描述流体静压力与深度关系的公式是()。
A. P = ρghB. P = ρgh²C. P = ρgh³D. P = ρg答案:A3. 在不可压缩流体中,连续性方程表明()。
A. 质量守恒B. 能量守恒C. 动量守恒D. 角动量守恒答案:A4. 流体力学中的雷诺数是用来描述()。
A. 流体的密度B. 流体的粘度C. 流体流动的层流与湍流状态D. 流体的压缩性答案:C5. 根据伯努利方程,流体在管道中流动时,流速增加会导致()。
A. 压力增加B. 压力减小C. 温度增加D. 密度增加答案:B二、填空题(每题2分,共10分)1. 流体力学中,流体的粘性系数通常用符号________表示。
答案:μ2. 当流体流动时,如果流体的流线不相交,则该流动称为________流动。
答案:层流3. 流体力学中,流体的惯性力与流体的________和________有关。
答案:密度,速度4. 流体力学中,流体的表面张力是由分子间的________力引起的。
答案:吸引力5. 流体力学中,流体的压缩性是指流体在压力作用下体积的________。
答案:变化三、简答题(每题10分,共20分)1. 简述流体力学中的边界层概念及其重要性。
答案:边界层是指流体在固体表面附近流动时,由于粘性作用,流体速度从零逐渐增加到与主流速度相近的区域。
边界层的存在对流体的流动特性、摩擦阻力和流体的传热、传质等过程有重要影响。
2. 描述流体力学中的能量守恒定律,并给出其数学表达式。
答案:能量守恒定律表明,流体系统中能量的总量在没有外力作用的情况下是守恒的。
数学表达式为:ρu(E + p/ρ + gz) = constant,其中ρ是流体密度,u是流体速度,E是单位质量流体的内能,p是压力,g是重力加速度,z是垂直高度。
流体试题及答案

流体试题及答案一、选择题(每题2分,共10分)1. 流体力学中,流体的粘性系数表示的是:A. 流体的密度B. 流体的压缩性C. 流体的粘滞性D. 流体的可压缩性答案:C2. 流体静力学中,液体压力随深度增加而:A. 减小B. 增大C. 不变D. 先增大后减小答案:B3. 流体动力学中,伯努利方程描述的是:A. 流体的粘性B. 流体的能量守恒C. 流体的动量守恒D. 流体的热力学性质答案:B4. 流体在管道中流动时,流速增加,压力会:A. 增加B. 减小C. 不变D. 先减小后增加答案:B5. 流体力学中,雷诺数是用来判断流体流动状态的无量纲数,它与流体的:A. 密度和粘度B. 密度和流速C. 粘度和流速D. 密度、粘度和流速答案:D二、填空题(每题2分,共10分)1. 流体力学中的连续性方程表明,流体的______和______在封闭管道中是守恒的。
答案:质量流量;动量2. 当流体的雷诺数小于2000时,流体的流动状态通常被认为是______流动。
答案:层流3. 流体在管道中流动时,若管道截面突然扩大,流体的流速将会______,压力将会______。
答案:减小;增加4. 流体力学中的纳维-斯托克斯方程描述了流体的______和______。
答案:动量守恒;质量守恒5. 在流体力学中,流体的粘性系数通常用希腊字母______表示。
答案:μ三、简答题(每题5分,共20分)1. 请简述流体力学中流体的粘性对流动的影响。
答案:流体的粘性会影响流体流动的阻力和流动状态。
粘性较大的流体在流动时会产生更大的内部摩擦力,从而增加流体流动的阻力,可能导致层流转变为湍流,影响流体的流动特性和能量损失。
2. 描述流体静力学中压力分布的特点。
答案:在流体静力学中,流体的压力随深度线性增加,且在同一点处,各个方向的压力相等。
这意味着流体内部的压强仅依赖于深度和流体的密度,而与流体的流动状态无关。
3. 解释伯努利方程在流体动力学中的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-1 两高度差z =20cm 的水管,与一倒U 形管压差计相连,压差计内的1 水面高差h =10cm ,试求下列两种情况A 、B 两点的压力差:(1)γ1为空气;2 (2)γ1为重度9kN/m 3的油。
3已已知知::z=20cm ,h=10cm 。
4解析:设倒U 型管上部两流体分界点D 处所在的水平面上的5 压力为p ',BC 间的垂直距离为l ,则有6)(A z l h p p +++'=水γ;l h p p 水γγ++'=1B 7以上两式相减,得 h z h p p 1B A )(γγ-+=-水8(1) 当γ1为空气时,气柱的重量可以忽略不计,则A 、B 两点的压力差为9Pa 2943)2.01.0(9810)(B A =+⨯=+=-z h p p 水γ10(2) 当γ1为重度9kN/m 3的油时,A 、B 两点的压力差为11Pa 20431.09000)2.01.0(9810)(1B A =⨯-+⨯=-+=-h z h p p γγ水122-2 U 形水银压差计中,已知h 1=0.3m ,h 2=13 0.2m ,h 3=0.25m 。
A 点的相对压力为p A =24.5kPa ,14 酒精的比重为0.8,试求B 点空气的相对压力。
15已已知知::h 1=0.3m ,h 2=0.2m ,h 3=0.25m 。
p A =24.5kPa ,S=0.8。
16解析:因为左右两侧的U 型管,以及中部的倒U 型管17 中1、2、3点所在的水平面均为等压面,依据题意列静力学方程,得 183B 3h p p 汞γ+=, 232h p p 酒精γ-=,19221h p p 汞γ+=, 121A )(p h h p =++水γ 20将以上各式整理后,可得到B 点空气的相对压力为21Pa10906.2)]25.02.0(6.132.08.0)2.03.0[(9810105.24)()(4332221A B ⨯-=+⨯-⨯++⨯+⨯=+-+++=h h h h h p p 汞酒精水γγγ 22 以mH 2O 表示为 O mH 96.2981010906.224B-=⨯-==水γp h232-3 如图所示,一洒水车等加速度a=0.98m/s2向前平驶,求水车内自由24 表面与水平面间的夹角a ;若B 点在运动前位于水面下深为h=1.0m ,距z 轴25 为xB= -1.5m ,求洒水车加速运动后该点的静水压强。
26 272829 解:考虑惯性力与重力在内的单位质量力为(取原液面中点为坐标原点) 30X = -a ; Y=0 ;Z= -g 31代入式()dp Xdx Ydy Zdz ρ=++得: 32dp= r (-adx -gdz ) 33积分得: p= -r (ax+gz )+C34在自由液面上,有: x=z=0 ; p=p 0 35得: C= p 0 =036代入上式得: ()ap x z gγ=-+ 37B点的压强为:38 2098()9800(( 1.5)( 1.0))11270/11.2798B a p x z N m kpa g γ⋅=-+=-⨯-+-==⋅ 39自由液面方程为(∵液面上p 0=0) 40ax+gz=0 41即:420.980.19.8545z a tg xgαα=-==='=432-4 一矩形水箱长为l =2.0m ,箱中静水面比箱顶低h =0.4m ,问水箱44 运动的直线加速度多大时,水将溢出水箱? 45已已知知::l =2.0m ,h=0.4m 。
46解析:建立坐标系如图所示,水箱中水所受单位质量力分47 别为48a f -=x , 0y =f , g f -=z49代入等压面微分方程(2-13)式,积分后得等压面方程为50C z g x a =+51由边界条件:当0=x 时,0=z ,得0=C 。
将l x 21-=,h z =代入上式得加速52 度为532m/s 924.30.24.081.922=⨯⨯==-=l gh g x z a 542-5 一盛水的矩形敞口容器,沿α=30°的斜面向上作加速度运动,加速度55 a =2m/s 2,求液面与壁面的夹角θ。
56已已知知::a =2m/s 2,α=30°。
57解析:建立坐标系如图所示,容器中水所受单位质量力分58 别为592x x s /m 732.130cos 0.2cos -=⨯-=-=-=αa a f 602z z s/m 81.1081.930sin 0.2sin -=-⨯-=--=--= g a g a f α61质量力的作用线与铅直线的夹角为621.981.10732.1tg tg1z x 1===--f f β 63由于质量力与自由液面(等压面)处处正交,所以,由图可得液面与壁面的夹角64 θ为659.501.9309090=--=--=βαθ662-6 已知矩形闸门高h =3m ,宽b =2m ,上游水深h 167 =6m ,下游水深h 2=4.5m ,求:(1)作用在闸门上的总静68 水压力;(2)压力中心的位置。
69已已知知::h=3m ,h 1=6m ,h 2=4.5m ,b=2m 。
70解析:(1) 闸门左侧所受的总压力为71kN264.8732)236(9810)2(1c11=⨯⨯-⨯=-==bhhh A h P γγ72左侧压力中心到闸门中心的距离为73m 167.032)236(1232)2(121313c1xc c1D11=⨯⨯-⨯⨯=-==-=bh h h bhAh I h h e74闸门右侧所受的总压力为75kN 58.76132)235.4(9810)2(2c22=⨯⨯-⨯=-==bh h h A h P γγ76右侧压力中心到闸门中心的距离为77m 25.032)235.4(1232)2(121323c2xc c2D22=⨯⨯-⨯⨯=-==-=bh h h bhAh I h h e78闸门所受的总压力为79kN 29.8858.17687.26421=-=-=P P P80总压力的方向指向右侧。
81(2) 为求压力中心的位置,设总压力的作用点距底部O 点的距离为a ,对O 点82 取矩,得83)2()2(2211e h P e hP Pa ---=84则85m 5.129.88)25.023(58.176)167.023(87.264)2()2(2211=-⨯--⨯=---=P e h P e h P a8687 2-7 已知矩形平面h=1m ,H=3m ,b=5m ,求F 的大小及作用点。
8889 解:1、解析法90c o o H h H h 3131F h A (h)b 9800(1)5392KN 2sin 302sin 30----=γ=γ+⨯⨯=⨯+⨯⨯= 9133o c c p c o c c o o12H h 5()1b ()112I h 12213sin 302y y m h 122H h y A sin 3035b 211sin 30sin 3022-⨯⨯⨯⨯=+=+=+=-⨯⨯⨯⨯ 9293 2-8 在倾角α=60°的堤坡上有一圆形泄水孔,孔口装一直径d =1m 的平板94 闸门,闸门中心位于水深h =3m 处,闸门a 端有一铰链,b 端有一钢索可将闸门95 打开。
若不计闸门及钢索的自重,求开启闸门所需的力F 。
96已已知知::d=1m ,h c =3m ,α=60°。
97解析:(1) 闸门所受的总压力为98kN 23.1N 1031.20.114.3413981042c =⨯=⨯⨯⨯⨯==A h P γ 99(2) 压力中心到闸门中心的距离为100m 018.031660sin 0.116sin 4sin 642c 22c4c xc c D =⨯⨯==⋅==-= hd d h d A y I y ye απαπ101(3) 对闸门上端a 点取矩,得 )2(cos e dP Fd +=α102则开启闸门所需要的力为103kN 93.2360cos 0.1)018.020.1(1031.2cos )2(4=⨯+⨯⨯=+= αd e d P F 104105 2-9一直径d=2000mm 的涵洞,其圆形闸门AB 在顶部A 处铰接,如图。
若门重106 为3000N ,试求: (1)作用于闸门上的静水总压力F ;(2)F 的作用点;(3)107 阻止闸门开启的水平力F'。
108109 解 (1)圆形闸门受压面形心到水面的距离为h 0=1.5+1.0=2.5m ;闸门的直径110 D 为2.83m (D=2/sin45°); 111闸门面积为:222(2.83)D 44A 6.28m ππ===112作用于圆形闸门上的总压力为: 113P=gh c A=9800´2.5 ´6.28=153860N114oc 2.5sin 45y 3.54m ==115(2)圆形闸门中心至ox 轴的距离为116圆形闸门面积A 对经闸门中心且平行于ox 轴之惯性矩I xc 为:11744xc 43.14(2.83)D 6464I 3.14m π===118cxc cx c p c p c I y AI 3.14y A3.546.28y y y y 0.14m ⨯=+-===得 119故总压力作用点在闸门中心正下方0.14m 处。
120(3)因铰点在A 处,则作用于闸门的所有外力对此点之力矩总和必为0,即121op 1.5sin 45F(y )G 1.0F' 2.00--⨯-⨯= 122得阻止闸门的开启力123153860(3.540.142.12)30001F 118511N 2+--⨯==124125 2-10 一圆柱形闸门,长l =10m ,直径D =4m ,上游126 水深h 1=4m ,下游水深h 2=2m ,求作用在该闸门上的静127 水总压力的大小与方向。
128已已知知::l =10m ,D=4m ,h 1=4m ,h 2=2m 。
129解析:(1) 闸门左侧面所受的水平分力为130N 10848.710449810212151x1⨯=⨯⨯⨯⨯==l D h P γ 131闸门右侧面所受的水平分力为132N 10962.11042981041212152x2⨯=⨯⨯⨯⨯=⋅=l D h P γ 133则,闸门所受的总水平分力为134N 10886.510)962.1848.7(55x2x1x ⨯=⨯-=-=P P P135(2) 依据题意可知,闸门左侧压力体的体积为21圆柱体,闸门右侧压力体的体136 积为41圆柱体,总压力体的体积为43圆柱体。
