截长补短法例题精编版
截长补短经典例题

截长补短经典例题
1. 问题:一个长方形的长是宽的2倍,如果长减少4厘米,宽增加6厘米,那么面积就会增加18平方厘米。
请问原来的长方形的长和宽各是多少厘米?
解:设原来的长方形的宽为x厘米,那么长为2x厘米。
根据题意,我们可以得到一个方程:
(x + 6) * (2x - 4) = 2x^2 + 18
解这个方程,我们得到:
2x^2 - 4x + 12x - 24 = 2x^2 + 18
10x = 42
x = 4.2
所以原来长方形的宽为4.2厘米,长为4.2 * 2 = 8.4厘米。
2. 问题:一个圆的半径是另一个圆半径的2倍,如果大圆的面积比小圆的面积大16π平方厘米,那么大圆和小圆的半径各是多少厘米?(π取
3.14)
解:设小圆的半径为r厘米,那么大圆的半径为2r厘米。
根据题意,我们可以得到一个方程:
π * (2r)^2 - π * r^2 = 16π
解这个方程,我们得到:
3.14 * (4r^2 - r^2) = 16π
3.14 * 3r^2 = 16π
3r^2 = 16
r^2 = 5.3333(保留四位小数)
所以小圆的半径约为2.3厘米,大圆的半径约为4.6厘米。
截长补短法

EDCA21N MED C BA截长补短法一、专项练习【板块一】截长1. 如图,在△ABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点.求证:AB -AC >PB -PC .2. 如图,△ABC 中,∠ABC =60º,AD 、CE 分别平分∠BAC ,∠ACB ,判断AC 的长与AE+CD 的大小关系并证明.3. 如图,已知点C 是∠MAN 的平分线上一点,CE ⊥AB 于E ,B 、D 分别在AM 、AN 上,且AE =21(AD +AB ).问:∠1和∠2有何关系?【板块二】补短4. 如图,已知△ABC 中,∠A =90º,AB =AC ,BE 平分∠ABC ,CE ⊥BD 于E ,求证:CE =21BD .EDCAFEDCBAEFDCAFE DCBAEDC BA【板块三】截长补短5. 如图所示:在△ABC 中,∠1=∠2,∠B =2∠C ,求证:AC =AB +BD .6. 如图,已知四边形ABCD 中,AD ∥BC ,若∠DAB 的平分线AE 交CD 于E ,连接BE ,且BE 恰好平分∠ABC ,判断AB 的长与AD +BC 的大小关系并证明.【板块四】拓展拔高7. ①正方形ABCD 中,点E 在CB 延长线上,点F 在DC 延长线上,∠EAF =45°.请问现在EF 、DF 、BE 有什么数量关系?②正方形ABCD 中,点E 在BC 延长线上,点F 在CD 延长线上,∠EAF =45°.请问现在EF 、BE 、DF 有什么数量关系?③正三角形ABC 中,E 在AB 上,F 在AC 上,∠EDF =60°,DB =DC ,∠BDC =120°.请问现在EF 、BE 、CF 有什么数量关系?ABCDEDCB AFEBAAB C E F 倍长中线法一、专项训练1. 如图,AD 为△ABC 的中线,求证:AB +AC >2AD .2. 如图,CB ,CD 分别是钝角△AEC 和锐角△ABC 的中线,且AC =AB . 求证:①CE =2CD .②CB 平分∠DCE .3、 如图已知△ABC ,AD 是BC 边上的中线,分别以AB 、AC 为直角边各向外作等腰直角三角形,求证:EF =2AD .4、 如图,△ABC 中,E 、F 分别在AB 、AC 上,DE ⊥DF ,D 是中点,试比较BE +CF 与EF 的大小.FE C B A FE DCB AGABCDFEFEDCBA5、 如图,在△ABC 中,D 是BC 边的中点,E 是AD 上一点,BE =AC ,BE 的延长线交AC 于点F ,求证:∠AEF =∠EAF .6、 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 中点,EF ∥AD 交CA 的延长线于点F ,交AB 于点G ,若BG =CF ,求证:AD 为△ABC 的角平分线.7、 (1)如图1,△ABC 和△BDE 均为等腰直角三角形,BA ⊥AC ,ED ⊥BD ,点D 在AB 边上.连接EC ,取EC 中点F ,连接AF 、DF ,猜测AF 、DF 的数量关系和位置关系,并加以证明.(2)如图2,将△BDE 旋转至如图位置,使E 在AB 延长线上,点D 在CB 延长线上,其他条件不变,则(1)中AF 、DF 的数量关系和位置关系是否发生变化,并加以证明.。
截长补短法经典例题

1.在解决几何问题时,截长补短法常用于:A.证明线段相等B.证明角度相等(答案)C.计算面积D.求解体积2.下列哪个图形问题最适合使用截长补短法来解决?A.求解圆的半径B.证明两个三角形全等(答案)C.计算长方体的表面积D.求解一次方程的根3.使用截长补短法时,通常需要:A.添加辅助线来构造相似图形B.延长或截取线段来构造等长线段(答案)C.使用勾股定理D.计算图形的周长4.在三角形ABC中,AB > AC,为了证明某条线段与AB相等,可以使用截长补短法,下列哪个步骤是正确的?A.延长AC至D,使得CD = ABB.截取AB的一部分,使其与AC相等(答案)C.在三角形外部构造一个与三角形ABC全等的三角形D.计算三角形ABC的面积5.截长补短法在解决哪类问题时特别有用?A.代数方程求解B.图形面积计算C.线段长度比较和证明(答案)D.体积计算6.下列哪个不是截长补短法的常见应用?A.证明线段和差关系B.构造平行线来证明角度相等C.通过截取和延长来构造等边三角形(答案,这更多是等边三角形的性质或构造法,不是截长补短法的直接应用)D.利用线段的相等关系来证明三角形的全等7.在使用截长补短法时,如果延长了某条线段,通常是为了:A.增加图形的面积B.构造一个与已知线段相等的线段(答案)C.改变图形的形状D.计算图形的周长8.下列哪个步骤是使用截长补短法证明线段相等时的常见策略?A.延长较短的线段至与较长线段相等B.计算两条线段的长度差C.通过截取较长线段的一部分来构造与较短线段相等的线段(答案)D.使用三角形的相似性质。
截长法和补短法的例题和解析

截长法和补短法的例题和解析说到截长法和补短法,很多人一听就觉得这又是个数学难题,哎呀,我可不想脑袋里塞满公式。
不过,今天咱们就轻松聊聊这两种方法,保准让你豁然开朗,甚至能在朋友面前抖个机灵,炫耀一下你的数学“绝技”。
先来聊聊截长法。
想象一下你在剪头发,朋友想要个“帅气”的短发,可是发量又不够,怎么办?这时候就得用截长法了!简单说,就是把长的部分“截”掉,然后用剩下的长度来拼凑出一个好的造型。
哎,你看,就像我之前跟我朋友一起去理发,剪了个“爆炸头”,结果出来的时候,我朋友的发型竟然比我还好!这就是截长法的魅力所在,把多余的剪掉,剩下的部分更显得精致。
再来说补短法。
这法子就像是给缺口的地方加点东西。
想象你在做一件手工活,刚好少了一块布,没关系,拿出一块颜色相近的布,补上去,不就成了吗?有一次我和朋友做DIY,差点没把东西做成四不像,结果我灵机一动,拿出一张彩纸,补了一下,嘿,瞬间变得生动有趣,朋友们都夸我有创意!补短法就是用好东西把不足的地方填上,让整体看起来更完美。
这两种方法其实在生活中无处不在。
比如你在做一道数学题,题目给了个长长的公式,哦,真是头疼。
可是如果你能截掉一些冗余的部分,简化一下,不就简单多了吗?或者遇到短缺的条件,你就得用补短法,想办法把缺的部分找回来,搞定问题。
数学就像生活,时不时需要用点创意。
那说到例题,咱们来试试吧!假设你有一根长度为10米的绳子,你想要做一个正方形的花坛。
你会发现,这绳子不够用,咋整?这就是截长法的好时机。
把花坛的边长从2米调整成1.5米,嘿,这一下绳子就够用了,花坛不但可以做出来,视觉效果也不错,真是一举两得。
再说补短法。
假设你在搞一个团体活动,每个人都要出一份稿子,结果发现有一个人写得特别少,怎么办?用补短法,大家一起帮他补充点内容,齐心协力,让整份稿子看起来完整,真是众人拾柴火焰高嘛。
这种方法特别适合团队合作,大家各展所长,凑成一份完美的作品。
哦,对了,还得提到一个小技巧。
截长补短经典例题20道

截长补短经典例题20道一、三角形中的截长补短例1:在△ABC中,∠ABC = 60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点O。
求证:AC = AE+CD。
解析:在AC上截取AF = AE,连接OF。
因为AD平分∠BAC,所以∠EAO = ∠FAO。
在△AEO和△AFO中,AE = AF,∠EAO = ∠FAO,AO = AO,所以△AEO≌△AFO(SAS)。
所以∠AOE = ∠AOF。
因为∠ABC = 60°,AD、CE分别平分∠BAC、∠ACB,所以∠BAC+∠ACB = 120°,则∠AOE =∠COD =∠AOF = 60°。
所以∠COF = 180° - ∠AOF - ∠COD=60°,即∠COF = ∠COD。
又因为CE平分∠ACB,所以∠FCO = ∠DCO。
在△FOC和△DOC中,∠FOC = ∠DOC,∠FCO = ∠DCO,CO = CO,所以△FOC≌△DOC(ASA)。
所以CD = CF。
因为AC = AF+CF,AF = AE,CF = CD,所以AC = AE + CD。
例2:已知:如图,在△ABC中,∠A = 90°,AB = AC,BD是∠ABC的平分线。
求证:BC = AB+AD。
解析:过点D作DE⊥BC于E。
因为BD是∠ABC的平分线,∠A = 90°,DE⊥BC,所以AD = DE。
因为AB = AC,∠A = 90°,所以∠C = 45°。
在Rt△DEC中,因为∠C = 45°,所以DE = EC。
又因为BD = BD,AD = DE,∠A = ∠BED = 90°,所以△ABD≌△EBD(HL)。
所以AB = BE。
因为BC = BE+EC,AB = BE,AD = EC,所以BC = AB+AD。
二、四边形中的截长补短例3:如图,在正方形ABCD中,E为BC上一点,F为CD上一点,且∠EAF = 45°。
截长补短法的经典例题

截长补短法的经典例题
首先,我们来看一个代数方程的例题:
假设我们有方程式 2x + 5 = 11,我们可以使用截长补短法来解决这个方程。
首先,我们注意到方程左侧有一个2x,我们可以通过减去5来“截长”,即:
2x + 5 5 = 11 5。
得到 2x = 6。
然后,我们得到了简化后的方程2x = 6,接下来我们可以继续使用截长补短法,将方程简化为x = 3。
这样,我们就得到了方程的解,x = 3。
接下来,我们来看一个不等式的例题:
假设我们有不等式 3y 7 < 8,同样可以使用截长补短法来解决这个不等式。
首先,我们注意到不等式左侧有一个3y,我们可以通过加上7来“补短”,即:
3y 7 + 7 < 8 + 7。
得到 3y < 15。
然后,我们得到了简化后的不等式3y < 15,接下来我们可以继续使用截长补短法,将不等式简化为y < 5。
这样,我们就得到了不等式的解,y < 5。
通过以上两个例题,我们可以看到截长补短法的经典应用。
这种方法在解决代数方程和不等式时非常实用,通过不断简化方程或不等式的形式,我们可以更清晰地看到方程或不等式的性质,从而更容易求解。
当然,在实际应用中,还需要注意不等式或方程的变形规则和注意事项,以确保推导的过程和结果的准确性。
正方形截长补短法的经典例题

正方形截长补短法的经典例题
正方形截长补短法是一种几何解题方法,通常用于解决面积或者长度的问题。
经典的例题可以是这样的:
假设有一个正方形花坛,边长为 10 米。
现在要在花坛的四周围上一圈砖石。
但是由于某些原因,只有 30 块砖石,无法完全围成一圈。
这时可以采用截长补短法来解决问题。
问,如何摆放这 30 块砖石,使得花坛的面积最大化?
这个问题可以通过截长补短法来解决。
首先,我们将正方形的一边截短,然后在截短的两端加上砖石,使得原来的正方形变成一个长方形。
然后,我们可以计算出长方形的面积,找到最大化面积的方法。
这个例题可以帮助学生理解截长补短法的应用和原理。
三角形全等之截长补短(习题)(完整资料).doc
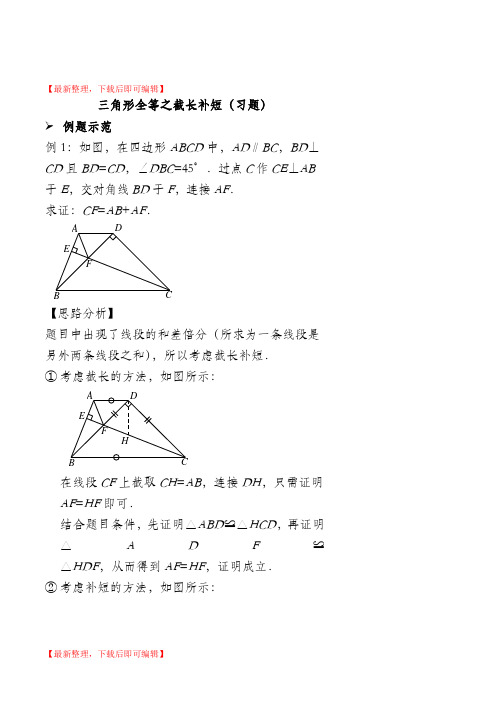
【最新整理,下载后即可编辑】三角形全等之截长补短(习题)➢ 例题示范例1:如图,在四边形ABCD 中,AD ∥BC ,BD ⊥CD 且BD =CD ,∠DBC =45°.过点C 作CE ⊥AB于E ,交对角线BD 于F ,连接AF . 求证:CF =AB +AF .【思路分析】题目中出现了线段的和差倍分(所求为一条线段是另外两条线段之和),所以考虑截长补短. ① 考虑截长的方法,如图所示:在线段CF 上截取CH =AB ,连接DH ,只需证明AF =HF 即可.结合题目条件,先证明△ABD ≌△HCD ,再证明△A D F ≌△HDF ,从而得到AF =HF ,证明成立. ② 考虑补短的方法,如图所示:FEDCBA A BCDEFH延长BA 交CD 的延长线于点H ,只需证明BH =CF ,AH =AF 即可.可结合题目条件,先证明△CDF ≌△BDH ,再证明△ADF ≌△ADH ,从而得到BH =CF ,AH =AF ,证明成立. 【过程书写】 (截长的方法)在线段CF 上截取CH =AB ,连接DH .∵BD ⊥CD ,BE ⊥CE ∴∠BEF =∠FDC =90° ∴∠EBF +∠EFB =90° ∠FCD +∠DFC =90° ∵∠EFB =∠DFC ∴∠EBF =∠FCD 在△ABD 和△HCD 中,FEDCB A H A BCDEFHAB HC ABD HCD BD CD =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△HCD (SAS ) ∴AD =HD ,∠ADB =∠HDC ∵AD ∥BC∴∠ADB =∠DBC =45° ∴∠HDC =45°∴∠HDF =∠BDC -∠HDC =45° ∴∠ADB =∠HDF 在△ADF 和△HDF 中,AD HD ADF HDF DF DF =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△HDF (SAS ) ∴AF =HF∴CF =CH +HF =AB +AF➢ 巩固练习1.如图,在△ABC 中,∠BAC =60°,∠ABC =80°,AD 是∠BAC 的平分线.求证:AC =AB +BD .ABCD A2.如图,AC 平分∠BAD ,CE ⊥AB 于E ,∠B +∠D =180°.求证:AE =AD +BE .CD ECD E3.如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD,连接EC.求证:BC=AB+CE.BE ADCBE ADC4.已知:如图,四边形ABCD是正方形,∠FAD=∠FAE.求证:BE+DF=AE.➢思考小结1.证明线段或角相等时,可以考虑把线段或角放到FEDC BA两个三角形中证明全等.如果题目中没有可能全等的三角形,往往考虑通过添加辅助线,构造全等三角形来证明.常见构造辅助线的方法:①___________:当已知条件中有中线(中点)时,往往考虑延长中线构造全等三角形.②_________:当题目中出现线段的和差倍分时,往往考虑把多条线段间的数量关系转化为两条线段的等量关系来处理.2.利用“截长补短”我们就可以证明直角三角形中非常重要的一个定理:30°角所对的直角边是斜边的一半.已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.求证:BC1AAB.230°【参考答案】➢巩固练习1.证明略提示:方法一:在AC上截取AE=AB,连接DE,证明△ABD≌△AED,再证明CE=DE;方法二:延长AB到E,使BE=BD,连接DE,证明△ADE≌△ADC.2.证明略提示:在AE上截取AF=AD,证明△CDA≌△CFA,再证明BE=FE.3.证明略提示:在BC上截取BF=BA,连接DF,证明△ABD ≌△FBD,再证明△DFC≌△DEC.4.证明略提示:延长CB至点G,使BG=DF,连接AG,证明△ABG≌△ADF,再证明AE=GE即可.➢思考小结1.倍长中线,截长补短2.证明略提示:延长BC到D,使BD=BA,得到△ABC 为等边三角形,AD=AB,根据三线合一,可得BC=12BD,所以BC=12AB.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
截长补短法
例1.
已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC .
求证:∠BAD +∠BCD =180°.
分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.
证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2 ∵BD 平分∠ABC ,∴DE =DF , 在Rt △ADE 与Rt △CDF 中,
⎩
⎨
⎧==CD AD DF
DE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF .
又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180°
例2. 已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD . 求证:∠BAP +∠BCP =180°.
分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造.
证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2
∵∠1=∠2,且PD ⊥BC ,∴PE =PD , 在Rt △BPE 与Rt △BPD 中,
⎩
⎨
⎧==BP BP PD
PE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .
∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE 即DC =BE -AB =AE .
F
E
D
C
B
A
图1-2
A
B
C
D
P
12
N
图3-1
P
12
N
A
B
C
D
E 图3-2
A
B
C D
图1-1
A
D
B
C
E
图2-1
在Rt △APE 与Rt △CPD 中,
⎪⎩
⎪
⎨⎧=∠=∠=DC AE PDC PEA PD PE ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180°
例3. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .
求证:CD =AD +BC .
分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的.
证明:在CD 上截取CF =BC ,如图2-2
在△FCE 与△BCE 中,
⎪⎩
⎪
⎨⎧=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE (SAS ),∴∠2=∠1.
又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°, ∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,
⎪⎩
⎪
⎨⎧∠=∠=∠=∠43DE
DE ADE FDE ∴△FDE ≌△ADE (ASA ),∴DF =DA , ∵CD =DF +CF ,∴CD =AD +BC .
A
D
B C
E
F
1
234图2-2
例4. 已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2.
求证:AB =AC +CD .
分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC .
证明:方法一(补短法)
延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2
∴∠ACB =2∠E ,
∵∠ACB =2∠B ,∴∠B =∠E , 在△ABD 与△AED 中,
⎪⎩
⎪
⎨⎧=∠=∠∠=∠AD AD E B 21 ∴△ABD ≌△AED (AAS ),∴AB =AE . 又AE =AC+CE =AC +DC ,∴AB =AC +DC . 方法二(截长法)
在AB 上截取AF =AC ,如图4-3 在△AFD 与△ACD 中,
⎪⎩
⎪
⎨⎧=∠=∠=AD AD AC AF 21 ∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD . 又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB . ∵AB =AF +FB =AC +FD ,∴AB =AC +CD .
D
C
B A 12
图4-1
E
D
C
B
A
12
图4-2
F
D
C
B A 12
图4-3。
