空间点阵群
名词解释

点群:一个结晶多面体所有的全部宏观对称要素的集合,称为该结晶多面体的点群。
对称型:晶体结构中所有点对称要素(对称面、对称中心、对称轴和旋转反伸轴)的集合称为对称型,也称点群。
空间群:空间群:指在一个晶体结构中所存在的一切对称要素的集合。
它由两部分组成,一是平移轴的集合(也就是平移群),另外是除平移轴之外的所有其他对称要素的集合(与对称型相对应)。
无规则网络假说:凡是成为玻璃态的物质和相应的晶体结构一样,也是由一个三度空间网络所构成。
这种网络是由离子多面体(三角体或四面体)构筑起来的。
晶体结构网是由多面体无数次有规律重复构成,而玻璃中结构多面体的重复没有规律性。
网络形成体:单键强度大于335KJ/mol的氧化物,可单独形成玻璃。
网络变性(改变)体:单键强度小于250KJ/mol的氧化物,这类氧化物不能形成玻璃,但是能改变网络结构。
从而使玻璃性质改变。
正尖晶石;二价阳离子分布在1/8四面体空隙中,三价阳离子分布在l/2八面体空隙的尖晶石。
反型尖晶石:二价阳离子分布在八面体空隙中,三价阳离子一半在四面体空隙中,另一半在八面体空隙中的尖晶石。
萤石结构(CaF2):F-填充在八个小立方体中心,8个四面体全被占据,八面体全空(有1+12*1/4=4个八面体空隙,其中有12个位于棱的中点,为4个晶胞所共用,1个位于体心) 。
可塑性:粘土与适当比例的水混合均匀制成泥团,该泥团受到高于某一个数值剪应力作用后,可以塑造成任何形状,当去除应力泥团能保持其形状,这种性质称为可塑性。
弗伦克尔缺陷:如果在晶格热振动时,一些能量足够大的原子离开平衡位置后,挤到晶格的间隙中,形成间隙原子,而原来位置上形成空位,这种缺陷称为弗伦克尔缺陷。
Frenkel缺陷的特点是:①间隙原子和空位成对出现;②缺陷产生前后,晶体体积不变。
网络形成剂:这类氧化物单键强度大于335KJ/mol,其正离子为网络形成离子,可单独形成玻璃。
液相独立析晶:是在转熔过程中发生的,由于冷却速度较快,被回收的晶相有可能会被新析出的固相包裹起来,使转熔过程不能继续进行,从而使液相进行另一个单独的析晶过程,就是液相独立析晶。
简述晶体结构与空间点阵之间的关系

简述晶体结构与空间点阵之间的关系晶体结构是指由原子、离子或分子按照一定的规律排列而形成的固体结构。
而空间点阵则是描述晶体结构的数学模型,用来表示晶体中原子、离子或分子的排列方式和间距。
晶体结构与空间点阵之间存在着密切的关系,下面将从晶体结构和空间点阵的定义、表示方法以及它们之间的关系三个方面来进行阐述。
一、晶体结构的定义和表示方法晶体结构是指由原子、离子或分子按照一定的规律排列而形成的固体结构。
在晶体中,原子、离子或分子之间的排列方式是非常有序的,各个粒子之间有着固定的位置关系和间距。
晶体结构可以通过实验方法如X射线衍射等来确定,也可以通过理论计算和模拟方法来推测。
晶体结构的表示方法主要有两种,一种是晶体结构的几何图形表示,另一种是用数学模型表示。
几何图形表示主要通过晶体的晶面、晶胞和晶格来描述晶体的结构。
晶面是晶体表面上的一个平面,晶胞是晶体中的最小重复单元,晶格是由相邻晶胞的重复堆积形成的一个无限延伸的空间网格。
数学模型表示主要是通过空间点阵来描述晶体的结构。
二、空间点阵的定义和表示方法空间点阵是一种数学模型,用来描述晶体中原子、离子或分子的排列方式和间距。
空间点阵是由一系列的基矢量和晶胞参数来表示的。
基矢量是一组线性无关的矢量,它们的线性组合可以表示出空间中的任意矢量。
晶胞参数包括晶胞的长度、角度和对称操作元素等。
空间点阵可以分为离散点阵和连续点阵两种。
离散点阵是指晶体中的原子、离子或分子按照一定的规律在空间中离散排列的情况,如简单立方晶体、体心立方晶体和面心立方晶体等。
连续点阵是指晶体中的原子、离子或分子在空间中连续排列的情况,如钻石晶体和金属晶体等。
三、晶体结构与空间点阵的关系晶体结构与空间点阵之间存在着密切的关系。
晶体结构可以通过空间点阵来描述和表示。
在晶体中,原子、离子或分子按照一定的规律排列,形成了一种具有周期性的结构。
这种周期性的结构可以通过空间点阵的平移操作来表示,即晶体结构是由空间点阵的平移操作所生成的。
空间点阵空间点阵到底有多少种排列形式?按照每个阵点的周围环境

-空间点阵空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如图1-8所示。
一般情况下单胞的选取有以图1-8 空间点阵及晶胞的不同取法图1-9面心立方阵胞中的固体物理原胞图1-10晶体学选取晶胞的原则下两种选取方式:1.固体物理选法在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征,如图1-9所示。
2.晶体学选法由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则(如图1-10所示):①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。
根据以上原则,所选出的14种布拉菲点阵的单胞(见图1-12)可以分为两大类。
一类为简单单胞,即只在平行六面体的 8个顶点上有结点,而每个顶点处的结点又分属于 8个相邻单胞,故一个简单单胞只含有一个结点。
另一类为复合单胞(或称复杂单胞),除在平行六面体顶点位置含有结点之外,尚在体心、面心、底心等位置上存在结点,整个单胞含有一个以上的结点。
14种布拉菲点阵中包括7个简单单胞,7个复合单胞。
图1-11 单晶胞及晶格常数根据单胞所反映出的对称性,可以选定合适的坐标系,一般以单胞中某一顶点为坐标原点,相交于原点的三个棱边为X、Y、Z三个坐标轴,定义X、Y轴之间夹角为γ,Y、Z之间夹角为α,Z、X轴之间夹角为β,如图1-11所示。
无机材料科学基础名词解释

名词解释肖特基缺陷:正常格点上的原子,热起伏过程中获得能量离开平衡位置迁移到晶体表面,晶体内正常格点上留下空位弗伦克尔缺陷:晶格热振动时,能量足够大的原子离开平衡位置,挤到晶格间隙中,形成间隙原子,原来位置上形成空位空间群:晶体结构中一切对称要素的集合称为空间群。
本征扩散:指空位来源于晶体结构中本征热缺陷而引起质点的迁移的扩散方式;非本征扩散是由不等价杂质离子取代造成晶格空位,由此而引起的质点迁移。
固溶体:在固态条件下,一种组分(溶剂)内“溶解”了其它组分(溶质)而形成的单一、均匀的晶态固体称为固溶体。
烧结与熔融:烧结是在远低于固态物质的熔融温度下进行的,熔融时全部组元都转变为液相,而烧结时至少有一组元是固态的。
等同点:在晶体结构中占据相同的位置和具有相同的环境的点点阵(空间点阵):空间点阵,一系列在三维空间按周期性排列的几何点结点间距:行列中两个相邻结点间的距离晶体:内部质点在三维空间按周期性重复排列的固体,具有格子构造的固体基本性质:结晶均一性、各向异性、自限性、对称性、最小内能性对称:物体中相同部分之间的有规律的重复宏观晶体的对称要素:对称轴、对称中心、对称面、倒转轴对称变换(对称操作):使对称物体中各相同部分作有规律重复的变换动作对称型(点群):宏观晶体中对称要素的集合,包含了宏观晶体中全部对称要素的总和以及它们相互间的组合关系晶胞:晶体结构中的平行六面体单位,其形状大小与对应的空间格子中的平行六面体一致。
单位晶胞:能够充分反映整个晶体结构特征的最小结构单位,其形状大小与对应的单位平行六面体完全一致。
配位数:晶体结构中,原子或离子的周围,与它直接相邻结合的原子个数或所有异号离子的个数。
固相反应:广义:固相参与的化学反应;狭义:固体与固体发生化学反应生成新的固体。
固相反应速度较慢、需要高温烧结:一种或多种固体粉末经过成型,在加热到一定温度后开始收缩,在低于熔点的温度下变成致密、坚硬的烧结体的过程,包括粉末颗粒表面的粘结和粉末内部物质的传递与迁移。
第2章晶体结构和空间点阵

(a) (b)
(c) (d) 一维周期排列的结构及其点阵(黑点代表点阵点) (a) Cu , (b) 石墨 , (c) Se , (d) NaC l
晶体结构的基本重复单位是晶胞,整个晶体 就是晶胞在三维空间周期地重复排列堆砌而成 的。只要将一个晶胞的结构剖析透彻,整个晶 体结构也就掌握了。
晶胞有两个要素: ⑴ 晶胞的大小和形状,由晶胞参数
a , b , c , α , β , γ 规定; ⑵晶胞内部各个原子的坐标位置,由原子坐标 参数 (x , y , z )规定。
第2章 晶体结构和空间点阵
➢ 内容
✓ 晶体结构的周期性与空间点阵。 ✓ 晶胞、晶列、晶面和晶面指数。 ✓ 倒易点阵 ✓ 晶体的对称性。 ✓ 7个晶系和14种Bravias空间格子。 ✓ 晶体缺陷
➢ 教学目标
通过本章学习,掌握晶体所具有的周期性结构与它的 点阵表示,倒易点阵,了解晶体对称性与空间群。
材料科学与工程
ห้องสมุดไป่ตู้
▪ 体心点阵,I
除8个顶点外,体 心上还有一个阵点, 因此,每个阵胞含 有两个阵点,000, 1/2 1/2 1/2
• 面心点阵。F
除8个顶点外,每 个面心上有一个 阵点,每个阵胞 上有4个阵点,其 坐标分别为000, 1/2 1/2 0, 1/2 0 1/2, 0 1/2 1/2
2. 2 晶体的周期性,晶胞
晶体结构(晶格) = 点阵 + 结构基元
原胞和晶胞
• 原胞(primitive cell):最小的重复单元。 • 晶胞(unit cell):体现所有对称性的最
浙江大学《材料科学基础》考研复习知识点

i
1 2
§2-2 位错 位错:原子行列间相互滑移,不再符合理想晶格的有序的排列,为线缺陷 (一)刃型位错 刃型位错:滑移面和未滑移面交界处的一条交界线,也即一个多余半原子面与滑
移面相交的交线上,由于原子失掉正常的相邻关系,形成的晶格缺陷。它 与滑移方向垂直。图 2- 6,图 2- 8 有正、负刃型位错
(1)对晶胞作晶轴X、Y、Z,以晶胞的边长作为晶轴上的单位长度。 (2)求出晶面在三个晶轴上的截距(如该晶面与某轴平行,则截距为∞)。例 如1、1、∞,1、1、1,1、1、1/2等。 (3)取这些截距数的倒数。例如110,111,112等。 (4)将上述倒数化为最小的简单整数, 并加上圆括号, 即表示该晶面的指数, 一般记为(hkl)。例如(110),(111),(112)等。如果所求晶面在晶轴上 的截距为负数,则在相应的指数上方加一负号,如(110)、(111)、(11 2 ) 等。
多的负离子包围它)和离子的相对大小((rC)与(rA)之比)决定
负离子配位多面体:以正离子为中心,将周围最近邻配置的各负离子的中心连起
来形成的多面体
正离子配位数:配置于正离子周围的负离子数 三者之间关系:
表 1- 9 rC/rA 0-0.155 0.155-0.225 0.225-0.414 0.414-0.732 0.732-1.0 正、负离子半径比,正离子配位数和配位多面体形之间的关系 正离子配位数 2 3 4 6 8 配位多面体类型 线性 三角形 四面体 八面体 立方体 举例 CO2 B2O3 SiO2 TiO2 CsCl
四、晶体的对称性 (一)对称要素 对称要素:反映晶体对称性的参数。晶体通过相应对称操作后的位置与原始位置
完全重合
宏观对称要素:反映出晶体外形和其宏观性质的对称性 微观对称要素:与宏观对称要素配合运用能反映出晶体中原子排列的对称性 所有对称要素归纳:
空间点阵示意图在晶体中凡是几何环...

四、晶带、晶面间距和晶面夹角
1.晶带
在晶体结构和空间点阵中平行于某一轴向的所有晶面均 属于同一个晶带,这些晶面叫做晶带面(共带面)。晶带面 的交线相互平行,其中通过坐标原点的那条平行直线叫做晶 带轴。晶带轴的指数即为该晶带的指数。
同一晶带中所有晶面的法线都与晶带轴垂直。通过矢量 概念可以导出,凡属于[υϖω]晶带的晶面,它们的指数(ηκλ) 都必须符合下式:
第二章 X射线衍射方向
§2-1 晶体几何学基础
一、空间点阵
在晶体中凡是几何 环境、物理环境完全相 同的点称为等同点。
这些等同点按连接 起来,按原晶体中的原 子(原子团)的排列完全 相同的骨架,称为空间 点阵。
图2-1 空间点阵示意图
许多阵点在三维空间内 有规律、周期性地排列而成 的一种空间图形。
③ 每个晶体都有自己特定的 ③ 许多晶体具有相同的点阵
晶体结构
结构(只有十四种)
意义内容基本相同的有:
晶体结构 ① 晶胞 ② 晶胞参数 ③ 三基矢 a b c ④ 晶胞常数 a b c ⑤ 晶轴夹角αβγ ⑥ 晶面、晶面指数 ⑦ 晶向、晶向指数 ⑧ 晶带、晶带轴定理
点阵结构 ① 点阵胞 ② 点阵参数 ③ 三基矢 a b c ④ 点阵胞常数 a b c ⑤ 点阵轴夹角αβγ ⑥ 点阵面、点阵面指数 ⑦ 点阵方向、点阵方向指数 ⑧ 点阵带、点阵带定理
④ 需要注意的是X射线的反射角不同于可见光的反射角,X 射线的入射线与反射线的夹角永远是2θ。
§2-3 布喇格方程的讨论
一、产生X射线的条件
衍射只产生在波长和散射种间距为同一数量级或更小 的时候。
nλ
2d
=
第六章 空间点阵
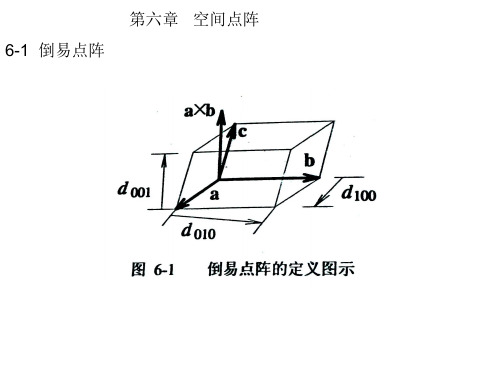
3
4 正点阵空间的位矢 R uvw u a v b w c 长度表示为 a u u 2 R uvw R uvw R uvw u , v , w b a b c v u , v , w G v w w c 5 h1 k 1l1 与 h 2 k 2 l 2 两平面夹角为两倒易矢 rh1 k 1 l1 * 与 rh 2 k 2 l 2 * 间
7
实际晶体中出现几率大
的是 Miller 指数小的晶面。
定义 2:一族晶面中离原点最 近的平面点阵在轴 a , b , c 上的 1 1 1 截距分别为 a , b , c 的 , , ,整数数组即为该晶面 的 Miller 指数。 h k l 定义 3:设一族点阵平面分别 将基矢 a , b , c 分为 h 段 , k 段 , l 段,则 该晶面的 Miller 指数为 hkl 。
a x a y a z a x a y a z ax ay az ax ay az 2 v a b c a b c bx by bz bx b y bz bx b y bz bx b y bz c c c c c c cx cy cz cx cy cz x y z x y z a a a b a c 2 1 b a b b b c det G 同理 v * det G * det G c a c b c c
Fourier
( x ua , y vb , z wc ) F hkl e
hkl
hkl
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Nr.Symbol Point group System Remarks 1P11triclinic 手性2P-1-1triclinic 中心3P22monoclinic 手性4P212monoclinic 手性5C22monoclinic 手性6Pm m monoclinic 非心7Pc m monoclinic 非心8Cm m monoclinic 非心9Cc m monoclinic 非心10P2/m2/m monoclinic 中心11P21/m2/m monoclinic 中心12C2/m2/m monoclinic 中心13P2/c2/m monoclinic 中心14P21/c2/m monoclinic 中心* 15C2/c2/m monoclinic 中心16P222222orthorhombic 手性17P2221222orthorhombic 手性* 18P21212222orthorhombic 手性* 19P212121222orthorhombic 手性* 20C2221222orthorhombic 手性* 21C222222orthorhombic 手性22F222222orthorhombic 手性23I222222orthorhombic 手性24I212121222orthorhombic 手性25Pmm2mm2orthorhombic 非心26Pmc21mm2orthorhombic 非心27Pcc2mm2orthorhombic 非心28Pma2mm2orthorhombic 非心29Pca21mm2orthorhombic 非心30Pnc2mm2orthorhombic 非心31Pmn21mm2orthorhombic 非心32Pba2mm2orthorhombic 非心33Pna21mm2orthorhombic 非心34Pnn2mm2orthorhombic 非心35Cmm2mm2orthorhombic 非心36Cmc21mm2orthorhombic 非心37Ccc2mm2orthorhombic 非心38Amm2mm2orthorhombic 非心39Abm2mm2orthorhombic 非心40Ama2mm2orthorhombic 非心41Aba2mm2orthorhombic 非心42Fmm2mm2orthorhombic 非心43Fdd2mm2orthorhombic 非心* 44Imm2mm2orthorhombic 非心45Iba2mm2orthorhombic 非心46Ima2mm2orthorhombic 非心47Pmmm mmm orthorhombic 中心48Pnnn mmm orthorhombic 中心49Pccm mmm orthorhombic 中心50Pban mmm orthorhombic 中心51Pmma mmm orthorhombic 中心52Pnna mmm orthorhombic 中心* 53Pmna mmm orthorhombic 中心54Pcca mmm orthorhombic 中心* 55Pbam mmm orthorhombic 中心56Pccn mmm orthorhombic 中心* 57Pbcm mmm orthorhombic 中心58Pnnm mmm orthorhombic 中心59Pmmn mmm orthorhombic 中心60Pbcn mmm orthorhombic 中心* 61Pbca mmm orthorhombic 中心* 62Pnma mmm orthorhombic 中心63Cmcm mmm orthorhombic 中心64Cmca mmm orthorhombic 中心65Cmmm mmm orthorhombic 中心66Cccm mmm orthorhombic 中心67Cmma mmm orthorhombic 中心68Ccca mmm orthorhombic 中心* 69Fmmm mmm orthorhombic 中心70Fddd mmm orthorhombic 中心* 71Immm mmm orthorhombic 中心72Ibam mmm orthorhombic 中心73Ibca mmm orthorhombic 中心74Imma mmm orthorhombic 中心75P44tetragonal 手性76P414tetragonal 手性* 77P424tetragonal 手性78P434tetragonal 手性* 79I44tetragonal 手性80I414tetragonal 手性* 81P-4-4tetragonal 非心82I-4-4tetragonal 非心83P4/m4/m tetragonal 中心84P42/m4/m tetragonal 中心85P4/n4/m tetragonal 中心* 86P42/n4/m tetragonal 中心* 87I4/m4/m tetragonal 中心88I41/a4/m tetragonal 中心* 89P422422tetragonal 手性90P4212422tetragonal 手性* 91P4122422tetragonal 手性92P41212422tetragonal 手性* 93P4222422tetragonal 手性*94P42212422tetragonal 手性* 95P4322422tetragonal 手性* 96P43212422tetragonal 手性* 97I422422tetragonal 手性98I4122422tetragonal 手性* 99P4mm4mm tetragonal 非心100P4bm4mm tetragonal 非心101P42cm4mm tetragonal 非心102P42nm4mm tetragonal 非心103P4cc4mm tetragonal 非心104P4nc4mm tetragonal 非心105P42mc4mm tetragonal 非心106P42bc4mm tetragonal 非心107I4mm4mm tetragonal 非心108I4cm4mm tetragonal 非心109I41md4mm tetragonal 非心110I41cd4mm tetragonal 非心* 111P-42m-42mm tetragonal 非心112P-42c-42mm tetragonal 非心113P-421m-42mm tetragonal 非心114P-421c-42mm tetragonal 非心* 115P-4m2-42mm tetragonal 非心116P-4c2-42mm tetragonal 非心117P-4b2-42mm tetragonal 非心118P-4n2-42mm tetragonal 非心119I-4m2-42mm tetragonal 非心120I-4c2-42mm tetragonal 非心121I-42m-42mm tetragonal 非心122I-42d-42mm tetragonal 非心123P4/mmm4/mmm tetragonal 中心124P4/mcc4/mmm tetragonal 中心125P4/nbm4/mmm tetragonal 中心* 126P4/nnc4/mmm tetragonal 中心* 127P4/mbm4/mmm tetragonal 中心128P4/mnc4/mmm tetragonal 中心129P4/nmm4/mmm tetragonal 中心* 130P4/ncc4/mmm tetragonal 中心* 131P42/mmc4/mmm tetragonal 中心132P42/mcm4/mmm tetragonal 中心133P42/nbc4/mmm tetragonal 中心* 134P42/nnm4/mmm tetragonal 中心* 135P42/mbc4/mmm tetragonal 中心136P42/mnm4/mmm tetragonal 中心137P42/nmc4/mmm tetragonal 中心* 138P42/ncm4/mmm tetragonal 中心* 139I4/mmm4/mmm tetragonal 中心140I4/mcm4/mmm tetragonal 中心141I41/amd4/mmm tetragonal 中心* 142I41/acd4/mmm tetragonal 中心* 143P33trigonal 手性144P313trigonal 手性145P323trigonal 手性146R33trigonal 手性147P-3-3trigonal 中心148R-3-3trigonal 中心149P31232trigonal 手性150P32132trigonal 手性151P311232trigonal 手性* 152P312132trigonal 手性* 153P321232trigonal 手性* 154P322132trigonal 手性* 155R3232trigonal 手性156P3m13m trigonal 非心157P31m3m trigonal 非心158P3c13m trigonal 非心159P31c3m trigonal 非心160R3m3m trigonal 非心161R3c3m trigonal 非心162P-31m-3m trigonal 中心163P-31c-3m trigonal 中心164P-3m1-3m trigonal 中心165P-3c1-3m trigonal 中心166R-3m-3m trigonal 中心167R-3c-3m trigonal 中心168P66hexagonal 手性169P616hexagonal 手性* 170P656hexagonal 手性* 171P626hexagonal 手性* 172P646hexagonal 手性* 173P636hexagonal 手性174P-6-6hexagonal 非心175P6/m6/m hexagonal 中心176P63/m6/m hexagonal 中心177P622622hexagonal 手性178P6122622hexagonal 手性* 179P6522622hexagonal 手性* 180P6222622hexagonal 手性* 181P6422622hexagonal 手性* 182P6322622hexagonal 手性* 183P6mm6mm hexagonal 非心184P6cc6mm hexagonal 非心185P63cm6mm hexagonal 非心186P63mc6mm hexagonal 非心187P-6m2-6m hexagonal 非心188P-6c2-6m hexagonal 非心189P-62m-6m hexagonal 非心190P-62c-6m hexagonal 非心191P6/mmm6/mmm hexagonal 中心192P6/mcc6/mmm hexagonal 中心193P63/mcm6/mmm hexagonal 中心194P63/mmc6/mmm hexagonal 中心195P2323cubic 手性196F2323cubic 手性197I2323cubic 手性198P21323cubic 手性* 199I21323cubic 手性200Pm-3m-3cubic 中心201Pn-3m-3cubic 中心* 202Fm-3m-3cubic 中心203Fd-3m-3cubic 中心* 204Im-3m-3cubic 中心205Ia-3m-3cubic 中心* 206Pa-3m-3cubic 中心* 207P432432cubic 手性208P4232432cubic 手性* 209F432432cubic 手性210F4132432cubic 手性* 211I432432cubic 手性212P4332432cubic 手性* 213P4132432cubic 手性* 214I4132432cubic 手性215P-43m-43m cubic 非心216F-43m-43m cubic 非心217I-43m-43m cubic 非心218P-43m-43m cubic 非心219F-43c-43m cubic 非心220I4-3d m-3m cubic 非心* 221Pm-3m m-3m cubic 中心222Pn-3n m-3m cubic 中心* 223Pm-3n m-3m cubic 中心224Pn-3m m-3m cubic 中心* 225Fm-3m m-3m cubic 中心226Fm-3c m-3m cubic 中心227Fd-3m m-3m cubic 中心* 228Fd-3c m-3m cubic 中心* 229Im-3m m-3m cubic 中心230Ia-3d m-3m cubic 中心*注:表中手性、非心、中心分别指该空间群属于手性、非中心对称或中心对称空间群。
