简谐振动-旋转矢量法教程文件
合集下载
简谐运动及其旋转矢量表示法简谐运动的能量

解:(1 )A6 1 2 0 m , /3 ,
1 Hz , 2 6
T 2 1 6s, /4
(2)势能 总能
Epkx2/2, EkA 2/2
由题意, k2 x/2k2 A /4, xA/ 24.2 41 02m
(3)从平衡位置运动到 xA/ 2
的最短时间为 T / 8。
即为 6/80.75s
) )
O
A/2
x
(B)
A/2
O
x
A
x 10-2cos( t /3 - /4),(SI)
五、两个同频率简谐运动的相位关系
x 10-2cos( t /3 - /4),(SI)
x2 比 x1 超前
简谐运动及其旋转矢量表示法简谐运动的能量
五、两个同频率简谐运动的相位关系
(或 x1 比 x2 落后 ) 的最短时间为 T / 8。
x Acos( t )
半径
圆周运动小球 角速度
振幅
角频率 简谐振动物体
角坐标
相位
例:一物体做谐振动,振幅为 A,在起始
时刻质点的位移为 A/2 且向 x 轴的正方向
运动,代表此谐振动的旋转矢量图为:
质点运动的周期和振幅。
五、两个同频率简谐运动的相位关系
= 2 v = 2 /T
质点运动的周期和振幅。
A
,振幅A=1 cm. t=0时,速度具有负最O大值,求振动表达式.
(C ) x A/2
(D)
A/2
O
x
A
[D]
四、简谐运动的能量
1. 动能
Ek
1 mv 2
2
1 kA2 sin 2( t )
2
掌握
Ek max
1 Hz , 2 6
T 2 1 6s, /4
(2)势能 总能
Epkx2/2, EkA 2/2
由题意, k2 x/2k2 A /4, xA/ 24.2 41 02m
(3)从平衡位置运动到 xA/ 2
的最短时间为 T / 8。
即为 6/80.75s
) )
O
A/2
x
(B)
A/2
O
x
A
x 10-2cos( t /3 - /4),(SI)
五、两个同频率简谐运动的相位关系
x 10-2cos( t /3 - /4),(SI)
x2 比 x1 超前
简谐运动及其旋转矢量表示法简谐运动的能量
五、两个同频率简谐运动的相位关系
(或 x1 比 x2 落后 ) 的最短时间为 T / 8。
x Acos( t )
半径
圆周运动小球 角速度
振幅
角频率 简谐振动物体
角坐标
相位
例:一物体做谐振动,振幅为 A,在起始
时刻质点的位移为 A/2 且向 x 轴的正方向
运动,代表此谐振动的旋转矢量图为:
质点运动的周期和振幅。
五、两个同频率简谐运动的相位关系
= 2 v = 2 /T
质点运动的周期和振幅。
A
,振幅A=1 cm. t=0时,速度具有负最O大值,求振动表达式.
(C ) x A/2
(D)
A/2
O
x
A
[D]
四、简谐运动的能量
1. 动能
Ek
1 mv 2
2
1 kA2 sin 2( t )
2
掌握
Ek max
简谐振动 旋转矢量法
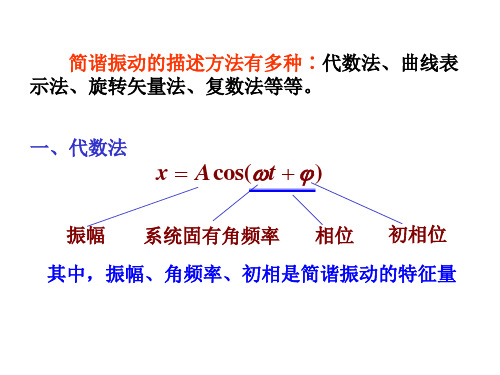
2 1 2 2
2 1 2k π (k 0 , 1, 2,)
x
x
A
A2
A1
o
o
T
t
A A 1 A 2
A A A 2 A1 A2 cos( 2 1 ) 2)相位差 2 1 (2k 1)π (k 0 , 1, )
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M P
A
x
注意:旋转矢量在第 2 象限 速度v < 0
M
P
A
x
注意:旋转矢量在第 3 象限 速度v 0
P M
A
<
x
注意:旋转矢量在第 3 象限 速度v 0
P x M
A
<
注意:旋转矢量在第 3 象限 速度v 0
( 1) 2 1 0, 称同相; (2) 2 1 , 称反相; (3) 2 1 0, 称振动2超前, 振动1落后; (4) 1 2 0, 称振动1超前, 振动2落后.
对于沿 x 轴振动的两个同频率的简谐振动:
用旋转矢量表示相位关系 同相位 反相位
对应关系
t
用旋转矢量图画简谐运动的
x t
图
T 2π (旋转矢量旋转一周所需的时间)
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M x
2 1 2k π (k 0 , 1, 2,)
x
x
A
A2
A1
o
o
T
t
A A 1 A 2
A A A 2 A1 A2 cos( 2 1 ) 2)相位差 2 1 (2k 1)π (k 0 , 1, )
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M P
A
x
注意:旋转矢量在第 2 象限 速度v < 0
M
P
A
x
注意:旋转矢量在第 3 象限 速度v 0
P M
A
<
x
注意:旋转矢量在第 3 象限 速度v 0
P x M
A
<
注意:旋转矢量在第 3 象限 速度v 0
( 1) 2 1 0, 称同相; (2) 2 1 , 称反相; (3) 2 1 0, 称振动2超前, 振动1落后; (4) 1 2 0, 称振动1超前, 振动2落后.
对于沿 x 轴振动的两个同频率的简谐振动:
用旋转矢量表示相位关系 同相位 反相位
对应关系
t
用旋转矢量图画简谐运动的
x t
图
T 2π (旋转矢量旋转一周所需的时间)
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M x
(优选)简谐振动旋转矢量法

初相位 : 也叫初位相或初相.
t=0时的相位, 描述初始时刻的 振动状态, 与初始条件有关.
相位差ΔΦ : 相位的差值.
单位: 弧度(rad)
4. 求解振幅和初相
设 t =0 时
x0 Acos , v0 Asin
x2 0
v2 0
2
A2 (sin 2 cos2 )
A2
振幅:
A
x0
2
v0
6cm x
解: A=12cm, T=2s, x0=6cm
(1)
2π π s1
x
x
o
to
o
t
t
相位差为 2 整数倍: 同步
相位差为 或 奇数倍: 反相
3. 用旋转矢量图画简谐运动的x t
例2: 一质点沿x轴作简谐运动 的振幅为12cm, 周期为2s. 当 t = 0 时, 位移为6cm, 且沿 x 轴 正方向运动. 求: (1) 振动表达式; (2) t = 0.5s时, 质点的位置, 速 度和加速度; (3) 如果在某时刻质点位于 x=-6cm, 且沿 x 轴负方向运 动, 求从该位置回到平衡位置 所需要的最短时间.
振子沿 x 轴负方向运动 2. 比较各振动之间的相位关系 不同振动同一时刻的相位差
x1 Acos( t ) x2 Acos(t )
x1 Acos( t1 ) x2 Acos( t2 ) Φ (t2 ) (t1 )
(t2 t1) ( ) t
Φ 2 1
Φ 0 同步
x
0 超前 Φ π反相 Φ 0 落后
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
t=0时的相位, 描述初始时刻的 振动状态, 与初始条件有关.
相位差ΔΦ : 相位的差值.
单位: 弧度(rad)
4. 求解振幅和初相
设 t =0 时
x0 Acos , v0 Asin
x2 0
v2 0
2
A2 (sin 2 cos2 )
A2
振幅:
A
x0
2
v0
6cm x
解: A=12cm, T=2s, x0=6cm
(1)
2π π s1
x
x
o
to
o
t
t
相位差为 2 整数倍: 同步
相位差为 或 奇数倍: 反相
3. 用旋转矢量图画简谐运动的x t
例2: 一质点沿x轴作简谐运动 的振幅为12cm, 周期为2s. 当 t = 0 时, 位移为6cm, 且沿 x 轴 正方向运动. 求: (1) 振动表达式; (2) t = 0.5s时, 质点的位置, 速 度和加速度; (3) 如果在某时刻质点位于 x=-6cm, 且沿 x 轴负方向运 动, 求从该位置回到平衡位置 所需要的最短时间.
振子沿 x 轴负方向运动 2. 比较各振动之间的相位关系 不同振动同一时刻的相位差
x1 Acos( t ) x2 Acos(t )
x1 Acos( t1 ) x2 Acos( t2 ) Φ (t2 ) (t1 )
(t2 t1) ( ) t
Φ 2 1
Φ 0 同步
x
0 超前 Φ π反相 Φ 0 落后
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
4-1-2简谐运动旋转矢量法简谐运动的动力学讲解

t 超前、落后以<
-A1
的相位角来判断。
1
2
, 2
0
1
3
2
,
2
0
2-1>0 ,x2比x1超前 π/2 1-2>0 ,x1比x2超前 3π/2
位 移 :x(t) Acos(t )
速 度 :(t) Asin(t )
加 速 度 :a(t) 2 x(t)
x、 、a
2A
A
A
x
o
-A
- A
dt
2
a(t)
d 2 x(t) dt 2
2 Acos(t
)
2 x(t)
m
加速度与位移成正比而反向
x、 、a
2A
A
A
x
o
-A
- A
- 2A
a < 0 a<0 加速
<0 >0 减速
o
x
x
>0 >0 加速
T t
>0 <0 减速
三. 描述简谐运动的特征量 x(t)=Acos( t+)
1.振幅A(amplitude) 偏离平衡位置的最大距离 其值与运动如何开始有关
波动与光学
第1章 振 动 (Vibration)
生活中观察的:摇曳的树枝、飘荡的小船, 人类发明中的:颤动的琴弦或鼓膜, 人类自身中的:声带、耳膜、心脏, 不易感觉的:传递声音的空气分子的振动、
传递温度的固体内原子的振动、 传递信息的天线中电子的振动…… 周期性过程:指不断有规律重复的过程或状态。
2.周期T (period) 振动往复一次所需时间 频率v (frequency) 单位时间内的振动次数
-A1
的相位角来判断。
1
2
, 2
0
1
3
2
,
2
0
2-1>0 ,x2比x1超前 π/2 1-2>0 ,x1比x2超前 3π/2
位 移 :x(t) Acos(t )
速 度 :(t) Asin(t )
加 速 度 :a(t) 2 x(t)
x、 、a
2A
A
A
x
o
-A
- A
dt
2
a(t)
d 2 x(t) dt 2
2 Acos(t
)
2 x(t)
m
加速度与位移成正比而反向
x、 、a
2A
A
A
x
o
-A
- A
- 2A
a < 0 a<0 加速
<0 >0 减速
o
x
x
>0 >0 加速
T t
>0 <0 减速
三. 描述简谐运动的特征量 x(t)=Acos( t+)
1.振幅A(amplitude) 偏离平衡位置的最大距离 其值与运动如何开始有关
波动与光学
第1章 振 动 (Vibration)
生活中观察的:摇曳的树枝、飘荡的小船, 人类发明中的:颤动的琴弦或鼓膜, 人类自身中的:声带、耳膜、心脏, 不易感觉的:传递声音的空气分子的振动、
传递温度的固体内原子的振动、 传递信息的天线中电子的振动…… 周期性过程:指不断有规律重复的过程或状态。
2.周期T (period) 振动往复一次所需时间 频率v (frequency) 单位时间内的振动次数
15 简谐振动 旋转矢量法

振动频率
ν 1 2 2π
k1k2
k1 k2m
P.20/35
作业
习题集:121、6、8、9、16
第5章 机械振动
P.21/35
P.3/35
§5.1 简谐运动
第5章 机械振动
5.1.1 简谐运动的特征及其运 动方程
弹簧振子——理想模型
简谐运动的受力
f kx
始终指向平衡位置(有心力)
简谐运动的动力学方程
单
摆
m d2x k x
dt 2
P.4/35
简谐运动动力学方程
m d2x k x 令 dt 2
2 k m
d2x dt2
arctavn0 0
x0
1
1
2
3
2 2
依题意, v<0
v 0.24 3 0 .20 m s 8 1
(为什么 不取π ?)
2
P.9/35
§5.2 简谐运动的旋转矢量 表示法
5.2.1 旋转矢量表示法
t
x
P
• 旋转矢量A的模即为简谐运 动的振幅.
第5章 机械振动
• 旋转矢量A与x轴的夹角(t+)
篇机械振动&机械波
第五章 机械振动
第5章 机械振动
为何讨论的重点是简谐运动 复杂振动可分解为若干简谐运动
振动的运动学规律
简谐振动的动力学特征
振动能量的周期性特征
P.2/35
振动和波动的关系: 波动——振动的传播 振动——波动的源头
机械振动, 电磁振荡 机械波, 电磁波 德布罗意波——几率波
振动学是波动学的基础
即为简谐运动的相位.
• 旋转矢量 A 的角速度 即
教案-旋转矢量
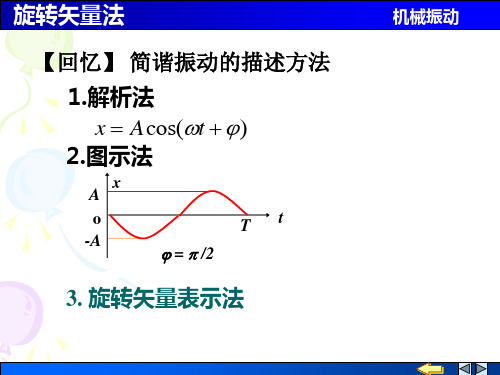
9.8 k g = = = 10rad / s ω= ∆l m 0.098
O x X
0
)
旋转矢量法
由初条件得
2 0
机械振动
)2 = 0.098m ω v0 m ϕ0 = arctg(− ) = 0或 π 者 ωx0 由x0=Acosϕ0=0.098>0 ∴ cosϕ0>0, 取ϕ0=0
A= x +(
v0
ω = 10rad / s
O x
振动方程为:x=9.8×10-2cos(10t) m 振动方程为: X (2)按题意 t=0 时 x0=0,v0>0 按题意 1 g ω x0=Acosϕ0=0 , cosϕ0=0 ϕ0=π/2或3π/2 ν = 2π = 2π ∆l z v0=-Aωsinϕ>0 , sin ϕ0 <0, 取ϕ0=3π/2 =1.6H 固有频率 ∴ x=9.8×10-2cos(10t+3π/2) m 不同, 对同一谐振动取不同的计时起点ϕ不同,但ω、A不变 不变
A 1
旋转矢量法 讨论
机械振动
相位差:表示两个相位之差 . 相位差:
2)对同一简谐运动,相位差可以给出两运动状 同一简谐运动, 简谐运动 态间变化所需的时间. 态间变化所需的时间. ∆ϕ = (ωt 2 + ϕ ) − (ωt1 + ϕ )
x = A cos(ωt1 + ϕ ) x = A cos(ωt 2 + ϕ )
π
6
)cm
x = Acos(ωt +ϕ0 ) π v = −ωAsin( ωt +ϕ0 ) = vm cos(ωt +ϕ0 + ) 2 −1 vm = ωA = 31.4cms
O x X
0
)
旋转矢量法
由初条件得
2 0
机械振动
)2 = 0.098m ω v0 m ϕ0 = arctg(− ) = 0或 π 者 ωx0 由x0=Acosϕ0=0.098>0 ∴ cosϕ0>0, 取ϕ0=0
A= x +(
v0
ω = 10rad / s
O x
振动方程为:x=9.8×10-2cos(10t) m 振动方程为: X (2)按题意 t=0 时 x0=0,v0>0 按题意 1 g ω x0=Acosϕ0=0 , cosϕ0=0 ϕ0=π/2或3π/2 ν = 2π = 2π ∆l z v0=-Aωsinϕ>0 , sin ϕ0 <0, 取ϕ0=3π/2 =1.6H 固有频率 ∴ x=9.8×10-2cos(10t+3π/2) m 不同, 对同一谐振动取不同的计时起点ϕ不同,但ω、A不变 不变
A 1
旋转矢量法 讨论
机械振动
相位差:表示两个相位之差 . 相位差:
2)对同一简谐运动,相位差可以给出两运动状 同一简谐运动, 简谐运动 态间变化所需的时间. 态间变化所需的时间. ∆ϕ = (ωt 2 + ϕ ) − (ωt1 + ϕ )
x = A cos(ωt1 + ϕ ) x = A cos(ωt 2 + ϕ )
π
6
)cm
x = Acos(ωt +ϕ0 ) π v = −ωAsin( ωt +ϕ0 ) = vm cos(ωt +ϕ0 + ) 2 −1 vm = ωA = 31.4cms
高二物理竞赛课件:简谐振动的旋转矢量图示法

单摆周期 T与角振幅 m的关系为:
T
T0
1
1 22
sin 2
m
2
1 22
32 42
sin 4
m
2
T0 为 m很小时单摆的周期。
根据上述周期的级数公式,可以将周期计算到 所要求的任何精度。
上页 下页 返回 退出
t 0
P
X
x
r
Ar 旋转的方向
逆时针方向
A 与参考方向X的夹角
振动相位
M 点在 X 轴上投影(P点)的运动规律:
x Acos(t 0 )
上页 下页 返回 退出
A
O
v0
X
O
v0
X
A
速度、加速度的旋转矢量表示法:
v
v, a沿X 轴的投
影为简谐运动的速度、 加速度表达式。
M 点:
vm A
am 2 A
23 6 t 0.83s
上页 下页 返回 退出
几种常见的谐振动
(1) 单摆
一根不会伸长的细线,上端固定,下端悬挂一个 很小重物,重物略加移动就可以在竖直平面内来回摆动。
上页 下页 返回 退出
单摆受力分析如右图所示,
根据牛顿第二运动定律可得
mg sin
ml
d2
dt 2
q 很小时(小于 5o),可取
sin
d2
dt 2
g
l
2
其中2 g
l
C
l F
of
mg
上页 下页 返回 退出
单摆在摆角很小时,在平衡位置附近作角谐振动,周期
T 2 2 g
l
转角q 的表达式可写为:
m cos(t 0 )
简谐振动旋转矢量法讲课文档

机械振动, 电磁振荡 机械波, 电磁波 德布罗意波——几率波
振动学是波动学的基础
第5章 机械振动
振动: 任何一个物理量(物体的位置, 电 流强度, 电场强度, 磁场强度等)在某一 固定值附近作往复变化. 机械振动: 物体在固定位置(平衡位置) 附近作来回往复的运动. 简谐运动: 是最基本, 最简单的振动.
ω 6π 6
第18页,共20页。
§ 5.3 单摆
O
l T
mg
小球受力矩:
Mmg siln
根据转动定律
M J
mgslinm2ldd2t2
化简得:
d2
dt2
gsin
l
0
当θ 很小时, sin
d2
dt2
g l
0
结论: 单摆振动是简谐运动
0 cos t
g
l
T 2π l g
θ为振动角位移,θ0叫做角振幅
第19页,共20页。
例3: 一简谐振动曲线如图所示, 则振动周期
x(m 4) 2
1
t(s)
2 4 cos
0 4cos
3
32
5
6
T 2 12 5
(A)2.62 s (B)2.40 s (C)0.42 s (D)0.382 s
答案: B
第20页,共20页。
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
依题意, v<0
v 0.24 3 0.208 m s1 2
第11页,共20页。
§5.2 简谐运动的旋转矢量 表示法
5.2.1 旋转矢量表示法
振动学是波动学的基础
第5章 机械振动
振动: 任何一个物理量(物体的位置, 电 流强度, 电场强度, 磁场强度等)在某一 固定值附近作往复变化. 机械振动: 物体在固定位置(平衡位置) 附近作来回往复的运动. 简谐运动: 是最基本, 最简单的振动.
ω 6π 6
第18页,共20页。
§ 5.3 单摆
O
l T
mg
小球受力矩:
Mmg siln
根据转动定律
M J
mgslinm2ldd2t2
化简得:
d2
dt2
gsin
l
0
当θ 很小时, sin
d2
dt2
g l
0
结论: 单摆振动是简谐运动
0 cos t
g
l
T 2π l g
θ为振动角位移,θ0叫做角振幅
第19页,共20页。
例3: 一简谐振动曲线如图所示, 则振动周期
x(m 4) 2
1
t(s)
2 4 cos
0 4cos
3
32
5
6
T 2 12 5
(A)2.62 s (B)2.40 s (C)0.42 s (D)0.382 s
答案: B
第20页,共20页。
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
依题意, v<0
v 0.24 3 0.208 m s1 2
第11页,共20页。
§5.2 简谐运动的旋转矢量 表示法
5.2.1 旋转矢量表示法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x 矢量以A o的为端原点点在,旋轴转
上的投影点的运动为 简谐运动.
A
t t 时
t
o
x
xAcots()
对应关系
A
t
←→ 振幅 ←→ 圆频率 ←→ 初相位 ←→ 相位
用旋转矢量图画简谐运动的xt图
T 2(π旋转矢量旋转一周所需的时间)
A
M Px
注意:旋转矢量在第 1 象限
速度v <0
A
简谐振动的描述方法有多种∶代数法、曲线表 示法、旋转矢量法、复数法等等。
一、代数法
xAcos(t)
振幅 系统固有角频率 相位 初相位 其中,振幅、角频率、初相是简谐振动的特征量
二、图示法: (振动曲线)
xAcots(0)
旋转矢量法
当t 0 时
A
o
x0 x
Hale Waihona Puke x0AcosAt t 时
t
o
x
xAcots()
由图可见
21
例题3 :
谐振子从 A/ 2 的位置过渡到 A 的位置, 最短历时是多少?
首先考查从 A/ 2 到 A 的相位差
从旋转矢量图上可以得出
210(3)3
由匀速运动的等时性 t T
2
所以,渡越时间为
t T1T 2 6
例题4: 简谐振动的振动曲线,写出其振动表达式.
xAcots(0)
A A 1 2A 2 22A 1A 2co2 s(1)
=A1cost 1+A2cost 2
A1cos1 A2cos2cos t A1sin1 A2sin2sint
tgA A11csion 11s A A22csion 2s2
两个同方向同频率简谐运动的合成
二、应用旋转矢量法:
x 1 A 1cot s1 ) ( x 2 A 2 co t s2 ) ( A2
M
PA
x
<
注意:旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
x0 A x0 A x0 A/ 2 正向运动
x0 A/2 正向运动
0 / 4
2/3
作参考圆
例题2 :
普通物理学教案
两振子 x10 A/ 2 , x20 A/2 都指向平衡位置运动。请判定它们的相位差。
解: 判定两振动之间的相位差,是一个在实 际工作中经常遇到的问题。
用旋转矢量法
(1) 21 0,称同;相 (2) 21 ,称反;相 (3) 21 0,称振2动 超前 ,振动 1落后 ; (4) 12 0,称振1动 超前 ,振动 2落后 .
用旋转矢量表示相位关系
同相位
反相位
r
r
A2
A1
x
r A2
r A
1
x
2 1
r
r
A2
A1
x
例题1 :
普通物理学教案
确定以下几种情况的初相位
解:
A = 5 (m); T = 2 (s),
2 (rad/s)
T
xAcots(0) t = 0 时: co 0sx0/A1/2,
0
3
初速度方向指向平衡位置,
v0Asin00,
0
3
A = 5 (m);
(rad/s)
x5cos(t3) (m)
例题5 :
普通物理学教案
某振子x-t 图和v-t 图如下,写出振子的 运动学方程。
A
P
x
注意:旋转M 矢量在第 2 象限
速度v <0
A
P
x
注意:旋转矢量在第 2 象限
M
速度v <0
A
P
x
注意:旋转矢量在第 2 象限
M
速度v <0
A
P
x
注意:旋转矢量在第 2 象限
速度v <0
M
A
P
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
注意:旋转矢量在第 2 象限
速度v <0
1)相位差 212kπ( k 0 , 1 , 2 , ) xx
oo
A1 A2
A
A A1 A2
T
t
A A 1 2 A 2 2 2 A 1 A 2 co 2 s1 )(
2)相位差 21 (2 k 1 )π(k 0 , 1 , )
xx
A1 o o
A
A2
A A1 A2
Tt
结论
A A 1 2A 2 22 A 1A 2co s(21)
A
xx1x2
xA cots ()
0
21
x2
x
A1
1
xx
A A 1 2 A 2 2 2 A 1 A 2 co 2 s1 )(
tanA A 1 1c sio n 1 1s A A 2 2s cio n2 2s
两个同方向同频 率简谐运动合成 后仍为简谐运动
讨论 A A 1 2 A 2 2 2 A 1 A 2 co 2 s1 )(
一、同方向、同频率谐振动的合成
某质点同时参与两个同频率且在同一条直线上的简谐运动
x1A1cost1 令 AsinA1sin1A2sin2
x2 A2c ost2
AcosA1co1 sA2cos2
合振动 xx1x2
x= A co cso tsA sin si nt
= A co st
1、应用解析法
x x1 x2
速度v 0
P x
A
M
<
注意:旋转矢量在第 4 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 4 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 4 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 4 象限
速度v 0
P
A
x
M
<
注意:旋转矢量在第 4 象限
速度v 0
P
A
x
M
<
注意:旋转矢量在第 4 象限
解: 由x - t 图,A = 2, x0 = -A / 2,向平衡位置移动
4 3
或 2
3
x-t 图上ω或T 信息不明确, 再看v-t 图 vmax 10m/s
由速度幅 vmax A, vmax/A5s-1
找到谐振动的特征量,问题就解决了。
振动方程为 x2cos(5t 2)
3
16-4 简谐振动的合成
M Px
注意:旋转矢量在第 1 象限
速度v <0
A
M
P
x
注意:旋转矢量在第 1 象限
速度v <0
M
A
P
x
注意:旋转矢量在第 1 象限
速度v
M
<
0
A
P
x
注意:旋转矢量在第 1 象限
M速度v < 0
A
P
x
注意:旋转矢量M在第 1 象限
速度v <0
A
P
x
注意:旋转矢M量在第 1 象限
速度v <0
速度v 0
A
M Px
一、二象限的旋转矢量对应的简谐振动速度沿负向 三、四象限的旋转矢量对应的简谐振动速度沿正向
相 位
对于沿 x 轴振动的两个同频率的简谐振动:
x 1 A 1 c o s (t 1 ) , x 2 A 2 c o s (t 2 ) ,
差 两者的相位差(即初相差)可能有下列四种情况:
