高中数学课时作业:对数与对数函数
对数与对数运算 课时作业(含解析) (9)
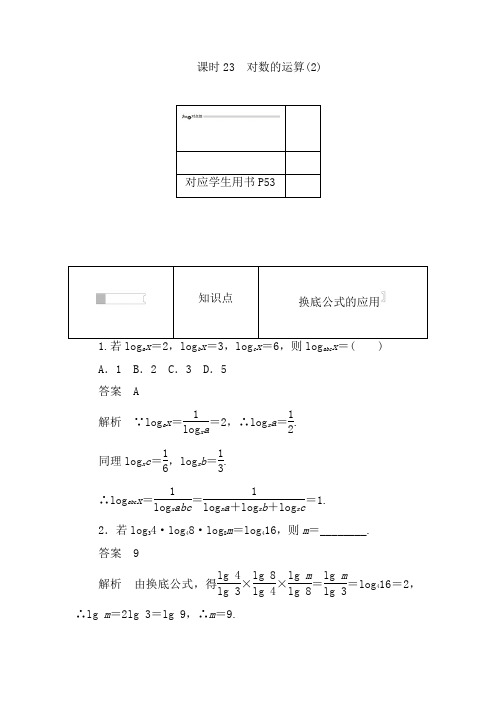
课时23 对数的运算(2)对应学生用书P53知识点换底公式的应用a b c abc A .1 B .2 C .3 D .5 答案 A解析 ∵log a x =1log x a =2,∴log x a =12.同理log x c =16,log x b =13.∴log abc x =1log x abc =1log x a +log x b +log x c =1.2.若log 34·log 48·log 8m =log 416,则m =________. 答案 9解析 由换底公式,得lg 4lg 3×lg 8lg 4×lg m lg 8=lg mlg 3=log 416=2,∴lg m =2lg 3=lg 9,∴m =9.3.设3x=4y=36,求2x +1y的值.解 由已知分别求出x 和y ,∵3x =36,4y =36,∴x =log 336,y =log 436, 由换底公式得:x =log 3636log 363=1log 363,y =log 3636log 364=1log 364,∴1x =log 363,1y=log 364,∴2x +1y=2log 363+log 364=log 36(32×4)=log 3636=1.4.计算:(1)log 89×log 2732; (2)log 927;(3)log 21125×log 3132×log 513;(4)(log 43+log 83)(log 32+log 92). 解 (1)log 89×log 2732=lg 9lg 8×lg 32lg 27=lg 32lg 23×lg 25lg 33=2lg 33lg 2×5lg 23lg 3=109; (2)log 927=log 327log 39=log 333log 332=3log 332log 33=32;(3)log 21125×log 3132×log 513=log 25-3×log 32-5×log 53-1 =-3log 25×(-5log 32)×(-log 53)=-15×lg 5lg 2×lg 2lg 3×lg 3lg 5=-15;(4)原式=⎝⎛⎭⎪⎫lg 3lg 4+lg 3lg 8⎝ ⎛⎭⎪⎫lg 2lg 3+lg 2lg 9 =⎝⎛⎭⎪⎫lg 32lg 2+lg 33lg 2⎝ ⎛⎭⎪⎫lg 2lg 3+lg 22lg 3 =12+14+13+16=54.易错点运用换底公式不熟练致误23A.14 B.12C .2D .4 易错分析 本题易在使用对数的运算公式时,尤其换底公式的使用过程中发生错误.答案 D正解 log 29×log 34=lg 9lg 2×lg 4lg 3=2lg 3lg 2×2lg 2lg 3=2×2=4.对应学生用书P53一、选择题 1.log 29log 23=( ) A.12 B .2 C.32 D.92 答案 B解析 由换底公式log 39=log 29log 23.∵log 39=2,∴log 29log 23=2.2.已知log 23=a ,log 37=b ,则log 27=( )A .a +bB .a -bC .ab D.ab答案 C解析 log 27=log 23×log 37=ab .3.设2a=5b=m ,且1a +1b=2,则m =( )A.10 B .10 C .20 D .100 答案 A解析 ∵2a =5b =m ,∴a =log 2m ,b =log 5m .1a +1b=log m 2+log m 5=log m 10=2,∴m 2=10. 又∵m >0,∴m =10,选A. 4.1log 1419+1log1513等于( )A .lg 3B .-lg 3 C.1lg 3 D .-1lg 3 答案C 解析 原式=log1914+log 1315=log 1312+log 1315=log 13110=log 310=1lg 3.选C. 5.已知2a =3b =k (k ≠1),且2a +b =ab ,则实数k 的值为( ) A .6 B .9 C .12 D .18 答案 D解析 a =log 2k ,b =log 3k ,由2a +b =ab 得2log 2k +log 3k =log 2k ·log 3k ,即2lg k lg 2+lg k lg 3=lg k 2lg 2lg 3,得2lg 3+lg 2=lg k ,即k =18.二、填空题6.方程log 3(x -1)=log 9(x +5)的解是________. 答案 4解析 由换底公式得log 9(x +5)=12log 3(x +5).∴原方程可化为2log 3(x -1)=log 3(x +5), 即log 3(x -1)2=log 3(x +5),∴(x -1)2=x +5.∴x 2-3x -4=0,解得x =4或x =-1.又∵⎩⎪⎨⎪⎧x -1>0,x +5>0,∴x >1,故x =4.7.若log a b ·log 3a =4,则b 的值为________. 答案 81解析 log a b ·log 3a =4,即log 3a ·log a b =4,即log 3b =4, ∴34=b ,∴b =81.8.已知2x=72y=A ,且1x +1y=1,则A 的值是________.答案 98解析 ∵2x =72y =A ,∴x =log 2A,2y =log 7A . ∴1x +1y =1log 2A +2log 7A =log A 2+2log A 7 =log A 2+log A 49=log A 98=1. ∴A =98. 三、解答题9.计算下列各式的值: (1)lg 2+lg 5-lg 8lg 5-lg 4;(2)lg 5(lg 8+lg 1000)+(lg 23)2+lg 16+lg 0.06.解 (1)原式=1-3lg 2lg 5-2lg 2=1-3lg 21-3lg 2=1;(2)原式=lg 5(3lg 2+3)+3(lg 2)2-lg 6+lg 6-2 =3lg 5×lg 2+3lg 5+3lg 22-2 =3lg 2(lg 5+lg 2)+3lg 5-2=3(lg 2+lg 5)-2=3-2=1.10.已知x ,y ,z 为正数,3x =4y =6z,2x =py . (1)求p ;(2)求证:1z -1x =12y.解 (1)设3x =4y =6z =k (显然k >0,且k ≠1),则x =log 3k ,y =log 4k ,z =log 6k .由2x =py ,得2log 3k =p log 4k =p ·log 3klog 34.∵log 3k ≠0,∴p =2log 34.(2)证明:1z -1x =1log 6k -1log 3k =log k 6-log k 3=log k 2=12log k 4=12y ,∴1z -1x =12y.►2.2.2 对数函数及其性质。
高三数学一轮复习 2.7《对数与对数函数》课时作业

对数与数函数一、选择题三、解答题10.已知f x=log a a x-1a>0,且a≠1.1求f x的定义域;2讨论函数f x的单调性.解析:1由a x-1>0,得a x>1.当a>1时,x>0;当0<a<1时,x<0.∴当a>1时,f x的定义域为0,+∞;当0<a<1时,f x的定义域为-∞,0.2当a>1时,设0<x1<x2,则1<ax1<ax2,故0<ax1-1<ax2-1,∴log a ax1-1<log a ax2-1,∴f x1<f x2,故当a>1时,f x在0,+∞上是增函数.类似地,当0<a<1时,f x在-∞,0上为增函数.12.已知函数f x=log4ax2+2x+3.1若f1=1,求f x的单调区间;2是否存在实数a,使f x的最小值为0?若存在,求出a的值;若不存在,说明理由.解析:1∵f1=1,∴log4a+5=1,因此a+5=4,a=-1,这时f x=log4-x2+2x+3.由-x2+2x+3>0得-1<x<3,函数定义域为-1,3.令g x=-x2+2x+3.则g x在-∞,1上递增,在1,+∞上递减,又y=log4x在0,+∞上递增,所以f x的单调递增区间是-1,1,递减区间是1,3.来源12.已知函数f x=log4ax2+2x+3.1若f1=1,求f x的单调区间;2是否存在实数a,使f x的最小值为0?若存在,求出a的值;若不存在,说明理由.解析:1∵f1=1,∴log4a+5=1,因此a+5=4,a=-1,这时f x=log4-x2+2x+3.由-x2+2x+3>0得-1<x<3,函数定义域为-1,3.来源来源令g x=-x2+2x+3.则g x在-∞,1上递增,在1,+∞上递减,又y=log4x在0,+∞上递增,所以f x的单调递增区间是-1,1,递减区间是1,3.。
高中数学4-2对数与对数函数4-2-3对数函数的性质与图象一课时作业新人教B版必修第二册

4.2.3 对数函数的性质与图象(一)1.(多选)下列函数为对数函数的是( )A .y =ln xB .y =log a (2x )(a >0且a ≠1)C .y =log (a -1)x (a >1且a ≠2)D .y =2log a x (a >0且a ≠1)2.若某对数函数的图象过点(4,2),则该对数函数的解析式为( )A .y =log 2xB .y =2log 4xC .y =log 2x 或y =2log 4xD .不确定3.函数f (x )=x -4lg x -1的定义域是( ) A .[4,+∞)B .(10,+∞)C.(4,10)∪(10,+∞)D .[4,10)∪(10,+∞)4.已知m ,n ∈R ,函数f (x )=m +log n x 的图象如图,则m ,n 的取值范围分别是( )A .m >0,0<n <1B .m <0,0<n <1C .m >0,n >1D .m <0,n >15.函数y =log a (x +1)-2(a >0且a ≠1)的图象恒过点________.6.函数f (x )=1-2log 5x 的定义域为________.7.(多选)若函数f (x )=a x -2,g (x )=log a |x |,其中a >0,且a ≠1,则函数f (x ),g (x )在同一坐标系中的大致图象可能是( )8.已知f (x )=⎩⎪⎨⎪⎧(3a -1)x +4a ,x ≤1,log a x ,x >1是(-∞,+∞)上的减函数,那么a 的取值范围是( )A.[17,13) B .[17,1) C .(0,1) D .(0,13) 9.(多选)已知实数a ,b 满足等式log 2a =log 3b ,则下列四个选项中,可能成立的有( )A .a >b >1B .a <b <1C .b <a <1D .a =b10.如果函数f (x )=(3-a )x ,g (x )=log a x 的增减性相同,则a 的取值范围是________.11.函数f (x )=log a x (a >0且a ≠1)在[2,3]上的最大值为1,则a =________.12.已知函数f (x )=log ax +1x -1(a >0,且a ≠1). (1)求f (x )的定义域;(2)判断函数的奇偶性.13.已知f (x )=|log 3x |,若f (a )>f (2),则a 的取值范围为________.14.已知函数f (x )=⎩⎪⎨⎪⎧3x ,x ≤0,log 3x ,x >0,则f (f (-1))=________;若f (f (x ))=x ,则x 的取值范围是______.4.2.3 对数函数的性质与图象(一)1.答案:AC解析:y =log a (2x )(a >0且≠1)的真数不符合对数函数定义,B 错误;y =2log a x (a >0且a ≠1)在对数形式前乘2,不符合对数函数定义,D 错误.2.答案:A解析:由对数函数的概念可设该函数的解析式为y =log a x ,则log a 4=2,解得a =2,故所求解析式为y =log 2x .3.答案:D解析:由⎩⎪⎨⎪⎧x -4≥0,lg x -1≠0,x >0,解得⎩⎪⎨⎪⎧x ≥4,x ≠10,x >0,∴x ≥4且x ≠10,∴函数f (x )的定义域为[4,10)∪(10,+∞).4.答案:C解析:由题中图象知函数为增函数,故n >1,又当x =1时,f (x )=m >0,故m >0.5.答案:(0,-2)解析:依题意,x +1=1,即x =0时,y =log a (0+1)-2=0-2=-2,故图象恒过定点(0,-2).6.答案:(0,5]解析:由1-2log 5x ≥0,得log 5x ≤12, 故0<x ≤5,所以定义域为(0,5].7.答案:AD解析:由题意知f (x )=a x -2是指数型函数,g (x )=log a |x |是对数型函数,且是一个偶函数.当0<a <1时,f (x )=a x -2单调递减,g (x )=log a |x |在(0,+∞)上递减,此时A 符合题意,当a >1时,f (x )=ax -2单调递增,g (x )=log a |x |在(0,+∞)上单调递增,此时D 符合题意,故选AD.8.答案:A解析:因为f (x )为(-∞,+∞)上的减函数,所以有⎩⎪⎨⎪⎧3a -1<00<a <1(3a -1)×1+4a ≥log a 1,解得17≤a <13. 9.答案:CD解析:实数a ,b 满足等式log 2a =log 3b ,即y =log 2x 在x =a 处的函数值和y =log 3x 在x =b 处的函数值相等,当a =b =1时,log 2a =log 3b =0,此时D 成立;令log 2a =log 3b=1,可得a =2,b =3,由此知A 不成立;令log 2a =log 3b =-1,可得a =12,b =13,由此知C 成立,B 不成立,综上知可能成立的有CD 两项.10.答案:(1,2)解析:若f (x ),g (x )均为增函数,则⎩⎪⎨⎪⎧3-a >1,a >1,即1<a <2. 若f (x ),g (x )均为减函数,则⎩⎪⎨⎪⎧0<3-a <1,0<a <1无解. 11.答案:3解析:当a >1时,f (x )的最大值是f (3)=1,则log a 3=1,∴a =3.当0<a <1时,f (x )的最大值是f (2)=1,则log a 2=1,∴a =2(不合题意舍去).综上得a =3.12.解析:(1)要使函数有意义,则有x +1x -1>0, 即⎩⎪⎨⎪⎧x +1>0,x -1>0,或⎩⎪⎨⎪⎧x +1<0,x -1<0, 解得x >1或x <-1,此函数的定义域为(-∞,-1)∪(1,+∞),关于原点对称.(2)f (-x )=log a -x +1-x -1=log a x -1x +1=-log a x +1x -1=-f (x ), ∴f (x )为奇函数.13.答案:(0,12)∪(2,+∞) 解析:作出函数f (x )的图象,如图所示,由于f (2)=f (12),故结合图象可知0<a <12或a >2.14.答案:-1 (-∞,1]解析:f (-1)=3-1>0,故f (f (-1))=f (3-1)=log 33-1=-1.当x ≤0时,f (x )=3x >0, f (f (x ))=f (3x )=log 33x =x ;当0<x <1时,f (x )=log 3x <0,f (f (x ))=f (log 3x )=3log 3x =x ;当x =1时,f (x )=log 31=0,f (f (x ))=f (0)=30=1;当x>1时,f(x)=log3x>0,f(f(x))=log3(log3x)≠x,故使f(f(x))=x的x的取值范围是(-∞,1].。
对数与对数运算 课时作业(含解析) (3)

[课时作业][A 组 基础巩固]1.2log 510+log 50.25= ( )A .0B .1C .2D .4解析:2log 510+log 50.25=log 5102+log 50.25=log 5(102×0.25)=log 525=2. 答案:C2.(lg 5)2+lg 2 lg 5+lg 20的值是( )A .0B.1 C .2 D .3解析:(lg 5)2+lg 2lg 5+lg 20=lg 5·(lg 5+lg 2)+lg 20=lg 5+lg 20=lg 100=2. 答案:C3.2321+2log 2的值是( )A .12 2 B.9+ 2C .9 2D .84 2 解析:∵12+2log 23=log 22+log 29=log 292,又∵a log a x =x ,∴原式=9 2.答案:C4.若log 513·log 36·log 6x =2,则x 等于( )A . 9B.19 C .25D .125 解析:原式=lg 13lg 5×lg 6lg 3×lg x lg 6=-lg x lg 5=2∴-lg x =2lg 5=lg 52=lg 25,∴x =125.答案:D5.设a ,b ,c 均为不等于1的正实数,则下列等式中恒成立的是( )A .log a b ·log c b =log c aB .log a b ·log c a =log c bC .log a (bc )=log a b ·log a cD .log a (b +c )=log a b +log a b +log a c 解析:由对数的运算公式log a (bc )=log a b +log a c 可判断选项C ,D 错误.选项A ,由对数的换底公式知log a b ·log c b =log c a ⇒lg b lg a ·lg b lg c =lg a lg c ⇒(lg b )2=(lg a )2,此式不恒成立.选项B ,由对数的换底公式知log a b ·log c a =lg b lg a ·lg a lg c =lg b lg c =log c b ,故恒成立.答案:B6.方程log 3(x -1)=log 9(x +5)的解是________.解析:由题意知⎩⎪⎨⎪⎧ x -1>0,x +5>0,(x -1)2=x +5,解之得x =4.答案:47.lg 3+2lg 2-1lg 1.2=________. 解析:原式=lg 3+lg 22-lg 10lg 1.2=lg 3+lg 4-lg 10lg 1.2=lg 3×410lg 1.2=1.答案:18.计算log 225·log 322·log 59的结果为________.解析:原式=lg 25lg 2·lg 22lg 3·lg 9lg 5=2lg 5lg 2·32lg 2lg 3·2lg 3lg 5=6.答案:69.计算:(1)lg 2+lg 5-lg 8lg 50-lg 40+log 222; (2)lg 5(lg 8+lg 1 000)+)2+lg 16+lg 0.06.解析:(1)原式=lg (2×5)-lg 8lg 54+log 2(2)-1 =lg 54lg 54-1=0.(2)原式=lg 5(3lg 2+3)+3(lg 2)2-lg 6+lg 6-2=3·lg 5·lg 2+3lg 5+3lg 22-2=3lg 2(lg 5+lg 2)+3lg 5-2=3lg 2+3lg 5-2=3(lg 2+lg 5)-2=3-2=1.10.已知2x =3y =6z ≠1,求证:1x +1y =1z .证明:设2x =3y =6z =k (k ≠1),则x =log 2k =lg k lg 2,y =log 3k =lg k lg 3,z =log 6k =lg k lg 6∴1x +1y =lg 2+lg 3lg k =lg 6lg k =1z .[B 组 能力提升]1.已知log 89=a ,log 25=b ,则lg 3等于( )A.a b -1B.32(b -1)C.3a 2(b +1)D.3(a -1)2b 解析:∵log 89=a ,∴a =lg 9lg 8=2lg 33lg 2,b =lg 5lg 2=1-lg 2lg 2,∴lg 2=1b +1, ∴lg 3=32a lg 2=3a 2×1b +1=3a 2(b +1). 答案:C2.若lg a ,lg b 是方程2x 2-4x +1=0的两个根,则(lg a b )2的值等于( )A .2 B.12 C .4 D .14解析:由韦达定理知⎩⎨⎧ lg a +lg b =2,lg a ·lg b =12,∴(lg a b )2=(lg a -lg b )2=(lg a +lg b )2-4lg a lg b =22-4×12=2.答案:A3.设lg a +lg b =2lg(a -2b ),则log 4a b 的值是________.解析:依题意,得a >0,b >0,a -2b >0,原式可化为ab =(a -2b )2,即a 2-5ab+4b 2=0,则⎝ ⎛⎭⎪⎫a b 2-5⎝ ⎛⎭⎪⎫a b +4=0,∴a b =4或a b =1.∵a -2b >0,a b >2,∴a b =4,∴log 4a b =1.答案:14.已知x ,y ,z 都是大于1的正数,m >0,且log x m =24,log y m =40,log xyz m =12,求log z m 的值.解析:log m (xyz )=log m x +log m y +log m z =112,而log m x =124,log m y =140,故log m z =112-log m x -log m y =112-124-140=160,即log z m =60.5.已知ab =8,a 2log b =4,求a 、b 的值.解析:由a 2log b =4两边取对数得log 2(a 2log b )=log 24⇒(log 2a )(log 2b )=2,①由ab =8得log 2(ab )=log 28⇒log 2a +log 2b =3.②由①②得⎩⎪⎨⎪⎧ log 2a =1,log 2b =2或⎩⎪⎨⎪⎧ log 2a =2,log 2b =1, 解得⎩⎪⎨⎪⎧ a =2,b =4或⎩⎪⎨⎪⎧ a =4,b =2.。
人教A版高中数学必修一对数与对数运算课时作业新

对数与对数运算基础达标1. 有以下四个结论:①lg(lg 10)=0;②ln (ln e)=0;③若10=lg x ,则x =10;④若e=ln x ,则x =e 2,其中正确的是( ).A .①③B .②④C .①②D .③④解析 lg(lg 10)=lg 1=0;ln(ln e)=ln 1=0,故①、②正确,若10=lg x ,则x =1010,③错误;若e =ln x ,则x =e e ,故④错误.答案 C2.在M =log (x -3)(x +1)中,要使式子有意义,x 的取值范围为( ).A .(-∞,3]B .(3,4)∪(4,+∞)C .(4,+∞)D .(3,4)解析 由题知⎩⎪⎨⎪⎧x +1>0,x -3>0,x -3≠1,解得3<x <4或x >4.答案 B3.若log 3(log 2x )=1,则等于( ).A.13B.123C.122D.133解析 ∵log 3(log 2x )=1,∴log 2x =3, ∴x =23=8,则=18=122答案 C4.log 6[log 4(log 381)]=________.解析 原式=log 6[log 4(log 334)]=log 6(log 44)=log 61=0. 答案 0 5.若2log 3x=14,则x 等于________. 解析 ∵2log 3x =14=2-2,∴log 3x =-2,∴x =3-2=19.答案 196.设log a 2=m ,log a 3=n ,则a2m +n的值为________.解析 ∵log a 2=m ,log a 3=n ,∴a m=2,a n=3, ∴a2m +n=(a m )2·a n=4×3=12.答案 12能力提升8.若log x 7y =z ,则( ).A .y 7=x zB .y =x 7zC .y =7x zD .y =z 7x解析 由log x 7y =z ,得x z=7y , ∴⎝⎛⎭⎫7y 7=(x z )7,则y =x 7z . 答案 B 9.已知=49(a >0),则a =________.解析 设a =x ,则a =,又=49,∴=,即,∴23x =2,解得x =3.答案 310.已知log a x=4,log a y=5(a>0,且a≠1),求A=(x·3x-1y2)12的值.解由log a x=4,得x=a4,由log a y=5,得y=a5,所以A=。
课时作业(九) 对数与对数函数 (3)

课时作业(九) 对数与对数函数 基础过关组 一、单项选择题1.函数y =log 3(2x -1)+1的定义域是( ) A .[1,2] B .[1,2)C .[23,+∞)D .(23,+∞)解析 由Error!即Error!解得x ≥23。
答案 C2.若函数y =f (x )是函数y =a x (a >0且a ≠1)的反函数,且f (2)=1,则f (x )=( ) A .log 2x B .12xC .log 12x D .2x -2解析 由题意知f (x )=log a x (a >0且a ≠1),因为f (2)=1,所以log a 2=1,所以a =2。
所以f (x )=log 2x 。
故选A 。
答案 A3.(2020·全国Ⅰ卷)设a log 34=2,则4-a =( ) A .116B .19C .18D .16解析 解法一:因为a log 34=2,所以log 34a =2,则有4a =32=9,所以4-a =14a =19。
故选B 。
解法二:因为a log 34=2,所以-a log 34=-2,所以log 34-a =-2,所以4-a =3-2=132=19。
故选B 。
解法三:因为a log 34=2,所以a 2=1log 34=log 43,所以4a2 =3,两边同时平方得4a =9,所以4-a =14a =19。
故选B 。
解法四:因为a log 34=2,所以a =2log 34=log 39log 34=log 49,4a =9,所以4-a =14a =19。
故选B 。
答案 B4.如果log12x <log 12y <0,那么( )A .y <x <1B .x <y <1C .1<x <yD .1<y <x解析 因为log 12x <log 12y <log 121,所以x >y >1。
高中数学 课时作业26 2.2.1.2 对数与对数运算(第2课时)新人教A版必修1
课时作业(二十六) 2.2.1.2 对数与对数运算(第2课时)1.log 35-log 345=( ) A.1 B.-1 C.2 D.-2答案 D2.若lgx =lga +2lgb -3lgc ,则x =( ) A.a +2b -3c B.2ab 3cC.ab 2c 3 D.ab 2-c 3答案 C3.当a>0,a ≠1时,下列说法正确的是( ) ①若M =N ,则log a M =log a N ; ②若log a M =log a N ,则M =N ; ③若log a M 2=log a N 2,则M =N ; ④若M =N ,则log a M 2=log a N 2. A.①与② B.②与④ C.② D.①②③④答案 C4.lg(100x)比lg x100大( )A.200B.104C.4D.1104 答案 C5.已知|lga|=lgb(a>0,b>0),那么( ) A.a =b B.a =b 或ab =1 C.a =±b D.ab =1答案 B6.已知2log 6x =1-log 63,则x 的值是( ) A. 3 B. 2 C.2或- 2 D.3或 2答案 B7.设方程lg 2x +(lg2+lg3)lgx +lg2·lg3=0的两根为x 1,x 2,那么x 1·x 2的值为( ) A.lg2·lg3B.lg2+lg3C.16D.-6答案 C解析 设lgx =t ,则t 2+(lg2+lg3)t +lg2lg3=0.据⎩⎪⎨⎪⎧t 1=lgx 1,t 2=lgx 2,又t 1+t 2=-lg2-lg3=lgx 1+lgx 2,∴x 1x 2=16.8.已知log 32=a ,log 35=b ,则log 310等于( ) A.a +b B.a -b C.ab D.a b答案 A解析 log 310=log 3(2×5)=log 32+log 35.9.已知lga =2.431 0,lgb =1.431 0,则ba 等于( )A.1100B.110C.10D.100答案 B解析 b a =101.431102.431=10-1=110,故选B.10.已知2x=3,log 25=y ,则x +y 等于( ) A.log 215 B.log 253C.log 235D.log 310答案 A解析 由已知x =log 23,x +y =log 23+log 25=log 215. 11.log 2322-log 22=________. 答案 5解析 原式=log 23222=log 232=5.12.(1)2log 510+log 50.25=________. 答案 2(2)log 2149+log 213-log 217=________. 答案 1解析 原式=log 2149×37=1.(3)lg75-lg5-lg3+lg2=________. 答案 1解析 原式=lg 75×25×3=1.13.求值:lg2.5-lg 58+lg 12=________.答案 lg214.(1)若lg2=a ,lg3=b ,则lg 23=________.答案 a -b解析 原式=lg2-lg3=a -b.(2)(log 3312)2+log 0.2514+9log 55-log 31=______.答案234解析 原式=(12)2+log 0.250.25+9log 5512-0=14+1+92=234.15.若ln x -ln y =a ,则ln(x 2)3-ln(y 2)3等于________.答案 3a 16.计算.(1)lg 37+lg70-lg3;(2)lg 22+lg5lg20-1;(3)lg52+23lg8+lg5·lg20+(lg2)2.答案 (1)1 (2)0 (3)3解析 (3)原式=2(lg5+lg2)+lg5(lg5+2lg2)+(lg2)2=2+(lg5+lg2)2=2+1=3. 17.若lga ,lgb 是方程2x 2-4x +1=0的两个根,则(lg a b )2的值等于( )A.2B.12C.4D.14答案 A解析 ∵lga +lgb =2,lga ·lgb =12,∴(lg a b )2=(lga -lgb)2=(lga +lgb)2-4lga ·lgb =2.►重点班·选做题18.已知log a 2=m ,log a 3=n. (1)求a2m -n的值; (2)求log a 18.解析 (1)∵log a 2=m ,log a 3=n ,∴a m=2,a n=3. ∴a2m -n=a 2m ÷a n =(a m )2÷a n =22÷3=43.(2)log a 18=log a (2×32)=log a 2+log a 32=log a 2+2log a 3=m +2n.log 618+2log 62的结果是( ) A.-2 B.2 C. 2 D.log 62答案 B解析 原式=log 618+log 62=log 636=2.。
高三数学一轮复习课时作业(9)对数与对数函数 江苏专版
课时作业(九) [第9讲 对数与对数函数][时间:45分钟 分值:100分]基础热身1.若lg2=a ,lg3=b ,则lg108=________,lg 1825=________(用a ,b 表示).2.用“<”“>”填空:log 0.27________log 0.29;log 35________log 65;(lg m )1.9________(lg m )2.1(其中m >10).3.函数y =log 2(x 2+2x )的单调递增区间为________.4.设f (x )=lg ⎝ ⎛⎭⎪⎫21-x +a 为奇函数,则a 的值是________.能力提升5.函数f (x )=log 2x 2+2的值域为________.6.[2011·江苏卷] 函数f (x )=log 5(2x +1)的单调增区间是________.7.在同一坐标系中,三个函数y =log a x ,y =log b x ,y =log c x 的图象如图K9-1所示,那么a ,b ,c 的大小关系是________.8.设f (x )=log 3(3x+1)+12ax 是偶函数,则a 的值为________.9.已知函数f (x )=log a x (a >0,a ≠1),若f (2)<f (3),则实数a 的取值范围是________.10.已知函数f (x )=a x+log a x (a >0且a ≠1)在[1,2]上的最大值与最小值之和为log a 2+6,则a 的值为________.11.[2011·宿迁模拟] 若函数f (x )=log (a 2-3)(ax +4)在[-1,1]上是单调增函数,则实数a 的取值范围是________.12.[2012·苏南四校联考] 已知函数f (x )=|log 2x |,正实数m ,n 满足m <n ,且f (m )=f (n ),若f (x )在区间[m 2,n ]上的最大值为2,则n +m =________.13.(8分)(1)用log a x ,log a y ,log a z 表示下列各式:log a xy z ;log a x 2y 3z;(2)求值:lg8+lg125-lg2-lg5lg 10lg0.1.14.(8分)(1)若log a 45<1(a >0且a ≠1),求实数a 的取值范围;(2)若log a 2<log b 2<0,求a 、b 、1三数的大小关系.15.(12分)在函数f (x )=log 12(x 2-2ax +3)中.(1)若其在[-1,+∞)内有意义,求实数a 的取值范围; (2)若其在(-∞,1]内为增函数,求实数a 的取值范围. 16.(12分)[2012·东海调研] 设函数f (x )的定义域是(0,+∞),对于任意正实数m ,n 恒有f (mn )=f (m )+f (n ),且当x >1时,f (x )>0,f (2)=1.(1)求f ⎝ ⎛⎭⎪⎫12的值; (2)求证:f (x )在(0,+∞)上是增函数; (3)求方程4sin x =f (x )的根的个数.课时作业(九)【基础热身】1.2a +3b 3a +2b -2 [解析] lg108=lg(22×33)=2lg2+3lg3=2a +3b , lg 1825=lg18-lg25=lg(2×32)-lg52=lg2+2lg3-2lg5=lg2+2lg3-2(1-lg2)=3lg2+2lg3-2=3a +2b -2.2.> > < [解析] 对于log 0.27与log 0.29的大小比较,可利用函数y =log 0.2x 在定义域内单调减;对于log 35与log 65的大小比较,可先利用y =log 5x 单调增,再结合倒数法则;而对于(lg m )1.9与(lg m )2.1的大小比较,要对lg m 与1的大小关系进行讨论,因为m >10,所以填“<”.3.(0,+∞) [解析] 令y =log 2u ,u =x 2+2x ,可知外函数为增函数,所以内函数也要为增函数且满足定义域,即:⎩⎪⎨⎪⎧x >-1,x 2+2x >0,所以单调递增区间为(0,+∞).4.-1 [解析] ∵f (x )是奇函数,∴f (0)=0,解得:a =-1. 【能力提升】5.⎣⎢⎡⎭⎪⎫12,+∞ [解析] 令u =x 2+2≥2,所以y =log 2u ≥12.6.⎝ ⎛⎭⎪⎫-12,+∞ [解析] 因为y =log 5x 为增函数,故结合原函数的定义域可知原函数的单调增区间为⎝ ⎛⎭⎪⎫-12,+∞. 7.a >c >b [解析] 在图象上作出直线y =1,则它与图象的交点的横坐标即为相应的a ,b ,c ,从左向右依次为b ,c ,a .所以a >c >b .8.-1 [解析] 由题意可得,f (-1)=f (1),即log 3(3-1+1)-12a =log 3(3+1)+12a ,解得a =-1.9.a >1 [解析] 若a >1时,函数f (x )=log a x 为单调递增函数,则f (2)<f (3)成立; 若0<a <1时,函数f (x )=log a x 为单调递减函数,则f (2)<f (3)不成立. 则实数a 的取值范围是a >1.10.2 [解析] 无论a >1还是0<a <1总有a 1+log a 1+a 2+log a 2=log a 2+6,解得a =2.11.(-2,-3)∪(2,4) [解析] 首先由a 2-3>0,可得a >3或a <- 3.当a >3时,函数g (x )=ax +4在[-1,1]上是增函数,则需a 2-3>1,故a >2.又函数g (x )=ax +4>0在[-1,1]上恒成立,故g (-1)=4-a >0,即2<a <4.当a <-3时,函数g (x )=ax +4在[-1,1]上是减函数,则需0<a 2-3<1,故-2<a <-3.又函数g (x )=ax +4>0在[-1,1]上恒成立,故g (1)=a +4>0,即a >-4.综上所述,实数a 的取值范围为(-2,-3)∪(2,4).12.52[解析] 本题结合函数的性质考查数形结合方法的应用:由函数f (x )=|log 2x |得到其图象如下图所示:又因为f (m )=f (n ),所以mn =1,∴m <1,n >1.再结合图象可知,最大值出现在x =m2或x =n 处.当最大值出现在x =m 2时,即m 2=14⇒m =12⇒f (m )=1=f (n )⇒n =2,∴⎩⎪⎨⎪⎧m =12,n =2,⇒m +n =52.当最大值出现在x =n 处时,即n =4⇒m =14,m 2=116,f (m 2)>2,不符合题意.故m +n=52. 13.[解答] (1)log a xy z=log a (xy )-log a z =log a x +log a y -log a z ; log ax 2y3z=log a (x2y )-log a 3z=log a x 2+log a y -log a 3z =2log a x +12log a y -13log a z .(2)原式=3lg2+3lg5-lg2-lg512×-1=2lg2+lg5-12=-4lg10=-4.14.[解答] (1)当a >1时,y =log a x 在(0,+∞)上是单调增函数,log a 45<log a a ,∴a >45,∴a >1.当0<a <1时,y =log a x 在(0,+∞)上是单调减函数,log a 45<log a a ,∴0<a <45,∴0<a <45.综上所述:实数a 的取值范围为⎝ ⎛⎭⎪⎫0,45∪(1,+∞). (2)用倒数法则将不等式log a 2<log b 2<0改写成0>log 2a >log 2b ,由对数函数的单调性可求得0<b <a <1.15.[解答] (1)命题等价于“u =g (x )=x 2-2ax +3>0对x ∈[-1,+∞)恒成立”.对函数g (x )的对称轴x 0=a 进行讨论有:⎩⎪⎨⎪⎧ a <-1,g -1>0或⎩⎪⎨⎪⎧a ≥-1,Δ=4a 2-12<0,解得⎩⎪⎨⎪⎧a <-1,a >-2或⎩⎨⎧a ≥-1,-3<a <3,∴a 的取值范围是(-2,3).(2)令g (x )=x 2-2ax +3,原命题等价于⎩⎪⎨⎪⎧gx 在-∞,1]上为减函数,g x >0对x ∈-∞,1]恒成立,于是有⎩⎪⎨⎪⎧x 0=a ≥1,g 1>0,解得⎩⎪⎨⎪⎧a ≥1,a <2,∴a 的取值范围是[1,2).16.[解答] (1)令m =n =1,则f (1)=f (1)+f (1), ∴f (1)=0.令m =2,n =12,则f (1)=f ⎝ ⎛⎭⎪⎫2×12=f (2)+f ⎝ ⎛⎭⎪⎫12,∴f ⎝ ⎛⎭⎪⎫12=f (1)-f (2)=-1.(2)证明:设0<x 1<x 2,则x 2x 1>1.∵当x >1时,f (x )>0,∴f ⎝ ⎛⎭⎪⎫x 2x 1>0. ∴f (x 2)=f ⎝ ⎛⎭⎪⎫x 1×x 2x 1=f (x 1)+f ⎝ ⎛⎭⎪⎫x 2x 1>f (x 1), ∴f (x )在(0,+∞)上是增函数.(3)∵y =4sin x又f (4)=f (2×2)=2,f (16)由y =f (x )在(0,+∞)上单调递增,且f (1)=0,f (16)=4, 可得y =f (x )的图象大致形状如上图所示,由图象在[0,2π]内有1个交点,在(2π,4π]内有2个交点,在(4π,5π]内有2个交点,又5π<16<6π,后面y =f (x )的图象均在y =4sin x 图象的上方.故方程4sin x =f (x )的根的个数为5个.。
人教A版高中数学第一册(必修1)课时作业2:4.4.1 对数函数的概念
4.4 对数函数 4.4.1 对数函数的概念1.给出下列函数:①y =223log x ;②y =log 3(x -1);③y =log (x +1)x ;④y =log πx .其中是对数函数的有( ) A .1个B .2个C .3个D .4个 考点 对数函数的概念 题点 对数函数的概念 『答 案』 A『解 析』 ①②不是对数函数,因为对数的真数不是仅有自变量x ;③不是对数函数,因为对数的底数不是常数;④是对数函数. 2.已知函数f (x )=11-x的定义域为M ,g (x )=ln(1+x )的定义域为N ,则M ∩N 等于( ) A .{x |x >-1} B .{x |x <1} C .{x |-1<x <1}D .∅考点 对数函数的定义域 题点 对数函数的定义域 『答 案』 C『解 析』 ∵M ={x |1-x >0}={x |x <1}, N ={x |1+x >0}={x |x >-1}, ∴M ∩N ={x |-1<x <1}.3.下列函数中,与函数y =x 相等的是( ) A .y =(x )2 B .y =x 2C .y =2log 2xD .y =log 22x『答 案』 D『解 析』 因为y =log 22x 的定义域为R ,且根据对数恒等式知y =x . 4.对数函数的图象过点M (16,4),则此对数函数的『解 析』式为( ) A .y =log 4x B .y =14log xC .y =12log xD .y =log 2x『答 案』 D『解 析』 由于对数函数的图象过点M (16,4), 所以4=log a 16,得a =2.所以对数函数的『解 析』式为y =log 2x ,故选D.5.已知函数f (x )=log a (x +2),若图象过点(6,3),则f (2)的值为( ) A .-2B .2C.12D .-12考点 对数函数的性质 题点 对数函数图象过定点问题 『答 案』 B『解 析』 代入(6,3),得3=log a (6+2)=log a 8, 即a 3=8,∴a =2.∴f (x )=log 2(x +2),∴f (2)=log 2(2+2)=2.6.若f (x )=log a x +a 2-4a -5是对数函数,则a =________. 『答 案』 5『解 析』 由对数函数的定义可知,⎩⎪⎨⎪⎧a 2-4a -5=0,a >0,a ≠1,解得a =5.7.函数y =()12log 3x a -的定义域是⎝⎛⎭⎫23,+∞,则a =________. 『答 案』 2『解 析』 由y =()12log 3x a -知,3x -a >0,即x >a3.∴a 3=23,即a =2.8.某公司为了业务发展制定了一个激励销售人员的奖励方案,在销售额为x 万元时,奖励y 万元.若公司拟定的奖励方案为y =2log 4x -2,某业务员要得到5万元奖励,则他的销售额应为________万元. 『答 案』 128『解 析』 由题意得5=2log 4x -2, 即7=log 2x ,得x =128. 9.求下列函数的定义域: (1)f (x )=log (x -1)(3-x ); (2)f (x )=2x +3x -1+log 2(3x -1). 解 (1)由题意知⎩⎪⎨⎪⎧3-x >0,x -1>0,x -1≠1,解得1<x <3,且x ≠2,故f (x )的定义域是(1,2)∪(2,3). (2)由题意知⎩⎪⎨⎪⎧2x +3≥0,x -1≠0,3x -1>0,解得x >13,且x ≠1.故f (x )的定义域是⎝⎛⎭⎫13,1∪(1,+∞).10.20世纪70年代,里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级M ,其计算公式为M =lg A -lg A 0.其中A 是被测地震的最大振幅,A 0是“标准地震”的振幅.(1)假设在一次地震中,一个距离震中1000千米的测震仪记录的地震最大振幅是20,此时标准地震的振幅是0.002,计算这次地震的震级;(2)5级地震给人的震感已比较明显,我国发生在汶川的8级地震的最大振幅是5级地震的最大振幅的多少倍?解 (1)M =lg A -lg A 0=lg A A 0=lg 200.002=lg104=4.即这次地震的震级为4级.(2)由题意得⎩⎪⎨⎪⎧5=lg A 5-lg A 0,8=lg A 8-lg A 0,所以lg A 8-lg A 5=3, 即lg A 8A 5=3.所以A 8A 5=103=1000.即8级地震的最大振幅是5级地震的最大振幅的1000倍.11.函数y =log 2(x -1)2-x的定义域是( )A .(1,2』B .(1,2)C .(2,+∞)D .(-∞,2) 『答 案』 B『解 析』 由⎩⎪⎨⎪⎧ x -1>0,2-x >0,得⎩⎪⎨⎪⎧x >1,x <2,∴1<x <2.∴函数的定义域为(1,2).12.某地为了抑制一种有害昆虫的繁殖,引入了一种以该昆虫为食物的特殊动物,已知该动物的繁殖数量y (只)与引入时间x (年)的关系为y =a log 2(x +1),若该动物在引入一年后的数量为100只,则7年后它们发展到( ) A .300只B .400只C .600只D .700只 『答 案』 A『解 析』 将x =1,y =100代入y =a log 2(x +1)得, 100=a log 2(1+1),解得a =100, 所以x =7时,y =100log 2(7+1)=300.13.若函数f (x )=(a 2-a +1)log (a +1)x 是对数函数,则实数a =________. 『答 案』 1『解 析』 由a 2-a +1=1, 解得a =0或a =1. 又底数a +1>0,且a +1≠1,所以a =1.14.函数f (x )=lg ⎝⎛⎭⎫2kx 2-kx +38的定义域为R ,则实数k 的取值范围是________. 『答 案』 『0,3)『解 析』 依题意,2kx 2-kx +38>0的解集为R ,即不等式2kx 2-kx +38>0恒成立,当k =0时,38>0恒成立,∴k =0满足条件.当k ≠0时,则⎩⎪⎨⎪⎧k >0,Δ=k 2-4×2k ×38<0,解得0<k <3. 综上,k 的取值范围是『0,3).15.函数f (x )=a -lg x 的定义域为(0,10』,则实数a 的值为( ) A .0B .10C .1D.110『答 案』 C『解 析』 由已知,得a -lg x ≥0的解集为(0,10』, 由a -lg x ≥0,得lg x ≤a , 又当0<x ≤10时,lg x ≤1, 所以a =1,故选C.16.国际视力表值(又叫小数视力值,用V 表示,范围是『0.1,1.5』)和我国现行视力表值(又叫对数视力值,由缪天容创立,用L 表示,范围是『4.0,5.2』)的换算关系式为L =5.0+lg V . (1)请根据此关系式将下面视力对照表补充完整;V 1.5 ② 0.4 ④ L①5.0③4.0(2)甲、乙两位同学检查视力,其中甲的对数视力值为4.5,乙的小数视力值是甲的2倍,求乙的对数视力值.(所求值均精确到小数点后面一位数,参考数据:lg2≈0.3010,lg3≈0.4771) 解 (1)因为5.0+lg1.5=5.0+lg 1510=5.0+lg3=5.0+lg3-lg22≈5.0+0.4771-0.3010≈5.2,所以①应填5.2;因为5.0=5.0+lg V,所以V=1,②处应填1.0;=5.0+lg4-1因为5.0+lg0.4=5.0+lg410=5.0+2lg2-1≈5.0+2×0.3010-1≈4.6,所以③处应填4.6;因为4.0=5.0+lg V,所以lg V=-1.所以V=0.1.所以④处应填0.1.对照表补充完整如下:(2)先将甲的对数视力值换算成小数视力值,则有4.5=5.0+lg V甲,所以V甲=10-0.5,则V乙=2×10-0.5.所以乙的对数视力值L乙=5.0+lg(2×10-0.5) =5.0+lg2-0.5≈5.0+0.3010-0.5≈4.8.。
高中数学4-2对数与对数函数4-2-1对数运算4-2-2对数运算法则课时作业新人教B版必修第二册
4.2.1 对数运算 4.2.2 对数运算法则1.将(12)3=18化为对数式正确的是( )A .log 123=18B .log 1218=3C .log 1812=3 D .log 312=182.设a =log 32,则log 38-2log 36用a 表示的形式是( ) A .a -2 B .3a -(1+a )2C .5a -2D .-a 2+3a -13.计算log 225·log 322·log 59的结果为( ) A .3 B .4 C .5 D .64.若x =60,则1log 3x +1log 4x +1log 5x 的值为( )A .1B .12C .2D .-15.求下列各式中x 的值. (1)log 5(log 3x )=0; (2)-ln e 2=x ;(3)lg [log 2(lg x )]=0; (4)log 3(2x -1)=1; (5)4x-2x +1-3=0.6.计算下列各式的值:(1)12lg 3249-43lg 8+lg 245; (2)lg 52+23lg 8+lg 5·lg 20+(lg 2)2.7.若lg x =m ,lg y =n ,则lg x -lg (y10)2的值等于( )A .12m -2n -2B .12m -2n -1 C .12m -2n +1 D .12m -2n +2 8.(多选)下列各等式正确的是( ) A .log 23×log 25=log 2(3×5) B .lg 3+lg 4=lg (3×4) C .log 2x y=log 2x -log 2yD .lg n m =1nlg m (m >0,n >1,n ∈N *)9.(多选)下列指数式与对数式互化正确的是( ) A .e 0=1与ln 1=0 B .8-13=12与log 812=-13C .lg 100=2与100错误!未定义书签。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业9 对数与对数函数一、选择题1.函数y =log 3(2x -1)+1的定义域是( C ) A .[1,2]B .[1,2)C.⎣⎢⎡⎭⎪⎫23,+∞ D.⎝ ⎛⎭⎪⎫23,+∞ 解析:由⎩⎪⎨⎪⎧log 3(2x -1)+1≥0,2x -1>0,即⎩⎪⎨⎪⎧log 3(2x -1)≥log 313,x >12,解得x ≥23.2.若函数y =f (x )是函数y =a x (a >0,且a ≠1)的反函数,且f (2)=1,则f (x )=( A )A .log 2x B.12x C .log 12 xD .2x -2解析:由题意知f (x )=log a x (a >0,且a ≠1),∵f (2)=1,∴log a 2=1,∴a =2.∴f (x )=log 2x .3.函数f (x )=x a 满足f (2)=4,那么函数g (x )=|log a (x +1)|的图象大致为( C )解析:由f (2)=2a =4,得a =2.所以g (x )=|log 2(x +1)|,则g (x )的图象由y =|log 2x |的图象向左平移一个单位得到,C 满足. 4.(惠州市调研)若a =20.5,b =log π3,c =log 2sin 2π5,则( D )A .b >c >aB .b >a >cC .c >a >bD .a >b >c解析:依题意,得a >1,0<b =log π3<log ππ=1,而由0<sin 2π5 <1,2>1,得c <0,故a >b >c ,故选D.5.若函数f (x )=lg(x 2-2ax +1+a )在区间(-∞,1]上递减,则a 的取值范围为( A )A .[1,2)B .[1,2]C .[1,+∞)D .[2,+∞)解析:令函数g (x )=x 2-2ax +1+a =(x -a )2+1+a -a 2,对称轴为x =a ,要使函数在(-∞,1]上递减,则有⎩⎪⎨⎪⎧ g (1)>0,a ≥1,即⎩⎪⎨⎪⎧2-a >0,a ≥1,解得1≤a <2,即a ∈[1,2).6.(洛阳市第一次联考)设a =log 36,b =log 510,c =log 714,则( D ) A .c >b >a B .b >c >a C .a >c >bD .a >b >c解析:因为a =log 36=log 33+log 32=1+log 32,b =log 510=log 55+log 52=1+log 52,c =log 714=log 77+log 72=1+log 72,因为log 32>log 52>log 72,所以a >b >c ,故选D.7.(贵阳市摸底考试)20世纪30年代,为了防范地震带来的灾害,里克特(C.F.Richter)制定了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级M ,其计算公式为M =lg A -lg A 0,其中A 是被测地震的最大振幅,A 0是“标准地震”的振幅.已知5级地震给人的震感已经比较明显,则7级地震的最大振幅是5级地震的最大振幅的( D )A .10倍B .20倍C .50倍D .100倍解析:根据题意有lg A =lg A 0+lg10M =lg(A 0·10M ),所以A =A 0·10M ,则A 0×107A 0×105=100.故选D.二、填空题8.(2018·全国卷Ⅰ)已知函数f (x )=log 2(x 2+a ).若f (3)=1.则a =-7.解析:由f (3)=1得log 2(32+a )=1,所以9+a =2,解得a =-7. 9.若log a 34<1(a >0,且a ≠1),则实数a 的取值范围是⎝ ⎛⎭⎪⎫0,34∪(1,+∞).解析:若a >1,则log a 34<0,不等式log a 34<1一定成立;若0<a <1,则log a 34<1=log a a ,根据对数函数性质可得a <34,又a >0,故0<a <34.所以a 的取值范围是⎝ ⎛⎭⎪⎫0,34∪(1,+∞).10.已知f (x )=2+log 3x ,x ∈[1,9],则函数y =[f (x )]2+f (x 2)的最大值是13. 解析:由f (x )=2+log 3x ,x ∈[1,9],得f (x 2)=2+log 3x 2,x 2∈[1,9],即x ∈[1,3],得函数y =[f (x )]2+f (x 2)的定义域为[1,3].y =(2+log 3x )2+2+log 3x 2,即y =(log 3x )2+6log 3x +6=(log 3x +3)2-3,令log 3x =t,0≤t ≤1,则y =(t +3)2-3,当t =log 3x =1,即x =3时,y max =13.三、解答题11.已知函数f (x )是定义在R 上的偶函数,f (0)=0,当x >0时,f (x )=log 12x .(1)求函数f (x )的解析式; (2)解不等式f (x 2-1)>-2.解:(1)当x <0时,-x >0,则f (-x )=log 12(-x ).因为函数f (x )是偶函数,所以f (-x )=f (x ).所以函数f (x )的解析式为f (x )=⎩⎪⎨⎪⎧log 12 x ,x >0,0,x =0,log 12(-x ),x <0.(2)因为f (4)=log 124=-2,f (x )是偶函数,所以不等式f (x 2-1)>-2可化为f (|x 2-1|)>f (4).又因为函数f (x )在(0,+∞)上是减函数,所以|x 2-1|<4,解得-5<x < 5.即不等式的解集为(-5,5).12.设f (x )=log a (1+x )+log a (3-x )(a >0,且a ≠1),且f (1)=2. (1)求a 的值及f (x )的定义域; (2)求f (x )在区间⎣⎢⎡⎦⎥⎤0,32上的值域.解:(1)∵f (1)=2,∴log a 4=2(a >0,且a ≠1),∴a =2.由⎩⎪⎨⎪⎧1+x >0,3-x >0,得x ∈(-1,3),∴函数f (x )的定义域为(-1,3). (2)f (x )=log 2(1+x )+log 2(3-x ) =log 2(1+x )(3-x )=log 2[-(x -1)2+4], ∴当x ∈(-1,1]时,f (x )是增函数; 当x ∈(1,3)时,f (x )是减函数,故函数f (x )在⎣⎢⎡⎦⎥⎤0,32上的最大值是f (1)=log 24=2.又f (0)=log 23,f (32)=log 2154,log 23<log 2154,∴函数f (x )在[0,32]上的最小值是f (0)=log 23.故函数f (x )在区间[0,32]上的值域为[log 23,2].13.(2018·全国卷Ⅲ)设a =log 0.20.3,b =log 20.3,则( B ) A .a +b <ab <0 B .ab <a +b <0 C .a +b <0<abD .ab <0<a +b解析:由a =log 0.20.3得1a =log 0.30.2,由b =log 20.3得1b =log 0.32,所以1a +1b =log 0.30.2+log 0.32=log 0.30.4,所以0<1a +1b <1,得0<a +b ab <1.又a >0,b <0,所以ab <0,所以ab <a +b <0.14.(成都诊断性检测)已知定义在R 上的奇函数f (x )满足f (x +2)+f (x )=0,且当x ∈[0,1]时,f (x )=log 2(x +1),则下列不等式正确的是( C )A .f (log 27)<f (-5)<f (6)B .f (log 27)<f (6)<f (-5)C .f (-5)<f (log 27)<f (6)D .f (-5)<f (6)<f (log 27)解析:f (x +2)+f (x )=0⇒f (x +2)=-f (x )⇒f (x +4)=-f (x +2)=f (x ),所以f (x )是周期为4的周期函数.又f (-x )=-f (x ),且有f (2)=-f (0)=0,所以f (-5)=-f (5)=-f (1)=-log 22=-1,f (6)=f (2)=0. 又2<log 27<3,所以0<log 27-2<1,即0<log 274<1, f (log 27)+f (log 27-2)=0⇒f (log 27)=-f (log 27-2) =-f (log 274)=-log 2(log 274+1)=-log 2(log 272), 又1<log 272<2,所以0<log 2(log 272)<1, 所以-1<-log 2(log 272)<0, 所以f (-5)<f (log 27)<f (6).尖子生小题库——供重点班学生使用,普通班学生慎用15.若A (a ,b ),B (e,c )(其中e 为自然对数的底数)是f (x )=ln x 图象上不同的两点,则下列各点一定在f (x )图象上的是( A )A .(a e,b +1)B .(a +e,b +1)C .(a +e,b )D .(a e,b )解析:∵A (a ,b ),B (e,c )是f (x )=ln x 图象上不同的两个点,∴ln a =b ,lne =1=c ,∴b +1=b +c =ln a +lne =ln(a e),∴(a e,b +1)在f (x )图象上,故选A.16.(湖北八校联考)已知π为圆周率,e =2.718 28…为自然对数的底数,则( B )A .πe <3eB .πlog 3e>3log πeC .3e -2π<3πe -2D .log πe>log 3e解析:对于A,∵函数y =x e 是(0,+∞)上的增函数,且π>3,∴πe >3e ,A 错误;对于B,πlog 3e>3log πe ⇔πln3>3lnπ⇔πlnπ>3ln3⇔ππ>33,B 正确;对于C,3e -2π<3πe -2⇔3e -3<πe -3,而函数y =x e -3是(0,+∞)上的减函数,C 错误;对于D,log πe>log 3e ⇔1lnπ>1ln3⇔lnπ<ln3,而函数y =ln x 是(0,+∞)上的增函数,D 错误.综上,故选B.。
