《勾股定理的应用》习题课
勾股定理及其应用习题及答案

勾股定理及其应用习题及答案一、选择题(每小题3分,共36分)1.如图所示,在边长为1个单位长度的小正方形组成的网格中,点A,B 都是格点,则线段AB的长度为( A )A.5B.6C.7D.25第1题图2.下列各组数中,以它们为边长不能构成直角三角形的是( D )A.60,80,100B.13,5,12C.0.3,0.4,0.5D.2,3,43.(2021泰安期中)如图所示,阴影部分是一个正方形,则此正方形的面积为( A )A.64B.32C.16D.128第3题图4.如图所示,把长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的边BC 长为( A )A.24B.22C.20D.30第4题图5.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,在△ABC中,∠ACB= 90°,AC+AB=10尺,BC=3尺,求AC的长.在这个问题中,AC的长为( C )A.4尺B.9尺2尺 D.5尺C.9120第5题图6.如图所示,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺,突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水深是( C )A.3.5尺B.4尺C.4.5尺D.5尺第6题图7.如图所示,高速公路上有A,B两点相距25 km,C,D为两村庄,已知DA=10 km,CB=15 km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C,D两村庄到E站的距离相等,则AE的长是( C ) A.5 km B.10 km C.15 km D.25 km第7题图8.在△ABC中,AB=15,AC=13,高AD=12,则BC等于( C )A.14B.4C.14或4D.9或59.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图所示).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9 cm,底面边长为4 cm,则这圈金属丝的长度至少为( D )A.8 cmB.10 cmC.12 cmD.15 cm第9题图10.如图①所示,美丽的弦图蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c.如图②所示,现将这四个全等的直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,则该飞镖状图案的面积为( C )A.6B.12C.24D.24√3第10题图11.如图所示,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使点A与BC的中点D重合,折痕为PQ,则线段BQ的长度为( C )A.53B.52C.4D.5第11题图12.给出下列四个说法:①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;②如果直角三角形的两边是5,12,那么第三边必是13;③如果一个三角形的三边是12,25,21,那么此三角形必是直角三角形;④如果三角形三边长分别是n2-4,4n,n2+4(n>2),那么此三角形是直角三角形.其中正确的说法是( C )A.①②B.①③C.①④D.②④二、填空题(每小题3分,共18分)13.已知在△ABC中,AB=5,BC=8,BC边上的中线AD=3,则AC= 5 .14.如图所示,AB,BC,CD,DE是四根长度均为5 cm的火柴棒,点A,C,E 共线.若AC=6 cm,CD⊥BC,则线段CE的长度是8 cm.第14题图15.如图所示,四边形ABCD是边长为9的正方形纸片,将纸片沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=3,则AM的长是 2 .第15题图16.如图所示,AB⊥BC于点B,DC⊥BC于点C,E是BC上一点,∠BAE= ∠DEC=60°,AB=3,CE=4,则AD= 10 .第16题图17.如图所示,A,B两个小镇在河流CD的同侧,到河边的距离分别为AC=10 km,BD=30 km,且CD=30 km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万元,在河流CD上选择水厂的位置为点M,使铺设水管的费用最节省,则总费用是150 万元.第17题图18.如图所示,在正方形网格中,A,B,C,D均为格点,则∠BAC-∠DAE= 45°.第18题图三、解答题(共46分)19.(8分)(2021泰安期中)如图所示的是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁从A 点沿着台阶面爬行到B点的最短路程为多少?解:如图所示,三级台阶平面展开图为长方形,长为20 dm,宽为(2+3)×3 dm,则蚂蚁从A点沿台阶面爬行到B点的最短路程是此长方形的对角线长.设蚂蚁从A点沿台阶面爬行到B点的最短路程为x dm,根据勾股定理,得x2=202+[(2+3)×3]2.解得x=25.即蚂蚁从A点沿着台阶面爬行到B点的最短路程为25 dm.20.(8分)(2021沂源期中)如图所示,在Rt△ABC中,∠ACB=90°, AB=20 cm,AC=16 cm,点P从点A出发,以每秒1 cm的速度向点C运动,连接PB,设运动时间为t s(t>0).(1)求BC的长;(2)当PA=PB时,求t的值.解:(1)在Rt△ABC中,∠ACB=90°,AB=20 cm,AC=16 cm,所以BC2=AB2-AC2.解得BC=12 cm.(2)设AP=t cm,则BP=AP=t cm,PC=(16-t)cm.在Rt△PCB中,因为∠PCB=90°,所以PC2+BC2=PB2,即(16-t)2+122=t2.解得t=12.5.所以当点P运动到PA=PB时,t的值为12.5.21.(8分)《中华人民共和国道路交通安全法实施条例》规定:机动车在同方向只有一条机动道的公路上行驶的速度不得超过 70 km/h.如图所示,一辆小汽车在同方向只有一条机动道的公路上行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30 m的C处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗? (参考数据转换:1 m/s=3.6 km/h)解:由题意,知△ABC是直角三角形,∠C=90°,AC=30 m,AB=50 m,根据勾股定理,有BC2+AC2=AB2,即BC2+302=502.解得BC=40 m.=20(m/s).所以小汽车的速度为40220 m/s=(20×3.6)km/h=72 km/h.因为72 km/h>70 km/h,所以这辆小汽车超速行驶.22.(10分)如图所示,一架25 m长的梯子AC斜靠在一面竖直的墙AB 上,这时梯子底端C到墙的距离BC为7 m.(1)求这架梯子的顶端距地面的高度AB的长;(2)如果梯子的顶端A沿墙下滑4 m到点A′,小明说梯子的底端C在水平方向向右也滑动4 m.你认为小明说的对吗?请说明你的理由. 解:(1)在Rt△ABC中,由勾股定理,得AB2+BC2=AC2,即AB2+72=252,所以AB=24 m,即这架梯子的顶端距地面的高度AB的长是24 m.(2)小明说的不对.理由:因为梯子的顶端A下滑了4 m至点A′,所以BA′=AB-AA′=24-4=20(m).在Rt△BA′C′中,由勾股定理,得BA′2+BC′2=A′C′2,即202+BC′2=252.所以BC′=15m,所以CC′=BC′-BC=15-7=8(m),即梯子的底端在水平方向向右滑动了8 m.23.(12分)我国海监船在某岛海域的巡航如图所示,OA⊥OB,OA= 45 n mile,OB=15 n mile,该岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向该岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.(1)请用直尺和圆规作出C处的位置;(2)求我国海监船行驶的航程BC的长.解:(1)如图所示,作AB的垂直平分线与OA交于点C.(2)连接BC,如图所示.由作图可得CD为AB的中垂线,则CB=CA.由题意可得OC=45-CA=45-CB.因为OA⊥OB,在Rt△BOC中,BO2+OC2=BC2,所以152+(45-BC)2=BC2,解得BC=25.故我国海监船行驶的航程BC的长为25 n mile.。
勾股定理及应用 练习题(带答案

勾股定理及应用 题集一、勾股定理与逆定理A. B. C. D.1.如图所示的一块地,,,,,,这块地的面积为( ).【答案】B 【解析】连接,在中,,∴,∵,,,∴是直角三角形,.【标注】【知识点】勾股逆定理的应用2.如图,在四边形中,,,,.求的度数.【答案】.【解析】连接,在中,,,∴,∴,∴,∵,,∴.在中,,∴是直角三角形,即,∵,∴.【标注】【知识点】勾股定理的逆定理【知识点】勾股定理的证明A.尺B.尺C.尺D.尺3.如图,有一个水池,其底面是边长为尺的正方形,一根芦苇生长在它的正中央,高出水面部分的长为尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部恰好碰到岸边,则这根芦苇的长是( ).【答案】C 【解析】苇长尺,则水深尺,∵尺,∴尺,∵中,.∴.【标注】【知识点】勾股定理与实际问题(1)(2)4.如图,一架云梯长米,斜靠在一面墙上,梯子靠墙的一端距地面米.这个梯子底端离墙有多少米.如果梯子的顶端下滑米,那么梯子的底部在水平方向也滑动了米吗?【答案】(1)(2)米.不是.【解析】(1)(2)由题意得此时米,米,根据,∴可求米.设滑动后梯子的底端到墙的距离为米,得方程,,解得,所以梯子向后滑动了米.综合得:如果梯子的顶端下滑了米,那么梯子的底部在水平方向不是滑米.【标注】【知识点】勾股定理的综合应用A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形5.若的三边长,,满足,则是( ).【答案】D【解析】∵,∴或.∴或.∴为等腰三角形或直角三角形.【标注】【知识点】勾股逆定理的应用A. B. C. D.6.如图,已知在中,,分别以、为直径作半圆,面积分别记为、,则等于( ).【答案】A【解析】由勾股定理可知:.,,∴.【标注】【知识点】勾股定理与几何问题(1)(2)7.下表中给出的每行三个数、、满足,根据表中已有的数的规律填空:当时, , .用含字母的代数式分别表示、,,.【答案】(1)(2);; 【解析】(1)(2)∵,∴,.∵,,;,,;,,;∴,.【标注】【知识点】勾股树(1)(2)(3)8.若一个直角三角形的两条直角边长为、,斜边为,斜边上的高为.求证:..以、、为边构成的三角形是直角三角形.【答案】(1)(2)(3)证明见解析证明见解析证明见解析【解析】(1)(2)(3)∵,,∴,代入得,∴.由,,则,∴,即,∴略【标注】【知识点】解直角三角形的综合应用二、勾股定理的方程思想1.如图,已知等腰的底边,是腰上一点,且,,求的周长.【答案】.【解析】由勾股定理逆定理得,是直角三角形.在中,应用勾股定理,设,代入数值得,.所以的周长=.【标注】【知识点】方程思想在勾股定理的应用2.如图,在中,,平分,,,求的长.【答案】.【解析】过作,∵平分,∴,∵,∴由勾股定理得,设,则,在由勾股定理得:,解得,∴.【标注】【知识点】方程思想在勾股定理的应用(1)(2)3.如图,在中,,,,的平分线与相交于点,过点作,垂足为.求的长.求的长.【答案】(1)(2)..【解析】(1)∵平分,,,∴,在和中,(2),∴≌,∴.∵,,,∴在中,,∴,.设,则,,在中,,,解得,∴.【标注】【知识点】方程思想在勾股定理的应用4.如图,在中,,,,求边上的高.【答案】.【解析】设为,则,∵为的高,∴在中,,在中,,∴.即,解得:.∴.∴在中,.【标注】【知识点】方程思想在勾股定理的应用(1)(2)5.如图,在中,,,,点为边上的动点,点从点出发,沿边往运动,当运动到点时停止,设点运动的时间为秒,速度为每秒个单位长度.若是直角三角形,求的值.若是等腰三角形,求的值.【答案】(1)(2)或.,或.【解析】(1)(2)当时,是直角三角形,,,故.∵,∴,即,,.当时,是直角三角形,此时与重合,∴,,综上所述,或.当时,即,解得,当时,取中点,连接.∵,∴,∴,∴,∴,即.当时,过点作于点.∵,,,∴,在中,,即,综上所述,的值为,或.【标注】【知识点】方程思想在勾股定理的应用6.如图,是一张直角三角形纸片,,两直角边、,现将折叠,使点与点重合,折痕为,则的长为 .【答案】【解析】依题可知≌,∴.设,则,在中,,,∴,解得,,∴.【标注】【知识点】翻折问题与勾股定理7.如图,在中,,,,将折叠,使点恰好落在斜边上,与点重合,为折痕,则 .【答案】 或【解析】在中,,∵将折叠得到,∴,,∴.设,则.在中,,∴,解得.∴.【标注】【知识点】解直角三角形的综合应用A. B. C. D.8.如图,在矩形中,,,将沿对角线翻折,点落在点处,交于点,则线段的长为( ).【答案】A【解析】设,则,∵四边形为矩形,∴,,,∴,由题意得:,∴,∴,由勾股定理得,即,解得:,∴,∴.【标注】【知识点】其它翻折问题9.如图,矩形中,,,点是边上一点,连接,把沿折叠,使点落在点处.当为直角三角形时,的长为 .【答案】或【解析】当为直角三角形时,有两种情况:图图①当点落在矩形内部时,如答图所示.连接,在中,,,,沿折叠,使点落在点处,,当为直角三角形时,只能得到,点、、共线,即沿折叠,使点落在对角线上的点处,,,,设,则,,在中,,,解得,;②当点落在边上时,如答图所示.此时为正方形,.综上所述,的长为或.故答案为:或.【标注】【知识点】四边形与折叠问题三、勾股定理与最短路径问题A. B. C. D.1.如图,长方体的长为,宽为,高为,点离点的距离为,一只蚂蚁如果要沿着长方体的表面从点爬到点,需要爬行的最短距离是( ).【答案】B【解析】将长方体展开,连接、,根据两点之间线段最短,()如图,,,由勾股定理得:.()如图,,,由勾股定理得,.()只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如图:∵长方体的宽为,高为,点离点的距离是,∴,,在直角三角形中,根据勾股定理得:∴.由于,故最短距离为.【标注】【知识点】勾股定理与展开图最短路径问题2.如图所示,无盖玻璃容器,高,底面周长为,在外侧距下底的点处有一蜘蛛,与蜘蛛相对的容器的上口外侧距开口的处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度.【答案】最短路线长为.【解析】如下图可知,最短路线的长度为线段的长度,作于,则,,∵底面周长为,∴,∴.∴最短路线长为.【标注】【知识点】勾股定理与展开图最短路径问题。
勾股定理的应用(习题及答案).

勾股定理的应用(习题)➢例题示范例1:如图,在四边形ABCD 中,∠B=90°,AB=3,BC=4,AD=12,CD=13,求四边形ABCD 的面积.解:如图,连接AC,在Rt△ABC 中,∠B=90°,AB=3,BC=4,由勾股定理,得AB2+BC2=AC2,∴32+42=AC2.∴AC=5.在△ACD 中,AC=5,AD=12,CD=13,∵52+122=132,∴AC2+AD2=CD2.∴△ACD 是直角三角形,且∠CAD=90°.∴S四边形ABCD =S△ACD-S△ABC=1AD ⋅AC -1AB ⋅BC2 2=1⨯12 ⨯ 5 -1⨯ 3⨯ 42 2= 24 .➢复习巩固1.已知甲、乙两人从同一地点出发,甲往东走了12 km,乙往南走了5 km,这时甲、乙两人之间的距离为.2.小明从家出发向正北方向走了150 m,接着向正东方向走到离家250 m 远的地方,则小明向正东方向走了m.3.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7 米,顶端距离地面2.4 米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2 米,则这条小巷的宽度为.第3 题图第4 题图4.如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面30 cm.突然一阵大风吹过,红莲被吹至一边,花朵下部刚好齐及水面,如果知道红莲移动的水平距离为60 cm,则水深是()cm.A.35 B.40 C.50 D.455.11 世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题:小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高30 肘尺(肘尺是古代的长度单位),另外一棵树高20 肘尺;两棵棕榈树的树干间的距离是50 肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且同时到达目标.则这条鱼出现的地方与较高的棕榈树之间的距离为.6.如图,有两只猴子在一棵树CD 上高5 m 的点B 处,它们都要到A 处的池塘去喝水,其中一只猴子沿树爬下走到离树10 m 处的池塘A 处,另一只猴子爬到树顶D 后直线跃向池塘的A 处.如果两只猴子所经过的路程相等,那么这棵树高有多少米?7.男孩戴维是城里的飞盘冠军,戈里是城里踩高跷的人,两人约定一比高低.戴维直立肩高 1 m,他投飞盘很有力,但需要在13 m 内才有威力;戈里踩高跷时鼻子离地13 m,他的鼻子是他唯一的弱点.戴维要通过击中对方的鼻子获胜,需离戈里的最远距离为()A.7 m B.8 m C.6 m D.5 m8.如图所示,小河的同一侧有A,B 两个村庄,它们到小河所在的直线的垂直距离分别为AA1=2 千米,BB1=5 千米,A1B1=24 千米,要在小河上修建一座小型发电站P,使它到A,B 两个村庄的电线之和最短,则这个最短距离是千米.9.如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5 m(踏板厚度忽略不计),右图是从侧面看,当秋千踏板荡起至点B 位置时,点离地面垂直高度BC 为1 m,离秋千支柱AD 的水平距离BE 为1.5 m(不考虑支柱的直径),求秋千支柱AD 的高.10.如图,一块四边形菜地ABCD,已知∠B=90°,AB=9 m,BC=12 m,AD=8 m,CD=17 m.求这块菜地的面积.11.据说古埃及人曾用下面的方法得到直角:如图所示,他们用13 个等距的结把一根绳子分成等长的12 段,一个工匠同时握住绳子的第1 个结和13 个结,两个助手分别握住第4 个结和第8 个结,拉紧绳子,就会得到一个直角三角形,其直角在第4 个结处.你能说说其中的道理吗?➢思考小结1.观察图中的3 个图案,设△ABC 的三边长分别为a,b,c,请根据三角形的形状,猜测a2,b2,c2 满足的条件.(1)如果△ABC 是直角三角形,则a2+b2c2;(2)如果△ABC 是锐角三角形,则a2+b2c2;(3)如果△ABC 是钝角三角形,则a2+b2c2.【参考答案】➢复习巩固1. 13 km2. 2003. 2.2 m4. D5.20 肘尺6.树高7.5 米7. D8. 259.秋千支柱AD 的高为3 m10.这块菜地的面积为114 m211.此三角形是直角三角形,理由略➢思考小结1. (1)= (2)>(3)<。
专题01 勾股定理的基本应用(解析版)

专题01 勾股定理的基本应用题型一 求面积1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设“赵爽弦图”中直角三角形较长直角边长为a ,较短直角边长为b ,若2()24a b +=,大正方形的面积为14,则小正方形的面积为( )A .2B .3C .4D .5【解答】解:设大正方形的边长为c ,则22214c a b ==+,2()24a b +=Q ,22224a ab b \++=,解得5ab =,\小正方形的面积是:1441425141042ab -´=-´=-=,故选:C .2.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A 、B 、D 的面积依次为6、10、24,则正方形C 的面积为( )A .4B .6C .8D .12【解答】解:由题意:A B E S S S +=正方形正方形正方形,D C E S S S -=正方形正方形正方形,A B D CS S S S \+=-正方形正方形正方形正方形Q 正方形A 、B 、D 的面积依次为6、10、24,24610C S \-=+正方形,8C S \=正方形.故选:C .3.如图,点C 是线段AB 上的一点,分别以AC 、BC 为边向两侧作正方形.设6AB =,两个正方形的面积和1220S S +=,则图中BCD D 的面积为( )A .4B .6C .8D .10【解答】解:设AC a =,BC b =,由题意得:6a b +=,2220a b +=,222()2a b a b ab +=+-Q ,22062ab \=-,8ab \=,BCD \D 的面积118422ab ==´=.图中BCD D 的面积为4.故选:A .4.正方形ABCD 的边长为1,其面积记为1S ,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为2S ,L 按此规律继续下去,则2022S 的值为( )A .20221()2B .20211()2C .2022D .2021【解答】解:在图中标上字母E ,如图所示.Q 正方形ABCD 的边长为1,CDE D 为等腰直角三角形,222DE CE CD \+=,DE CE =,221S S S \+=.观察,发现规律:2111S ==,211122S S ==,321124S S ==,431128S S ==,¼,11()2n n S -\=.当2022n =时,202212021202211()()22S -==,故选:B .5.如图,以正方形ABCD 的边AD 为直径作一个半圆,点M 是半圆上一个动点,分别以线段AM 、DM 为边各自向外作一个正方形,其面积分别为1S 和2S ,若正方形的面积为10,随点M 的运动12S S +的值为( )A .大于10B .小于10C .等于10D .不确定【解答】解:AB Q 为半圆的直径,90AMD \Ð=°,22210AM DM AD \+==,21S AM =Q ,22S DM =,1210S S \+=.故选:C .6.如图,在四边形ABDE 中,//AB DE ,AB BD ^,点C 是边BD 上一点,BC DE a ==,CD AB b ==,AC CE c ==.下列结论:①ABC CDE D @D ;②90ACE Ð=°;③四边形ABDE 的面积是21()2a b +;④22111()2222a b c ab +-=´;⑤该图可以验证勾股定理.其中正确的结论个数是( )A .5B .4C .3D .2【解答】解://AB DE Q ,AB BD ^,DE BD \^,90B D \Ð=Ð=°.在ABC D 和CDE D 中,90AB CD B D BC DE =ìïÐ=Ð=°íï=î,()ABC CDE SAS \D @D,A DCE \Ð=Ð,ACB E Ð=Ð.90A ACB Ð+Ð=°Q ,90DCE ACB \Ð+Ð=°.180DCE ACB ACE Ð+Ð+Ð=°Q ,90ACE \Ð=°,故①②正确;//AB DE Q ,AB BD ^,\四边形ABDE 的面积是21()2a b +;故③正确;Q 梯形ABDE 的面积-直角三角形ACE 的面积=两个直角三角形的面积,\22111()2222a b c ab +-=´,222a b c \+=.故③④⑤都正确.故选:A .7.如图,Rt ABC D 中,90C Ð=°,AD 平分BAC Ð,交BC 于点D ,6CD =,12AB =,则ABD D 的面积是( )A .18B .24C .36D .72【解答】解:作DH AB ^于D ,如图,AD Q 平分BAC Ð,DH AB ^,DC AC ^,6DH DC \==,1126362ABD S D \=´´=.故选:C .8.如图,Rt ABC D 中,90C Ð=°,5AC =,12BC =,分别以AB 、AC 、BC 为边在AB 的同侧作正方形ABEF 、ACPQ 、BCMN ,四块阴影部分的面积分别为1S 、2S 、3S 、4S ,则1234S S S S +++等于( )A .60B .80C .90D .120【解答】解:连接PF ,过点F 作FD AK ^于点D ,AB EB =Q ,90ACB ENB Ð=Ð=°,而90CBA CBE EBN CBE Ð+Ð=Ð+Ð=°,CBA EBN \Ð=Ð,()CBA NBE AAS \D @D ,故4ABC S S D =;同理ADF ABC D @D ,AC DF AQ CP \===,90QAC KDF PCD Ð=Ð=Ð=°Q ,//AQ DF \,\四边形CDFP 是矩形,90CPF \Ð=°,180QPC CPF \Ð+Ð=°,Q \,P ,F 三点共线,又FA AB =Q ,90FDA ACB Ð=Ð=°,而90FAD CAB CAB ABC Ð+Ð=Ð+Ð=°,FAD ABC \Ð=Ð,()FAD ABC AAS \D @D ,同理可证ACT FDK D @D ,2FDA ABC S S S D D \==,同理可证TPF KME D @D ,AQF ABC D @D ,13ADF ABC S S S S D D \+==,综上所证:1234133125902ABC S S S S S D +++==´´´=.故选:C .9.如图,直线l 上有三个正方形a ,b ,c ,若a ,c 的面积分别为4和10,则b 的面积为 14 .【解答】解:如图,a Q 、b 、c 都为正方形,BC BF \=,90CBF Ð=°,24AC =,210DF =,1290Ð+Ð=°Q ,2390Ð+Ð=°,13\Ð=Ð,在ABC D 和DFB D 中,13BAC FDB BC FB Ð=ÐìïÐ=Ðíï=î,ABC DFB \D @D ,AB DF \=,在ABC D 中,2222241014BC AC AB AC DF =+=+=+=,b \的面积为14.故答案为14.10.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,90BAC Ð=°,3AB =,4AC =,点D ,E ,F ,G ,H ,I 都在矩形KLMJ 的边上,则空白部分的面积为 60 .【解答】解:如图,延长AB 交KF 于点O ,延长AC 交GM 于点P ,所以,四边形AOLP 是正方形,90BAC Ð=°Q ,3AB =,4AC =,347AO AB AC \=+=+=,3710KL \=+=,4711LM =+=,因此,矩形KLMJ 的面积为1011110´=,\空白部分的面积为22211034560---=,故答案为:60.11.我国古代著作《周髀算经》中记载了“赵爽弦图”.如图,若勾6AE =,弦10AD =,则小正方形EFGH 的面积是 4 .【解答】解:如图,Q 勾6AE =,弦AD =弦10AB =,\股8BE ==,\小正方形的边长862=-=,\小正方形的面积224==.故答案是:4.12.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A 、C 、D 的面积依次为4、6、18,则正方形B 的面积为 8 .【解答】解:由题意:A B E S S S +=正方形正方形正方形,D C E S S S -=正方形正方形正方形,A B D CS S S S \+=-正方形正方形正方形正方形Q 正方形A 、C 、D 的面积依次为4、6、18,4186B S \+=-正方形,8B S \=正方形.故答案为:8.13.如图,在同一平面内,直线l 同侧有三个正方形A ,B ,C ,若A ,C 的面积分别为9和4,则阴影部分的总面积为 6 .【解答】解:如图,作LM FE ^交FE 的延长线于点M ,交JI 的延长线于点N ,Q 四边形A 、B 、C 都是正方形,且正方形A 、C 的面积分别为9、4,90EKI EDR IHG \Ð=Ð=Ð=°,29DE =,24HI =,3DE \=,2HI =,1809090EDK KHI Ð=Ð=°-°=°Q ,90DKE KHI HIK \Ð=°-Ð=Ð,在EDK D 和KHI D 中,EDK KHI DKE HIK EK KI Ð=ÐìïÐ=Ðíï=î,()EDK KHI AAS \D @D ,2DK HI \==,3DE HK ==,13232EDK KHI S S D D \==´´=;90DEF HIJ Ð=Ð=°Q ,18090DEM DEF \Ð=°-Ð=°,18090HIN HIJ Ð=°-Ð=°,90KEL KIL Ð=Ð=°Q,90MEL DEK KEM \Ð=Ð=°-Ð,90NIL HIK KIN Ð=Ð=°-Ð,//EF l Q ,//IJ l ,//EF IJ \,90EML EMN N \Ð=Ð=Ð=°,在EML D 和EDK D 中,MIL DEK EML EDK EL EK Ð=ÐìïÐ=Ðíï=î,()EML EDK AAS \D @D ,EM ED EF \==,3EFL EML EDK S S S D D D \===;在LNI D 和KHI D 中,NIL HIK N KHI IL IK Ð=ÐìïÐ=Ðíï=î,()LNI KHI AAS \D @D ,IN IE IJ ==Q ,3LJI LNI KHI S S S D D D \===,336EFL LJI S S D D \+=+=,\阴影部分的总面积为6.14.如图,正方形ABDE 、CDFI 、EFGH 的面积分别为25、9、16,AEH D 、BDC D 、GFI D 的面积分别为1S 、2S 、3S ,则123S S S ++= 18 .【解答】解:DF DC =Q ,DE DB =,且180EDF BDC Ð+Ð=°,过点A 作AJ EH ^,交HE 的延长线于点J ,90J DFE \Ð=Ð=°,90AEJ DEJ DEJ DEF Ð+Ð=Ð+Ð=°Q ,AEJ DEF \Ð=Ð,AE DE =Q ,()AEJ DEF AAS \D @D ,AJ DF \=,EH EF =Q ,AHE DEF S S D D \=,同理:BDC GFI DEF S S S D D D ==,1233AHE BDC GFI DEF S S S S S S S D D D D ++=++=´,13462DEF S D =´´=,12318S S S \++=.故答案为:18.题型二 求线段长15.一个大正方形,被两条线段分割成两个小正方形和两个小长方形,若两个小正方形的面积分别为10和6,则小长方形的对角线AB 的长为( )A .4B .6C .10D .16【解答】解:如图,Q 两个小正方形的面积分别为10和6,26AC \=,210BC =,由勾股定理得,4AB ===.故选:A .16.如图,在Rt ABC D 中,90ABC Ð=°,以AB 为边在ABC D 外作正方形,其面积为9,以BC 为斜边在ABC D 外作等腰直角三角形,其面积为4,过点B 作BD AC ^交AC 于点D ,则(AD = )A .85B .94C .95D .2【解答】解:Q 以AB 为边的正方形的面积为9,29AB \=,Q 以BC 为斜边的等腰直角三角形的面积为4,\等腰直角三角形的腰长为216BC \=,在Rt ABC D 中,90ABC Ð=°,则5AC ===,1122ABC S AB AC AC BD D =´´=´´Q ,\1134522BD ´´=´´,解得:125BD =,由勾股定理得:95AD ===,故选:C .17.如图,在Rt ABC D 中,90ACB Ð=°,CD AB ^于D .已知15AB =,Rt ABC D 的周长为15+,则CD 的长为( )A .5BC .D .6【解答】解:如图所示:Rt ABC D Q 的周长为15+,90ACB Ð=°,15AB =,AC BC \+=,222215225AC BC AB +===,22()AC BC \+=,即222405AC AC BC BC +´+=,2405225180AC BC \´=-=,90AC BC \´=,Q 1122AB CD AC BC ´=´,90615AC BC CD AB ´\===;故选:D .18.若ABC=,高24=,则BC的长为( )cm.AD cmAC cmD中,30AB cm=,26A.28或8B.8C.28D.以上都不对Q为边BC上的高,【解答】解:AD\Ð=Ð=°.90ADB ADCBD===,在Rt ABDD中,18CD===.在Rt ACDD中,10当点D在线段BC上时,如图1,181028=+=+=;BC BD CD当点D在线段CB的延长线上时,如图2,18108=-=-=.BC BD CD\的长为28或8.BC故选:A.19.如图,在ABCBC=,6AB=,4AC=,则DE的^于D,且5D中,CE是AB边上的中线,CD AB长 2 .【解答】解:设BD x=-,=,则5AD x在Rt ACD D 中,222CD AC AD =-,在Rt BCD D 中,222CD BC BD =-,2222AC AD BC BD \-=-,即22226(5)4x x --=-,解得,12x =,则12BD =,2DE BE BD \=-=,贵答案为:2.20.如图,锐角三角形ABC 中,2C B Ð=Ð,AB =,8BC CA +=,则ABC D 的面积为 【解答】解:过A 作AE BC ^于E ,延长BC 到D 使CD AC =,则CAD D Ð=Ð,ACB D CAD Ð=Ð+ÐQ ,2ACB D \Ð=Ð,2C B Ð=ÐQ ,B D \Ð=Ð,AB AD \=,BE DE \=,8BC CA +=Q ,8BD BC CD BC AC \=+=+=,4BE \=,AE \==,222AE CE AC \+=,即228(4)(8)BC BC +-=-,解得:5BC =,ABC \D 的面积11522BC AE ==´´=g故答案为:.21.如图所示,ABC D 的顶点A 、B 、C 在边长为1的正方形网格的格点上,BD AC ^于点D ,则BD 的长为 3 .【解答】解:由图形可知,5BC =,BC 边上的高为3,ABC \D 的面积1155322=´´=,由勾股定理得,5AC ==,则115522BD ´´=,解得,3BD =,故答案为:3.22.如图,在Rt ABC D 中,90B Ð=°,3AB =,6BC =,AC 的中垂线DE 交AC 于点D ,交BC 于点E .延长DE 交AB 的延长线于点F ,连接CF .(1)求出CD 的长;(2)求出CF 的长.【解答】解:(1)在Rt ABC D 中,90B Ð=°,3AB =,6BC =,则AC ===,DE Q 是AC 的中垂线,12CD AC \==(2)DF Q 是AC 的中垂线,FA FC \=,3AB =Q ,33FB FA CF \=-=-,在Rt FBC D 中,222CF BC FB =+,即2226(3)CF CF =+-,解得:152CF =.23.如图,在ABC D 中,AB AC =,AD BC ^于点D ,45CBE Ð=°,BE 分别交AC ,AD 于点E 、F .(1)如图1,若13AB =,10BC =,求AF 的长度;(2)如图2,若AF BC =,求证:222BF EF AE +=.【解答】(1)解:如图1,AB AC =Q ,AD BC ^,BD CD \=,10BC =Q ,5BD \=,Rt ABD D 中,13AB =Q ,12AD \==,Rt BDF D 中,45CBE Ð=°Q ,BDF \D 是等腰直角三角形,5DF BD \==,1257AF AD DF \=-=-=;(2)证明:如图2,在BF 上取一点H ,使BH EF =,连接CF 、CH 在CHB D 和AEF D 中,Q 45BH EFCBH AFE BC AF=ìïÐ=Ð=°íï=î,()CHB AEF SAS \D @D ,AE CH \=,AEF BHC Ð=Ð,CEF CHE \Ð=Ð,CE CH \=,BD CD =Q ,FD BC ^,CF BF \=,45CFD BFD \Ð=Ð=°,90CFB \Ð=°,EF FH \=,Rt CFH D 中,由勾股定理得:222CF FH CH +=,222BF EF AE \+=.24.如图,在ABC D 中,AD BC ^,垂足为点D ,13AB =,5BD =,15AC =.(1)求AD 的长;(2)求BC的长.【解答】解:(1)AD BC ^Q ,90ADB CDA \Ð=Ð=°.在Rt ADB D 中,90ADB Ð=°Q ,222AD BD AB \+=,222144AD AB BD \=-=.0AD >Q ,12AD \=.(2)在Rt ADC D 中,90CDA Ð=°Q ,222AD CD AC \+=,22281CD AC AD \=-=.0CD >Q ,9CD \=.5914BC BD CD \=+=+=.题型三 通过勾股定理设方程25.如图,四个全等的直角三角形围成正方形ABCD 和正方形EFGH ,即赵爽弦图.连接AC ,分别交EF 、GH 于点M ,N ,连接FN .已知3AH DH =,且21ABCD S =正方形,则图中阴影部分的面积之和为( )A .214B .215C .225D .223【解答】解:21ABCD S =Q 正方形,221AB \=,设DH x =,则33AH DH x ==,22921x x \+=,22110x \=,根据题意可知:AE CG DH x ===,3CF AH x ==,32FE FG CF CG x x x \==-=-=,2FGN CGNS S D D \=AEM CGN S S D D =Q ,FGN AEM CGN S S S D D D \=+,\阴影部分的面积之和为:()12NGFM S NG FM FG =+×梯形1()2EM MF FG =+×12FE FG =×21(2)2x =´22x =215=.故选:B .26.如图,在ABC D 中,90C Ð=°,点M 是AB 的中点,点N 在AC 上,MN AB ^.若8AC =,4BC =,则NC 的长为( )A .3B .4C .5D .【解答】解:如图,连接BN ,AB Q 的垂直平分线交AB 、AC 于点M 、N ,AN BN \=,设NC x =,则8AN BN x ==-,在Rt BCN D 中,由勾股定理得:222BN BC CN =+,即222(8)4x x -=+,解得:3x =,即3NC =,故选:A .27.如图,由四个全等的直角三角形拼成的图形,设CE a =,HG b =,则斜边BD 的长是()A B C .a b +D .a b-【解答】解:设CD x =,则DE a x =-,HG b =Q ,AH CD AG HG DE HG a x b x \==-=-=--=,2a bx -\=,22a b a bBC DE a -+\==-=,2222222()()222a b a b a b BD BC CD +-+\=+=+=,BD \=,故选:B .28.在长方形ABCD 中,52AB =,4BC =,CE CF =,延长AB 至点E ,连接CE ,CF 平分ECD Ð,则BE = 76 .【解答】解:如图,延长CF ,BA 交于点G ,连接EF ,过点F 作FH CE ^于H ,过点E 作EM CF ^于M ,Q 四边形ABCD 是矩形,且52AB =,4BC =,//AB CD \,52AB CD ==,90D ABC CBE Ð=Ð=Ð=°,DCF G \Ð=Ð,CF Q 平分ECD Ð,DCF FCE \Ð=Ð,FH DF =,G ECF \Ð=Ð,EC EG \=,ECG \D 是等腰三角形,CM MG \=,CE CF =Q ,ECF \D 是等腰三角形,EM CF ^Q ,FH CE ^,EM \和FH 是等腰三角形腰上的高,EM FH DF \==,Rt CDF Rt CME(HL)\D @D ,52CM CD \==,5CG \=,Rt CBG D 中,3BG ===,设BE x =,则3EC EG x ==+,Rt CBE D 中,222(3)4x x +=+,解得:76x =,76BE \=.故答案为:76.29.如图是“赵爽弦图”, ABH D ,BCG D ,CDF D 和DAE D 是四个全等的直角三角形,四边形ABCD 和EFGH 都是正方形,如果10AB =,且:3:4AH AE =.那么AH 等于 6 .【解答】解:10AB =Q ,:3:4AH AE =,设AH 为3x ,AE 为4x ,由勾股定理得:222222(3)(4)(5)AB AH AE x x x =+=+=,510x \=,2x \=,6AH \=,故答案为:6.30.[阅读理解]如图,在ABC D 中,4AB =,6AC =,7BC =,过点A 作直线BC 的垂线,垂足为D ,求线段AD 的长.解:设BD x =,则7CD x =-.AD BC ^Q ,90ADB ADC \Ð=Ð=°.在Rt ABD D 中,222AD AB BD =-,在Rt ACD D 中,222AD AC CD =-,2222AB BD AC CD \-=-.又4AB =Q ,6AC =,222246(7)x x \-=--.解得2914x =,2914BD \=.AD \==.[知识迁移](1)在ABC D 中,13AB =,15AC =,过点A 作直线BC 的垂线,垂足为D .)i 如图1,若14BC =,求线段AD 的长;)ii 若12AD =,求线段BC 的长.(2)如图2,在ABC D 中,AB =,AC =,过点A 作直线BC 的垂线,交线段BC 于点D ,将ABD D 沿直线AB 翻折后得到对应的ABD D ¢,连接CD ¢,若252AD =,求线段CD ¢的长.【解答】解:(1))i 设BD x =,则14CD x =-,AD BC ^Q ,90ADB ADC \Ð=Ð=°,在Rt ABD D 中,222AD AB BD =-,在Rt ACD D 中,222AD AC CD =-,2222AB BD AC CD \-=-,13AB =Q ,15AC =,22221315(14)x x \-=--,5x \=,5BD \=,12AD \===;)ii 在Rt ABD D 中,5BD ===,在Rt ACD D 中,9CD ===,当ABC Ð为锐角时,如图11-,5914BC BD CD =+=+=,当ABC Ð为钝角时,如图12-,954BC BD CD =-=-=;(2)如图2,连接DD ¢交AB 于点N ,则DD AB ¢^,过点D ¢作D H BD ¢^于H ,在Rt ABD D 中,254BD ==;在Rt ACD D 中,5CD ==,AB Q 垂直平分DD ¢,254D B DB ¢\==,2D D DN ¢=,1122ABD S AD BD AB DN D =×=×Q ,\252524DN ´=,DN \=2D D DN ¢\==,设HB m =,则254HD HB BD m =+=+,22222D H D D HD D B HB ¢¢¢=-=-Q ,22222525(()44m m \-+=-,154m \=,154HB \=,152541544HC HB BD CD \=++=++=,5D H ¢===,D C ¢\===.。
18[1].1勾股定理的应用(习题课)——10年3月18日
![18[1].1勾股定理的应用(习题课)——10年3月18日](https://img.taocdn.com/s3/m/a8e61ee3aeaad1f346933f47.png)
A D B C
B
D A
C
例7(2)如图,有一块直角三角形纸片,两 直角边AC=6cm,BC=8cm,现将直角边AC沿直 线AD折叠,使它落在斜边AB上,且与AE重合, A 求CD的长. 方程思想:直角三 角形中,已知一直 6 角边,以及另一直 角边和斜边的等量 关系,可建立方程 C x 求解. 6
C
A
B
D
变式2、在等腰△ABC中,AB=AC=13cm , BC=10cm,求△ABC的面积和AC边上的高.
A
A
A
两个直角三角形中,如果有一条公共边,可 利用勾股定理建立方程求解 . B C B C B D
E
变式3、已知:如图,△ABC中,AB=26, BC=25,AC=17,求△ABC的面积.
B
E
A
例5(1)已知直角三角形的两边长分别是3和 4, 则第三边长为 5 或 7 . (2)三角形ABC中,AB=10,AC=17,BC边上的高线 AD=8,求BC 21 或9
A
8 6 15
8 6
D
17
10 B C
15
练习5(1)已知直角三角形两边的长分别 是3cm和6cm,则第三边的长是 . (2)△ABC中,AB=AC=2,BD是AC边 上的高,且BD与AB的夹角为300,求CD 的长.
1
教材改编题
教材67页探究2:如图,一架长为10m的梯子AB斜靠在墙上,梯 子的顶端距地面的垂直距离为8m. 问题:如果梯子的顶端下滑1m,那么它的底端是否也滑动1 m?
变式一:当梯子的顶端下滑多少米时,梯子顶端下滑的距离AC 会等于梯子底端下滑的距离BD? 变式二:如果设梯子的长度为c米,AO=b米,BO=a米,请 用含a、b的式子表示当梯子顶端下滑多少米时,梯子顶端下滑 的距离AC会等于梯子底端下滑的距离BD?
北师大版八年级(上)数学《勾股定理的应用》课堂练习(含答案)
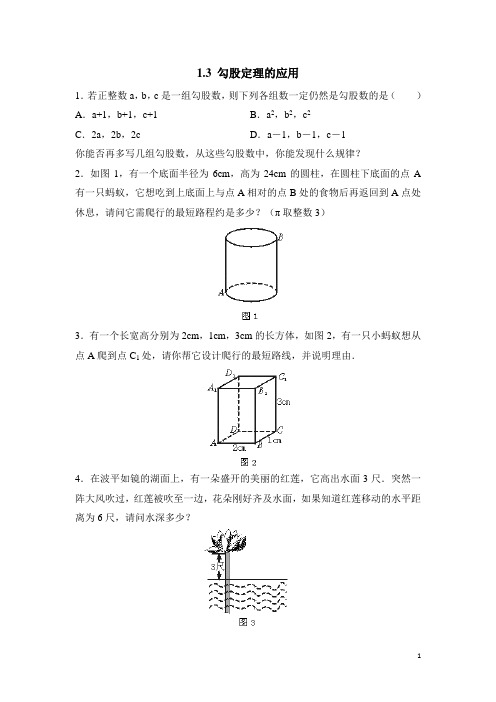
1.3 勾股定理的应用1.若正整数a,b,c是一组勾股数,则下列各组数一定仍然是勾股数的是()A.a+1,b+1,c+1 B.a2,b2,c2C.2a,2b,2c D.a-1,b-1,c-1你能否再多写几组勾股数,从这些勾股数中,你能发现什么规律?2.如图1,有一个底面半径为6cm,高为24cm的圆柱,在圆柱下底面的点A 有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物后再返回到A点处休息,请问它需爬行的最短路程约是多少?(π取整数3)3.有一个长宽高分别为2cm,1cm,3cm的长方体,如图2,有一只小蚂蚁想从点A爬到点C1处,请你帮它设计爬行的最短路线,并说明理由.4.在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,请问水深多少?参考答案1.C若a,b,c为一组勾股数,那么ka,kb,kc(k≠0,k为常数)也是勾股数.2.解:如下图:将圆柱沿着过A点的高AC剪开,并将侧面展开.1·2πr=π·r≈18(cm)则AC=24cm,BC=2∴在Rt△ABC中,AB2=AC2+BC2=242+182,∴AB=30(cm)∴它最短的爬行路程约为30×2=60(厘米)3.(1)当蚂蚁在侧面A1ABB1和侧面B1BCC1上爬行时,爬行的最短路线的长设为d1,则d12=(2+1)2+32=18(2)当蚂蚁在侧面A1ABB1和上底面A1B1C1D1上爬行时,由A到C1的最短路线的长设为d2,则d22=22+(3+1)2=20(3)同理可求得蚂蚁在侧面A1ADD1和D1DCC1上爬行时,d32=32+(1+2)2=18,蚂蚁在底面ABCD,侧面D1DCC1上爬行时,d32=22+(1+3)2=20所以,蚂蚁可沿A—M—C1爬行,如下图:或蚂蚁沿A—N—C1爬行,如下图:4.解:设水深为x尺如图,Rt△ABC中,AB=h,AC=h+3,BC=6由勾股定理得:AC2=AB2+BC2,即(h+3)2=h2+62∴h2+6h+9=h2+36,解得:h=4.5答:水深4.5尺.。
2024年第十七章第2课时-勾股定理的应用课堂练习题及答案

B.82+(x+4)2=x2
C.82+(x-4)2=x2
D.x2+82=(x+4)2
7
8
9
第2课时 勾股定理的应用
8.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个
小圆孔,则一条长16的直吸管露在罐外部分a的长度(罐壁的厚度和小
圆孔的大小忽略不计)范围是 3≤a≤4
45°角,作业时调整为60°角(如图所示),则梯子的顶端A沿墙面升高
5
5
3- 2
了__________m.
2
2
1
2
3
4
5
6
第2课时 勾股定理的应用
4.“儿童散学归来早,忙趁东风放纸鸢”.又到了放风筝的最佳时节.某校八年
级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度
CE(如图),他们进行了如下操作:①测得水平距离BD的长为8米;
1
2
3
4
5
6
第2课时 勾股定理的应用
(2)如果小明想风筝沿CD方向下降9米,则他应该往回收线多少米?
解:如图,由题意,得CM=9米,
∴DM=15-9=6(米).
∴BM= DM2 +BD2 = 6 2 +8 2 =10(米).
∴BC-BM=17-10=7(米).
答:他应该往回收线7米.
1
2
3
4
5
6
第2课时 勾股定理的应用
第十七章 勾股定理
第十七章 勾股定理
17.1 勾股定理
第2课时 勾股定理的应用
第2课时 勾股定理的应用
人教版八年级下册数学习题课件. 勾股定理第二课时 勾股定理的应用

11.如图,在高3米,斜边长为5米的楼梯的表面铺地毯,地毯的长度 至少为__7__米.
第11题图 12.如图,A 点表示的实数为___3______.
第12题图
13.(2020·扬州)《九章算术》是中国传统数学的重要著作之一,奠定 了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题: “今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一 根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺, 试问折断处离地面多高?答:折断处离地面____4_.5_5______尺高.
17.如图,公路MN和公路PQ在点P处交汇,已知∠QPN=30°,点A 处有一所小学,AP=160米,假使拖拉机行驶时,周围100米内受到噪音 的影响,那么拖拉机在公路上沿PN方向行驶时,学校是否受到噪音影响? 若受影响,假使拖拉机的速度为18千米/时,那么学校受影响的时间为多 少秒?
题图答图Biblioteka 解:如图,过A作AB⊥PN,在△PAB中,∠QPN=30°,PA=160米, ∴AB=80米<100米,∴学校会受噪音影响.设拖拉机到C处开始受影响, 则CA=100米,则BC2=CA2-BA2,∴BC=60米,拖拉机行到D处后恰 好不影响学校,则BC=BD,CD=120米,∵拖拉机的速度为18千米/时 =5米/秒,∴学校受影响的时间为120÷5=24(秒)
志之所趋,无远勿届,穷山复海不能限也;志之所向,无坚不摧。
贫成困功能 往造往就偏C男向子于.气有1概准3。备c的m人 D.16 cm
石看纹理山看脉,人看志气树看材。 丈夫志气薄,儿女安得知? 壮志与毅力是事业的双翼。 远大的希望造就伟大的人物。 胸无大志,枉活一世。 一个人如果胸无大志,既使再有壮丽的举动也称不上是伟人。 在年轻人的颈项上,没有什么东西能比事业心这颗灿烂的宝珠。 志之所趋,无远勿届,穷山复海不能限也;志之所向,无坚不摧。 志气和贫困是患难兄弟,世人常见他们伴在一起。 有志的人战天斗地,无志的人怨天恨地。 不为穷变节,不为贱易志。 卒子过河,意在吃帅。 有志者能使石头长出青草来。
