向量和向量的基本运算
向量的基本运算公式大全

向量的基本运算公式大全下面是向量的基本运算公式大全:1.向量加法:o a + b = b + a(交换律)o(a + b) + c = a + (b + c)(结合律)2.向量减法:o a - b = a + (-b)3.向量数量乘法:o ka = ak(交换律,其中k是标量)o(kl)a = k(la)(结合律)4.零向量:o a + 0 = ao a + (-a) = 05.向量点乘(内积):o a·b = b·a(交换律)o(ka)·b = k(a·b) = a·(kb)(分配律)o a·(b + c) = a·b + a·c(分配律)6.向量叉乘(外积):o a×b = -(b×a)(反对称性)o a×(b + c) = a×b + a×c(分配律)o(ka)×b = k(a×b) = a×(kb)(分配律)7.向量混合积:o a·(b×c) = b·(c×a) = c·(a×b)8.长度(模):o||a|| = √(a·a)9.单位向量:o一个向量除以其长度得到单位向量: a/||a||10.平行和垂直:o两个向量平行:a与b平行,当且仅当存在标量k,使得a = kb或b = ka。
o两个向量垂直:a与b垂直,当且仅当a·b = 0。
这些是向量的基本运算公式,它们形成了向量运算的基础,可以用于解决向量计算和几何问题。
需要注意的是,这些公式适用于向量的二维、三维或更高维度空间。
具体运用时,根据具体的向量运算要求和问题,选择合适的公式和运算规则。
向量的基本运算及应用教案

向量的基本运算及应用教案引言:向量是数学中的一种重要概念,广泛应用于物理学、工程学和计算机科学等领域。
本教案旨在通过教授向量的基本运算和应用,让学生们深入理解向量的概念和运算法则,培养他们对向量运算的应用能力。
一、向量的基本概念1. 向量的定义向量是有大小和方向的量,用箭头表示,在平面上可以表示为带有起点和终点的有向线段。
2. 向量的表示方法向量可以使用坐标表示法和分量表示法进行表示。
3. 向量的运算法则(1)向量的加法:将两个向量的对应分量相加,得到新的向量。
(2)向量的减法:将两个向量的对应分量相减,得到新的向量。
(3)向量的数量乘法:将向量的每个分量都乘以一个标量,得到新的向量。
二、向量的基本运算实例1. 向量的加法实例假设有向量 A(2, 3) 和向量 B(4, -1),则它们的向量和为:A +B = (2+4, 3+(-1)) = (6, 2)2. 向量的减法实例假设有向量 A(5, 7) 和向量 B(3, 2),则它们的向量差为:A -B = (5-3, 7-2) = (2, 5)3. 向量的数量乘法实例假设有向量 A(3, 4),要将其乘以 2,则结果为:2A = (2*3, 2*4) = (6, 8)三、向量的应用1. 向量的平移通过向量的加法运算,可以实现对向量的平移操作。
例如,将向量A(2, 3) 平移到点 (5, 7),可以得到平移后的向量为:A' = A + (5-2, 7-3) = (3, 4)2. 向量的线性组合向量的线性组合是指将多个向量按照一定比例相加的操作。
例如,向量 A(2, 3) 和向量 B(4, 1) 的线性组合可以表示为:cA + dB = (c*2, c*3) + (d*4, d*1) = (2c+4d, 3c+d),其中 c 和 d 为标量。
3. 向量的内积和外积向量的内积和外积是向量运算中的两个重要概念。
(1)向量的内积:也称为点积,可以用来计算两个向量间的夹角。
向量的运算的所有公式

向量的运算的所有公式向量运算是数学中的一个重要概念,它可以用来描述力学、物理、几何等领域中的各种现象。
本文将介绍向量的基本运算公式,涵盖向量的加法、减法、数乘、点积、叉积等运算。
1.向量的加法:向量的加法是指将两个向量相加得到一个新的向量。
设有两个向量A 和B,它们的加法可以表示为:A+B=(A1+B1,A2+B2,...,An+Bn)其中,A1、A2...An和B1、B2...Bn分别是向量A和B的各个分量。
2.向量的减法:向量的减法是指将一个向量减去另一个向量得到一个新的向量。
设有两个向量A和B,它们的减法可以表示为:A-B=(A1-B1,A2-B2,...,An-Bn)其中,A1、A2...An和B1、B2...Bn分别是向量A和B的各个分量。
3.向量的数乘:向量的数乘是指将一个向量的每个分量乘以一个常数得到一个新的向量。
设有一个向量A和一个实数k,它们的数乘可以表示为:kA=(kA1,kA2,...,kAn)其中,A1、A2...An是向量A的各个分量,k是一个实数。
4.向量的点积(内积):向量的点积是指将两个向量的对应分量相乘再求和得到一个标量。
设有两个向量A和B,它们的点积可以表示为:A·B=A1B1+A2B2+...+AnBn其中,A1、A2...An和B1、B2...Bn分别是向量A和B的各个分量。
5.向量的叉积(外积):向量的叉积是指将两个向量进行运算得到一个新的向量。
设有两个三维向量A和B,它们的叉积可以表示为:A×B=(A2B3-A3B2,A3B1-A1B3,A1B2-A2B1)其中,A1、A2、A3和B1、B2、B3分别是向量A和B的三个分量。
6.向量的模(长度):向量的模是指向量的大小或长度,可以通过向量的分量计算得到。
设有一个n维向量A,它的模可以表示为:A,=√(A1^2+A2^2+...+An^2)7.向量的投影:向量的投影是指将一个向量在另一个向量上的投影,得到一个标量。
平面向量加减法口诀
向量的加法口诀: 首尾相连,首连尾,方向指向末向量。
以第一个向量的起点为起点,以第二个向量的终点为终点的向量是两向量的和向量。
二、向量的减法两向量做减法运算,图像如下图所示:向量的减法口诀: 首首相连,尾连尾,方向指向被减向量。
以第一个向量的终点为起点,以第二个向量的终点为终点的向量是两向量的差向量。
向量的学习是高一数学必修四第二章的内容,要求同学们会向量的基本运算,其中就包括加法、减法、数乘。
要求大家能根据运算法则解决基本的向量运算,学会运用图像解决向量加减法,向量的数乘等问题。
向量的相关题目难度也不是很大,只要大家认真学习,认真做好笔记,认真做做题目,总结做题规律,那么当我们遇到类似题目时就会似曾相识,做起来也很顺手,再细心点的话,得满分也没有问题。
学习方法很多,重要的事找到适合自己的方法,当然适合自己方法就是最好的方法。
附一;三角形定则解决向量加减的方法将各个向量依次首尾顺次相接,结果为第一个向量的起点指向最后一个向量的终点。
注:两个向量相减,则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。
平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣>1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上伸长为原来的λ∣倍;当∣λ∣<1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律:(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa.数对于向量的分配律(第二分配律):λ(a+b)=λa+λb.数乘向量的消去律:① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义:已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义:两个向量的数量积(内积、点积)是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉;若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示:a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a(交换律);(λa)·b=λ(a·b)(关于数乘法的结合律);(a+b)·c=a·c+b·c(分配律);向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即:(a·b)·c≠a·(b·c);例如:(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即:由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义:两个向量a和b的向量积(外积、叉积)是一个向量,记作a×b.若a、b不共线,则a×b的模是:∣a×b∣=|a|·|b|·sin〈a,b〉;a×b的方向是:垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质:∣a×b∣是以a和b为边的平行四边形面积.。
向量代数的基本概念及运算法则

向量代数的基本概念及运算法则向量代数是线性代数的重要部分,涉及了向量的基本概念及其运算法则。
本文将介绍向量的概念、向量的加法和减法运算法则、向量的数乘运算法则,并讨论一些常见的向量运算性质。
一、向量的概念向量是具有大小和方向的物理量,常用有向线段表示。
通常将向量用字母加箭头表示,例如,向量a用记号“→a”表示。
向量有两个重要的属性,即大小(模)和方向。
向量的大小表示向量的长度或大小,用|→a| 或||→a|| 表示,读作“模a”或“a的模”。
向量的方向表示指向何处,可以用角度、弧度或者其他方式进行表示。
二、向量的加法和减法运算法则向量的加法运算是指将两个向量进行求和的运算,其法则可以用平行四边形法则和三角法则表示。
平行四边形法则可以简要描述如下:设有向量→a和→b,取→a的起点作为平行四边形的一个顶点,将→b 平移至→a的终点,以→a和→b的起点为相对顶点形成平行四边形,平行四边形的对角线所表示的向量,即为向量→a和→b的和向量→a+→b。
三角法则可以简要描述如下:将→a和→b的起点相接,以→a的终点为直角,连接→b的终点和→a的起点,所得的向量即为向量→a和→b的和向量→a+→b。
向量的减法运算是指将两个向量进行相减的运算,可以通过向量的加法和取负得到。
设有向量→a和→b,向量→a减去向量→b即为向量→a加上向量→b的负向量,即→a-→b=→a+(-→b)。
三、向量的数乘运算法则向量的数乘运算是指将一个向量乘以一个实数的运算,用以改变向量的长度或方向。
设有向量→a和实数k,向量→a与k的乘积,记作k→a,即为把向量→a的长度伸缩为原来的|k|倍,并在原来的方向上(若k>0)或相反方向上(若k<0)。
四、常见的向量运算性质1. 交换律:向量加法满足交换律,即→a+→b=→b+→a。
2. 结合律:向量加法满足结合律,即(→a+→b)+→c=→a+(→b+→c)。
3. 分配律:向量的数乘运算满足分配律,即k(→a+→b)=k→a+k→b。
向量的基本运算和性质

向量的基本运算和性质在数学的广阔领域中,向量是一个极其重要的概念,它不仅在几何、物理等学科中有着广泛的应用,也是我们理解和解决许多实际问题的有力工具。
接下来,让我们一起深入探索向量的基本运算和性质。
向量,简单来说,就是既有大小又有方向的量。
比如,力就是一个常见的向量,它既有大小(力的强度),又有方向(力的作用方向)。
在数学中,我们通常用有向线段来表示向量,线段的长度表示向量的大小,箭头所指的方向表示向量的方向。
向量的基本运算主要包括加法、减法和数乘。
向量的加法是将两个向量首尾相连,从第一个向量的起点指向第二个向量的终点所得到的向量就是它们的和向量。
举个例子,如果有向量 A 和向量 B,将向量 A 的终点与向量 B 的起点相连,那么从向量 A 的起点到向量 B 的终点所构成的向量就是 A + B。
向量加法满足交换律和结合律,也就是说 A + B = B + A,(A + B) + C = A +(B+ C)。
这就好比我们走路,先向东走一段距离,再向北走一段距离,和先向北走一段距离,再向东走一段距离,最终到达的位置是一样的。
向量的减法可以看作是加法的逆运算。
向量 A 减去向量 B,就等于向量 A 加上向量 B 的相反向量(大小相等,方向相反)。
比如,要计算 A B,我们可以把它转化为 A +(B)。
数乘向量则是将一个实数与一个向量相乘。
当这个实数大于 0 时,得到的向量与原向量方向相同,大小是原向量的倍数;当实数小于 0 时,得到的向量与原向量方向相反,大小是原向量的倍数的绝对值;当实数为 0 时,得到的是零向量。
数乘向量满足分配律,即 k(A + B)= kA + kB。
向量还有一些重要的性质。
首先是向量的模。
向量的模就是向量的长度,对于向量 A =(x, y),它的模可以用公式√(x²+ y²) 来计算。
模的大小反映了向量的长度,模为 0 的向量就是零向量。
其次是向量的点积。
高三数学平面向量向量及向量的基本运算

孩子从母亲那里,得到最初的食物和衣着,看到世上第一张欢颜,听到人间第一句笑语……小小的心,像一只薄而透明的钵,盛满了乳色的爱,悄悄涟漪着。以孩子的智力,必认为这些都是上天无缘无故倾倒的琼浆玉液,是与生俱来的赠品。 作为施与的一方,母爱有时也是本能以致盲
目愚蠢的代名词。母爱单纯也复杂,清澈也浑浊,博大也狭窄,无偿也有偿。体验这种以血为缘的爱,感知它的厚重深远,纪念它的无私无畏,弘扬它的旗幡,播撒它的甘霖,需要灵敏的悟力和细腻的柔情。世人只知给予艰难,其实接受也非易事,需要虚怀若谷的智慧。只有容纳得多,
成人还是少年,我们都曾欢欣地接受过母爱,我们也都可以成为辐射母爱的源泉。 柔 和 ? “柔和”这个词,细想起来挺有意思的。先说“和”字,由禾苗和口两问部分组成,那涵义大概就是有了生长着的禾苗,嘴里的食物就有了保障,人就该气定神闲,和和气气了。 这个规律,在农
耕社会或许是颠扑不破的。那时只要人的温饱得到解决,其他的都好说。随着社会和科技的发达进步。人的较低层次需要得到满足之后,单是手中的粮,就无法抚平激荡的灵魂了。中国有句俗话,叫作“吃饱了撑的——没事找事”。可见胃充盈了之后,就有新的问题滋生,起码无法达到
想起了母亲。当我们想起母亲的时候,其实是想起了无边无际云蒸霞蔚的爱。当我们想起爱的时候,其实是想起了如天宇般宽广淳厚的温暖和一种伟大神圣的责任。当我们想起责任的时候,其实是在宁静致远地思索人生的真谛和生命的尊严。 世上没有关于“家”的节日,好在有一个
“母亲节”,让我们飘荡的心有所附丽。每年这一天,人们心心相印地隆重纪念这个民间节日,感念一种饱含沧桑的爱。 最初发起为母亲设定一个节日的人,定是一位成年的男人或是女人。太小的孩子,我以为是无法理解母爱的。婴儿的热爱的涌起,更多地是源于一种生命本能的驱动。
向量代数的基本公式

向量代数的基本公式向量代数是数学中的一个分支,主要研究在向量空间中向量的代数运算及其相关性质。
向量代数中包括很多基本公式,这些公式不仅是向量代数研究中的重要内容,也是我们日常生活中常常用到的数学工具。
在这篇文章中,我们将介绍向量代数中的一些基本公式及其重要性。
1. 向量加法的基本公式向量加法是向量代数中最基本的运算之一,它表达了两个向量相加的结果。
对于任意两个向量a和b,它们的和向量c可以表示为:c = a + b该公式意味着,当我们把向量a和向量b相加时,向量c的大小和方向取决于a和b的大小和方向。
这个公式在计算中非常实用,因为在求解向量问题时,通常需要将多个向量相加或相减。
2. 向量数量积的基本公式向量数量积指的是两个向量的标量积,也称为点积。
对于向量a和向量b,它们的数量积可以表示为:a·b = |a||b|cosθ其中,|a|和|b|分别表示向量a和b的模长,θ表示它们之间的夹角,cosθ表示它们之间的夹角的余弦值。
该公式的意义在于,它为我们提供了两个向量之间的度量方法。
例如,我们可以使用该公式计算两个向量之间的夹角,也可以计算出它们之间的投影等。
3. 向量矢量积的基本公式向量矢量积指的是两个向量的向量积,也称为叉积。
对于向量a和向量b,它们的向量积可以表示为:a×b = |a||b|sinθn其中,|a|和|b|分别表示向量a和b的模长,θ表示它们之间的夹角,n表示一个垂直于a和b所在平面的单位向量,sinθ表示它们之间夹角的正弦值。
该公式的重要性在于它可以用于计算平面区域、体积和方向向量等问题。
例如,在计算三角形面积时,我们可以利用向量积的大小。
此外,在物理学、工程学等领域中,向量积的应用也非常广泛。
4. 向量三角函数的基本公式向量三角函数指的是向量和角度之间的关系。
与传统的三角函数类似,向量三角函数包括正弦、余弦、正切等。
对于向量a和向量b,它们的三角函数可以表示为:sinθ = |a×b|/|a||b| cosθ = a·b/|a||b| tanθ = |a×b|/a·b其中,sinθ表示向量a和b的夹角的正弦值,cosθ表示它们之间的夹角的余弦值,tanθ表示它们之间的夹角的正切值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向量及向量的基本运算一、教学目标:1.理解向量的有关概念,掌握向量的加法与减法、实数与向量的积、向量的数量积及其运算法则,理解向量共线的充要条件.2.会用向量的代数运算法则、三角形法则、平行四边形法则解决有关问题.不断培养并深化用数形结合的思想方法解题的自觉意识.二、教学重点:向量的概念和向量的加法和减法法则. 三、教学过程: (一)主要知识: 1)向量的有关概念①向量:既有大小又有方向的量。
向量一般用c b a,,……来表示,或用有向线段的起点与终点的大写字母表示,如:AB 。
向量的大小即向量的模(长度),记作|AB |。
②零向量:长度为0的向量,记为0 ,其方向是任意的,0与任意向量平行。
<注意与0的区别>③单位向量:模为1个单位长度的向量。
④平行向量(共线向量):方向相同或相反的非零向量。
任意一组平行向量都可以移到同一直线上。
相反向量:我们把与向量a 长度相等,方向相反的向量叫做a的相反向量。
记作-a 。
⑤相等向量:长度相等且方向相同的向量。
相等向量经过平移后总可以重合,记为b a=。
2)向量加法①求两个向量和的运算叫做向量的加法。
设b a==,,则a +b =+=。
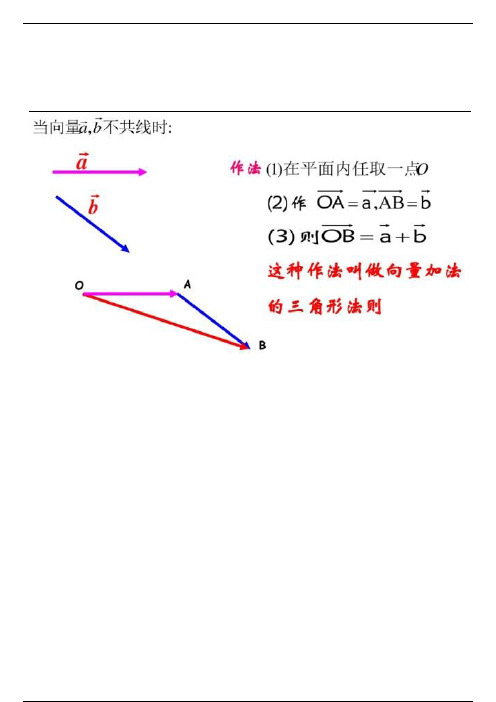
向量加法有“三角形法则”与“平行四边形法则”。
说明:(1)a a a=+=+00;(2)向量加法满足交换律与结合律; 3)向量的减法① 相反向量:与a 长度相等、方向相反的向量,叫做a 的相反向量。
记作a-,零向量的相反向量仍是零向量。
关于相反向量有: (i ))(a --=a; (ii)a +(a -)=(a -)+a =0 ;(iii)若a 、b是互为相反向量,则a =b -,b =a -,a +b =0 。
②向量减法:向量a 加上b 的相反向量叫做a 与b的差,记作:)(b a b a -+=-。
求两个向量差的运算,叫做向量的减法。
b a -的作图法:b a -可以表示为从b 的终点指向a 的终点的向量(a 、b有共同起点)。
注:(1)用平行四边形法则时,两个已知向量是要共始点的,和向量是始点与已知向量的始点重合的那条对角线,而差向量是另一条对角线,方向是从减向量指向被减向量。
(2) 三角形法则的特点是“首尾相接”,由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和;差向量是从减向量的终点指向被减向量的终点。
4)实数与向量的积①实数λ与向量a 的积是一个向量,记作λa,它的长度与方向规定如下:(Ⅰ)a a⋅=λλ;(Ⅱ)当0>λ时,λa 的方向与a 的方向相同;当0<λ时,λa 的方向与a的方向相反;当0=λ时,0=a λ,方向是任意的。
②数乘向量满足交换律、结合律与分配律。
实数与向量的积的运算律:设λ、μ为实数,则①λ(μa )=(λμ) a②(λ+μ) a =λa +μa③λ(a +)=λa+λ 5)两个向量共线定理向量b 与非零向量a共线⇔有且只有一个实数λ,使得b =a λ。
6)平面向量的基本定理如果21,e e 是一个平面内的两个不共线向量,那么对这一平面内的任一向量a,有且只有一对实数21,λλ使:2211e e a λλ+=其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底。
7)特别注意:(1)向量的加法与减法是互逆运算。
(2)相等向量与平行向量有区别,向量平行是向量相等的必要条件。
(3)向量平行与直线平行有区别,直线平行不包括共线(即重合),而向量平行则包括共线(重合)的情况。
(4)向量的坐标与表示该向量的有向线条的始点、终点的具体位置无关,只与其相对位置有关。
(二)主要方法:1.充分理解向量的概念和向量的表示; 2.数形结合的方法的应用;3.用基底向量表示任一向量唯一性; 4.向量的特例0和单位向量,要考虑周全. (三)例题分析:例1、判断下列各命题是否正确(1)零向量没有方向 (2)若b a b a ==则, (3)单位向量都相等 (4) 向量就是有向线段(5)两相等向量若共起点,则终点也相同 (6)若b a =,c b =,则c a=;(7)若b a //,c b //,则c a// (8)若四边形ABCD 是平行四边形,则DA BC CD B ==,A(9)已知A (3,7),B (5,2),将AB 按向量a =(1,2)平移后得到的向量B A ''的坐标为(3,-3)(10)b a =的充要条件是||||b a =且b a //;解:(1) 不正确,零向量方向任意, (2) 不正确,说明模相等,还有方向 (3) 不正确,单位向量的模为1,方向很多 (4) 不正确,有向线段是向量的一种表示形式 (5)正确, (6)正确,向量相等有传递性 (7)不正确,因若0=b ,则不共线的向量c a ,也有0//a,c //0。
(8) 不正确, 如图DA BC CD B ≠=,A (9)不正确,∵a =(1,2),∴平移公式是⎩⎨⎧+='+='21y y x x ,将A (3,7),B (5,2)分别代入可求得)4,6(),9,4(B A '',故B A ''=(6,4)-(4,9)=(2,-5)。
(10)不正确,当b a //,且方向相反时,即使||||b a =,也不能得到b a=;[点评]正确理解向量的有关概念例2、如图平行四边形ABCD 的对角线OD,AB 相交于点C ,线段BC 上有一点M 满足BC=3BM,线段CD 上有一点N 满足CD =3CN,设MN ON OM b a b OB a OA ,,,,,表示试用==解:()()b a OB OA BA BM BA BC BM -=-==∴==616161,6131 b a BM OB OM 6561+=+=∴ . OD CD ON CD CN 3234,31==∴=()()b a OB OA OD ON +=+==∴323232 b a OM ON MN 6121-=-=∴[点评]根据向量的几何加减法则,能对图形中的向量进行互相表示练习: △ABC中,.,//,32N DE BC AM E AC BC DE AB AD 于边上中线交是于交=,,b AC a AB ==设 用AN AM DN DE BC AE b a ,,,,,,分别表示向量.如图 解:()()a b DN a b DE a b BC b AE -=-=-==31,32,,32 ()()a b AN a b AM +=+=31,21例3、一条渔船距对岸4km ,以2km/h 的速度向垂直于对岸的方向划去,到达对岸时,船的实际航程为8km ,求河水的流速.解:设AB 表示垂直于对岸的速度,BC 表示水流速度,则AC 为实际速度 航行时间为4km ÷2km/h=2h 在△ABC 中3242===BC AC AB所以, 河水的流速为h km /32[点评]求合力或分力,合速或分速问题用向量解是一种常见问题,要善于运用平行四边形和三角形法则例4、在△ABC 中,D 、E 分别为AB 、AC 的中点,用向量的方法证明: DE 平行且等于0.5BC分析:要证明DE 平行且等于0.5BC,只要BC DE 21= 解:如图AB Ac BC AD AE DE -=-=, 又D,E 为中点AC AE AB AD 21,21==∴ 即()BC AB AC AD AE DE 2121=-=-=所以DE 平行且等于210.5BC[点评]几何问题可以转化为向量问题的证明,往往会变的简单明了练习: 已知G 是△ABC 的重心,求证:0=++GC GB GA证明:以向量GC GB ,为邻边作平行四边形GBEC ,则GD GE GC GB 2==+,又由G 为△ABC 的重心知GD AG 2=,从而GD GA 2-=,∴022=+-=++GD GD GC GB GA 。
例5、设21,e e 是不共线的向量,已知向量2121212,3,2e e CD e e CB e k e AB -=+=+=,若A,B,D 三点共线,求k 的值 分析:使BD AB λ=解:214e e -=-=, 使λ=)4(22121e e e k e -=+∴λ 得84,2-=⇒-==k k λλ[点评]共线或平行问题,用向量或坐标平行的充要条件解决例3. 经过OAB ∆重心G 的直线与,OA OB 分别交于点P ,Q ,设,OP mOA OQ nOB ==,,m n R ∈,求11n m+的值。
解:设,OA a OB b ==,则1()3OG a b =+,PQ nb ma =-11()33PG OG OP m a b =-=-+由,,P G Q 共线,得存在实数λ,使得PQ PG λ=,即11()33nb ma m a b λλ-=-+从而1()313m m n λλ⎧-=-⎪⎪⎨⎪=⎪⎩,消去λ得:113n m +=(四)巩固练习:1.已知梯形ABCD 中,||2||AB DC =,M ,N 分别是DC 、AB 的中点,若AB 1e =,2AD e =,用1e ,2e 表示DC 、BC 、MN .解:(1)1122eDC AB ==(2)211122BC BA AC AB AC AD DC AB AD AB e e =+=-+=+-=-=- (3)1211114244MN MD DA AN AB AD AB AB AD e e =++=--+=-=-2. (1)设两个非零向量1e 、2e 不共线,如果12121223,623,48AB e e BC e e CD e e =+=+=-, 求证:,,A B D 三点共线.(2)设1e 、2e 是两个不共线的向量,已知1212122,3,2AB e ke CB e e CD e e =+=+=-,若,,A B D 三点共线,求k 的值.(1)证明:因为1212623,48BC e e CD e e =+=-AM D CNBG •QOBPA所以121015BD e e =+ 又因为1223AB e e =+ 得5BD AB =即//BD AB 又因为公共点B所以,,A B D 三点共线;(2)解:121221324DB CB CD e e e e e e =-=+-+=-122AB e ke =+ 因为,,A B D 共线所以//AB DB 设DB AB λ=所以212k λ=⎧⎪⎨=-⎪⎩ 即12k =-;四、小结:1)向量的有关概念: ①向量②零向量③单位向量④平行向量(共线向量)⑤相等向量 2)向量加法减法: 3)实数与向量的积 4)两个向量共线定理5)平面向量的基本定理, 基底五、作业:。
