第六章 双像投影测图
大地测量学第六章高斯投影及其计算

第六章 高斯投影 及其计算
中国矿业大学环境与测绘学院
第六章 高斯投影及其计算概述
1、椭球面上计算复杂; 2、椭球面上表示点位的经度、纬度大地线长、大地
方位角等对大比例尺测图不适应; 3、为了测绘地形图和计算的方便,需通过地图投影
的方法将椭球面上的元素化算到平面上; 4、本章主要介绍正形投影的特性以及高斯投影建立
应用大地测量学
§6.2.2 高斯投影的长度比和长度变形
1、用大地坐标表示的高斯投影长度比m
式中:
2、用平面坐标表示的高斯投影长度比m
m
1
y2 2R 2
y4 24R4
式中y为投影点的横坐标,R为该点处椭球平均曲率半径。
应用大地测量学
§6.2.2 高斯投影的长度比和长度变形
3、长度变形m-1与横坐标y的关系
5 5′
应用大地测量学
§6.3 高斯投影坐标计算
高斯投影坐标正算——由(B,L)求(x,y) 高斯投影坐标反算——由(x,y)求(B,L)
应用大地测量学
§6.3.1 高斯投影坐标正算公式
(6-26)
式中,X为由赤道至纬度B的子午线弧长, 为计算点P点与中央子午线
的经差。N为卯酉圈曲率半径,t=tanB, η=e′cosB。 L-L0若以度为单位,则ρ=57.295779513; L-L0若以分为单位,则ρ=3437.7467708; L-L0若以秒为单位,则ρ=206264.80625。
平面直角坐标系的方法、观测元素的化算、高斯 投影坐标计算。
第六章 高斯投影及其计算
第一节 地图投影概念和正形投影性质 第二节 高斯投影与国家平面直角坐标系(基础) 第三节 高斯投影坐标计算(重点) 第四节 椭球面上的方向和长度归算至高斯投影平面
应用大地测量学第六章-高斯投影及其计算

20
21
22
23
78° 84° 90° 96° 102° 108° 114° 120° 126° 132° 138° 27 29 31 33 35 37 39 41 43 45
2 3
应用大地测量学
§6.2.3 高斯投影的分带
6°带带号N和中央子午线经度 LN的关系式:LN=6N-3 3°带带号n和中央子午线经度 Ln的关系式:Ln=3n
2、将椭球面上起算元素和观测元素归算至高斯投 影平面,然后解算平面三角形,推算各边坐标方位角, 在平面上进行平差计算,求解各点的平面直角坐标。
§6.2.4 高斯投影的计算内容
第二种方法的具体推算内容如下:
应用大地测量学
1、将起算点的大地坐标(B1,L1)换算为高斯平面坐标(x1,y1)——高 斯投影坐标计算。 2、将起算边的大地方位角A12改换为平面坐标方位角T12; T12=A12-γ+δ12 式中,γ为子午线收敛角,δ12为方向改正。 3、将起算边的大地线长度S12归算为高斯平面上的直线长度D12: D12=S12+△S 式中△S为距离改正。 4、对于椭球面上三角网的各观测方向和观测边长分别进行方向改正和距离 改正,归算为高斯平面上的直线方向和直线距离。组成平面三角网,平差计 算,推求各控制点的平面直角坐标。
应用大地测量学
§6.3 高斯投影坐标计算
高斯投影坐标正算——由(B,L)求(x,y)
高斯投影坐标反算——由(x,y)求(B,L)
y2 y4 m 1 2 2R 24R 4
式中y为投影点的横坐标,R为该点处椭球平均曲率半径。
应用大地测量学
§6.2.2 高斯投影的长度比和长度变形
3、长度变形m-1与横坐标y的关系
第6章轴测图

6.3斜二等轴测图 6.3斜二等轴测图 6.3.1轴向伸缩系数和轴间角 6.3.2斜二等轴测图的画法
6.3.1轴向伸缩系数和轴间角 6.3.1轴向伸缩系数和轴间角
如图6-4所示, 如果使物体的XOZ坐 如图 所示, 如果使物体的 所示 坐 标面对轴测投影面处于平行的位置, 标面对轴测投影面处于平行的位置, 采 用平行斜投影法也能得到具有立体感的 轴测图, 轴测图, 这样所得到的轴测投影就是斜 二等测轴测图,简称斜二测图。 二等测轴测图,简称斜二测图。
图 6- 4
斜二等测轴测图
1.轴向伸缩系数 轴向伸缩系数
国标规定,轴向伸缩系数 国标规定,轴向伸缩系数p=r=1, , q=0.5,O1Y1轴的轴向伸缩系数与轴间角 , 轴的轴向伸缩系数与轴间角 无关,如图6-4所示 所示。 无关,如图 所示。
2.轴间角 轴间角
轴间角∠X1O1Z1=90°, 轴间角∠ ° ∠X1O1Y1=∠Z1O1Y1=135°,如图 所 ∠ ° 如图6-4所 示。
第六章 轴测图
第6章轴测图
6.1
轴测图的基本知识
6.2
正等轴测图
6.3
斜二等轴测图 轴测剖视图
6.4
6.1轴测图的基本知识 6.1轴测图的基本知识 6.1.1轴测投影的形成 6.1.2轴测图的分类 6.1.3轴间角和轴向伸缩系数 6.1.4轴测图的基本性质
6.1.1轴测投影的形成 6.1.1轴测投影的形成
2.切割法 切割法
画切割体的轴测图时, 画切割体的轴测图时,先画出其完整 形体的轴测图, 形体的轴测图,再按形体形成的过程逐一 切去多余的部分而得到所求的轴测图, 切去多余的部分而得到所求的轴测图,这 种方法称为切割法。 种方法称为切割法。 当平面立体上的平面多数和坐标平面 平行时,可采用叠加或切割的方法绘制, 平行时,可采用叠加或切割的方法绘制, 画图时,可先画出基本形体的轴测图,然 画图时,可先画出基本形体的轴测图, 后再用叠加切割法逐步完成作图。 后再用叠加切割法逐步完成作图。
第6章 对映异构

比旋光度 (Specific Rotation)
t
B l
:旋光度 B :质量浓度(g/ml) l :盛液管的长度(dm)
8
:光源的波长
t :测定时的温度
说明
•比旋光度[]:体现物质特性,可在手册中查到 •一般用钠灯(D)作光源,λ=589.3nm,t=20℃ •物质的旋光度,需要通过改变浓度或者改变盛液管长度 的方式测定两次,才能确定。 •溶液一般为稀溶液,否则测出的α值不准 •若溶剂不是水,则要在后面标出溶剂及相应浓度 右旋酒石酸: (乙醇, 5%)
25
CH3 C HO H CH2CH3 HO
CH3 C CH2CH3 H HO
CH2CH3 C H CH3
S
R
R
S
≡ ≡
A B C
≡
B
B
A
C
D
D
R
D A C
≡
A
D B
26
C
Fischer投影式中R、S的简便确定法: •若最小基团d在竖线上,则a,b,c顺时针旋转为R型, 逆时针为S型; •若最小基团d在横线上,则a,b,c顺时针旋转为S型, 逆时针为R型。 使用费歇尔投影式应注意的问题: •在纸面上转动180°或偶数倍,构型不变。
n
﹡
﹡
I
≡
II
III
IV
关系:对映体:III和IV
内消旋体:I和II
非对映体:I和III,II和III,I和IV,II和IV
33
内消旋体(meso):分子内部形成对映两半的化合物 (有) 内消旋体无旋光性(抵消), 不能分离成光活性物质
mp
(+)-酒石酸 (-)-酒石酸 170oc 170oc
第六章 组合体的视图及尺寸标注
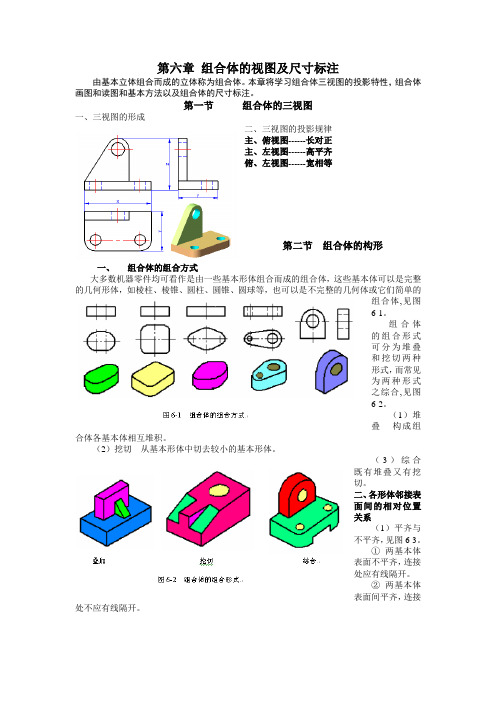
第六章组合体的视图及尺寸标注由基本立体组合而成的立体称为组合体。
本章将学习组合体三视图的投影特性,组合体画图和读图和基本方法以及组合体的尺寸标注。
第一节组合体的三视图一、三视图的形成二、三视图的投影规律主、俯视图------长对正主、左视图------高平齐俯、左视图------宽相等第二节组合体的构形一、组合体的组合方式大多数机器零件均可看作是由一些基本形体组合而成的组合体,这些基本体可以是完整的几何形体,如棱柱、棱锥、圆柱、圆锥、圆球等,也可以是不完整的几何体或它们简单的组合体,见图6-1。
组合体的组合形式可分为堆叠和挖切两种形式,而常见为两种形式之综合,见图6-2。
(1)堆叠构成组合体各基本体相互堆积。
(2)挖切从基本形体中切去较小的基本形体。
(3)综合既有堆叠又有挖切。
二、各形体邻接表面间的相对位置关系(1)平齐与不平齐,见图6-3。
①两基本体表面不平齐,连接处应有线隔开。
②两基本体表面间平齐,连接处不应有线隔开。
(2)相交当两基本体表面相交时,其相交处交线一定要画出来,如图6-4所示,(3)相切当两基本体表面相切时,其相切处是圆滑过渡,应不画线,如图6-5所示,图中底板前端平面与圆弧面相切其平面上的棱线末端应画至切点为止。
切点位置由投影关系确定,相切处无线。
第三节组合体视图的画法一、形体分析画组合体视图之前,应对组合体进行形体分析,了解组合体的各基本体的形状、组合形式、相对位置以及在某个方向上是否对称,以便对组合体的整体形状有个概念,为画图做准备。
(a) 轴承座(b) 形体分析图6-6 画组合体视图从图6-6中可以看出,该组合体由四棱柱底板、空心圆柱体、等腰梯形柱的支承板、直角梯形柱和四棱柱叠合的肋板组成。
支承板与空心圆柱体外表面相切,叠放在底板上,它与底板后面平齐。
肋板叠放在底板上,其上与圆筒外面相结合,后面与支承板紧靠,两侧面与圆柱面相交。
整个组合体左右对称。
注意:画图时不要把组合体看成是由各零散的基本体“拼接”而成。
第六章轴测投影图

(1)平行于V面的圆仍为圆,
Z1
反映实形。
(2)平行于H面的圆为椭圆,
长轴对O1X1轴偏转7°, 长轴≈1.06d,
X1
短轴≈0.33d。
(3)平行于W面的圆与平行
Y1
于H面的圆的椭圆形状相同, 长轴对O1Z1轴偏转7°。
由于两个椭圆的作图相当繁,所以当物体这两 个方向上有圆时,一般不用斜二轴测图,而采用正 等轴测图。
S
O
Y
轴测轴: V
O1X1、O1Y1、O1Z1 轴间角: 轴测轴之间的夹角
轴向伸缩系数: X A
O1A1 p=
OA O1B1 q= OB O1C1 r=
OC
Z C
O B X1 A1Y
P
Z1 C1
B1 Y1
二、轴测图的种类
轴测图
正轴测图
斜轴测图
正等测 p = q = r 正二测 两个轴向变化率相等 正三测 三个轴向变化率都不等
二、平面立体正等测图的画法
1.坐标法: ①选定坐标原点;③按点的坐标画点;
②画轴测轴; ④连接A1B1C1D1E1F1,完成顶面;
f
2e
Xa
d
O
H H
F1 X1 A1
E1 O1
D1 C1
B1
Y1
1
bL c
M
Y
⑤过A1B1C1D1E1F各点向下作直线 平行O1Z1并截取H,定出底面上的 点,顺次连接,整理完成全图。
6.4 轴测剖视图
为了表示零件的内部结构和形状,常用 两个剖切平面沿两个坐标面方向切掉零件的 四分之一。
3.4.1 画图步骤
⒈ 先画外形再剖切 ⒉ 先画断面的形状, 后画可见轮廓。
第六章 轴测投影图
2、圆柱:
x 例2:已知圆柱的投影,作正等测轴测图。 z z o4 作图如下:
O`
o1 x
O`0
o o3
o2
t1
x
o o0
o1
t1
y
公切线 (转向线)
y 3、将o1、o2、 o4及 切点t1、t2下降同一 o4 Z尺寸 4、作底圆 o0 o2 5、作上下 t2 圆的公切线
t2
1、作顶圆 2、定底圆圆心o0
例1、已知门洞的投影,作斜二测轴测图 x
1
1
0
45°
z
O`2 O1` O2
z
O1
x
O`
x
O2
o
y取0.5
x
o O1 y
公切线 0.5 y 作图如下: 作图如下: 1、定圆心O1,作 前面图形 2、将O1向后取1/2Y 尺寸得 O2 3、以O2为圆心画后 面大小圆弧 y 4、将各角点向后作 1/2Y 尺寸
作图如下: 作长方体 作正垂面 作铅垂面 连交线 加粗
0 x
y
y
轴测图的仰视 仰视画法:已知如图 仰视
z z x a` b` x a c` 0`
0x
B A C
y
b y
c
0
轴测图的四种投影方向 四种投影方向及图示效果: 四种投影方向
Z 0 X X Y b)由左前上向 右后下投影 Z 0 X 左后上投影 Y 0 c) 由右前上向 左后下投影 Z X 0 Y Z Y
第六章 轴测投影图
一、概述 二、正轴测投影图 三、斜轴测投影图
一、概述:
在工程中,由于正投影图度量性好、绘图方 便,常用来绘制施工图。但正投影图缺乏立体 感,不易看懂。因此,常绘制形体的轴测投影 轴测投影 图作为辅助图样。 (一)轴测投影图的形成:如下图
六图像重建PPT课件
一个豪斯费尔德等于水的衰减系数的0.1%,标度 上选择 H(水)=0
H
(组织) (水) (水)
1000
对于空气 H=-1000 骨骼 H=+1000 早期的断层成像是用机械方法得到,如下图所示:
图 6—2 常规断层摄影的原理示意图
z3
• §6.2 解联立方程组方法
A
B
C
D z6
F E
z5 z1
z2 z3 z4
Z1=9 Z2=18 Z3=12 Z4=9 Z5=9 Z6=10
• 特点:
• 运算简单
• 每个重建像素值包含邻近像素的灰 度值成分,以更小的比例包含更远 的像素灰度值成分,“未聚焦”产 生结构模糊。
6.3 经典断层成像
•
“以前医生做手术前可能只是画一下,制定一个大致的方案,手
术中遇到的突发情况只能靠医生的临床经验和应变能力了”,领衔该
项目的珠江医院肝胆一科主任方驰华教授说,新的仿真手术系统则可
以重建三维模型,与患者本人的腹部脏器完全吻合,还可以任意角度
旋转观察,可以设置脏器的透明化来观察患者肿瘤与内部动脉、静脉、
• 6.1 概述 • 1、图像重建的理论基础 • 二维或三维物体能够通过其无限多个
投影来确定。
• 1972,第一台X射线断层摄影装置
• 1974 年被正式命名为计算机断层摄影 术(CT: Computed Tomography)
• 1979年,获得Nobel医学奖
• 对于有些截面信息无法确知的物体, 可以设法得到一组投影数据,然后通 过图像重建技术来得到其截面图像, 典型应用如CT技术、无损检测等
有机化学 第六章 对映异构
有对称中心的分子非手性,实物与镜可重叠,没 有对映体和旋光性。
(3)对称轴 Cn ——若通过分子画一轴线,当分子绕此轴 旋转360º /n后,得到与原来分子相同的形象,此轴线就 是该分子的几重对称轴。
O H 球体 H 水 H
N
H H
氨
C∞
C2
C3
H
H H Cl
Cl Cl Cl
Cl
Cl C2
H
有无对称轴不能 作为判断分子有 无手性的依据。
第七节 不含手性碳原子的化合物的对映异构
一、丙二烯型分子
a C
b c
a 或 C
b
a
C
C
d
C
C
b
当任何一个双键上连接相同基团,则分子无手性
二、联苯型化合物
分子有 对称面, 无手性
当某些分子单键之间的自由旋转受到阻碍时产生的 光活性异构体,称位阻异构现象.
其它
R1 N R2
R3 R4
第八节 外消旋体的拆分
第六章 对映异构
构造异构 同分异构
碳干异构 位置异构 官能团异构 互变异构 构型异构 顺反异构 对映异构
立体异构 构象异构
对映异构:是指分子式、构造式相同,构型不同,互 呈镜像对映关系的立体异构现象。实物与其镜象不能 重叠的分子成为一对对映体。
CH3 C HO H CH2CH3
镜子 CH3 C H OH CH2CH3 左旋-2-丁醇
第二节 对映异构现象与分子结构的关系
一、对映异构现象的发现 1848年法国巴黎师范大学化学家、微生物学家 在研究酒石酸钠铵晶体时,发现有两种不同的晶体.
两种晶体互为实物和镜像的关系,相似不重合,将其 分开分别溶于水中,一种左旋一种右旋,比旋光度相 等。
第六章 由投影重建图像 1.断层摄影图像的获取 2.重建图像的几种方法
2) 反投影法
2) 反投影法
例如:把与A象素有关的z1 ,z3 ,z5叠加起来,可
知 A的值将和总和成正比。其他各个象素也一
样,事实上,叠加的结果都包含有 9 个象素的 总和,为保持射线密度的平均值不变,可以用 总象素数 9 去除总和,从而获得一个相应象素 的平均密度值,即重建图像的各个象素值分别
1)减少未知数数目
2)增加扫描路径
3)改变扫描路径
1) 解联立方程组方法
对于本问题,只有第三种 方程组为:
A B D z1 D E F z4 C D z2 B E z5 A B C z3 A C E z6
图(c)是改变扫描路径的情况,此时获得的新联立
些改变,但其基本原理还是相同的。下面我们
仅就 T-R 型扫描方式,讨论几种图像重建的方
法。
2. 重建图像的几种方法
常用的几种由投影重建图像的方法:
l解联立方程组方法 l反投影法 l利用傅立叶变换进行图像重建 l利用卷积进行图像重建
l图像重建的逐步逼近法
l最优化重建 l扇形投影数据的重建
1) 解联立方程组方法
复技术。如把投影看成是一种劣化过程,而重
建则是一种复原过程。具体来说,ห้องสมุดไป่ตู้投影时我
们丢失了沿射线方向的分辨能力(只剩1—D信
息),而重建则利用多个投影恢复了2—D的分
辨力。
第六章 由投影重建图像
从投影重建图像的技术在许多科学领域,包括从分子
量级(借助电子显微镜)到宇宙量级(射电天文学)都得 到了应用。它极大地增强了人类观察物体内部结构的
收敛于对应象素值)而引起的结构模糊。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双像投影测图
主要内容:立体像对的特殊点、线、面, 立体像对的相对定向元素和模型的绝对 定向元素,立体测图仪上像对的相对定 向,立体测图仪上模型的绝对定向。 重点:立体像对的特殊点、线、面,像 对的相对定向及模型的绝对定向。 难点:像对的相对定向 学时安排:授课 4,实验 2。
第一节
概述
在立体摄影测量中,利用立体像对的两张像 片进行投影,有可能建立按比例缩小的地面 几何模型。量测几何模型,可直接测绘出符 合规定比例尺的地形原图。设想利用两个投 影器,将立体像对的两张像片分别投影时, 如果能保证投影光束与摄影光束完全相似, 而且两投影器连同像片还原到两摄影站上, 并与摄影时的摄影机空间方位一致,亦即恢 复了两张像片的内、外方位元素的情况下, 则同名点的投影射线必然对对相交,而形成 实地的几何模型。
(一)移动dbx的影响 当微动dbx螺旋,投影器在X方向移动dbx时,承 影面上各投影点在X方向都移动dbx,但在Y方 向不产生位移,如图6-6所示。 位移分量 : (a) dX dbx dY 0
(二)移动dby的影响 当微动dby螺旋,投影器在Y方向移动dby时,承 影面上各投影点在X方向都移动dby,但在X方 向不产生位移,如图6-7所示。 位移分量: dX 0 (b) dY dby
二、绝对定向元素 绝对定向元素是确定相对定向所建立的几何模型的 比例尺和恢复模型空间方位的元素。相对定向所建 立的几何模型的比例尺是任意的,要改变投影基线 b的长度,使之符合测图比例尺;然后把两像片 (两投影器)看成一个整体,连同建立的模型在空 间进行平移和旋转,间接地恢复左像片的外方位元 素:XS、YS、ZS、φ、ω、κ,同时右像片的外方 位元素也就恢复了。模型的平移是通过图底的平移 和高程分划尺上读数的安置来完成的;模型的旋转 一般是绕仪器的Y轴和X轴分别旋转Φ和Ω角度以及 图底旋转K来完成的。因而可归纳为七个绝对定向 元素:XS、YS、ZS、Φ、Ω、Κ和b。 一般来讲,每个像对有十二个外方位元素,可分成 两组:五个相对定向元素和七个绝对定向元素。
XY XY Y Q d d H (1 2 )d Xd X d H H H
Y X Y Y 2 Q db dbz d H (1 2 )d X d y H H H
二、定向点的选择 在式(6-3)和(6-4)中包含五个待定值 (相对定向元素),从理论上讲,观测出五 个定向点的坐标和Q值以后,列出五个方程 式,就可解求出相对定向元素。在模拟测图 仪上进行像对相对定向,通常是在立体观察 下,运用投影器的运动逐点消除所出现的上 下视差来完成。同样需要有五个定向点。为 了有所检核,需要增加一个检查点,共六个 点。
第三节 立体测图仪上像对的相对定向
相对定向的目的:是恢复两张像片的相对位置,达 到同名射线对对相交,建立起与地面相似的几何模 型。在模拟测图仪上,像对的相对定向通常是在立 体观察下运动投影器,使得五个定向点的同名射线 对对相交。图6-5所示,当观察到承影面上某定向点 的投影点M和M′在仪器Y轴方向错开时,则说明同名 射线SM和S′M′不相交,而Y与Y′坐标之差也称为上 下视差,用Q(=Y-Y′)表示。如果只是在X轴方向 错开,说明同名射线还是相交的,不过相交点不在 承影面上。
基线延长线与左、右像片的交点k1、k2称为 核点。通过摄影基线S1S2与任一地面点A所 作的平面WA,称为点A的核面。核面与像片 的交线称为核线,对于同一核面的左右像片 上的核线,如k1a1、k2a2称为同名核线。像 片上诸核线均会聚于核点。通过像主点的核 面称为主核面。一般情况下,通过左右像片 主点的两个主核面不重合,分别称为左主核 面和右主核面。通过像底点的核面,称为垂 核面。因为左右像片的底点与摄影基线B位于 同一铅垂面内,所以一个像对只有一个垂核 面。垂核面与像片面的交线称为核线。
当投影器转动dφ时,投影点M移到M′,β改 变为β+dβ,dβ=dφ,而θ不变,微分上式:
H dX d 2 cos
由图可知: Htgtg sec d dY
cos H
2 2
X H 考虑到dβ=dφ,则位移分量:
tg
Y X2 H2
X tg H
(六)移动dω的影响 当微动ω螺旋,承影面上位于Y轴上的各 点沿Y轴移位,其他各点沿着双曲线的轨 迹移位,如图6-13所示。 位移分量:参照在dφ影响下相类似的推导, XY (f) 可得出: dX d
X X XY dX dbx dbz H (1 2 )d d Yd H H H
而 Q = Y – Y′ = dY′ – dY 当左投影器不动时,认为dY = 0,并参考式(62),则 (6-3) 式中:X′、Y′是右像片的投影点的坐标。 当保持投影基线不动,进行单独像对的相对 定向时,运用两投影器的角运动dφ、dκ、dφ′、 dκ′、dω′来消除上下视差,同理得: (6-4) 2
通过立体观察,可直接量测几何模型并绘出 1 比例尺为 M 的地形原图。这种方法的基本思 想是模拟空中摄影过程,或者说是摄影过程 的几何反转。本着这种思想测图所设计的立 体测图仪称为模拟型立体测图仪(模拟测图 仪)。在我国习惯上称之为全能型立体测图 仪(全能仪)。“全能”的涵义是指在这种 仪器上能测绘出地物和等高线。 立体摄影测量,也称双像测图,是由两相邻 摄影站所摄取的、具有一定重叠度的一对像 片为量测单元。这样的两张像片称为立体像 对(简称像对)。
立体像对也有一些特殊的点、线和面。 图6-2表示一个像对的相关位置。S1和S2是 左像片P1和右像片P2的投影中心。两投影中 心的连线B称为摄影基线,o1、o2为左、右 像片的像主点。a1、a2是地面上任一点A在 左、右像片上的构像,称为同名像点。射线 AS1a1和AS2a2称为同名射线。
第三张像片相对于所取像空间辅助坐标系的五个方 位元素:by、bz、φ、ω、κ称为连续像对的相对定 向元素。by、bz是连续像对右投影中心Si+1相对于 左投影中心Si的两个基线分量,随着基线分量bx的 大小而变化;φi+1、ωi+1、κi+1则是相对于航带统 一的像空间辅助坐标系的像对相对定向角元素。 在模拟测图仪上进行像对的相对定向,目的只是 恢复两张像片的相对位置,达到同名射线对对相交; 这要通过投影器的运动来安置五个相对定向元素来 完成,至于这几个元素的数值是无需知道的,也不 是绝对的,对同一个像对而言,五个相对定向元素 的数值随着所取像空间辅助坐标系的不同而有所不 同。还应指出,相对定向的角元素与以前所定义的 外方位角元素是不相同的,但习惯上采用相同的符 号。
(三)移动dbz的影响 当微动dbz螺旋,投影器升降dbz,承影面 上各投影点沿辐射方向位移,其中位于负 重铅垂方向的投影点位不变,如图6-8 所示。 X dX dbz 位移分量: (c) H
Y dY dbz H
式中H为投影距离。
(四)移动dκ的影响 当微动κ螺旋,承影面上各投影点均绕像 主点的投影作圆周运动,像主点的的投影 点位不变,如图6-9所示。 位移分量从图6-10得: X = r· κ cos Y = r· κ sin
dX Yd dY Xd
(d)
(五)移动dφ的影响 当微动φ螺旋,投影光束绕通过投影中 心的Y轴旋转dφ时,承影面上位于X轴 上的各点沿X轴移位,其他各点沿着双 曲线的轨迹移位,如图6-11所示。 从图6-12得: X =Htgβ
Y X 2 H 2 tg ( Htg ) 2 H 2 tg H tg sec
要按实长恢复像片外方位三个线元素是不可 能的,但可按一定比例缩小,亦即将摄影B缩 小到若干分之一作为投影基线b。按投影基线 b来安置两投影器,并保持原来的空间方位不 变,则两张像片上同名像点的投影射线仍然 是对对相交,只是对于每一点由摄影基线形 成的交会三角形变成以投影基线形成的交会 三角形,大小改变了,但保持它们之间的相 似性。综合所有的交会点,形成与地面相似 的几何模型,此时模型的比例尺为 b 1(图 B M 6-1)。
这一步骤称为模型的绝对定向。进行模型的 绝对定向,至少要有适当分布的三个地面控 制点,作为模型绝对定向的依据。 一、相对定向元素 相对定向元素是确定像对两张像片相对位置 的元素。相对定向元素随着所取像空间辅助 坐标系的不同而有所不同。基本上有两种形 式:
1、保持投影基线不动,取它作为像空间辅助坐标 系的X轴,以左方投影中心S作为坐标原点,通过原 点与左方主核面相垂直的方向线作为Y轴,如图6-3 所示。相对于这样一个像空间辅助坐标系而言,方 位元素有五个:φ1、κ1、φ2、κ2、ω2,并称它们 为单独像对的相对定向元素。 2、在某些类型的模拟测图仪上,可将相邻像对连 续地进行相对定向,建立起航带模型。如,在一航 线中的第一个像对(像片1、2)完成相对定向后, 接着进行第二个像对(像片2、3)的相对定向。这 时要保持第二张像片(第二个投影器)不动,并且 取与第一个像对所取的像空间辅助坐标系平行的 S2-X2Y2Z2,作为第二个像对的像空间辅助坐标系, 如图6-4所示。
第二节立体像对的相对定向元素和模 型的绝对定向元素
模拟型立体测图仪测图的原理,是应用光线或机械 的投影方式来模拟一个像对的摄影过程,进行几何 反转。这需要恢复两张像片的内、外方位元素,只 是其中外方位的线元素均按一定的比例缩小,因而 在相应的核面内形成的前方交会三角形按同一比例 缩小,但仍然保持同名射线对对相交,形成与地面 相似的几何模型。利用投影器恢复像片的内方位元 素不难实现,可是外方位元素通常不知道,事实上 无法直接完成,但可用间接的办法来实现摄影过程 的几何反转。
首先恢复两张像片(两投影器)的相对位置, 暂不考虑模型比例尺,可粗略地安置投影基 线,运用两个投影器的运动,使得像对重叠 范围内适当分布的五对同名点的射线对对相 交,就可保证所有同名射线对对相交,亦即 恢复了两张像片的相对位置,形成地面的几 何模型。这一作业过程称为像对的相对定向。 完成了相对定向,并没有恢复两张像片的外 方位元素,而建立起来的几何模型,它的比 例尺和空间方位都是任意的,即模型可能是 倾斜的,因此还要确定(或调整)模型比例 尺,并将模型置平。
